Imaging the impact on cuprate superconductivity of varying the interatomic distances within individual crystal unit cells

Abstract

Many theoretical models of high-temperature superconductivity focus only on the doping dependence of the CuO₂-plane electronic structure. However, such models are manifestly insufficient to explain the strong variations in superconducting critical temperature, T_c, among cuprates that have identical hole density but are crystallographically different outside of the CuO₂ plane. A key challenge, therefore, has been to identify a predominant out-of-plane influence controlling the superconductivity, with much attention focusing on the distance d_A between the apical oxygen and the planar copper atom. Here we report direct determination of how variations in interatomic distances within individual crystalline unit cells affect the superconducting energy-gap maximum Δ of Bi₂Sr₂CaCu₂O_8+δ. In this material, quasiperiodic variations of unit cell geometry occur in the form of a bulk crystalline “supermodulation.” Within each supermodulation period, we find ≈9 ± 1% cosinusoidal variation in local Δ that is anticorrelated with the associated d_A variations. Furthermore, we show that phenomenological consistency would exist between these effects and the random Δ variations found near dopant atoms if the primary effect of the interstitial dopant atom is to displace the apical oxygen so as to diminish d_A or tilt the CuO₅ pyramid. Thus, we reveal a strong, nonrandom out-of-plane effect on cuprate superconductivity at atomic scale.

The superconductive copper oxide materials exist in a variety of complex crystal forms (1). Introduction of ≈16% holes into the insulating CuO₂ crystal plane by chemical doping generates superconductors with the highest critical temperature, T_c, known. However, the maximum T_c varies widely between crystals sharing the same basic in-plane electronic structure, by up to a factor of 10 at the same hole density in monolayer cuprates (1). These variations obviously cannot be due to the doping-dependence of CuO₂ in-plane electronic structure, and it has long been hypothesized (2) that there must be a key out-of-plane influence that controls the basic electronic structure of cuprates. Identification of such an out-of-plane influence may be pivotal to finding a route to higher-T_c cuprate superconductors.

Much attention has been focused on the “apical” oxygen atom as a primary candidate for the cause of such out-of-plane effects. This atom is positioned at the apex of the CuO₅ pyramid (Fig. 1A), the key chemical unit within the unit cell of bi- and trilayer cuprates (monolayer cuprates contain an analogous CuO₆ octahedron). Hybridization of the p_z orbital on the apical oxygen and the out-of-plane Cu d_3r²–z² orbital should be quite strong (3). The importance of the apical oxygen location is supported empirically by experiments involving chemical substitution of cations at adjacent sites (4, 5), which result in dramatic effects on T_c. Because the substituted cations have the same valence but different radii, their primary effect is a geometrical displacement of the apical oxygen atom. Similarly, the effects of hydrostatic pressure (6–8)—although their microscopic interpretation is not always clear—generate large changes in T_c in response to distortion of the crystal geometry. Taken together, these experiments imply that distortion of the CuO₅ pyramidal geometry might be the source for the dramatic out-of-plane effects on maximum T_c.

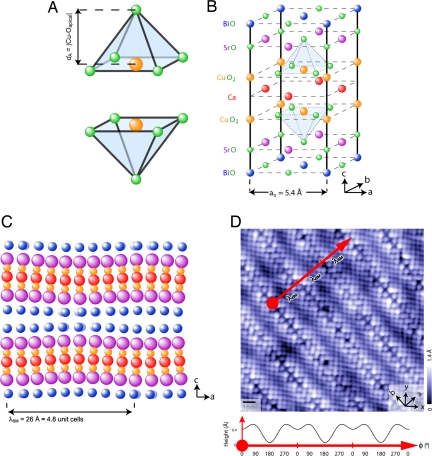
Fig. 1.

Crystal structure and periodic unit cell distortion due to bulk incommensurate supermodulation. (A) The CuO₅ pyramidal coordination of oxygen atoms surrounding each copper atom in Bi₂Sr₂CaCu₂O_8+δ. (B) Top half of the Bi₂Sr₂CaCu₂O_8+δ unit cell (the lower half is identical except for a translation by a₀/2 along the a axis). Crystal axes a, b, and c are indicated. (C) Schematic view along the b axis of the crystal, showing representative displacements of all non-O atoms (adapted from ref. 14). Supermodulation displacements can be seen in both the a and c directions. (D) A 14.6-nm-square topographic image of the exposed BiO layer of a cleaved crystal of Bi₂Sr₂CaCu₂O_8+δ. The x and y axes (aligned along the Cu–O bonds), and the crystalline a and b axes, are indicated in the figure. The c axis supermodulation effect is visible as corrugations of the surface. A simulated cross-section is shown, illustrating the periodic profile of the modulations. [Profile calculated by phase-averaging the topographic height and fitting the first two harmonics of the resulting function z(φ).]

Changes in interatomic distances within the unit cell should, in theory, have major effects on both the underlying electronic structure and the superconducting state (2, 9). For example, based on calculation of Madelung (electrostatic) site potentials, Ohta et al. (2) argue that the geometry of the pyramidal unit—in particular the displacement of the apical oxygen d_A (Fig. 1A)—determines the relative energy levels of key electronic orbitals of the apical and in-plane O atoms and the Cu atoms. These energy-level shifts affect hole propagation through the stability of the Zhang–Rice singlet state (10), such that the state of the apical oxygen atom is directly correlated with T_c. Further, Pavarini et al. (9) derive a relationship between d_A and T_c by considering translationally invariant changes in unit cell geometry on the in-plane hopping rates t along (1, 0) and t′ along (1, 1). Finally, Nunner et al. (11) have proposed that such geometrical distortions of the unit cell may locally alter the electron-pairing interactions. Until now, however, no direct test of such theories has been possible because techniques whereby picometer changes in interatomic distances could be compared directly with the superconducting electronic structure inside the same unit cell did not exist.

To investigate how the geometry of a CuO₅ pyramid affects superconductivity locally, an ideal experiment would be to continuously perturb the dimensions of a single unit cell (Fig. 1B) and measure the resulting changes in superconducting properties within that same unit cell. At first glance, this might seem merely a gedanken experiment. Fortunately, however, significant variations in cell dimensions and geometry occur naturally at the nanoscale in the Bi₂Sr₂Ca_n−1Cu_nO_4+2n (n = 1, 2, 3) family. These variations take the form of a bulk incommensurate periodic modulation (12–17) perturbing the atoms from their mean positions (18), as shown schematically in Fig. 1 C and D. This so-called crystal “supermodulation” is believed to originate from a misfit between the preferred bond lengths of the perovskite and rock-salt layers of the crystal. In each of the 14 layers of the Bi₂Sr₂CaCu₂O_8+δ (Bi-2212) unit cell, atoms are displaced from their mean locations (i.e., where they would be located in an idealized average unit cell) by up to 0.4 Å, following a functional form repeating, on average, every 26 Å (≈4.8 unit cells) along the a axis. These distortions are represented schematically in Fig. 1C. Here we exploit the associated modulations of interatomic distances (whose largest fractional change is to the Cu–O_apical distance) to directly explore associated changes to the superconducting state.

Results

Topographic and Spectroscopic Imaging of Bi-2212.

We use floating-zone-grown single crystals of Bi-2212, cleaved in cryogenic ultrahigh vacuum to reveal the BiO layer (Fig. 1B). These crystals are inserted into the scanning tunneling microscope (STM) head at 4.2 K. The CuO₂ plane is ≈5 Å beneath the BiO surface and separated from the STM tip by insulating BiO and SrO layers. Fig. 1D shows a 14.6-nm-square topographic image of the BiO surface, revealing the distorted, grid-like arrangement of Bi atoms; the Cu atoms lie ≈5 Å below each Bi atom. The blotchy appearance of the topograph is due to the heterogeneous high-energy spectral weight shifts near each dopant atom (19). Most importantly, the effects of the crystal supermodulation at the BiO layer can be seen in Fig. 1D as a surface corrugation. A simulated cross-section of this surface corrugation along the red line in the figure is displayed below the topograph and shows the primary BiO modulation with its weaker second harmonic. We choose to label the phase of the supermodulation as φ = 0° (180°) where the first-order maximum (minimum) c axis Bi atom positions occur [see supporting information (SI) Text for details].

Homogeneous Low-Energy Excitations with E = Δ Nanoscale Electronic Disorder.

To explore the CuO₂ electronic local density of states (LDOS) (r, E) at each point within the supermodulation, we use STM-based imaging of the differential conductance g(r, V) ≡ dI/dV(r). If spatial variations of the tunneling matrix elements do not predominate, this technique results in a spatial image of LDOS (r, E = eV) ∝ g(r, V). To generate an atomic resolution “gap map,” we then determine, at each point, half the energy difference between the two peaks in each g(r, V) spectrum (Fig. 2G Inset) and ascribe this difference to the maximum value of the d-wave superconducting energy gap Δ(r). For this work, we studied gap maps from 11 distinct samples of Bi-2212 at a sequence of different hole-dopings, 0.08 < p < 0.23. Fig. 2 B, E, and H shows gap maps produced from three representative samples at p ≈ 0.13, 0.15, and 0.17. An identical color scale represents Δ in these panels. The panels exhibit intense disorder in the gap maxima, with values ranging from 20 to >70 meV within adjacent ≈3-nm-diameter domains; the disorder in gap maxima occurs in association with the nonstoichiometric dopant oxygen atom locations (19), with gap values strongly increased in their vicinity. However, this disorder in gap maxima always coexists with a dI/dV (r, E) that is spatially homogeneous below some lower energy (20–22) [because the Δ(k) for any range of energies where quasiparticle interference (23, 24) is detected must be spatially homogeneous throughout that region]. The detailed agreement between results from g(r, V) imaging (21) and angle-resolved photoemission (25) provides confidence that tunneling matrix element effects do not prevent the STM from accessing an undistorted k-space electronic structure.

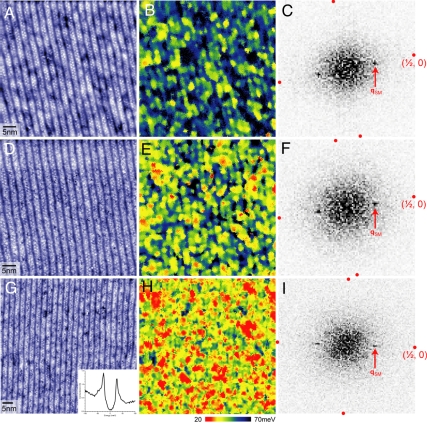
Fig. 2.

Appearance of gap modulations at the same wavevector q_SM as the crystal supermodulation. Topographic images of underdoped (mean gap, 5 meV) (A), optimally doped (mean gap, 47 meV) (D), and overdoped (mean gap, 37 meV) (G) samples of Bi₂Sr₂CaCu₂O_8+δ. Gap maps B, E, and H correspond to adjacent topographs A, D, and G, respectively, alongside their respective Fourier transforms C, F, and I. Clear peaks are visible in the Fourier-transformed gap maps at q_SM (indicated). Points corresponding to (±½, 0) and (0, ±½) are indicated, in units of 2π/a₀.

In all Δ(r), we find a variation of the gap magnitude that has the same wavevector q_SM as the crystal supermodulation. The three gap maps of Fig. 2 B, E, and H are presented alongside their simultaneously acquired topographs (Fig. 2 A, D, and G). In the three topographs, each ≈45 nm square, the minima (φ = 180°) of the supermodulation distortion can be seen as a series of dark parallel lines ≈2.6 nm apart. The mean gap energy falls from the underdoped sample (Fig. 2B; 55 meV), through the near-optimally doped sample (Fig. 2E; 47 meV), to the moderately overdoped sample (Fig. 2H; 37 meV). Careful comparison of the gap maps with the topographs reveals that each gap map exhibits periodic features with the same wavevector q_SM as its simultaneous topograph. This becomes more obvious in the Fourier transforms of the gap maps (Fig. 2 C, F, and I), which exhibit clear peaks, labeled q_SM, at positions corresponding to the average wavevector of the crystalline supermodulation. The obvious difficulty is how to quantify the local relationship between the supermodulation and Δ variations at q_SM in the presence of both the irregularity in the supermodulation and the dopant-induced gap disorder.

Supermodulation Phase Map.

The supermodulation itself is an incommensurate, approximately periodic, displacive modulation of the atomic sites of the crystal. The periodicity and direction of the modulation can be given (14) by wavevector q_SM = q₁a* + q₂b* + q₃c*, where a*, b*, and c* are the reciprocal basis vectors of the lattice, q₁ = 0, q₂ ≈ 0.212, and q₃ = 1. The effect of the supermodulation is to displace each atom, μ, whose unperturbed position within the unit cell we denote x^μ, by a displacement vector u^μ(φ). We call φ the “supermodulation phase,” and set u^μ(φ) = u^μ(φ + 2π) for all φ. The supermodulation phase at an atomic site μ is given by φ = 2πq · (n + x^μ), where n is the position of the unit cell in which the atom resides. Thus, because of the periodicity of the displacements u^μ(φ), the dimensions of any unit cell at r in the crystal can be labeled by φ(r), and all unit cells with the same value of φ will, in general, have the same interatomic dimensions. If the supermodulation were sufficiently regular, knowing q_SM and the phase φ₀ at any point r would be sufficient to determine its phase and thus the unit cell dimensions at all r. However, the supermodulation is quite irregular—its spatial phase slips and meanders (see SI Fig. 5A) throughout the field of view. No matter what values of q_SM and φ₀ are chosen, the degree of disorder present means that the actual supermodulation will slip quickly out of phase, rendering standard Fourier analysis techniques unreliable.

To address this challenge, we developed a technique that accurately tracks the local phase of the supermodulation, extracting the value of the supermodulation phase at every location: a supermodulation phase map φ(r). With it, we correctly parameterize the dimensions of the unit cell at every r (see SI Text). The latter can be achieved because the actual bond length changes in each unit cell are determined from φ(r), using knowledge from x-ray crystallography. Such studies (12–16) have established that the Cu–O_apical bond length d_A varies with φ (as defined here) by as much as 12%, peak to peak. If we consider only the first harmonic in atomic displacements within the most widely accepted refinements of the crystal supermodulation, this variation in d_A occurs because the amplitude of the c axis supermodulation is greater in the CuO₂ layer than in the adjacent SrO layer containing the apical oxygen. Within this simplified picture, the apical oxygen distance d_A is thus minimal at φ = 0° and maximal around φ = 180°. We note that a small number of studies (14) present a different crystal refinement. Nevertheless, changes in d_A represent the largest fractional change of any bond length within the unit cell (in-plane bond lengths being much less affected) and occur with a primary periodicity of the supermodulation plus small additional departures occurring in the second harmonic (13).

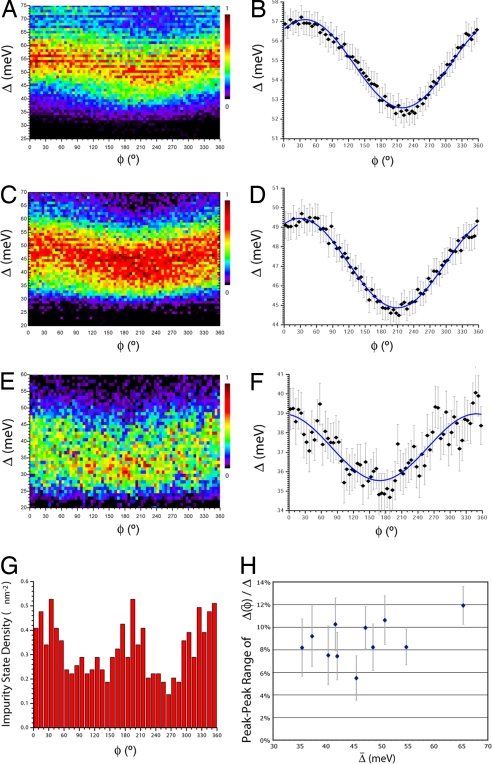
Using this crystal modulation phase-map technique, we next determine φ(r) and Δ(r) simultaneously in each field of view. Each pixel is then labeled by its local value of φ and Δ. Next, we generate two-dimensional histograms showing the frequency with which each pair of φ:Δ values occurs (Fig. 3A, C, and E). Fig. 3 B, D, and F represent the mean gap energy of each of these distributions, plotted again vs. φ. The striking fact revealed by this analysis is that the superconducting energy gap varies significantly, varying cosinusoidally with the unit cell dimension as labeled by φ. The data in Fig. 3 demonstrate a direct atomic-scale influence of the unit cell geometry on the local superconducting state of a cuprate. In all 11 samples studied over a wide range of doping, the Δ(r) vary in the same fashion with supermodulation phase, with gap maxima in the vicinity of φ = 0° and minima near φ = 180°. The measured functions Δ(φ) were well fit by the single harmonic function Δ(φ) = Δ̄[1 + A · cos(φ + α)], as shown by the blue fit lines in Fig. 3 B, D, and F [we note that this technique would reveal any higher harmonics in Δ(φ) if they existed above the noise level]. By using such fits, the mean peak-to-peak range 2A was found to be 9 ± 2%, with no apparent dependence on doped hole density (Fig. 3H).

Fig. 3.

Gap magnitude as a function of crystal supermodulation phase. (A, C, and E) Two-dimensional histograms giving the frequency with which each value of Δ (in meV) occurs at a given phase of the supermodulation φ (in degrees) for the underdoped (A), optimally doped (C), and overdoped (E) samples analyzed in Fig. 2. The color scale gives the relative frequency as a fraction of the maximum. Taking any vertical cut through these two-dimensional histograms results in an approximately Gaussian-profiled one-dimensional histogram of Δ distribution for a specific value of φ. (B, D, and F) The mean value of Δ for each value of φ is plotted as a function Δ(φ) for each sample from A, C, and E, respectively. Error bars represent 95% confidence intervals. (G) Dopant impurity state density vs. supermodulation phase, showing a typical two-peaked distribution. (H) The magnitude of the supermodulation effect on gap energy is represented by the peak-to-peak range 2A of the cosinusoidal fit to Δ(φ) (expressed as a percentage of the average) for each sample studied. There is no clear relationship to the hole density.

Dopant-Induced Electronic Disorder.

Nonstoichiometric dopant atoms are associated with random disorder in the gap maxima, with the gap energy increasing strongly in their vicinity (19). These effects do not appear to be caused by variations in local carrier density because, in that case, accumulation of holes near the negatively charged dopants would cause the gap values to be diminished; however, the opposite is observed. Instead, Nunner et al. (11) have proposed that the primary effect of dopant atoms is to enhance the pairing interactions near each dopant; however, no consensus has yet emerged regarding which microscopic mechanism might cause this to occur.

A potential cause of the periodic gap modulations reported here could merely be that the dopant density is modulated with the same period as the supermodulation. To examine this point, high-energy, g(r, V ≈ –1 V) maps [from which the locations O(r) of the dopant-atom-induced impurity states are identified (19)] were measured in the same field of view as the gap maps, while the topography of the surface was simultaneously recorded. The relationship between O(r) and the supermodulation phase φ(r) was then analyzed by determining the probability of finding a dopant-induced impurity state at each value of φ. In Fig. 3G, we show that the dopant density is somewhat correlated with φ, but with peaks at both φ = 0° and φ = 180°. Because Δ(φ) has only a single peak around φ = 0°, The data in Fig. 3G are inconsistent with periodic dopant-density variations being the primary cause of the gap modulation at q_SM.

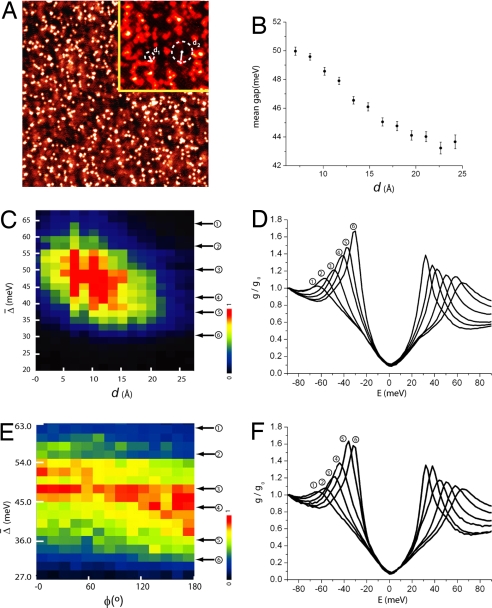
On the other hand, a comparison of the details of g(V) spectral variations at dopant atoms with those due to the supermodulation reveals startling similarities in the response of the superconductivity to these apparently different perturbations. Fig. 4A shows a g(r, V) map at V = −0.9 V that is believed to reveal the locations (19) of interstitial dopant ions in Bi-2212. Fig. 4A Inset provides two examples of the definition of d, the distance of any point to the nearest dopant atom: all points on the surface r can be labeled with a particular value of d(r). The g(r, V) spectra are then sorted according to d(r), with the results shown in Fig. 4 B, C, and D. Fig. 4B shows the mean gap value as a function of d, falling >7 meV within a d range of 2 nm. Fig. 4C shows the histogram of gap values vs. d, whereas Fig. 4D shows the average spectra associated with various d (as labeled in Fig. 4C). For the range of gap variations due to dopant disorder, the key spectra are labeled 2, 3 and 4. For comparison, Fig. 4E shows the gap magnitudes sorted by the phase of the supermodulation φ(r) (in the same sample), and Fig. 4F shows the average spectra associated with different values of φ(r) (as labeled in Fig. 4E). Here, the key spectra are labeled 2, 3, 4, and 5. Comparing Fig. 4 D and F, we see that the anticorrelation between coherence peak height and Δ seen in the random gap disorder (19, 20, 22) (Fig. 4D) appears indistinguishable, although the primary perturbation is not random dopant atoms but the crystalline supermodulation. Empirically, then, we detect no difference between the evolution of g(V) spectra as a function of dopant distance d and supermodulation phase φ.

Fig. 4.

Response of gap to interstitial dopant ions and supermodulation. (A) A dI/dV(r, V) map at V = −0.96 V, showing locations of dopant ions. Inset, two examples of the definition of d, the distance from any point to the nearest dopant atom. (B) Mean gap value as a function of d. (C) Histogram of gap values vs. d. (D) Average spectra associated with different nearest-dopant-atom distances, as labeled in C. (E) Gap magnitudes sorted by the phase of the supermodulation. (F) Average spectra associated with different values of supermodulation phase, as labeled in E. We emphasize that the spectra in D and F are not sorted by gap values. The arrows in C and E are merely guides to indicate the resulting average gap values after the spectra are sorted by d and φ, respectively.

Discussion and Conclusions

In these studies, we show a direct link between the dimensions of individual unit cells and the local gap maximum in a high-temperature superconductor. The gap maxima Δ are modulated cosinusoidally by the changes in unit cell dimensions of Bi-2212, with the gap maxima occurring in association with the minima of O_apical–Cu distance (when only the first harmonic of the crystal refinement is considered). The range of the gap modulation is found to be ≈9% of the mean gap maximum independent of doping. We note that the modulating superconducting gap, albeit induced by a crystal modulation, now makes it possible to study a “pair-density wave” (26–29) in cuprates. Overall, our data confirm directly at atomic scale the theoretical concept of a strong influence of unit cell geometry on cuprate electronic structure and superconductivity (2, 9, 11).

However, a key question emerging from these studies is whether the random gap disorder associated with the dopant atoms (19) and the periodic gap modulations herein could be caused by the same atomic-scale mechanism. In neither case are the observations consistent with variations of in-plane hole density because the high Δ regions occur when the negatively charged oxygen atom (dopant or apical) is most attractive to holes and should, therefore, tend to diminish Δ, but the opposite is detected in both cases. For this reason, both types of Δ variations appear to be more consistent with some other strong out-of-plane effect unrelated to hole density variations. This issue is important because, if there is a single out-of-plane influence that can alter gap magnitudes by large factors, it is obviously key to understanding the superconductivity and achieving maximum T_c. An important observation is that the modulation in Δ reported here also preserves the anticorrelation between coherence peak height and Δ seen in the random gap disorder (19, 20, 22) (Fig. 4F): the spectra evolve in both cases from having small gaps and sharp coherence peaks to wide gaps and low coherence peaks, as if both gap energy and quasiparticle lifetimes are affected in opposite directions by a single parameter. Thus, there is no empirical reason to conjecture two different microscopic mechanisms for the dopant disorder-induced effects and the new supermodulation-induced effects reported here. Conversely, the supermodulation effects on Δ would be empirically consistent with those of the random dopant disorder on Δ if (i) the supermodulation's first-harmonic of atomic displacements predominates, and (ii) the proposal that the interstitial dopant atoms displace the apical oxygen atom (30) and tilt the CuO₅ pyramid is correct. In that case, dopant- and supermodulation-induced gap variations would have a closely related out-of-plane trigger effect, probably involving either the alteration of d_A or the tipping to the CuO₅ cage, which is central to the electron-pairing process.

Studies of local variations in superconducting electronic structure are becoming a key area for atomic-scale tests of proposed mechanisms for cuprate superconductivity (31–35). But because such analysis has, in the past, relied on correlations between random dopant locations (19) and electronic disorder, definite conclusions have been difficult to achieve. With the finding of a nonrandom modulation in superconducting electronic structure due to unit cell dimension modulations, we point to a far more controlled avenue for testing models of the pairing mechanism at atomic scale. Theoretical approaches (36–38) to this challenge have emerged rapidly. Yin and Ku (36) derive an effective one-band Hamiltonian but emphasizing the effects of out-of-plane apical oxygen atoms by using a Wannier function and LDA+U approach. The parameters emphasize an intersite “superrepulsion” term V_ij, which is controlled by the energy of the apical oxygen p_z orbital; V_ij weakens local pairing strength. These authors propose that the dopant atoms and the crystal supermodulation both perturb the energy levels of the apical oxygen p_z orbital (2), which in turn modulates V_ij and thus Δ. Andersen et al. (37) use a d-wave Bardeen–Cooper–Schrieffer Hamiltonian whose pairing strength is modulating along with the supermodulation reproducing the effects reported here. This type of model has been quite successful in reproducing the random effects due to dopant disorder (11). Although dopant-disorder and supermodulation effects on Δ can, therefore, be consistent within the model, the microscopic cause of the pairing modulation and dopant effect has not yet been identified. Yang et al. (38) use a t-t′-J model within a renormalized mean field theory to account for the strong correlations. This model appears to be related to that used by Zhu (34) to describe dopant-disorder effects. Here, by modulating t, t′, and J along with the crystalline supermodulation, a Δ modulation can be simulated in agreement with experiment, but with the t′ modulation leading to a significant carrier concentration modulation. Yang et al. ascribe the random gap disorder (19–22, 31–35) to a different microscopic effect, possibly emerging from local hole-density variation through Sr/Bi intersubstitution.

Identification of a predominant out-of-plane influence controlling the superconductivity could transform both the material science approach to raising T_c and efforts to understand the microscopic electron-pairing mechanism in cuprate high-T_c superconductivity (1). The powerful and nonrandom effects on superconductivity of varying the interatomic distances within individual crystal unit cells, as reported here, provide opportunities to address both this issue and the physics of pair density waves directly at the atomic scale. The small spatial scale on which these effects occur also means that sophisticated quantitative, but numerically intensive, theoretical models can now be brought to bear on the observations. An immediate challenge for this research focus will be to relate a controlled change in T_c to electronic structure changes resulting from interatomic distance alterations, as determined directly by spectroscopic imaging scanning tunneling microscopy.