Modulated pairs in superconducting cuprates

High-temperature cuprate superconductors are well known to the general science community for the simple reason that their transition temperature, T_c, is much higher than that of other superconductors. Perhaps less well known is the fact that T_c varies dramatically from one family of cuprates to the next. Understanding this dependence of T_c on crystalline structure would obviously be key to designing even higher temperature superconductors, but the origin of this variation is still not well understood, even after two decades of study. In this issue of PNAS, Slezak et al. (1) take an important step toward such understanding by using scanning tunneling microscopy (STM) to find a direct correlation between the size of the energy gap characterizing the superconducting state and a modulation of the atomic positions in the material. In doing so, they have also made the first definitive observation at zero magnetic field of a modulated superconducting state known as a “pair density wave” (2).

Investigation of the relationship between superconductivity and atomic structure has a long history. When the now-accepted microscopic theory of superconductivity was proposed in 1957 by Bardeen, Cooper, and Schrieffer (3), it was criticized by Bernd Matthias (4) because of its inability to correlate the superconducting T_c with known structural properties. Eventually, the theorists did catch up, to an extent, with the experimentalists; the strong coupling generalization of the Bardeen–Cooper–Schrieffer (BCS) theory is now known to give a reasonable estimate of the T_c of classical superconductors (5).

The layered cuprates, however, are a different story. Because there is no accepted microscopic theory related to these materials, it has been difficult to understand the dramatic variation in the maximum T_c from one family of cuprates to another. At ambient pressure, this maximum ranges from 26 K for the single-CuO₂-layered oxychlorides to 135 K for the three-CuO₂-layered mercury compounds (6). This variation, which is even larger if one considers materials under pressure, has been a real puzzle to theorists because the low-energy electronic structure is known to be due to a single band of carriers resulting from hybridization of a copper 3d_x²–y² orbital with 2p_x,y orbitals on four planar coordinated oxygens (7). All cuprate families have this property. Where they differ is in the variation in crystal structure between the CuO₂ layers. This difference dramatically affects T_c, despite the fact that it has only an indirect effect on the planar electronic structure.

Over the past decade, this T_c variation has been addressed quantitatively, by both theory and experiment. The copper atoms can be planar-coordinated, pyramidal-coordinated, or octahedral-coordinated; the nonplanar oxygens are known as apical oxygens. It has been appreciated for some time that a direct correlation exists between T_c and these apical oxygens (8). In a pioneering study, Pavarini et al. (9) proposed, from band theory, that this correlation is due to the indirect effect that the apical oxygens—and other atoms that do not sit in the CuO₂ planes—have on the effective electronic structure of the CuO₂ planes. In particular, interlayer coupling is due primarily to hybridization between the Cu 4s orbital with other orbitals, such as the 2p_z orbital on the apical oxygens. This hybridized orbital then affects the various hoppings within the CuO₂ planes. In turn, the apical oxygens themselves are sensitive to intrinsic disorder in the cuprates. Eisaki et al. (6) have shown that disorder close to the apical oxygens has the most dramatic effect on T_c.

To gain further insight, it is necessary to probe the local electronic structure. In their study, Slezak et al. (1) exploited the atomic precision of STM to examine the material Bi₂Sr₂CaCu₂O₈, also known as Bi-2212. This material is often used in surface electronic probes such as STM and photoemission because it possesses a natural cleavage plane between the two BiO layers. However, the mismatch between the BiO planes and the CuO₂ planes causes this material to have a complex superstructure modulation that is incommensurate with the underlying CuO₂ lattice. In the past, this characteristic has presented a complication, but Slezak et al. turned it to their advantage. From structural studies, this modulation is known to have a significant impact on the location of the apical oxygens (the atoms in the CuO₂ layers are much less affected). The question then arises whether this modulation also affects superconductivity. The authors found that this was indeed the case. Superconductivity is characterized by an energy gap, and it is known that the maximal T_c for any given family of cuprates correlates with the size of this gap (as expected from BCS theory). Slezak et al. used STM to measure the energy gap as a function of position. They then performed Fourier transformation and found that the energy gap has a modulation with the same period as the supermodulation—that is, the Cooper pairs exhibit a density wave. Such a pair density wave state was previously proposed by Chen et al. (2) to explain the earlier STM studies of Hoffman et al. (10), who found a different modulated state associated with the vortex cores in a magnetic field. However, the modulated state discovered by Slezak et al. has no connection with vortices because the measurements were done at zero magnetic field.

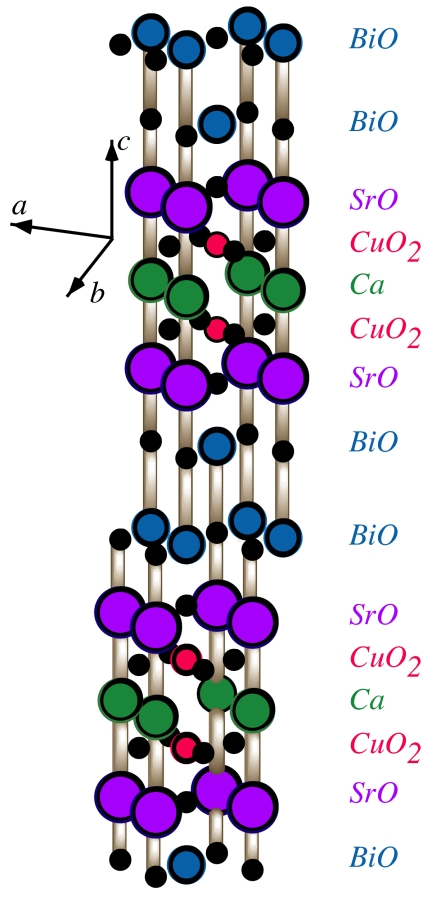
How should these new results be interpreted? On the basis of several structural refinements, Slezak et al. (1) suggest that the energy gap is anticorrelated with the distance between the copper and apical oxygen atoms. This important observation is somewhat of a surprise, given that the opposite correlation was suggested by Pavarini et al. (9). Of particular concern is the fact that not all structural refinements of Bi-2212 support this interesting conjecture, although the conjecture has gained recent support from electronic structure calculations (11). Moreover, most refinements indicate a strong second harmonic contribution that is not observed in the gap modulation. In fact, the actual crystal structure of Bi-2212 (Fig. 1) is still an object of contention after 20 years of study because of its complexity. It is hoped that the new results of Slezak et al. will motivate a more precise determination of the crystal structure.

Fig. 1.

A simplified tetragonal representation of the crystal structure of Bi-2212. The actual material is orthorhombic, with a long-period modulation wave along the b axis that is incommensurate with respect to this simplified representation. The superconducting energy gap associated with the CuO₂ planes has a modulation that matches this superlattice, and the size of the gap is conjectured to be anticorrelated with the distance between the copper atoms and the apical oxygen atoms (1). The microscopic origin of this anticorrelation effect could be an important key in deciphering the mystery of the high superconducting transition temperature seen in this material.

What do these results imply for other measurements? Angle-resolved photoemission probes momentum space rather than real space, and the superlattice modulation is seen very clearly in these materials as ghost images of the Fermi surface displaced by the superlattice wavevector (12). It was thought that these images were due to diffraction of the outgoing photoelectrons by the surface BiO layer, but Slezak et al. (1) suggest that the superlattice actually alters the intrinsic electronic structure. Therefore, a close look at the electronic structure where these ghost images cross the Fermi surface (in the usually avoided X quadrant of the Brillouin zone) could be most instructive. In addition, another photoemission study (13) found a dichroism signal in Bi-2212 in the pseudogap phase from which superconductivity emerges—the relationship between the pseudogap and the superconducting gap being a subject of much debate in the field (14). From these measurements, it was not possible to determine whether this signal was due to breaking of time-reversal or inversion symmetry, but a recent x-ray dichroism study (15) suggests the latter. However, calculations based on several structural refinements could not reproduce this dichroism signal (16), again calling for a more precise determination of the crystal structure of Bi-2212.

The modulated state discovered by Slezak et al. has no connection with vortices.

Finally, what does all this have to say about the theory of cuprates? As might be expected, the observations of Slezak et al. (1), along with earlier observations by the same group of a correlation of the energy gap with dopant atoms (17), have already motivated a number of theoretical proposals. Modulations of the pairing potential (18, 19), the hopping between copper and planar oxygen atoms (20), and the superexchange interaction between copper ions (21) have all been proposed. If we are lucky, one of these suggestions will turn out to be the primary explanation for the gap modulation, from which we can hope to identify the most important microscopic parameter that controls T_c. The step from this explanation to a proper microscopic theory of cuprate superconductivity could be relatively straightforward. If we are unlucky, however, multiple parameters may be found to affect the gap modulation, and then we would not be as close to the truth as we could hope. Such dilemmas are common in the cuprate field, and only time will reveal the most important direction to pursue. Regardless of future outcomes, however, the study by Slezak et al. is another important step in understanding the microscopic nature of cuprate superconductivity.