Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2008 Dec 1.
Published in final edited form as: J Struct Biol. 2007 Aug 24;160(3):353–361. doi: 10.1016/j.jsb.2007.08.008

Automatic lattice determination for two-dimensional crystal images

Xiangyan Zeng 1, Bryant Gipson 1, Zi Yan Zheng 1, Ludovic Renault 1, Henning Stahlberg 1,*
PMCID: PMC2265636  NIHMSID: NIHMS35272  PMID: 17904383

Abstract

Electron crystallography determines the structure of membrane proteins and other periodic samples by recording either images or diffraction patterns. Computer processing of recorded images requires the determination of the reciprocal lattice parameters in the Fourier transform of the image. We have developed a set of three programs 2dx_peaksearch, 2dx_latfind and 2dx_getlat, which can determine the reciprocal lattice from a Fourier transformation of a 2D crystal image automatically. 2dx_peaksearch determines a list of Fourier peak coordinates from a processed calculated diffraction pattern. These coordinates are evaluated by 2dx_latfind to determine one or more lattices, using a-priori knowledge of the real-space crystal unit cell dimensions, and the sample tilt geometry. If these are unknown, then the program 2dx_getlat can be used to obtain a guess for the unit cell dimensions. These programs are available as part of the 2dx software package for the image processing of 2D crystal images at http://2dx.org.

Keywords: electron crystallography, 2D membrane protein crystals, computer image processing, lattice determination

Introduction

Electron crystallography determines the structure of two-dimensional (2D) crystals of membrane proteins or other periodically arranged samples, using cryo-electron microscopy (cryo-EM) data collection and computer image processing (Henderson et al., 1990; Henderson & Unwin, 1975). The electron microscope can be used in either the imaging or the diffraction mode. In imaging mode, real-space images of the crystalline samples are recorded on the instrument’s CCD camera or photographic film. The latter need to be digitized with a scanner before further processing. Digitized images can then be numerically Fourier transformed, producing complex datasets, which contain amplitudes and phases. Since computational correction of 2D crystal defects in the image can be done by computational “unbending” (Crowther et al., 1996), useful real-space images can also be recorded for crystal samples of limited order. Nevertheless, the resolution of such real-space images is affected by beam-induced sample charging and drum-head movement, as well as by sample vibration or drift. While phases obtained from Fourier-transformed 2D crystal real-space images are of relatively good quality, the amplitudes are affected by the electron microscope’s contrast transfer function, and are therefore less well determined.

Alternatively, the electron microscope can record electron diffraction patterns of the 2D crystal samples, which are preferably recorded onto CCD cameras due to their superior dynamic range. The electron diffraction patterns are then evaluated similarly to X-ray diffraction (XRD) patterns in X-ray crystallography; which yield the intensities of the diffracted rays, and thereby contain the information about the structure’s amplitudes. Phase information is not contained in the diffraction pattern, and has to be acquired by different means. Electron diffraction data collection, in contrast, generally does not suffer from sample charging or sample movement during the data collection. Since 2D crystal image unbending cannot be done with a diffraction pattern, in practical terms electron diffraction can only be done with larger, well-ordered 2D crystal samples.

Electron crystallography structure reconstruction of membrane proteins ideally utilizes real-space images to obtain an initial dataset with amplitudes and phases, and then continues completing the dataset with high-resolution amplitudes from electron diffraction patterns alone. The phases for the high-resolution components are then generated or refined by phase extension or molecular replacement, similar to the procedures used in X-ray diffraction structure determination (Grigorieff et al., 1996).

The atomic models for seven membrane proteins and tubulin have so far been determined by electron crystallography: BR (Henderson et al., 1990) LHCII (Kühlbrandt et al., 1994), AQP1 (Murata et al., 2000; Ren et al., 2001), nAChR (Miyazawa et al., 2003), AQPO (Gonen et al., 2004; Gonen et al., 2005), AQP4 (Hiroaki et al., 2006), MGST1 (Holm et al., 2006), and Tubulin (Nogales et al., 1998). Several other membrane proteins classified as transporters, ion pumps, receptors and membrane bound enzymes have been studied by electron crystallography at lower resolution allowing localization of secondary structure motifs such as transmembrane helices, and are likely to produce atomic models in the near future (e.g. Hirai et al., 2002; Kukulski et al., 2005; Schenk et al., 2005; Tate et al., 2003; Vinothkumar et al., 2005). Computer image processing in almost all above-mentioned cases has been performed with the so-called “MRC programs” for image processing (Crowther et al., 1996). Computer processing of recorded images generally requires the determination of the crystal lattice using spots visible in the Fourier transform of the images. For the processing of electron crystallography images, this determination of the lattice vectors is usually done manually, and represents a time-intensive step, especially if many images are to be processed.

X-ray crystallography diffraction patterns show spots if their reciprocal position overlaps sufficiently with the Ewald sphere. The complex indexing process of XRD is done with robust automated software, such as the program DENZO as a part of the diffraction-image processing suite HKL2000 (Otwinowski & Minor, 1997; Otwinowski & Minor, 2001; Rossmann & van Beek, 1999), MOSFLM (Leslie, 1992), and d*TREK (Pflugrath, 1999). Important representatives of autoindexing algorithms are either based on Fourier analysis (Steller et al., 1997) or direct indexing of difference vectors (Higashi, 1990; Kabsch, 1988; Kim, 1989). The general principle behind Fourier analysis methods is that the projection of a protein lattice in a chosen direction has a periodic distribution. The periodicity is determined by Fourier analysis. Structural details are encoded in the regular lattice in Fourier space. The basis vectors defining the reciprocal lattice in Fourier space are found by exploring all possible directions. In XRD autoindexing, Fourier-based methods need a few hundred spots to get reliable results, although in some favorable cases as few as 50 can be sufficient (Leslie, 2006). Difference vector methods first sort and estimate the crude base vectors according to their lengths and angle constraints. The selected bases are iteratively refined using estimated positions of observed diffraction spots. Both, Fourier-based and difference vector methods cannot identify single lattices in double- or poly-crystals. In this case, spots of a single lattice have to be selected manually beforehand.

There have been many algorithms for indexing diffraction spots in X-ray crystallography. However, there is little work reported for that task in electron crystallography. Unlike X-ray diffraction patterns, electron crystallography gives real space images that have a very low signal to noise ratio, and the Fourier transformations show usually less than 100 visible spots. The common methods of difference vector analysis may not find the accurate basis. (Kabsch, 1993), has proposed a robust solution that takes into account the moderate accuracy of the automatically determined lattice points and tolerates a small number of artifacts among them. This approach, however, cannot handle multiple crystal lattices.

We present here two new algorithms for determination of the reciprocal lattice of a 2D crystal image. These algorithms are also applicable to poly-crystal images. In addition, we present a refined tool for manual lattice identification in 2dx_image.

The lattice determination algorithm

The first algorithm presented requires and makes use of a-priori knowledge of the lattice dimensions and lattice angle of the crystal sample in real-space, as well as of the sample tilt geometry under which the image was recorded. This algorithm determines the reciprocal lattice in the Fourier transformation (FFT) of the image in two steps: A first program 2dx_peaksearch compiles a list of peak coordinates from the FFT, and another program 2dx_latfind uses these peak coordinates to determine one or more lattices. If the unit cell parameters are unknown, a second algorithm is implemented in the program 2dx_getlat, which guesses a lattice without any a-priori knowledge.

2dx_peaksearch

As a first step, 2dx_peaksearch compiles a list of coordinates of peaks in the power spectrum (PS; the squared amplitude component of the calculated FFT) of an edge-tapered 2D crystal image (Fig. 1A). To obtain reliable peak spots, the pixels on the X- and Y-axis and at high resolution outside of a circular mask are replaced by the average grey value, and the resulting masked PS is low-pass and high-pass filtered to flatten potential variations from the contrast transfer function of the microscope, and to reduce the noise (Fig. 1B). The central X- and Y-axis are then again masked to eliminate potential “cross-wire” artifacts. Continuous streaks are then recognized by a pixel-wise neighbor search starting from the origin in the original PS and masked (Fig. 1C). Since the bright and dark center areas in Fig. 1B are masked with the average, the contrast of the PS is enhanced in Fig. 1C. A set of peak coordinates is then obtained through two peak search processes, each of which finds the specified numbers of peaks that are a local maxima in a 3×3 square, while ignoring other local peaks within a 10 pixel radius or found peaks. The first search process is used to find initial peaks. For each of these identified peak positions, a copy of the PS is shifted so that each peak becomes the new center. These shifted PS images are then averaged, weighted according to the central peak height. The effect of image shift to the distribution of peaks is shown in Fig. 1D. The resulting average PS image usually has a full coverage of low-resolution spots without any systematic absences, and therefore facilitates lattice determination. In addition, this average image has a better signal to noise ratio. This step of shifting-and-averaging PS follows the processing from the MRC program autoindex (Crowther et al., 1996), which identifies the initial peaks using a static threshold and then searches for two independent low-resolution vectors directly in the averaged PS. However, 2dx_peaksearch subjects this averaged PS image to a second peak search, with the list of peaks coordinates and their amplitudes (heights) written out for further processing by the programs 2dx_latfind or 2dx_getlat.

Figure 1.

Figure 1

Open in a new tab

Automatic lattice determination of a crystal. (A) The original power spectrum (PS). (B) The program 2dx_peaksearch replaces pixels on the X- and Y-axes and at high-resolution outside of a circular mask with the average grey value. This masked PS is then high- and low-pass filtered. (C) Streak artifacts together with X- and Y-axes are again masked with the mean in (C). (D) The origin-shifted and weighted averaged PS. (E) The first (circles) and second (squares) lattices are overlaid over the original PS, as automatically determined by 2dx_findlat. The first vector of each lattice u=(1,0) is plotted in red, the second one v=(0,1) in dark blue. Note that the brightest diffraction spots in the original PS were correctly recognized by 2dx_findlat as second order spots with coordinates (1,1), (2,0) and (−1,1), corresponding to a rectangular real-space lattice of a=81Å, b=136Å, and γ=90°. (F) The program 2dx_getlat in this example reported a lattice that covers most but not all lattice nodes, and is a wrongly indexed lattice due to the lack of additional information. This lattice, however, can still be transferred into the correct lattice as shown in (E) with the script “Evaluate Lattice” in 2dx_image (see text).

2dx_latfind

As second step, 2dx_latfind uses the list of peak coordinates for the search of the best fitting lattice. This is done by calculating a hypothetical test lattice, based on the given real-space unit cell dimensions and included angle, considering the potential distortions due to the sample tilt. The crystal sample parameters are given as a,b for the unit cell dimensions and γ for the unit cell angle, and the tilt geometry is defined as in the MRC software by TLTANG and TLTAXIS (Crowther et al., 1996). The reciprocal lattice vectors U=(u1,u2) and V=(v1,v2) are then initially set to:

u1=0u2=d/(a∗mag∗sin(γ))v1=d∗cos(π−γ)/(b∗mag∗sin(γ))v2=d∗sin(π−γ)/(b∗mag∗sin(γ)) (1)

where d is the image pixel size and mag is the magnification.

This test lattice (U, V) is then rotated in the sample plane in small angle increments Θ to give (U′, V′):

U′=(cos(Θ)sin(Θ)−sin(Θ)cos(Θ))U (2)

and equivalently for V′, and the expected lattice distortion due to the tilt geometry is then applied, to give (U″, V″) for each rotation step:

U″=(cos(TLTAXIS)−sin(TLTAXIS)sin(TLTAXIS)cos(TLTAXIS))(00cos(TLTANG)−1cos(TLTANG)−1)(cos(TLTAXIS)sin(TLTAXIS)−sin(TLTAXIS)cos(TLTAXIS))U′ (3)

and equivalently for V″. In addition, the magnification mag is varied in a raster search of stepsize λ, to accommodate potential inaccuracies in the scale of the lattice or magnification.

Given a set of n peaks Pi = (xi, yi, zi), with peak coordinates (x, y) and peak heights z, a score value F is determined for each rotated, distorted and magnification-varied test-lattice, by summation of the peak values of peaks that lay within a given radius of the listed peak coordinates.

F=∑i=1ng(zi) (4)

where g(z)={z         ; if   spot   on   lattice0         ;   otherwise, and i denotes the peak numbers.

A peak with the coordinates (xi, yi), is accepted as “on the lattice”, if

∣P1−xi∣<δh2+k2, and   ∣P2−yi∣<δh2+k2 (5)

Where P1 = u1*h + v1*k, and P2 = u2*h + v2*k, with h, k being the Miller indices of spots in the averaged PS, and δ being a tolerance constant. The condition (5) allows a larger deviation of spots from the lattice with increasing radius (resolution). This gives high-resolution spots a higher chance of contributing to the lattice vectors than low-resolution spots, in contrast to the method used by (Kabsch, 1993), that is using a constant threshold |P1−xi| < δ.

Any lattice candidate that covers a sufficiently large number nmin of low-resolution peaks is further refined. The peak spots in the lattice are first mapped into the lattice coordinates (RMi, RNi), using

RMi=xiv1−yiv2u1v1−u2v2,         RNi=xiu1−yiu2v1u1−v2u2 (6)

Then the refined lattice vectors are obtained by minimizing the residuals

∑i=1n[(int(RMi)u1+int(RNi)v1−xi)2+(int(RMi)u2+int(RNi)v2−yi)2] (7)

where Int(x) takes the nearest integer value of a real number x. For the refined lattice, a final scoring value F is then calculated as in equation (4).

From all the rotated, tilt-distorted, magnification-varied, and then refined lattices, that pair of lattice vectors with the highest scoring value is selected as the final lattice. By excluding the peaks that overlap with this identified lattice from the peak set, the algorithm is iteratively re-applied to the remaining peaks to find other potential lattices of multi-layered crystals or poly crystals (Fig. 1E).

2dx_getlat

If the unit cell parameters of the crystal sample and/or the tilt geometry are unknown, an alternative algorithm is implemented in the program 2dx_getlat, which is used to identify candidate lattice vectors for the refinement and scoring evaluation.

2dx_getlat requires only the peak list of the averaged PS generated by 2dx_peaksearch. Using this, a set of difference vectors between certain low-resolution peak positions is generated, from which the most likely pair of lattice-generating vectors is found. This pair is then used as the basis for an iterative refinement process (usually requiring a maximum of 2 or 3 steps) assigning miller indices to found peaks which are then used in a least squares refinement of the basis vectors for the next round of refinement.

The strongest peak in the average PS image will necessarily fall on the strongest of any present lattices, and will very likely be a lattice-generating basis vector itself. As such, 2dx_getlat compiles a list of every possible pair of points drawn from a list of all peaks occurring closer to the origin than the farthest of the k strongest peaks. Each such pair is then used to form basis vectors that generate separate candidate lattices, which are then individually compared against the full peak list. The parameter k can be changed to decrease the total calculation time and is usually set to 4 or 8 as the ideal basis vectors are almost always contained within the set of peak-vectors which are shorter than the longest of the 8 brightest peaks.

Lattice fitness for each candidate lattice, defined by vectors u⃑ and v⃑, is determined by first transforming each peak from the full peak list into a generalized Miller space via multiplication with the inverse of the 2×2 matrix [u⃑, v⃑] (with u⃑ and v⃑ the lattice generating column vectors). The computed Euclidean distances from integer values for each transformed peak are then summed, with each term in the summation multiplied by the strength of the peak in question. For lattices where the included angle Θ between the vectors u⃑ and v⃑ is smaller than a certain limit (Θ ≤ ΘMax) a penalty weighting-factor of e(ΘMax − Θ) is multiplied to each term. A value of ΘMax = 10° was found suitable. This factor is applied to prevent trivial solution lattices, which have tightly spaced nodes and achieve artificially high apparent fitness. This problematic fitting occurs if the resulting lattice nodes approach continuity such that all peaks in the PS inevitably fall within reasonable distances of a node.

The two vectors, which generate the lattice with the lowest error are then transformed into the shortest lattice-defining right-handed lattice that lies in the right half of the FFT: First, by inverting vectors with negative x-values, then by iteratively either subtracting the shorter of the two vectors from the other if the included angle is smaller than 90°, or by adding them if the included angle is greater than 90°, until convergence to the shortest solution is reached. These resulting vectors are then ordered canonically, with the first vector defined as the one being closer to the negative y-axis.

Using this basis, all peaks in the average PS are then transformed into the generalized Miller space, which is defined by the inverse of the 2×2 matrix of the newly found lattice vectors [u⃑,v⃑]. These transformed peaks will then be assigned a given Miller index if they fall within ε of the integer values associated with this index. An ε of 0.0707 corresponds to 10% of the maximally possible error of 12, and is usually sufficient to exclude peaks from artifacts or other lattices. Finally, a peak assigned to a given index is discarded if another peak is found to lie closer to the index in question. Using the generated Miller index/peak position pairs, a least squares fit is then performed to refine the lattice [u⃑,v⃑]. This process is then iteratively repeated until the method converges to a final lattice, which usually is reached within 2 or 3 iterations. As this method requires nothing beyond the peak list itself, it is highly sensitive to errors or absences found in this list.

Manual lattice indexing

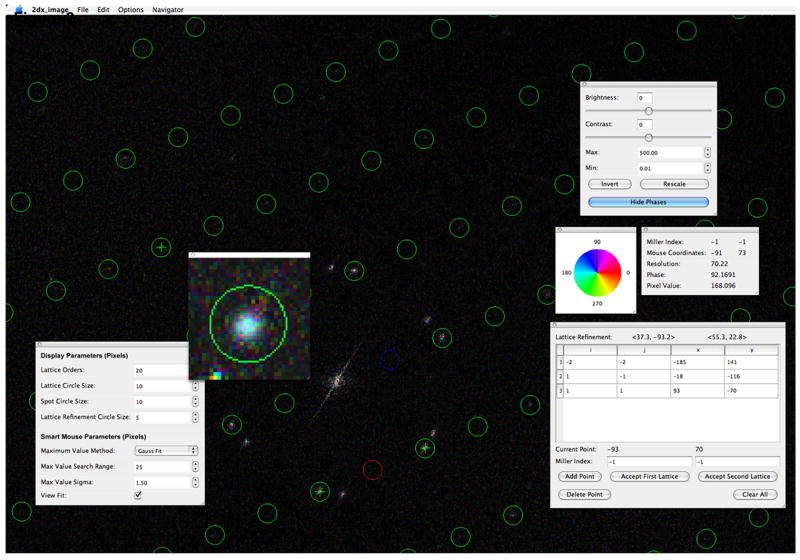
To assist the user in manual indexing of the reciprocal lattice, we have implemented a lattice refinement function into the full-screen browser of 2dx_image (Fig. 2), with design and function largely inspired by the functions and development work found in the MRC program Ximdisp.exe (Smith, 1999). 2dx_image allows displaying of phase information in the calculated Fourier transformation of an image as color code. In cases of very well ordered 2D crystal images, true diffraction peaks can be recognized by coherent phase information of neighboring pixels, while noise peaks have generally more random phases (Amos et al., 1982). The manual lattice indexing function further supports the user by pre-entering the most likely Miller coordinates of the chosen peak location, so that in most cases the user can confirm that Miller index by simply hitting the “Enter” key on the keyboard. A smart mouse function in the full-screen browser is activated upon double-clicking into the Fourier transformation. This function will then either correct the click-location to the strongest pixel within a given radius, or will perform a peak-search within that given radius with a Gaussian profile of a given half-width. In addition, 2dx image offers a set of lattice-arithmetic functions in the “Evaluate Lattice” script, which allow the user to swap the primary and secondary reciprocal lattices, scale, skew, or rotate the reciprocal lattice, as well as invert the handedness of the current reciprocal lattice. This script also allows calculating the corresponding real-space lattice, and can give feedback on the agreement of the chosen lattice with the determined peak-locations in the averaged PS.

Figure 2.

Figure 2

Open in a new tab

The manual lattice determination function of the full-screen browser in 2dx_image. The calculated FFT of an image is displayed, here optionally with color-coded phase information (top right panel). The currently valid lattice is indicated by circles, with spot (1,0) in red, and (0,1) in blue. The information of the current mouse pointer location is displayed in the panel on the right. The user can manually identify individual peak positions by mouse-click and then assign Miller indices to the peak, while the most likely Miller indices based on the current lattice estimate are automatically pre-entered as default values (bottom right panel). Double-clicking close to a peak in the FFT will activate the smart-mouse function, which either selects the highest peak within a given radial distance, or will perform a Gauss profile peak search over the pixels within the given radius (here 25 pixels) and select the best fitting location as click-location. Parameters for the smart mouse function can be adjusted in the panel bottom left. The Gauss peak fit at the automatically re-centered location is displayed in the zoomed window (center left panel).

Results

The performance of these algorithms has been tested on a variety of images from non-tilted and tilted 2D crystals of various lattice dimensions and signal-to-noise levels.

Table 1 shows the results of applying the first algorithm (2dx_findlat) to different electron micrographs of 2D membrane protein crystals. For the first peak search in the original PS, 40 peaks were selected to generate the average shifted PS image and 140 peaks were selected from the latter to determine the lattice vectors. 2dx_latfind found lattices in all test images using a stepsize of Θ = 0.1° for the rotational angle increment of the test lattice, a magnification variation of λ = mag * 0.006, a minimal number of required lattice peaks of nmin = 8, and a tolerance value of δ = 3 pixels in reciprocal space (px−1) for the spot acceptance. The normalized root-mean-square deviation (RMSDN) of the locations of peaks that fit the final lattice is calculated and normalized by the unit cell length

Table 1.

Performance of the automatic lattice determination by 2dx_findlat for different images.

Data set Number of crystals Tilt geometry [TLTANG, TLTAXIS]& Real-space lattice (a, b, γ) Lattice error [%]
AmtB 2* 0°,0° 81Å, 136Å, 90° 1.51277
1.39484
BR 1 0°,0° 62Å, 62Å, 120° 1.30567
AQP2 1 0°,0° 98Å, 98Å, 90° 1.18784
AQP2 2* 33.85°, 63.04° 98Å, 98Å, 90° 0.75341
0.86334
AQP2 1 45.36°, 60.73° 98Å, 98Å, 90° 2.45832
Open in a new tab
*

) These lattices were overlaid and correctly identified in the same image.

&

) Angle definition as in the MRC software (Henderson & Unwin, 1975).

RMSDN=2n∑i=1n∥L·m⇀i−x⇀i∥max(∥u⇀+v⇀∥,∥u⇀−v⇀∥) (8)

where L = [u⃑ v⃑], the matrix whose columns are formed by the reciprocal lattice vectors, and m⃑i = [hi ki]T are the miller indices of spot i and x⃑i = [xi yi]T represent the positions of the peaks in reciprocal space. In addition to this criterion, all the lattices were visually verified.

The combination of the streak-removal routine in 2dx_peaksearch and the algorithm used in 2dx_findlat was found to be insensitive to artifact peaks or streaks in the PS. The degree of tolerance of artifact peaks is related to the parameter δ, which should be chosen according to the confidence in the peak spot locations, i.e. the sharpness of the peaks and the signal-to-noise ratio in the PS. A small δ should be chosen in case of a PS with strong and sharp peaks, which then will give a high accuracy of the determined lattice vectors. A larger δ is recommended if the peaks in the PS are broad and noisy, to allow the algorithm to still find approximate lattice bases. Experiments were carried out with a dataset of peak spots of an AQP2 2D crystal with the vector length of 119 px−1. The peak coordinates were deliberately distorted by Gaussian distributed offsets. 2dx_findlat failed to find the correct lattice from peak locations that had been disturbed with a position deviation of σ = 10 px−1, when using a δ = 3.0 px−1, but could still find the correct lattice with a δ = 6.0 px−1 (Table 2).

Table 2.

Lattice vector identification of an AQP2 image, where the peak positions were displaced by random amounts with a Gaussian distribution with standard deviation σ. The image was from a sample tilted at TLTANG=45.36°, with TLTAXIS=60.73°, with a=b=98Å, γ =90°. The tolerance value of δ=3.0 px−1 was sufficient to identify the correct lattice for smaller peak distortions, but a larger tolerance of δ=6.0 px−1 was required for strongly distorted peak coordinates. At larger peak deviations σ, the resulting lattice unavoidably has a larger RMSDN. Nevertheless, the correct lattice was found as visually verified, except in the one mentioned case.

Peak deviations σ [px−1] Lattice tolerance δ [px−1] U V Lattice Error [%]
2.0 3.0 18.895, −89.272 110.294, −4.216 2.78121
5.0 3.0 18.651, −89.157 109.903, −4.143 2.92306
8.0 3.0 18.782, −88.957 110.359, −4.229 3.24457
10.0 3.0 19.939, −98.402 116.967, −12.795 wrong lattice
10.0 6.0 19.323, −90.239 110.596, −6.014 4.13556
Open in a new tab

Tests were also done to investigate the tolerance to the errors in the tilt geometry and the unit cell length, using an image of a tilted AQP2 2D crystal with a=b= 98Å, γ=90°, and a tilt angle of 45°. The lattice could be correctly identified with tilt angle and axis variations of ± 8°, and with the unit cell length varying between 93Å and 106Å (data not shown).

The difference-vector based algorithm implemented in 2dx_getlat does not require a-priori knowledge of an expected lattice or tilt geometry. Since this second algorithm does not perform an exhaustive search, but rather guesses the lattice from direct calculations, this algorithm was found to be 100 to 1000 times faster in computational costs, and was still able in most cases to correctly identify the lattice. Only cases of PS with significant absences of lattice nodes caused 2dx_getlat to fail to report the correctly indexed lattice. One such case is shown in Figure 1F.

Discussions

The peaks from the averaged PS allow much better identification of the lattice than the peaks from the original PS. Our algorithm as implemented in 2dx_peaksearch follows the developments for the average PS that were also implemented in the MRC program autoindex before (Crowther et al., 1996). In addition, 2dx_peaksearch also removes streaks, which can arise from image edge effects, or, as in the case for Figure 1, from the edges of a negatively stained 2D crystal itself. The resulting averaged PS usually shows a pattern without absences of a much-increased signal-to-noise level, from which peak coordinates are evaluated for further processing.

The results presented here show that the informed exhaustive search implemented in 2dx_findlat can accurately identify one or more lattices in images of 2D crystals, including those of tilted and polycrystalline crystals. The ability of distinguishing multi-layer crystals arises from the fact that 2dx_findlat makes use of a-priori known information about the 2D crystal lattice, such as the unit cell dimensions and the tilt geometry. The required dimensions of the real unit cell can be obtained either manually from one easier-to-index non-tilted image, or by using the difference vector based algorithm implemented in 2dx_getlat, which does not require any a-priori knowledge.

Identifying the lattices in a large number of 2D crystal images can be done first by indexing the lattice of one good non-tilted image with 2dx_getlat, or manually. In most cases, 2dx_getlat will find the correct lattice. However, in case of tricky lattices with systematic absences, 2dx_getlat might report a lattice that assigns wrong indices to the correctly identified lattice nodes (as shown for example in Figure 1F). In this case, the graphical user interface (GUI) of the 2dx_image software (Gipson et al., 2007) offers a script called “Evaluate Lattice”, which allows modification of the identified lattice. This script allows the user to scale the lattice by doubling or halving one or both lattice vectors, skewing the lattice by replacing one vector with the sum or difference of both vectors, rotating the lattice clock or anti-clock wise (for square or hexagonal lattices), as well as changing the handedness of the lattice. This script can be used to transform the automatically determined lattice into the visually chosen one. This script also compares the current lattice with the list of closest peak positions to report the precision of the current lattice in the form of RMSDN. It also reports the corresponding real-space lattice dimension and included angle, which can then be entered into the 2dx_image database into the default configuration file 2dx_image.cfg. This then creates the a-priori knowledge that is required for using the exhaustive search algorithm in 2dx_findlat, which should from then on automatically identify the correct lattice in images of highly tilted samples or those with tricky lattices. For difficult lattices in highly tilted images, 2dx_findlat was usually capable of identifying the lattice more reliable than a manual user.

With the real-space lattice dimensions known, the script “Evaluate Lattice” also calculates the tilt geometry that would correspond to the given lattice when compared to the real-space lattice dimensions. This is done with a slightly adapted version of the program EMTILT, which is part of the MRC software (Crowther et al., 1996; Shaw & Hills, 1981; Valpuesta et al., 1994).

When large tolerance boundaries for the magnification and lattice tolerance are used, 2dx_findlat might report the correct lattice, but have assigned the basis vectors incorrectly. For example, the reported lattice could have a wrong handedness assignment (i.e. u and v are exchanged). In the case of a tilted sample, this could then result in EMTILT reporting a wrong tilt geometry. Comparison of the EMTILT-determined tilt geometry with the defocus-gradient based tilt geometry allows identifying the correct lattice indexation. In practice, the user can use the script “Evaluate Lattice” to quickly cycle through different lattice indexations until the resulting tilt geometry agrees with the defocus-gradient determined geometry, as displayed in the Status panel in the 2dx_image GUI.

The precision of the determined lattices as determined by 2dx_latError and measured in RMSDN for us was always higher for lattices determined by either of the automatic algorithms than for lattices that we indexed manually.

Conclusions

A set of three programs 2dx_peaksearch, 2dx_latfind and 2dx_getlat was created, which allow the automatic determination of a 2D crystal lattice from a real-space image. 2dx_peaksearch determines a list of Fourier peak coordinates, which are used by 2dx_latfind to determine one or more lattices, using a-priori knowledge of the real-space crystal unit cell dimensions and the sample tilt geometry. If these are unknown, the program 2dx_getlat can be used to rapidly determine the most likely lattice, and thereby obtain a guess for the unit cell dimensions. Alternatively, the user can manually identify a lattice, while being supported by a set of functions in the full-screen browser of 2dx_image. These programs are available as part of the 2dx software package for the user-friendly image processing of 2D crystal images (Gipson et al., 2007), and are available at http://2dx.org.

Table 3.

Comparison of the performance of 2dx_findlat and 2dx_getlat. The algorithms were applied to 7 images from 5 different samples and different tilt angles. The Lattice Error is calculated as RMSDN of the distance of peak locations from the chosen lattice. Only peaks closer than a given threshold (see text) are included in this calculation. The Number of Peaks indicates how many peaks fulfilled the selection criteria (used), and how many peaks from the averaged PS were given to the algorithms (allowed). Node Density indicates the calculated number of lattice nodes for a given area relative to the number of peaks that fall within this area. (Ideally this number should be close to one and is a measure of whether the found lattice is too big or small by integer amounts. This measure also describes the number of layers present in the image for multi-layer crystals.) The computation times for 2dx_findlat are about three orders of magnitude longer than for 2dx_getlat, while the precision of both algorithms is comparable and usually better than a human operator can perform. However, in one image (AmtB*), 2dx_getlat failed to recognize the correct lattice, and chose a lattice twice as large instead, see Figure 1. This still produced a lattice where 34 out of 140 spots could be used to report an acceptable RMSDN, since this lattice had some 34 spots that were precisely fitting to this lattice. Nevertheless, the peak indexing was wrong, while 2dx_findlat identified the correct lattice.

Protein Tilt Angle [°] Lattice Error [%] Number of Peaks (used/allowed) Node Density [Nodes/Peaks]
2dx_findlat 2dx_getlat 2dx_fndlat 2dx_getlat 2dx_findlat 2dx_getlat
AQP2 0.0 1.56784 1.6402 128/140 128/140 2.85953 2.85883
AmtB 0.0 1.51277 1.45631 74/300 74/300 1.35132 1.35226
AmtB* 0.0 1.39484 wrong lattice 50/140 28/140 1.99996 1.13391
BR 0.0 1.30567 0.959057 101/140 95/140 0.78599 0.860895
OmpF 1 -Layer 0.0 1.95961 1.97492 69/140 68/140 0.764223 0.800325
Synthetic 0.0 0.761587 0.761232 140/140 140/140 1.12429 1.12407
V0 20.0 0.543959 0.543976 88/140 88/140 1.46933 1.46932
Open in a new tab

Acknowledgments

This work was supported by the NSF, grant number MCB-0447860 and by the NIH, grant number U54-GM074929. We thank Richard Henderson for his explanations of the algorithms used in autoindex. Development of some of these algorithms was started in the laboratories of Jacques Dubochet in Lausanne, and Andreas Engel in Basel, Switzerland.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Amos LA, Henderson R, Unwin PN. Three-dimensional structure determination by electron microscopy of two-dimensional crystals. Prog Biophys Mol Biol. 1982;39:183–231. doi: 10.1016/0079-6107(83)90017-2. [DOI] [PubMed] [Google Scholar]
  2. Crowther RA, Henderson R, Smith JM. MRC image processing programs. J Struct Biol. 1996;116:9–16. doi: 10.1006/jsbi.1996.0003. [DOI] [PubMed] [Google Scholar]
  3. Gipson B, Zeng X, Zhang ZY, Stahlberg H. 2dx-User-friendly image processing for 2D crystals. J Struct Biol. 2007;157:64–72. doi: 10.1016/j.jsb.2006.07.020. [DOI] [PubMed] [Google Scholar]
  4. Gonen T, Cheng Y, Sliz P, Hiroaki Y, Fujiyoshi Y, Harrison SC, Walz T. Lipid-protein interactions in double-layered two-dimensional AQP0 crystals. Nature. 2005;438:633–638. doi: 10.1038/nature04321. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Gonen T, Sliz P, Kistler J, Cheng Y, Walz T. Aquaporin-0 membrane junctions reveal the structure of a closed water pore. Nature. 2004;429:193–197. doi: 10.1038/nature02503. [DOI] [PubMed] [Google Scholar]
  6. Grigorieff N, Ceska TA, Downing KH, Baldwin JM, Henderson R. Electron-crystallographic refinement of the structure of bacteriorhodopsin. J Mol Biol. 1996;259:393–421. doi: 10.1006/jmbi.1996.0328. [DOI] [PubMed] [Google Scholar]
  7. Henderson R, Baldwin JM, Ceska TA, Zemlin F, Beckmann E, Downing KH. Model for the structure of Bacteriorhodopsin based on high-resolution electron cryo-microscopy. J Mol Biol. 1990;213:899–929. doi: 10.1016/S0022-2836(05)80271-2. [DOI] [PubMed] [Google Scholar]
  8. Henderson R, Unwin PN. Three-dimensional model of purple membrane obtained by electron microscopy. Nature. 1975;257:28–32. doi: 10.1038/257028a0. [DOI] [PubMed] [Google Scholar]
  9. Higashi T. Auto-indexing of oscillation images. J Appl Cryst. 1990;23:253–257. [Google Scholar]
  10. Hirai T, Heymann JA, Shi D, Sarker R, Maloney PC, Subramaniam S. Three-dimensional structure of a bacterial oxalate transporter. Nat Struct Biol. 2002;9:597–600. doi: 10.1038/nsb821. [DOI] [PubMed] [Google Scholar]
  11. Hiroaki Y, Tani K, Kamegawa A, Gyobu N, Nishikawa K, Suzuki H, Walz T, Sasaki S, Mitsuoka K, Kimura K, Mizoguchi A, Fujiyoshi Y. Implications of the aquaporin-4 structure on array formation and cell adhesion. J Mol Biol. 2006;355:628–639. doi: 10.1016/j.jmb.2005.10.081. [DOI] [PubMed] [Google Scholar]
  12. Holm PJ, Bhakat P, Jegerschold C, Gyobu N, Mitsuoka K, Fujiyoshi Y, Morgenstern R, Hebert H. Structural basis for detoxification and oxidative stress protection in membranes. J Mol Biol. 2006;360:934–945. doi: 10.1016/j.jmb.2006.05.056. [DOI] [PubMed] [Google Scholar]
  13. Kabsch W. Automatic processing of rotation diffraction data from crystals of initially unknown symmetry and cell constants. J Appl Cryst. 1993;26:795–800. [Google Scholar]
  14. Kabsch W. Automatic processing of rotation diffraction patterns. J Appl Cryst. 1988;21:67–71. [Google Scholar]
  15. Kim S. Auto-indexing oscillation photographs. J Appl Cryst. 1989;22:53–60. [Google Scholar]
  16. Kühlbrandt W, Wang DN, Fujiyoshi Y. Atomic model of plant light-harvesting complex by electron crystallography. Nature. 1994;367:614–621. doi: 10.1038/367614a0. [DOI] [PubMed] [Google Scholar]
  17. Kukulski W, Schenk AD, Johanson U, Braun T, de Groot BL, Fotiadis D, Kjellbom P, Engel A. The 5Å structure of heterologously expressed plant aquaporin SoPIP2;1. J Mol Biol. 2005;350:611–616. doi: 10.1016/j.jmb.2005.05.001. [DOI] [PubMed] [Google Scholar]
  18. Leslie AG. The integration of macromolecular diffraction data. Acta Cryst D Biol Crystallogr. 2006;62:48–57. doi: 10.1107/S0907444905039107. [DOI] [PubMed] [Google Scholar]
  19. Leslie AGW. Recent changes to the MOSFLM package for processing film and image plate data. Joint CCP4 + ESF-EAMCB. News-letter Prot Cryst. 1992;26:22–33. [Google Scholar]
  20. Miyazawa A, Fujiyoshi Y, Unwin N. Structure and gating mechanism of the acetylcholine receptor pore. Nature. 2003;424:949–955. doi: 10.1038/nature01748. [DOI] [PubMed] [Google Scholar]
  21. Murata K, Mitsuoka K, Hirai T, Walz T, Agre P, Heymann JB, Engel A, Fujiyoshi Y. Structural determinants of water permeation through aquaporin-1. Nature. 2000;407:599–605. doi: 10.1038/35036519. [DOI] [PubMed] [Google Scholar]
  22. Nogales E, Wolf SG, Downing KH. Structure of the alpha beta tubulin dimer by electron crystallography. Nature. 1998;391:199–203. doi: 10.1038/34465. [DOI] [PubMed] [Google Scholar]
  23. Otwinowski ZM, Minor W. DENZO and SCALEPACK. In: Rossmann MG, Arnold E, editors. International tables for crystallography. Vol. F: Crystallography of biological macromolecules. Kluwer Academic Publishers; Dordrecht, The Netherlands: 2001. pp. 226–235. [Google Scholar]
  24. Otwinowski ZM, Minor W. Processing of X-ray diffraction data collected in oscillation mode. Meth Enzymol. 1997;276:307–326. doi: 10.1016/S0076-6879(97)76066-X. [DOI] [PubMed] [Google Scholar]
  25. Pflugrath JW. The finer things in X-ray diffraction data collection. Acta Cryst D Biol Crystallogr. 1999;55:1718–1725. doi: 10.1107/s090744499900935x. [DOI] [PubMed] [Google Scholar]
  26. Ren G, Reddy VS, Cheng A, Melnyk P, Mitra AK. Visualization of a water-selective pore by electron crystallography in vitreous ice. Proc Natl Acad Sci USA. 2001;98:1398–1403. doi: 10.1073/pnas.041489198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rossmann MG, van Beek CG. Data processing. Acta Cryst D Biol Crystallogr. 1999;55:1631–1640. doi: 10.1107/s0907444999008379. [DOI] [PubMed] [Google Scholar]
  28. Schenk AD, Werten PJ, Scheuring S, de Groot BL, Müller SA, Stahlberg H, Philippsen A, Engel A. The 4.5 A structure of human AQP2. J Mol Biol. 2005;350:278–289. doi: 10.1016/j.jmb.2005.04.030. [DOI] [PubMed] [Google Scholar]
  29. Shaw PJ, Hills GJ. Tilted specimen in the electron microscope: A simple specimen holder and the calculation of tilt angles for crystalline specimens. Micron. 1981;12:279–282. [Google Scholar]
  30. Smith JM. Ximdisp--A visualization tool to aid structure determination from electron microscope images. J Struct Biol. 1999;125:223–228. doi: 10.1006/jsbi.1998.4073. [DOI] [PubMed] [Google Scholar]
  31. Steller L, Bolotovsky R, Rossmann MG. An algorithm for automatic indexing of oscillation images using Fourier analysis. J Appl Cryst. 1997;30:1036–1040. [Google Scholar]
  32. Tate CG, Ubarretxena-Belandia I, Baldwin JM. Conformational changes in the multidrug transporter EmrE associated with substrate binding. J Mol Biol. 2003;332:229–242. doi: 10.1016/s0022-2836(03)00895-7. [DOI] [PubMed] [Google Scholar]
  33. Valpuesta JM, Carrascosa JL, Henderson R. Analysis of electron microscope images and electron diffraction patterns of thin crystals of phi 29 connectors in ice. J Mol Biol. 1994;240:281–287. doi: 10.1006/jmbi.1994.1445. [DOI] [PubMed] [Google Scholar]
  34. Vinothkumar KR, Smits SH, Kühlbrandt W. pH-induced structural change in a sodium/proton antiporter from Methanococcus jannaschii. EMBO J. 2005;24:2720–2729. doi: 10.1038/sj.emboj.7600727. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES