Genome Partitioning of Genetic Variation for Height from 11,214 Sibling Pairs

Abstract

Height has been used for more than a century as a model by which to understand quantitative genetic variation in humans. We report that the entire genome appears to contribute to its additive genetic variance. We used genotypes and phenotypes of 11,214 sibling pairs from three countries to partition additive genetic variance across the genome. Using genome scans to estimate the proportion of the genomes of each chromosome from siblings that were identical by descent, we estimated the heritability of height contributed by each of the 22 autosomes and the X chromosome. We show that additive genetic variance is spread across multiple chromosomes and that at least six chromosomes (i.e., 3, 4, 8, 15, 17, and 18) are responsible for the observed variation. Indeed, the data are not inconsistent with a uniform spread of trait loci throughout the genome. Our estimate of the variance explained by a chromosome is correlated with the number of times suggestive or significant linkage with height has been reported for that chromosome. Variance due to dominance was not significant but was difficult to assess because of the high sampling correlation between additive and dominance components. Results were consistent with the absence of any large between-chromosome epistatic effects. Notwithstanding the proposed architecture of complex traits that involves widespread gene-gene and gene-environment interactions, our results suggest that variation in height in humans can be explained by many loci distributed over all autosomes, with an additive mode of gene action.

Research into the genetics of complex traits has moved from the estimation of genetic variance in populations to the detection and identification of variants that are associated with or directly cause variation. The standard paradigm has been to perform linkage studies in pedigrees, followed by fine-mapping or candidate-gene studies with the use of association. Recently, genomewide association (GWA) studies, which rely on linkage disequilibrium between observed and causal variants, have become a reality—in particular, for the study of common disease in human populations.^1–4 The success of both linkage and association studies depends on the frequency and distribution of individual gene effects in the population. Rare variants with large effects can most readily be mapped in pedigrees, whereas common variants with moderate effects can be mapped using an association study. Multiple rare variants in the same gene, each with a moderate effect on the phenotype, can be detected using linkage studies but would be hard to find in an association study.

Despite the large research effort in the past decade or so, the nature of complex-trait variation—in terms of the number of causal variants, their frequency in the population, and the size of their effects—is still largely unknown.⁵ Emerging evidence suggests that there are common variants with effects large enough to be detected for a range of phenotypes across a number of species, but the number of identified causal variants remains small.^6,7 Other evidence suggests that multiple rare variants in the same gene may segregate in the population, each with an effect large enough to increase susceptibility to disease.⁸ In human populations, there has frequently been inconsistency of linkage to disease and quantitative phenotypes across multiple samples and populations, with few examples of clear-cut replication. One possible explanation is that, for most phenotypes, the effects of causal variants are too small to be detected by linkage—that is, that most studies have been underpowered. Association analyses are much more powerful for detecting small effects but, again, are dependent on the actual distribution of effect sizes. Recent reports of associated and replicated SNPs from GWA studies show that the effect sizes of individual common variants are typically small.^1–4 Both linkage and association studies suffer from a multiple-testing problem, because they are generally hypothesis generating. There is also a conceptual problem with the null hypothesis in nearly all gene-mapping studies. The null hypothesis for a test at a given location in the genome is that there is no genetic variation associated with that location, despite the fact that we know that there is heritability, often considerable, for the phenotype in question. Hence, a priori, the null hypothesis cannot be true for all test locations. This assumption is particularly worrisome for linkage studies because of the strong linkage disequilibrium within families, such that many linked genes of small effects would result in false evidence of a major gene of large effect.⁹ We recently showed that a number of these problems disappear if the emphasis is on estimation of variance rather than on hypothesis testing.¹⁰

The actual genomewide relationship between pairs of relatives varies because of segregation and can be estimated using dense genetic markers for each pair. For full siblings, for example, the average proportion of the genome shared identical by descent (IBD) is 50%, with a range of ∼38% to ∼62%.¹⁰ By calculating the covariance between the proportion of the genome shared and the similarity of siblings for the phenotype, we were able to estimate the genetic variance free from assumptions about nongenetic sources of resemblance between relatives.¹⁰ In this study, we apply the principle of chromosome- and genomewide-realized relationships^10,11 to partition genetic variance across the genome. We use a very large sample of sibling pairs with genomewide marker genotypes, a well-studied¹² quantitative phenotype in humans (i.e., height), and the independent segregation of chromosomes, to partition genetic variation across chromosomes. We show that at least six chromosomes are responsible for genetic variation but that the hypothesis that all chromosomes contribute variation cannot be rejected. We find no evidence of dominance or epistatic variation. Thus, our data are consistent with a large number of underlying variants acting additively across all chromosomes to affect height in humans.

The data comprised quasi-independent sibling pairs (QISPs) from three studies in Australia (AU), the United States (US), and the Netherlands (NL). All individuals were of European descent. Pairs of MZ twins were excluded, but QISPs, including a single MZ individual, were maintained. Descriptions of the pedigrees, phenotypes, and genotypes have all been given elsewhere.^10,13–15 In brief, for each of the three samples, QISPs were created from pairs of siblings within a nuclear family. Pairs were included if they had both phenotypic and genomewide genotypic information, with a minimum of 210 microsatellite markers per individual and an average of >400 markers for each of the studies.^10,13–15 Height measurements were adjusted for sex and for age at measurement, and standardized residuals (Z scores) were calculated for each individual for each sample separately, to avoid the influence of heterogeneous variances across populations. There were 5,952, 3,996, and 1,266 QISPs for the AU, US, and NL samples, respectively, with a total sample size of 11,214. There were 1,936 brother-brother pairs, 4,011 sister-sister pairs, and 5,267 brother-sister pairs. After adjustment for sex and age, the sibling correlations for the AU, US, and NL samples were 0.432, 0.502, and 0.451, respectively, and the sibling correlation in the entire sample was 0.461. The brother-brother, sister-sister, and brother-sister correlations in the entire sample, after adjustments for age (and for the mean difference in sex in the brother-sister pairs), were 0.494, 0.479, and 0.435, respectively.

Additive coefficients of relationship were calculated using Merlin¹⁶ for each chromosome and genomewide for all three samples, as described elsewhere.¹⁰ For the X chromosome, IBD probabilities were estimated using ^MINX. The genetic length of the chromosomes was taken from independent pedigree data.¹⁷ We estimated from the marker data the proportions of individual chromosomes and of the genome as a whole that are shared IBD between all 11,214 pairs of siblings.^10,13,14 These proportions are coefficients of additive relationship, which are, on average, 0.5 for full siblings but which vary considerably around their expectation, both between chromosomes for the same full-sib pair and between full-sib pairs for the same chromosome.^10,18 The mean±SD of genomewide additive relationships in our sample of 11,214 sibling pairs was 0.4994±0.036 and the range was 0.309 to 0.644, consistent with previous results and with theory.¹⁰

Variance components were estimated by maximum likelihood, as implemented in the statistical package Mx¹⁹ and described elsewhere.¹⁰ Mixed linear models were fitted, including nongenetic family effects, chromosome and genomewide additive genetic effects, and residual effects. We first estimated genetic variance associated with the entire genome, by fitting a model that estimated the covariation between phenotypic similarity and the coefficient of additive relationship. For this whole-genome analysis, we confirmed our previous results,¹⁰ which were based on a smaller data set of 4,919 pairs from only one source of data. The estimate of heritability for stature from genomewide IBD from the sample of 11,214 sibling pairs was 0.86 (95% CI 0.49–0.95; P<.00001). The estimate of the proportion of phenotypic variation due to nongenetic family effects was 0.03 (P=.38), which is statistically nonsignificant. In addition to the genomewide additive effect, we fitted a genomewide dominance effect, using the probability of sharing two alleles IBD, averaged across the genome.¹⁰ The estimated proportions of variance due to additive and dominance effects were 0.699 and 0.160, respectively, but the dominance component was not significantly different from zero (P=.35). However, statistical power to separate these effects is low in our sibling-pair design, since the genomewide additive and dominance coefficients are highly correlated (r=0.911; n=11,214), as predicted by theory.¹⁰

After the genomewide analyses, we estimated genetic variance associated with individual chromosomes, using chromosomewide coefficients of additive relationship. The proportion of additive genetic variance explained by a particular chromosome was estimated in two ways—first, by fitting a full model that included effects due to a single chromosome and a reduced model in which no chromosomal effects were fitted, and, second, by fitting a full model containing effects for all 22 autosomes and a reduced model that fitted 21 autosomes only. Table 1 shows that, for the individual-chromosome analyses, 6 of 22 estimates of chromosomal heritability were significantly different from zero at P<.05 and of these 3 at P<.01. The six most significant chromosomes were, in order of the size of the test statistic, 17, 4, 3, 18, 15, and 8. This order is not the same as that of estimated chromosomal heritability, because SEs of estimates are larger for longer chromosomes.¹⁰ The estimate of the proportion of variance due to nongenetic family effects (f²) in the single-chromosome analyses captures the variation due to the other autosomes not fitted—for all 22 estimates, the sum of the estimates of f² and (1/2)h² was ∼0.459, the observed overall sibling correlation. Very similar estimates and test statistics were obtained from a full model with 22 additive genetic-variance components, from which chromosomal heritabilities were dropped one by one (table 1), consistent with the absence of any large between-chromosome epistatic effects.

Table 1. .

Estimates of Variance Proportions from Single-Chromosome Analyses and a Joint Analysis of All 22 Autosomes

	Single-Chromosome Analyses					Combined-Chromosome Analysis
Chromosome	f2a	h2ib	e2c	LRTd	P	h2i	LRTe	P
1	.4285	.0607	.5108	1.201	.137	.0633	1.418	.117
2	.4525	.0131	.5344	.065	.399	.0097	.037	.424
3	.4023	.1134	.4843	5.704	.008	.1160	6.269	.006
4	.4036	.1124	.4840	5.938	.007	.1082	5.705	.008
5	.4458	.0264	.5278	.319	.286	.0196	.191	.500
6	.4336	.0506	.5158	1.294	.128	.0508	1.370	.500
7	.4284	.0616	.5100	2.019	.078	.0630	2.230	.068
8	.4234	.0708	.5058	2.778	.048	.0856	4.172	.021
9	.4482	.0216	.5302	.277	.299	.0325	.663	.500
10	.4590	.0000	.5410	.000	.500	.0000	.000	.500
11	.4590	.0000	.5410	.000	.500	.0000	.000	.500
12	.4365	.0451	.5184	1.121	.145	.0489	1.434	.500
13	.4545	.0089	.5366	.056	.406	.0006	.000	.500
14	.4427	.0323	.5250	.728	.197	.0185	.246	.500
15	.4241	.0703	.5056	3.353	.034	.0760	4.028	.022
16	.4556	.0069	.5375	.035	.426	.0180	.251	.308
17	.4023	.1142	.4834	9.019	.001	.1124	8.967	.001
18	.4237	.0703	.5060	3.753	.026	.0622	3.013	.041
19	.4437	.0309	.5253	.759	.192	.0317	.840	.500
20	.4575	.0031	.5395	.008	.464	.0037	.012	.456
21	.4590	.0000	.5410	.000	.500	.0000	.000	.500
22	.4590	.0000	.5410	.000	.500	.0000	.000	.500
Total	…	.9126	…	38.427	…	.9205	40.846	…

^aProportion of variance due to sibling resemblance not accounted for by single-chromosomal genetic effects.

^bProportion of variance due to additive genetic effects on the chromosome.

^cProportion of variance due to individual environmental effects.

^dThe likelihood-ratio test (LRT) statistic from comparing a full model fitting three variance components with a reduced model fitting two variance components. The P value was calculated assuming that the LRT statistic is distributed as 0 or χ²₁, each with a probability of 1/2.

^eThe LRT statistic from comparing a full model fitting 24 variance components (22 additive genetic, 1 common environmental, and 1 residual) with a reduced model fitting 23 variance components, by dropping the ith additive genetic-variance component. The P value was calculated in the same way as that in the single-chromosome analyses.

We estimated variance on the X chromosome separately from the autosomes and separately for brother-brother, sister-sister, and brother-sister pairs, because the expected additive genetic covariance between siblings depends on their sex and on assumptions regarding dosage compensation.²⁰ There was no evidence of additive genetic variance for height on the X chromosome for all three groups. The estimates of the proportion of variance due to additive effects on the X chromosome was 0.007 in brother-brother pairs (P=.47), 0.081 in sister-sister pairs (P=.39), and 0.00 in brother-sister pairs (P=.50).

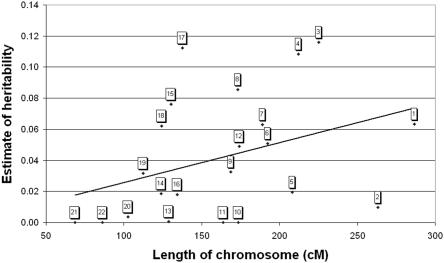
Figure 1 shows the relationship between the genetic length of the chromosome and the estimate of the proportion of additive genetic variance attributed to it in the single-chromosome analyses. In general, the longer the chromosome, the more variation it explains. A weighted least-squares regression was performed, with use of the empirical variance of chromosomal additive coefficients as weights, because this variance is inversely proportional to the sampling variance of the estimate of heritability.¹⁰ The relationship was highly statistically significant in a no-intercept model (F test, P<.0001), and adding an intercept after the regression was not statistically significant (P=.683). The slope of the regression line (0.03 heritability per 100 cM) is consistent with what would be expected if variance were apportioned according to genetic length, with the assumption of 0.86 for the overall heritability and a total sex-averaged map length of 2,864 cM for the autosomes.¹⁷ The correlation (r=0.23) between our estimates of chromosomal heritability and the number of genes per chromosome, obtained from Ensembl build 36, was smaller than the correlation with chromosomal length. The estimates and log-likelihoods of models in which all 22 additive genetic components were fitted were compared with those for the model in which a single genomewide additive genetic component was fitted. The drop in the log-likelihood of the data was 19.2 (P=.57, χ² test with 21 df), which means that the more parsimonious model of variance contributed by chromosomes proportional to their length was not rejected.

Figure 1. .

Estimate of chromosomal heritability from a joint analysis of all 22 autosomes (labeled on graph) as a function of the genetic length of the chromosome. The figure shows that there is a relationship between the genetic length of a chromosome and the amount of variance it explains. P<.0001 for the regression coefficient from a weighted least-squares analysis if no intercept is fitted. P=.683 if an intercept is fitted after the regression.

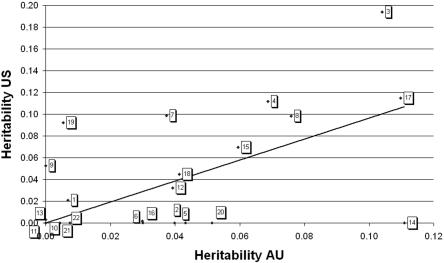
What is the minimum number of chromosomes needed to explain genetic variance for height? To address this question, we ordered chromosomes according to the amount of genetic variance they explained from the joint analysis (table 1) and, in a stepwise procedure, added one chromosome at a time. We compared the log-likelihoods, stopping when the addition of an extra chromosome did not improve the fit after accounting for the number of parameters in the model. To compare models, we used Akaike’s information criterion (AIC), calculated as −2(difference in log-likelihood) + 2(number of additive genetic-variance components), between the model and the null model of no additive genetic-variance components. In all models, a nongenetic family effect (f²) was fitted. The best and most parsimonious model, based on AIC, includes six chromosomes: 17, 4, 3, 18, 15, and 8, in order of statistical significance. The scaled AIC values for fitting 1–8 chromosomes were −7.02, −10.41, −13.73, −15.35, −16.36, −19.09, −19.03, and −18.51, with a minimum of six fitted genetic-variance components. Hence, our data indicate that at least 6 but as many as 22 chromosomes may contribute to additive genetic variation for height. For internal validation, we estimated the proportion of additive genetic variance attributable to each chromosome separately for the two largest data sets (AU and US). Figure 2 shows that the estimates are positively correlated. The slope of the regression line for the 22 pairs of heritability estimates in a no-intercept model is close to unity (0.96) and is highly significantly different from zero (P<.0001), which indicates that the estimates are generally similar across the two data sets. The partial correlation between the heritability estimates after conditioning on the length of the chromosome remained positive and significant (partial r=0.54; P=.011, two-sided), supporting the consistency of heritability estimates across data sets. Variable heritability estimates between chromosomes in excess of sampling variation imply that chromosomes do not contribute equally to additive genetic variance, even after an adjustment for their length.

Figure 2. .

Relationship between heritability estimates from the AU and US data sets. There is a highly significant correlation between the estimates of chromosomal heritability from the two data sets (no-intercept model, P<.0001; model with intercept, P=.009). The relationship remains significant when conditioning on the length of the chromosome (partial correlation 0.540; P=.011, two-sided).

We next investigated whether the proportion of variance explained by an autosome in our data is correlated with the number of times that suggestive or significant linkage²¹ has been reported for that chromosome in the literature, excluding reports that are partially or wholly based on the data in this study. For each chromosome, the number of LOD scores >1.9, defined as being “suggestive” of linkage,²¹ were counted from reported whole-genome linkage scans for height.^22–30 From these scans, there were 2, 7, 5, 2, and 6 chromosomes for which 0, 1, 2, 3, and 4 linkages were reported, respectively, for an average of 2.1 linkages per autosome. We found a positive and significant correlation between our estimate of chromosomal heritability and the number of reported linkages from independent studies (Spearman’s nonparametric rank correlation 0.586; P=.002, one-tailed). This relationship remained significant after a linear adjustment of the latter for the length of the chromosome (P=.013). For three of the six most significant chromosomes in our data—namely, 3, 4, and 15—there have been at least three independent reports of suggestive or significant linkage, although, for our most significant chromosome (17), there has been only a single report of suggestive linkage in the literature. Counting the number of peak LOD scores from the literature may be an inaccurate quantification of assessing the importance of individual chromosomes in explaining variation because of reporting bias and because more false-positive results are likely to be reported for longer chromosomes. Nevertheless, even after an adjustment for chromosome length and despite the large sampling errors of estimates, we found a significant (but not perfect) relationship between our estimates of chromosomal heritability and the number of times suggestive or significant linkage had been reported.

To our knowledge, this is the first attempt to attribute additive genetic variation for a complex trait in humans to specific chromosomes by partitioning the total variance. We estimate that additive genetic variation for height in humans is contributed by all autosomes, with a minimum of six that are responsible, and that there is no significant evidence against the hypothesis that all chromosomes contribute to genetic variance in proportion to their length. For five of these (chromosomes 3, 4, 8, 15, and 18), there have been multiple independent reports of linkage in the literature.

Estimates of the effects of individual chromosomes on variation in a quantitative trait have been reported for Drosophila,^31,32 and a method to estimate variance associated with whole chromosomes was proposed for experimental line crosses.³³ For human pedigrees, a method to estimate the contribution of chromosome regions or whole chromosomes to variation in a quantitative trait, by the estimation of IBD sharing of sibling pairs from (sparse) marker data, was described elsewhere.³⁴ The principle of genome partitioning and whole-genome analysis, as a multistage approach toward individual QTL mapping, was proposed by Schork.¹¹ We have performed the first large-scale application of such methods to the quantitative trait height and have shown how additive genetic variance in three populations is distributed over chromosomes.

If indeed all chromosomes contribute variance in proportion to their length, then the best-case scenario for gene mapping is that all of them harbor a single QTL. For such an “average” QTL that explains, say, 3.9% (∼0.90 of 23) of the phenotypic variance, a linkage study with 57,830 sib pairs would be needed to detect it with a probability of 0.80 at a type I error rate of 0.0001.³⁵ This is much larger than the sample sizes in all reported genomewide linkage studies for height in humans. The largest study comprises data from ∼4,000 equivalent full-sib pairs plus >10,000 more-distantly related (and therefore less informative) relative pairs, with approximately sufficient power to detect QTLs explaining 10% of the phenotypic variance in a genome linkage scan.¹³ A number of genome linkage scans have been reported with smaller sample size (typically <1,000 sibling pairs), and a number of loci, notably those on chromosome 9 and on the X chromosome, appear to be “replicated.”^14,24–27 There is no evidence of genetic variation associated with chromosome 9 or with the X chromosome in our study. The study by Liu et al.,¹³ who reported significant linkage results on chromosomes 9 and X, was based on large extended pedigrees, whereas, in our study, we have extracted the linkage information from only the full-sibling pairs from that sample. Large pedigrees contain many more contrasts between relatives and therefore have more power to detect a QTL than does an analysis based on the full-sib pairs only. Statistical replication in linkage studies for complex traits is problematic because of the imprecision with which loci are mapped.³⁶ Most of the reported studies, apart from that by Liu et al.,¹³ are characterized by small sample size and by analysis of data for males and females separately, thereby effectively creating even smaller samples. There is some evidence of a sex-by-genotype interaction for height in humans,^37,38 but the additive genetic correlation across the sexes is ∼0.8–0.9,³⁸ so we would expect that most trait loci have similar effects in males and females. From the brother-brother, sister-sister, and brother-sister correlations in our data—0.494, 0.479, and 0.435, respectively—and with the assumption of a pure additive model of family resemblance, we estimate a genetic correlation coefficient across the sexes of 0.435/√(0.494×0.479)=0.894.

Our results have implications for GWA studies for height and other complex traits, including disease. GWA studies are typically powered to detect loci that explain at least 0.5%–1% of the phenotypic variation. If the total genetic variance explained per chromosome is ∼5%, this puts an upper bound to the effect sizes that can be detected. Many complex traits, including most diseases, have lower heritabilities than that of height, typically 30%–50%; so, if the genetic variance for these complex traits is distributed over all chromosomes, individual chromosomes will explain only of the order of 1%–3% of the phenotypic variation. Further, if the partitioning of variation across chromosomes, implying many trait loci, can be extrapolated to the partitioning of variation on an individual chromosome (for which we currently have no evidence), then the effect sizes at individual loci or over small intervals may become too small to be detected. In the near future, we will be able to test these hypotheses for quantitative traits, using GWA studies that are currently being conducted. From our study, we predict that, if GWA studies of height are successful in locating significant loci, then the associated variants are likely to be on chromosomes 3, 4, 8, 15, 17, and 18.

The main limitation of our study, as in most studies of the genetics of complex traits in humans, is sample size. Despite having a sample of >11,000 sibling pairs with genomewide marker data and a highly heritable phenotype, we have insufficient power to estimate precisely the contribution of each chromosome to genetic variance and to estimate nonadditive genetic variance. However, since height is a phenotype that is easy to measure and is collected in many cohort studies, and since researchers are willing to collaborate to increase sample size, it should be feasible in the near future to further dissect quantitative genetic variation for height by linkage and/or by association with the use of sample sizes of tens of thousands of individuals.

In conclusion, with a large sample size of 11,214 sibling pairs, we estimated how genetic variance is apportioned in the genome. The hypothesis that chromosomes explain additive genetic variance in proportion to their length could not be rejected in our data. Despite the recent suggestion that variation due to epistasis is too-often neglected in complex-trait studies,³⁹ we found no evidence of any nonadditive genetic variance for height, the complex trait we studied. Our results imply, at least for the quantitative trait height in humans, that genetic variation can be explained by many loci distributed over all the autosomes with an additive mode of gene action.