Family-Based Association Tests for Genomewide Association Scans

Abstract

With millions of single-nucleotide polymorphisms (SNPs) identified and characterized, genomewide association studies have begun to identify susceptibility genes for complex traits and diseases. These studies involve the characterization and analysis of very-high-resolution SNP genotype data for hundreds or thousands of individuals. We describe a computationally efficient approach to testing association between SNPs and quantitative phenotypes, which can be applied to whole-genome association scans. In addition to observed genotypes, our approach allows estimation of missing genotypes, resulting in substantial increases in power when genotyping resources are limited. We estimate missing genotypes probabilistically using the Lander-Green or Elston-Stewart algorithms and combine high-resolution SNP genotypes for a subset of individuals in each pedigree with sparser marker data for the remaining individuals. We show that power is increased whenever phenotype information for ungenotyped individuals is included in analyses and that high-density genotyping of just three carefully selected individuals in a nuclear family can recover >90% of the information available if every individual were genotyped, for a fraction of the cost and experimental effort. To aid in study design, we evaluate the power of strategies that genotype different subsets of individuals in each pedigree and make recommendations about which individuals should be genotyped at a high density. To illustrate our method, we performed genomewide association analysis for 27 gene-expression phenotypes in 3-generation families (Centre d'Etude du Polymorphisme Humain pedigrees), in which genotypes for ∼860,000 SNPs in 90 grandparents and parents are complemented by genotypes for ∼6,700 SNPs in a total of 168 individuals. In addition to increasing the evidence of association at 15 previously identified cis-acting associated alleles, our genotype-inference algorithm allowed us to identify associated alleles at 4 cis-acting loci that were missed when analysis was restricted to individuals with the high-density SNP data. Our genotype-inference algorithm and the proposed association tests are implemented in software that is available for free.

Rapid advances in genotyping technology and the availability of very large inventories of SNPs are making new strategies for genetic mapping possible.^1–3 It is now practical to examine hundreds of thousands of SNPs, representing a large fraction of the common variants in the human genome,^4,5 in very large numbers of individuals. Genetic association studies, which traditionally focused on relatively small numbers of SNPs within candidate genes or regions, can now be performed on a genomic scale.

These technological advances, which are revolutionizing human genetics, will greatly impact analytical strategies for family-based association studies. For example, some of the most popular techniques for association analysis of family data are the transmission/disequilibrium test and its extensions,^6–10 which focus on the transmission of alleles from heterozygous parents to their offspring. The strategy results in association tests that are robust to population stratification, even when a single marker is examined, at the cost of a substantial loss in power on a per-genotype basis.^11,12 Loss of power occurs because these methods rely on a single marker to simultaneously provide evidence of association and guard against population stratification. When genotype data are available on a genomic scale, methods that use multiple markers to evaluate the effects of population structure, such as genomic control¹³ or structured association mapping,¹⁴ are likely to provide a more cost-effective way to guard against population stratification. Thus, as association studies performed on a genomic scale become the norm, we expect that association tests that focus on allelic transmission from heterozygous parents will be replaced by tests that use genomic data to control for stratification.

Another feature that we expect will become important in association tests in the future is the ability to incorporate phenotypes of relatives that are not directly measured for the marker of interest when evidence of association is evaluated.^15–17 Since related individuals share a large fraction of their genetic material, genotypes for one or more individuals in a family can be used to estimate genotypes of their relatives. If flanking-marker data are available, missing genotypes often can be imputed with very high accuracy, and the imputed genotypes provide substantial gains in power.¹⁵ However, even without flanking-marker data, genotypes of relatives can be estimated and used to increase the power of genetic association studies.¹⁷ Unfortunately, most of the currently available family-based association tests consider only the phenotypes of individuals for whom genotype data are available.

Here, we describe two efficient approaches to testing for association between a genetic marker and a quantitative trait that incorporate phenotype information for relatives and that readily allow genomic data to be used to control for stratification. In one approach, evidence of association is evaluated within a computationally demanding maximum-likelihood framework. In another approach, evidence of association is evaluated using a rapid score test that substantially reduces computational time at the expense of a slight loss of power. When evidence of association at a genetic marker is evaluated, both approaches not only examine individuals for whom genotype and phenotype data are available, but also examine the phenotypes of their relatives, if available. In addition, both approaches can use genotype data at flanking markers to improve estimates of unobserved genotypes and to further increase power. The proposed approaches do not focus on alleles transmitted from heterozygous parents. Instead, to control for stratification in admixed samples, they rely on estimates of the ancestry of each individual to be provided as covariates. These estimates can be computed from genomic data.^14,18 Our approaches can accommodate many distinct pedigree configurations (each with potentially different subsets of genotyped and phenotyped individuals), and, in the “Results” section, we illustrate some of the possibilities through the analysis of simulated and real data sets.

Methods

Definitions

We consider a phenotype of interest, measured in a set of pedigrees, each including one or more related individuals. We let Y_ij and x_ij denote the observed trait and covariates, respectively, for individual j in family i. Similarly, we let G_ijm denote the observed genotype at marker m for individual j in family i. Different amounts of data may be available or missing for each individual. For example, for some individuals, both phenotype and genotype data may be available; for others, only phenotype data or only genotype data may be available; and, for yet others, neither may be available. Further note that, in each individual for whom genotype data are available, genotypes may be available for only a subset of markers.

Model for Association

For each of the genotyped SNP markers, we are interested in testing whether observed genotypes and phenotypes are associated. For the SNP being tested, we label the two alleles “A” and “a” and define a genotype score, g_ijm, as 0, 1, or 2, depending on whether G_ijm=a/a, A/a, or A/A, respectively. To avoid unnecessary cumbersome notation, and because we evaluate the evidence of association one SNP at a time, we drop the index m in our presentation below. We consider the model

Here, μ is the population mean, β_g is the additive effect for each SNP, and β_x is a vector of covariate effects. Recall that the additive genetic effect corresponds to the average change in the phenotype when an allele of type a is replaced with an allele of type A (for details, see the work of Boerwinkle et al.¹⁹). To allow for correlation between different observed phenotypes within each family, we define the variance-covariance matrix Ω_i for family i as

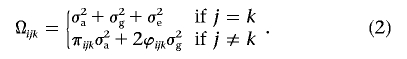Here, the parameters σ²_a, σ²_g, and σ²_e are variance components^20–22 defined to account for linked major gene effects, background polygenic effects, and environmental effects, respectively. As usual, π_ijk denotes identical-by-descent (IBD) sharing between individuals j and k at the location of the SNP being tested, and ϕ_ijk denotes the kinship coefficient between the same two individuals. The model defined in equations (1) and (2) or very similar models form the basis of many family-based association tests.^9,12 These tests perform well when SNP genotypes are available for all (or nearly all) phenotyped individuals, and, below, we extend two of these tests to accommodate individuals for whom genotypes at the SNP being tested are missing. First, we show how estimates of unobserved genotypes can be obtained. Then, we show how these estimates can be incorporated into variance-components–based likelihood-ratio and score tests.

Estimating Unobserved Genotypes

High-throughput SNP genotyping data can be costly and time consuming to generate. When data of this type are generated only for a subset of individuals in each family, it is desirable to estimate genotypes for other individuals in the family, so as to incorporate all available phenotype information in tests of association. One way to accomplish this is to estimate a conditional distribution of the missing genotypes for every individual in the family. In addition to the observed genotypes, this conditional distribution will depend on a vector of intermarker recombination fractions, θ, and a vector of allele frequencies for each marker, F. The intermarker recombination fractions θ can be obtained from one of the publicly available genetic maps^23,24 or can be estimated from physical maps, by use of the approximation 1 cM≈1 Mb.^23,24 Our software implementation can rapidly calculate maximum-likelihood allele-frequency estimates for each locus in most small pedigrees.²⁵

Consider the situation in which G_ijm (the genotype at marker m for individual j in family i) is unobserved, and let G_i denote all the observed genotype data for family i. Let Pr(G_i|θ,F) be a function that provides the probability of the observed genotypes G_i conditional on a specific vector of intermarker recombination fractions θ and allele frequencies F. This function can be calculated using the Elston-Stewart²⁶ or Lander-Green²⁷ algorithms, or it can be approximated using Monte-Carlo methods.^28,29 Then, note that

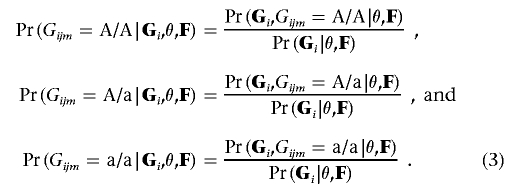One approach¹⁵ for dealing with unobserved genotypes is to check whether any of these conditional probabilities exceeds a predefined threshold (say, 0.99) and then to impute the corresponding genotype. Although this approach would work well in some settings, it could still result in the discarding of useful information. Instead of imputing the most likely genotype, we impute the expected genotype score, 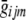, which we define as

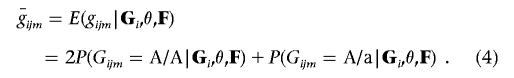As detailed below, whenever a genotype is not observed, this expected genotype score 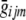can be used in place of the observed genotype g_ijm. Whatever approach is used to calculate the likelihood of the different genotype configurations, note that all genotype configurations whose likelihoods are evaluated differ by only one or two genotypes; thus, many portions of the likelihood calculation can be reused. By use of our implementation of the Lander-Green algorithm,^25,30 these expected genotype scores can be calculated very rapidly in most small pedigrees (typically, only a few seconds are required to calculate expected genotype scores for ∼500,000 markers in a small sibship). The Lander-Green algorithm assumes that the likelihood calculation can be updated one marker at a time and that its complexity increases exponentially with pedigree size. For larger pedigrees (e.g., those with >15 individuals), we have implemented an Elston-Stewart version of the approach, complete with genotype elimination.³¹ The Elston-Stewart algorithm is designed for pedigrees with no inbreeding and assumes that the likelihood calculation can be factored by individual. Its complexity increases exponentially with the number of markers being analyzed, so that only a subset of the available flanking markers can be used to estimate each unobserved genotype (typically, 5–10 flanking markers can be used, depending on the pattern of missing data in the pedigree). Both implementations are available with source code from our Web sites (Ghost and Merlin).

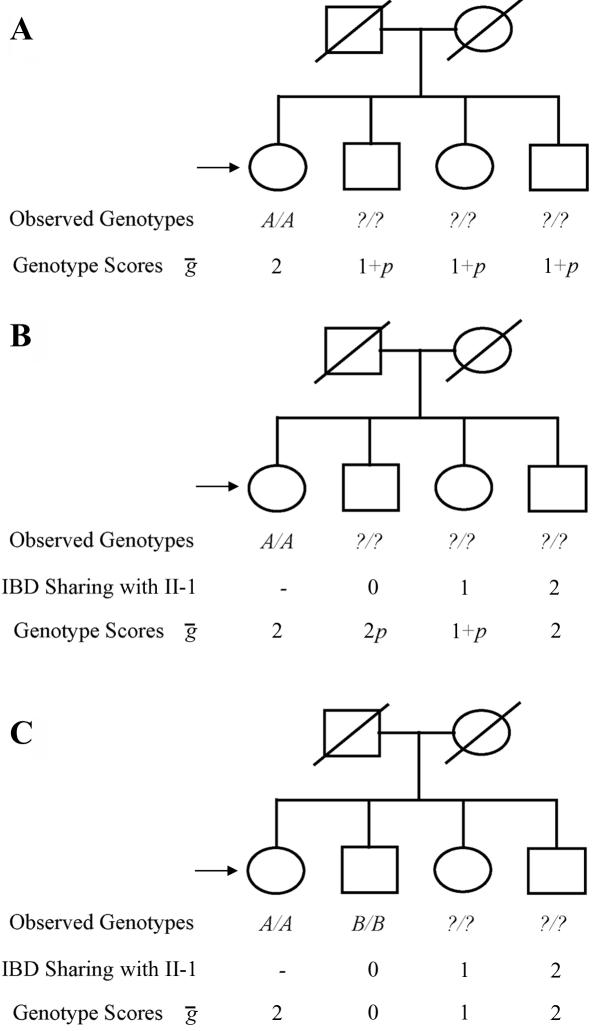
Figure 1 provides an example of how the expected genotype scores are coded. In figure 1A, only the first sibling is genotyped, and no genotype information is available for the three siblings. Thus, the first sibling is assigned a genotype score of 2 (corresponding to two copies of allele A), whereas the other siblings are assigned identical genotype scores of 1+p (where p is the population frequency of allele A). In figure 1B, information at flanking markers is available for all individuals, specifying IBD sharing patterns in the family and resulting in distinct expected genotype scores for each of the siblings (note that, in this case, genotypes could only be inferred for the fourth sibling). In figure 1C, genotype information at the candidate marker is available for one additional sibling, and all genotype scores become integers. In the situation depicted in figure 1C, it would actually be possible to impute genotypes for the third and fourth siblings as A/a and A/A.

Figure 1. .

Exemplar scoring of expected genotype scores. In each panel, the first sibling (individual II-1) is marked with an arrow. In panel A, only the first sibling is genotyped, and no flanking-marker data are available. In panel B, hypothetical flanking-marker data are available and can be used to characterize IBD sharing between the genotyped individual and her siblings. In panel C, two individuals are genotyped, providing further information.

Extended Model for Association

To accommodate individuals with missing genotype data, we extend our model by replacing equation (1) with

In this setting, although the above equality holds, the variance-components model given in equation (2) is only approximate (because the variance of each Y_ij around E(Y_ij) will be slightly smaller when the genotype score is known and the marker being tested is associated with the trait than when the genotype score is estimated). However, we note that (i) simulations suggest our method appears to perform correctly and (ii) since most genotypes will have no impact or only a small impact on the trait, the differences between our approximation and more-accurate but cumbersome approaches should be slight.

Tests of Association

One natural way to test association is to consider the multivariate normal likelihood

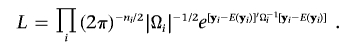Here, n_i is the number of phenotyped individuals in family i and |Ω_i| is the determinant of matrix Ω_i. The likelihood can be maximized numerically, with respect to the parameter μ and the coefficients β_g and β_x—which together define the expected phenotype vector for family i, E(y_i)—and the variance components σ²_a, σ²_g, and σ²_e—which together define the variance-covariance matrix for family i, Ω_i. To test for association, we first maximize the likelihood under the null hypothesis with the constraint that β_g=0 and denote the resulting likelihood as L₀. We then repeat the procedure without constraints on the parameters, to obtain L₁. Then, a likelihood-ratio test (LRT) statistic that is asymptotically distributed as χ² with 1 df can be used to evaluate the evidence of association:

The LRT statistic above requires that L₀ and L₁ be maximized numerically for each SNP, a procedure that can become computationally prohibitive on a genomewide scale. Maximization of L₀ is required because estimates of σ²_a depend on the observed patterns of IBD sharing at each location. When available computing time is limited, an alternative approach is to first fit a simple variance-components model to the data (with parameters μ, β_x, σ²_g, and σ²_e but without parameters β_g and σ²_a). This model provides a vector of fitted values for each family, which we denote E(y_i)^(base), and an estimate of the variance-covariance matrix for each family, which we denote Ω^(base)_i. Using these two quantities, we define the score statistic

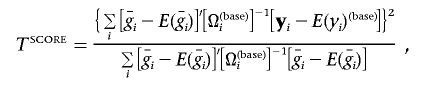where 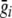is a vector with expected genotype scores for each individual in the ith family, calculated conditional on the available marker data, and 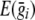is a vector with identical elements that give the unconditional expectation of each genotype score. This expectation is 2p, or twice the frequency of allele A at the SNP being tested. The value 2p arises from the assumption of Hardy-Weinberg equilibrium in the population; before conditioning on genotypes of related individuals, we have probability p² of observing genotype A/A and probability 2p(1-p) of observing genotype A/a. Thus, for any i and j, we have 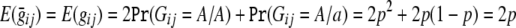. T^SCORE is approximately distributed as χ² with 1 df. In contrast to the T^LRT statistic, which requires one round of numerical maximization for each marker, the T^SCORE statistic requires only a single round of numerical optimization to estimate Ω^(base)_i and E(y_i)^(base). Thus, the T^SCORE statistic should provide a useful and computationally efficient screening tool for genomewide studies. In our preliminary analyses, it allows genomewide association scans in data sets that include thousands of individuals in modest-sized pedigrees (⩽15 individuals) to be completed within a few hours. It is important to note that the distribution of T^SCORE will deviate from χ² when σ²_a is large. In practice, T^SCORE should be used for an initial screening phase in genomewide studies, and promising findings should be reevaluated with the T^LRT statistic to avoid an excess of false-positive results in regions of strong linkage. The number of promising statistics that can be reevaluated with T^LRT will depend on the available computational resources. We recommend that at least those statistics selected for further follow-up should be evaluated with T^LRT.

Simulations

To evaluate the performance of our approach, we simulated different types of pedigrees and patterns of missing genotype data at the SNP being tested for association. Unless otherwise specified, we simulated a SNP with a minor-allele frequency (MAF) of 0.30 that explained 5% of the trait variance and simulated background polygenic effects that accounted for a further 35% of the trait variability. In addition, we simulated genotype data for a 0.3-cM grid of 50 equally spaced flanking SNPs, each with two equally frequent alleles. This should be approximately analogous to using 10,000 SNP markers across the genome to genotype individuals not selected for high-density scanning. We implemented our simulation engine within Merlin^,25,30 allowing others to easily reproduce our results and simulations. To summarize analyses of simulated data, we report expected LOD scores (ELODs), which were calculated as the average of the LOD scores estimated after analysis of each replicate. As usual, LOD scores were defined as χ²/2ln(10).

Exemplar Data Set

To examine the performance of our method in a real data set, we reanalyzed the data of Cheung et al.³² The original analysis of Cheung et al.³² used genotypes generated by the International HapMap Consortium¹ to search for SNPs that regulate mRNA levels of 27 different transcripts. The analysis focused on individuals for whom both high-density SNP genotype data and gene-expression data were available. These individuals form part of extended 3-generation pedigrees, and measurements of mRNA levels, as well as limited genotype data, are available for many additional individuals in the pedigrees.³³ Thus, we used our approach to combine all the available information (i.e., mRNA levels for 156 individuals, 6,728 SNP genotypes for all 168 individuals, and 864,360 additional SNP genotypes for each of the 90 individuals genotyped by the HapMap Consortium).

Results

Type I Error Rates

Before evaluating power for our proposed approach, we checked type I error rates in a variety of settings, including different family sizes and subsets of genotyped individuals. In each simulated replicate, we tested for association at a SNP in linkage equilibrium with the QTL but tightly linked to it (recombination fraction θ=0). Table 1 summarizes the performance of the method for nuclear families with four offspring each and with different subsets of genotyped individuals (results were similar for other family configurations, including nuclear families with different numbers of offspring and a variety of small 3-generation pedigrees; data not shown). To generate each row in the table, we examined 100,000 replicates, each with a simulated QTL explaining 5% of the quantitative-trait variation and a total trait heritability of 40%. It is clear from the table that both the proposed LRT and score test (SCORE) have type I error rates very close to their target α levels. In fact, when the 1.8 million replicates that were analyzed to generate table 1 are considered together, we observed average type I error rates of 0.00008 (LRT) and 0.00009 (SCORE test) at the α=0.0001 level. In this combined set of 1.8 million replicates, type I error rates for both tests also appeared to be well controlled at more-stringent significance levels. Specifically, we observed 15 replicates significant at α=10^-5 (vs. 18 expected) and none significant at α=10^-6 (vs. 1.8 expected). Marker spacing and allele frequencies did not appear to have a significant impact on type I error rates for the LRT and SCORE test statistics.

Table 1. .

Type I Error Rates for Nuclear Families with Four Offspring and Different Subsets of Individuals Genotyped at the Candidate SNP (100,000 Simulations)

	Type I Error Rate when
	α = .01				α = .001				α = .0001
		Imputed Genotypes				Imputed Genotypes				Imputed Genotypes
Family Structure and No. of Children Genotyped at the Candidate SNP	Observed Genotypes LRT	SCORE	LRT	Combined	Observed Genotypes LRT	SCORE	LRT	Combined	Observed Genotypes LRT	SCORE	LRT	Combined
Both parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4 children	.010	.011	.010	.010	.0012	.0013	.0012	.0012	.00007	.00008	.00007	.00007
3 children	.010	.010	.010	.009	.0010	.0011	.0009	.0009	.00005	.00012	.00010	.00009
2 children	.010	.010	.010	.010	.0009	.0012	.0011	.0011	.00011	.00012	.00011	.00011
1 child	.010	.011	.010	.010	.0009	.0009	.0008	.0008	.00012	.00007	.00007	.00006
0 children	.010	.010	.010	.009	.0008	.0009	.0009	.0009	.00005	.00007	.00009	.00007
One parent genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4 children	.009	.010	.010	.010	.0009	.0011	.0009	.0009	.00005	.00008	.00010	.00007
3 children	.010	.011	.010	.010	.0011	.0011	.0010	.0010	.00011	.00008	.00007	.00006
2 children	.010	.011	.010	.010	.0010	.0012	.0011	.0010	.00013	.00006	.00006	.00006
1 child	.009	.011	.010	.010	.0009	.0010	.0009	.0009	.00009	.00010	.00008	.00008
0 children	.010	.010	.010	.010	.0011	.0008	.0008	.0008	.00011	.00007	.00011	.00007
No parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4 children	.009	.010	.009	.009	.0009	.0011	.0010	.0010	.00014	.00007	.00006	.00006
3 children	.010	.011	.010	.010	.0011	.0011	.0009	.0009	.00008	.00010	.00009	.00009
2 children	.009	.010	.009	.009	.0008	.0009	.0009	.0008	.00004	.00008	.00008	.00007
1 child	.010	.011	.010	.010	.0010	.0010	.0009	.0009	.00009	.00012	.00010	.00010
No parents genotyped; phenotype and flanking-marker data available for offspring only:
4 children	.010	.011	.010	.010	.0009	.0010	.0009	.0009	.00012	.00014	.00012	.00012
3 children	.009	.010	.010	.009	.0010	.0009	.0008	.0008	.00005	.00003	.00003	.00003
2 children	.010	.010	.009	.009	.0010	.0010	.0008	.0008	.00007	.00010	.00009	.00009
1 child	.010	.011	.010	.010	.0009	.0009	.0007	.0007	.00006	.00008	.00008	.00007

When varying the genetic model, we observed that the type I error rate for the SCORE test increased slightly when the effect of the tightly linked QTL was large (e.g., when the simulated QTL explained >20% of the trait variance). This is expected because the SCORE test does not take IBD sharing into account when modeling the correlation between relatives. In practice, we recommend that the SCORE test be used as a computationally efficient screening tool for genomewide studies and that interesting results (i.e., those for which the SCORE test P value is <.01 or some other appropriate threshold) be followed up with the LRT. In our simulations, this two-stage procedure resulted in power and type I error rates equivalent to application of the LRT to the entire data set.

Power for Sib-Pair Families

After evaluating type I error rates, we proceeded to evaluate the power of our proposed approach in small families and its efficiency for different subsets of genotyped individuals. Table 2 shows the expected LOD scores for the LRT and SCORE statistics when association was evaluated in a sample of 350 nuclear families, each with two offspring. In each row, a different subset of individuals was genotyped for the marker being tested for association. By comparison of test statistics calculated using only genotyped individuals (table 2, columns 2 and 4) with those calculated using estimated genotype counts for other individuals (table 2, columns 3 and 5), it is clear that genotype inference increases power, irrespective of whether the LRT or SCORE test is used (increases in expected LODs ranged from ∼15% to ∼32%, depending on the individuals selected for genotyping when flanking-marker data are available).

Table 2. .

Power for Nuclear Families with Two Offspring and Different Sets of Individuals Genotyped at the Candidate SNP^[Note]

	Power (α=10-7) for Genotypes				ELOD for Genotypes				ELOD per Genotype (×1,000) for Genotypes
	Observed		Imputed		Observed		Imputed		Observed		Imputed
Family Structure and No. of Children Genotyped at the Candidate SNP	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT
Both parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and both siblings:
2 children	99.4	99.4	99.4	99.4	13.31	13.68	13.31	13.68	9.51	9.77	9.51	9.77
1 child	95.3	96.2	99.0	99.1	10.72	11.09	12.80	13.15	10.21	10.56	12.19	12.52
0 children	75.2	76.4	87.8	88.9	7.81	8.05	9.11	9.41	11.16	11.50	13.01	13.44
One parent genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and both siblings:
2 children	95.1	95.6	98.4	98.4	10.46	10.73	12.08	12.39	9.96	10.22	11.50	11.80
1 child	68.8	70.7	91.4	91.9	7.40	7.66	9.64	9.84	10.57	10.94	13.77	14.06
0 children	9.7	12.5	19.9	21.2	3.93	4.06	4.66	4.75	11.23	11.60	13.31	13.57
No parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and both siblings:
2 children	68.2	70.2	86.2	86.2	7.39	7.57	8.87	9.05	10.56	10.81	12.67	12.93
1 child	10.8	13.8	34.4	36.9	4.00	4.14	5.50	5.58	11.43	11.83	15.71	15.94
No parents genotyped; phenotype and flanking-marker data available for offspring only:
2 children	68.2	70.1	68.2	70.1	7.39	7.57	7.39	7.57	10.56	10.81	10.56	10.81
1 child	10.8	13.8	25.0	26.6	4.00	4.14	4.88	4.96	11.43	11.83	13.94	14.17

Note.— Power, the ELOD, and the ELOD per genotype were evaluated by executing 1,000 simulations for each cell. A total of 350 families, each with two offspring, were simulated. The associated SNP had MAF of 0.30 and explained 5% of the trait variability. The associated SNP was flanked by 50 SNPs (with 0.3-cM spacing), which were used to help infer missing genotypes. Background polygenic effects accounted for 35% of the trait variability. Simulated data sets were analyzed first with use of only the observed genotypes and then, again, with use of our expected genotype score approach.

In absolute terms, the most powerful approach is to genotype all individuals for the SNP being tested, resulting in an expected LOD of 13.68 (LRT) and power >99% (table 2). However, this is also likely to be the most costly strategy, because it requires the largest genotyping effort. Genotyping the candidate SNP in two parents and one offspring reduces the amount of genotyping required by 25% and results in only a slight decrease in the ELOD, to 13.15 (a 4% decrease from the LRT ELOD), and still retains power >99% (table 2).

Strategies that involve genotyping fewer individuals result in further losses of power but can be even more cost effective on a per-genotype basis. For example, genotyping only one offspring per family results in an ELOD per genotype that is ∼60% higher than when all individuals are genotyped (ELOD of 0.0159 vs. 0.0098 per genotype). This means that, given fixed genotyping resources, it usually will be better to genotype only a few individuals per family in a large number of families than to genotype a subset of the available families more extensively. When two individuals per family are genotyped, the most cost-effective strategy is to genotype one parent and one offspring per family (ELOD of 0.014 per genotype). This choice of individuals provides good information about phases for three of the four haplotypes segregating in the family, and allows our method to take advantage of flanking-marker data to fill in the missing genotypes for the other two individuals. Other choices, such as genotyping two parents or genotyping two siblings, provide less-accurate phase information and result in estimates of the missing genotypes that are less good.

The last two rows of table 2 show that the method is attractive even when parental data are not available. In this case, when only one child is genotyped, it is very hard to infer the genotype of the other child (because the two will be IBD only 25% of the time). Nevertheless, note that the ELOD per genotype is 0.0108 when both children are genotyped but increases to 0.0142 when only one child is genotyped and our approach is used (an ∼30% increase in efficiency on a per-genotype basis). Further, it is important to note that, although the availability of flanking-marker information clearly improves the performance of our method, the approach is still valuable when flanking-marker data are not available. When we repeated the analysis without flanking-marker data, the ELOD per genotype decreased to 0.0130 when only one child was genotyped, but this is still ∼20% higher than the ELOD of 0.0108 when only the observed genotypes are used in the association analysis. Thus, our approach of using expected genotype scores in the analysis can lead to gains in power even when there is substantial uncertainty about all the missing genotypes.

Power for Larger Nuclear Families

We next evaluated the performance of our method in larger nuclear families, each with four offspring (table 3). In this setting, each genotyped individual provides information about a larger number of ungenotyped individuals, and the potential efficiency gains are larger. Including ungenotyped individuals in the analysis resulted in substantial increases in the expected test statistic (ranging from ∼15% to ∼60%, depending on the subset of individuals selected for genotyping). In addition, for the ELOD on a per-genotype basis, the most effective strategy was again to genotype just one child per family (ELOD per genotype is 0.0159 in the families with two offspring examined [table 2] and is 0.0194 in the families with four offspring examined [table 3]). With a fixed set of 250 families, this strategy provided 36% of the total ELOD for ∼17% (one-sixth) of the genotyping effort. Collecting genotypes for one parent and one offspring per family was also very efficient (ELOD per genotype of 0.0176), providing ∼65% of the total ELOD for ∼33% of the genotyping effort. Finally, note that, when two parents and one offspring are genotyped, ∼92% of the expected test statistic can be recovered for 50% of the genotyping effort.

Table 3. .

Power for Nuclear Families with Four Offspring and Different Sets of Individuals Genotyped at the Candidate SNP^[Note]

	Power (α=10-7) for Genotypes				ELOD for Genotypes				ELOD per Genotype (×1,000) for Genotypes
	Observed		Imputed		Observed		Imputed		Observed		Imputed
Family Structure and No. of Children Genotyped at the Candidate SNP	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT
Both parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4 children	99.5	99.5	99.5	99.5	13.25	13.47	13.25	13.47	8.83	8.98	8.83	8.98
3 children	96.9	97.2	99.5	99.5	11.44	11.70	13.16	13.38	9.15	9.36	10.53	10.70
2 children	90.4	91.2	99.0	99.2	9.62	9.90	12.90	13.11	9.62	9.90	12.90	13.11
1 child	68.9	71.6	98.4	98.5	7.49	7.76	12.21	12.41	9.99	10.35	16.28	16.55
0 children	35.5	37.9	62.0	64.8	5.48	5.65	7.04	7.31	10.96	11.30	14.08	14.62
One parent genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4 children	97.7	97.8	99.4	99.5	11.50	11.66	13.00	13.21	9.20	9.33	10.40	10.57
3 children	91.2	91.4	99.2	99.3	9.63	9.84	12.50	12.69	9.63	9.84	12.50	12.69
2 children	69.4	71.0	97.6	97.6	7.46	7.67	11.32	11.47	9.95	10.23	15.09	15.29
1 child	29.3	33.2	84.7	85.4	5.18	5.38	8.72	8.80	10.36	10.76	17.44	17.60
0 children	2.5	3.5	6.1	7.0	2.84	2.95	3.66	3.75	11.36	11.80	14.64	15.00
No parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4 children	90.3	90.6	97.5	97.7	9.51	9.62	11.43	11.56	9.51	9.62	11.43	11.56
3 children	67.3	69.1	93.6	93.8	7.42	7.56	10.39	10.49	9.89	10.08	13.85	13.99
2 children	29.8	31.6	78.7	78.6	5.22	5.36	8.25	8.29	10.44	10.72	16.50	16.58
1 child	2.5	3.8	24.3	24.3	2.90	3.01	4.86	4.86	11.60	12.04	19.44	19.44
No parents genotyped; phenotype and flanking-marker data available for offspring only:
4 children	90.3	90.6	90.3	90.6	9.51	9.62	9.51	9.62	9.51	9.62	9.51	9.62
3 children	67.3	69.1	86.0	86.4	7.42	7.56	8.89	8.98	9.89	10.08	11.85	11.97
2 children	29.8	31.7	67.5	68.1	5.22	5.36	7.43	7.48	10.44	10.72	14.86	14.96
1 child	2.5	3.8	17.6	18.0	2.90	3.01	4.55	4.55	11.60	12.04	18.20	18.20

Note.— Power, the ELOD, and the ELOD per genotype were evaluated by executing 1,000 simulations for each cell. A total of 250 families, each with four offspring, were simulated. The associated SNP had MAF of 0.30 and explained 5% of the trait variability. The associated SNP was flanked by 50 SNPs (with 0.3-cM spacing), which were used to help infer missing genotypes. Background polygenic effects accounted for 35% of the trait variability. Simulated data sets were analyzed first with use of only the observed genotypes and then, again, with use of our expected genotype score approach.

Additional Simulations

We considered a variety of other configurations for simulated pedigrees, including larger sibships and 3-generation pedigrees. Table 4 summarizes the results for situations in which the associated SNP had a lower or higher MAF (0.05 or 0.50, respectively). The results are in good agreement with the results in table 3, showing that the most-effective genotyping strategies are to examine one offspring (if only one individual per family is genotyped at a high density), one parent and one offspring (two individuals per family), or both parents and one offspring (three individuals per family). In all settings we examined, incorporation of phenotypes of ungenotyped individuals in the analysis increased the power and efficiency (on a per-genotype basis). As expected, power gains were largest in large sibships or 3-generation pedigrees. Nevertheless, even when only a few ungenotyped relatives were available, we found that estimating the missing genotypes provided meaningful increases in power (tables 2 and 3). We also observed that, on average, the LRT statistic was slightly more powerful than the SCORE statistic and that this advantage appeared to be enhanced in larger pedigrees.

Table 4. .

Power in Nuclear Families with Four Offspring when MAF at Associated SNP Is 0.05 or 0.5^[Note]

	Power (α=10-7) for Genotypes				ELOD for Genotypes				ELOD per Genotype (×1,000) for Genotypes
	Observed		Imputed		Observed		Imputed		Observed		Imputed
MAF at Trait-Associated SNP, Family Structure, and No. of Genotyped Children	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT	SCORE	LRT
MAF = .05:
Both parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4	97.8	98.0	97.8	98.0	13.19	13.41	13.19	13.41	8.79	8.94	8.79	8.94
3	97.4	97.4	97.9	98.0	11.42	11.70	13.15	13.37	9.14	9.36	10.52	10.70
2	87.4	88.7	97.8	97.9	9.54	9.82	13.09	13.31	9.54	9.82	13.09	13.31
1	68.3	70.3	97.6	97.7	7.52	7.79	12.92	13.14	10.02	10.38	17.22	17.52
0	36.2	40.2	62.3	65.4	5.66	5.84	7.07	7.35	11.31	11.69	14.14	14.70
One parent genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4	96.5	96.7	97.3	97.5	11.53	11.71	12.99	13.21	9.22	9.37	10.39	10.56
3	88.1	88.9	97.0	97.1	9.56	9.77	12.61	12.81	9.56	9.77	12.61	12.81
2	66.4	68.2	95.9	95.9	7.46	7.67	11.77	11.94	9.94	10.22	15.69	15.92
1	32.1	34.8	88.2	88.4	5.26	5.47	9.83	9.93	10.53	10.93	19.65	19.85
0	3.4	4.4	8.3	9.7	2.91	3.03	3.60	3.68	11.63	12.11	14.39	14.73
No parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4	85.8	85.9	96.7	96.8	9.39	9.52	12.19	12.37	9.39	9.52	12.19	12.37
3	66.8	67.5	94.0	94.2	7.35	7.49	11.10	11.23	9.79	9.98	14.80	14.98
2	29.3	32.3	81.9	82.2	5.23	5.37	8.86	8.93	10.46	10.75	17.72	17.86
1	4.3	5.9	24.0	24.2	2.89	3.01	4.83	4.82	11.56	12.04	19.31	19.28
No parents genotyped; phenotype and flanking-marker data available for offspring only:
4	85.8	85.9	85.8	85.9	9.39	9.52	9.39	9.52	9.39	9.52	9.39	9.52
3	66.8	67.4	82.6	82.7	7.35	7.48	8.88	8.99	9.79	9.98	11.84	11.98
2	29.3	32.3	66.6	67.3	5.23	5.37	7.47	7.54	10.46	10.75	14.95	15.08
1	4.3	5.9	19.7	20.9	2.89	3.01	4.52	4.54	11.56	12.04	18.10	18.16
MAF = .50:
Both parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4	99.2	99.2	99.2	99.2	13.09	13.30	13.09	13.30	8.73	8.87	8.73	8.87
3	96.9	97.3	99.2	99.3	11.48	11.75	12.98	13.19	9.19	9.40	10.39	10.55
2	90.7	91.3	99.2	99.2	9.55	9.83	12.69	12.90	9.55	9.83	12.69	12.90
1	70.2	72.2	98.9	99.0	7.53	7.80	11.89	12.09	10.05	10.40	15.86	16.11
0	35.0	38.1	60.9	63.3	5.50	5.68	6.94	7.21	11.01	11.36	13.89	14.43
One parent genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings
4	97.1	97.0	99.1	99.1	11.55	11.72	12.82	13.02	9.24	9.37	10.25	10.42
3	88.8	89.6	99.0	99.0	9.58	9.79	12.23	12.41	9.58	9.79	12.23	12.41
2	70.8	72.7	96.8	97.0	7.48	7.69	10.95	11.08	9.97	10.25	14.60	14.78
1	29.5	33.7	80.3	80.6	5.16	5.36	8.32	8.39	10.32	10.71	16.63	16.78
0	3.1	4.3	5.7	7.2	2.87	2.98	3.58	3.66	11.48	11.93	14.32	14.65
No parents genotyped at candidate SNP; phenotype and flanking-marker data available for both parents and 4 siblings:
4	89.8	90.0	96.9	97.2	9.41	9.52	11.15	11.27	9.41	9.52	11.15	11.27
3	70.9	72.5	94.0	93.8	7.55	7.69	10.11	10.20	10.06	10.26	13.48	13.59
2	27.3	30.3	76.3	75.4	5.13	5.26	8.04	8.07	10.26	10.53	16.08	16.14
1	2.6	2.9	23.2	23.3	2.88	2.99	4.83	4.82	11.50	11.95	19.32	19.30
No parents genotyped; phenotype and flanking-marker data available for offspring only:
4	89.8	90.0	89.8	90.0	9.41	9.52	9.41	9.52	9.41	9.52	9.41	9.52
3	70.9	72.4	85.0	85.8	7.55	7.69	8.81	8.90	10.06	10.26	11.74	11.86
2	27.3	30.4	66.4	66.3	5.13	5.26	7.34	7.38	10.26	10.53	14.68	14.77
1	2.6	2.9	18.4	17.9	2.88	2.99	4.53	4.53	11.50	11.95	18.12	18.11

Note.— Power, the ELOD, and the ELOD per genotype were evaluated by executing 1,000 simulations for each cell. A total of 250 families, each with four offspring, were simulated. The associated SNP had MAF of 0.05 or 0.50 and explained 5% of the trait variability. The associated SNP was flanked by 50 SNPs (with 0.3-cM spacing), which were used to help infer missing genotypes. Background polygenic effects accounted for 35% of the trait variability. Simulated data sets were analyzed first using only the observed genotypes and then, again, using our expected genotype score approach.

Analysis of Exemplar Data Set

As a complement to the simulation studies presented above, we reanalyzed publicly available data for 27 gene-expression traits.^32,33 The data consist of gene-expression measurements for 156 individuals in 20 3-generation CEPH pedigrees, each with 12–17 individuals. Genotypes for 864,360 SNPs were generated for a subset of 90 individuals in these families in phase I of the International HapMap Project¹ (all individuals genotyped by the HapMap Consortium were in the grandparental or parental generation). Genotypes for 6,728 SNPs for the complete families, including 168 individuals, were also genotyped previously by the SNP Consortium.²³ There are 12 individuals with genotype data but no gene-expression data.

In their original analysis, Cheung et al.³² focused on a subset of unrelated individuals from the grandparental generation to evaluate the impact of each SNP on gene expression, using a simple linear regression. We repeated their analysis, using our approach, first without inference of any missing genotypes (i.e., using only the observed genotypes for individuals in the parental and grandparental generations) and then with use of expected genotype scores for all individuals. To reduce the impact of outliers and nonnormal trait distributions on our analyses, we used quantile normalization to convert each phenotype to approximate normality.³⁴ For computational convenience, we used our implementation of the Elston-Stewart algorithm to infer missing genotypes by use of eight flanking markers. We decided on eight flanking markers to balance computational constraints for our implementation of the Elston-Stewart algorithm (whose complexity increases exponentially with the number of markers) and accuracy of estimated allele counts. By use of exactly the same 3-generation pedigree structure as used by Cheung et al.,³² our simulations showed that eight SNPs with high heterozygosity extracted nearly the same information as did an infinitely dense map of fully informative markers (such that a map of fully informative markers would change test statistics by <3%; authors' unpublished data). Estimation of genotype counts for all individuals and calculation of the T^SCORE statistic at each SNP for all 27 traits took <23 h by use of a 2.33-GHz Pentium Workstation. The analyses were conducted one chromosome at a time and required <256 Mb of RAM.

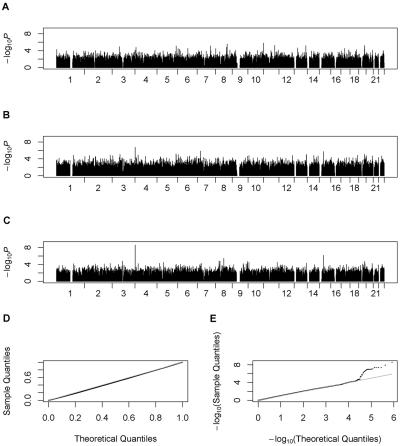
Figure 2 summarizes our results for the analysis of CTBP1 expression level, 1 of the 27 phenotypes analyzed. The CTBP1 gene maps to chromosome 4. Figure 2A shows results for the simplest analysis strategy, which focuses on a subset of 60 unrelated individuals and uses ordinary least-squares regression. This analysis ignores much of the available data and does not provide a clear association signal. Figure 2B shows the use of observed genotypes for the 90 individuals genotyped by the HapMap Consortium¹ and shows a peak of association on chromosome 4 at SNP rs11247978, which is within 18.8 kb of the CTBP1 gene. The peak corresponds to a P value of 1.8×10^-7. Figure 2C provides results for our preferred approach, which uses the expected genotype scores to extract information from relatives of genotyped individuals who themselves may not have been genotyped for the marker of interest. This analysis considers a total of 156 individuals and again provides a clear signal of association on chromosome 4 at SNP rs11247978, with a P value of 2.6×10^-9.

Figure 2. .

Genome scan for CTBP1 expression levels. The gene maps to the beginning of chromosome 4. A, Genome scan using 60 unrelated individuals only. B, Genome scan using all 90 individuals genotyped by the HapMap Consortium. C, Genome scan that augmented the observed genotypes with expected genotype scores for other individuals, resulting in a total sample size of 156 individuals. All analysis were performed using the computationally efficient SCORE statistic. D, Q-Q plot. E, log Q–log Q plot. The plots show that the statistic is behaving adequately.

Figure 2D, which presents a Q-Q plot for the statistics in figure 2C, shows that, overall, the SCORE P values are distributed uniformly between 0 and 1. In figure 2E, the log Q–log Q plot for the statistics in figure 2C focuses attention on the tail of the distribution. There are some clear outliers, with 25 P values <10^-5. Among these, 22 correspond to the cis association signal and map within 100 kb of the CTBP1 gene.

Thus, our proposed association test appears to behave correctly in this real data set. The top associated SNP mapped in cis of the CTBP1 gene in genome scans with use of the SCORE statistic and either the expected genotype scores (fig. 2C) or all available genotypes (fig. 2B) but not when analysis was restricted to a subset of unrelated individuals (fig. 2A). Also note that the contrast between the strength of the cis signal and background noise is clearest in figure 2C, where expected genotypes are used to extract information from individuals with missing genotype data.

A similar pattern was observed for the other traits. Table 5 lists the SNP showing the most significant association with each trait (transcript expression level) when analyses were performed using only a subset of 60 unrelated individuals and ordinary least-squares regression (columns 3–5), when analyses were performed using genotypes for 90 individuals genotyped by the HapMap Consortium for whom gene expression data were available (columns 6–8), and when analyses were performed using all available data by incorporating expected genotype scores into the analysis (columns 9–12). The top SNP association for each transcript was selected by analyzing all available SNPs by use of the SCORE test. P values and variance explained by the top SNP (per trait) were then estimated using the full likelihood model. Since we have scanned the whole genome for association, it is extremely unlikely that the peak of association would occur in cis purely by chance, and we expect that the number of cis signals detected is a reasonable proxy for the relative power of the different analyses.

Table 5. .

Summary of Reanalysis of Data from Cheung et al.,³² with Different Analytical Strategies^[Note]

		Strategy Using Founder Genotypes Only			Strategy Using All Observed Genotypes			Strategy Using Imputed Genotype Scores
Transcript	Chromosome	Top SNP	Distance or Positiona	P	Top SNP	Distance or Positiona	P	Top SNP	Distance or Positiona	P	H2
LRAP	5	rs10051637	25.8 kb	<10−20	rs1981846	10.6 kb	<10−19	rs27307	84.8 kb	<10−28	73.1
POMZP3	7	rs2005354	In transcript	<10−16	rs2005354	In transcript	<10−14	rs2005354	In transcript	<10−22	70.6
IRF5	7	rs7789423	31.1 kb	<10−10	rs6969930	40.2 kb	<10−8	rs10239340	79.0 kb	<10−17	47.4
HSD17B12	11	rs4755741	74.9 kb	<10−8	rs4755741	74.9 kb	<10−10	rs1878851	In transcript	<10−16	42.2
AA827892	20	rs1739646	11.6 kb	<10−8	rs1739646	11.6 kb	<10−11	rs1739646	11.6 kb	<10−16	45.1
RPS26	12	rs2271194	39.7 kb	<10−10	rs2271194	39.7 kb	<10−7	rs2271194	39.7 kb	<10−14	50.6
HLA-DRB2	6	rs9275141	16.5 kb	<10−9	rs9275141	16.5 kb	<10−8	rs9275141	16.5 kb	<10−14	48.2
PSPHL	7	rs2419485	9.0 Mbb	<10−13	rs2419485	9.0 Mbb	<10−9	rs2419485	9.0 Mbb	<10−14	60.5
CPNE1	20	rs6060535	In transcript	<10−7	rs6058296	16.4 kb	<10−9	rs6060578	63.8 kb	<10−13	38.6
CSTB	21	rs880987	28.2 kb	<10−10	rs2276246	14.6 kb	<10−9	rs2838393	37.0 kb	<10−12	32.7
CTSH	15	rs1369324	2.4 kb	<10−6	rs1036938	.2 kb	<10−11	rs1369324	2.4 kb	<10−10	30.6
PPAT	4	rs2161041	Trans, chr 3	<10−6	rs2139512	25.2 kb	<10−6	rs2139512	In transcript	<10−10	37.0
CTBP1	4	rs11246311	Trans, chr 11	<10−5	rs11247978	18.8 kb	<10−6	rs11247978	18.8 kb	<10−9	30.3
CHI3L2	1	rs755467	In transcript	<10−6	rs1325284	In transcript	<10−7	rs2477578	In transcript	<10−9	33.4
IL16	15	rs6698333	Trans, chr 1	<10−5	rs731908	Trans, chr 13	<10−6	rs731908	Trans, chr 13	<10−8	22.6
ZNF85	19	rs1869051	Trans, chr 2	<10−5	rs10454111	In transcript	<10−6	rs11672610	.8 kb	<10−8	25.8
DDX17	22	rs7004029	Trans, chr 8	<10−5	rs10401935	Trans, chr 19	<10−6	rs3756726	Trans, chr 5	<10−6	20.7
GSTM2	1	rs1005932	Trans, chr 2	<10−5	rs1074334	Trans, chr 14	<10−5	rs412543	12.0 kb	<10−6	23.4
TCEA1	8	rs1960350	Trans, chr 11	<10−6	rs1046995	Trans, chr 1	<10−6	rs952194	105.2 kb	<10−6	22.2
GSTM1	1	rs3118590	Trans, chr 9	<10−5	rs9428368	113.6 Mbc	<10−6	rs412543	.5 kb	<10−5	21.6
VAMP8	2	rs1835307	Trans, chr 1	<10−6	rs254677	Trans, chr 5	<10−6	rs3755015	40.7 kb	<10−5	20.8
SMARCB1	22	rs3861946	Trans, chr 1	<10−5	rs1517492	Trans, chr 2	<10−5	rs4497390	Trans, chr 11	<10−5	11.9
ICAP-1A	2	rs4713169	Trans, chr 6	<10−5	rs7739016	Trans, chr 6	<10−6	rs10501853	Trans, chr 11	<10−5	18.4
S100A13	1	rs9586149	Trans, chr 13	<10−6	rs1502430	Trans, chr 16	<10−4	rs2571343	Trans, chr 12	<10−5	16.1
TM7SF3	12	rs7934888	Trans, chr 11	<10−6	rs7934888	Trans, chr 11	<10−5	rs7637623	Trans, chr 3	<10−5	25.2
EIF3S8	16	rs2973361	Trans, chr 5	<10−6	rs878724	Trans, chr 9	<10−4	rs12552044	Trans, chr 9	<10−5	18.1
CGI-96	22	rs1519568	Trans, chr 3	<10−6	rs6765660	Trans, chr 3	<10−5	rs1880693	Trans, chr 11	<10−4	20.0

Note.— The three columns under the first strategy show the marker with strongest association, its position relative to the transcript, and the associated P value when unrelated individuals are selected from each family (the grandparents, for a total of 60 individuals) and are analyzed using linear regression. The next three columns show the marker with strongest association, its position relative to the transcript, and the associated P value when all individuals genotyped by the HapMap Consortium are included in analysis (90 individuals in the grandparental and parental generations). In this instance, our proposed score test but no estimates of missing genotypes were used to perform association analyses. The last four columns summarize the results for our recommended strategy, incorporating estimated genotypes for all individuals. Our score test was used to evaluate all SNPs, and a follow-up analysis of the SNP showing the strongest association was performed using the LRT (which was used to produce the reported P value and the proportion of variance explained by association with each SNP, H²). chr = Chromosome.

^aUnless stated otherwise, the SNPs map to the same chromosome as the transcript.

^bThe rs2419485 SNP and the PSPHL transcript are separated by the centromere of chromosome 7. Other SNPs closer to the transcript are in strong LD with rs2419485 and also show association with expression levels.

^cThis cis association result is probably a false-positive result.

The evidence of association reaches genomewide significance (nominal P=5.7×10^-8, by use of an overall α=0.05 and a Bonferroni correction) for 15 of the 27 expression levels by use of our approach, for 12 expression levels by use of only observed genotypes, and for 10 expression levels by use of genotypes of unrelated individuals only. All significant genomewide associations identified were in cis of the putatively regulated gene. Each approach identified an additional 2–4 expression levels for which the top associated SNP mapped in cis of the putatively regulated probe but did not reach genomewide significance. One curious finding in our results is the association between PSPHL transcript levels and rs2419485, for which the cis association appears to be quite distant from the gene. However, the PSPHL gene and rs2419485 actually map to opposite sides of the centromere for chromosome 7 and are in a region of very extensive linkage disequilibrium. In fact, rs2419485 is in strong linkage disequilibrium with SNPs that are much closer to PSPHL and could very well be a surrogate for them.

In addition to the 15 cis associations reported by Cheung et al.,³¹ we found 4 cis associations in our study, for phenotypes CTBP1, ZNF85, TCEA1, and VAMP8. In total, among the 19 peak cis-associated SNPs identified using our approach, 4 map within the gene, and all but one (PSPHL) map to a region within 106 kb of the gene. We expect that most of the identified cis associations are real, in that they reflect an association between specific SNPs and the strength of the mRNA hybridization signal. Thus, we interpret the fact that our proposed approach identified more cis associations as evidence that it provides a more powerful analytical strategy. In fact, three of the four new cis signals we report (CTBP1, ZNF85, and VAMP8) were replicated in an independent set of ∼400 individuals examined with a different expression array and genotyped with a different technology (all P values <10^-9).³⁵

We also compared the findings from the genome scan for the 27 phenotypes in table 5 with those from the linkage scans by Morley et al.³² Morley et al. report that all 27 phenotypes show evidence of cis linkage. As noted above, for 19 of the phenotypes, we identified evidence of cis association, which is consistent with the linkage signals. For eight others, we did not uncover evidence of cis association, despite the evidence of linkage reported by Morley et al.³² In these cases, the linkage signal could be artifactual, the regulatory alleles may not be in strong disequilibrium with the phase I HapMap SNPs examined, or there may be multiple causal alleles involved—a setting that might require haplotype tests for successful association analysis.

Discussion

We describe two family-based association tests. One relies on computationally intensive maximum-likelihood estimation. The other uses a computationally efficient score test to rapidly evaluate evidence of association at hundreds of thousands of markers. Although our tests can be used for samples in which all individuals are genotyped at all markers of interest, both of our proposed family-based association tests can accommodate phenotype data for individuals for whom genotype data are not available. Whenever one or more relatives of these individuals are genotyped at the marker of interest, expected genotype counts are calculated for the ungenotyped individual and are used to improve the power of subsequent association analysis. Our approach allows family samples collected for linkage studies or for studies of parent-of-origin effects to be used effectively in genomewide association studies. For the same number of genotyped individuals, genotyping a small number of individuals in each family and estimating the genotypes for their relatives provides more power than does simply examining the unrelated individuals. Thus, the approach described here is especially attractive in situations where the number of individuals to be examined is limited by cost considerations, such as when new technologies are evaluated (such as higher-density SNP chips or genome resequencing chips).

Consistent with previous results,^15,17 our results show that estimating genotypes for phenotyped individuals with missing genotype data can produce substantial increases in power. We also show that, in the analysis of gene-expression data, incorporation of estimated genotypes for phenotyped individuals with incomplete genotype data resulted in more findings of cis associations. The quality of the estimated genotypes will depend on the availability of flanking-marker data. In many cases, these data will be readily available because of a previous linkage scan. Even when flanking-marker data are not available, phenotypes of related individuals can be incorporated in the analysis because our method uses expected genotype counts, which can be estimated even when there is uncertainty about the identity of the missing genotypes. Our use of expected genotype counts allows for great flexibility in the choice of which individuals to genotype in each family.

Our method does not provide a built-in safeguard against population stratification (in contrast to the transmission/disequilibrium test⁷ and related methods). We decided not to include this built-in safeguard, so as to increase power. Our approach already has been applied successfully to study quantitative traits related to complex disease in humans.^35–37 In practice, we recommend that the distribution of test statistics across the genome be inspected—if a deviation from the null is suspected, the analysis could be repeated, incorporating estimates of individual ancestry^14,18 as covariates in the analysis, or the test statistics could be adjusted using a suitable genomic-control method.¹³ Naturally, after covariates are included and the analysis is repeated, the distribution of statistics across the genome should be inspected again. We expect that use of individual ancestry as a covariate will be an appropriate strategy for avoiding the effects of population stratification at most markers but may be insufficient for markers at a few loci (such as the human leukocyte antigen locus [HLA]) that show very strong differentiation even among closely related populations and ethnic groups. In these cases, it may be prudent to rely on traditional transmission/disequilibrium–based methods whose false-positive error rates are insensitive to any form of population structure.

Our simulation results provide guidance to investigators who plan to genotype a subset of individuals in an existing family collection. If only one individual can be genotyped in each nuclear family, our results show that genotyping one child provides the most power. If two individuals are to be genotyped per nuclear family, genotyping one parent and one child will provide the most power on a per-genotype basis. With three genotyped individuals per family, the best choice is to genotype two parents and one child. We recognize that other considerations are important in deciding whom to genotype. For example, sometimes it may be desirable to genotype two parents (but no offspring), to facilitate haplotype analyses that rely on unrelated individuals. In other cases, the choice of which individuals to genotype may be guided by the availability of DNA samples. In yet other cases, it may be desirable to use prior evidence of linkage to guide the choice of which individuals to genotype.³⁸ Our software implementation is general and will use arbitrary sets of genotyped individuals to estimate genotypes for their relatives.

To estimate missing genotypes, our association test relies on standard pedigree likelihood calculations, which we implemented using the Lander-Green²⁷ or Elston-Stewart²⁶ algorithm. Our implementations naturally take advantage of computational enhancements to these algorithms—for example, our Lander-Green implementation uses the method of Idury-Elston to speed up multipoint calculations,³⁹ the method of Abecasis et al.³⁰ to take advantage of recurring terms in likelihood calculations, and the methods of Abecasis and Wigginton²⁵ to model linkage disequilibrium within clusters of tightly linked markers.

Since the key calculations involved in implementing our method rely on existing algorithms, we were also able to implement our method for the X chromosome with minimal effort. Our X-chromosome implementation models kinship coefficients on the X chromosome as described elsewhere³⁴ and assumes that average phenotypic values for hemizygous males are the same as for homozygous females.

It has been proposed that appropriately designed family-based association tests can be used to perform screening and replication analysis using one set of families.⁴⁰ If our method is used to evaluate the evidence of association after a subset of individuals is genotyped (stage 1), investigators may consider genotyping the remainder of the individuals to follow up promising findings (stage 2). If a replication analysis is desired, estimated genotype counts from the first stage of the analysis (estimated using stage 1 genotype data only) can be included as covariates when the complete genotype data are analyzed. In this way, it will be possible to use a subset of individuals to screen for association and then to replicate the finding by genotyping additional individuals from the same family sample. It is important to note that a combined analysis of the stage 1 and stage 2 data, with a stringent significance threshold, often will provide more power than simply using the stage 2 data to replicate stage 1 findings.⁴¹

In the results presented here, we have focused on imputing genotypes for all individuals in each family when a subset of individuals is genotyped at the marker of interest. Whenever possible, we relied on flanking-marker data and the Lander-Green or Elston-Stewart algorithm to identify shared segments of chromosome among the individuals in each family and thus to impute the missing genotypes. In principle, genotype inference can be extended to the population level—a setting in which shared segments of chromosome are likely to be much shorter but should still exist.⁴² For example, our implementation allows genotype scores to be estimated for markers that are completely ungenotyped whenever these markers are in linkage disequilibrium with nearby typed markers and when estimates of population haplotype frequencies are provided to describe the relationship between the ungenotyped markers and other nearby markers. In the current implementation, this imputation of ungenotyped markers relies on a cluster-based linkage-disequilibrium model described elsewhere.²⁵

It is also important to note that, although we designed our approach to use expected genotype scores (so that we deal with uncertainty in missing genotypes in a manner that is somewhat similar to the approach used by Zaykin et al.⁴³ to deal with uncertain haplotype phase in case-control association tests), it should, in theory, be possible to implement a full likelihood-based approach that integrates over the joint distribution of missing genotypes for each family and estimates genetic model parameters simultaneously. Although we considered it, we decided that this full likelihood approach would be cumbersome when used for the analysis of whole-genome scans, particularly when a polygenic component is also included in the model to explain residual resemblance between relatives. For discrete traits, the LAMP program^16,44 integrates over all missing genotypes in each family jointly to estimate genetic model parameters and provides an alternative to our approach.

Computer programs implementing the approaches described here are available at our Web sites (Ghost and Merlin). We hope they will be helpful for investigators planning to perform quantitative-trait genomewide association studies of existing family samples.