Abstract
Mathematical models for hepatitis C viral (HCV) RNA kinetics have provided a means of evaluating the antiviral effectiveness of therapy, of estimating parameters such as the rate of HCV RNA clearance, and they have suggested mechanism of action against HCV for both interferon and ribavirin. Nevertheless, the model that was originally formulated by Neumann et al. (Science 1998: 282, 103-107) is unable to explain all of the observed HCV RNA profiles under treatment e.g., a triphasic viral decay and a viral rebound to baseline values after the cessation of therapy. Further, the half-life of productively HCV-infected cells, estimated from the second phase HCV RNA decline slope, is very variable and sometimes zero with no clear understanding of why. We show that extending the original model by including hepatocyte proliferation yields a more realistic model without any of these deficiencies. Further, we define and characterize a critical drug efficacy, such that for efficacies above the critical value HCV is ultimately cleared, while for efficacies below it, a new chronically infected viral steady state level is reached.
Keywords: mathematical modeling, hepatitis C virus, viral kinetics, critical drug efficacy, liver regeneration
1. Introduction
Hepatitis C virus (HCV) infect about 200 millions people worldwide (World Health Organization 2000). About 15-30% of asymptomatic patients (Villano et al., 1999) and more than 50% of symptomatic patients (Gerlach et al., 2003) with acute hepatitis C spontaneously clear the virus during the early phase of infection, with the remainder progressing to chronic hepatitis infection. Chronic HCV infection is the main cause of chronic liver disease and cirrhosis leading to liver transplantation or death (Alter et al., 1992).
Antiviral therapy has been used to treat chronically HCV infected patients, with successful therapy resulting in undetectable virus for more than 6 months after treatment cessation. Typical therapy response begins with a rapid viral decline followed by a second slower decline until the virus becomes undetectable (Colombatto et al., 2003; Neumann et al., 1998; Pawlotsky et al., 2004). In some patients a triphasic decline has been observed, consisting of a rapid initial decline in the viral load followed by a “shoulder phase” (4 – 28 days) – in which viral load decays slowly or remains constant – and a third phase of resumed viral decay (Bekkering et al., 2001; Herrmann et al., 2003; Sentjens et al., 2002). However, in approximately 50% of HCV treated patients with current therapy, consisting of pegylated interferon and ribavirin, the virus is not eradicated (termed partial responders) and either rebounds to pretreatment levels during therapy, or converges to a lower viral plateau during treatment and then returns to pretreatment levels upon therapy cessation (Fried et al., 2002; Manns et al., 2001).
A model of HIV infection (Perelson et al., 1996; Wei et al., 1995) was adapted by Neumann et al. (1998) to study the kinetics of chronic HCV infection during treatment. Since then viral kinetics modeling has played an important role in the analysis of HCV RNA decay during antiviral therapy (see review (Perelson et al., 2005). The original model for HCV infection (Neumann et al., 1998) includes three differential equations (here termed the original model) representing the populations of target cells, productively-infected cells, and virus. A simplified version of the model (here termed the two-equation model) that assumes a constant population of target cells was used to estimate the rates of viral clearance and infected cell loss by fitting the observed biphasic decline of HCV RNA in patients during therapy. The analytic solution of the two-equation model, when target cells were held constant, showed that the first phase decline in viral load depends mainly on the viral clearance rate and treatment effectiveness, and that the second phase decline depends mainly on the loss rate of infected cells and to a less extent on treatment effectiveness. Fitting the analytic solution to patient data, the half life of HCV infected cells was estimated to span a large range from 1.7 days to greater than 70 days (Neumann et al., 1998). However, in this model, the data from partial responders, exhibiting a flat second phase, can only be fitted under the assumption that infected cells do not die or that they have an unrealistically long half-life. Moreover, the model can not explain a triphasic viral decay nor does it predict viral load resurgence to the baseline level upon cessation of therapy.
The assumption of a constant population of target cells during therapy is an approximation and is only valid for a short duration (Neumann et al., 1998). Since hepatocytes have been suggested to be the major producers of HCV (Dahari et al., 2005a; Powers et al., 2006), we assume that target cells are hepatocytes. The liver is an organ that regenerates, and thus we expect that due to homeostatic mechanisms (Fausto 2004; Michalopoulos et al., 1997), any loss of infected hepatocytes would be compensated for by the proliferation of hepatocytes (Dahari et al., 2005b).
Here, we extend the original model of HCV infection under therapy (Neumann et al., 1998) to account for the proliferation of hepatocytes (Fig. 1) (here termed the extended model), as was recently used to model HCV RNA kinetics in primary infection in chimpanzees (Dahari et al., 2005b). We then compare the behavior of the two-equation model, the original model and the extended model. We show that the extended model can explain both biphasic and triphasic viral decays, the response seen in “flat partial responders” in which virus decay is characterized by a flat second phase, as well as the rebound of virus to its pre-treatment or baseline level on the cessation of therapy. We also show that there exists a critical drug efficacy such that for efficacies below the critical value a flat partial response will occur, whereas for efficacies above the critical value ultimate HCV elimination should occur.
Figure 1. Diagrammatic representation of the model of chronic viral infection.
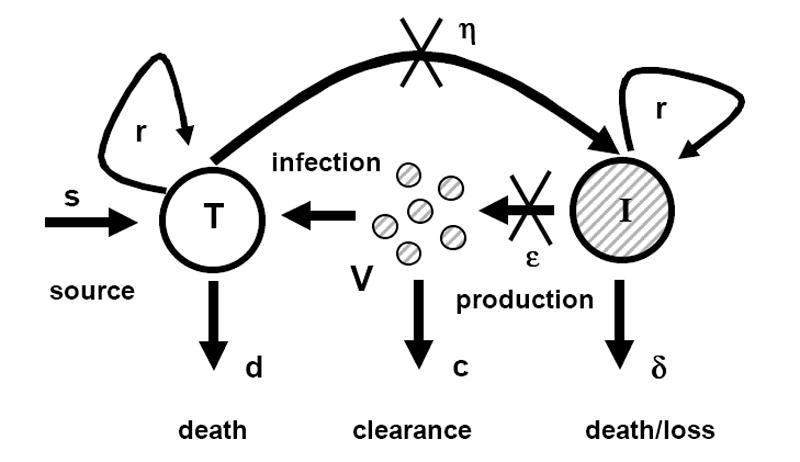
The original Neumann et al. (1998) model assumes that there is no proliferation of target and infected cells (i.e., r=0). The extended model that we introduce here accounts for target and infected cell proliferation (i.e., r > 0). T, and I represent target and infected cells, respectively, and V represents free virus.
2. Original model during antiviral therapy
Neumann et al. (1998) modeled HCV infection and treatment with the following system of differential equations (Fig. 1):
| (1) |
| (2) |
| (3) |
where T represents uninfected hepatocytes, I represents infected hepatocytes and V represents virus. The model assumes that uninfected hepatocytes are produced at a constant rate s, die at rate, d, per cell and are infected at constant rate β. Infected hepatocytes are lost at a rate δ per cell. Viral particles (virions) are produced at rate p per infected hepatocyte and cleared at rate c per virion. Chronic HCV infection is treated using interferon-α in combination with the antiviral drug ribavirin. Interferon-α acts primarily by blocking the production/release of new virus, although we also allow for a treatment effect in blocking de novo infection. The efficacy of treatment in blocking virion production and reducing new infections are described by two parameters, εp and η, respectively. For example, a treatment efficacy in blocking virion production of 95% corresponds to εp = 0.95.
2.1 Two-equation model
The non-linear system in equations (1) - (3) does not have a closed form analytic solution. However, if one assumes the target cell population remains constant during the course of therapy, the resulting two-equation model:
| (4) |
| (5) |
where T0 is the target cell level at the start of therapy, can be solved exactly under the assumption that the system was in quasi-steady at the start of therapy, i.e., pβT0=cδ (Neumann et al., 1998).
2.1.1 Steady states of the two-equation model
The two-equation model admits two steady states before therapy initiation (i.e., εp=η=0): an uninfected steady state with no virus and no infected cells (i.e., I=V=0) and total number of uninfected hepatocytes equal to T0, and an infected steady state with
| (6) |
where V0 represents any given baseline pre-therapy HCV level.
2.1.2 Analytical solution of the two-equation model
Assuming a patient is in the infected steady state and then begins treatment at time t=0, so that T0 = cδ/(pβ), V(0) = V0 and I(0) = cV0/p, the solutions of Eqs. (4) and (5) are:
| (7) |
| (8) |
where
and
According to Eqs. (7) and (8), the viral load under treatment will always decrease to the uninfected steady state following a double exponential decay, with rates λ1 and λ2. The infected cell population also decreases to the uninfected steady state. However, current estimates of model parameters obtained from comparisons with experimental data (Neumann et al., 1998), suggest c ≫ δ. Under these conditions, λ1≫λ2, B ~ 0, and I(t) follows an approximate single exponential decay, with rate λ2. In most patients, the viral load data under treatment does in fact show a two phase decline until the virus becomes undetectable, and Eq. (7) can be fitted to the data. These fits are usually done assuming η = 0, and yield estimates for εp, c and δ (Neumann et al., 1998). The assumption η = 0 is made because it can be shown that for large values of εp, as are obtained by many therapies, the effect of η on Eq. (7) is negligible (Neumann et al., 1998). The value of η can also be fixed to non-zero values, but in general the available data are insufficient to estimate it.
2.1.3 Flat partial responses to therapy
In patients that partially respond to therapy, an initial decrease in viral load is followed by a flat second phase with no additional decreases (e.g. patients 1A, 1F and 1H in Neumann et al. (1998)). Equation (7) can fit this pattern only if δ is very small or zero, such that λ2 ~ 0. However, this is clearly not biologically realistic because there must be a finite positive loss rate of infected cells.
2.1.4 HCV kinetics after treatment cessation
In most treated individuals the virus returns to its pretreatment levels within 1-2 weeks after cessation of treatment (Gretch et al., 1995; Sentjens et al., 2002). The dynamics of viral recovery can easily be predicted from Eqs. (4) and (5). Assume therapy is given until time te. To study what occurs after therapy ends, we solve the two-equation model, Eqs. (4) and (5), with initial conditions I(0)=I(te) and V(0)=V(te). Since and εp=η=0 for t>te, Eqs. (4) and (5) can be rewritten as:
with solution
| (9) |
At the eventual steady state obtained after cessation of therapy, which we denote by the use of the subscript ∞, dV/dt=0 so from Eq. (5) pI∞ = cV∞. Thus, pI∞ + δV∞ = (c + δ)V∞, and the new viral steady state after treatment cessation can be written as
| (10) |
where V(te) and I(te) can be calculated using Eqs. (7) and (8), respectively.
A more intuitive expression can be obtained if we assume that virus is in quasi-steady state during therapy, which tends to be a good assumption as long as c ≫ δ. Then, at the last time treatment is present, te, or
| (11) |
Substituting Eq. (11) into Eq. (10), we obtain
| (12) |
However, since ,
| (13) |
Thus, the two-equation model predicts that after cessation of therapy the viral load will only increase by a factor 1/(1-εp) (Fig. 2A), and not necessarily return to its pre-treatment level, V0, as observed in patients (Gretch et al., 1995; Sentjens et al., 2002).
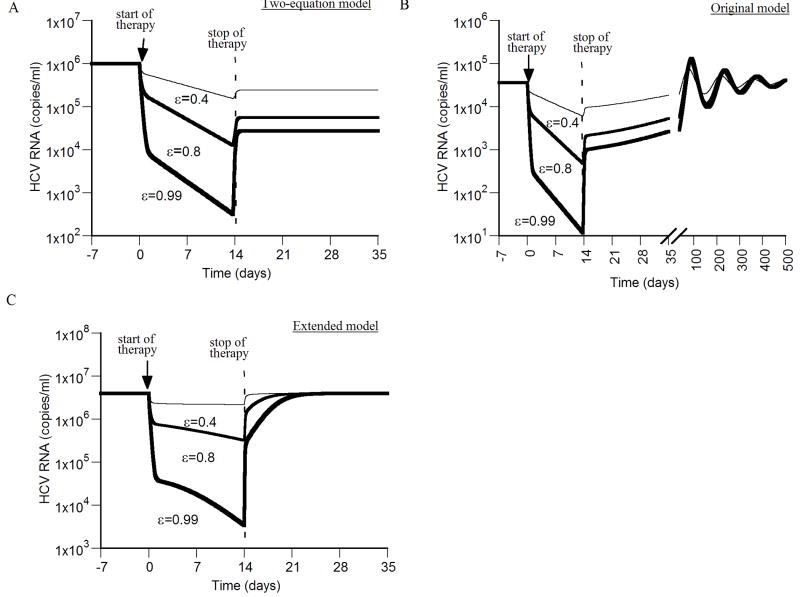
Figure 2. Viral kinetics after therapy cessation.
We simulated virus resurgence post therapy cessation using the two-equation model (A), the original model (B), and the extended model (C). Different drug efficacies (ε = 0.4, 0.8 and 0.99) were assigned at time 0 for 14 days, and then set to ε=0 for the rest of the simulation. In all simulations the following parameters were held fixed: d = 0.0026 day-1, p = 2.9 virions/day, β = 2.25×10-7 ml day-1 virions-1, c = 6.0 day-1, δ = 0.26 day-1. A) During therapy (ε > 0) the virus concentration V(t) can be calculated using Eq. (7). Here the initial condition V(0) = V0 = 106/ml was used. Upon cessation of therapy at time te = 14 days, V increases from V(te) to a new steady-state level V(te)/(1-ε), but not to its pretreatment level, as explained in section 2.1.4. B) Using the original model, with s = 2.6×104 cell ml-1 day-1, the virus resurges to pretreatment levels with damped oscillations. The curve for virus increase after therapy cessation with drug efficacies of ε = 0.99 and ε = 0.8 largely superimpose. The virus resurges to pretreatment viral load levels in a significant shorter time with higher values of p and/or β (not shown). C) Using the extended model, with s = 2.6×104 cell ml-1 day-1, r = 4.2 day-1 and Tmax = 1.0 × 107 cells, the virus resurges to pretreatment levels within a week post therapy cessation.
In summary, the two-equation model can not predict the observed flat partial viral response with a realistic positive value for the death rate of infected cells and can not predict viral resurgence to pretreatment levels. The question still remains of whether the original three-equation model, system (1)-(3), without assuming that dT/dt = 0, can explain these phenomena.
2.2 Steady states of the original three-equation model
The original model, Eqs. (1) - (3), admits two steady states: an uninfected steady state with I=V=0 and total number of uninfected hepatocytes equal to
| (14) |
It also has an infected steady state given by
| (15) |
Before treatment the drug efficacy is zero (η = εp = 0), while during antiviral therapy, 0≤η≤1, 0≤εp≤1. In Eq. (15), we combined the terms for drug efficacy into a single term 1−ε = (1−εp)(1−η) where ε represents the overall drug efficacy.
2.3 Stability analysis of the original model during therapy
During antiviral therapy, the model given by Eqs. (1) - (3) predicts that viral load evolves to one of the two steady states: complete viral eradication (cure) as given in Eq. (14) or persistent viral infection, as described in Eq. (15). The local stability of the two steady states is determined by linearizing the equations of the model around each steady state and examining the corresponding eigenvalues. Such analysis indicates that there exists a transcritical bifurcation point at
| (16) |
that separates the region of stability for the infected steady state from the region of stability for the uninfected steady state. When the left hand side of Eq. (16) is less than the right hand side, the uninfected steady state is stable (Callaway et al., 2002; Huang et al., 2003). Given the population of hepatocytes in the uninfected steady state , and the population of uninfected hepatocytes in chronic infection prior to treatment the bifurcation point, termed the critical efficacy, εc, can be rewritten as:
| (17) |
where T̄/T̄0 is the ratio of the number of uninfected hepatocytes in a chronically infected individual before treatment to the total number of hepatocytes in an uninfected individual. In the case of successful drug therapy ε > εc, and the viral load will approach zero. Otherwise (ε < εc), the system will converge to a new infected steady state with lower levels of virus and infected cells as given by equation Eq. (15). The critical condition ε > εc is also equivalent to the standard condition from epidemiology that the basic reproductive number R0 < 1, where (Callaway et al., 2002).
2.4 Eigenvalues close to the uninfected steady-state
Upon successful treatment, i.e., ε > εc, the viral load converges to the uninfected steady state at a rate given by the eigenvalues of Eqs. (1) - (3) linearized around the uninfected steady state. To simplify the calculation of the eigenvalues, we assume that the viral load is in quasi-steady state during therapy, i.e., . This assumption can be justified because the virus clearance rate, c, is much larger than the death rate of infected cells, δ. Thus, the original model (Eqs. (1) - (3)) is reduced to the following system of differential equations:
| (18) |
| (19) |
where . Equations (18) and (19) can be linearized about the uninfected state-state (Eq. (14)). The Jacobian is
| (20) |
Thus, close to the uninfected state-state of the system, we obtain the following linear equations
| (21) |
| (22) |
where T’ and I’ represent the values of T and I near the uninfected steady state, i.e. T = T̄ + T’ and I = Ī + I’, where the steady-state values are T̄ and Ī. Using the definition , Eq. (22) can be rewritten as
| (23) |
Thus, after an initial transient that depends on c and εp (first phase decline far from the uninfected equilibrium), the viral load during the second phase, which is proportional to the number of infected cells, converges to the uninfected steady state with eigenvalue . Note that in the case of successful treatment , (Eq. 17). For values of drug efficacy ε ~ 1, λ ≈ -δ. For drug efficacies near the critical efficacy, ε ~ εc<1, the viral decline close to the uninfected steady state will be slow and affected by the fraction of infected hepatocytes, 1−T̄0/T̄.
2.5 Viral decline during treatment
Solving the original three-equation model numerically during therapy, i.e., without making a quasi-steady state assumption as above, with antiviral efficacy higher than the critical efficacy, i.e., ε > εc, we confirm that for ε ~ 1, the second phase viral decline slope represents the death rate of infected hepatocytes, δ, but for efficacies near the critical the second phase decline slope is much less than δ (Fig. 3A). However, this model and its solutions do not predict the triphasic viral decay observed in some patients, as noted before (Herrmann et al., 2003).
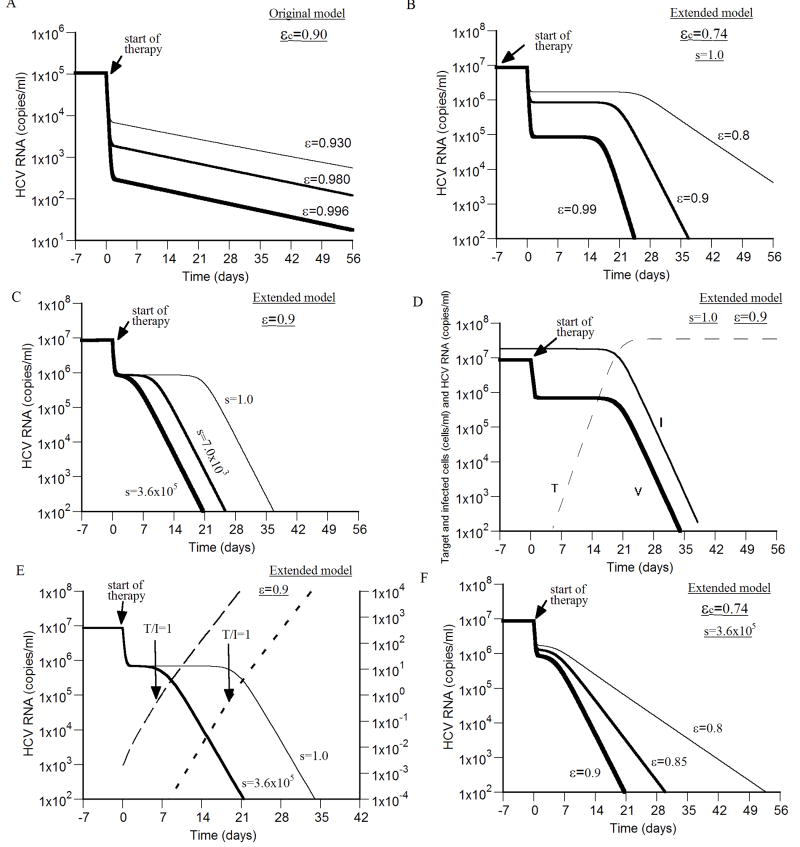
Figure 3. Viral kinetics during successful antiviral treatment.
We simulated virus decay during therapy using the original model (A), and the extended model (B - F), with different drug efficacies higher than the critical efficacy (ε > εc), and (unless otherwise stated) d = 0.01 day-1, p = 2.9 virions/day, β = 2.25×10-7 ml day-1 virions-1, δ = 1.0 day-1, c = 6.0 day-1, r = 2.0 day-1, s=1.0 cell ml-1 day-1 and Tmax = 3.6 × 107 cells ml-1. A) With drug efficacies (i.e., ε = 0.93, 0.98 and 0.996) higher than the critical efficacy (εc=0.90), a biphasic viral decline is shown which lead to viral eradication. Based on simulation results, the second phase viral decline slopes under the three efficacies (i.e., ε=0.93, 0.98 and 0.996) are 0.047 day-1, 0.050 day-1 and 0.051 day-1, respectively (i.e., 91%, 98% and 99% of the death rate of infected cells used here (δ = 0.052 day-1). Tmax = 1.0 × 107 cells ml-1, s=2.6×104 cell ml-1 day-1 and d = 0.0026 day-1. B) With drug efficacies (i.e., ε = 0.80, 0.90 and 0.99) higher than the critical efficacy (εc=0.74), a triphasic viral decay is shown that consists of a first phase with rapid virus decline followed by a “shoulder phase” in which virus load remains constant and a third phase of faster viral decay. For the three efficacies 0.80, 0.90 and 0.99 the third phase viral decline slopes are 0.04 day-1, 0.34 day-1 and 0.82 day-1, respectively, i.e., 4%, 34% and 82% of the infected cell death rate used here (δ=1.0 day-1). C) Higher influx rates of new hepatocytes, s, shrinks the “shoulder phase” and even eliminates it giving rise to a biphasic viral decline. The drug efficacy was fixed, ε=0.90, in the three simulation curves. Note, over a large range of values for s, i.e., 1.0×105 - 3.6×105 cells ml-1 day-1, with the above parameter values, the critical drug efficacy εc = 0.742 − 0.743, and thus does not change significantly. D) The viral (thick line) shoulder phase is maintained by a quasi-steady-state level of infected cells (thin line) until the target cell population level (dashed line) reaches that of infected cell population. E) A shoulder phase is observed when the level of infected cells is much higher than the target cell level at baseline (i.e., T/I ≪ 1 before therapy; (short-dashed line)). The shoulder phase ends when T/I ~ 1. T/I ratio for the shorter shoulder-phase is represented by a long-dashed line. F) With a higher influx rate of new hepatocytes, s = 3.6×105 cell ml-1 day-1, and drug efficacies ε = 0.80, 0.85 and 0.90, higher than the critical efficacy (εc=0.74), a biphasic viral decay is shown that leads to viral eradication. The second phase viral decline slopes for the three efficacies ε = 0.80, 0.85 and 0.90 are 0.20 day-1, 0.38 day-1 and 0.57 day-1, respectively, i.e., 20%, 38% and 57% of the infected cell death rate used here (δ=1.0 day-1).
2.6 Flat second phase slope in partial responders
Solving the original model numerically during therapy with antiviral efficacy lower than the critical efficacy, i.e., 0 < ε < εc, one obtains a flat second phase in the viral decline without making the assumption that δ ~ 0 (Fig. 4A).
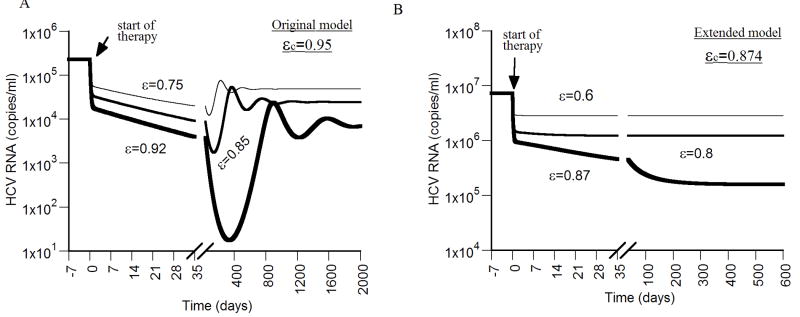
Figure 4. Viral kinetics with drug efficacy below the critical efficacy.
We simulated virus decay during therapy using the original model (A), and the extended model (B), with different drug efficacies below the critical efficacy (ε < εc), and η = 0, d = 0.0026 day-1, p = 2.9 virions/day, β = 2.25×10-7 ml day-1 virions-1, and c = 6.0 day-1. The critical efficacies for the original model and the extended model were calculated using Eqs. (17) and (29), respectively. With the original model, (A), after an initial rapid viral decrease upon start of therapy, the virus decays in a slower second phase during the first weeks of therapy until it reaches a viral nadir and then rebounds to a lower viral plateau. Higher values of p and/or β lead to shorter times until the lower plateau is reached (not shown). In (A), δ = 0.052 day-1 and s = 2.6×104 cell ml-1 day-1. With the extended model (B), after a rapid viral decrease upon start of therapy, the virus decays in a slower phase during the first weeks of therapy until it reaches a lower viral plateau. A lower value of r, e.g.,<0.05 day-1, leads to viral oscillation, until it reaches the lower viral plateau (not shown). δ = 0.26 day-1, Tmax = 1.0×107 cells, s = 2.6×105 cell ml-1 day-1 and r = 1.0 day-1.
2.7 Viral kinetics after treatment cessation
Unlike the two-equation model (Fig. 2A), the three-equation model predicts virus resurgence to pretreatment levels (with damped oscillations) after cessation of therapy (Fig. 2B).
3. Extended model
The original Neumann et al. (1998) model of chronic hepatitis infection and treatment assumes a source of hepatocytes but ignores proliferation of both infected and uninfected cells. Here we include density-dependent proliferation terms for both infected and uninfected hepatocytes (Fig. 1) that only allow growth of the liver until a maximum size, Tmax, is reached (Dahari et al., 2005b). The extended model is given by
| (24) |
| (25) |
| (26) |
where uninfected (T) and infected (I) hepatocytes can proliferate with maximum proliferation rate r, under a blind homeostasis process, in which there is no distinction between infected and uninfected cells in the density-dependent term. Because HCV infection is non-cytopathic and viral production rates in vivo appear to be low, there is no reason to suppose that infected cells can not proliferate. In principle, the maximum proliferation rate r, could be different for infected and uninfected cells, and this generalization will be pursued elsewhere.
3.1 Steady states of the extended model
The extended model admits two steady states: an uninfected steady state with I=V=0 and total number of uninfected hepatocytes equal to
| (27) |
where r > d and s ≤ dTmax in order to have a physiologically realistic model (i.e., T̄0 ≤ Tmax), and an infected steady state with
| (28) |
where
3.2 Stability analysis of the extended model during therapy
The local stability of the two steady states is determined by examining the corresponding eigenvalues, as before. Standard analysis shows that there still exists a transcritical bifurcation point, but now it is at
| (29) |
The transcritical bifurcation separates the region of stability for the infected steady state from the region of stability for the uninfected steady state.
3.3 Eigenvalues close to the uninfected steady-state
Again assuming the virus is in quasi-steady state, then upon successful treatment, i.e., ε>εc, the viral load converges, again after an initial transient (first phase decline), to the uninfected steady state at a rate determined by the eigenvalue
| (30) |
Note that , because of the condition ε > εc. For values of drug efficacy ε ~ 1, λ is close to -δ, while for drug efficacies near the critical efficacy (εc ~ ε), λ is close to 0.
3.4 Triphasic and biphasic viral decline
Solving the extended model numerically assuming ε > εc, we find that for certain parameter values the viral decay is triphasic (Fig. 3B), with the third phase decline slope close to the death rate of infected hepatocytes (δ) for ε ~ 1. As the influx rate of new hepatocytes, s, is made larger the “shoulder phase” of the triphasic viral decay shrinks eventually yielding a biphasic viral decay (Fig. 3C).
The best way to understand why this extended model can give rise to a triphasic decay is to focus on the shoulder or flat second phase. During this period the infected cell level is maintained approximately constant, i.e., the loss of infected cells is compensated for by infected cell proliferation. The viral levels stay constant because they are in quasi-steady state with the infected cells that produce virus (Fig. 3D). However, uninfected cells also proliferate and are assumed to be generated de novo from precursors at rate s. Thus, during the shoulder phase target cell numbers also increase (Fig. 3D), and when the target cell level approaches that of infected cells they start causing a decrease in the infected cell proliferation rate due to density-dependent form of the proliferation term. As the infected cell proliferation rate falls, the infected cell levels fall and the shoulder phase ends. Thus, shoulder phases, and hence triphasic responses, are only seen when the number of infected cells is much higher than the number of target cells before therapy (i.e., T/I ≪ 1). The shoulder phase persists until the ratio between target cells and infected cells is approximately one (T/I ~ 1) (Fig. 3E). When the ratio of target cells to infected cells before therapy is greater then one, i.e., T/I > 1, the shoulder phase does not exist (not shown). In addition, for drug efficacies close to 1, the second phase (in the biphasic viral decay; Fig 3F) or the third phase (in the triphasic viral decay; Fig. 3B) slope is close to the death rate of infected hepatocytes, δ.
3.5 Flat second phase in partial responders can be generated with a reasonable infected cell death rate (δ)
Solving the extended model numerically with 0 < ε < εc, a flat second phase can be obtained with a realistic infected hepatocyte half-life and a rapid viral convergence to a lower viral plateau (Fig. 4B).
3.6 Viral kinetics after treatment cessation
As shown for the original model (section 2.7), the extended model predicts virus resurgence to pretreatment levels after cessation of therapy (Fig. 2C). Also, the inclusion of proliferation in the model tends to blunt the predator-prey type oscillations seen in the original three-equation model (Fig. 2B). The kinetics of viral resurgence thus tend to mimic that observed in patients taken off therapy.
3.7 Model agreement with patient data
To show that the extended model is consistent with experimental data, we fitted the model to HCV RNA data from interferon treated patients that exhibits a biphasic decline (Neumann et al., 1998) (Fig. 5A), a triphasic decline (Herrmann et al., 2003)(Fig. 5B) and a flat partial response (Neumann et al., 1998) (Fig. 5C).
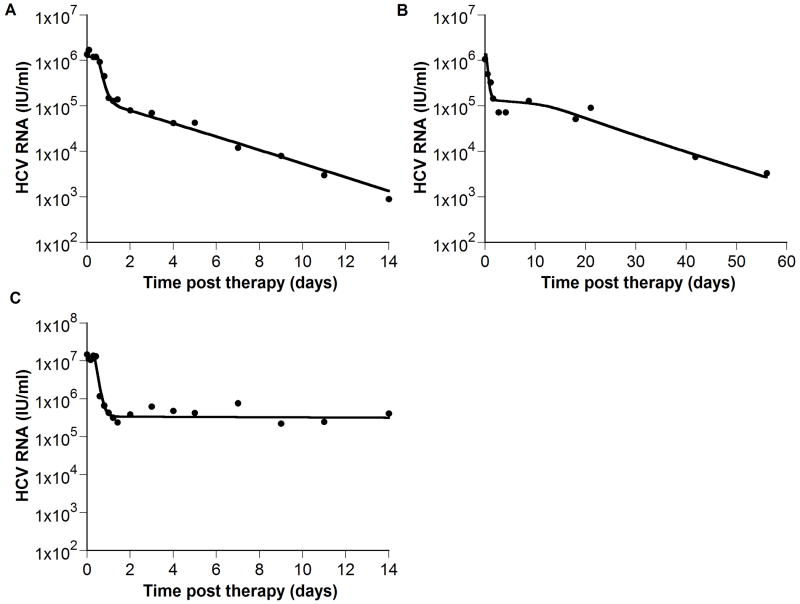
Figure 5. The model is consistent with experimental data.
(●) exhibiting biphasic (A), triphasic (B) and flat partial (C) viral decays. We fit (A) HCV RNA levels from a chronic HCV patient treated with interferon α-2b from Neumann et al., 1998, (B) digitized HCV RNA levels of a patient treated with pegylated interferon α-2a (shown in figure 2B of Hermann et al., 2003), and (C) HCV RNA levels from a second patient treated with interferon α-2b from Neumann et al., 1998. The analytical solution for V(t), i.e., Eq. (7) in Neumann et al., 1998 was first fitted to the HCV RNA, using Berkeley-Madonna (version 7.0.2; www.berkeleymadonna.com), to estimate the delay time before viral decay begins, t0, the IFN effectiveness, ε, and the viral clearance rate constant, c. Then, we fitted our model (Eqs. 24 - 26; solid line) to the HCV RNA data (●) with t0, ε, and c held fixed at their previously estimated values, and found values for the parameters s, d, δ, p, r, Tmax, and β for each patient that generated viral load decays consistent with the data. Parameter values found in (A), (B) and (C) respectively are: Tmax = 0.7 × 107, 0.51 × 107 and 0.6 × 107 ml-1; s = 8.0 × 105, 1.5 × 103 and 3.7 × 104 day-1 ml-1; d = 4.7 × 10-3, 9.3 × 10-3 and 2.4 × 10-3 day-1; δ = 0.30, 0.49 and 0.06 day-1; β = 0.6 × 10-7, 3.8 × 10-7 and 1.8 × 10-7 virions-1 day-1; r = 0.45, 0.54, and 0.73 day-1; c = 5.9, 3.5, and 13.9 day-1; t0 = 0.6, 0.3, and 0.4 days; p = 5.4, 7.1 and 13.9 virions day-1; ε = 0.906, 0.899 and 0.9675.
4. Discussion
Hepatitis C infection is an important infectious disease affecting millions of people and with high levels of morbidity and mortality (NIH. 2002). However, there are now therapies that use interferon-α and ribavirin, which clear the virus in a substantial number of patients (Fried et al., 2002; Manns et al., 2001). Unfortunately, in some patients especially those affected with HCV genotype 1 or of African-American descent, treatment is much less successful (Dixit et al., 2004). Thus, better understanding of treatment effects on viral load and its correlates of success will have direct clinical impact.
Here we have examined in detail the model currently used to analyze viral load during HCV treatment (Neumann et al., 1998). We specifically addressed two shortcoming of this model, namely its incompleteness in explaining the viral load profile in patients that respond to treatment only partially with a flat second phase of decline and the impossibility to fit with such model the viral load of those patients that show a triphasic profile in virus decay (Herrmann et al., 2003). We analyzed the model, without the linearization imposed by assuming a constant level of uninfected hepatocytes during therapy. Moreover, we used an extended model that includes density-dependent proliferation of hepatocytes, as previously implemented in a study to explain HCV RNA kinetics during primary HCV infection in chimpanzees (Dahari et al., 2005b). Here, we show that the inclusion of proliferation of hepatocytes in existent HCV kinetic models, can better predict viral kinetics in chronic HCV patients during and after antiviral therapy. These terms also make the model more biologically realistic, as it is well known that small transplanted livers quickly grow by cell proliferation to reach the size suitable for the patients (Fausto 2004; Michalopoulos et al., 1997).
In the field of HIV therapy the notation of a critical drug efficacy has been introduced (Callaway et al., 2002; Huang et al., 2003; Wein et al., 1998). If efficacy is not high enough, i.e., below its critical value, then theory predicts that HIV rather than declining monotonically during therapy, will decline initially, possibly rebound, and then stabilize at a therapy-induced set-point lower than the pre-treatment baseline. Here we extend this idea into the field of HCV infection and show the existence of a transcritical bifurcation point in models for HCV infection that defines whether the treatment will be successful leading to HCV eradication, or if it will lead only to a partial response. We were also able to show that the period (4 – 28 days) of approximately constant viral load after the rapid early decline and before the late third phase observed in some patients, occurs when hepatocytes proliferation is included (i.e., the extended model) and the majority of the liver is infected by the virus (i.e., T̄/Ī ≪ 1 before therapy) with a small influx (s) of new hepatocytes.
The extended model proposed here to analyze HCV RNA decay under treatment includes more parameters than the simplified version of the two-equation model (Neumann et al., 1998). Whether we will be able to use these models to fit viral load data in practice remains to be seen, although the model is clearly consistent with the data (Fig. 5). However, our results present some new insights on the possible mechanisms for the gamut of viral load profiles observed in the clinic. It is our hope that the systematic application of this type of model will lead to a better understanding of treatment success and failure in HCV infection.
Acknowledgments
This research was performed under the auspices of the U.S. Department of Energy under contract DE-AC52-06NA25396 and supported by National Institutes of Health (NIH) grant RR06555 (to A.S.P). R.M.R and H.D were supported by grant P20-RR18754 from the National Center for Research Resources (NCRR), a component of the NIH. This study is solely the responsibility of the authors and does not necessarily represent the official views of NCRR or NIH.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alter MJ, Margolis HS, Krawczynski K, Judson FN, Mares A, Alexander WJ, Hu PY, Miller JK, Gerber MA, Sampliner RE. The natural history of community-acquired hepatitis C in the United States. The Sentinel Counties Chronic non-A, non-B Hepatitis Study Team. N Engl J Med. 1992;327(27):1899–1905. doi: 10.1056/NEJM199212313272702. [DOI] [PubMed] [Google Scholar]
- Bekkering FC, Neumann AU, Brouwer JT, Levi-Drummer RS, Schalm SW. Changes in anti-viral effectiveness of interferon after dose reduction in chronic hepatitis C patients: a case control study. BMC Gastroenterol. 2001;1:14. doi: 10.1186/1471-230X-1-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaway DS, Perelson AS. HIV-1 infection and low steady state viral loads. Bull Math Biol. 2002;64(1):29–64. doi: 10.1006/bulm.2001.0266. [DOI] [PubMed] [Google Scholar]
- Colombatto P, Civitano L, Oliveri F, Coco B, Ciccorossi P, Flichman D, Campa M, Bonino F, Brunetto MR. Sustained response to interferon-ribavirin combination therapy predicted by a model of hepatitis C virus dynamics using both HCV RNA and alanine aminotransferase. Antivir Ther. 2003;8(6):519–530. [PubMed] [Google Scholar]
- Dahari H, Feliu A, Garcia-Retortillo M, Forns X, Neumann AU. Second hepatitis C replication compartment indicated by viral dynamics during liver transplantation. J Hepatol. 2005a;42(4):491–498. doi: 10.1016/j.jhep.2004.12.017. [DOI] [PubMed] [Google Scholar]
- Dahari H, Major M, Zhang X, Mihalik K, Rice CM, Perelson AS, Feinstone SM, Neumann AU. Mathematical modeling of primary hepatitis C infection: Noncytolytic clearance and early blockage of virion production. Gastroenterology. 2005b;128(4):1056–1066. doi: 10.1053/j.gastro.2005.01.049. [DOI] [PubMed] [Google Scholar]
- Dixit NM, Layden-Almer JE, Layden TJ, Perelson AS. Modelling how ribavirin improves interferon response rates in hepatitis C virus infection. Nature. 2004;432(7019):922–924. doi: 10.1038/nature03153. [DOI] [PubMed] [Google Scholar]
- Fausto N. Liver regeneration and repair: hepatocytes, progenitor cells, and stem cells. Hepatology. 2004;39(6):1477–1487. doi: 10.1002/hep.20214. [DOI] [PubMed] [Google Scholar]
- Fried MW, Shiffman ML, Reddy KR, Smith C, Marinos G, Goncales FL, Jr, Haussinger D, Diago M, Carosi G, Dhumeaux D, Craxi A, Lin A, Hoffman J, Yu J. Peginterferon alfa-2a plus ribavirin for chronic hepatitis C virus infection. N Engl J Med. 2002;347(13):975–982. doi: 10.1056/NEJMoa020047. [DOI] [PubMed] [Google Scholar]
- Gerlach JT, Diepolder HM, Zachoval R, Gruener NH, Jung MC, Ulsenheimer A, Schraut WW, Schirren CA, Waechtler M, Backmund M, Pape GR. Acute hepatitis C: high rate of both spontaneous and treatment-induced viral clearance. Gastroenterology. 2003;125(1):80–88. doi: 10.1016/s0016-5085(03)00668-1. [DOI] [PubMed] [Google Scholar]
- Gretch DR, dela Rosa C, Carithers RL, Jr, Willson RA, Williams B, Corey L. Assessment of hepatitis C viremia using molecular amplification technologies: correlations and clinical implications. Ann Intern Med. 1995;123(5):321–329. doi: 10.7326/0003-4819-123-5-199509010-00001. [DOI] [PubMed] [Google Scholar]
- Herrmann E, Lee JH, Marinos G, Modi M, Zeuzem S. Effect of ribavirin on hepatitis C viral kinetics in patients treated with pegylated interferon. Hepatology. 2003;37(6):1351–1358. doi: 10.1053/jhep.2003.50218. [DOI] [PubMed] [Google Scholar]
- Huang Y, Rosenkranz SL, Wu H. Modeling HIV dynamics and antiviral response with consideration of time-varying drug exposures, adherence and phenotypic sensitivity. Math Biosci. 2003;184(2):165–186. doi: 10.1016/s0025-5564(03)00058-0. [DOI] [PubMed] [Google Scholar]
- Manns MP, McHutchison JG, Gordon SC, Rustgi VK, Shiffman M, Reindollar R, Goodman ZD, Koury K, Ling M, Albrecht JK. Peginterferon alfa-2b plus ribavirin compared with interferon alfa-2b plus ribavirin for initial treatment of chronic hepatitis C: a randomised trial. Lancet. 2001;358(9286):958–965. doi: 10.1016/s0140-6736(01)06102-5. [DOI] [PubMed] [Google Scholar]
- Michalopoulos GK, DeFrances MC. Liver regeneration. Science. 1997;276(5309):60–66. doi: 10.1126/science.276.5309.60. [DOI] [PubMed] [Google Scholar]
- Neumann AU, Lam NP, Dahari H, Gretch DR, Wiley TE, Layden TJ, Perelson AS. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science. 1998;282(5386):103–107. doi: 10.1126/science.282.5386.103. [DOI] [PubMed] [Google Scholar]
- NIH. National Institutes of Health Consensus Development Conference: management of hepatitis C: 2002. Hepatology. 2002;36(5 Suppl 1):S3–20. doi: 10.1053/jhep.2002.36992. [DOI] [PubMed] [Google Scholar]
- Pawlotsky JM, Dahari H, Neumann AU, Hezode C, Germanidis G, Lonjon I, Castera L, Dhumeaux D. Antiviral action of ribavirin in chronic hepatitis C. Gastroenterology. 2004;126(3):703–714. doi: 10.1053/j.gastro.2003.12.002. [DOI] [PubMed] [Google Scholar]
- Perelson AS, Herrmann E, Micol F, Zeuzem S. New kinetic models for the hepatitis C virus. Hepatology. 2005;42(4):749–754. doi: 10.1002/hep.20882. [DOI] [PubMed] [Google Scholar]
- Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271(5255):1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- Powers KA, Ribeiro RM, Patel K, Pianko S, Nyberg L, Pockros P, Conrad AJ, McHutchison J, Perelson AS. Kinetics of hepatitis C virus reinfection after liver transplantation. Liver Transpl. 2006;12(2):207–216. doi: 10.1002/lt.20572. [DOI] [PubMed] [Google Scholar]
- Sentjens RE, Weegink CJ, Beld MG, Cooreman MC, Reesink HW. Viral kinetics of hepatitis C virus RNA in patients with chronic hepatitis C treated with 18 MU of interferon alpha daily. Eur J Gastroenterol Hepatol. 2002;14(8):833–840. doi: 10.1097/00042737-200208000-00004. [DOI] [PubMed] [Google Scholar]
- Villano SA, Vlahov D, Nelson KE, Cohn S, Thomas DL. Persistence of viremia and the importance of long-term follow-up after acute hepatitis C infection. Hepatology. 1999;29(3):908–914. doi: 10.1002/hep.510290311. [DOI] [PubMed] [Google Scholar]
- Wei X, Ghosh SK, Taylor ME, Johnson VA, Emini EA, Deutsch P, Lifson JD, Bonhoeffer S, Nowak MA, Hahn BH, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature. 1995;373(6510):117–122. doi: 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- Wein LM, D’Amato RM, Perelson AS. Mathematical analysis of antiretroviral therapy aimed at HIV-1 eradication or maintenance of low viral loads. J Theor Biol. 1998;192(1):81–98. doi: 10.1006/jtbi.1997.0622. [DOI] [PubMed] [Google Scholar]
- World Health Organization. Hepatitis C—global prevalence (update) Weekly Epidemiol Rec. 2000;75:18–19. [PubMed] [Google Scholar]