Abstract
Normal muscle has a resting potential of −85 mV, but in a number of situations there is depolarization of the resting potential that alters excitability. To better understand the effect of resting potential on muscle excitability we attempted to accurately simulate excitability at both normal and depolarized resting potentials. To accurately simulate excitability we found that it was necessary to include a resting potential–dependent shift in the voltage dependence of sodium channel activation and fast inactivation. We recorded sodium currents from muscle fibers in vivo and found that prolonged changes in holding potential cause shifts in the voltage dependence of both activation and fast inactivation of sodium currents. We also found that altering the amplitude of the prepulse or test pulse produced differences in the voltage dependence of activation and inactivation respectively. Since only the Nav1.4 sodium channel isoform is present in significant quantity in adult skeletal muscle, this suggests that either there are multiple states of Nav1.4 that differ in their voltage dependence of gating or there is a distribution in the voltage dependence of gating of Nav1.4. Taken together, our data suggest that changes in resting potential toward more positive potentials favor states of Nav1.4 with depolarized voltage dependence of gating and thus shift voltage dependence of the sodium current. We propose that resting potential–induced shifts in the voltage dependence of sodium channel gating are essential to properly regulate muscle excitability in vivo.
INTRODUCTION
Loss of excitability of skeletal muscle is a central feature of critical illness myopathy (Rich et al., 1996, 1997; Bird and Rich, 2002). In the animal model of critical illness myopathy, inactivation of sodium channels plays a central role in the loss of excitability (Rich et al., 1998; Rich and Pinter, 2001). A major contributor to inactivation of sodium channels is depolarization of the resting potential (Rich and Pinter, 2003). We currently lack a detailed understanding of how changes in resting potential alter cellular excitability. While depolarization of the resting potential reduces excitability by increasing the fraction of sodium channels undergoing both fast and slow inactivation, it could also increase excitability by moving the membrane potential closer to potentials at which sodium channels activate (Sejersted and Sjogaard, 2000).
We previously studied the effect of resting potential on excitability of skeletal muscle and found a reproducible series of changes that occur as muscle is depolarized (Rich and Pinter, 2003). These changes progress in the following order: a reduction in action potential peak, an increase in threshold for action potential initiation, a dependence of action potential amplitude on stimulus strength and finally, inexcitability. To learn more about possible underlying mechanisms, we simulated the changes in excitability that occur during depolarization. To accurately simulate changes in muscle excitability during depolarization, it was necessary to include a resting potential–induced shift in the voltage dependence of sodium channel activation and fast inactivation. To determine whether such a shift occurred in vivo, we recorded sodium currents from muscle fibers and found that prolonged changes in holding potential induced a shift in the voltage dependence of sodium channel gating that was similar in magnitude to the shift necessary to correctly simulate muscle fiber excitability at all resting potentials. The role such mechanisms may play in determining muscle fiber excitability is considered.
MATERIALS AND METHODS
Modeling of Action Potentials
Muscle fiber action potentials were simulated using a cable model consisting of 21 compartments that incorporated passive and active membrane properties. Each compartment included separate passive elements representing surface membrane and the t-tubule system. T-tubule and surface membrane passive properties are each represented by a capacitance and leak conductance in parallel per compartment, and these conductance–capacitance pairs are connected by an “access” conductance. This compartmental configuration is identical to that used in earlier modeling studies (Cannon et al., 1993). Voltage-dependent properties (GNa and GK) were placed in surface membrane and t-tubule portions of each compartment. The sodium conductance at the beginning of each run was adjusted to reflect the amount of slow inactivation occurring at the resting potential of the fiber.
As a starting point, values used in modeling action potentials were taken from a previous study (Cannon et al., 1993). Current injections were placed at the middle of the simulated fiber. Specific membrane capacitance was constant at 1 μF/cm2. For all simulations, it was assumed that the t-tubule system represented 8/9 of the total surface area. This is based on previous estimates for frog muscle fibers that the surface area of the t-tubule system is seven- to eightfold greater than the area of surface membrane (Mobley and Eisenberg, 1975; Peachey, 1975). For simplicity, the resistivity of surface and t-tubule membranes was assumed to be identical. In all simulations, fiber length was maintained at 10 mm; fiber diameter was 40 μm.
Active properties are modeled using the equations for describing voltage-dependent behavior of model membranes taken directly from Hodgkin and Huxley (Hodgkin and Huxley, 1952) and have been used to model motoneuron action potentials (Cooley and Dodge, 1973), axonal action potentials (Cooley and Dodge, 1966), and muscle fibers (Cannon et al., 1993). Differential equations were integrated numerically using the Runga-Kutta method to provide starting values for the Adams-Moulton predictor-corrector method (Carnahan et al., 1969), with adjustable step sizes of 1–4 μs. These numerical methods have been used previously for modeling calcium transients in cells (Nowycky and Pinter, 1993).
Tissue Preparation and Perfusion
Adult female Wistar rats were killed by carbon dioxide inhalation and the extensor digitorum longus (EDL) muscle was dissected tendon to tendon. Muscle fibers were labeled with 10 μM 4-Di-2-ASP and visualized using an upright epifluorescence microscope as previously described (Rich et al., 1998; Rich and Pinter, 2001). For all experiments, the recording chamber was continuously perfused with solution containing (in millimoles per liter) NaCl, 118; KCl, 3.5; CaCl2, 1.5; MgSO4, 0.7; NaHCO3, 26.2; NaH2PO4, 1.7; glucose, 10.8 (pH 7.3–7.4, 20–22°C) equilibrated with 95% O2 and 5% CO2. In some experiments, muscle fibers were depolarized using 12 mM K+ in the external solution. Muscles were bathed with the solution containing elevated KCl for 15 min before recording to allow muscle to equilibrate. All animal protocols were done in accordance with Emory University IACUC guidelines.
Loose Patch Voltage Clamp
Loose patch voltage recording and analysis was performed as previously described (Rich and Pinter, 2001, 2003; Filatov and Rich, 2004). Fibers were not impaled to measure the resting potential before seal formation. Instead the resting potential was assumed during voltage protocols and then measured after patch recordings were complete. The difference between the assumed and measured resting potential was then used to correct step voltages used during data acquisition. By impaling the muscle fiber after patch recordings were complete, potential problems related to issues of muscle damage and depolarization due to impalement were avoided. Patches in which the maximal inward current was >50 nA were discarded.
During our initial studies of the voltage dependence of fast inactivation, the step used to activate sodium channels was to −30 mV. During our initial studies of the voltage dependence of activation, the prepulse was to −120 mV. For calculation of sodium conductance, the sodium reversal potential was assumed to be +40 mV (Pappone, 1980; Kirsch and Anderson, 1986). In most fibers, the most depolarized pulse used to activate sodium currents was −10 mV; however, when the holding potential was −60 or −70 mV, the depolarized shift in the voltage dependence of activation made it necessary is some cases to include a pulse to 0 mV.
For experiments in which the voltage dependence of activation and fast inactivation were measured, fibers were held at each potential for 10 min before measurements. In some cases the changes in the voltage dependence of activation and fast inactivation were not complete by 10 min. Thus, the measures presented may represent underestimates of the steady-state effect of changing holding potential on the voltage dependence of sodium channel gating. In a few fibers, only activation was studied so the number of fibers for activation is slightly higher than for inactivation.
RESULTS
Modeling Action Potentials at Normal and Depolarized Resting Potentials
The first goal of this study was to identify model parameters needed to produce an accurate simulation of action potential failure in muscle fibers during depolarization. To accomplish this, we began by studying how action potentials fail during depolarization of normal muscle fibers. Muscle fibers normally have a resting potential close to −85 mV. At this potential, most sodium channels are not inactivated and the resting potential is ∼20 mV from levels at which significant sodium channel activation begins to occur (Rich and Pinter, 2003). The 20-mV difference between the resting potential and initial sodium channel activation ensures that fibers are electrically silent unless they are triggered to fire an action potential. Once triggered by sufficient depolarization, action potentials are all or none events that move the muscle resting potential near the sodium reversal potential (Fig. 1, row A, column 1, [A1]). As the resting membrane potential is depolarized by raising external potassium, reduction of excitability manifests in several ways: threshold for action potential initiation moves toward more depolarized potentials (from between −60 and −70 mV to between −40 and −50 mV), peak of the action potential becomes less positive (from between +30 and +40 mV to between +5 and +20 mV) and the action potential becomes wider (Fig. 1, A2). As excitability is further reduced by increasing depolarization, action potentials are no longer all or none; instead amplitude is graded and depends on the strength of the stimulus (Rich and Pinter, 2003). Finally muscle fibers become inexcitable. Repetitive firing of muscle fibers (myotonia) and firing of an action potential after termination of a hyperpolarizing current pulse (anode break excitation) are never seen during depolarization of innervated muscle fibers (Fig. 1, A3 and A4).
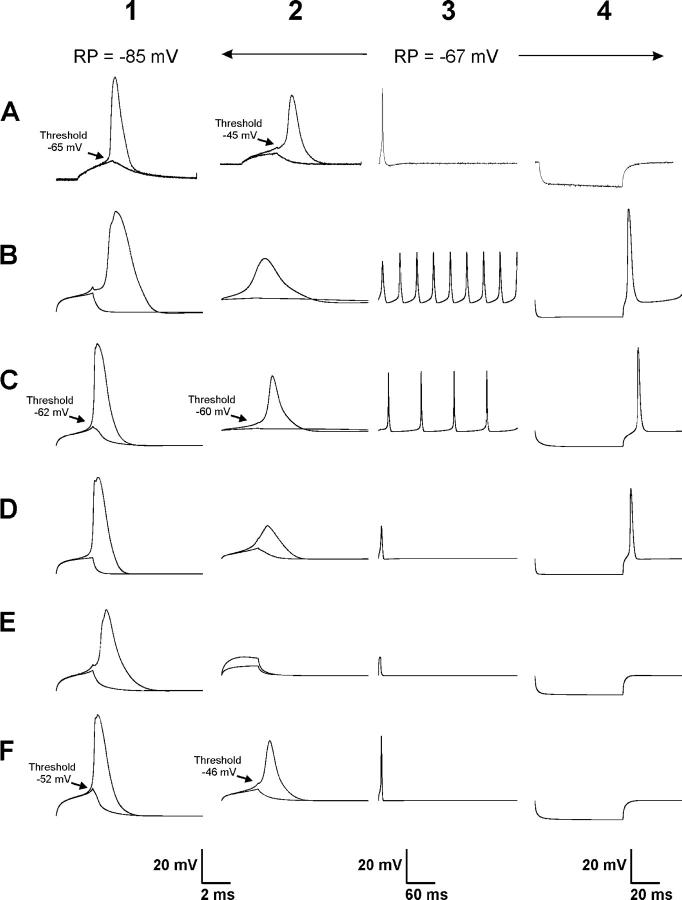
Figure 1.
Real and simulated action potentials at resting potential of −85 and −67 mV. (A) Shown are action potentials evoked at a resting potential of −85 mV (column 1, A1) and a resting potential of −67 mV in solution containing elevated extracellular K (column 2, A2). Superimposed on each action potential trace is the trace representing the largest depolarization that failed to elicit an action potential. Shown in column 3 is an action potential evoked at a resting potential of −67 mV on a long time-base (A3). In normal muscle, only a single action potential is evoked. In column 4 is a trace showing the response of the fiber to a 60-ms hyperpolarizing pulse (A4). In normal muscle, no action potential is evoked upon termination of the hyperpolarizing pulse (anode break excitation). (B) Shown are simulated action potentials that result using previously published parameters (Cannon et al., 1993). The action potentials are too wide at resting potentials of −85 and −67 mV (B1 and B2). Furthermore, a run of action potentials (myotonia) is evoked following a single depolarizing pulse at a resting potential of −67 mV (B3). Finally, there is anode break excitation following a hyperpolarizing stimulus pulse (B4). (C) After adjustment of kinetic parameters for sodium and potassium channels, simulated action potentials at a resting potential of −85 mV more closely resemble those from real fibers (C1). However, at a resting potential of −67 mV, the threshold is very close to the resting potential (C2). This results in both myotonia (C3) and anode break excitation (C4). (D) When a lower specific membrane resistance of 1,333 Ωcm2 is used, the simulated action potential at a resting potential of −85 mV looks normal (D1), but at −67 mV it is small and wide (D2). While no myotonia is present (D3), anode break excitation remains (D4). (E) When the midpoint of slow inactivation is set at −99 mV with a slope of 6 mV (Simoncini and Stuhmer, 1987; Ruff, 1996, 1999), the simulated action potential at −85 mV has a slow rise time and is somewhat wide (E1). Muscle is inexcitable at a resting potential of −67 mV (E2–4). (F) When the voltage dependence of sodium channel activation and fast inactivation are shifted by 7 mV to values of −66 and −30 mV, respectively, simulated action potentials are accurately modeled at a resting potential of −67 mV (F2). Furthermore, both myotonia and anode break excitation are prevented (F3, F4). However, at a resting potential of −85 mV, threshold for action potential initiation is too positive (F1).
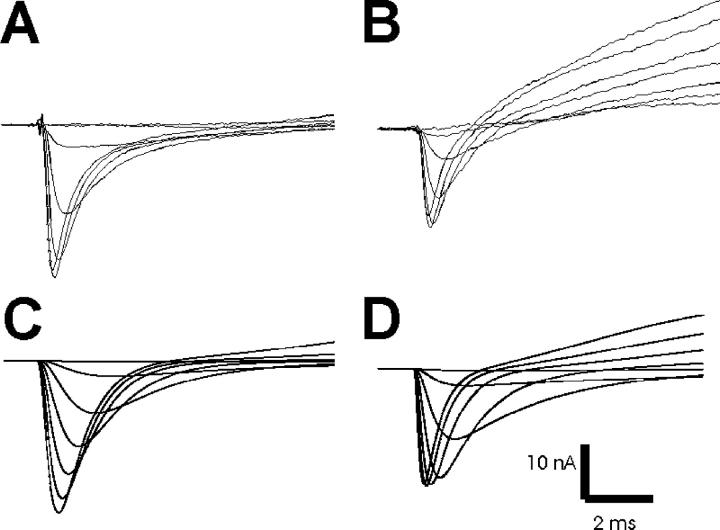
Figure 2.
Real and simulated patch currents. Shown on the top row are patch currents obtained from muscle fibers near the endplate (A) and away from the endplate (B). The outward potassium current is larger away from the endplate. On the bottom row are patch currents simulated with parameters used previously to model muscle fiber action potentials (Cannon et al., 1993) (C) and simulated currents in which rate parameters have been adjusted to speed sodium and potassium channel gating (D). Previously used parameters resulted in potassium currents that were too small and sodium currents that peaked too slowly. In both the real and modeled currents, the traces shown represent currents evoked after steps to −70 mV up to −10 mV in 10-mV increments. In both the real currents and the optimized modeled currents, the peak current was evoked following a step to −20 mV.
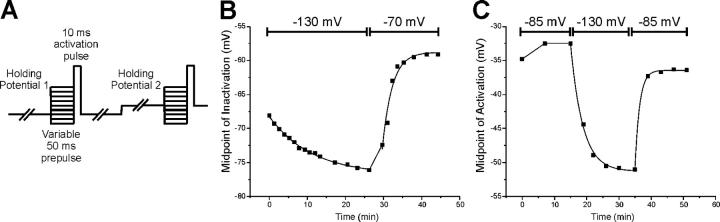
Figure 3.
Holding potential–induced shifts in the voltage dependence of sodium channel activation and fast inactivation. (A) Shown is the pulse protocol used to measure holding potential–induced changes in the voltage dependence of sodium current inactivation. A series of pulses to measure the voltage dependence of fast inactivation are run at the first holding potential. This series is repeated every 1–2 min to follow changes in the voltage dependence of fast inactivation. The holding potential is then changed and the measures of fast inactivation are repeated every 1–2 min. (B) Time course of holding potential–induced changes in the midpoint of inactivation measured in a selected muscle fiber. The fiber was initially at its resting potential of −85 mV. The midpoint of inactivation was measured and then the holding potential was set at −130 mV, followed by a holding potential of −70 mV. As the patch was held at −130 mV, there was a shift in the midpoint of fast inactivation from a value of −66 mV to a value of −76 mV with a time constant of 11.2 min. When the holding potential was set at −70 mV, the midpoint of inactivation shifted to a value of −59 mV with a time constant of 2.5 min. (C) The time course of holding potential–induced changes in the midpoint of activation. The patch was initially held at −85 mV, holding potential was then set at −130 mV and then returned to −85 mV. With a holding potential of −130 mV, the Km of activation shifted from a value of −34 mV to a value of −52 mV with a time constant of 3.7 min. After the holding potential was returned to −85 mV, the Km of activation shifted to a value of −36 mV with a time constant of 1.4 min.
To simulate action potential failure, we sought model parameters that would provide accurate simulation at both the normal resting potential of skeletal muscle (−85 mV) and at a resting potential at which muscle fiber excitability is about to fail (−67 mV) (Rich and Pinter, 2003). We initially used parameters that had been used previously to model action potentials in skeletal muscle (Table I; Cannon et al., 1993). These parameters resulted in action potentials at a resting potential of −85 mV that were wider than action potentials recorded from muscle fibers at the same resting potential (Fig. 1, A1 vs. B1). Also, even though slow inactivation was not included in this model, action potentials were wide and small at a resting potential of −67 mV (Fig. 1, B2). Despite having small action potentials, muscle was hyperexcitable at a resting potential of −67 mV and both myotonia and anode break excitation were present (Fig. 1, B3 and B4). When slow inactivation was included, muscle fibers were inexcitable at a resting potential of −67 mV (traces not shown). Thus, parameters from earlier modeling studies did not provide accurate simulation of action potentials at a resting potential of −67 mV, independent of whether slow inactivation was incorporated into the model.
TABLE I.
Parameters Used in Modeling Action Potentials
| Parameter/Units | Previously used values (Cannon et al., 1993) | Our values |
|---|---|---|
| αm/ms−1 | .288 | 1.0 |
| βm/ms−1 | 1.38 | 2.0 |
| Midpoint of NaCh activation/mV | −40 | −37 |
| Kαm/mV | 10 | 10 |
| Kβm/mV | 18 | 18 |
| αh/ms−1 | .0081 | .0081 |
| βh/ms−1 | 4.38 | 8.0 |
| Midpoint of NaCh inactivation/mV | −80 | −73 |
| Kαh/mV | 14.7 | 14.7 |
| Kβh/mV | 9 | 9 |
| αn/ms−1 | .0131 | .020 |
| βn/ms−1 | .067 | .067 |
| Midpoint of K activation/mV | −23.7 | −39.3 |
| Kαh/mV | 7 | 7 |
| Kβh/mV | 40 | 40 |
| Leak conductance/mS/cm2 | .75 | .25 |
| Maximum Na conductance/mS/cm2 | 150 | 500 |
| Midpoint of NaCh slow inactivation/mV | No slow inactivation | −87 |
| Slope of slow inactivation/mV | – | 9.8 |
| Maximum K conductance/mS/cm2 | 21.6 | 30 |
| Resting potential (Rm)/mV | −85 | −85 |
| Total conductance at Rm/mS/cm2 | 2 | .25 |
| ENa/mV | 48 | 40 |
| EK/mV | −95 | −85 |
| Internal resistivity/Ωcm | Not a cable model | 185 |
Note, we report the midpoint of NaCh channel activation and inactivation and K channel activation rather than the values for the voltage dependence of the parameters m, h, and n as was done previously. This was done to make it easier to compare modeled data to values recorded from real muscle fibers. Internal resistivity was taken from Farnbach and Barchi (1977). Data for slow inactivation was taken from Rich and Pinter (2003). For our modeling, we used values for specific membrane resistance (4,000 Ωcm2 = .25 mS/cm2), slow inactivation (h infinity midpoint −87 mV, slope 9.8 mV) based on previous studies (Kirsch and Anderson, 1986; Featherstone et al., 1996; Rich et al., 1998; Rich and Pinter, 2001, 2003; Vilin et al., 2001). For fast inactivation and activation we used midpoints of −73 and −37 mV based on our previous measures at a holding potential of −110 mV (Rich and Pinter, 2003).
To improve modeling of action potentials, we recorded patch currents from muscle fibers and used these to derive a set of parameters for modeling sodium and potassium currents at various resting potentials. One difficulty in modeling patch currents in muscle fibers is that the amount of potassium current present in a patch of membrane is highly variable. In general, the amplitudes of these currents are large when recorded at locations away from the endplate, whereas near the endplate there is often little to no potassium current (Fig. 2, A and B). For modeling of action potentials, we used parameters that yielded a potassium current density between that found near endplates and that found away from endplates.
Modeling of patch currents showed that action potentials were abnormally wide in our initial simulations because sodium and potassium currents activated too slowly (Fig. 2 C). Using previous parameters (Cannon et al., 1993), sodium currents peaked at 800 μs rather than the experimentally observed 300 μs following a step to −20 mV, while potassium currents were only beginning to activate at the end of a 10-ms pulse. Because of this difference, we changed a number of kinetic parameters for sodium and potassium currents and set the midpoints of sodium channel activation and inactivation to fit those measured previously at our standard holding potential of −110 mV (Table I; Rich and Pinter, 2003; Filatov and Rich, 2004). These changes resulted in currents that more closely resembled those obtained from intact muscle fibers. After the changes in parameters, sodium currents peaked ∼300 μs following a voltage step to −20 mV (Fig. 2 D).
A major difficulty in modeling action potentials is deciding values to use for the numerous other parameters in the model. Previous estimates of maximal sodium conductance from muscle fibers in vivo vary by up to fivefold. Based on loose patch data, we have calculated that maximal sodium conductance is close to 600 mS/cm2 in muscle fibers in vivo (Rich and Pinter, 2003). In contrast, estimates of maximal sodium conductance are two- to fivefold lower when using data from previous studies and assuming ENa = 40 mV (Pappone, 1980; Kirsch and Anderson, 1986; Ruff et al., 1987; Simoncini and Stuhmer, 1987). We found that the lower estimates of maximal sodium conductance produced inexcitability when action potentials were simulated at a resting potential of −67 mV. We thus used a value of 500 mS/cm2 that was closer to our estimates than those of previous studies. In our initial simulation of action potentials we used a value for specific membrane resistance based on our previous measurements (Rich et al., 1998) that was 4–10-fold higher than most previous estimates (Table I; Albuquerque and Thesleff, 1968; Lorkovic and Tomanek, 1977; Palade and Barchi, 1977). We also used lower values for specific membrane resistance, but use of lower values led to small, wide action potentials at a resting potential of −67 mV (Fig. 1, D2). Although myotonia was prevented by use of a low specific membrane resistance (Fig. 1, D3), anode break excitation remained (Fig. 1, D4). We used the higher value for specific membrane resistance for all subsequent simulations since this value led to better simulation of the action potential waveform at a resting potential of −67 mV.
Choosing values for the voltage dependence of slow inactivation are also problematic since values for Nav1.4 differ by close to 20 mV between various studies. Some studies found a midpoint between −80 and −90 mV (Kirsch and Anderson, 1986; Featherstone et al., 1996; Vilin et al., 2001; Rich and Pinter, 2003), whereas other studies reported midpoints more negative than −100 mV (Simoncini and Stuhmer, 1987; Ruff, 1996). The more positive values of slow inactivation are similar to those observed previously at 37°C (Ruff, 1999). When we used the more positive values for slow inactivation and kinetic parameters derived from modeling patch currents, we obtained action potentials at a resting potential of −85 mV that closely resembled those of real muscle fibers with a similar resting potential (Fig. 1, C1 and C2). However, hyperexcitability was present at a resting potential of −67 mV. The threshold for action potential initiation was very close to the membrane potential, and both myotonia and anode break excitation were observed (Fig. 1, C3 and C4). Use of the more negative published value for the midpoint for slow inactivation led to inexcitability at a resting potential of −67 mV (Fig. 1, row E). Thus, despite our ability to accurately model action potentials at a resting potential of −85 mV, we could find no combination of parameters for the specific membrane resistance, slow inactivation, and maximal sodium conductance that also allowed us to accurately simulate muscle fiber excitability at a resting potential of −67 mV. At a resting potential of −67 mV, fibers were either inexcitable or hyperexcitable.
To obtain action potentials with appropriate amplitude and threshold at a resting potential of −67 mV, we found it necessary to use values for midpoints of fast inactivation (−66 mV) and activation (−30 mV) that were more positive than we had previously measured from intact muscle fibers held at −110 mV. Use of the more positive values of activation and inactivation resulted in a threshold for action potential initiation close to −45 mV with a peak at +5 mV (Fig. 1, F2) and prevented both myotonia and anode break excitation (Fig. 1, F3 and F4). These values for action potential threshold and peak agreed well with values we have observed previously in muscle fibers depolarized to near −67 mV using extracellular potassium (Rich and Pinter, 2003). However, midpoint values for activation and fast inactivation that worked well at a resting potential of −67 mV did not provide accurate simulation of action potentials at a resting potential of −85 mV. At −85 mV, these parameters resulted in a threshold for action potential initiation of −52 mV, which is 13 mV more positive than the threshold seen in real muscle fibers (Fig. 1, F1 vs. A1). Thus, the only way we were able to accurately model action potentials at resting potentials of both −85 and −67 mV was to use a different set of parameters for the voltage dependence of activation and fast inactivation for each resting potential.
Holding Potential-dependent Changes in the Voltage Dependence of Sodium Channel Activation and Fast Inactivation
The modeling studies above show that shifts in the voltage dependence of sodium channel activation and fast inactivation are needed to accurately simulate muscle fiber excitability during depolarization of the resting potential. If such shifts occur in muscle fibers in vivo, they may be of crucial importance for regulating excitability. Holding potential–induced changes in the voltage dependence of activation and fast inactivation in skeletal muscle have been noted during studies of slow inactivation of sodium currents from rat muscles (Simoncini and Stuhmer, 1987; Ruff et al., 1988). However, the significance of the effect was unclear and because increased extracellular calcium reduced the effect, subsequent studies were performed in high extracellular calcium (Simoncini and Stuhmer, 1987; Ruff et al., 1988). Our modeling studies suggest that this effect might be necessary to appropriately regulate muscle fiber excitability, so we performed further studies using normal extracellular calcium levels.
To study the effects of holding potential on the voltage dependence of inactivation, we held fibers for up to 30 min at various holding potentials. At each holding potential, we measured the midpoint of the voltage dependence of fast inactivation every 1 to 2 min using the voltage protocol shown in Fig. 3 A. We found that changing the holding potential caused a shift in the voltage dependence of fast inactivation (Fig. 3 B). A similar effect was observed for the voltage dependence of activation (Fig. 3 C).
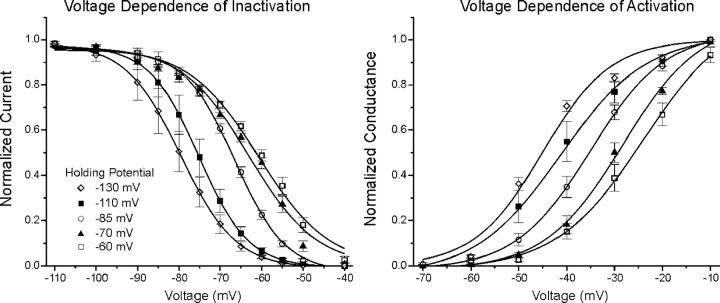
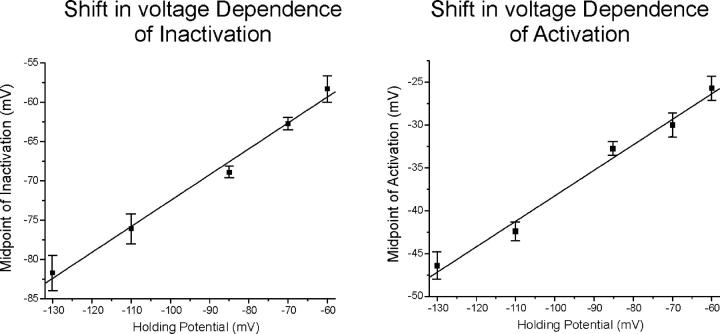
We examined the magnitude of the shift in the voltage dependence of inactivation and activation as the holding potential was varied from −130 to −60 mV. The effect is quite large; the voltage dependence of both activation and inactivation shift >20 mV when the holding potential is changed from −130 to −60 mV (Table II; Fig. 4). We plotted the midpoint of both fast inactivation and activation versus the holding potential for holding potentials ranging from −130 to −60 mV (Fig. 5) . The data were well represented by linear fits for both activation (R = 0.99, P < 0.01, slope = 0.29) and inactivation (R = 0.99, P < 0.01, slope = 0.29). Using the slope of the linear fit, we estimated that the magnitude of the shift between resting potentials of −85 mV and −67 mV would be >5 mV for both activation and fast inactivation. This is close to the 7-mV shift that was required to accurately model muscle fiber excitability at resting potentials of both −85 and −67 mV. Thus, data from muscle fibers studied in vivo support the prediction from our modeling study that the voltage dependence of sodium channel gating is modulated by resting potential.
Figure 4.
The voltage dependence of inactivation and activation at various holding potentials. On the left is the plot of the voltage dependence of inactivation at holding potentials ranging from −130 to −60 mV. On the right is the plot of the voltage dependence of activation over the same range of holding potentials. As the holding potential becomes more depolarized, the voltage dependence of both inactivation and activation shift to more depolarized potentials.
Figure 5.
The voltage dependence of shifts in the midpoint of sodium channel gating. Shown on the left is the plot of the midpoint of fast inactivation versus holding potential. On the right is the plot of the midpoint of activation versus holding potential. Both sets of data are fit well (R = 0.99, P < 0.01) with a linear fit with a slope of 0.29. For the number of fibers at each holding potential refer to Table II
TABLE II.
Holding Potential Dependence of Activation and Inactivation
| V hold (mV) | Km act (mV) | Slope | N | Km inact (mV) | Slope | N |
|---|---|---|---|---|---|---|
| −60 | −25.7 ± 1.4 | 7.8 ± 0.9 | 8 | −58.3 ± 1.7 | 7.9 ± 0.7 | 4 |
| −70 | −30.9 ± 1.0 | 6.8 ± 0.4 | 7 | −62.4 ± 0.6 | 10.1 ± 0.8 | 7 |
| −85 | −32.8 ± 0.4 | 7.0 ± 0.4 | 14 | −68.9 ± 0.7 | 6.3 ± 0.3 | 10 |
| −110 | −41.7 ± 1.9 | 7.6 ± 0.3 | 6 | −74.3 ± 0.8 | 5.3 ± 0.2 | 5 |
| −130 | −46.6 ± 1.6 | 7.0 ± 0.4 | 6 | −79.2 ± 1 | 5.6 ± 0.2 | 5 |
Changes in the voltage dependence of the midpoint of activation (Km act) and fast inactivation (Km inact) for sodium channels in muscle fibers at various holding potentials (V hold). N = the number of muscle fibers studied at each holding potential.
Effects of Brief Prepulse and Test Pulse Amplitude on Voltage Dependence
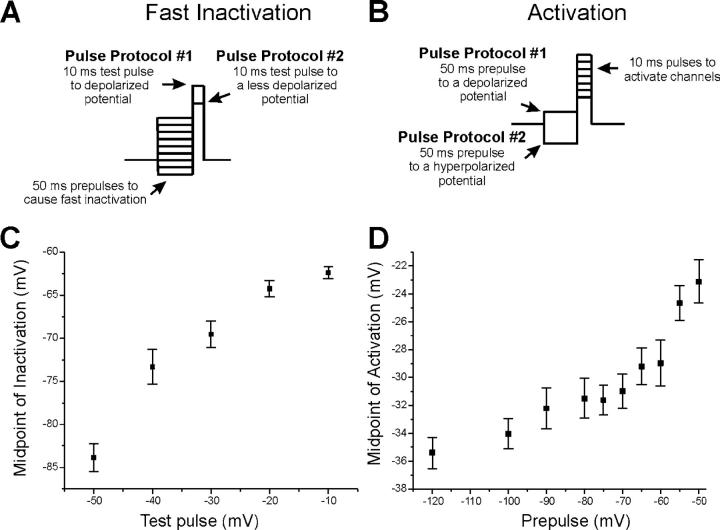
During the course of experiments, we noticed that different test potential amplitudes (Fig. 6 A) produced differences in the apparent voltage dependence of inactivation. Similarly, changing the prepulse amplitude (Fig. 6 B) produced differences in the apparent voltage dependence of activation. This was unexpected since evidence presented above suggested that shifts in the voltage dependence of activation and inactivation take minutes to occur. Previously, a dependence of inactivation on the test pulse amplitude was observed during tight seal recording from cardiac myocytes, and the authors suggested this might be due to the presence of populations of sodium channels with differences in the voltage dependence of activation and inactivation (Kimitsuki et al., 1990). To further characterize these effects in skeletal muscle we determined the relationships between prepulse and test pulse amplitudes and the voltage dependence of activation and inactivation. As shown in Fig. 6 C, as the test pulse amplitude was made more positive, the measured voltage dependence of inactivation shifted toward more depolarized potentials. Similarly, as more depolarized prepulses were used, the measured voltage dependence of activation shifted toward more depolarized potentials (Fig. 6 D). These results demonstrate that the measured voltage dependence of activation and inactivation is directly related to the amplitude of prepulses and test pulses used during the protocols. Evidence presented above indicates that changes in voltage dependence require minutes to occur after changes in holding potential. Thus, the results shown in Fig. 6 (C and D) indicate that either multiple populations of channels exist with differences in the voltage dependence of activation and inactivation or that a distribution of voltage dependences exists within the population of channels.
Figure 6.
The measured voltage dependence of sodium channel inactivation and activation depends on the pulse protocol used. (A) Examples of two pulse protocols used to measure the voltage dependence of fast inactivation. In protocol 1, a depolarized test potential is used that activates all sodium channels. Thus when prepulses are altered to measure the voltage dependence of fast inactivation, the measured voltage dependence of fast inactivation is affected by all Nav1.4 sodium channels. In protocol 2, a more hyperpolarized activation pulse is used that only activates channels that gate at hyperpolarized potentials. In protocol 2, the voltage dependence of inactivation will preferentially measure the voltage dependence of inactivation of sodium channels that have a hyperpolarized voltage dependence of activation. (B) Examples of two pulse protocols used to measure the voltage dependence of activation. In protocol 1, a depolarized prepulse preferentially inactivates sodium channels that inactivate at hyperpolarized potentials. Thus protocol 1 will preferentially measure the voltage dependence of activation of sodium channels that have a depolarized voltage dependence of inactivation. Protocol 2 will not inactivate any sodium channels so that the voltage dependence of activation includes both sodium channels that inactivate at hyperpolarized potentials and sodium channels that inactivate at depolarized potentials. (C) The midpoint of inactivation is plotted against the test pulse used to activate sodium channels in a patch held at −80 mV. Use of a test pulse of −50 mV yields a midpoint of inactivation of close to −84 mV. Use of more depolarized test pulses yielded more depolarized midpoints of inactivation. (D) The midpoint of activation is plotted against the prepulse potential used to inactivate sodium channels before measurement of the voltage dependence of activation in a patch held at −80 mV. As the prepulse becomes increasingly depolarized, the measured voltage dependence of activation shifts toward depolarized potentials. For inactivation, n for each test potential is (−50:5, −40:9, −30:13, −20:10, −10:12). For activation, n for each prepulse is (−120:9, −100:10, −90:7, −80:7, −75:10, −70:8, −65:8, −60:8, −55:9, −50:9).
Controls for the Loose Patch Recording Technique
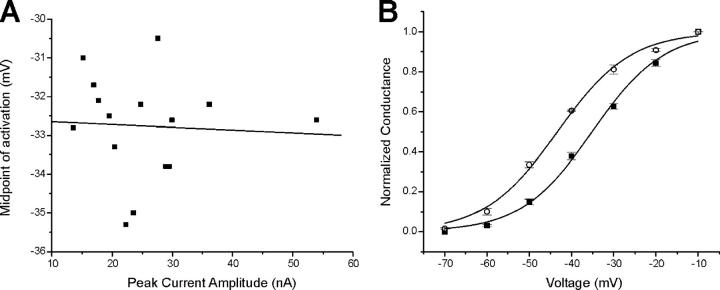
To study sodium channel gating in skeletal muscle in vivo, we used the loose patch technique to acquire the data presented above. Loose patch studies have the advantage that they allow study of sodium channel gating in vivo with minimal perturbation of the muscle fiber. However, loose patch studies in which the holding potential is altered are complicated by changes in the amplitude of the sodium current over time due to changes in the fraction of sodium channels that are slow inactivated. Since the interior of the muscle fiber is not clamped during loose patch measurement of currents, large inward sodium current can cause depolarization of the fiber and underestimation of the voltage step. Our studies of fast inactivation were not significantly affected by this problem since we used a voltage step to −30 mV to activate the sodium current. Following a step to −30 mV, depolarization of the fiber by as much as 20 mV causes little change in current amplitude since the current is near maximal (Rich and Pinter, 2003). Measures of the voltage dependence of activation, however, could be affected by lack of voltage control of the muscle fiber interior. To determine whether depolarization of the muscle fiber was shifting our measurements of activation midpoint, we examined the effect of sodium current amplitude on the measured voltage dependence of sodium channel activation. If an absence of interior voltage control was a contributing factor, we reasoned that patches in which currents were larger should have a more negative voltage dependence of activation. We plotted the midpoint of activation measured at a holding potential of −85 mV versus the amplitude of the peak current and found no significant correlation (Fig. 7 A, R = −0.06, P = 0.85). It thus appears unlikely that lack of voltage control of the muscle fiber interior affected our measures of the voltage dependence of activation. Nevertheless, we discarded data from patches in which the maximal inward current was >50 nA to limit any possible contributions of uncontrolled internal depolarization.
Figure 7.
Holding potential–dependent shifts in sodium channel gating are not due to artifacts of the loose patch technique. (A) Scatterplot of the midpoint of activation versus the peak inward current for 15 patches held at −85 mV. There is no correlation between the amplitude of the current and the midpoint of inactivation. The linear fit of the data yields an R value of −0.06 with a P value of 0.85. The mean of the data shown is presented in Table II. For data included in Table II the patch with the maximal inward current of 55 nA was discarded. (B) Shown is the average voltage dependence of activation for three muscle fibers at holding potentials of −130 mV (open circles) and −110 mV (filled squares). All recordings were performed in solution containing 12 mM potassium. Resting potentials were between −55 and −60 mV such that sodium channels under poor voltage control were mostly inactivated. In patches held at −130 mV, the prepulse was to −80 mV, and the average maximal current amplitude was 9.4 ± 0.9 nA. For patches held at −110 mV, the prepulse was to −90 mV and the average maximal current amplitude was 16.5 ± 0.1 nA. In this group of patches, the average current was larger in cells held at the more depolarized holding potential. Thus, the shift in the voltage dependence of activation cannot be accounted for by lack of voltage clamp of the interior of the muscle fiber. Values shown represent the means ± SEM.
Another potential artifact during loose patch studies involves channels that are under poor voltage control near the edge of the pipette (Stuhmer et al., 1983; Roberts and Almers, 1984). Sodium channels under poor voltage control near the edge of the pipette can activate during depolarizing steps and thus complicate measures of the voltage dependence of activation. This is particularly problematic during the most depolarizing voltage steps. To reduce the contribution from channels under poor voltage control, we depolarized fibers to resting potentials between −50 and −60 mV using 12 mM external potassium. This caused slow inactivation of sodium channels along the length of the fiber. By holding patches at various potentials hyperpolarized to the resting potential, slow inactivation was selectively relieved in channels under good voltage control. Under these conditions, holding potential–induced shifts in the voltage dependence of activation were still observed (Fig. 7 B).
DISCUSSION
We report here that altering the holding potential of skeletal muscle membrane for prolonged periods induces a shift in the voltage dependence of sodium channel activation and fast inactivation. Experiments in which the amplitude of prepulses or test potentials was altered suggest that a distribution may exist in the voltage dependence of gating of Nav1.4 sodium channels at any given holding potential. Based on these results, we propose that holding potential–induced shifts in the voltage dependence of sodium channel gating are due to shifts in the distribution of voltage dependences of Nav1.4 gating within the population of sodium channels. Computer simulation of action potentials suggests that a resting potential–induced shift in the voltage dependence of sodium channel gating is necessary to appropriately regulate muscle excitability.
Technical Considerations
We used loose patch recording methods to study the voltage dependence of sodium channel gating. One concern is that the shift in the voltage dependence of sodium channel gating that we report is due to an artifact of loose patch recording. This concern is heightened by the fact that a holding potential–induced shift in the voltage dependence of sodium channel gating has not been widely noted despite numerous studies of sodium channel gating using tight seal patch recording. One potential explanation for why holding potential–induced shifts in gating have not been more widely reported is that the effect occurs very slowly and thus requires prolonged changes in holding potential. In most studies of sodium channel gating behavior, a single holding potential is used throughout the experiment so that any changes due to alterations of holding potential will be missed. Furthermore, many recordings of sodium currents are performed in the whole cell mode or use two-electrode voltage clamp in oocytes. In both situations, factors that regulate sodium channel gating in vivo may be absent. In the whole cell recording mode, as the intracellular milieu is washed out, shifts in the voltage dependence of Nav1.4 gating occur (Wang et al., 1996) that could obscure holding potential–dependent shifts.
When the results of loose patch recording of cardiac sodium currents have been directly compared with the results of tight seal patch recording, it appears that the loose patch technique avoids shifts in sodium channel gating induced by formation of the tight seal (Eickhorn et al., 1994). Thus, one advantage of loose patch recording is that it avoids some of the artifacts associated with the formation of a tight seal and thus allows for measurement of sodium channel gating with minimal perturbation of the cell. A disadvantage of loose patch is the potential artifacts that may appear due to lack of internal voltage clamp or poor voltage control. However, our control experiments suggest that neither of these potential problems contributed to our results. Moreover, there is evidence that the shifts we report do in fact occur when using tight seal recording methods under appropriate conditions (Kimitsuki et al., 1990).
Effects of Holding Potential on Gating
We propose both that holding potential affects the voltage dependence of sodium channel gating and that there is a distribution of voltage dependences of gating of individual Nav1.4 channels at a given holding potential. Thus, shifts in the voltage dependence of gating with changes in holding potential likely represent shifts in the average of a population of voltage dependences.
Although this is the first study in which a holding potential–induced shift in the voltage dependence of gating has been studied in detail, there have been studies in which the phenomenon has been noted (Simoncini and Stuhmer, 1987; Ruff et al., 1988; Kimitsuki et al., 1990). In two of the studies, the phenomenon was thought to be an artifact of the loose patch technique (Simoncini and Stuhmer, 1987; Ruff et al., 1988). As it was noted in those studies that high extracellular Ca minimized the effect, further experiments were performed in elevated extracellular Ca. In the third study, the effect could not be ascribed to the loose patch technique, and it was proposed that the effect was due to an artifact caused by interaction of sodium channels with fixed negative charges on the glass of the pipette (Kimitsuki et al., 1990). Ours is the first study to propose that the effect described is real and of biologic importance.
The time course of the effects of holding potential we have shown here are similar to the time course of slow inactivation (Ruff et al., 1987; Simoncini and Stuhmer, 1987; Ruff, 1999). Thus, it is possible that the effect is related to slow inactivation. However, several considerations indicate that slow inactivation is distinct. Since the shift in gating occurs in channels that are not slow inactivated, it must be distinct from slow inactivation. It is possible, however, that the process represents transitions between multiple nonslow inactivated states similar to the multiple slow inactivated states that exist (Toib et al., 1998; Vilin and Ruben, 2001). However, high extracellular calcium does not prevent slow inactivation (Simoncini and Stuhmer, 1987; Ruff et al., 1988), whereas it significantly reduces holding potential–induced changes in the voltage dependence of sodium channel gating (Simoncini and Stuhmer, 1987; Ruff et al., 1988; Kimitsuki et al., 1990).
A number of studies have found that holding for prolonged periods at depolarized potentials causes hyperpolarized shifts in the voltage dependence of gating of sodium and potassium channels (Bezanilla et al., 1982; Ji et al., 1994; Chang et al., 1996; Olcese et al., 1997). In some studies of sodium channels this was termed modal gating and was associated with two states with markedly different kinetics of gating (Ji et al., 1994; Chang et al., 1996). We report a phenomenon that is distinct from modal gating in that depolarized holding potentials cause depolarized shifts in the voltage dependence of gating that are not associated with clear changes in kinetics (unpublished data).
We also found that changing the amplitude of the prepulse or test pulse leads to a change in the measured voltage dependence of activation and inactivation, respectively. It has previously been reported that changes in amplitude of the prepulse potential alter the kinetics of potassium and sodium channel activation (Cole and Moore, 1960; Taylor and Bezanilla, 1983). This is known as the Cole-Moore effect (Taylor and Bezanilla, 1983) and the focus was on kinetics, whereas we have focused on the change in voltage dependence. Our results showing test potential affects the measured voltage dependence of sodium channel inactivation are similar to those from previous studies (Hoyt and Adelman, 1970; Kimitsuki et al., 1990). It has recently been reported that altering the prepulse alters the voltage dependence of HCN channel gating (Mannikko et al., 2005).
Our findings suggest that the gating properties of individual Nav1.4 channels may be heterogeneous. There is no single channel evidence of which we are aware that suggests such heterogeneity in the voltage dependence of gating of individual sodium channels of a given isoform within individual cells. However, there is evidence from single channel studies in adult frog skeletal muscle in vivo that gating kinetics of individual sodium channels can switch over prolonged time periods (Patlak and Ortiz, 1986, 1989; Patlak et al., 1986). We propose that prolonged changes in holding potential modify the voltage sensitivity of individual Nav1.4 channels. This results in a shift in the distribution of voltage dependences in the population of Nav1.4 channels in a patch of membrane and results in a shift in the average voltage dependence of the sodium current.
Functional Implications
The ability to alter the voltage dependence of Na channel gating may serve an important role in maintaining excitability under various conditions. The gating behavior we report here could be important in diseases where muscle resting potential becomes depolarized, such as hyperkalemic periodic paralysis (Cannon, 2002; Jurkat-Rott et al., 2002) and critical illness myopathy (Rich et al., 1998; Rich and Pinter, 2001, 2003; Filatov and Rich, 2004). Resting potential–dependent shifts in sodium channel gating may also be important in maintaining excitability of muscle during periods of intense exercise when K+ accumulates extracellularly (Cannon et al., 1993; Green et al., 2000; Sejersted and Sjogaard, 2000). Changes in intracellular pH that reduce chloride conductance may also help prevent loss of excitability during periods of intense exercise (Pedersen et al., 2004, 2005). Our modeling suggests that resting potential–dependent shifts in the voltage dependence of gating may be necessary to prevent hyperexcitability when muscle becomes depolarized.
Resting potential–dependent regulation of sodium channel gating may also play a role in diseases of excitability in brain and heart. The phenomenon has been reported in the Nav1.5 isoform (expressed in cardiac muscle) (Kimitsuki et al., 1990) and may occur in the Nav1.2 isoform (expressed in neurons) (Majumdar et al., 2004). Changes in the voltage dependence of gating of the Nav1.5 sodium channel could play an important role in preventing arrhythmias during cardiac depolarization due to ischemia. In neurons, shifts in the voltage dependence of sodium channel gating could play an important role in modulating excitability in diseases such as epilepsy.
It has previously been suggested that the presence of multiple sodium channel isoforms and regulation of sodium channel isoforms through processes such as phosphorylation allow for diversity in the gating characteristics of sodium channels (Cantrell and Catterall, 2001; Goldin, 2001; Waxman, 2001). Our findings suggest that there is even more diversity and regulation of sodium channel gating than has been suspected. Additional studies are needed to determine whether similar resting potential–dependent modulation of gating also occurs in voltage-gated potassium and calcium channels.
Acknowledgments
We would like to thank Criss Hartzell for helpful comments.
This work was supported by National Institutes of Health grant NS040826 (M.M. Rich).
Olaf S. Andersen served as editor.
References
- Albuquerque, E.X., and S. Thesleff. 1968. A comparative study of membrane properties of innervated and chronically denervated fast and slow skeletal muscles of the rat. Acta Physiol. Scand. 73:471–480. [DOI] [PubMed] [Google Scholar]
- Bezanilla, F., R.E. Taylor, and J.M. Fernandez. 1982. Distribution and kinetics of membrane dielectric polarization. 1. Long-term inactivation of gating currents. J. Gen. Physiol. 79:21–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bird, S.J., and M.M. Rich. 2002. Critical illness myopathy and polyneuropathy. Curr. Neurol. Neurosci. Rep. 2:527–533. [DOI] [PubMed] [Google Scholar]
- Cannon, S.C. 2002. An expanding view for the molecular basis of familial periodic paralysis. Neuromuscul. Disord. 12:533–543. [DOI] [PubMed] [Google Scholar]
- Cannon, S.C., R.H. Brown Jr., and D.P. Corey. 1993. Theoretical reconstruction of myotonia and paralysis caused by incomplete inactivation of sodium channels. Biophys. J. 65:270–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantrell, A.R., and W.A. Catterall. 2001. Neuromodulation of Na+ channels: an unexpected form of cellular plasticity. Nat. Rev. Neurosci. 2:397–407. [DOI] [PubMed] [Google Scholar]
- Carnahan, B., H.A. Luther, and J.O. Wilkes. 1969. Applied Numerical Methods. Wiley, New York. 604 pp.
- Chang, S.Y., J. Satin, and H.A. Fozzard. 1996. Modal behavior of the mu 1 Na+ channel and effects of coexpression of the β1-subunit. Biophys. J. 70:2581–2592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole, K.S., and J.W. Moore. 1960. Potassium ion current in the squid giant axon: dynamic characteristic. Biophys. J. 1:1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooley, J., and F. Dodge. 1966. Digital computer solutions for excitation and propagation of the nerve impulse. Biophys. J. 6:583–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooley, J., and F. Dodge. 1973. Action potential of the motorneuron. IBM Journal of Research and Development. 17:219–229. [Google Scholar]
- Eickhorn, R., C. Dragert, and H. Antoni. 1994. Influence of cell isolation and recording technique on the voltage dependence of the fast cardiac sodium current of the rat. J. Mol. Cell. Cardiol. 26:1095–1108. [DOI] [PubMed] [Google Scholar]
- Farnbach, G.C., and R.L. Barchi. 1977. Determination of muscle cable parameters from a single membrane voltage response. J. Membr. Biol. 32:133–149. [DOI] [PubMed] [Google Scholar]
- Featherstone, D.E., J.E. Richmond, and P.C. Ruben. 1996. Interaction between fast and slow inactivation in Skm1 sodium channels. Biophys. J. 71:3098–3109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filatov, G.N., and M.M. Rich. 2004. Hyperpolarized shifts in the voltage dependence of fast inactivation of Nav1.4 and Nav1.5 in a rat model of critical illness myopathy. J. Physiol. 559:813–820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldin, A.L. 2001. Resurgence of sodium channel research. Annu. Rev. Physiol. 63:871–894. [DOI] [PubMed] [Google Scholar]
- Green, S., H. Langberg, D. Skovgaard, J. Bulow, and M. Kjaer. 2000. Interstitial and arterial-venous [K+] in human calf muscle during dynamic exercise: effect of ischaemia and relation to muscle pain. J. Physiol. 529(Pt 3):849–861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin, A.L., and A.F. Huxley. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoyt, R.C., and W.J. Adelman Jr. 1970. Sodium inactivation. Experimental test of two models. Biophys. J. 10:610–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji, S., W. Sun, A.L. George Jr., R. Horn, and R.L. Barchi. 1994. Voltage-dependent regulation of modal gating in the rat SkM1 sodium channel expressed in Xenopus oocytes. J. Gen. Physiol. 104:625–643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurkat-Rott, K., H. Lerche, and F. Lehmann-Horn. 2002. Skeletal muscle channelopathies. J. Neurol. 249:1493–1502. [DOI] [PubMed] [Google Scholar]
- Kimitsuki, T., T. Mitsuiye, and A. Noma. 1990. Negative shift of cardiac Na+ channel kinetics in cell-attached patch recordings. Am. J. Physiol. 258:H247–H254. [DOI] [PubMed] [Google Scholar]
- Kirsch, G.E., and M.F. Anderson. 1986. Sodium channel kinetics in normal and denervated rabbit muscle membrane. Muscle Nerve. 9:738–747. [DOI] [PubMed] [Google Scholar]
- Lorkovic, H., and R.J. Tomanek. 1977. Potassium and chloride conductances in normal and denervated rat muscles. Am. J. Physiol. 232:C109–C114. [DOI] [PubMed] [Google Scholar]
- Majumdar, S., G. Foster, and S.K. Sikdar. 2004. Induction of pseudo-periodic oscillation in voltage-gated sodium channel properties is dependent on the duration of prolonged depolarization. Eur. J. Neurosci. 20:127–143. [DOI] [PubMed] [Google Scholar]
- Mannikko, R., S. Pandey, H.P. Larsson, and F. Elinder. 2005. Hysteresis in the voltage dependence of HCN channels: conversion between two modes affects pacemaker properties. J. Gen. Physiol. 125:305–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley, B.A., and B.R. Eisenberg. 1975. Sizes of components in frog skeletal muscle measured by methods of stereology. J. Gen. Physiol. 66:31–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowycky, M.C., and M.J. Pinter. 1993. Time courses of calcium and calcium-bound buffers following calcium influx in a model cell. Biophys. J. 64:77–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olcese, R., R. Latorre, L. Toro, F. Bezanilla, and E. Stefani. 1997. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. J. Gen. Physiol. 110:579–589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palade, P.T., and R.L. Barchi. 1977. Characteristics of the chloride conductance in muscle fibers of the rat diaphragm. J. Gen. Physiol. 69:325–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pappone, P.A. 1980. Voltage-clamp experiments in normal and denervated mammalian skeletal muscle fibres. J. Physiol. 306:377–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak, J.B., and M. Ortiz. 1986. Two modes of gating during late Na+ channel currents in frog sartorius muscle. J. Gen. Physiol. 87:305–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak, J.B., and M. Ortiz. 1989. Kinetic diversity of Na+ channel bursts in frog skeletal muscle. J. Gen. Physiol. 94:279–301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak, J.B., M. Ortiz, and R. Horn. 1986. Opentime heterogeneity during bursting of sodium channels in frog skeletal muscle. Biophys. J. 49:773–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peachey, L.D. 1975. Structure and function of the T-system of vertebrate skeletal muscle. The Nervous System. Vol. 1. D.B. Tower, editor. Raven Press, New York. 81–89.
- Pedersen, T.H., O.B. Nielsen, G.D. Lamb, and D.G. Stephenson. 2004. Intracellular acidosis enhances the excitability of working muscle. Science. 305:1144–1147. [DOI] [PubMed] [Google Scholar]
- Pedersen, T.H., F. de Paoli, and O.B. Nielsen. 2005. Increased excitability of acidified skeletal muscle: role of chloride conductance. J. Gen. Physiol. 125:237–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich, M.M., and M.J. Pinter. 2001. Sodium channel inactivation in an animal model of acute quadriplegic myopathy. Ann. Neurol. 50:26–33. [DOI] [PubMed] [Google Scholar]
- Rich, M.M., and M.J. Pinter. 2003. Crucial role of sodium channel fast inactivation in muscle fibre inexcitability in a rat model of critical illness myopathy. J. Physiol. 547:555–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich, M.M., J.W. Teener, E.C. Raps, D.L. Schotland, and S.J. Bird. 1996. Muscle is electrically inexcitable in acute quadriplegic myopathy. Neurology. 46:731–736. [DOI] [PubMed] [Google Scholar]
- Rich, M.M., S.J. Bird, E.C. Raps, L.F. McCluskey, and J.W. Teener. 1997. Direct muscle stimulation in acute quadriplegic myopathy. Muscle Nerve. 20:665–673. [DOI] [PubMed] [Google Scholar]
- Rich, M.M., M.J. Pinter, S.D. Kraner, and R.L. Barchi. 1998. Loss of electrical excitability in an animal model of acute quadriplegic myopathy. Ann. Neurol. 43:171–179. [DOI] [PubMed] [Google Scholar]
- Roberts, W.M., and W. Almers. 1984. An improved loose patch voltage clamp method using concentric pipettes. Pflugers Arch. 402:190–196. [DOI] [PubMed] [Google Scholar]
- Ruff, R.L. 1996. Single-channel basis of slow inactivation of Na+ channels in rat skeletal muscle. Am. J. Physiol. 271:C971–C981. [DOI] [PubMed] [Google Scholar]
- Ruff, R.L. 1999. Effects of temperature on slow and fast inactivation of rat skeletal muscle Na+ channels. Am. J. Physiol. 277:C937–C947. [DOI] [PubMed] [Google Scholar]
- Ruff, R.L., L. Simoncini, and W. Stuhmer. 1987. Comparison between slow sodium channel inactivation in rat slow- and fast-twitch muscle. J. Physiol. 383:339–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff, R.L., L. Simoncini, and W. Stuhmer. 1988. Slow sodium channel inactivation in mammalian muscle: a possible role in regulating excitability. Muscle Nerve. 11:502–510. [DOI] [PubMed] [Google Scholar]
- Sejersted, O.M., and G. Sjogaard. 2000. Dynamics and consequences of potassium shifts in skeletal muscle and heart during exercise. Physiol. Rev. 80:1411–1481. [DOI] [PubMed] [Google Scholar]
- Simoncini, L., and W. Stuhmer. 1987. Slow sodium channel inactivation in rat fast-twitch muscle. J. Physiol. 383:327–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuhmer, W., W.M. Roberts, and W. Almers. 1983. The loose-patch clamp. Single Channel Recording. B. Sakmann and E. Neher, editors. Plenum Press, New York. 123–132.
- Taylor, R.E., and F. Bezanilla. 1983. Sodium and gating current time shifts resulting from changes in initial conditions. J. Gen. Physiol. 81:773–784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toib, A., V. Lyakhov, and S. Marom. 1998. Interaction between duration of activity and time course of recovery from slow inactivation in mammalian brain Na+ channels. J. Neurosci. 18:1893–1903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vilin, Y.Y., and P.C. Ruben. 2001. Slow inactivation in voltage-gated sodium channels: molecular substrates and contributions to channelopathies. Cell Biochem. Biophys. 35:171–190. [DOI] [PubMed] [Google Scholar]
- Vilin, Y.Y., E. Fujimoto, and P.C. Ruben. 2001. A single residue differentiates between human cardiac and skeletal muscle Na+ channel slow inactivation. Biophys. J. 80:2221–2230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, D.W., A.L. George Jr., and P.B. Bennett. 1996. Comparison of heterologously expressed human cardiac and skeletal muscle sodium channels. Biophys. J. 70:238–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waxman, S.G. 2001. Transcriptional channelopathies: an emerging class of disorders. Nat. Rev. Neurosci. 2:652–659. [DOI] [PubMed] [Google Scholar]