The NH₂ Terminus of RCK1 Domain Regulates Ca²⁺-dependent BK_Ca Channel Gating

Abstract

Large conductance, voltage- and Ca²⁺-activated K⁺ (BK_Ca) channels regulate blood vessel tone, synaptic transmission, and hearing owing to dual activation by membrane depolarization and intracellular Ca²⁺. Similar to an archeon Ca²⁺-activated K⁺ channel, MthK, each of four α subunits of BK_Ca may contain two cytosolic RCK domains and eight of which may form a gating ring. The structure of the MthK channel suggests that the RCK domains reorient with one another upon Ca²⁺ binding to change the gating ring conformation and open the activation gate. Here we report that the conformational changes of the NH₂ terminus of RCK1 (AC region) modulate BK_Ca gating. Such modulation depends on Ca²⁺ occupancy and activation states, but is not directly related to the Ca²⁺ binding sites. These results demonstrate that AC region is important in the allosteric coupling between Ca²⁺ binding and channel opening. Thus, the conformational changes of the AC region within each RCK domain is likely to be an important step in addition to the reorientation of RCK domains leading to the opening of the BK_Ca activation gate. Our observations are consistent with a mechanism for Ca²⁺-dependent activation of BK_Ca channels such that the AC region inhibits channel activation when the channel is at the closed state in the absence of Ca²⁺; Ca²⁺ binding and depolarization relieve this inhibition.

INTRODUCTION

BK_Ca channels, encoded by the Slo1 gene (Atkinson et al., 1991; Adelman et al., 1992; Butler et al., 1993; Tseng-Crank et al., 1994), are dually activated by voltage and cytosolic Ca²⁺, allowing outward K⁺ current to repolarize the membrane and prevent further entry of Ca²⁺ ions into the cell through voltage-dependent Ca²⁺ channels (Marty, 1981; Pallotta et al., 1981; Hudspeth and Lewis, 1988b; Robitaille et al., 1993; Cui et al., 1997; Yazejian et al., 1997). They play key regulatory roles in diverse physiological functions involving cellular [Ca²⁺]_i, such as neurotransmitter release (Robitaille et al., 1993; Yazejian et al., 1997), cochlear hair-cell tuning (Hudspeth and Lewis, 1988a,b; Fettiplace and Fuchs, 1999; Duncan and Fuchs, 2003), arterial smooth muscle tone regulation (Nelson et al., 1995; Brenner et al., 2000), and immunity (Ahluwalia et al., 2004). Recently, it was found that a mutation in the BK_Ca α-subunit is linked to generalized epilepsy and paroxysmal dyskinesia by altering Ca²⁺ sensitivity of the channel (Du et al., 2005).

BK_Ca possesses common structural features of homotetrameric voltage-gated K⁺ channels, including an ion-selective pore formed by transmembrane segments S5 and S6 and a selectivity filter from four α-subunits, and a voltage-sensing module formed by transmembrane segments S1–S4. In addition, the Slo1 protein has a long intracellular COOH terminus that may form a Ca²⁺-sensing module. Based on the X-ray crystallographic structures of the K⁺ channel in Escherichia coli and an archeon Ca²⁺-activated K⁺ channel, MthK, as well as the homology of BK_Ca with these channels, it is proposed that the intracellular COOH terminus of each Slo1 protein may contain two consecutive RCK domains (RCK1 and RCK2), which form a gating ring in the tetrameric channel (Jiang et al., 2001, 2002a). Three possible divalent binding sites have been identified in the Slo1 protein (Zeng et al., 2005) of which two putative Ca²⁺ binding sites for the intracellular Ca²⁺-sensing module are proposed to be located in the RCK1 domain (Bao et al., 2002; Xia et al., 2002) and in Ca²⁺ bowl, a COOH-terminal motif that contains repeated Asp residues (Schreiber and Salkoff, 1997; Schreiber et al., 1999; Bian et al., 2001; Bao et al., 2004). Mutation of residues in these proposed Ca²⁺ binding sites reduces or abolishes Ca²⁺ sensitivity of channel activation (Schreiber and Salkoff, 1997; Bao et al., 2002, 2004; Xia et al. 2002; Zeng et al., 2005).

While the identification of Ca²⁺ binding sites has been a focus of recent research on BK_Ca activation (Bian et al., 2001; Braun and Sy, 2001; Shi and Cui, 2001; Zhang et al., 2001; Bao et al., 2002, 2004; Piskorowski and Aldrich, 2002; Shi et al., 2002; Xia et al., 2002; Qian and Magleby, 2003; Zeng et al., 2005), the molecular process of how Ca²⁺ binding is coupled to channel opening has been less studied. Nevertheless, the proposed mechanism of MthK activation based on its structure provides an excellent model for this aspect of BK_Ca channel activation. In the MthK channel, RCK domains in the gating ring interact with one another at two interfaces, a fixed interface and a flexible interface (Jiang et al., 2002a). By comparing the structures of MthK and the RCK domain of the E. coli K⁺ channel, it is proposed that Ca²⁺ binding to the MthK channel alters the orientation among RCK domains in the gating ring by rearranging the flexible interface, which changes the conformation of the gating ring and opens the channel by pulling the linker between the inner helix and the gating ring (Jiang et al., 2001, 2002a). The Ca²⁺-dependent gating mechanism of BK_Ca is suggested to be similar to this mechanism by a recent study demonstrating that the gating properties of BK_Ca depend on the length of the linker between S6 and gating ring and which may be pulled by a conformational change in the gating ring during Ca²⁺-dependent activation (Niu et al., 2004). However, the nature of conformational changes in the BK_Ca gating ring during Ca²⁺-dependent activation may not be identical to that in the MthK channels. This is evident based on many differences between the function and structure of these two channels, including the affinity and location of the Ca²⁺ binding sites (Moczydlowski and Latorre, 1983; McManus and Magleby, 1991; Cox et al., 1997; Cui et al., 1997; Schreiber et al., 1999; Bao et al., 2002; Jiang et al., 2002a,b; Xia et al., 2002). In BK_Ca channels, the structural relationship between Ca²⁺ binding sites and the flexible interface is not clear. Whether a similar conformational change occurs at the flexible interface upon Ca²⁺ binding to the BK_Ca channel needs to be explored.

Here, by comparing structure and function between BK_Ca homologues mSlo1 (Butler et al., 1993) and dSlo1 (Adelman et al., 1992), we have identified a region in the NH₂ terminus of RCK1, called AC region, that modulates Ca²⁺ sensitivity of channel activation. We found that the difference in Ca²⁺ sensitivity between mSlo1 and dSlo1 was not due to differences in metal binding sites between the two channels. Instead, conformational differences in this AC region caused activation energy to change. The effects of AC region on channel gating depend on Ca²⁺ occupancy and activation state of the channel, suggesting that AC region is important in the energetic coupling between Ca²⁺ binding and the opening of the activation gate. In the crystal structure of the gating ring, the AC region of each RCK domain does not interact with any structure in other RCK domains and is distant from the flexible interface (Jiang et al., 2002a). The above observation, along with our findings, indicate that conformational changes occur in each individual RCK domain during BK_Ca activation upon Ca²⁺ binding. Regardless of whether such conformational changes within each RCK domain may either be driven by or combine with the reorientation among different RCK domains at the flexible interfaces, the conformational change in the AC region is a very important step in the allosteric machinery linking Ca²⁺ binding to channel opening.

An abstract of this work has been presented in the 49th Annual Meeting of Biophysical Society.

MATERIALS AND METHODS

Mutagenesis and Expression

The mbr5 splice variant of the mouse Slo1 BK_Ca channel (Butler et al., 1993) and the A1C2E1G3I0 splice variant of the Drosophila Slo1 channel (Adelman et al., 1992) were used to make mutant and chimeric channels. The wild-type (WT) mSlo1 and dSlo1 sequences included in each of the chimeras, given as the residue numbers in the primary sequence of the respective proteins are as follows: Chim1, dSlo1:1-611, mSlo1:631-1169; Chim2, dSlo1:1-475, mSlo1:462-1169; Chim3, dSlo1:1-432, mSlo1:419-1169; Chim4, dSlo1:1-389, mSlo1:376-1169; Chim5, dSlo1:1-336, mSlo1:323-1169; Chim6, dSlo1:1-271, mSlo1:257-1169; Chim7, dSlo1:71-127, mSlo1:1-43 and 114–1169; d[mAC], dSlo1:1-333 and 433–1164, mSlo1:320-418; m[dAC], dSlo1:334-432, mSlo1:1-319 and 419–1169. All mutant and chimeric constructs were made using overlap-extension PCR (Shi et al., 2002) with Pfu polymerase (Stratagene). The PCR-amplified regions were verified by sequencing. RNA was transcribed in vitro with T3 polymerase for mSlo1 and T7 polymerase (Ambion) for dSlo1 constructs. Xenopus laevis oocytes were each injected with 0.05–50 ng of RNA and incubated in 18°C for 2–6 d before recording.

Electrophysiology

Macroscopic currents were recorded from inside-out patches using Axopatch 200-B patch-clamp amplifier (Axon Instruments) and PULSE acquisition software (HEKA Electroniks), low-pass filtered at 5 kHz with the amplifier's built-in four-pole Bessel filter and digitized at 20-μs intervals. Solution compositions were as follows: external (extracellular), 140 mM K-methanesulphonic acid, 20 mM Hepes, 2 mM KCl, 2 mM MgCl₂, pH ∼7.20; basal internal (intracellular), 140 mM K-methanesulphonic acid, 20 mM Hepes, 2 mM KCl, 1 mM EGTA, pH ∼7.20. The “0 [Ca²⁺]_i” had the same composition as basal internal solution except that it contained 5 mM EGTA to give a free [Ca²⁺]_i of ∼0.5 nM, which is too low to produce BK_Ca channel activation (Cui et al., 1997). Required [Ca²⁺]_i and [Mg²⁺]_i were obtained by adding appropriate volumes of CaCl₂ and MgCl₂ solutions to basal internal solution. The actual free [Ca²⁺]_i was measured using a Ca²⁺-sensitive electrode (Orion). All currents were recorded at room temperature (22–25°C).

Analysis

Relative conductance was calculated from tail current amplitudes at −50 mV. Conductance–voltage (G-V) relations were fitted with the Boltzmann distribution

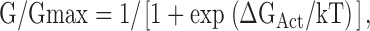(1)

where k is Boltzmann's constant, T is absolute temperature, and ΔG_Act is the free energy of channel opening. ΔG_Act is the total energy increase provided by voltage (ΔG_V = −zeV, where e is elementary charge and z is the number of equivalent gating charges) and Ca²⁺ and Mg²⁺ binding (ΔG_Ca and ΔG_Mg). In the absence of Ca²⁺ and Mg²⁺ at 0 mV, ΔG_Act = ΔG₀ (Cui and Aldrich, 2000). Hence,

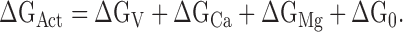(2)

The change in the contribution of Ca²⁺ binding to ΔG_Act as a result of an increase in [Ca²⁺]_i, ΔΔG_Ca, was measured at a constant [Mg²⁺]_i and vice-versa. ΔΔG_Ca and ΔΔG_Mg were calculated as a measure of the shift and change in shape of the G-V relation between two specified values of [Ca²⁺]_i or [Mg²⁺]_i as

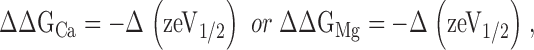(3)

where V_1/2 is the voltage at half maximum of the G-V relation (Figs. 1, 3, and 4). ΔΔG_Ca and ΔΔG_Mg represent the Ca²⁺ sensitivity and Mg²⁺ sensitivity, respectively, of a channel measured between two specified Ca²⁺ or Mg²⁺ concentrations. While in general the Ca²⁺ sensitivity and Mg²⁺ sensitivity of the channel should be evaluated between 0 and saturating concentrations of metal ions, our results show that ΔΔG_Ca of dSlo1 is consistently larger than that of mSlo1 between any pair of [Ca²⁺]_i used in our experiments (see Figs. 1, 4, 6, and 10). Mean ΔΔG_Ca of WT and mutant channels was measured and calculated at 0 [Mg²⁺]_i and two [Ca²⁺]_i values that allowed us to obtain a complete G-V relation. In Figs. 4 and 6, mean ΔΔG_Ca of mutant channels was then divided by the mean ΔΔG_Ca of WT mSlo1 under the same conditions of [Ca²⁺]_i and [Mg²⁺]_i. In Fig. 10 C, ΔG_V values were measured and calculated at V = V_1/2.

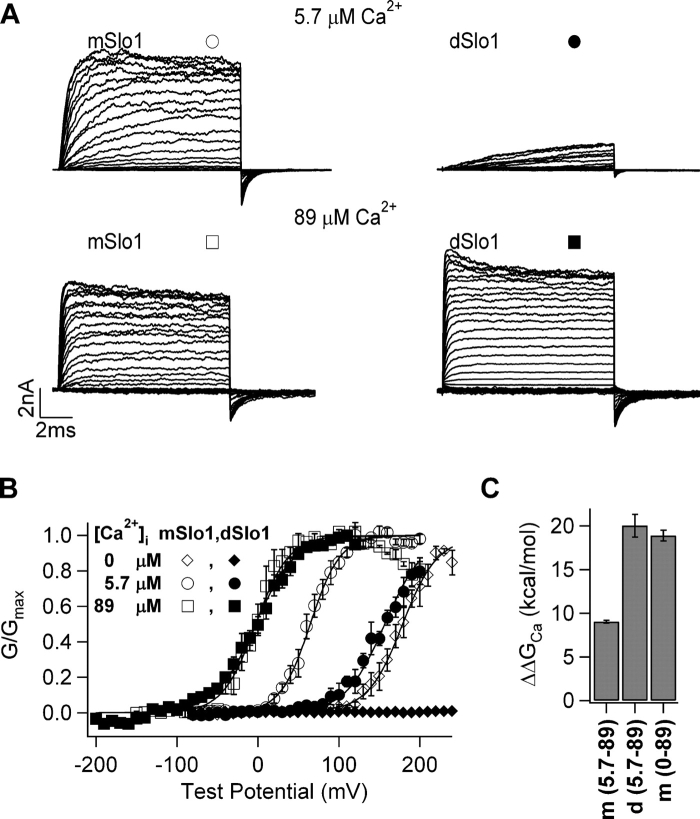
Figure 1.

dSlo1 activation exhibits higher Ca²⁺ sensitivity than mSlo1. (A) Current traces of mSlo1 and dSlo1. Test potentials were −80 to +200 mV and −150 to +200 mV for 5.7 μM and 89 μM [Ca²⁺]_i, respectively, holding and repolarization potentials were −50 mV. (B) Steady-state G-V relations of mSlo1 and dSlo1. Smooth curves are fits of the Boltzmann equation (see MATERIALS AND METHODS) with parameters for mSlo1, in 0 [Ca²⁺]_i: V_1/2 = 179 mV, z = 1.2, in 5.7 μM [Ca²⁺]_i, V_1/2 = 64.6 mV, z = 1.4, in 89 μM [Ca²⁺]_i, V_1/2 = −2.8 mV, z = 1.2; for dSlo1, in 5.7 μM [Ca²⁺]_i, V_1/2 = 157 mV, z = 1.3, in 89 μM [Ca²⁺]_i, V_1/2 = −2.9 mV, z = 1.1. (C) Free energy provided by Ca²⁺ binding for channel activation when [Ca²⁺]_i changes from 0 or 5.7 μM to 89 μM, as indicated in parentheses under the abscissa. m, mSlo1; d, dSlo1.

Figure 3.

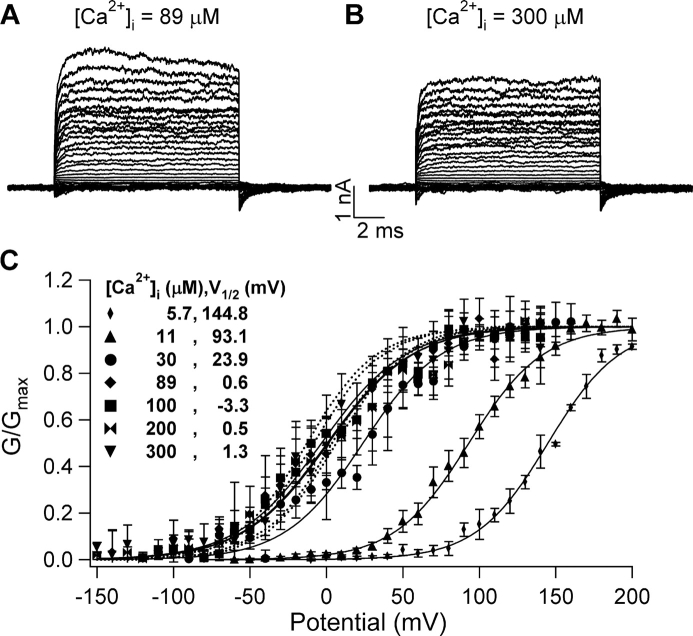
Activation of dSlo1 saturates around 89 μM [Ca²⁺]_i. (A and B) Current traces of dSlo1 for indicated [Ca²⁺]_i elicited by voltages from −150 to 200 mV. (C) Steady-state G-V curves of dSlo1. Solid curves are fits of the Boltzmann equation. V_1/2 obtained from the fits of the G-V relations at each [Ca²⁺]_i is indicated. Dotted lines indicate MWC model simulations of the G-V relation at [Ca²⁺]_i 89, 100, 200, and 300 μM using the same parameters as indicated in Fig. 10 C.

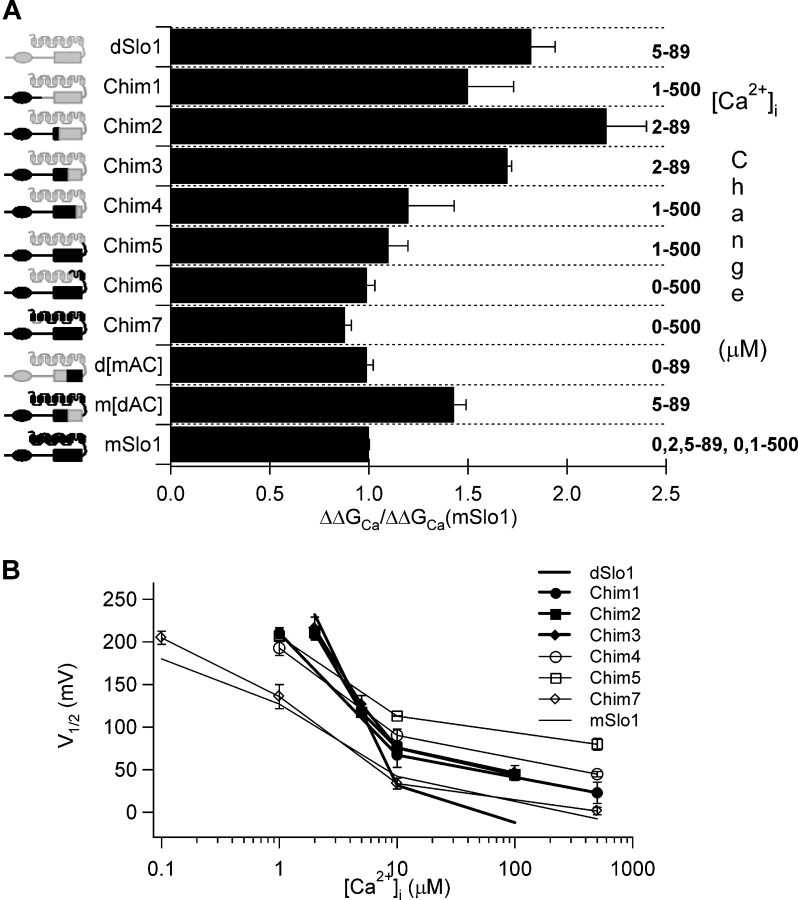
Figure 4.

The AC region in the RCK1 domain is important for Ca²⁺ sensitivity. (A) Ca²⁺ sensitivity of activation in chimeric channels of mSlo1 and dSlo1. The vertical axis shows schematic representation of chimera constructs with dSlo1 portions shaded gray and mSlo1 black. Rectangles are transmembrane segments or RCK1 domains (Jiang et al., 2002a), ovals are the Ca²⁺ bowl (Schreiber et al., 1999). Free energy increase in response to increase in [Ca²⁺]_i (shown at the right) for each chimera and WT channel was normalized against that for mSlo1. (B) Plot of V_1/2 versus [Ca²⁺]_i for mSlo1 (thin black line), dSlo1 (thick black line), and the chimeric channels as defined in A. V_1/2 values are obtained by fitting the G-V relations of the channels at various [Ca²⁺]_i with the Boltzmann equation.

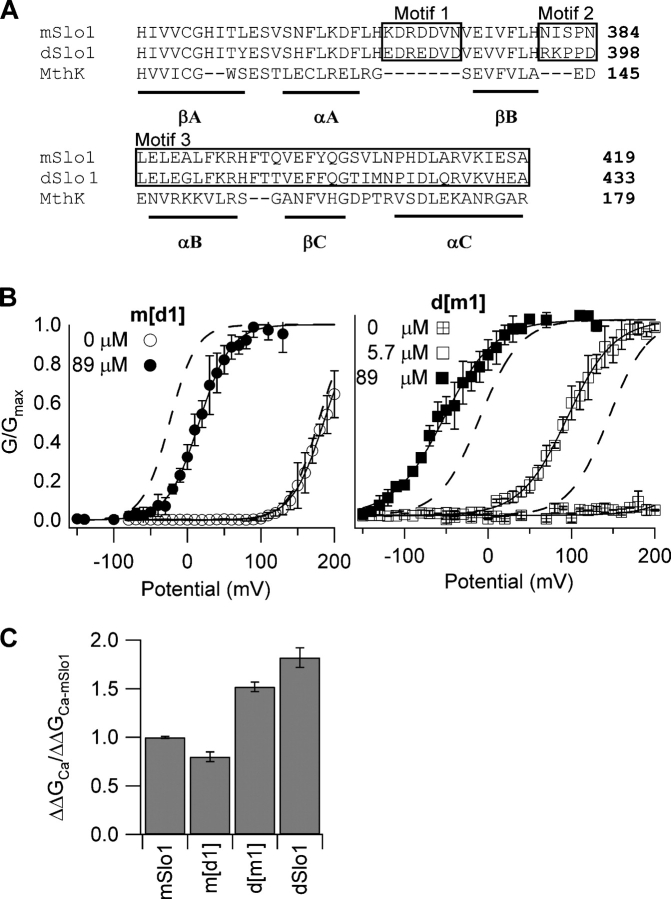
Figure 6.

Ca²⁺ sensitivity change is not related to the Ca²⁺ binding site in the AC region. (A) Sequence alignment of the AC region of the RCK1 domain (Jiang et al., 2002a) from mSlo1 (Butler et al., 1993), dSlo1 (Adelman et al., 1992), and the archeon MthK (Jiang et al., 2002a). Numbers indicate the position of the rightmost residues in the primary sequence of respective proteins. Secondary structures βA-C and αA-C are indicated by underlines. Boxed amino acids labeled as motifs 1, 2, and 3 are regions showing significant sequence differences between mSlo1 and dSlo1. Motif 1 is important for Ca²⁺-dependent activation (Shi et al., 2002; Xia et al., 2002). Effects of switching motif 1 between mSlo1 and dSlo1 are shown in B and C. (B, left) Steady-state G-V relations of the mutant channel m[d1] (motif 1 from dSlo1 in the mSlo1 background). Solid lines are fits of the Boltzmann equation with the following parameters: at 0 [Ca²⁺]_i, V_1/2 = 185 mV, z = 1.2; at 89 μM [Ca²⁺]_i, V_1/2 = 15.9 mV, and z = 1.2. Dotted lines are G-V relations of mSlo1. (B, right) Steady-state G-V relations of the mutant channel d[m1] (motif 1 from mSlo1 in the dSlo1 background). Solid lines are fits of the Boltzmann equation with the following parameters: at 89 μM [Ca²⁺]_i, V_1/2 = −52.5 mV, z = 0.83; at 5.7 μM [Ca²⁺]_i, V_1/2 = 95.1 mV and z = 0.89; at 0 [Ca²⁺]_i, the G-V relation was too right shifted for z and V_1/2 values to be determined. Dotted lines are G-V relations of dSlo1. (C) Free energy of activation provided by Ca²⁺ binding in mSlo1, d[m1], m[d1], and dSlo1 when [Ca²⁺]_i increased from 0 to 89 μM (for m[d1]) and from 5.7 to 89 μM (for d[m1] and dSlo1), normalized against corresponding free energy values for mSlo1.

Figure 10.

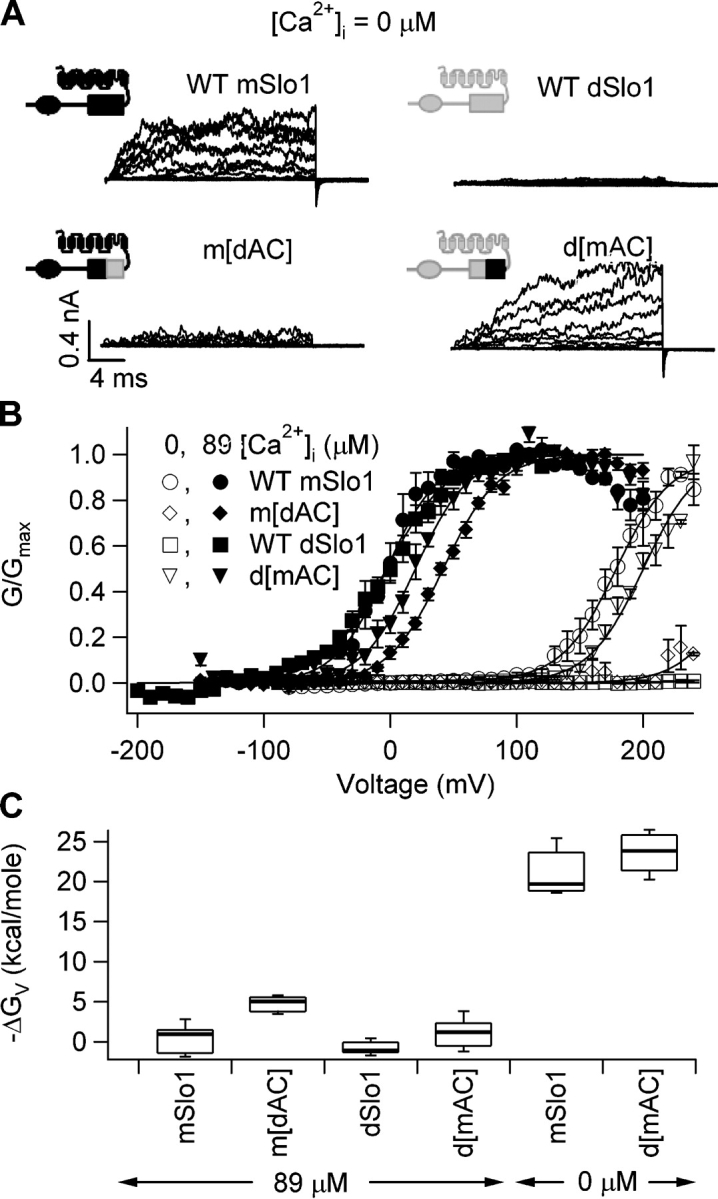
Modulation of BK_Ca activation by the AC region depends on Ca²⁺ occupancy. (A) Current traces of mSlo1, dSlo1, d[mAC], and m[dAC] at 0 [Ca²⁺]_i. Test voltages were from −80 to 200 mV with a holding and repolarization potential of −50 mV. (B) Steady-state G-V relations of above channels at 0 (open symbols) and 89 μM (filled symbols) [Ca²⁺]_i. Smooth curves are fits to the Boltzmann equation. At 89 μM [Ca²⁺]_i, for mSlo1: V_1/2 = −2.8 mV, z = 1.2; for d[mAC]: V_1/2 = 7.7 mV, z = 1.4; for dSlo1: V_1/2 = −2.9 mV, z = 1.1; for m[dAC]: V_1/2 = 41.6 mV, z = 1.2. At 0 [Ca²⁺]_i, for mSlo1: V_1/2 = 179 mV, z = 1.2; for d[mAC]: V_1/2 = 181 mV, z = 1.3. The voltage range of dSlo1 and m[dAC] activation at 0 [Ca²⁺]_i is too positive to record any current. (C) Box plot of ΔG_V = zV_1/2 for the above channels at 0 and 89 μM [Ca²⁺]_i. The percentile values shown are 10, 25, 50, 75, and 90 for each channel. ΔG_V for m[dAC] and dSlo1 at 0 [Ca²⁺]_i are too large to be determined.

Ca²⁺ sensitivity in BK_Ca channel activation is sometimes evaluated by fitting the response of P_o to [Ca²⁺]_i to Hill equation at a fixed voltage to obtain K_1/2 and Hill coefficient. Ca²⁺ sensitivity determined in such a manner is pertinent only to the specific voltage at which the data is analyzed. It does not reflect the overall Ca²⁺ sensitivity of a channel because for the same channel Ca²⁺ sensitivity defined by the fit of Hill equation is different at different voltages (Cui et al., 1997; Bian et al., 2001; Zhang et al., 2001). When the voltage range of activation is shifted by a mutation, at a fixed voltage the Ca²⁺ sensitivity estimated by Hill equation would naturally change even if the overall Ca²⁺ sensitivity of the channel is actually not changed. The error bars in all figures show standard error of means from three to nine patches of data.

Monod-Wyman-Changeux (MWC) Model

In Fig. 11, MWC model fits used the following equation:

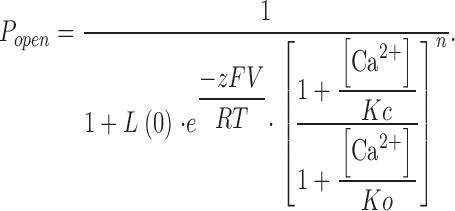(4)

Figure 11.

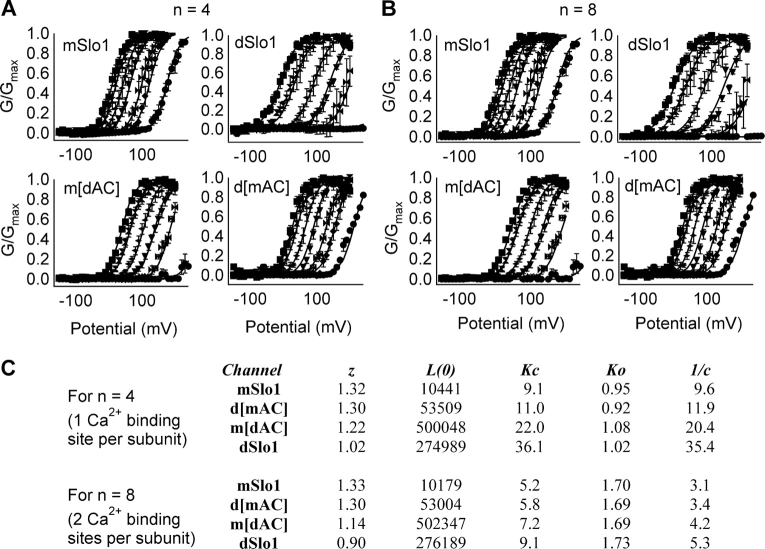
The AC region affects Ca²⁺ binding to closed channels. (A and B) G-V relations of mSlo1, dSlo1, d[mAC], and m[dAC] channels at [Ca²⁺]_i of 0, 1.7, 2.3, 5.7, 11.2, 28.5, and 89 μM. Each dataset was fit (smooth curves) by the MWC model (Eq. 4), n = 4 (A) or 8 (B). (C) Parameters of fits obtained from A and B.

K_c = dissociation constant of [Ca²⁺] in the closed state; K_o = dissociation constant of [Ca²⁺] in the open state; c = K_o/K_c is a measure of Ca²⁺ sensitivity of activation; L(0) = [C]/[O] at 0 [Ca²⁺]_i; n = 4 or 8. MWC model code was written and executed in MATLAB 6.5 (The Mathworks Inc.).

Molecular Dynamics

The first step to computationally simulate the mSlo1 and dSlo1 AC region was to create structural models for each protein. Using the MthK structure as a starting point (PDB code 1ID1), we created the required mutations and small insertions using PLOP (Jacobson et al., 2004). Using the molecular dynamics package Gromacs (Lindahl et al., 2001) we first minimized both structures using the OPLS/AA force field and explicit SPC solvent. The systems were then heated in 50 K steps to 300 K, equilibrated at 300 K for 10 ns, and followed by production runs of 20 ns. In all cases we used 2 fs time steps with bond constraints, Particle Mesh Ewald, and coordinates were saved every 1 ps. To compare the dynamics of these two domains, we used Principal Component Analysis. The covariance matrix calculated from each production run was diagonalized and the eigenvectors corresponding to the largest eigenvalue (i.e., the most significant mode) were used. The motion along the principal eigenvectors of each protein showed marked dynamical differences between mSlo1 and dSlo1. To further quantify this dynamical difference, we computed the root mean square fluctuations of the α carbons for each protein. Since the proteins are of identical length and have the same secondary structure, this comparison highlights the effect of sidechain substitutions on the motion of the protein backbone.

RESULTS

dSlo1 Exhibits Greater Ca²⁺ Sensitivity than mSlo1

BK channel homologues mSlo1 and dSlo1 exhibit high sequence homology and amino acid identity (Adelman et al., 1992, Butler et al., 1993). However, there are significant differences in their channel activation and macroscopic current properties in response to changes in voltage and [Ca²⁺]_i as shown in Fig. 1. In the absence of [Ca²⁺]_i (see MATERIALS AND METHODS), significant currents could be evoked in mSlo1 at positive potentials (the voltage at half maximum activation, V_1/2 ∼180 mV), whereas, virtually no current was evoked in dSlo1 for the same condition, with the result that voltage dependence of channel activation was far-right shifted on the voltage axis and could not be determined (Fig. 1 B). Similarly, when [Ca²⁺]_i was increased to 5.7 μM, the same voltage protocol elicited larger mSlo1 currents than dSlo1 (Fig. 1 A, top). However, at 89 μM [Ca²⁺]_i, comparable amounts of mSlo1 and dSlo1 currents were observed (Fig. 1 A, bottom), such that at this [Ca²⁺]_i, the voltage dependence of open probability was the same for both mSlo1 and dSlo1 (Fig. 1 B). Thus, the same amount of increase in [Ca²⁺]_i (0–89 μM or 5.7–89 μM) results in a more pronounced increase of dSlo1 activation than that of mSlo1 for the same voltage protocols (Fig. 1, A and B). The voltage range of channel activation for dSlo1 exhibits a larger leftward shift (ΔV_1/2 ∼160 mV) than mSlo1 (ΔV_1/2 ∼68 mV) for the same change of [Ca²⁺]_i from 5.7 to 89 μM (Fig. 1 B), imparting higher Ca²⁺ sensitivity to dSlo1 as compared with mSlo1 (see MATERIALS AND METHODS for more details). Higher Ca²⁺ sensitivity of dSlo1 as compared with mSlo1 is also seen in the free energy of channel activation contributed by Ca²⁺ binding when [Ca²⁺]_i increases. The increase in [Ca²⁺]_i from 5.7 to 89 μM contributes ∼20 kcal/mole to dSlo1 activation as compared with ∼9 kcal/mole to mSlo1 activation (Fig. 1 C). More importantly, the ΔΔG_Ca contributed to dSlo1 activation by an increase in [Ca²⁺]_i from 5.7 to 89 μM is about the same as the ΔΔG_Ca contributed to mSlo1 activation by an increase in [Ca²⁺]_i from 0 to 89 μM (Cui and Aldrich, 2000) (Fig. 1 C). The above results demonstrate that (1) the activation properties of dSlo1 and mSlo1 channels in the absence of Ca²⁺ are vastly different, and (2) the Ca²⁺ sensitivity of dSlo1 is higher compared with mSlo1.

NH₂-terminal Region in the RCK1 Domain Modulates Ca²⁺ Sensitivity of Activation

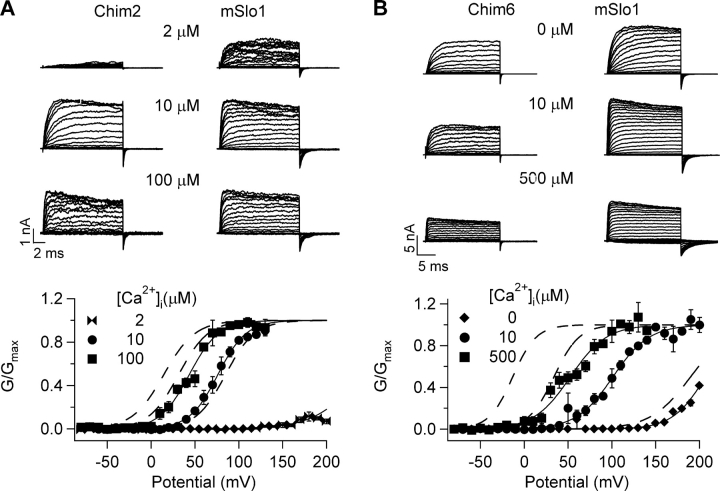
A comparison of the sequences of mSlo1 and dSlo1 shows differences at many locations throughout the entire peptide (Adelman et al., 1992; Butler et al., 1993). To determine the structural basis of the higher Ca²⁺ sensitivity of dSlo1, we constructed chimeric channels of mSlo1 and dSlo1, named Chim1 to Chim7, by replacing parts of the sequence of the dSlo1 protein with corresponding sequences of mSlo1. The aim was to identify the structural domain in the mSlo1 protein that would reduce Ca²⁺ sensitivity of the background dSlo1 channel. To compare Ca²⁺ sensitivity of the chimeric channels with that of dSlo1 and mSlo1, it is desirable that Ca²⁺ sensitivity for each channel is measured over the complete range of [Ca²⁺]_i, from zero to saturating levels. However, it was not possible to measure Ca²⁺ sensitivity over the same Ca²⁺ range for all the chimeric channels because, like dSlo1 (Fig. 1 B), the voltage range of activation of some chimeric channels is too positive to be measured at low [Ca²⁺]_i. This is illustrated in Fig. 2 for two of the chimeric channels, Chim2 and Chim6 (for description and sequence information of chimeric channels, refer to MATERIALS AND METHODS). We observed that the channel activation properties of Chim2 are similar to that of dSlo1 as seen in Fig. 1. At 0 [Ca²⁺]_i the channel could not be activated even at voltages more positive than 250 mV. In this case, the lowest [Ca²⁺]_i at which we could measure a portion of the G-V relation of Chim2 was 2 μM (Fig. 2 A). Therefore, the Ca²⁺ sensitivity was measured between a [Ca²⁺]_i change from 2 μM to a saturating level for this channel. Fig. 2 A shows that for an identical change in [Ca²⁺]_i from 2 to 100 μM, the G-V relation of mSlo1 shifts much less on the voltage axis than that of Chim2. On the other hand, Chim6 exhibits channel properties more similar to mSlo1, such that for the same voltage protocols, the currents evoked are comparable to mSlo1 at all [Ca²⁺]_i (Fig. 2 B, current traces). Although the G-V relation of Chim6 at all [Ca²⁺]_i is right shifted as compared with mSlo1 (Fig. 2 B, bottom), a portion of the G-V relation at 0 [Ca²⁺]_i can be measured. Therefore, the Ca²⁺ sensitivity was measured between a full range of [Ca²⁺]_i change from 0 to a saturating level for this channel. Similar to Chim2, the Ca²⁺ sensitivity of Chim6 is compared with that of the WT mSlo1 measured at the same [Ca²⁺]_i range (Fig. 2 B).

Figure 2.

Chimeric channels of mSlo1 and dSlo1 retain features of their native WT channels. (A, top) Current traces of Chim2 and mSlo1 at [Ca²⁺]_i of 2, 10, and 100 μM. Test potentials were −80 to +200 mV, holding and repolarization potentials were −50 mV. (Bottom) Steady-state G-V relations of Chim2 and mSlo1. Smooth curves are fits of the Boltzmann equation with parameters for Chim2, in 2 μM [Ca²⁺]_i: V_1/2 = 240.1 mV, z = 0.95, in 10 μM [Ca²⁺]_i: V_1/2 = 76.1 mV, z = 1.5, in 100 μM [Ca²⁺]_i: V_1/2 = 43.5 mV, z = 1.5; for mSlo1, in 2 μM [Ca²⁺]_i: V_1/2 = 84.8 mV, z = 1.5, in 10 μM [Ca²⁺]_i: V_1/2 = 31.4 mV, z = 1.5, in 100 μM [Ca²⁺]_i: V_1/2 = 14.4 mV, z = 1.4. (B, top) Current traces of Chim6 and mSlo1 at [Ca²⁺]_i of 0, 10, and 500 μM. Test potentials were −80 to +200 mV, holding and repolarization potentials were −50 mV. (Bottom) Steady-state G-V relations of Chim6 and mSlo1. Smooth curves are fits of the Boltzmann equation with parameters for Chim6, in 0 [Ca²⁺]_i: V_1/2 = 206.7 mV, z = 1.3, in 10 μM [Ca²⁺]_i: V_1/2 = 101.1 mV, z = 1.2, in 500 μM [Ca²⁺]_i: V_1/2 = 52.5 mV, z = 1.2; for mSlo1, in 0 [Ca²⁺]_i: V_1/2 = 189.7 mV, z = 1.1, in 10 μM [Ca²⁺]_i: V_1/2 = 33.8 mV, z = 1.7, in 500 μM [Ca²⁺]_i: V_1/2 = −13.2 mV, z = 1.8.

To compare the Ca²⁺ sensitivity of chimeric channels with that of mSlo1 within the maximum [Ca²⁺]_i range, we needed to find the saturating [Ca²⁺]_i for channel activation. It has been shown previously that the high affinity Ca²⁺ binding sites for mSlo1 activation is nearly saturated at [Ca²⁺]_i ≥ 80 μM (Cox et al., 1997; Cui et al., 1997). Fig. 3 shows that Ca²⁺-dependent activation of dSlo1 also saturates at similar [Ca²⁺]_i. Fig. 3 (A and B) shows that the current traces of WT dSlo1 recorded at 89 and 300 μM are very similar. The steady-state G-V relations of WT dSlo1 at [Ca²⁺]_i 5.7, 11.2, 28.5, 89, 100, 200, and 300 μM are shown in Fig. 3 C. Doubling [Ca²⁺]_i from 89 to 200 μM caused little shift in the G-V relation while a doubling of [Ca²⁺]_i from 5.7 to 11.2 μM caused a G-V shift of −50 mV, suggesting that at 89 μM [Ca²⁺]_i, the activation is close to being saturated. We also fitted the data at [Ca²⁺]_i of 89, 100, 200, and 300 μM with the MWC model using the same parameters indicated in Fig. 10 (Fig. 3 C), which also suggest that at 89 μM [Ca²⁺]_i, the activation is close to being saturated. These results indicate that the activation of both mSlo1 and dSlo1 channels saturates at [Ca²⁺]_i ≥ 89 μM and the activation differs little within the [Ca²⁺]_i range between 89 and 300 μM. Therefore, we have used [Ca²⁺]_i between 89 and 500 μM as the saturating [Ca²⁺]_i in the experiments involving measurement of Ca²⁺ sensitivity.

Based on the observations similar to those described above, we measured the Ca²⁺ sensitivity (ΔΔG_Ca) between the maximum [Ca²⁺]_i intervals possible for each chimeric channel, and then compared it to the ΔΔG_Ca measured for WT mSlo1 between the same [Ca²⁺]_i intervals. Fig. 4 A plots the ΔΔG_Ca values of dSlo1 and chimeric channels normalized against that of mSlo1 measured between the same [Ca²⁺]_i intervals, respectively. Shown at the left are cartoons illustrating the mSlo1 domain substituting dSlo1 counterpart in each chimera and on the right are the [Ca²⁺]_i intervals at which ΔΔG_Ca was measured (Fig. 4 A). In chimeric channels Chim1–Chim7, replacement of dSlo1 started with the tail of mSlo1 in Chim1 and progressively covered all the important regions that have been shown in previous studies to affect the Ca²⁺ sensitivity of BK_Ca channels. Replacing the tail of dSlo1 with its mSlo1 counterpart (Chim1), which included Ca²⁺ bowl, the putative Ca²⁺ binding site (Schreiber and Salkoff, 1997; Schreiber et al., 1999; Bian et al., 2001; Bao et al., 2004), did not have much effect on Ca²⁺ sensitivity; nor did Chim2 and Chim3, where the COOH terminus of the RCK1 domain was included in the replacement. However, Chim4, in which the replacement included the NH₂-terminal part of the RCK1 domain, brought the Ca²⁺ sensitivity closer to that of WT mSlo1. Further addition of mSlo1 sequence did not significantly alter the Ca²⁺ sensitivity further, as seen in Chim5, Chim6, and Chim7. In addition to the lowest and highest possible [Ca²⁺]_i for each chimeric channel, we also measured channel activation at one or more intermediate [Ca²⁺]_i and compared the V_0.5–[Ca²⁺]_i plots with that of WT mSlo1 and dSlo1 as shown in Fig. 4 B. The maximal slope of the V_0.5–[Ca²⁺]_i for dSlo1 (thick black line) is significantly larger than for mSlo1 (thin black line), indicating higher Ca²⁺ sensitivity. As in Fig. 4 A for Ca²⁺ sensitivity, Chim1, Chim2, and Chim3 exhibit a maximal slope of V_0.5–[Ca²⁺]_i similar to dSlo1 (thick lines), while Chim4 to Chim7 have a maximal V_0.5–[Ca²⁺]_i slope similar to mSlo1 (thin lines) (Fig. 4 B).

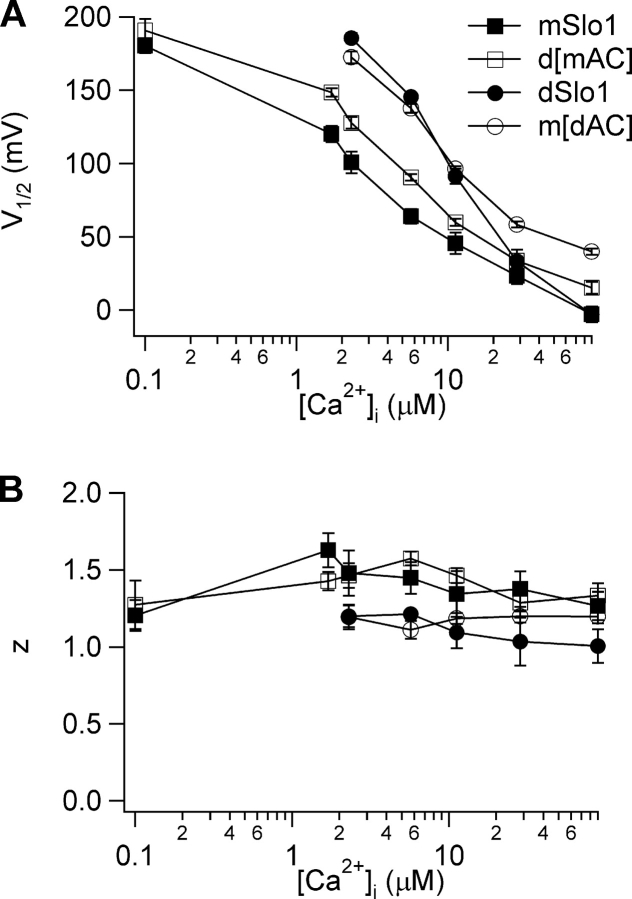
Thus, a difference of a 43 amino acid stretch in the RCK1 domain (αB-αC, Fig. 6 A), between Chim3 and Chim4, switched the Ca²⁺ sensitivity of the channel from being dSlo1-like to being mSlo1-like (Fig. 4). To examine if this stretch is sufficient to switch Ca²⁺ sensitivity of the BK_Ca channel, we replaced just the NH₂-terminal part of the RCK1 domain (βA-αC, henceforth referred to as AC, Fig. 6 A) in dSlo1 by its mSlo1 counterpart (d[mAC]). Fig. 4 A shows that the AC stretch from mSlo1 alone is able to reduce Ca²⁺ sensitivity of dSlo1. Conversely, when the same region in mSlo1 was replaced by the dSlo1 counterpart (m[dAC]), the Ca²⁺ sensitivity increased (Fig. 4 A). To confirm whether the AC region is able to switch the Ca²⁺ sensitivity between mSlo1 and dSlo1 at all [Ca²⁺]_i and not just at the extremities, we measured and plotted the voltage for half-maximal activation, V_1/2 as well as the equivalent charge, z, versus [Ca²⁺]_i for a range of [Ca²⁺]_i from 0 to 89 μM (Fig. 5, A and B). Both plots confirm the observation from Fig. 4 that switching the AC region between mSlo1 and dSlo1 was sufficient to switch the phenotype of Ca²⁺ sensitivity between the channels for all [Ca²⁺]_i between 0 and saturating levels.

Figure 5.

The AC region switches Ca²⁺ sensitivity between mSlo1 and dSlo1. Plot of (A) V_1/2 and (B) z versus [Ca²⁺]_i for mSlo1, dSlo1, m[dAC], and d[mAC]. V_1/2 and z are obtained by fitting the G-V relations of the channels at various [Ca²⁺]_i with the Boltzmann equation.

We observe that the extent of increase in Ca²⁺ sensitivity in m[dAC] is not equal to the extent of decrease in Ca²⁺ sensitivity in d[mAC] (Fig. 4 A). We postulate that this is because the modulation of Ca²⁺ sensitivity involves many parts of the channel protein and replacing just one of the components in mSlo1 by dSlo1 (in this case, the AC region) is not enough to result in a complete gain of function, i.e., an increase in Ca²⁺ sensitivity. A loss of function is however more easily obtained by changing one of the components and this is seen by the significant decrease in Ca²⁺ sensitivity of d[mAC] compared with WT dSlo1. Hence, results of Figs. 4 and 5 indicate that the AC region of the RCK1 domain is important in determining the Ca²⁺ sensitivity of channel activation in mSlo1 and dSlo1.

Metal Binding Sites in the AC Region Are Not Responsible for the Difference in Ca²⁺ Sensitivity

Previous studies demonstrated that Ca²⁺ activates BK_Ca channels by an allosteric mechanism, i.e., Ca²⁺ binds to sites distant from the activation gate and opens the channel by changing the conformation of channel protein (McManus and Magleby, 1991; Cox et al., 1997; Jiang et al., 2002a,b). Thus, an alteration of either the Ca²⁺ binding sites or the structure linking binding sites to the activation gate can change Ca²⁺ sensitivity of BK_Ca gating. At present, the location of the Ca²⁺ binding sites for BK_Ca activation has not been completely elucidated. Previous results have led to the proposal that perhaps more than one site per subunit contribute to channel gating and are located in the cytosolic regions (Xia et al., 2004), possibly in the Ca²⁺ bowl (Schreiber and Salkoff, 1997) and the RCK domains (Bao et al., 2002; Xia et al., 2002), or in the core of the channel that includes transmembrane segments and connecting loops (Braun and Sy, 2001; Piskorowski and Aldrich, 2002). Sequence differences between mSlo1 and dSlo1 at these putative Ca²⁺ binding sites are not likely to be responsible for the differences in Ca²⁺ sensitivity because switching sequences between the two channels in these locations failed to alter Ca²⁺ sensitivity (Chim 1, Chim 5, and Chim 7 in Fig. 4).

Closer inspection of the AC regions of mSlo1 and dSlo1 highlighted three groups of amino acids, Motif1, Motif2, and Motif3, which show significant differences in amino acid identity (Fig. 6 A). Of these, Motif1 contains a putative Ca²⁺ binding site (Xia et al., 2002), which is conserved between mSlo1 and dSlo1 (D367 in mSlo1 or D381 in dSlo1), but differs in amino acids flanking this conserved site (Fig. 6 A). It is reasonable to suppose that differences in one or all of these motifs are responsible for reversing the Ca²⁺ sensitivity phenotype between mSlo1 and dSlo1. To test this hypothesis, we made chimeric mutant channels where the three motifs were switched between mSlo1 and dSlo1 either individually or in combination. Figs. 6 and 7 summarize the observations of the effect of motif switching on the phenotype of Ca²⁺ sensitivity. Neither d[m1] nor m[d1] showed any change in Ca²⁺ sensitivity when compared with their respective native phenotype (Fig. 6, B and C). The free energy of channel activation provided by Ca²⁺ binding, ΔΔG_Ca, is dependent on the background but not motif1 of the channel such that ΔΔG_Ca of m[d1] is similar to that of WT mSlo1, whereas ΔΔG_Ca of d[m1] is similar to WT dSlo1 (Fig. 6 C). At 0 [Ca²⁺]_i, the voltage-dependent activation of m[d1] has similar characteristics as WT mSlo1, while that of d[m1] is similar to WT dSlo1 (Fig. 6 B). Switching Motif2 or Motif3 of mSlo1 to dSlo1 did not affect Ca²⁺ sensitivity of mSlo1 (Fig. 7 A). Additionally, the mutant channels in which motif pairs were switched also failed to switch the Ca²⁺ sensitivity phenotype (Fig. 7 B). In each case, the ΔΔG_Ca value matched that of its native mSlo1 channel (Fig. 7 C). In all cases, the mutations shifted the positions of the G-V on the voltage axis from that of the WT channels at all [Ca²⁺]_i (Fig. 6 B and Fig. 7, A and B). However, these shifts are relatively small and did not significantly affect the free energy of channel activation provided by Ca²⁺ binding. The results of Figs. 6 and 7 indicate that the reversal of phenotype seen as a result of a switch of the AC regions between mSlo1 and dSlo1 is not the result of changes to the Ca²⁺ binding site or individual amino acid differences between mSlo1 and dSlo1 in the AC region. Rather, the AC region as a whole is responsible for the differences in Ca²⁺ sensitivity between mSlo1 and dSlo1 channels.

Figure 7.

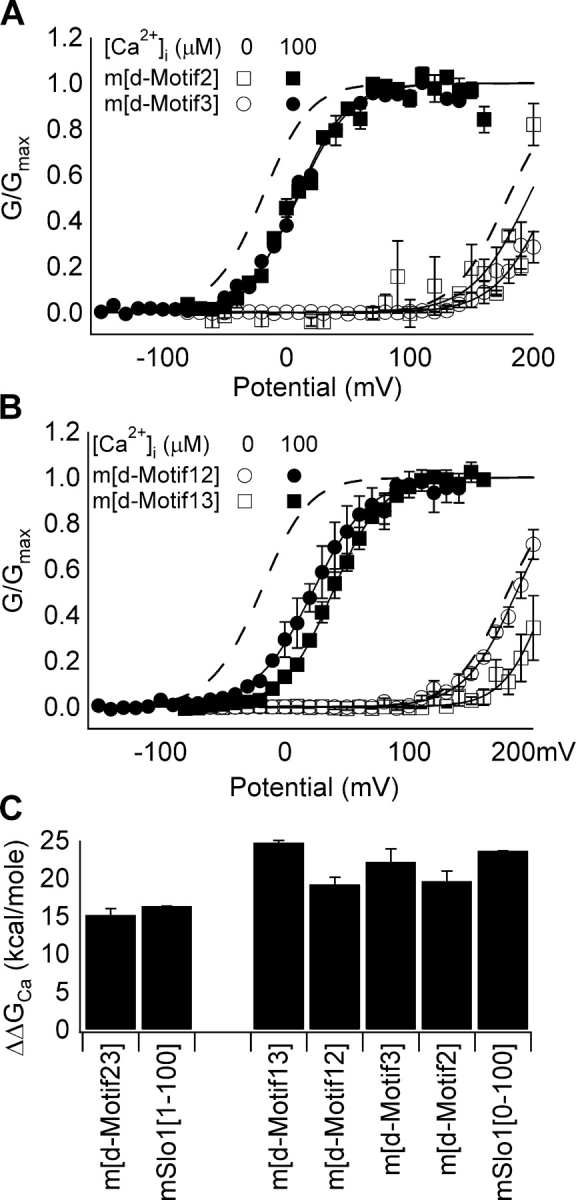
Switching sequence differences in AC region between mSlo1 and dSlo1 either singly or in combination does not switch Ca²⁺ sensitivity of BK_Ca gating. (A) Steady-state G-V relations of m[d-Motif2] and m[d-Motif3]. Dotted lines are G-V relations of mSlo1. Parameters of the Boltzmann fits (solid lines): for m[d-Motif2], at 0 [Ca²⁺]_i, V_1/2 = 195.7 mV, z = 1.1; at 100 μM [Ca²⁺]_i, V_1/2 = 8.2 mV, z = 1.2; for m[d-Motif3], at 0 [Ca²⁺]_i, V_1/2 = 213.2 mV, z = 1.1; at 100 μM [Ca²⁺]_i, V_1/2 = 9.2 mV, z = 1.2. (B) Steady-state G-V relations of m[d-Motif12] and m[d-Motif13]. Dotted lines are G-V relations of mSlo1. Parameters of the Boltzmann fits (solid lines): for m[d-Motif12], at 0 [Ca²⁺]_i, V_1/2 = 186.5 mV, z = 1.2; at 100 μM [Ca²⁺]_i, V_1/2 = 22.2 mV, z = 1.1; for m[d-Motif13], at 0 [Ca²⁺]_i, V_1/2 = 211.9 mV, z = 1.4; at 100 μM [Ca²⁺]_i, V_1/2 = 38.4 mV, z = 1.3. (C) Free energy of activation provided by Ca²⁺ binding for the chimeric channels. Free energy change for each channel was in response to [Ca²⁺]_i change shown in parentheses for mSlo1 plotted alongside each group.

Besides the differences in the boxed motifs (Fig. 6 A), the AC region of mSlo1 and dSlo1 contains a conserved Mg²⁺ site (Shi et al., 2002; Xia et al., 2002). Intracellular Mg²⁺ activates mSlo1 and dSlo1 similarly by binding to this low-affinity metal binding site (K_d ∼ mM), which is nonspecific to divalent cations (Shi et al., 2002; Xia et al., 2002) (Fig. 8 A). We considered the possibility that the affinity of this metal binding site for Ca²⁺ might increase in dSlo1 such that the excess Ca²⁺ sensitivity observed in dSlo1 could be the effect of Ca²⁺ binding to this conserved metal site, even when Ca²⁺ is present only in micromolar concentrations. To test this hypothesis, we made a mutation in the Mg²⁺ binding site, E413R in dSlo1. E413R not only effectively abolishes Mg²⁺ sensitivity in dSlo1 (Fig. 8, B and C) but also leaves the Ca²⁺ sensitivity of the channel unchanged from WT dSlo1 (Fig. 8 D). This result demonstrates that the increased Ca²⁺ sensitivity in dSlo1 seen in Fig. 1 is not due to Ca²⁺ binding to the low affinity metal binding site.

Figure 8.

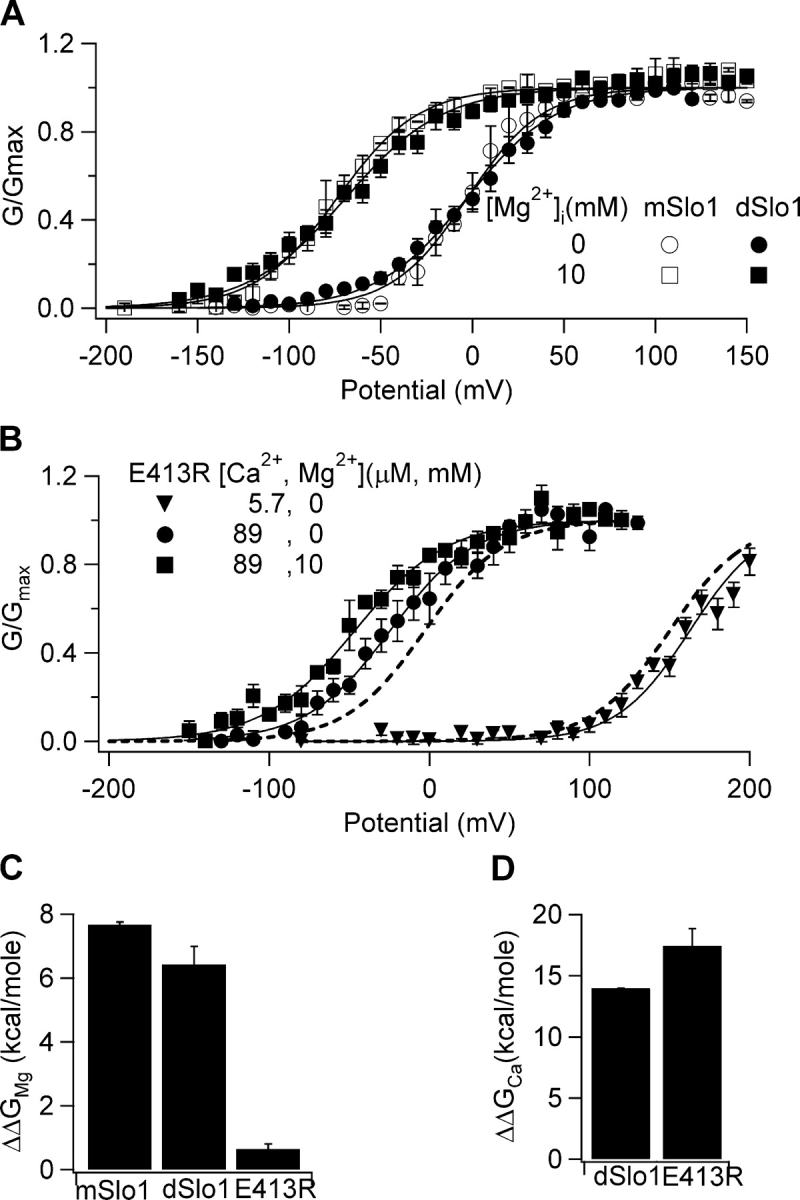
High Ca²⁺ sensitivity in dSlo1 is not related to the low affinity metal binding site. (A) Steady-state G-V relations of mSlo1 and dSlo1 at 89 μM [Ca²⁺]_i and indicated [Mg²⁺]_i. Boltzmann fits (smooth curves) gave following parameters: mSlo1, for 0 [Mg²⁺]_i, V_1/2 = −2.8 mV, z = 1.2, for 10 mM [Mg²⁺]_i, V_1/2 = −73.8 mV, z = 1.1; dSlo1, for 0 [Mg²⁺]_i, V_1/2 = −2.9 mV, z = 1.1, for 10 mM [Mg²⁺]_i, V_1/2 = −69.2 mV, z = 0.94. (B) Steady-state G-V relations of the E413R mutant dSlo1 channel. Boltzmann fits (solid curves) gave the following: E413R, for 5.7 μM [Ca²⁺]_i, V_1/2 = 163 mV, z = 1.1, for 89 μM [Ca²⁺]_i, 0 [Mg²⁺]_i, V_1/2 = −24.6 mV, z = 0.95, for 89 μM [Ca²⁺]_i, 10 mM [Mg²⁺]_i, V_1/2 = −46.7 mV, z = 0.87. Dotted lines are G-V relations for dSlo1 at 5.7 μM [Ca²⁺]_i and 89 μM [Ca²⁺]_i, 0 [Mg²⁺]_i. (C) Free energy provided by Mg²⁺ binding for channel activation in mSlo1, dSlo1, and E413R dSlo1 when [Mg²⁺]_i changes from 0 to 10 mM, measured at [Ca²⁺]_i of 89 μM. (D) Free energy provided by Ca²⁺ binding for channel activation in WT and E413R dSlo1 when [Ca²⁺]_i changes from 5.7 to 89 μM.

Conformational Differences in AC Region May Cause the Difference in Ca²⁺ Sensitivity between mSlo1 and dSlo1

The results in Figs. 4–7 suggest that, instead of affecting Ca²⁺ binding, AC region may act as a structure linking binding sites to the activation gate and modulate Ca²⁺ sensitivity of BK_Ca channels. Consistent with this mechanism, we found that only when the sequence comprising the AC region as a whole was exchanged between mSlo1 and dSlo1, was the phenotype of Ca²⁺ sensitivity also exchanged (Figs. 4–7). This result suggests that a combination of all the sequence differences in AC region may contribute and lead to a different conformation of the AC region between mSlo1 and dSlo1, which then results in altered conformational transitions during channel activation and hence Ca²⁺ sensitivity. Presently, there is no structural information available to allow a direct comparison between the conformations of mSlo1 and dSlo1. To examine if the conformation of the AC region in mSlo1 is different than in dSlo1 we performed molecular dynamics simulations on the AC region of dSlo1 and mSlo1 (Fig. 9), using homology models based on the crystal structure of MthK (Jiang et al., 2002a) (see MATERIALS AND METHODS). We observed that dSlo1 AC appears more compact than the mSlo1 AC, and that the range of motion in the first principal eigenmode is significantly different for the two proteins (Fig. 9, top). Further, the two structures show considerable differences in the fluctuations of their backbone throughout the AC region (Fig. 9, bottom). These simulations were performed on isolated AC regions, indicating that the AC regions from dSlo1 and mSlo1 have intrinsic differences in their conformation and dynamics even without considering effects of possible interactions between AC region and other parts of the channel.

Figure 9.

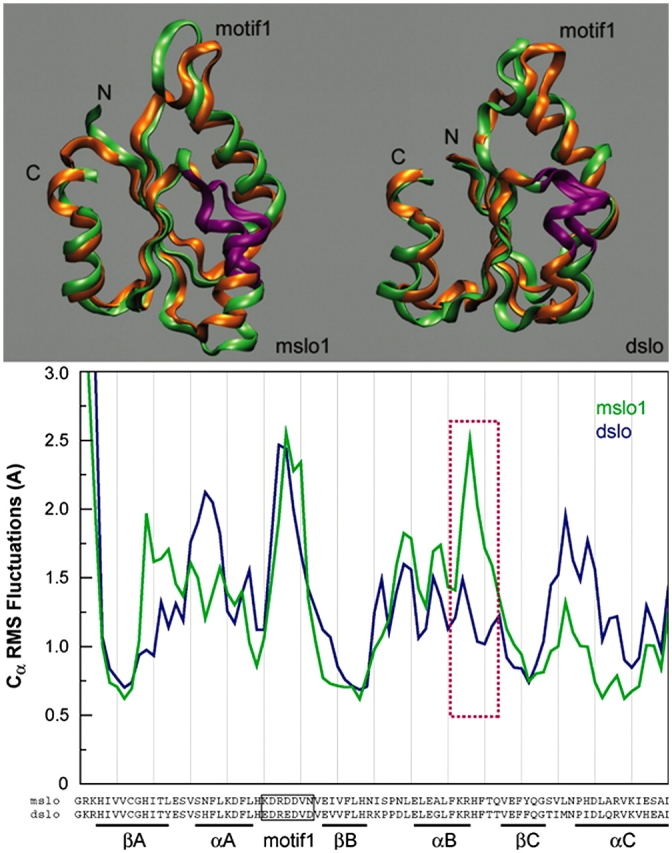
Molecular dynamics simulations of the AC region of mSlo1 and dSlo1. Top panels show the extrema (green and orange) of the motion along the principal eigenvector for the AC region from mSlo1 (left) and dSlo1 (right) (see MATERIALS AND METHODS). Part of helix B highlighted in purple shows the region of largest dynamic difference between the structures of mSlo1 and dSlo1. Bottom panel shows the RMS fluctuations for the C_α's of the above structure. The purple box denotes the same region (αB) highlighted above. Amino acid in the sequence at the bottom corresponds to the C_α whose dynamics are plotted above. Molecular graphics were produced using visual molecular dynamics (VMD) (Humphrey et al., 1996).

AC Region Modulates Channel Activation Depending on Ca²⁺ Binding and States of Gating

If AC region modulates Ca²⁺-dependent gating by altering the conformational changes induced by Ca²⁺ binding, it may affect channel gating differently depending on whether or not the Ca²⁺ binding sites are occupied. This is what we observed (Fig. 10) when we studied the activation of mSlo1, dSlo1, m[dAC], and d[mAC] at 0 and 89 μM [Ca²⁺]_i, where the Ca²⁺ binding sites are either empty or nearly saturated (Fig. 3) (Cox et al., 1997; Cui et al., 1997). In Fig. 10 A, it is immediately apparent that AC region affects the voltage-dependent channel activation at 0 [Ca²⁺]_i. When the channel contains AC region of dSlo1 (WT dSlo1 and m[dAC]), little current could be measured even at +240 mV, whereas the same voltage protocol elicited substantial currents in the channels containing AC region of mSlo1 (WT mSlo1 and d[mAC]). Subsequently, the G-V relation at 0 [Ca²⁺]_i for d[mAC] is similar in slope and voltage range to that of WT mSlo1, whereas, in m[dAC], as in WT dSlo1, the G-V curve was so far right shifted that the shape could not be determined (Fig. 10 B). On the other hand, voltage dependence of activation for all four channels at nearly saturating (89 μM) [Ca²⁺]_i are similar (Fig. 10 B). Fig. 10 C shows that at nearly saturating [Ca²⁺]_i, when Ca²⁺ binding sites are occupied, free energy of activation provided by voltage (ΔG_V) is about the same for all four channels, regardless of the origin of AC region. At 0 [Ca²⁺]_i, however, ΔG_V for WT mSlo1 and d[mAC] is similar while that for WT dSlo1 and m[dAC] is too large to be measured. Thus, changing AC region in the channel causes a large difference in voltage-dependent energy required to open the channel when Ca²⁺ binding sites are empty, but has little effect on channel gating when Ca²⁺ binding sites are occupied.

To further investigate the effects of AC region on Ca²⁺ sensitivity we obtained G-V relations of mSlo1, dSlo1, m[dAC], and d[mAC] channels at various [Ca²⁺]_i between 0 and 89 μM and fit them (Fig. 11) with the 10-state MWC model (Cox et al., 1997). Although the MWC model does not precisely describe the voltage and Ca²⁺-dependent gating of BK_Ca channels (Horrigan and Aldrich, 2002), it has been successfully used to describe major characteristics of BK_Ca gating (Cox et al., 1997; Magleby, 2003) and alterations by mutations and coexpression with β subunits (Cox and Aldrich, 2000; Zhang et al., 2001; Shi and Cui, 2001; Bao et al., 2002; Xia et al., 2002; Magleby, 2003). In the model, the conformation of the Ca²⁺ binding site(s) changes from the closed state to the open state, resulting in a different dissociation constant, K_c and K_o, for Ca²⁺ binding to the closed and open states, respectively. Ca²⁺ binds to the open channel with higher affinity, hence it shifts the closed–open equilibrium toward the open conformation by factor “c” (c = K_o/K_c). Since more than one high-affinity Ca²⁺ binding site in each Slo1 subunit could contribute to activation, Fig. 11 A shows the fits obtained for the G-V relations using the MWC model of four Ca²⁺ binding sites (n = 4), one per subunit, and Fig. 11 B shows the fits obtained for eight Ca²⁺ binding sites (n = 8), two per subunit with similar K_d's (Bao et al., 2002; Xia et al., 2002).

In both cases, n = 4 and n = 8, dSlo1 has smaller values for the c factor than mSlo1, signifying that dSlo1 is more sensitive to the effects of Ca²⁺ binding than mSlo1 (Fig. 11 C). The value of the c factor depends on the origin of AC region (Fig. 11 C). Switching AC region of mSlo1 to that of dSlo1 (m[dAC]) increased Ca²⁺ sensitivity. Conversely, replacing AC region of dSlo1 by its mSlo1 counterpart (d[mAC]) decreased Ca²⁺ sensitivity. These results suggest that higher Ca²⁺ sensitivity in dSlo1 is due to the greater ability of its AC region to change Ca²⁺ binding affinity during channel gating in comparison with that of mSlo1.

It is striking that the value of K_o, the dissociation constant for Ca²⁺ binding to the open state, for all four channels is similar, regardless of the origin of AC region (Fig. 11 C). However, the dissociation constant of Ca²⁺ binding to the closed state, K_c, of dSlo1 is higher than that of mSlo1, implying that Ca²⁺ binds with greater affinity to mSlo1 than to dSlo1 in the closed state. Such a difference in K_c can be largely accounted for by the switch of AC region (m[dAC] and d[mAC]; Fig. 11 C). These results suggest that the conformation of AC region influences the conformation of Ca²⁺ binding sites that is apparent only when the channel is closed, but with little effect when the channel is open.

DISCUSSION

AC Region Is a Crucial Link in the Allosteric Machinery that Couples Ca²⁺ Binding to Channel Opening

We found that dSlo1 has higher Ca²⁺ sensitivity than mSlo1 such that for an identical increase in [Ca²⁺]_i the energy of activation provided by Ca²⁺ binding, ΔΔG_Ca, in dSlo1 was about twice that of mSlo1 (Fig. 1). This differential sensitivity was not due to a different Ca²⁺ binding site in these channels because of two observations. (1) Sequence differences in all putative metal binding sites did not alter Ca²⁺ sensitivity (Figs. 4, 5, 6, and 8). (2) The value of K_o, the dissociation constant of Ca²⁺ binding in the open conformation, is the same (∼1 μM) for both mSlo1 and dSlo1 (Fig. 11). Rather, we find that the differences in conformation and dynamics of the NH₂-terminal (AC) region of the RCK1 domain is responsible for the differential Ca²⁺ sensitivity (Figs. 4, 5, and 9) such that when switched between mSlo1 and dSlo1, the voltage- and Ca²⁺-dependent gating properties of these channels are largely reversed (Figs. 4, 5, 10, and 11). Consistent with this mechanism, modulation by AC region is Ca²⁺ dependent as well as activation state dependent (Figs. 10 and 11); the identity of AC region matters only when the Ca²⁺ binding sites are empty (Fig. 10) and in the closed states (Fig. 11). These effects of AC region result in dSlo1 having a larger free energy change provided by Ca²⁺ binding during channel opening (Figs. 1 and 10), i.e., dSlo1 has higher Ca²⁺ sensitivity of activation. These results demonstrate that AC region is important in the allosteric coupling between Ca²⁺ binding and channel opening and may determine the phenotype of Ca²⁺-dependent activation.

The role of AC region in allosteric coupling between Ca²⁺ binding and channel opening is also consistent with its position in the structure of gating ring. The crystal structure of MthK shows that RCK domains in the gating ring interact with one another only at the fixed and flexible interfaces, both of which are formed by amino acids outside of AC region (Jiang et al., 2002a). The NH₂ terminus of AC region is directly connected to the S6 activation gate (Liu et al., 1997; Webster et al., 2004) through a short peptide linker while the COOH terminus is upstream to α-D and α-E that form the fixed interface with another adjacent RCK domain (Jiang et al., 2002a). A recent study demonstrated that the linker between S6 and the RCK1 domain in BK_Ca channels is important in controlling channel gating, suggesting that BK_Ca channels may have a similar mechanism for Ca²⁺-dependent gating as MthK such that a conformational change in the gating ring induced by Ca²⁺ binding opens the channel by pulling the activation gate (Niu et al., 2004). The structural arrangement suggests that both the linker and AC region may be pulled during the conformational change in the gating ring, while the fixed interface acts as a pivotal point. Consistent with the importance of the AC region in Ca-dependent activation found in this study, a mutation in the AC region has been shown to alter Ca²⁺ sensitivity of the channel and is linked to epilepsy and paroxysmal dyskinesia (Du et al., 2005).

Possible Mechanisms of AC Region Function in Ca²⁺-dependent Gating of BK_Ca

Niu et al. (2004) showed that the voltage dependence of BK_Ca channel open probability (P_o–V relation) in the absence of Ca²⁺ exhibits a linear shift in voltage range with respect to the length of the linker between the inner helix and the gating ring. Based on this observation, they proposed that the channel is gated by a spring-like mechanism and the change of linker length changes the force of the spring. The structural identity of the spring, however, was not clear. We find that the changes in voltage dependence and Ca²⁺ sensitivity caused by a change in the AC region from mSlo1 to dSlo1 are similar to the reported functional changes caused by an increased linker length (Niu et al., 2004), i.e., a shift in the voltage dependence to more positive voltage ranges in the absence of Ca²⁺ (Fig. 10) and an increased Ca²⁺ sensitivity (Figs. 1, 4, 5, 10, and 11). Furthermore, in both studies, the voltage dependence of channel activation is affected much more prominently at 0 [Ca²⁺]_i than at saturating [Ca²⁺]_i (Niu et al., 2004) (Fig. 10). Based on these similarities, it is reasonable to suppose that the AC region functions as a likely spring component in controlling voltage dependence and Ca²⁺ sensitivity of BK_Ca gating. Thus, changing the linker length alters the compression of the spring and hence the force on channel gating (Niu et al., 2004), while exchanging the AC region between dSlo1 and mSlo1 may alter either the compression or the stiffness of the spring.

It is not known at present how AC region couples Ca²⁺ binding to channel opening. Based on the results from Figs. 10 and 11, we propose a likely mechanism of such coupling. When the channel is not bound to Ca²⁺, AC regions from mSlo1 and dSlo1 cause a large difference in the free energy of the channel gating (Fig. 10), indicating that channel function is very sensitive to the conformational and dynamical differences between AC regions. However, it is striking that such an energetic change derived from the structural variation largely disappeared when the channel was saturated with Ca²⁺ (Fig. 10). This result could only be explained by two possibilities. (1) Ca²⁺ binding changes channel conformation in a manner that AC region no longer contributes to the free energy of channel activation. Hence the structural variations in AC region no longer matter. (2) AC region contributes energetically to channel gating at all [Ca²⁺]_i's. However, although the structural variations are critical to channel gating at low [Ca²⁺]_i, they matter little to channel gating at high [Ca²⁺]_i. The latter explanation seems unlikely given that the response to low [Ca²⁺]_i is sensitive to sequence variation throughout the AC region (Figs. 4–7, 9, and 11); and it is difficult to imagine that the sum contribution of these multiple differences would coincidentally be equal in saturating [Ca²⁺]_i.

Therefore, these results left us with the more likely conclusion that AC region may not contribute energetically to channel gating at saturating [Ca²⁺]_i. This conclusion is equivalent to a mechanism wherein AC region inhibits the channel in the absence of Ca²⁺, while Ca²⁺ binding relieves the inhibition and allows the channel to gate by less voltage-dependent free energy. This mechanism is consistent with the findings in the cAMP modulation of HCN channel gating, where the COOH-terminal cyclic nucleotide-binding domain (CNBD) inhibits channel activation and the binding of cAMP relieves this inhibition (Wainger et al., 2001). Similar mechanism for BK_Ca channel activation by the Ca²⁺ bowl has been previously proposed (Schreiber et al., 1999). In addition, we have also observed that the difference in the AC region structure alters channel conformation at closed state but not open state (Fig. 11), which is consistent with the mechanism that the AC region inhibits channel from opening by stabilizing the closed state.

A model on the mechanism of how AC region modulates BK_Ca gating can be used to summarize the above discussions (Fig. 12). In this model, AC region stabilizes the closed conformation when the Ca²⁺ binding sites are empty. When the Ca²⁺ binding sites are saturated or the channel is in the open state, AC region no longer affects BK_Ca gating (Fig. 12), which, in terms of a spring model, is as if a spring were slackened. However, the model in Fig. 12 does not require that AC region behaves like a spring. Regardless of whether or not AC region per se changes conformation during channel gating, the model will be similar as long as the conformational changes of the channel induced by Ca²⁺ binding result in AC region no longer affecting the activation gate. It is worth pointing out that this model requires a conformational change in the closed state upon Ca²⁺ binding, which differs from the MWC-based models that assume a conformational change only occurring during the closed–open transition.

Figure 12.

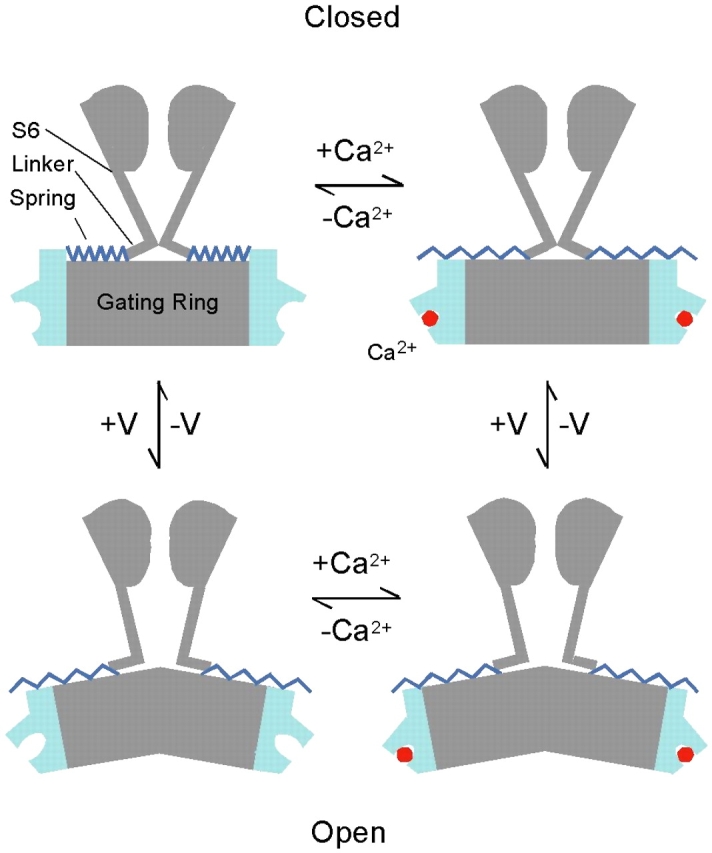
Spring effect of the AC region in channel gating. In the absence of bound Ca²⁺ and in the closed conformation, the AC region adopts a conformation that inhibits channel opening. Ca²⁺ binding (+Ca²⁺) or channel opening by depolarization (+V) removes this inhibition, rendering the channel gate more favorable to the open conformation. In the open conformation or when the Ca²⁺ binding sites are occupied, the AC region has little effect on channel gating.

An interesting outcome of the parameter fits to the MWC model is the 20-fold difference in the values of L(0) between mSlo1 and dSlo1 (Fig. 11 C). In the MWC model used here, L(0) is a lumped parameter representing the steady-state equilibrium of the voltage-dependent closed–open transition that occurs in the absence of Ca²⁺ binding. Thus, L(0) may be taken as a measure of the voltage-dependent activation energy that combines the energy of voltage sensor activation as well as channel opening. While the L(0) value for mSlo1 is consistent with those published before (Cox et al., 1997; Cui and Aldrich, 2000; Shi and Cui, 2001), no such reference exists for dSlo1. However, we note the higher value of L(0) as being consistent with the experimental observation that in the absence of Ca²⁺ binding, the voltage dependence of activation of the channel is extremely right shifted (Fig. 1 B and Fig. 10). Indications of such differences have been also observed in previous studies (Adelman et al., 1992; Wei et al., 1994; Silberberg et al., 1996; Moss et al., 1999). This could be interpreted as a suggestion that the allosteric mechanisms involved in the voltage-dependent gating of dSlo1 may be quite different from that of mSlo1. Exploring this aspect of dSlo1 activation in more detail warrants a different set of experiments and probably a different set of kinetic schemes, which is beyond the scope of the present study. The change in voltage dependence, however, should not affect our fitting results on the Ca²⁺ sensitivity using the MWC model because it has been shown that Ca²⁺ and voltage activate the channel through separate activation pathways, and the change of one pathway by mutations or β-subunit association does not affect the other significantly (Cox and Aldrich, 2000; Cui and Aldrich, 2000; Shi and Cui, 2001; Horrigan and Aldrich, 2002; Niu and Magleby, 2002; Hu et al., 2003; Orio and Latorre, 2005).

Recent structural studies demonstrate that the ionic pore and the activation gate of various ion channels adopt a similar structure (Doyle et al., 1998; Jiang et al., 2002b, 2003; Kuo et al., 2003), while they are associated with different gating modules that sense various stimuli such as voltage and intracellular ligands to control the closed–open transitions of the channel. BK_Ca is activated by both voltage and intracellular divalent cations. It is likely that a general and conserved principle of BK_Ca gating in coupling the stimuli to channel gate is adopted by both the intracellular gating ring and the transmembrane voltage sensor. If AC region modulates BK_Ca channel gating by inhibiting channel from opening while Ca²⁺ binding relieves this inhibition as suggested in the above model (Fig. 11), the voltage-dependent mechanism may also activate the channel by relieving an inhibition, similar to a mechanism suggested for voltage-gated Shaker K⁺ channels (Armstrong, 2003). Obviously, further investigation is required to test such models.