Concerted vs. Sequential. Two Activation Patterns of Vast Arrays of Intracellular Ca²⁺ Channels in Muscle

Abstract

To signal cell responses, Ca²⁺ is released from storage through intracellular Ca²⁺ channels. Unlike most plasmalemmal channels, these are clustered in quasi-crystalline arrays, which should endow them with unique properties. Two distinct patterns of local activation of Ca²⁺ release were revealed in images of Ca²⁺ sparks in permeabilized cells of amphibian muscle. In the presence of sulfate, an anion that enters the SR and precipitates Ca²⁺, sparks became wider than in the conventional, glutamate-based solution. Some of these were “protoplatykurtic” (had a flat top from early on), suggesting an extensive array of channels that activate simultaneously. Under these conditions the rate of production of signal mass was roughly constant during the rise time of the spark and could be as high as 5 μm³ ms⁻¹, consistent with a release current >50 pA since the beginning of the event. This pattern, called “concerted activation,” was observed also in rat muscle fibers. When sulfate was combined with a reduced cytosolic [Ca²⁺] (50 nM) these sparks coexisted (and interfered) with a sequential progression of channel opening, probably mediated by Ca²⁺-induced Ca²⁺ release (CICR). Sequential propagation, observed only in frogs, may require parajunctional channels, of RyR isoform β, which are absent in the rat. Concerted opening instead appears to be a property of RyR α in the amphibian and the homologous isoform 1 in the mammal.

INTRODUCTION

The signal in ion signaling may be the moving ion or its electric charge. Channels involved in electric signaling are often spatially separate, and can be modeled as members of statistical ensembles (e.g., Sigworth, 1994). One reason is that relaxation of net charge in aqueous media is fast, so that ion fluxes need not be locally dense to produce rapid cell-wide electric signals. By comparison, ion diffusion is slow, hence the paradigm of Ca²⁺ signaling is the “microdomain,” appropriate to diffusion in a time scale of milliseconds (e.g., Ríos and Stern, 1997). To reach targets by diffusion, high local concentration swings become necessary, often requiring channels of high conductance, assembled in arrays. Their tight packing could serve not just to concentrate the flux, but to synchronize their command. Instead of statistical ensembles, interchannel interactions must be contemplated.

In skeletal muscle, Ca²⁺ signals are most demandingly tuned for magnitude and rate. Much of the controlled speed of the signals is already present in Ca²⁺ sparks (Cheng et al., 1993; Tsugorka et al., 1995), building blocks of the Ca²⁺ transient (Cheng et al., 1993; Lacampagne et al., 1999) in cardiac muscle and in skeletal muscle of many taxa.

In intact fibers, sparks require sources of one to five channels (for review see Baylor, 2005), while events observed in cut fibers require many more (Ríos et al., 1999; González et al., 2000b). Sparks open-source times are modally distributed (Wang et al., 2002; Rengifo et al., 2002), therefore their generator is not Markovian, having instead some time-keeping provision that synchronizes closure. The implication is that in sparks channels interact, but it is not clear how.

An opportunity to unravel these interactions is presented by the different molecular endowment of mammals, with a set of isoform 1 RyR channels facing voltage sensors across the junction between SR and T tubule, versus amphibians, which additionally have isoform 3, or β (Ogawa et al., 2002), in a parajunctional position (Felder and Franzini-Armstrong, 2002).

We used video rate confocal imaging techniques to compare the time course of Ca²⁺ sparks in amphibian and mammalian muscle at high temporal resolution. The anion sulfate, which is used to increase the frequency of sparks in mammals, was found to cause substantial changes in morphology of events in the frog. Unexpectedly, a combination of sulfate and low [Ca²⁺]_cyto induced instead a strikingly different mode of channel interaction.

MATERIALS AND METHODS

Ca²⁺ events were imaged at 17–20°C in saponin-permeabilized skeletal muscle fibers from Rana pipiens semitendinosus muscle and Rattus norvegicus EDL muscle. Adult frogs and rats were killed by double pithing under anesthesia and CO₂ inhalation, respectively. Procedures were approved by Rush University's IACUC. Procedures and solutions for fiber dissection and mounting are published (Zhou et al., 2003a). The internal solutions used for frog were three: a “reference,” with glutamate as main anion; “sulfate,” with sulfate as main anion and 100 nM free [Ca²⁺], and “sulfate/low Ca²⁺.” The compositions of reference and sulfate are given in Zhou et al. (2003a), Table I. Sulfate/low Ca²⁺ had the same composition as sulfate but only 0.102 mM CaCl₂, for a [Ca²⁺] of 50 nM. Rat fibers were imaged in rat sulfate, with composition given in the same paper. All internal solutions had 100 μM fluo-4.

TABLE I.

Morphology of Sparks in Amphibian and Mammalian Muscle. The Effect of Sulfate

	Scanning	Peak amplitude	FWHM	Rise T	Ṁ	N events	N cells
			μm	ms	μm3ms−1
Frog glutamate	Conventional	0.88	1.53	5.55		1890	12
		0.06	0.07	0.41
Rat, combined	Conventional	0.64	2.01	7.64		4537	24
		0.02	0.04	0.19
Frog SO4	Conventional	0.63	2.02	7.31		359	6
		0.03	0.02	0.32
Frog glutamate	Video rate	0.71	1.53	4.6	0.87	23	2
		0.05	0.05	0.33	0.14
Frog SO4	Video rate	0.60	2.11	3.56	3.63	12	5
		0.16	0.19	0.59	0.60
Rat SO4	Video rate	0.52	1.95	3.50	2.60	51	4
		0.02	0.05	0.30	0.37

Average and SEM of morphologic parameters in sparks recorded in line scans at two temporal resolutions: conventional (2 ms per line, MRC 1000) or video rate (0.64 ms per line, Nikon RCM8000), of amplitude >0.4. Signal mass rate is the average of Ṁ(t) during the rise time. The entries for “Rat, combined” are equal weight averages of the numbers given separately for glutamate and SO₄ (which were not significantly different) in Zhou et al. (2003a). Entries for “Frog glutamate, conventional” are also from Zhou et al. (2003a).

Line scans were obtained with a conventional confocal scanning microscope (MRC 1000, Bio-Rad Laboratories) using a 40×, 1.2 NA water immersion objective (Carl Zeiss MicroImaging, Inc.) or a video rate scanner (RCM8000, Nikon) using a 40×, 1.15 NA water immersion objective (CF UV, Nikon), both in fluo-4 configuration. Images shown are of fluorescence F(x, t) determined at 2-ms or 64-μs intervals and pixel distances of 0.143 or 0.167 μm along a line perpendicular to the fiber axis for conventional and video rate scanning, respectively, usually normalized to its resting average F ₀(x). Sparks are located on a spatially filtered version of the normalized image as previously described (Zhou et al., 2003a). Parameters measured on the unfiltered image for every event include the following: amplitude (peak minus local average before the event), FWHM (spatial width of the region exceeding half amplitude at the time of peak), and rise time (between 0.1 and peak, on a spline interpolate).

Signal mass of events was calculated as a function of time t by the approximation M ≈ 1.206 × ΔF/F ₀ (t, x = 0) × FWHM(t)³ (Chandler et al., 2003). x = 0 is the spatial location of the spark's peak. FWHM(t) is 2(2 ln2)^0.5 σ, where σ is the standard deviation of a Gaussian fitted to the spatial profile ΔF/F ₀ (t, x) at each t. The assumption needed, Gaussian profiles with spherical symmetry, will not apply in general. Arguments and conclusions that depend on these estimates, however, should remain valid in spite of large errors. Signal mass production rate, Ṁ(t), was calculated numerically from M. For Fig. 2, Ṁ(t) was calculated similarly for a spark simulated as described by Csernoch et al. (2004) with a current of 75 pA, lasting 4 ms, originating at a cylindric source of 1.0 μm length and 0.1 μm radius, with axis on the scanning line. Resting [Ca²⁺] was 50 nM. Other parameters values are listed in table 1 of the same reference. Images shown are digitally filtered at corner frequencies equal to 0.33 of the Nyquist frequencies.

Figure 2.

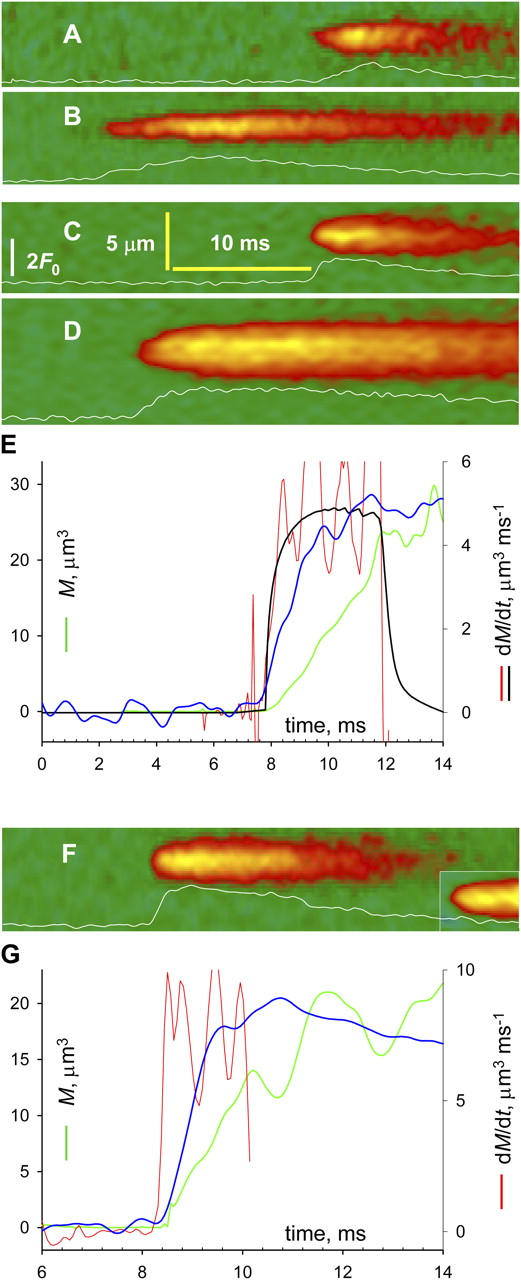
Sparks at high temporal resolution. Line scans transversal to fiber axis, obtained with the video-rate confocal system. Traces plot ΔF/F ₀ averaged at three central pixels. (A and B) Frog cells in glutamate. (C and D) Frog cells in sulfate. (F) Rat cells in sulfate. (E and G) Evolution of variables, calculated for sparks in D and F, respectively. Blue, ΔF/F ₀ (full scale is 2 and 2.4 in E and G); green, signal mass M(t); red, Ṁ(t); black, Ṁ (t) in simulation with source of 75 pA, open for 3 ms. Identifiers: A, 091302a4; B, 112902a76; C–E, 032802a3, 2; F and G, 032002a24 and 032002d17.

Kurtosis, κ, is a measure of peakedness of a distribution (Kenney and Keeping, 1962). It was applied to spark spatial profiles f(x) and calculated as

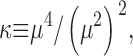where μⁿ are the n-th order central moments of f

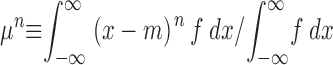and m is the mean value of x with distribution f(x). Functions that are approximately Gaussian have κ ∼ 3, and are called mesokurtic. Greater and lesser values of kurtosis correspond respectively to peakier, or leptokurtic and flatter, or platykurtic functions.

RESULTS

On average, Ca²⁺ sparks of permeabilized rat skeletal muscle are of lower amplitude and greater spatial width than the frog's, as documented in the first two rows of Table I, which summarize data of Zhou et al. (2003a). Standard solutions use glutamate as main anion. Surprisingly, when SO₄ ²⁻ was substituted for glutamate, frog sparks adopted the morphology of the rat's. The third row lists the properties of frog sparks in sulfate. Spatial width increased while amplitude decreased, resulting in events similar to those of the rat. Sulfate does not change the morphology of rat sparks (Zhou et al., 2003a).

Platykurtic Sparks in Mammalian and Amphibian Muscle

Sparks recorded in the frog in glutamate are illustrated in Fig. 1 A. The vast majority were bell shaped, approximately Gaussian. The kurtosis (a measure of peakedness defined in MATERIALS AND METHODS) of the three spatial profiles in Fig. 1 A is between 3.05 and 3.59, hence they are mesokurtic or slightly leptokurtic. By contrast, with sulfate solutions and transversal scanning, a fraction of sparks had flatter tops (examples in Fig. 1 B). Their kurtosis is correspondingly lower, 1.17 and 1.25 for the curves in Fig. 1 B. They are platykurtic. In simulations with a point source of Ca²⁺ current, sparks are mesokurtic until Ca²⁺ builds up sufficiently to saturate the dye; then, upon saturation, they become platykurtic (Izu et al., 2001). Panels B and C exemplify instead sparks of flat top right from the scan of first detection (named “protoplatykurtic” or PPK). These suggest the involvement of an extensive source. Fig. 1 C illustrates PPK sparks in rat muscle (which were observed whether sulfate was present or not).

Figure 1.

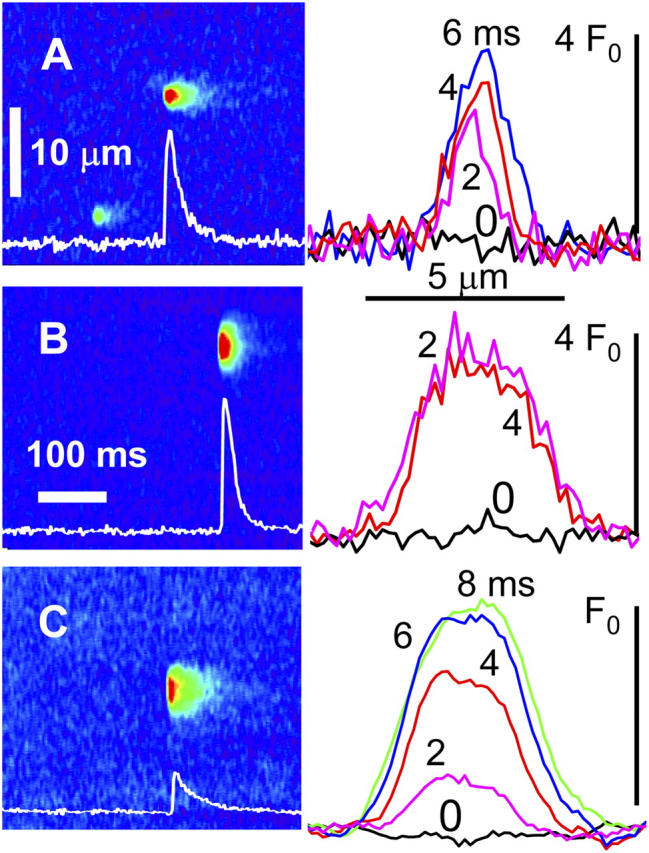
Protoplatykurtic sparks in frogs and rats. (A) Normalized fluorescence F/F ₀, in an image of a permeabilized frog fiber immersed in reference solution. Graph, spatial profiles of event in A at times indicated (ms). Kurtosis κ was 3.25, 3.05, and 3.59 at 2, 4, and 6 ms, respectively. (B) F/F ₀ in a frog fiber in “sulfate” solution. κ was 1.17 and 1.25 at 2 and 4 ms. (C) Spark in a rat fiber in sulfate. κ was 2.16 at 2 ms. Sparks in B and C are therefore protoplatykurtic. Identifiers of cell and image: A, 102901a306; B, 111301a1_2; C, 082702b411.

Some sparks had a high rate of rise. Especially for PPK sparks, this requires a large release current. Signal mass M (Sun et al., 1998; ZhuGe et al., 2000, 2002; Chandler et al., 2003) is a proportional indicator of underlying Ca²⁺ release, robust against variations in dye concentration. As done for sparks of smooth muscle by ZhuGe et al. (2000)(2002) and Zou et al. (2004), we will take its rate of change Ṁ(t) to be a proportional measure of release current. As shown in APPENDIX, the use can also be justified for the conditions of skeletal muscle. At peak fluorescence, signal mass was 9.8, 110, and 32 μm³, respectively, for the events of Fig. 1 (A, B, and C). Ṁ (t) peaked at a value 45 times greater in B than in A.

Sparks at High Temporal Resolution

The evolution of sparks and their mass was best recorded with the high temporal resolution of a video rate confocal microscope. Fig. 2 shows line scans from frog muscle in glutamate (A and B) or sulfate (C and D). Sparks in the rat, which were recorded at video rates only in sulfate, are illustrated in F. The lower rows in Table 1 list their average parameters, which were close to those determined by conventional scanning. Normalized fluorescence F(t)/F ₀ (blue), M(t) (green) and Ṁ (t) (red) of the sparks in D and F are plotted in E and G. In these and many other sparks of frog or rat, the early evolution of M was roughly linear. Ṁ (t) oscillated from the beginning of the spark near 5 (E) or 8 μm³ms⁻¹ (G). The table lists the average Ṁ. Sulfate increased it in frogs about fourfold, to a value close to that of rat sparks.

Because Ṁ relates to flux independently of dye concentration, it can be compared across fibers under the assumption that Ca²⁺ removal properties are similar. Eq. A7 in the Appendix shows under simple assumptions proportionality between Ca²⁺ release current and Ṁ [Ca²⁺]₀. This can be combined with simulations to calibrate Ṁ in terms of release current. A simulation with a Ca²⁺ source of 2.5 pA at [Ca²⁺]₀ = 50 nM results in average Ṁ of 0.25 μm³ms⁻¹ (Baylor, 2005). This is almost exactly proportional to the result of Csernoch et al. (2004) with a source of 0.5 pA at double the resting [Ca²⁺]₀ (0.02 μm³ms⁻¹). Averaging these two determinations yields a conversion factor of 0.22 pA per unit of Ṁ (μm³ms⁻¹) per nM [Ca²⁺]₀. If linearity held, the observed Ṁ of 5 μm³ms⁻¹ (at [Ca²⁺]₀ = 50 nM) would require a release current of 55 pA. The black trace in the figure plots Ṁ simulated with a source of 75 pA. While the result will vary with the assumptions, it seems clear that release from a very large group of channels is at the source of these events, as concluded for rat sparks by Zhou et al.(2003a). In the example of Fig. 2 E and others, signal mass increased linearly with time, as if driven by a constant current. An approximately linear increase of signal mass was also shown by ZhuGe et al. (2002) during the onset of a spark of amphibian smooth muscle. A constant Ṁ requires that the channels involved open nearly in unison. Therefore, the conclusion of Lacampagne et al. (1999), that opening of spark sources is effectively instantaneous, applies also to wide PPK events, a surprising conclusion as these may involve 100 channels or more.

There is almost certainly contact between RyRs in triads (Yin et al., 2005). Hence allosteric interactions, proposed to couple gating of RyRs in bilayers (Marx et al., 1998), could underlie concerted opening. While the mechanism of this coupling is not clear (Xin et al., 2002; Fill and Copello, 2002), it seemed interesting to test here the effects of rapamycin, which disrupts coupled gating in bilayers. Four frog fibers in sulfate were compared before and after exposure to 20 μM rapamycin. The drug caused no immediate effect. After 25 min, FWHM decreased, not significantly, from 1.95 μm (SEM 0.03, 1870 events) to 1.77 μm (0.15, 88). The frequency decreased significantly, but large PPK sparks remained even after 35 min in rapamycin. These modest effects leave unsettled a possible link between concerted opening in sparks and coupled gating in bilayers.

Sequentially Propagating Ca²⁺ Events

Activation of a linear array of channels by CICR should be sequential, with channels opening one after another as trigger Ca²⁺ reaches them by diffusion. Events that move at measurable speed have been described in frog muscle (Brum et al., 2000). Consistent with CICR, they were promoted by caffeine.

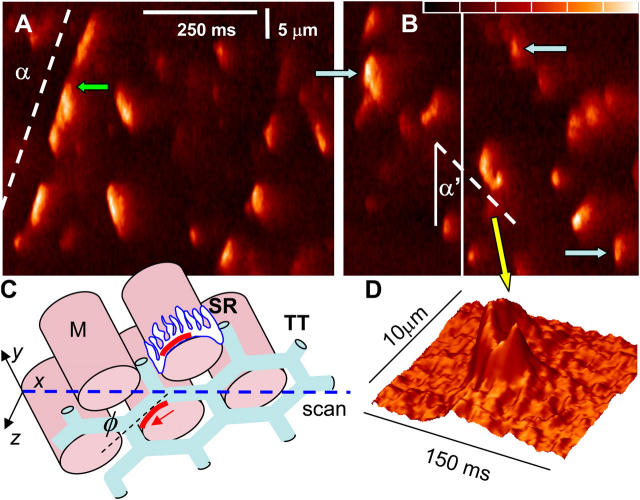
In the frog, moving events became very frequent in a cytosolic solution combining sulfate and a reduced [Ca²⁺] (50 nM). Line scans in Fig. 3 (A and B) were obtained after 2 min in this solution. The events propagated at nearly constant velocity, sometimes over distances spanning several myofibrils. Activity as shown could persist for 30 min, then drift toward uncontrolled release. Sequentially propagated events coexisted with regular sparks. Some of these were PPK (blue arrows in Fig. 3 B).

Figure 3.

Propagating activation of release channels. (A and B) Normalized fluorescence in selected areas of line scans of a frog fiber in “sulfate/low Ca²⁺.” Color scale spans the range 0.8–2.4. Activation propagates at a speed proportional to cot α. (C) Scheme of structures: M, myofibrils; TT, T tubules; SR, sarcoplasmic reticulum, with channel arrays or couplons in red. Transversal scans proceed along x axis (blue). If the direction of propagation separates from the scan line at an angle N (red arrow), then α will increase (e.g., α' in B). Propagating events coexist with others that widen rapidly and reach higher F (blue arrows in B). (D) 3-D representation of event in B where activation appears to turn around a myofibril. Identifiers: A, selected area of 082902b322; B, selected areas of 082902b309, 315.

As argued, sparks involve the activation of groups of channels essentially in unison. These sequentially propagated events are evidently different. Do the differences require distinct propagation mechanisms? An answer was reached through the analysis of propagation velocity.

The “lateral velocity” v _L of event propagation, the velocity in the x (scanning) direction, is proportional to the cotangent of the angle α between direction of propagation and scan axis (Fig. 3 A). v _L is equal to actual velocity v only when events propagate parallel to the scan line. As illustrated in Fig. 3 C, if the T tubule and its associated couplon (Stern et al., 1997) form an angle φ > 0 with the scan line, then v _L will be lower—α will increase. Increases in α were seldom observed, probably because the narrow field of the confocal microscope limits the height of the visible slice. One event in Fig. 3 B, highlighted in D, features such increase; afterwards the path turns back, delineating perhaps junctional SR around a myofibril. In spite of these exceptions, α was stable within events and reproducible in different events, suggesting that v _L was usually close to v, which in turn was essentially constant.

The v _L of individual events was examined as a way of separating propagation patterns. The rationale was that a continuum of velocities, ranging from finite to immeasurably high, would suggest a single propagation mechanism with variable efficiency. A sharp mode at a finite velocity, instead, would require a sequential mechanism different from the one synchronizing concerted activation.

An automatic procedure was devised to objectively evaluate propagating events. In line scans such as Fig. 4 A, events were first detected by criteria common to sparks (González et al., 2000a). A closed contour was constructed joining the pixels at the edge of the suprathreshold footprint of each detected event. Automatic examination of the contour identified events of measurable v _L as those with flat or convex leading edge (concavity suggesting multiple origins of propagation) and sufficient spatial extent to define a velocity (x span > 3 μm). In Fig. 4 A, the suitable events have a red footprint; those marked with contour only were rejected for their concave edge; those without a contour were spatially too small.

Figure 4.

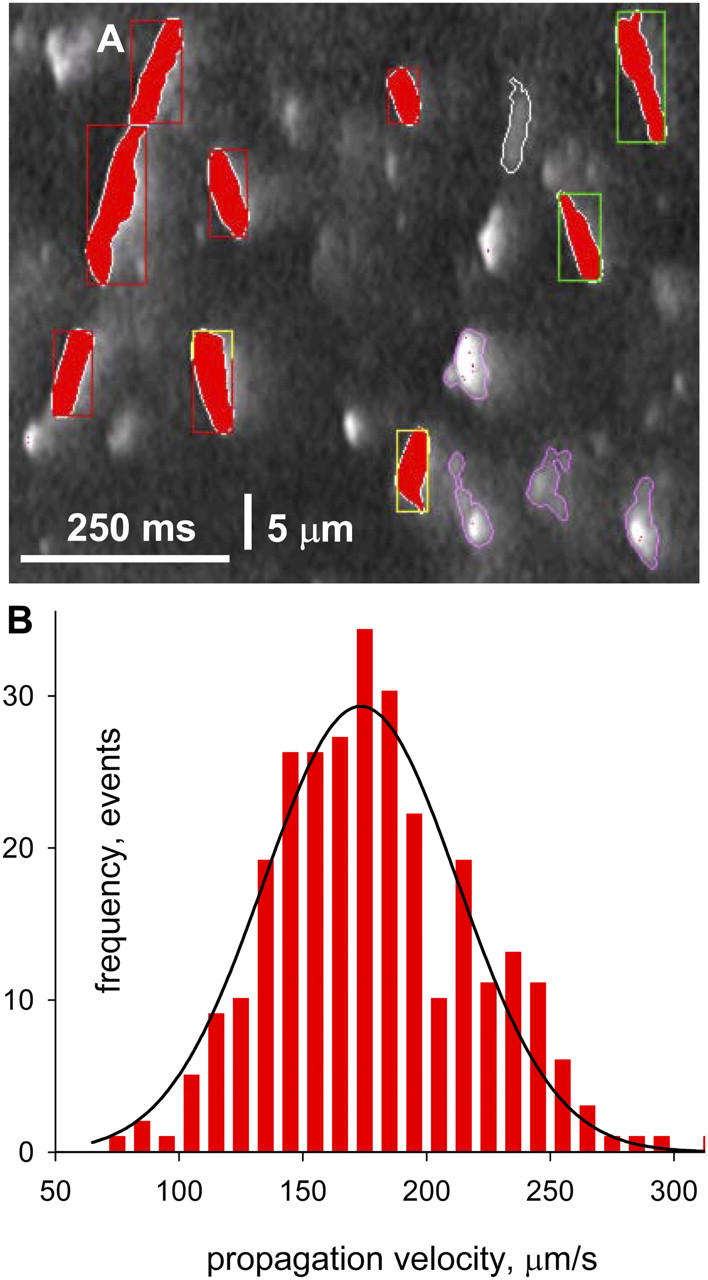
Propagation velocity. (A) Line scan image with markings by analysis software. In red are silhouettes of propagating events of measurable lateral velocity. Contours mark events classified as multifocal. Events without contours had insufficient width to define a velocity. (B) Histogram of propagation velocities, with Gaussian fit. Identifier: 082902b.

262 events satisfied the criteria in 60 images of the same fiber. The histogram of velocities, in Fig. 4 B, is well fitted by a Gaussian centered at 173 μm/s, with standard deviation of 39 μm/s. Averages of smaller groups of events in other fibers ranged from 120 to 246 μm/s. This finite, bell-shaped distribution of velocity sharply distinguishes sequential propagation from the seemingly instantaneous concerted mode.

Interaction between Patterns

Propagating events were also recorded in the video rate scanner. Fig. 5 A shows one example (repeated at right in a compressed time scale). The parallelogram-shaped event image reflects a transient that propagates at constant velocity and lasts about the same at all locations. In the event in Fig. 5 B both patterns may be at work: there is sequential activation at early times (dashed line); two discrete increases of intensity then intervene (arrows) and interrupt the propagation, which continues with the same velocity and direction after the increases subside (second dashed segment). The time-compressed version at right shows that the sudden increases in fluorescence result in rapid widening, followed by an interruption of propagation (bracket). It looks as if a temporary halt in propagation may be a consequence of the greater local [Ca²⁺].

Figure 5.

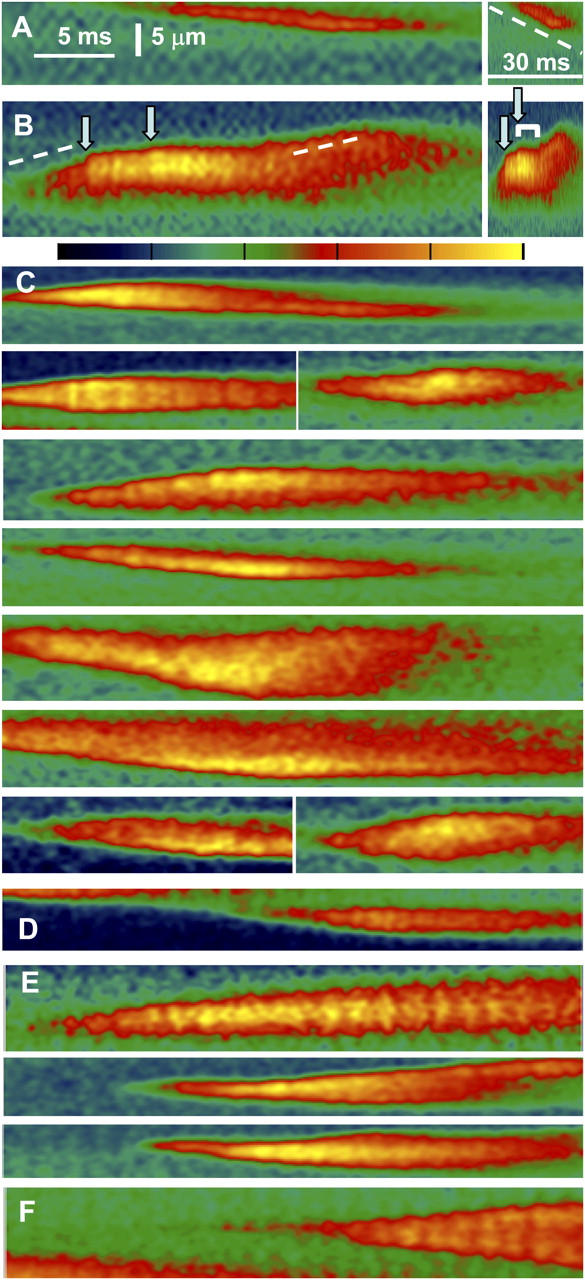
Events of mixed propagation imaged at high temporal resolution in frog muscle. Video rate line scan images of fluorescence in “sulfate/low Ca²⁺,” with color scale shown between B and C. (A) A sequentially propagated event. (B) A mixed event, in which sequential activation (dashed line) alternates with sudden increases in fluorescence (arrows). The image is repeated at right in a compressed time scale, to show that the sudden increases result in rapid widening, followed by transient interruption of propagation (bracket). (C) Examples of events in which a local increase in fluorescence accompanies a stop in propagation. (D) An event with a stop and no intensification of fluorescence (a second example is in A). (E) Events where increases in fluorescence do not stop propagation. (F) Example of propagated events that have neither interruptions of propagation nor increases in intensity. Identifiers: A and B, 091102c93, 104; C, 090502c, 091002a, 091102c; D, 091102c33; E, 091102c32, 36, 83; F, 091102c92.

For an objective test of this correlation, we tabulated propagated events having either or both of two features: instances of interruption of sequential propagation and intensification visible by eye. 49 such events were identified in five fibers. 51 interruptions or terminations of propagation were visible in 46 of these events. Among the 51 interruptions, 45 were accompanied or immediately preceded by an intensification of fluorescence and 6 were not. Additionally, there were 5 intensifications not associated with interruption. The bottom panels in Fig. 5 illustrate these features. C and D have events with interruptions of propagation, which in C are associated with intensification and in the events in D (and A) are not. Increases in intensity not altering propagation are in Fig. 5 E. The event in F represents those that were not included in the analysis because they had neither interruptions nor intensifications. They were veritable waves, which could propagate over long distances.

In all, there was clear association between a local increase in intensity and the stop of propagation. The correlation suggests that concerted activation will impinge negatively on the sequential process. The large uninterrupted waves of low intensity are also consistent with the idea that the increase in [Ca²⁺]_cyto above a certain level is inhibitory.

DISCUSSION

The central finding here is the coexistence of two patterns of propagation of activation along arrays of Ca²⁺ release channels. Both require plasma membrane permeabilization and immersion in nonphysiological salines. The concerted pattern results in essentially simultaneous opening of a large number of channels, as deduced from the large spatial width and rate of production of signal mass of these events.

The activation of such arrays appears instantaneous relative to the temporal resolution of the imaging technique. In the event of Fig. 2 E Ṁ reaches a roughly steady value in ∼0.5 ms, a rise reproduced by a simulation where the activation was truly instantaneous. Thus, these 0.5 ms reflect dye reaction time rather than propagation lag. The current in the simulation was 75 pA and it reached Ṁ = 4.7 μ³ms⁻¹. The average Ṁ (3.6 μ³ms⁻¹) would require instead 57.5 pA, or 115 channels of 0.5 pA (Kettlun et al., 2003). A 1 μm long couplon fits ∼60 junctional α channels, plus an equal number of parajunctional channels (assuming equal density of isoforms), for a total of 120 channels. Assuming that all of them contribute, 1 μm will be a lower bound for the length of array activated in <0.5 ms. A conservative estimate of propagation velocity in concerted gating is therefore 1 μm/0.5 ms, or 2,000 μm/s.

By contrast, the sequential mode of propagation (Figs. 3–5) has a finite velocity, distributed between 100 and 250 μm/s. This large discrepancy in speed is evidence that the two forms of propagation involve different mechanisms, or two sharply diverging manifestations of the same mechanism.

Possible Mechanisms of Propagation

Sequential propagation is probably mediated by CICR. This is indicated by the speed of the sequential events, somewhat greater than that of Ca²⁺-mediated Ca²⁺ waves in cardiomyocytes with high SR load (Lukyanenko and Györke, 1999). An additional argument is that sequential activation depends crucially on conditions, sulfate and [Ca²⁺]_cyto, that should affect the unitary release current and local cytosolic [Ca²⁺]. The much faster spread of concerted opening requires either a radically different regimen of CICR or conformational coupling among channels in physical contact.

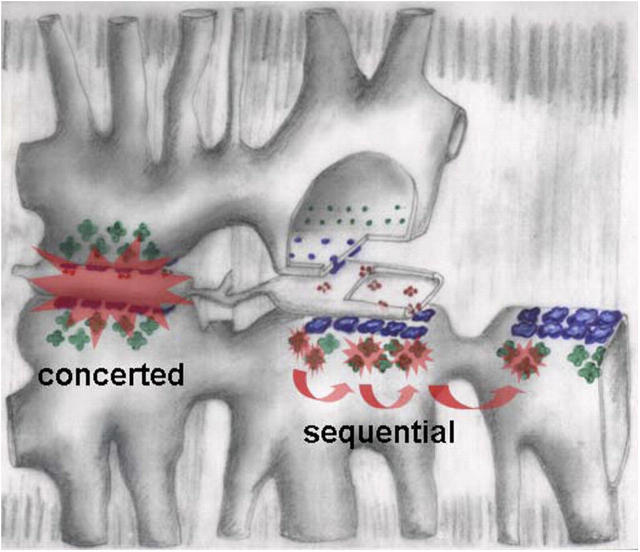
A molecular underpinning for dual mechanisms is suggested by the absence of sequential events in the rat, where sulfate only alters event frequency (Zhou et al., 2003a). As sketched for frog muscle in Fig. 6, concerted events, virtually identical in both species, should originate at the junctional arrays of α or RyR1 isoforms. Sequential activation should instead require β channels, green in the diagram.

Figure 6.

Hypothetical mechanisms of two activation patterns in frog fibers. Triads are drawn progressively separated and stripped of components from left to right. α channels, in blue, are grouped in couplons that face the junctional gap. They undergo concerted activation, pictured as a Ca²⁺-mediated interaction that propagates very rapidly in the narrow gap, then stops at the edges of the couplon. Sequential activation is attributed to β channels (green), facing the wide parajunctional space. Ca²⁺-mediated activation there should propagate more slowly, but freely, without defined structural bounds. “Mixed” events are not excluded in this view.

The idea is appealing mechanistically because α and β channels face cytosolic pools of different geometry (Felder and Franzini-Armstrong, 2002). [Ca²⁺]_cyto near an open source will spread faster within the triadic gap than in the wider cytosol. Therefore, CICR may be especially efficient in the gap, appearing as concerted activation, and propagate more slowly parajunctionally, mediating sequential activation. The idea naturally sets limits to the expanse of concerted activation, the boundaries of a couplon, limits that should not apply to the sequential process. It therefore explains well the different spatial extent of the two patterns.

In spite of the potential for propagation, in intact frog cells sparks involve only one to five channels (for review see Baylor, 2005), while in the mammal sparks do not seem to occur physiologically (Ríos, 2005). Two inhibitory mechanisms may be at work. RyR1 channels are physiologically inhibited by the DHPR or other junctional structures (Shirokova et al., 1999; Zhou et al., 2003b, 2004; Pérez et al., 2005; Szappanos et al., 2005). Additionally, and as seen above, high local [Ca²⁺]_cyto inhibits activation, an effect well documented for cell-averaged Ca²⁺ release (for review see Pizarro and Ríos, 2004). This mechanism may be especially important for parajunctional channels.

In addition to intracellular Ca²⁺ channels, membrane molecules that assemble in ordered arrays include aquaporins (Carmosino et al., 2001), acetylcholine receptors (Kistler and Stroud, 1981), gap junction channels (Sosinsky, 1996), SERCA (Castellani et al., 1989), and bacteriorhodopsin (Belrhali et al., 1999). The functional consequences of such ordered clustering have been elusive so far. Here we demonstrated opening of tens, perhaps hundreds, of channels in <0.5 ms. Although this occurred under nonphysiological conditions, the observation puts in evidence a mechanism uniquely suited to rapidly generate a microdomain of high [Ca²⁺].

APPENDIX

Signal Mass Production Rate

The goal is to demonstrate that the time derivative of signal mass is approximately proportional to the Ca²⁺ release current I and derive an expression for the proportionality constant.

Signal mass is defined as the volume integral of the increase in normalized fluorescence

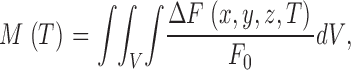where dV is dx dy dz and the integral extends over all space. Note the difference with the literature of smooth muscle, where mass is defined in terms of absolute fluorescence (ZhuGe et al., 2000).

In simulations, the mass produced at the end of a source current pulse of duration T is approximately proportional to total Ca²⁺ release, varied by changing I (between 2 and 6 pA) or T (between 2 and 12 ms; Chandler et al., 2003). For this limited set of T and (constant) I the result can be represented as

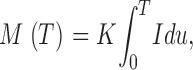(A1)

where K is a constant. Eq. A1 can be reasonably assumed to apply to all possible constant currents within the explored range, therefore to any time sequence of constant segments. Because all continuous functions I(t) within the relevant bounds of intensity and time can be approximated uniformly by a sequence of constant segments, Eq. A1 applies to varying I

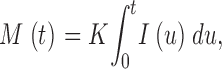(A2)

which amounts to proportionality between current and rate of signal mass production in the same range

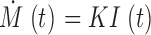(A3)

This conclusion is consistent with simulations of ZhuGe et al. (2000) and calibrations of Zou et al. (2004) in amphibian smooth muscle.

Except at very low [Ca²⁺], the fluorescence of fluo-4 is approximately proportional to [CaFluo](x,y,z,t). Therefore

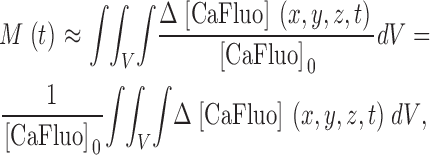(A4)

where [CaFluo]₀ is the concentration at rest. Then

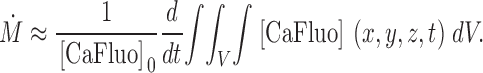(A5)

From A3 and A5

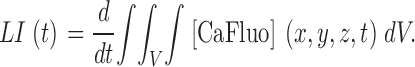(A6)

L ≡ K [CaFluo]₀, is the constant relating the rate of change in total Ca-bound dye to the release current. Because this rate is approximately proportional to total dye concentration [Fluo]_T, and so is [CaFluo]₀, it follows that K is roughly independent of dye concentration.

Eq. A6 can be used to calibrate Ṁ in terms of calcium current when the dye is far from saturation. Let L = S[Fluo]_T, where S is a constant. Substituting in A6

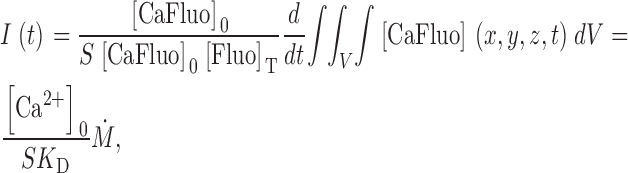(A7)

where K _D is the dissociation constant of dye and calcium.

In conclusion, the rate of signal mass production monitors I(t) proportionally. This is not a trivial result, in view of the fact that it becomes valid at times shorter than the characteristic times of dye reaction. As illustrated by the simulation in Fig. 2, when I undergoes a step increase, Ṁ follows, reaching 80% of the change with a lag of 0.52 ms.

Note that the constant of proportionality includes the resting cytosolic Ca²⁺ concentration. The conversion factor 1/SK _D is evaluated in the text.