A Quantum Mechanic/Molecular Mechanic Study of the Wild-Type and N155S Mutant HIV-1 Integrase Complexed with Diketo Acid

Abstract

Integrase (IN) is one of the three human immunodeficiency virus type 1 (HIV-1) enzymes essential for effective viral replication. Recently, mutation studies have been reported that have shown that a certain degree of viral resistance to diketo acids (DKAs) appears when some amino acid residues of the IN active site are mutated. Mutations represent a fascinating experimental challenge, and we invite theoretical simulations for the disclosure of still unexplored features of enzyme reactions. The aim of this work is to understand the molecular mechanisms of HIV-1 IN drug resistance, which will be useful for designing anti-HIV inhibitors with unique resistance profiles. In this study, we use molecular dynamics simulations, within the hybrid quantum mechanics/molecular mechanics (QM/MM) approach, to determine the protein-ligand interaction energy for wild-type and N155S mutant HIV-1 IN, both complexed with a DKA. This hybrid methodology has the advantage of the inclusion of quantum effects such as ligand polarization upon binding, which can be very important when highly polarizable groups are embedded in anisotropic environments, for example in metal-containing active sites. Furthermore, an energy terms decomposition analysis was performed to determine contributions of individual residues to the enzyme-inhibitor interactions. The results reveal that there is a strong interaction between the Lys-159, Lys-156, and Asn-155 residues and Mg²⁺ cation and the DKA inhibitor. Our calculations show that the binding energy is higher in wild-type than in the N155S mutant, in accordance with the experimental results. The role of the mutated residue has thus been checked as maintaining the structure of the ternary complex formed by the protein, the Mg²⁺ cation, and the inhibitor. These results might be useful to design compounds with more interesting anti-HIV-1 IN activity on the basis of its three-dimensional structure.

INTRODUCTION

Human immunodeficiency virus type 1 (HIV-1) integrase (IN) is an attractive target for the development of anti-AIDS (autoimmune deficiency syndrome) drugs (1–5). It catalyzes the integration of double-stranded viral DNA into the host cell's genomic DNA (2,3). The integration reaction requires three biochemical steps: assembly of a stable preintegration complex at the termini of the viral DNA and two sequential transesterification reactions (2,3). Both reactions consist of a nucleophilic attack of a hydroxyl group on a phosphodiester bond with the participation of a divalent metal ion (Mg²⁺ or Mn²⁺) as cofactor (1). The catalytic core domain comprises the amino acids 50–212, and it contains the conserved DDE motif (D64, D116, and E152). The mutation of any of these three amino acid residues inhibits enzyme's activity (1,5).

A great number of compounds bearing a β-diketo acid motif (DKAs) with anti-HIV-1 IN activity have been reported (5–8). These compounds represent one of the most promising classes of IN inhibitors in terms of potency and selectivity (7), L-731,988 and S-1360 being two of the most promising ones (8). Recently, one DKA analog (5CITEP), a well-known bioisoester (9), has been crystallized with the enzyme (Protein Data Bank (PDB) code 1QS4) (6). In this x-ray structure, a single Mg²⁺ ion is chelated by Asp-64, Asp-116, and water molecules in an octahedral coordination. Computational studies have been performed on DKA compounds by means of classical molecular dynamics (MD) (10,11) and docking (12–22) studies. In particular, 5-CITEP and L-731,988 inhibitors have been investigated by quantum chemical calculations (23) and by classical MD simulation of a full-length HIV-1 IN dimer complexed with viral DNA (24). Nevertheless, understanding the molecular mechanism is far from complete.

Recently, mutation studies have been reported (25–28) and have shown that a certain degree of viral resistance to DKAs appears when some amino acid residues of the IN active site are mutated. In this sense, Hazuda and co-workers have provided evidence that L-870,810 and DKA inhibitors (Scheme 1) exhibit discordant sensitivity to resistant mutations (25). However, they showed that in HIV-1 IN only the mutation of Asn-155 by serine (N155S) confers significant cross-resistance to both inhibitors. In fact, N155S mutation makes the protein 20- and 12-fold less sensitive to the L-870,810 and diketo acid, respectively. More recently, Briggs and co-workers (29–32) have performed classical MD simulations on double mutant enzyme IN T66I/M154I complexed with both 5CITEP and L-731,988 inhibitors. These studies suggest that the conformational changes in the loop 138–149 are responsible for the mechanism of inhibitor resistance in HIV-1 IN.

SCHEME 1.

Structure of the DKA-containing HIV-1 IN inhibitor.

Searching for adequate mutations remains a fascinating experimental challenge, and we invite others to perform theoretical simulations to disclose unexplored features of enzyme reactions. The aim of this work is to understand the molecular mechanisms of HIV-1 IN drug resistance, which will be useful for designing anti-HIV inhibitors with unique resistance profiles. In this work, we employed a combined quantum mechanical/molecular mechanical (QM/MM) approach to determine the protein-ligand interaction energy for wild-type and N155S HIV-1 IN mutant, both complexed with a DKA (Scheme 1). A detailed analysis of the interactions of each inhibitor with the key residues inside the binding pocket are carried out from the computational simulations.

The consideration of protein flexibility may be indispensable for a critical evaluation of ligand-binding affinity (33–36). Usually, docking techniques ignore the flexibility of the receptor, and only the ligand is allowed to suffer conformational changes during the docking procedure. This limitation can be partially overcome considering several receptor structures conveniently picked up from a simulation. However, cooperative structural changes induced between the ligand and the receptor are not considered in this strategy. On the other hand, MD methods can be used to calculate the free energy of protein/ligand binding, including the flexibility of the full system (37). The main problem associated with this methodology is the computational effort required to adequately sample the full configurational space and also to parameterize each new ligand essayed. Here we investigate a strategy to overcome these two computational bottlenecks based on the use of combined QM/MM methods (38–40). These methods are now widely used for the analysis of enzymatic reactions (41,42). In hybrid QM/MM methods, the ligand/substrate species may be described by a QM model, whereas the protein and solvent environment is represented by MM force fields. This hybrid methodology avoids most of the work needed to obtain new force field parameters for each new species. Treating the ligand quantum mechanically and the protein molecular mechanically has the additional advantage of the inclusion of quantum effects, such as ligand polarization upon binding (43,44). Moreover, as the largest part of the system is described classically, enough sampling can be obtained at reasonable computational cost. There are some recent computational studies that successfully applied the combined QM/MM method to the study of protein-ligand interactions in the HIV-1 protease system (45), the trypsin system (46), and cyclin-dependent kinase 2 (47). More recently, we successfully used this methodology to study the relationship between protein-ligand interaction energies and anti-HIV-1 IN activity (48).

METHODS

Model

The initial structure was built from the A-chain of the x-ray crystal structure complexed with the 5CITEP inhibitor (PDB 1QS4; (6)). This chain was used as a starting point for our calculations; we changed only the substrate molecule by the diketo acid depicted in Scheme 1. The Asn-155 residue was replaced by serine in N155S mutant HIV-1 IN. All the missing residues (141–144) were added using the HYPERCHEM facility (49). Hydrogen atoms were placed in the protein according to the predicted pK_a of the amino acids at pH 7. For this purpose, a statistical treatment of electrostatic potential calculations was performed, as implemented by Field and co-workers. (See Antosiewicz et al. (50)—where the method is explained and its accuracy compared with that obtained with other methods—and Gilson (51).) In this case, no unusual ionization states were found. The carboxylic group of the inhibitor is deprotonated in water because of its low pK_a value, and consequently it has been modeled in a deprotonated form (9).

QM/MM MD simulations

After adding the hydrogens to the structure, a series of optimization algorithms (steepest descent, conjugated gradient, and LBFGSB) were applied. To avoid a denaturalization of the protein structure, all the heavy atoms of the protein and the inhibitor were restrained by means of a Cartesian harmonic umbrella with a force constant of 1000 kJ mol⁻¹ Å⁻². Afterward, the system was fully relaxed, with the exception of restraining the peptidic backbone with a lower constant (100 kJ mol⁻¹ Å⁻²). After this procedure, the positions of the initially missing atoms (hydrogen atoms) are optimized, avoiding large distortions of the protein that could invalidate the following simulations. The optimized protein was placed in a cubic box (80 Å sides) of preequilibrated waters, using the principal axis of the protein-inhibitor complex as the geometrical center (Fig. 1). Any water with an oxygen atom lying within a radius of 2.8 Å from a heavy atom of the protein was deleted. The remaining water molecules were then relaxed using optimization algorithms. Finally, 50 ps of hybrid QM/MM Langevin-Verlet MD (canonical or NVT ensemble) at 300 K was used to equilibrate the model. For the hybrid QM/MM calculations, only the atoms of the inhibitor were selected for QM analysis, using a semiempirical Austin Model 1 (AM1) Hamiltonian (52). The rest of the system (protein plus water molecules) was described using the all atoms OPLS potential (OPLS-AA) (53) and TIP3P (54) force fields, as implemented in the DYNAMO (55,56) library.

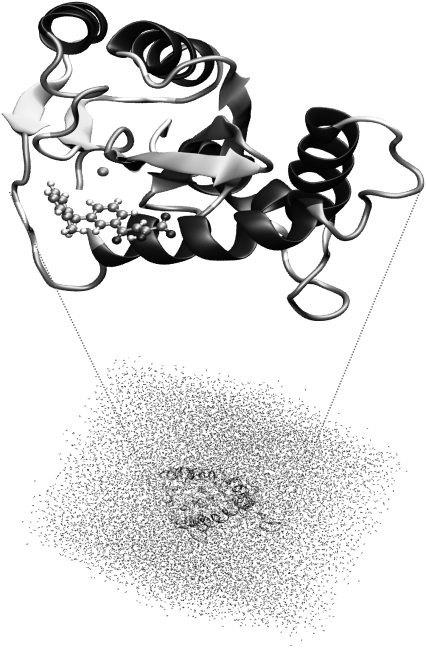
FIGURE 1.

Overall view of wild-type HIV-1 IN complexed with a DKA (in ball and sticks, top) and the full molecular system solvated in a cubic box of 80 Å side (bottom).

Due to the number of degrees of freedom, any residue 25 Å apart from any of the atoms of the initial inhibitor was selected to be kept frozen in the remaining calculations (10,235 mobile atoms). Cutoffs for the nonbonding interactions were applied using a switching scheme, within a radius ranging 11–13 Å.

Afterward, each system was equilibrated by means of 900 ps of QM/MM MD at a temperature of 300 K. The computed root mean-square deviation for the protein during the last 200 ps renders a value that is always below 0.9 Å. Furthermore, the root mean square of the temperature along the different equilibration steps was always lower than 2.5 K, and the variation coefficient of the potential energy during the dynamics simulations was never higher than 0.3%.

Interaction energy calculations

To obtain the interaction energy between the inhibitor and the solvated enzymatic system, we must keep in mind the expression of the hybrid QM/MM potential energy:

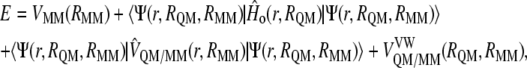(1)

where represents the energy of the MM force field; 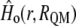is the in vacuo Hamiltonian for the selected QM method; is the polarized wave function due to the presence of an external and flexible electric field, generated by the protein and the solvent molecules; and finally, 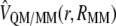and are the electrostatic and van der Waals coupling operators between the QM and MM parts (the van der Waals interaction term does not involve electronic coordinates and thus does not need to be evaluated in the self-consistent field (SCF) procedure). The interaction energy can be then calculated from the analysis of the MD trajectories as the energy difference between the full QM/MM system and the separated QM and MM subsystems. Taking into account that in nonpolarizable force fields the MM energy exactly cancels out we can write

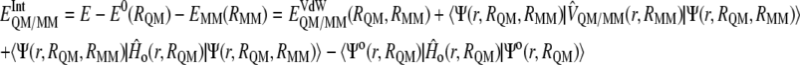(2)

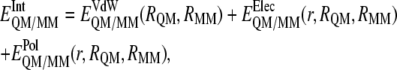(3)

which means that in vacuo single-point energy calculation must be carried out for given nuclear configurations of the quantum atoms along the trajectory, and then this energy must be subtracted from the QM/MM energy. Note that according to our definition of the polarization energy (third term in Eq. 3) as the gas phase energy difference between the polarized and unpolarized wave functions, this is a positive contribution.

This scheme for obtaining the interaction energy was applied in a following 100 ps QM/MM MD run at 300 K, using a time step of 1 fs to solve the equation of motion. In the calculations here, a switched cutoff region from 11.0 to 13.5 Å was used to calculate the nonbonding interaction energies. The polarized wave functions are conveniently stored during the MD simulations, whereas the unpolarized wave functions are obtained a posteriori using saved coordinates of the QM subsystem. Finally, the decomposition of the interaction energy term among the different residues of the protein was carried out using the polarized wave function. For this purpose we evaluated the interaction of the polarized system with the MM centers belonging to a particular residue. This procedure provides only the electrostatic and Lenard-Jones contribution to the interaction energy of a given residue. Thus, the global polarization energy must be derived from the difference between the total interaction energy and the sum of the local contribution of each residue. As stated before, this term is always positive. The described computational procedure was applied for the investigated wild-type and N155S mutant complexed with the diketo acid inhibitor.

DFT(B3LYP)/MM calculations

To check the reliability of the structures and the interaction energy calculations by residue obtained by means of AM1/MM methods, potential energy optimizations were also carried out using density functional theory (DFT) to describe the quantum region in the hybrid QM/MM scheme. The B3LYP function (57,58) was employed together with the 6-31G* basis set to describe the QM region of the system, which includes all atoms of the ligand and the Mg²⁺ ion, whereas the OPLS-AA force field was used for the MM part. This strategy has been used by Guo et al. (59) to study the stability of the metal ligand bonds.

The potential energy of our scheme is derived from the standard QM/MM formulation:

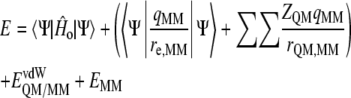(4)

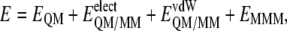(5)

where 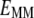is the energy of the MM subsystem terms, 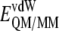is the van der Waals interaction energy between the QM and MM subsystems and includes both the coulombic interaction of the QM nuclei (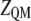) and the electrostatic interaction of the polarized electronic wave function (Ψ) with the charges of the protein (), and E_QM is the gas phase energy of the polarized wave function. To take advantage of powerful optimizations algorithms (see Marti et al. (60)), we substituted the electrostatic interaction term by a pure coulombic one in which the charges of the QM atoms are obtained by means of electrostatic potential fit methods based on the electronic density (61). Thus the final potential energy can be approximated by

(6)

Finally, the interaction energy between the inhibitor and the environment is evaluated as the difference between the QM/MM energy and the energies of the separated, noninteracting QM and MM subsystems with the same geometry. Considering that the MM part is described using a nonpolarizable potential, the interaction energy is given by the following expression:

(7)

where 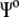is the gas phase wave function of the inhibitor.

RESULTS AND DISCUSSION

As explained in Methods, hybrid QM/MM MD simulations of 1.0 ns for wild-type and N155S mutant HIV-1 IN complexed with DKA (Scheme 1) were performed. Table 1 shows the values of ligand-protein interaction energies for these systems as well as the ligand-protein interaction energies' decomposition into the electrostatic and polarization energy terms. The reported values are averaged over 100,000 configurations from the last 100 ps of the QM/MM MD simulations. Both geometrical data and energy terms were averaged during the production run, and the standard deviation is provided in parenthesis accompanying the average value. The final structures obtained from the 1.0 ns MD simulations are depicted in Fig. 2, a and b, and the contribution of individual residues to the total interaction energy is displayed in Fig. 3, a–c. In the latter figure, negative values correspond to stabilizing effects. At this point, it must be noted that the analysis of binding affinity is done based on ligand-protein interaction energies (electrostatic and van der Waals). Other possible steric effects or more complex cooperative effects were not considered in this approach although, to some extent, change on solvent-substrate interaction energies upon mutations can be considered indirect effects. So, experimentally observed free energy changes can differ from estimations based on interaction energies, but the purpose here is to find the possible origin of these effects, not to quantify then.

TABLE 1.

Averaged QM/MM interaction energies in kJ mol⁻¹

	Interaction energy (kJ mol−1)	Elec (kJ mol−1)	Pol (kJ mol−1)
Wild-type	−776.0 (±38.6)	−813.7	37.7
N155S	−738.4 (±39.7)	−772.9	34.5

Values in parentheses correspond to the standard deviations. The corresponding electrostatic (Elec) and polarization (Pol) terms are also reported in kJ mol⁻¹.

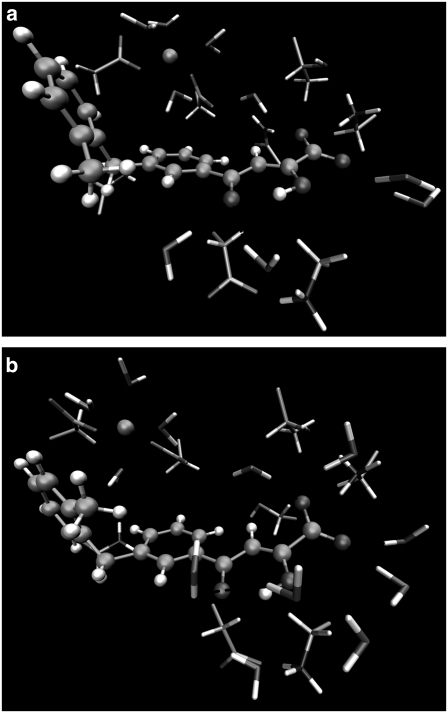
FIGURE 2.

Representation of the most important interactions between the wild-type HIV-1 IN (a) and its N155S mutant (b), both complexed with a DKA, obtained by means of the B3LYP (6-31G*)/MM method. Ball and stick representation corresponds to the QM region, and the licorice represents the MM residues and water molecules.

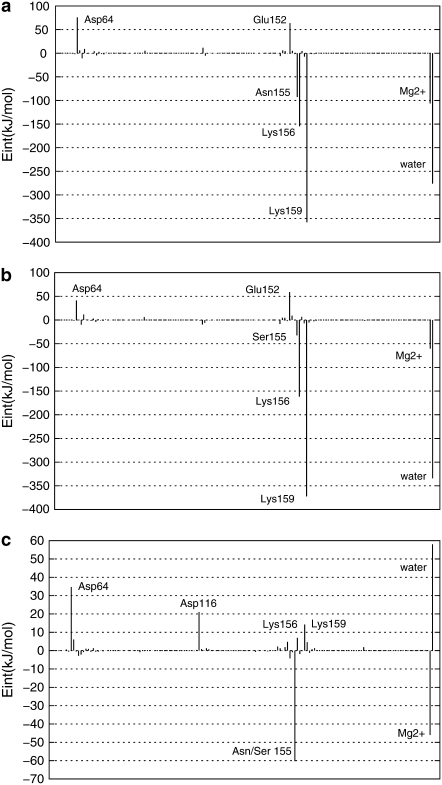
FIGURE 3.

Contributions of individual amino acid residues to inhibitor binding (in kJ mol⁻¹) of the wild-type HIV-1 IN (a), its N155S mutant (b), and interaction energy differences between both (c) obtained by means of the B3LYP(6-31G*)/MM method. “Water” refers to the effect of all the water molecules in the active site.

Due to computer limitations, no hybrid QM/MM MD simulations were carried out within a DFT Hamiltonian. Nevertheless, single geometry optimizations at the B3LYP/6-31G*/MM level were carried out for these compounds, followed by the corresponding analysis of protein-substrate interactions. In general, AM1/MM and DFT/MM calculations render quite similar results, thus confirming the reliability of the former.

Wild-type HIV-1 IN complex

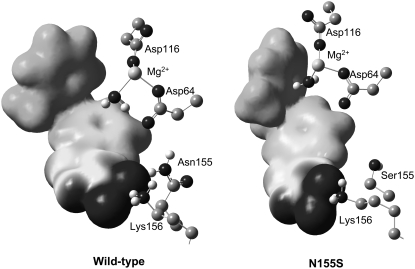
From Fig. 2 a and Table 2 we can observe how the carboxylic group interacts, through hydrogen bonds, with the pocket created by Asn-155, Lys-156, and Lys-159 residues. These interactions favor the stabilization of the protein-inhibitor complex as reflected in Fig. 3 a. In particular, Asn-155 interacts with Asp-64 and one of the oxygen atoms of the carboxylic group of the inhibitor; this interaction appears to be essential for the maintenance of the structure of the protein-metal-ligand complex. In fact, Hazuda and co-workers (25) have suggested that a mutation of Asn-155 could directly affect the interaction with the inhibitors by disrupting metal binding, in accordance with our results. Thr-66 does not interact directly with the ligand (Fig. 2 a) but stabilizes the cavity created by the three aforementioned residues through a hydrogen bond with Lys-159. Another residue that seems to be essential for catalysis (5) but does not participate in substrate binding (as worked out from Fig. 3 a) is the negatively charged Glu-152 residue. Its role seems to be similar to Thr-66: it interacts with Lys-156 and Gln-148 residues, thus stabilizing the cavity structure around the inhibitor.

TABLE 2.

Averaged distances (in Å) between key atoms/groups of the integrase active site of wild-type and the N155S form of the protein and the ligand

	Wild-type	N155S
MG-ASP-116	1.883 (0.042)	1.880 (0.041)
MG-ASP-64	1.906 (0.044)	1.916 (0.046)
MG-WAT	2.026 (0.061)	2.022 (0.063)
MG-WAT	2.021 (0.067)	2.026 (0.066)
MG-WAT	2.022 (0.060)	2.044 (0.068)
MG-WAT	2.024 (0.068)	2.026 (0.067)
O1-LYS-159	1.874 (0.170)	2.206 (0.329)
O1-WAT	2.087 (0.285)	–
O3-LYS-159	2.269 (0.298)	2.033 (0.286)
O3-ASN-155	1.993 (0.179)	–
O3-WAT	2.038 (0.205)	2.015 (0.202)
O12-H15	2.111 (0.129)	2.092 (0.132)
O12-WAT	2.130 (0.252)	2.200 (0.346)

Values in parentheses correspond to the standard deviations.

Both benzene rings of the inhibitor interact with the Mg²⁺ cation through an electrostatic attraction between the quadrupole moment created by the π-electrons of the aromatic moiety and the Mg²⁺ cation, as previously suggested by Dougherty (62,63). In fact, we can observe that the benzene rings and the Mg²⁺ cation are close to each other, as demonstrated by the averaged distance between the center of mass of the two benzene rings and the Mg²⁺cation, which are 5.17 Å and 5.60 Å, respectively. This favorable interaction is reflected in Fig. 3 a and may explain the metal-dependent inhibition by DKAs and DKA-like compounds (64–66). Correspondingly, the same argument can be used to explain the electrostatic repulsion observed between negative Asp-64 and the benzene ring.

These results are compatible with previous experimental studies. Thus, structure-activity relationship studies show that the aromatic portion is crucial for potency (64) and strand-transfer selectivity (65,66). Mutagenesis studies show that Asn-155 and Lys-159 are critical for IN/DNA binding (67–69), and photo cross-linking studies (70) suggest that the conserved adenosine binding in the vicinity of Lys-159 and Glu-152 and the 5′-adenosine overhang should be in contact with Gln-148.

Finally, as observed in Fig. 2 a and Table 2, there are some water molecules that interact with the inhibitor, stabilizing the complex as deduced from Fig. 3 a. In particular, one of the water molecules, which takes part of the coordination sphere of the ion Mg²⁺, interacts with the π-electrons of the central benzene ring. A second water molecule is involved by hydrogen bonds with the keto motif. A third water molecule interacts with the enol and Lys-156; and the rest of the water molecules depicted in Fig. 2 a interact with the carboxylic group by hydrogen bonds. McCammon et al. (10) and Briggs et al. (29–32) have found that water molecules are important in the stabilization of the L-731,988 and IN complex, in accordance with our theoretical simulations. Analysis of the complete protein-ligand structure reveals that this inhibitor adopts an orientation in which it may physically block the possible interface of the IN-DNA complexes, in accordance with the model suggested by Pommier and co-workers (8). In addition, this orientation is similar to the one adopted by 5CITEP in the crystal structure (6) and recently reported by us for L-731,988 and other derivatives (48) and S-1360 (71).

N155S HIV-1 IN mutant complex

The structure of the N155S mutant is similar to wild-type, but the absence of the interaction with Asn-155 provokes some changes in the interactions. First of all, the smaller size of Ser-155 creates a hole in the cavity that allows increasing the interaction with water molecules. The lack of interaction established between Ser-155 and Asp-64 causes the nonfavorable interaction between this latter residue and the inhibitor to decrease, as deduced when comparing Fig. 2 a with b. However, as a related effect, the Mg²⁺ cation moves away from the inhibitor, and the interaction with the inhibitor is diminished. However, the inhibitor remains bound within the N155S IN active site; this is in accordance with drug-resistance data reported by Hazuda and co-workers (26). The analysis of the average distance between the Mg²⁺ cation and the center of mass of the central benzene ring increases from 5.17 Å in the wild-type to 6.10 Å in N155S IN, whereas the distance between the Mg²⁺ cation and the distal benzene ring goes from 5.60 Å to 5.17 Å. These changes trigger a loss of ligand-protein interaction energy by 37.6 kJ/mol (see Table 1). Therefore, the loss of ligand-protein interaction, mainly through Ser-155 and the Mg²⁺ cation in N155S IN, may be responsible for the high resistance to the diketo acid. In fact, it has been experimentally observed that the N155S mutant is 20-fold less sensitive for this inhibitor (25). Obviously, these analyses are done with internal energy calculations and not free energies, which means that only qualitative results can be obtained; a reduction in binding affinity by a factor of 20 correspond to a much lower reduction in binding free energy (∼4 kJ/mol). The discrepancy between both quantities is due, on one hand, to the difficulties associated with obtaining well-converged internal energies and, on the other hand, to the fact that apart from protein-ligand electrostatic interactions other terms must be considered. So, we must also keep in mind the large interaction of the ligand with the solvation waters (see Fig. 3 c) and the entropic contributions that could partly cancel the changes in the internal energy observed upon mutation.

For the results obtained we can observe that the structures and energies for residues obtained with both AM1/MM and B3LYP/MM methods are comparable. However, the hydrogen-bond interactions established between water molecules and the inhibitor, obtained with the AM1/MM method, are weaker than those obtained at the B3LYP/MM level.

To check the robustness of the interactions analyzed previously, the time evolution of protein-inhibitor interaction energy obtained along the QM/MM MD simulations was studied (as shown in the Supplementary Material). The resulting plot shows no important fluctuations in either of the two compounds, the wild-type and the N155S mutant, thus supporting the conclusions obtained from the static interactions analysis.

Three-dimensional molecular electrostatic potential

Recently, we observed that the charges on some key atoms are important in quantitative structure-activity relationship studies of flavonoid compounds with anti-HIV activity (72,73). In addition, previous QM/MM studies for other inhibitors confirm this hypothesis (48,71). Therefore, in this work we also calculated the electronic density with the aim of understanding how structural changes can affect substrate charge distributions. Fig. 4 displays the three-dimensional molecular electrostatic potential (MEP) surfaces for the DKA shown in Scheme 1. The MEPs were generated with the Gauss View program (74) from the B3LYP/MM optimized structures. These surfaces correspond to the isodensity value of 0.002 a.u. The nucleophilic regions (negative electronic potential, in black) can be found around the carboxylic and keto-enol groups and the benzene ring, whereas the electrophilic regions (positive electrostatic potential, in light gray) can be found around the hydrogen and carbon atoms. From Fig. 4 we can observe a much more intense region of negative electrostatic potential around the carboxylic group and benzene ring. We can observe that electron-donating substituents at the aromatic ring (−CH₃) increase the region of negative electrostatic potential at the aromatic ring; and, therefore, it constitutes a more attractive cation-binding site. In fact, in previous work (48), we observed that DKA inhibitors with electron-donating substituents in the aromatic ring provoke higher values of total ligand-inhibitor interactions, which is related to very high values for anti-HIV activity in cells (75). The charges of the Mg²⁺ ion and ligand in both the wild-type and N155S complex obtained from the electrostatic potential (61) (provided in the Supplementary Material) are almost invariant.

FIGURE 4.

MEPs derived from B3LYP(6-31G*)/MM calculations for the inhibitor in HIV-1 IN and its N155S mutant. The increase of negative charges goes from positive (light gray) to negative (black).

CONCLUSIONS

This work provides insight into the activity of a potential inhibitor against HIV-1 IN. Hybrid QM/MM MD calculations were carried out for wild-type and N155S HIV-1 IN complexed with diketo acid to determine the protein-ligand interaction energy. As observed in the analysis of individual interactions, the influence of Asn-155, Lys-156, and Lys-159 seems to be crucial, with the interaction established between the inhibitor and the latter being especially important. These interactions, together with the one established with water molecules of the cavity created by the protein and the Mg²⁺, might be responsible for the anti-HIV activity. On the other hand, the orientation of the inhibitor in both the wild-type and N155S HIV-1 IN complex is close to the orientation adopted by 5CITEP in the crystal structure. The structure found for the N155S mutant was similar to wild-type, but the absence of the interaction with Asn-155 promoted an important loss in the interactions. This may be responsible for the high resistance observed experimentally in diketo acid.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.