Quantitative Determination of Size and Shape of Surface-Bound DNA Using an Acoustic Wave Sensor

Abstract

DNA bending plays a significant role in many biological processes, such as gene regulation, DNA replication, and chromosomal packing. Understanding how such processes take place and how they can, in turn, be regulated by artificial agents for individual oriented therapies is of importance to both biology and medicine. In this work, we describe the application of an acoustic wave device for characterizing the conformation of DNA molecules tethered to the device surface via a biotin-neutravidin interaction. The acoustic energy dissipation per unit mass observed upon DNA binding is directly related to DNA intrinsic viscosity, providing quantitative information on the size and shape of the tethered molecules. The validity of the above approach was verified by showing that the predesigned geometries of model double-stranded and triple-helix DNA molecules could be quantitatively distinguished: the resolution of the acoustic measurements is sufficient to allow discrimination between same size DNA carrying a bent at different positions along the chain. Furthermore, the significance of this analysis to the study of biologically relevant systems is shown during the evaluation of DNA conformational change upon protein (histone) binding.

INTRODUCTION

Duplex DNA can be analyzed by a variety of techniques to characterize DNA-protein interactions. Parameters assessed during the binding interaction include the sequence specificity of the proteins and the extent to which DNA is deformed. This latter point is of interest due to the biological relevance of DNA plasticity. Protein binding can affect the shape and thus the activity of DNA: protein-driven DNA bending has been shown to facilitate assembly of nuclear protein complexes and plays a fundamental role in the control of transcription and replication (1). Conversely, the intrinsic bending of DNA and the inherent deformability associated with specific base sequences can affect protein recognition and binding (2). Characterization of the extent to which DNA is bent intrinsically and on interaction with proteins is an ongoing process which increases the understanding of many aspects of DNA metabolism. In addition, development of a quantitative approach for the rapid detection of DNA bending could lead to screening for potential drugs that affect transcription and regulation by affecting the protein-driven bending.

The most commonly employed methods for measuring DNA curvature are electrophoretic mobility and cyclization assays. The cyclization assays, based on measurements of the rate at which DNA can form enzymatically sealed closed circles, have the potential to be developed as high-throughput methods. The electrophoretic mobility assays are not based on a complete theory and, therefore, are not sufficiently detailed to accurately predict mobility as a function of DNA bending (3). Three-dimensional crystal structures of proteins bound to DNA provide the most detailed insights into the mechanism of protein-driven DNA bending, but this information is obtained only through a long and labor-intensive process. Solution-based structural analysis via NMR likewise provides detailed information, but it is a method not applicable to all cases and unsuitable for rapid assays. Low-resolution structural information can be obtained from atomic force microscopy images (4,5).

End-tethered DNA has been studied by fluorescence to characterize the conformation of both small and large DNA molecules. Confocal microscopy of large DNA molecules with intercalated dye, measuring fluorescence intensity as a function of height for a population of molecules, has provided evidence that the radius of gyration of end-tethered molecules is the same as that for molecules in solution (6). Fluorescence interference measurements, with short DNA end labeled with a fluorophore, give a measure of the height of the fluorescent label within the DNA layer, which provides indirect evidence with regard to the tilt of double-stranded DNA (dsDNA), the shape of single-stranded DNA (ssDNA), and the extent of hybridization (7). This procedure has the advantage that it is compatible with the large-scale arrays that are currently employed for analysis of DNA hybridization.

The goal of the work presented here is to develop an experimental approach that, together with a suitable mathematical treatment, will provide quantitative information on the conformation of surface-tethered DNA molecules using a label-free real-time sensor which is sensitive to the presence of adsorbed molecules. DNA is employed here both for its intrinsic interest and for its value as a model system: it can be prepared at controlled lengths and attached at known points, thus providing well-regulated modified surfaces to facilitate data interpretation and assess validity of models developed to explain the sensor response. One additional requirement, of course, is for a sensor that will respond to conformational changes. Such changes do not appear as changes in the total adsorbed mass; detection, therefore, requires a system that is sensitive to alternative parameters. Sensors based on optical measurements typically measure average optical density, which is treated as being directly proportional to adsorbed mass, and are therefore unsuitable for the task here (8). Acoustic sensors, however, are sensitive both to changes in adsorbed mass and to changes in the viscosity of the device/liquid interface (9).

The relationship between viscosity and molecular shape and size is well established for polymer molecules in solution (10,11), leading to the prospect that sensors detecting viscous losses due to tethered molecules will be likewise sensitive to changes in molecular conformation. This concept has been applied in the past during the modeling of protein-bound molecules to the surface of a Love wave acoustic device (12) and during the study of the kinetics of interfacial nucleic acid hybridization using a thickness shear mode (TSM) acoustic wave sensor (13), a device similar to the quartz crystal microbalance (QCM). In this work the acoustic response is monitored during the systematic variation of the length, attachment mode, and shape of both dsDNA and triple-helix DNA molecules. Acoustic measurements involve monitoring of the velocity (i.e., phase) of the wave, which is proportional to adsorbed mass (9), and the dissipation (i.e., amplitude) of the acoustic energy, which is a measure of the viscosity at the solid/liquid interface (9,12). Classical solution viscosity theory, applied in combination with acoustic measurements, reveals that this approach can provide essential information on the conformation of surface-tethered DNA molecules and distinguish between DNA with the same mass but different shapes in a quantitative manner; moreover, the excellent agreement found between theoretical predictions and experimentally verified DNA conformations proves the validity of this approach. Finally, well-known changes in DNA conformation as a result of protein binding were detected and validated based on the proposed model.

MATERIALS AND METHODS

Acoustic wave device

Love wave acoustic devices were prepared by photolithography using single-crystal Y-cut z-propagating 0.5-mm-thick quartz, with a 100 nm gold overlayer and a 20 nm chromium adhesion layer. The input and output interdigitated transducers (IDTs) consisted of 192 pairs of split fingers with a periodicity of 32 μm. The operating frequency of the uncoated device was 155 MHz. A 0.4-μm-thick waveguide layer of polymethyl methacrylate (PMMA) was deposited on the surface of the acoustic device by spin coating at 4,000 rpm with an 8% (w/w) solution of medium molecular weight PMMA in 2-ethoxyethylacetate (Aldrich, Milwaukee, WI). The PMMA-covered devices were heated to 195°C for 2 h to promote solvent evaporation. A 20 nm gold layer was deposited on the region between the IDTs by sputter coating with a Bal-Tec SCD 050 sputter coater (Bal-Tec, Balzers, Liechtenstein). The gold layer was etched immediately before the acoustic experiments to ensure a clean surface. Devices were reused by etching to clean off adsorbed sample; a new layer of gold was added by sputter coating.

Instrumentation and experimental set-up

An Agilent E5061A network analyzer (Agilent, Santa Clara, CA) was used to measure the insertion loss (amplitude) and phase of the output signal with respect to a reference one. Experiments were performed at 25°C, and data were collected using LabVIEW interface software (National Instruments, Austin, TX). A perspex flow cell and a silicone rubber gasket were used to hold the solution in place over the region between the IDTs, exposing an area of 12 mm².

dsDNA design and preparation

Different sets of biotinylated and nonbiotinylated primers high performance liquid chromatography (HPLC; highest purity) were designed by FastPCR software (University of Helsinki, Helsinki, Finland) and obtained from metabion (Martinsried, Germany) to produce dsDNA molecules of various lengths (75 bp, 132 bp, 167 bp, 198 bp) by polymerase chain reaction (PCR) amplification. Plasmid pBR322 obtained from Minotech (Heraklion, Greece) was used as template in standard PCR reactions containing each different set of primers. PCR products were purified using a nucleospin kit (Macherey-Nagel, Düren, Germany). A 20-basepair (bp) dsDNA was produced by annealing a biotinylated oligonucleotide with a 10-fold excess of its nonbiotinylated complementary strand in an annealing buffer with 1 mM MgCl₂ and 20 mM Tris-HCl pH 8. The mixture was vortexed, heated at 95°C for 5 min, and then cooled slowly at room temperature for ∼10 min (SYNTHEGEN protocol). Two 90-mer oligonucleotides that are known to have different degrees of intrinsic curvature were designed based on sequences from previous studies. Each sequence was flanked by 20 bases to be amplified by a PCR reaction according to the conditions described previously. The sequences of the two oligos are the following:

• “Straight” (out of phase): 5′-tcttgctggc gttcgcgacg aaacgcgcgc gcaaaaaacg cgcgcgcaaa aaacgcgcgc gcaaaaaacg cgttgcaggc catgctgtcc-3′

• “Bent-1/2” (in phase): 5′-tcttgctggc gttcgcgacg cgaaaaaacg cgaaaaaacg cgaaaaaacg cgaaaaaacg cgaaaaaacg cgttgcaggc catgctgtcc-3′

• “Bent-1/3” (in phase): 5′-tcttgctggc gttcgcgacg gcggagagaa ttcccaaaaa tgtcaaaaaa taggcaaaaa atgccaaaaa cgttgcaggc catgctgtcc-3′. This sequence is part of a minicircle DNA from the kinetoplast body of the protozoan Leishmania tarentolae (14).

Curvature analysis of the two 90-bp products was performed using DNA curvature analysis (15) and GSVIEW software and verified by mobility differences on a 12% polyacrylamide gel under native conditions.

Triple-helix DNA design and preparation

Oligonucleotide-directed triple-helix formation was accomplished by binding two distal DNA sites separated by 10 bp, with oligonucleotides containing two DNA-binding domains separated by a short linker of 4 and 10 bases length. dsDNA was 50-bp long and was prepared by annealing a 5′-biotinylated oligo with its complementary strand. HPLC-purified oligos were purchased from metabion with the following sequences:

• First strand: 5′-Biotin-aattcagagaggaggagagagcggtgcggtaggagagagagaggaggatc-3′

• Second strand: 5′-gatcctcctctctctctcctaccgcaccgctctctcctcctctctgaatt-3′

• Triplex-forming oligo 4 (“bent”): 5′-tctctcctcctctcttttttcctctctctctcct-3′ (c is 5-methyl cytosine)

• Triplex-forming oligo10 (“straight”): 5′-tctctcctcctctcttttttttttttcctctctctctcct-3′ (c is 5-methyl cytosine)

Triple-helix formation was performed by incubating 200 picomoles of the modified oligo with the 50-bp DNA at 22°C for at least 1 h. The reaction volume was 10 μl in Mes buffer (45 mM 2-[N-morpholino] ethanesulphonic acid, pH 5.5, 1 mM MgCl₂). Incubated samples were loaded directly on a neutravidin-modified sensor surface equilibrated in the same buffer.

Real-time acoustic detection of neutravidin and DNA binding

A continuous flow of buffer (50 mM Tris, pH 7.5, 10 mM MgCl₂, 10 mM KCl for the dsDNA, and the aforementioned Mes buffer for the triplex DNA) was pumped over the surface of the gold-coated devices at a flow rate of 20 μl/min (shear rate 1.9 s⁻¹). The signal was allowed to equilibrate before the first addition, and all samples were added in the same buffer. Neutravidin (Pierce, Rockford, IL; specific activity 11–17 μg biotin bound/mg protein) was added at a concentration of 100 μg/ml for 10 min, long enough to saturate the surface with a large excess of protein. The amount of bound neutravidin was measured using Reichert SR7000 surface plasmon resonance (SPR; Reichert, Depew, NY). After a buffer rinse, DNA samples were added at a range of concentrations varying between 1.2 and 14 μg/ml.

Real-time acoustic detection of DNA-histone binding

After neutravidin addition, 5 μg/ml of 198-bp dsDNA was added to the device surface under conditions similar to those described in the section “Real-time acoustic detection of neutravidin and DNA binding”. A solution of 250 μg/ml of Hv1 protein (H6881, Sigma-Aldrich, St. Louis, MO) in 50 mM Tris buffer (pH 7.5, 2.5 mM MgCl₂, 10 mM KCl) was pumped over the 198-bp dsDNA surface at a rate of 20 μl/min until equilibrium was reached.

Acoustic wave sensor and measurements

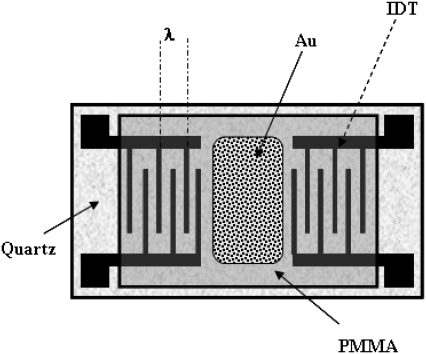
The work described here was carried out with a Love wave device, a waveguide configuration based on a surface acoustic wave sensor (Fig. 1). A guided shear horizontal surface acoustic wave is associated with a shear-oscillating displacement confined at the surface of an acoustic wave solid device overlaid by a polymer waveguide layer. Addition of the polymer layer to the device surface offers increased sensitivity to surface perturbations (16). The presence of an analyte at the device surface affects the propagation characteristics of the wave, thus providing a method for monitoring surface interactions.

FIGURE 1.

Representation of the biosensor device. Top view: the quartz piezoelectric crystal with the imprinted IDTs (where λ is the wavelength of the acoustic wave, equal to 32 μm), the PMMA, and gold layers.

The change in phase or frequency, related to the velocity of the acoustic wave, is proportional to adsorbed mass (9). Application of a viscous liquid to the device surface results primarily in energy dissipation and, to a lesser degree, in phase change (9,12). The penetration depth δ of the wave inside the liquid sample is the depth at which the wave amplitude has decayed to 1/e of its initial value and is given by

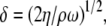(1)

where η and ρ are the solution viscosity and density, respectively, and ω is the oscillation angular frequency. At an operating frequency of 155 MHz of the Love wave device in pure water, δ is 45 nm.

The interaction between shear mode surface acoustic waves with continuous, firmly attached elastic layers such as metal films (17) and/or homogeneous viscous solutions of small solute molecules (17–19) has been described both theoretically and experimentally. Biomolecules attached to a surface, though, do not fall into either of these categories and a mathematical theory has not been fully developed yet.

RESULTS

Experimental data

DNA molecules, with conformation either predicted by their base sequence or already determined experimentally, were bound to a neutravidin-modified device surface by using biotin attached to the end of the DNA molecule through a hinge of 11 carbon atoms. Experiments were performed in a flow-through system which allowed continuous additions of DNA samples and buffer in an alternating way. The DNA attachment to the device surface was considered specific since control experiments performed with nonbiotinylated DNA gave no detectable signal. Acoustic results were expressed as the ratio of amplitude change over phase change (ΔA/ΔPh); this ratio is a measure of the energy dissipation per coupled unit mass and provides insight on viscosity changes (20) occurring at the sensor/liquid interface as a result of DNA binding.

Acoustic detection of straight dsDNA molecules of the same shape but various sizes

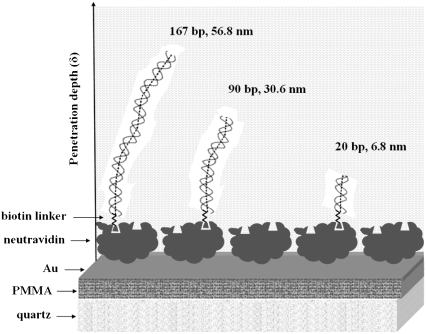
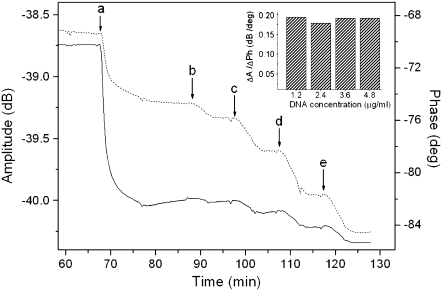
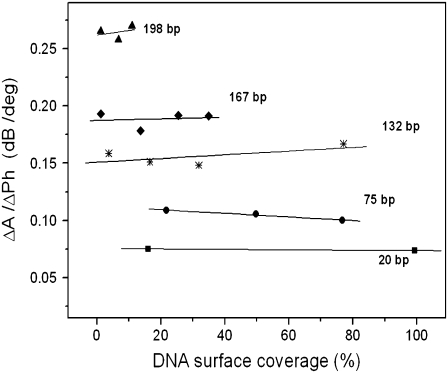
dsDNA samples applied to the surface of the acoustic devices had bp lengths of 20, 75, 90, 132, 167, and 198, with corresponding contour lengths of 6.8, 25.5, 30.6, 44.9, 56.8, and 67.3 nm (Fig. 2). Acoustic ratios were measured from real-time binding curves recorded during the loading of the DNA samples (Fig. 3). Results showed that the ratio ΔA/ΔPh at equilibrium was constant and independent of sample concentration (Fig. 3, inset). Furthermore, this ratio was found to be different and characteristic for each one of the DNA molecules attached to the surface (Fig. 4). This observation holds despite the fact that both amplitude and phase vary with the percentage of surface coverage (data not shown).

FIGURE 2.

Representation of the biosensor device surface/liquid interface: straight dsDNA molecules of various lengths are attached to the neutravidin-modified gold surface through a biotin linker incorporating an 11-carbon hinge. Three of the six different lengths used in this work are shown in the picture drawn using the GSVIEW software package (not drawn to scale). The white shade surrounding the DNA chains indicates the hydration layer of each molecule.

FIGURE 3.

Real-time binding curve of amplitude and phase change during the application of (a) neutravidin 100 μg/ml, followed by 167-bp DNA samples of (b) 1.2, (c) 2.4, (d) 3.6, and (e) 4.8 μg/ml. Buffer-washing steps following each deposition are not shown in the graph. Amplitude and phase are depicted with a dotted and solid line, respectively. (Inset) Acoustic ratio of amplitude change versus phase change (ΔA/ΔPh) measured for each DNA addition.

FIGURE 4.

Plot of the acoustic ratio (ΔA/ΔPh) versus the % of DNA surface coverage for the 198 (▴), 167 (♦), 132 (*), 75 (•), and 20 (▪) bp dsDNA molecules corresponding to a contour length of 67.3, 56.8, 44.9, 25.5, and 6.8 nm, respectively. The y and x axes are equivalent to 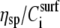or [η] and 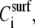respectively (see section on model analysis).

DNA surface coverage was calculated as the fraction of the maximum available number of neutravidin binding sites. Known amounts of ³²P-labeled surface-bound DNA (mass measured by gel densitometry) were correlated to its radioactivity (counts/min), and a linear calibration curve was obtained. From this calibration curve the DNA mass bound to the sensor's active area was estimated each time and, again, linearly correlated (R = 0.94) to the measured change in the wave phase ΔPh (the proportionality constant is 27.4 ng/cm² DNA per 1 deg phase change). This way, changes in phase directly give the bound amount (of thereafter unlabeled) DNA mass. The number of neutravidin binding sites is equal to the number of neutravidin molecules required for complete surface coverage, determined from SPR measurements to be 295 ng/cm² or 4.9 × 10⁻¹² moles/cm², assuming that approximately one site is available for DNA binding on each protein molecule. The dimensions of neutravidin molecules are ∼5.6 × 5 × 4 nm (21) so that on the surface they would be ∼6–7 nm apart center-to-center at a full coverage including the hydration layer. A 1:1 DNA/neutravidin ratio was assumed since electrostatic repulsion and steric hindrance considerations do not allow higher ratios; the distance between adjacent sites is very close to that of the diameter of the hydrated negatively charged DNA rods (that is ∼2.0 nm) (22), as other studies have indicated (20).

Fig. 4 gives the acoustic ratio for all straight dsDNA molecules tested in this work as a function of surface coverage. A striking feature of the system is that the measured ratio of each DNA molecule was independent of the device history; adding the DNA samples in random order had no effect in the measured values, suggesting that this measurement reflects only intrinsic properties of each molecule.

Acoustic detection of dsDNA molecules of the same size but various shapes

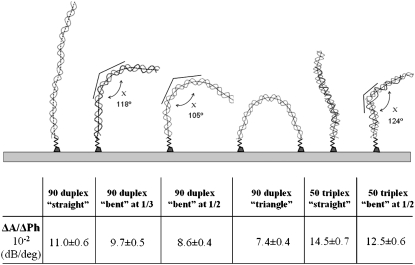
A series of 90-bp DNA molecules were prepared to produce molecules with the same MW and contour length, but different shape. The sequences were chosen so that the molecules were straight (out of phase) and bent (in phase) with a curvature that appears either at half length (−1/2) or at one third (−1/3) (Fig. 5). Although energetically speaking DNA bending is a costly process (e.g., for a 100-bp strand bending by 90° requires ∼1.1 kcal/mol), this is not the case when the sequence is specifically chosen to produce it (23). In addition, the bent DNA was prepared having both ends biotinylated and was also attached to the surface of the acoustic device to form a “triangle”. The value ΔA/ΔPh was measured for depositions of the three samples during the course of one experiment and for depositions on freshly prepared surfaces in separate experiments; the average acoustic results from six different experiments are summarized in Fig. 5. The bent-1/3, bent-1/2, and triangle DNA had significantly different ΔA/ΔPh values, 88%, 78%, and 67%, respectively, from that of the straight DNA.

FIGURE 5.

Characteristic acoustic ratios (ΔA/ΔPh) of i), the 90-bp dsDNA used with three different conformations, i.e., a straight, bent, and triangle shape; and ii), the 50-bp triple-helix DNA in a straight and bent conformation. The 90-bp dsDNA molecules were drawn using the GSVIEW software package (not drawn to scale). The experimental conditions (buffer, substrate) are different for the dsDNA and triple-stranded DNA; so comparison of values should not be made directly (error bars from same surface experiments).

Acoustic detection of triple-helix DNA molecules of the same size but various shapes

To further validate the correlation between acoustic measurements and DNA conformation, two triplex-forming oligos were combined with 50-bp-long DNA molecules. As a result, two triple DNA molecules were produced with a known straight and bent architecture (24) (Fig. 5). The acoustic ratio ΔA/ΔPh was measured for the two triple-helix DNA samples after their deposition in separate experiments repeated four times. The mean ΔA/ΔPh value for the bent one was found to be 86% of the corresponding value for the straight one.

Model analysis

In an effort to describe the experimental results, we focus on the quantitative side of how the viscosity of the sensed volume (layer δ) is affected by the presence of DNA molecules at the various stages of surface coverage. The viscosity of a fluid, by its definition, reflects its resistance to flow; addition of large molecules in the fluid increases viscosity in a manner dependent on three parameters: concentration, size, and structure, i.e., molecular weight and shape, of these molecules. Associated with this resistance is a certain amount of energy being dissipated in the particular system (11). If changes in energy dissipation, measured by this acoustic device as amplitude change, are taken to reflect changes in viscosity at the substrate/liquid interface and within the sensed volume, then changes in this value should closely follow changes in the above-mentioned three parameters.

The theory of macromolecule solution viscosity (10,11) gives

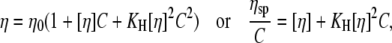(2)

where η is the solution viscosity at a particular solute concentration C, η₀ is the viscosity of the solvent (i.e., water plus buffer), [η] is the intrinsic viscosity for the particular solute (i.e., DNA), K_H is the so-called Huggins constant, and 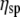is the specific viscosity.

An equivalent treatment, also extensively used (12,25), is one leading to the Simha equation, which is also valid for dilute enough solutions with noninteracting particles:

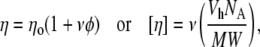(3)

where ν, 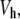MW, and ϕ are the shape factor, hydrated volume, molecular weight, and volume fraction, respectively, of a macromolecule in the solution. For Eq. 3 to be valid, two main assumptions are necessary. First, the distortion of flow by one particle does not interfere with that of the others, i.e., requiring dilute enough solutions; and second, a random orientation of the particles is assumed, i.e., use of low-flow velocities is called for so that no major orientation of the molecules in solution is caused. It is known from direct measurements of viscosity that changes in flow rate do cause changes in the measured intrinsic viscosity, and reported values are extrapolations to zero rate (11). Nevertheless for the very slow flow rates used in this work and taking into account that very big changes are needed for [η] to change appreciably, it can be safely assumed that this is not a major concern in our system.

The following data analysis, then, is based on two assumptions: a) that ΔA corresponds to viscosity η or 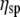(since 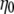is just a constant for the buffer solution), and b) that ΔPh corresponds/is equivalent to the macromolecule (surface) concentration 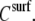As seen from Fig. 4, the ratio ΔA/ΔPh is independent of the surface coverage, i.e., surface concentration, for all the straight DNA molecules; the same holds true for the bent, triangle, and triple-helical molecules (data not shown). The equivalent observation based on Eq. 2 would suggest that K_H is zero, or very nearly so, for the 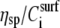versus 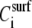plot to be almost horizontal, for each specific, different type of DNA molecule i. There is good reason for that to hold true here. The Huggins constant is a dimensionless constant indicative, among other things, of the hydrodynamic interactions of separate polymer chains in a particular solution; it decreases with higher solvent quality or decreased probability of entanglement (26,27). In our case, DNA chains are kept apart and complete rotational motions are prohibited since the molecules are anchored on the protein substrate. Their movement is expected to be a synchronized oscillation after the oscillation of the crystal surface at various tilt angles from the normal, depending on surface coverage.

DNA chains, carrying negative charges at pH 7.5, would also exhibit electrostatic repulsions among each other and with the negatively charged surface (neutravidin's pI = 6.3). A parameter often used to quantify the range of electrostatic interactions is the Debye-Huckel screening length, κ⁻¹, which in our case is calculated to be ∼1.0 nm, which is very short in comparison with ∼6–7 nm, the closest possible spacing of the anchored individual DNA chains. Given that the possibility of lateral interactions is obviously greatly diminished for the two-point attached triangular DNA and the low surface coverage of all other DNA and the experimental observation that ΔA/ΔPh has the same value for high coverage (Fig. 4), it can be safely assumed that K_H is indeed zero for all DNA molecules used here.

Since ΔPh is proportional to the total mass bound per surface area, using Eq. 2 with K_H = 0 we get

(4)

where 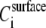represents the concentration of any particular type of DNA molecule i, anchored on the crystal surface (area S) within the acoustically sensed volume V = Sδ, whereas the mass is given by definition as (No. rods anchored)MW_i/N_A = dV_i, d being the (constant) density of DNA, V_i the volume of each DNA rod, and N_A Avogadro's number.

Straight rods

In the case of straight rods, the well-known Mark-Houwink relation may be used, correlating the intrinsic viscosity with the molecular weight of a macromolecule in a particular solvent:

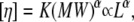(5)

where α is a factor indicative of the shape, ranging from ∼0.5 for random coils to ∼1.8 for straight stiff rod molecules, and L is the length of the straight DNA rod. The dsDNA persistence length is assumed to be between 50 and 80 nm (23,28); so the strands used in this study may be safely considered short stiff rods.

Taking the logarithm and differentiating Eq. 5, through Eq. 3, and the observation that MW 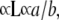we get to calculate the value of α for each DNA straight rod from (10):

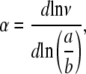(6)

where the shape factors ν are taken from the Simha equation, approximating the shape of stiff DNA molecules with that of a prolate ellipsoid with a and b the major and minor semiaxes of the ellipsoid:

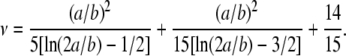(7)

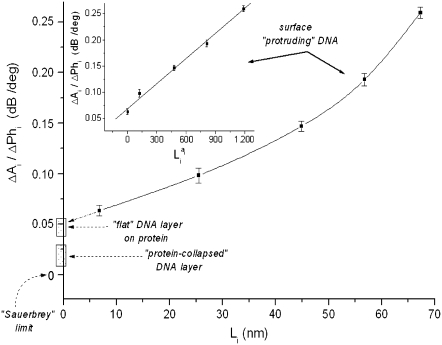
Fig. 6 shows a plot of (ΔA/ΔPh) versus length for each straight DNA molecule used. The experimentally obtained curved line should be turned into a straight line (according to Eq. 5) if the coefficient α calculated from Eqs. 6 and 7 is used, different for each length, assuming the theory predicts the behavior of the system well enough; as can be seen an excellent fit is obtained validating the above approach. It should be noted that Eq. 7 holds true for ratios a/b > 10. Correcting for the shorter DNA (20 and 75 bp where a/b is < 10), using the Hirota approximation (25) or the values from the Simha model (10), causes no significant changes (<4%) on the results and does not affect our analysis.

FIGURE 6.

Plot of the ratio ΔA/ΔPh versus contour length 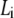of straight DNA molecules; 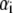values are calculated for each length 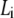from Eq. 6. The straight line (inset) is a linear fit (R = 0.997) of the data. Also indicated, as boxes on the y axis, are the various cases of formed layer rigidity (see text). The y axis is equivalent to 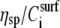or [η] (see Model Analysis).

Bent and triangle rods

The relationship in Eq. 4 shows that the energy dissipated per unit mass is proportional to the intrinsic viscosity of the molecule at hand and does not depend on the extent of surface coverage. Direct comparison of this ratio, for molecules with the same mass but different shapes, to the ratio of their respective intrinsic viscosities should be one way to validate the theory employed. Here, this is done by comparing straight DNA segments to bent DNA strands placed in different attachment modes on the surface (Fig. 5).

Bent rods (compared to straight rods of diameter D and length L) have been modeled as having two rod-like arms of lengths L₁ and L₂ joined end-to-end at an angle χ. The two components have the same diameter D and total length L, where L = L₁ + L₂. Their hydrodynamic behavior has been extensively studied theoretically using a “bead” model wherein the macromolecules are composed of spherical “elements”-beads and various different shapes can be studied (29,30). Calculations based on this model can produce values for the ratio [η]_bent/[η]_straight, which depends on the angle χ. Since in our approach this ratio is equivalent to the acoustic ratio (ΔA/ΔPh)_bent/(ΔA/ΔPh)_straight, the critical test would be to compare the two. The experimentally measured acoustic ratio of 0.78 ± 0.05 for the bent-1/2 requires an angle of 105° ± 6°. This value is clearly a very reasonable one as can be seen in Fig. 5 where the molecule is realistically drawn based on DNA-curvature analysis predicted by the GSVIEW software. The technique is sensitive enough to distinguish this DNA conformation from the bent-1/3 one, which gives a ratio of 0.88 ± 0.03 and a corresponding angle of 118° ± 6°.

An even more direct comparison is feasible in the case of a 50-bp triple-stranded DNA which is again considered a rod. The angle χ predicted here for the bent molecule based on the above approach is 124° ± 7°; this is in very good agreement with the value of 119° ± 3° reported in the literature, measured by phasing analysis (24).

For the case of the 90-bp DNA molecule placed in a triangular conformation (anchored on the surface by two biotin hinges instead of one; see Fig. 5) using an approximation for the triangle shape within the context of the bead model again, the corresponding theoretical ratio [η]_triangle/[η]_straight is in the range of 0.74–0.48; the experimentally measured value for the ratio (ΔA/ΔPh)_triangle/(ΔA/ΔPh)_straight is 0.67 ± 0.04 and falls correctly in the predicted range.

DNA-histone interaction

The biological relevance of our approach was tested during the study of protein binding on the conformation of immobilized DNA. Hv1 is a core histone H2A variant from the protozoan Tetrahymena thermophila, positively charged at pH 7.5, with MW ≈ 15 kD and <5–7 nm in length (31,32). It is well known that histones interact electrostatically with DNA regardless of sequence (33), causing large changes (bending) to these rod-shaped molecules. Changes in interfacial viscosity (acoustic data) are used to provide structural insight into the histone-DNA complex formation.

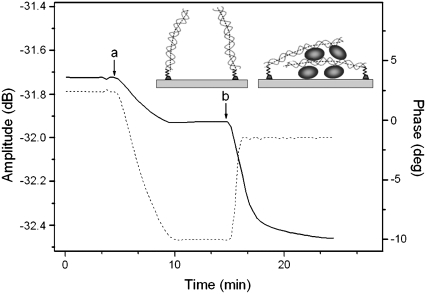
In these experiments Hv1 protein was pumped over a 198-bp dsDNA-coated surface, again attached on the sensor's surface via the neutravidin-biotin interaction. It is clear from Fig. 7 that the interaction of DNA with the histone does not follow the pattern of “higher mass-higher dissipation” of Fig. 3. Although with DNA addition both phase and amplitude decrease, with the ratio ΔA/ΔPh given earlier (0.26 dB/deg for 198 bp; Fig. 6), this is not the case with Hv1 addition. Now, whereas the phase decreases, as expected for mass added onto the surface, the amplitude increases, giving a final ratio for the complex of ∼0.018 dB/deg, i.e., more than a 10-fold decrease. Such low values of ΔA/ΔPh are indicative of rather compact systems dissipating little energy in relation to the surface mass (20,34); DNA is not dangling free, protruding from the sensor's surface outward anymore but, with the addition of Hv1, forms complexes that force it to bend and then collapse into a low dissipating structure (see drawing in Fig. 7).

FIGURE 7.

Real-time binding curve of amplitude and phase change during the application of neutravidin (not shown) followed by (a) 198-bp dsDNA sample of 5 μg/ml and (b) 250 μg/ml of histone Hv1. Amplitude and phase are depicted with a dotted and solid line, respectively. Also shown is a schematic representation of the DNA configuration on the surface before and after the addition of the histone.

Based on the acoustic ratio measurements reported here, four possible cases can be distinguished for the formed layers on a sensor's surface (Fig. 6):

1. A perfectly rigid film which dissipates no energy, i.e., with an acoustic ratio = 0 dB/deg; this is the classical Sauerbrey limiting case (9), something not observed in our experiments.

2. A less rigid, compact layer with a ratio ≈0.018 ± 0.009 dB/deg; this is the case of DNA molecules collapsed due to protein (histone) addition, resulting in a cross-linked layer; layers formed by pure protein also fall in this range of ratios, e.g., neutravidin, on the gold.

3. A semirigid layer with a ratio ≈0.046 ± 0.01 dB/deg; this is the case for a surface layer created when histone is added first and (nonbiotinylated) DNA follows (i.e., in the reverse order from above). This is a layer of DNA molecules lying flat, or nearly so, on the surface preformed by the histone and apparently has a stiffness intermediate between that of outward oriented, free-dangling DNA and that of a histone-collapsed one. The expected value for marginal cases (protruding length L ≈ 0, i.e., flat-lying DNA) falls exactly in this range; the extrapolated intercept value on the y axis is indeed ∼0.053 dB/deg.

4. A layer of distinct, free-dangling, straight DNA molecules whose ratio follows the curved line in accordance with the theoretical model presented earlier; cases for bent or triangle DNA also fall in this area but with smaller ratio values, again according to our modeling analysis.

The acoustic method and theory employed here quantitatively distinguish all these cases via the measured acoustic ratio values.

DISCUSSION

The goal of this work was to analyze solution samples of DNA by monitoring the interaction of these samples with the surface of an acoustic device. The parameters of interest here for DNA in solution were the length of the molecules and their shape. One question that must be considered is the extent to which these variables are affected by the surface interaction. Neutravidin has a pI of 6.3, making it negatively charged at pH 7.5, which helps to prevent nonspecific adsorption of the negatively charged DNA. The specificity of DNA binding via the 5′ biotin label has been demonstrated by control experiments; at pH 5.5, for triplex DNA, the small amount of nonspecific electrostatically adsorbed DNA was readily washed off during the buffer rinse step. The conformation of the DNA should therefore not be affected by the surface interaction, so that measurements on the tethered DNA should be valid for DNA in solution.

All DNA molecules used in this study are expected to be probed by the acoustic wave. Previous studies using a fluorescence technique have shown that end-tethered dsDNA of 21 or 50 bp lengths sits at an average orientation of ∼50° but very slanted positions are not excluded (7). Another work reported neutron reflectivity data for 25-bp-long dsDNA molecules also anchored on gold through a linker and spaced ∼6 nm from each other, suggesting an average 30° deviation from the normal (28). In accordance, the end-tethered DNA molecules through flexible hinges applied in this work will most likely adopt a tilted orientation on the device surface; it is, therefore, expected that all DNA should be well within the penetration depth δ of the acoustic device (δ > 45 nm since η at the interface is obviously greater than that of pure water for any DNA surface coverage).

A key parameter in the analysis of our data is the assumption that amplitude change is related only to viscosity changes. The mechanism of energy loss through viscous coupling can emerge by looking closely at the surface (Fig. 2). The movement of the tethered DNA rods including their tightly bound hydration layer (due to the crystal oscillation) is not expected to be identical to that of the entrained water within δ; DNA molecules are attached through the very strong biotin-avidin connection, whereas water molecules interact with the surface via less strong H-bonds and van der Waals forces. On the other hand, the transmission of this oscillation from water molecule to water molecule, as we move away from the surface toward the outer limit of δ, is mediated by H-bonds, whereas for dsDNA it is covalent bonds within the helical structure. Due to frictional (viscosity) forces acting on the DNA rod movement, a hysteresis is expected to exist between different parts of the molecule, say the bottom part close to the flexible hinge and its distal end. The relative motion of the discrete DNA molecules adds to the viscosity of the layer δ, which is the source of the observed energy dissipation measured through amplitude (dB) changes.

In attributing ΔA solely to viscosity changes and ΔPh solely to the added DNA mass, one should also examine alternative mechanisms of acoustic wave/matter interaction reported in the literature. Devices with textured surfaces, either randomly rough or regularly patterned, literally trap a quantity of fluid in excess of that viscously entrained by a smooth surface. Trapped liquid moves synchronously with the oscillating crystal surface rather than undergoing a progressive phase lag, as occurs with viscously coupled liquid, thus behaving like an ideal mass layer contributing almost no change to the dissipated energy (35). The system here of DNA rods protruding away from the surface could, of course, be seen as creating a corrugated/rough surface; but it cannot in any obvious manner be seen as confining any amount of water in between them (besides the individual hydration layers) to the extent that this water moves in synchrony with the surface/DNA structure and so contributes to mass effects, i.e., to the phase change ΔPh. Additionally, entrapment of water would have to be a function of surface coverage, i.e., proximity of DNA rods, something not experimentally observed here.

Finally, although studying the hydrodynamics of the system at hand in detail is clearly beyond the scope of this research, the following points are also of interest. Many studies (36–38) have revealed that parameters such as the spacing of cylinders in an array and the possible existence of internal structures on them are defining parameters for a particular flow rate. If the surface's features have dimensions close to δ, these protrusions could generate turbulent flow or compressional waves which act as additional dissipation mechanisms. For the flow rates used in this work, we do not anticipate a nonlaminar contribution due to compressional wave generation. The Reynolds numbers—due to a) the flow created by the crystal surface oscillation ranges from picometer to nanometer amplitudes (35,39) (Re ≪ 1), and b) the flow due to the pump flow rate (Re ≈ 0.15 as calculated for the specific geometry of our system)—are too low to cause turbulent flow even for solid roughness/protrusions comparable to δ (35).

Studies in similar systems (DNA bound through biotin/streptavidin at a QCM device surface) have modeled the formation of a ssDNA layer as a thin, homogeneous film; following this different approach, viscosity changes were calculated via a viscoelastic model. An increase of η with time, i.e., with surface coverage, was also observed (20). Interestingly, partial hybridization of the anchored ssDNA with complementary strands produced a further increase in the calculated viscosity. A higher energy dissipation per coupled mass unit for dsDNA (30-bp long) compared with the ssDNA has also been reported (34) and was attributed to further water entrapment. The “coil”-to-“stiff rod” structural transition, although not invoked by these studies, could be a cause for their observations since a coil has a smaller exponent α value than a rod of equal length, resulting in smaller [η] values.

Frequency changes measured with a TSM acoustic wave device were related to the DNA concentration-dependent viscosity change within the acoustic wave decay length region δ (13). Using classical viscosity theory, the authors successfully predicted the value 1.8 for the Mark-Houwink exponent α (Eq. 5), suggestive of a stiff rod conformation for their hybridized strands.

In this work, it is shown that energy dissipation per unit mass can be used as a direct measure of the intrinsic viscosity of the surface-attached DNA molecules. Systematic variation of the length of the straight DNA molecules gave excellent agreement between acoustic measurements and macromolecule solution viscosity theory, assuming that the shape of straight DNA molecules is that of a rod (Fig. 6, inset). Bent and triangle DNA molecules confirmed that the theory works quite well in describing systems of various shapes. Our results suggest that plots like the one shown in Fig. 6 can be used as a calibration curve to obtain accurate information on the length of straight dsDNA samples tethered to the device surface. Likewise, it would be possible to derive similar plots for surface-attached DNA molecules of various shapes upon careful design of the corresponding nucleic acids. The importance of the shape (i.e., shape factor) of DNA and DNA complexes has long been recognized in pharmaceutical practice, and similar approaches in its measurements, i.e., through viscosity, have been described (25).

In practice, the acoustic ratio is found here to be independent of the surface coverage, increasing the potential usefulness of acoustic sensors as analytical tools; solution samples can be analyzed without controlling for concentration or amount. In addition, multiple samples can be applied sequentially to one device. This can be exploited to detect signal differences that are too small to be detected reliably with measurements on separate devices by incorporation of an internal standard.

An area of great interest is the detection of protein-driven DNA bending to characterize DNA binding proteins such as transcription factors. In a recent study (40) an acoustic sensor was used to investigate the interaction between DNA and proteins, and an effort was made to evaluate conformational changes in the system, although not quantitatively. In contrast, the combined application of acoustic measurements with the theoretical analysis presented in this work showed that addition of histone, a well-known DNA-binding protein that forms compact structures through DNA wrapping around the protein, produces an acoustic change that corresponds to a compact DNA film rather than DNA upstanding structures. The results presented in this work suggest that acoustic biosensors can be developed into a powerful biophysical tool for studying DNA conformational changes.