Abstract
A theory is presented to study fluorescence correlation spectroscopy for particles with size comparable to the beam waist of the observation volume. Analytical correlation curves are derived for some experimentally interesting particle geometries. It is found that the finiteness of the particle generally decreases the value of the correlation amplitude and increases the correlation time compared to a point particle model. Furthermore, not only the size but also the distribution of fluorophores affects the shape of the correlation function. This is experimentally demonstrated with surface and internally labeled fluorescent spheres. In addition, experiments are performed on fluorescent spheres of different radii to validate the model by comparing the results to theoretical predictions.
INTRODUCTION
Fluorescence correlation spectroscopy (FCS) (1) is a noninvasive method for investigating kinetic processes and molecular interactions by statistical analysis of equilibrium fluctuations. The technique exploits fluorescence intensity fluctuations of molecules that pass through a very small optical observation volume. FCS has been widely applied in studying translational and rotational diffusion (2,3), flow (4), protein-protein interactions (5), protein conformational fluctuations (6), and many other phenomena.
Conventional FCS theory assumes pointlike particles with sizes much smaller than the observation volume. However, there are many potential applications of FCS where the particle size is comparable to the observation volume such that the point particle approximation is not necessarily valid anymore. For example, viral particles with lengths exceeding 100 nm are approaching the waist of the diffraction-limited observation volume. An FCS study of viruses labeled with fluorescent proteins needs to examine the effect of size on the autocorrelation function. In fact, a recent FCS study of phage-protein interactions discussed potential artifacts in data interpretation, because the size of the phage exceeded the beam waist (7). Lipid vesicles are another example of large particles. The potential of FCS for studying the binding of peptides and proteins to large unilamellar vesicles (LUVs) has been demonstrated by many studies (8,9). Because the diameter of LUVs is >100 nm, the effect of the finite size on FCS experiments is of interest.
Attempts to extend FCS to finite-sized particles have been described previously (10,11). However, only an approximate solution is derived for small disklike particles, and the investigation was primarily based on a Monte Carlo simulation for large particles. A formulation of FCS theory based on the dynamic structure factor (10) has recently been used to study intrachain dynamics of large semiflexible DNA molecules with a hydrodynamic radius larger than the waist of the observation volume (12,13). In this article, we use the same approach for calculating the autocorrelation function of particles with finite size and arbitrary fluorophore distribution. Analytical correlation functions are derived for a few specific cases. We explicitly consider surface- and internally labeled disks and spheres. The theory is validated with FCS experiments on fluorescently labeled spheres of various sizes.
The analysis shows that both the finite and point-particle FCS model fit the experimental correlation curves, but the point-particle model recovers biased parameters for large particles, which affects the interpretation of the diffusion coefficient, the hydrodynamic size, brightness, and particle concentration. This study also provides information about the critical size above which the shape and size need to be accounted for in FCS experiments.
THEORY
Consider a suspension of finite-sized particles that are labeled with fluorescent dyes. For simplicity, we assume that all particles are identical. The distribution of fluorophores within the particle is characterized by the function, 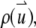 where
where 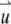 is measured with respect to the center of the particle. Assume that there are a total of NT particles freely diffusing in a very large volume, V. In this article, we use the normalized point spread function,
is measured with respect to the center of the particle. Assume that there are a total of NT particles freely diffusing in a very large volume, V. In this article, we use the normalized point spread function, 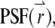 to describe the profile of the observation volume. For two-photon excitation,
to describe the profile of the observation volume. For two-photon excitation,  is given by the square of the illumination intensity profile, whereas for one-photon excitation, it is the product of the illumination intensity profile and the collection profile (14). Suppose the center of the jth particle is located at position
is given by the square of the illumination intensity profile, whereas for one-photon excitation, it is the product of the illumination intensity profile and the collection profile (14). Suppose the center of the jth particle is located at position 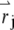 at time t. The fluorescence intensity emitted by the particle is given by
at time t. The fluorescence intensity emitted by the particle is given by
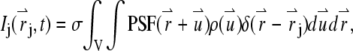 |
(1) |
where 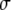 is the brightness of a single fluorescent dye that labels the sphere. Typically,
is the brightness of a single fluorescent dye that labels the sphere. Typically, 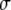 is the product of the absorption cross section, the fluorescence quantum yield, and the detection efficiency of the fluorophore.
is the product of the absorption cross section, the fluorescence quantum yield, and the detection efficiency of the fluorophore. 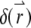 is the Dirac δ-function in the d-dimension. If we replace the δ-function by its Fourier transform and change the integration variable from
is the Dirac δ-function in the d-dimension. If we replace the δ-function by its Fourier transform and change the integration variable from 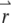 to
to 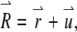 we obtain
we obtain
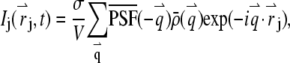 |
(2) |
where 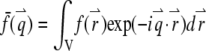 is the Fourier transform of the function
is the Fourier transform of the function 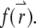 The total fluorescence from NT particles is
The total fluorescence from NT particles is
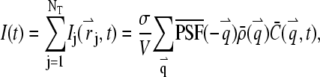 |
(3) |
where 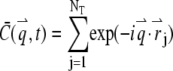 is the Fourier transform of the local particle concentration
is the Fourier transform of the local particle concentration 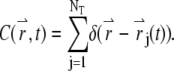 It is straightforward to verify that the average concentration is given as
It is straightforward to verify that the average concentration is given as 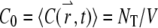 with this definition. We define
with this definition. We define 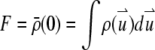 as the total number of fluorophores contained in one particle and
as the total number of fluorophores contained in one particle and 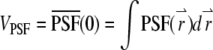 as the observation volume conventionally used in fluorescence fluctuation spectroscopy experiments. The average fluorescence is given by
as the observation volume conventionally used in fluorescence fluctuation spectroscopy experiments. The average fluorescence is given by 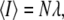 where
where 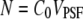 is the average occupation number in the observation volume, and
is the average occupation number in the observation volume, and 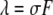 is the total brightness of the particle.
is the total brightness of the particle.
For a stationary and homogenous system, the correlation of the concentration fluctuation 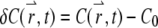 is translational invariant in time. If we further assume that the particle satisfies the diffusion equation, we obtain the correlation function (see Appendix A)
is translational invariant in time. If we further assume that the particle satisfies the diffusion equation, we obtain the correlation function (see Appendix A)
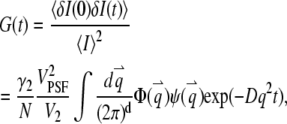 |
(4) |
where we define the normalized form factor (15) of the particle as 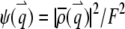 and the normalized PSF filter function as
and the normalized PSF filter function as 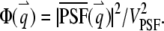 The
The 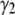 -factor in fluorescence fluctuation spectroscopy is defined as
-factor in fluorescence fluctuation spectroscopy is defined as 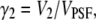 where
where 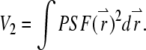 FCS theory based on the dynamic structure factor has been previously described (10). Here, we followed the same approach but focused explicitly on the effects due to the finiteness and fluorophore distribution of a particle.
FCS theory based on the dynamic structure factor has been previously described (10). Here, we followed the same approach but focused explicitly on the effects due to the finiteness and fluorophore distribution of a particle.
To calculate the correlation function, we need to specify the shape of the 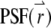 and the distribution function of the fluorophore
and the distribution function of the fluorophore 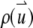 within the particle. A two-dimensional or three-dimensional Gaussian profile for s-photon (
within the particle. A two-dimensional or three-dimensional Gaussian profile for s-photon (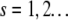 ) excitation is conventionally used in the FCS literature to model the PSF (1,16):
) excitation is conventionally used in the FCS literature to model the PSF (1,16):
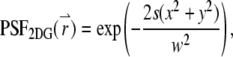 |
(5a) |
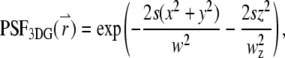 |
(5b) |
with beam waists of w and wz. The filter functions for these model PSFs are
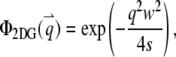 |
(6a) |
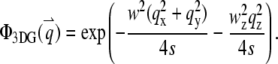 |
(6b) |
To illustrate the application of Eq. 4, we consider a disk with radius A diffusing through a 2D Gaussian PSF. First, we assume that the fluorophores only distribute on the edge of the disk, which implies 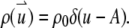 We call such a structure of fluorophores a “ring.” The total number of fluorophores within one ring is
We call such a structure of fluorophores a “ring.” The total number of fluorophores within one ring is 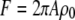 and the normalized form factor is
and the normalized form factor is 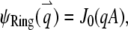 where
where 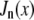 is the nth-order Bessel function of the first kind. Plugging
is the nth-order Bessel function of the first kind. Plugging 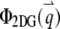 and
and 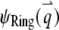 into Eq. 4, we obtain
into Eq. 4, we obtain
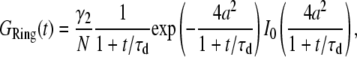 |
(7) |
where we have defined the dimensionless radius 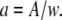 The diffusion time
The diffusion time 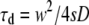 represents a natural timescale for the FCS experiment and characterizes the time it takes for the particle to diffuse through the waist of the observation volume.
represents a natural timescale for the FCS experiment and characterizes the time it takes for the particle to diffuse through the waist of the observation volume. 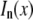 is the nth-order modified Bessel function of the first kind.
is the nth-order modified Bessel function of the first kind.
When the radius of the ring is small,  we can approximate Eq. 7 by its Taylor expansion. With a little rearrangement, we arrive at
we can approximate Eq. 7 by its Taylor expansion. With a little rearrangement, we arrive at
 |
(8) |
where 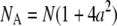 and
and 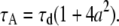 Equation 8 implies that the correlation function of the ring is well approximated by that of a point particle if the radius is small compared to the beam waist. The parameters NA and τA, however, represent an apparent number of molecules and an apparent diffusion time, which depends on the size of the particle.
Equation 8 implies that the correlation function of the ring is well approximated by that of a point particle if the radius is small compared to the beam waist. The parameters NA and τA, however, represent an apparent number of molecules and an apparent diffusion time, which depends on the size of the particle.
We used the same procedure to determine the correlation function of a fluorescent sphere, shell, and disk. The normalized form factor, the correlation function, and its small particle expansion are listed in Appendix B. The small parameter expansion reduced in all cases to the form of the point-particle correlation function, with apparent parameters for the diffusion time and the number of molecules.
Another useful parameter available from FCS is brightness, which is defined as the average photon counts detected per particle (17). We now consider the influence of particle size on brightness. FCS determines the brightness, λ, from the fluorescence intensity by 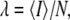 once the average number of particles, N, is known. For point particles, the number of particles,
once the average number of particles, N, is known. For point particles, the number of particles, 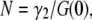 is directly obtained from the correlation amplitude, which leads to
is directly obtained from the correlation amplitude, which leads to  However, for finite-sized particles, this relationship is not valid anymore, because the number of particles depends not only on the fluctuation amplitude, but also on the size of the particle. For a ring structure, it is straightforward to derive from Eq. 7 the relation between the correlation amplitude and the brightness,
However, for finite-sized particles, this relationship is not valid anymore, because the number of particles depends not only on the fluctuation amplitude, but also on the size of the particle. For a ring structure, it is straightforward to derive from Eq. 7 the relation between the correlation amplitude and the brightness, 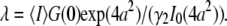 Thus, a point-particle model would underestimate the brightness of a ring-shaped particle by a factor of
Thus, a point-particle model would underestimate the brightness of a ring-shaped particle by a factor of 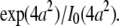 The brightness of disks, shells, and spheres can be derived similarly with the help of the equations provided in Appendix B.
The brightness of disks, shells, and spheres can be derived similarly with the help of the equations provided in Appendix B.
MATERIAL AND METHODS
The instrument for the fluorescence fluctuation experiments consists of a Zeiss Axiovert 200 microscope (Thornwood, NY) and a mode-locked Ti:sapphire laser (Tsunami, Spectra-Physics, Mountain View, CA) pumped by an intracavity doubled Nd:YVO4 laser (Millennia Vs, Spectra-Physics, Mountain View, CA). A 63× Plan-Apochromat oil immersion objective (NA 1.4) is used to focus the laser beam and collect the fluorescence. The light passes through an optical filter and is detected with an avalanche photodiode (SPCM-AQ-14, Perkin-Elmer, Dumberry, Québec, Canada). The output of the avalanche photodiode, which produces transistor-transistor logic pulses, was directly connected to a data acquisition card (FLEX02, Correlator.com, Bridgewater, NJ). The recorded photon counts were stored and later analyzed with programs written in IDL version 5.4 (Research Systems, Boulder, CO). A program written in Fortran with a nonlinear least-squares optimization routine from the Port Library (available at http://www.netlib.org) is used to fit the theoretical model to the experimental autocorrelation function.
The internally labeled green fluorescent spheres are bought from Duke Scientific (Fremont, CA), and the surface-labeled spheres carrying fluorescein are a kind gift from microParticles (Berlin, Germany). The particles are suspended in a buffer with 0.5% sodium dodecyl sulfate and 14.7% sucrose. The buffer has a viscosity of η = 1.54 centipoises at room temperature. To avoid sedimentation, the density of the buffer is adjusted by adding sucrose to 1.06 g/mL, which is equal to that of the fluorescent spheres. We estimated that the Rayleigh number of the system is <100, which implies that drift introduced by thermal convection is not important. If necessary, the presence of drift can be identified by scanning FCS (4). To ensure monodispersion, the suspension is vortexed vigorously and sonicated three times in a water bath for 10 min before performing measurements. An excitation wavelength of 905 nm was selected for all experiments.
RESULTS
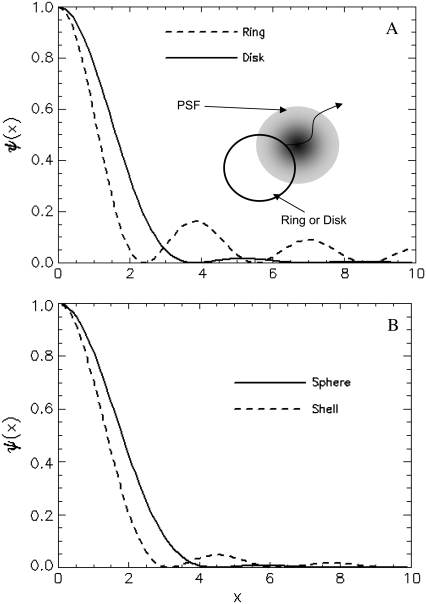
The contribution of the finiteness of the particle to the autocorrelation function is summarized by its form factor, which depends on the particle size and the fluorophore distribution inside the particle. In Fig. 1, we plot the normalized form factor 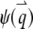 for a ring, disk (Fig. 1 a), shell, and sphere (Fig. 1 b). Generally, the form factor is an oscillatory and decaying function. It is interesting to note that the oscillatory behavior of the hollow structures, like a ring and a shell, persists much longer than that of the solid counterparts, like the disk and sphere. This is because the distribution function of the hollow structure is sharp and therefore it contains many more Fourier components. Since the normalized form factor,
for a ring, disk (Fig. 1 a), shell, and sphere (Fig. 1 b). Generally, the form factor is an oscillatory and decaying function. It is interesting to note that the oscillatory behavior of the hollow structures, like a ring and a shell, persists much longer than that of the solid counterparts, like the disk and sphere. This is because the distribution function of the hollow structure is sharp and therefore it contains many more Fourier components. Since the normalized form factor, 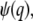 is a decaying function, we expect that the finiteness of the particle will in general decrease the value of the correlation function. On the other hand, the contribution of different wave vectors, q, to the integration is confined, according to Eq. 4, to within
is a decaying function, we expect that the finiteness of the particle will in general decrease the value of the correlation function. On the other hand, the contribution of different wave vectors, q, to the integration is confined, according to Eq. 4, to within 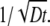 Thus, when the time, t, is large, only small wave vectors contribute to the integration. For small values of q, the normalized form factor approaches 1, which implies that the finiteness of the particle has no influence on the correlation function for large lag times t.
Thus, when the time, t, is large, only small wave vectors contribute to the integration. For small values of q, the normalized form factor approaches 1, which implies that the finiteness of the particle has no influence on the correlation function for large lag times t.
FIGURE 1.
(A) Normalized form factor for a ring (dashed line) and a disk (solid line), with cartoon of a ring or disk structure with size comparable to the beam waist diffusing through the point spread function. (B) Normalized form factor for a shell (dashed line) and a sphere (solid line).
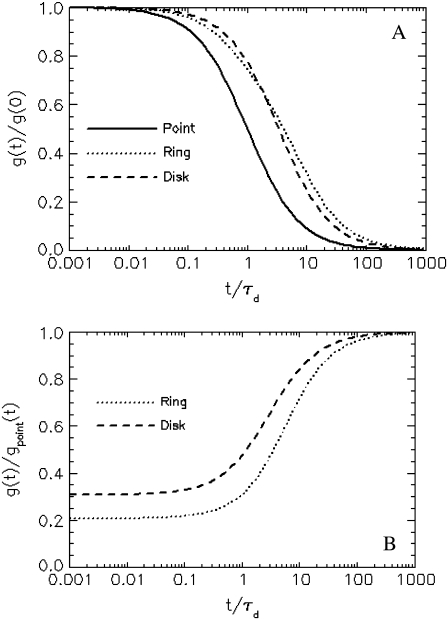
To support the above argument, we compare the autocorrelation function of a point particle to those of a ring and a disk with radius equal to the beam waist (a = 1). In Fig. 2 A, we plot the normalized autocorrelation function to investigate the shape of the correlation function. First, we notice that the correlation function of a ring or disk decays much slower than that of the corresponding point particle with the same diffusion time. It is also clear that correlation functions of a ring and disk have slightly different shapes, which solely originates from the difference in the form factor. In Fig. 2 B, we divide the correlation function of the ring and disk by that of the corresponding point particle, which characterizes the overall correction due to the finiteness of the particles. First, we notice that for small lag times t, the correlation function of a finite-sized particle has a reduced value when compared to the correlation function of the point particle. The difference in the fluctuation amplitude between a finite and a point particle defines a correction factor that needs to be taken into account in the proper determination of particle concentrations. It is also clear that for the same particle size, the correction arising from a ring is stronger than that from a disk. We have explained that this occurs because the form factor of a hollow structure decays faster for small wave vectors q and contains many more Fourier components for large q than the form factor of a solid object. This is because the fluorescence of the ring originates from the edge of the circle, causing a big change in the intensity when the ring moves slightly. As the particle diffuses through the observation volume, there is a strong correlation between the two edges, which makes the correlation persists longer. To summarize, the finiteness of a particle decreases the correlation amplitude and increases the correlation time.
FIGURE 2.
Comparison of the correlation functions between a finite-sized object and a point particle. (A) The normalized correlation functions of a point particle (solid line), a ring (dotted line), and a disk (dashed line) are plotted as a function of time. We set the radius of the particle equal to the beam waist of the PSF, A = w, or a = 1. The correlation function of a finite-sized object decays much more slowly than the corresponding correlation function of a point particle. The shape of the correlation function is different between a ring and a disk. (B) We divide the autocorrelation functions of a ring and a disk by the corresponding function for a point particle to characterize the overall effect of finiteness in the form of a correction function. A value different from 1 indicates that a correction is required to account for the size of the particle. At short times (t), the finite size decreases the value of the correlation function, whereas no correction is required at long times. The hollow ring decreases the correlation function much further than the solid disk.
To test the theory presented in this article, we performed FCS experiments on fluorescently labeled spheres. The diffusion coefficient, D, of the sphere is determined by the Stokes-Einstein relation (Eq. A5). The experimental quantity directly accessible from FCS experiments is the diffusion time, τd, which depends on the radius of the sphere as well as the beam waist, w, of the PSF. If we plug in the parameters used in the experiment (T = 23°C, η = 1.54 centipoises), we obtain a direct relationship between the diffusion time, τd, the radius of the sphere, A, and the beam waist, w: τd = 890Aw2, where A and w are in units of micrometers and τd is in unit of milliseconds. To determine the beam waist, w, we first measure the autocorrelation function of fluorescent microspheres with known radius A = 0.25 μm. The autocorrelation curve (data not shown) is fit using Eq. B3b, with the radius A fixed to its known value. The fit determined a beam waist of w = 0.42 μm and squared beam waist ratio as 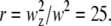 Using a point particle model (Eq. B2c) for calibration provides the same result for the beam waist, because finite size corrections are not important for these small particles. Below, we fix w and r to the calibrated value while allowing the radius of the sphere to vary as a free fitting parameter.
Using a point particle model (Eq. B2c) for calibration provides the same result for the beam waist, because finite size corrections are not important for these small particles. Below, we fix w and r to the calibrated value while allowing the radius of the sphere to vary as a free fitting parameter.
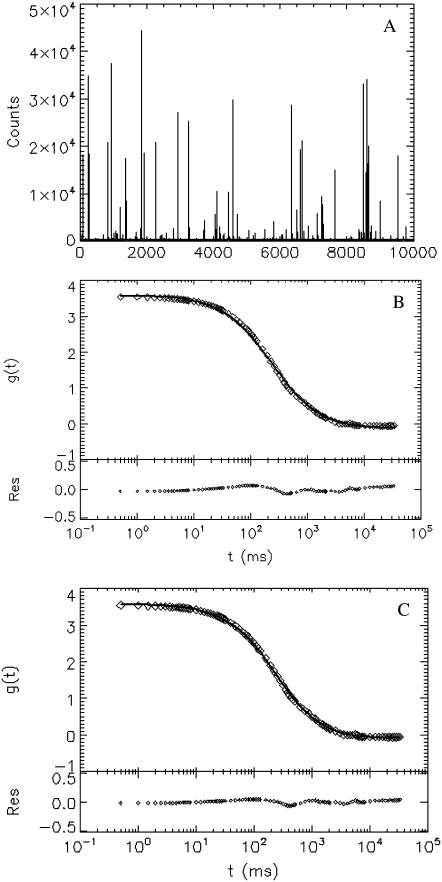
Next, we measure internally labeled spheres with a known radius A = 0.5 μm (provided by the manufacturer), which is larger than the beam waist, w. Fig. 3 A shows a plot of the intensity trace with many spikes. Each spike represents the passage of a sphere across the PSF. There are only a few hundred spikes in a 3-h period, which is a consequence of the extremely low concentration of the sphere. In Fig. 3, B and C, we plot the experimental autocorrelation function (○), together with its fit (solid line). The fit to the unphysical point particle model (Fig. 3 B) yields τd = 238 ± 27 ms or A = 1.53 ± 0.17 μm, which significantly overestimates the size of the particle. If the same data is fit to a sphere model (Fig. 3 C), we obtain the radius of the sphere, A = 0.48 ± 0.02 μm, and the diffusion time, τd = 75 ± 4 ms. From the Stokes-Einstein relation, we expect the diffusion time to be τd = 78 ms, which is in excellent agreement with the fit.
FIGURE 3.
FCS experiment of internally labeled spheres with radius A = 0.5 μm. (A) The intensity trace of the data taken at 2 kHz for 3 h. Each spike represents a sphere passing through the observation volume. (B and C) The experimental correlation function (○) and its fit (solid line) to the point particle model (B) and solid sphere model (C). The beam waist of the PSF is fixed to 0.42 μm, which is determined by calibration with a sample of 0.025-μm spheres, as described in the text. The fit to a point particle model yields a radius A = 1.53 ± 0.17 μm and a diffusion time τd = 238 ± 27 ms, which overestimates the size threefold. If the same data is fit to a solid sphere model, we obtain A = 0.48 ± 0.02 μm and a diffusion time τd = 75 ± 4 ms, which agrees very well with the prediction based on the Stokes-Einstein relation.
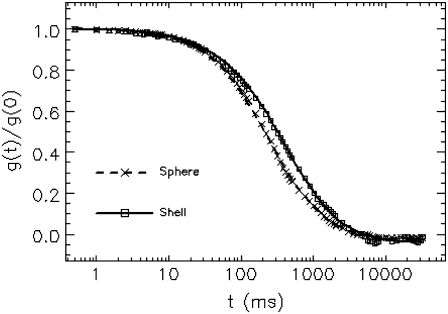
To demonstrate the effect of fluorophore distribution on the correlation function, we perform experiments with internally labeled and surface-labeled spheres of the same radius A = 0.5 μm. In Fig. 4, we plot the normalized experimental autocorrelation curve (symbols) together with the fit to the corresponding model (lines) for both samples. The correlation curve of surface-labeled spheres decays slower than that of the internally labeled ones, which is due to the difference in their form factors. The fitting result of the internally labeled sphere has been discussed above (Fig. 3). For the surface-labeled sphere, the fit to a shell model (Eq. B2b) returns a diffusion time τd = 77 ± 1 ms and a radius A = 0.50 ± 0.01 μm, which agrees with the predicted value from the Stokes-Einstein relation and the input radius of the sphere. If the data is fit instead to a point particle model, we recover τd = 361 ± 8 ms and a radius A = 2.32 ± 0.05 μm, which is much larger than the true value. A fit of the same data to a solid sphere model recovers a diffusion time τd = 88 ± 1 ms and radius A = 0.57 ± 0.01 μm, which deviates from the theoretical values by more than the experimental uncertainty.
FIGURE 4.
Comparison between internally and surface-labeled spheres of the same radius. Autocorrelation curves of internally labeled (cross) and surface-labeled (square) spheres both with radius 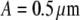 are measured. The fitting result of internally labeled spheres is given in Fig. 3. For surface-labeled spheres, the fit to a shell model returns a radius of
are measured. The fitting result of internally labeled spheres is given in Fig. 3. For surface-labeled spheres, the fit to a shell model returns a radius of 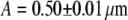 and τd = 77 ± 1 ms, which agrees well with the theoretically expected values.
and τd = 77 ± 1 ms, which agrees well with the theoretically expected values.
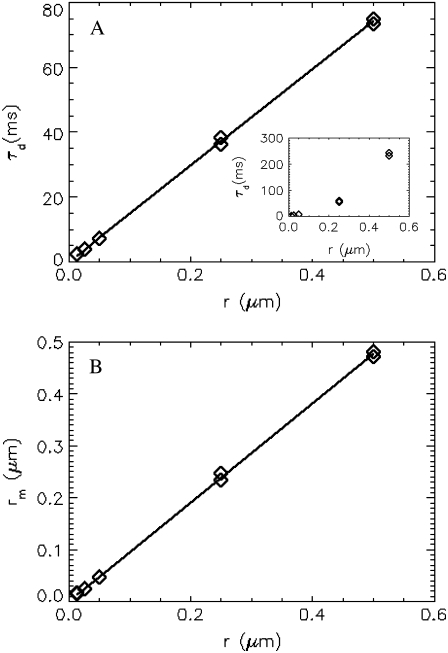
To check the robustness of the technique, we performed experiments with internally labeled spheres of different radii, ranging from 0.013 μm to 0.5 μm. We fit the correlation curve to the solid sphere model as described above. The fitted diffusion time (diamonds) is plotted as a function of the radius (Fig. 5 A). A fit of the data to a straight line (solid line) yields a slope of 149 ms/μm, which agrees well with theory, as the Stokes-Einstein relation predicts a slope of 156 ms/μm. The diffusion times returned from fits to a point particle model is plotted in the inset, which leads to a diffusion time that is apparently not linearly related to the radius of the sphere. In Fig. 5 B, the fitted radius (diamonds) is graphed as a function of the radius provided by the manufacturer. A linear fit (solid line) to the curve yields a slope of 0.98, which is close to the theoretical value of 1. The experiment shows that the theory describes the data over a wide range of particle sizes.
FIGURE 5.
FCS measurement of spheres with different sizes. In this experiment, internally labeled spheres with a radius of 0.013 μm, 0.025 μm, 0.05 μm, 0.25 μm, and 0.5 μm, (provided by manufacturer) were measured. The data acquisition times for these spheres are 10 min, 10 min, 10 min, 1 h, and 3 h, respectively. (A) The diffusion times returned from the fit are plotted as a function of the known radii of the spheres. Fitting the data to a straight line results in a slope of 149 ms/μm, whereas the slope predicted by the Stokes-Einstein relation is 156 ms/μm. (Inset) Diffusion time returned from fits to a point-particle model, which leads to an unphysical nonlinear relationship between diffusion time and radius of the sphere. (B) The measured radius is plotted as a function of the physical radius. The solid line is a fit to a linear model with slope of 0.98, which agrees closely with the expected slope of 1.
DISCUSSION
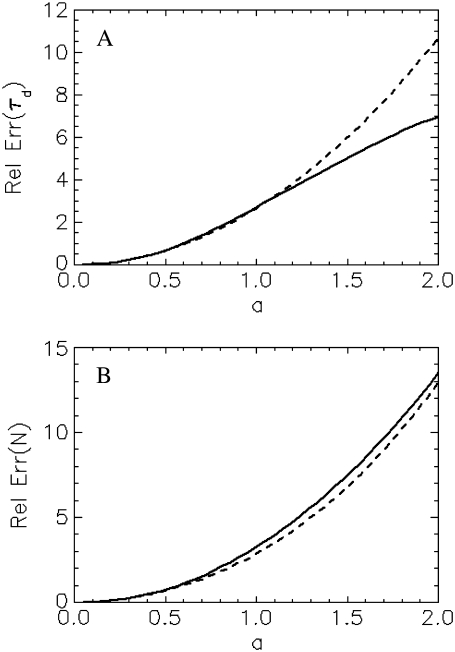
For an experimentalist, it is crucial to know about a model's limitations and range of applications. As we have shown in Fig. 3 B, a point-particle model describes well the experimental correlation curve of an extended particle. If one is not aware of the finite size effect, incorrect conclusion about the particle size, concentration, and brightness would be drawn from the data. Therefore, it is useful to draw a threshold for the particle size beyond which finite size effects have to be taken into account. To gauge the bias resulting from the point-particle model we generate theoretical correlation curves of particles with different sizes and fit these curves to the point-particle model. We define the relative error of a parameter as the difference between its fitted and exact value divided by its exact value. Fig. 6 A shows the relative error (solid line) of the diffusion time for a shell as a function of reduced radius a. The relative error increases with the size of the shell. If we choose a 10% error as a threshold indicating the importance of finite size effect, we obtain a corresponding threshold for the reduced radius of 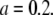 In other words, if the reduced radius of the shell exceeds 0.2, the point-particle model will bias the diffusion time by >10%. In our experimental conditions, this size corresponds to a shell particle with a radius of 80 nm. In Fig. 6 B, we plotted the relative error (solid line) for the number of particles, N, as a function of reduced radius a. Just as for the diffusion coefficient, the relative error exceeds 10% for a reduced radius >0.2.
In other words, if the reduced radius of the shell exceeds 0.2, the point-particle model will bias the diffusion time by >10%. In our experimental conditions, this size corresponds to a shell particle with a radius of 80 nm. In Fig. 6 B, we plotted the relative error (solid line) for the number of particles, N, as a function of reduced radius a. Just as for the diffusion coefficient, the relative error exceeds 10% for a reduced radius >0.2.
FIGURE 6.
The relative error in the fit parameters introduced by the point-particle model. The theoretical autocorrelation curve for a shell is fitted assuming a point-particle model, which leads to a bias in the fitted parameters. The solid line shows the relative error of the diffusion time (A) and the number of molecules (B) as a function of reduced particle size. The dotted lines represent the expected relative error based on the small-particle expansion (Eq. B2c), which is given by 8a2/3 for τd and by 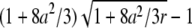 for N.
for N.
We found that the point-particle model described the experimental correlation functions of extended particles. This observation is consistent with the small-particle expansion of the theory. For all geometries discussed, the correlation function of the small-particle expansion has the same shape as the point-particle correlation function. However, unlike the point-particle model, the parameters NA and τA do not directly represent the number of particles, N, and the diffusion time, τd, but also depend on the shape and size of the particle. For example, the small-particle expansion for a shell given by Eq. B2.C leads to a relative error between τA and the diffusion time,τd, of 8a2/3 (Fig. 6 A, dotted line). Remarkably, the relative error (or deviation) between τA and the diffusion time is well approximated by the small-particle expansion for a < 1.2.
In Fig. 6 B, we have plotted the relative error between the parameter NA and the number of particles, N. Again the small-particle expansion predicts the relative error very accurately for a wide range of particle sizes. The above results suggest another way of analyzing FCS data for intermediate-sized particles. The correlation curve is first fit with a point-particle model. The fit parameters are subsequently corrected with the equations provided by the small-particle expansion to yield the correct diffusion time and the number of particles.
The same analysis presented in Fig. 6 has also been performed for the solid sphere model (data not shown), with similar results as for the shell model. The point-particle model fits the theoretical correlation function, and the small-particle expansion accurately describes the relative error over a wider range of particle sizes. In the solid sphere case, the threshold for a 10% error from the point-particle model is a = 0.25, which corresponds to a radius of 100 nm in our experimental setup.
Brightness has been successfully applied to study protein oligomerization (5,18), ligand binding (19), and molecular aggregation (20,21). By comparing the brightness of a particle carrying multiple fluorophores to that of a single fluorophore, it is possible to infer the total number of fluorescent molecules within the particle (5). To perform brightness analysis on large particles like viruses or LUVs, it is important to consider the effect of size on the analysis as pointed out in the Theory section.
Below, we discuss the assumptions made in deriving the correlation function for finite-sized particles. First, we assumed that the particle satisfies the diffusion equation with a constant diffusion coefficient, which is valid only for timescales larger than the velocity correlation time (15). We estimated, for our experimental conditions, that the velocity correlation time is on the order of 10−5 s for a sphere with a radius of 0.5 μm. For smaller spheres, the velocity correlation time is even shorter. The diffusion time for a 0.5-μm sphere is ∼80 ms, and the sampling time of the experiment is 0.5 ms. Thus, for the experiments considered in this article, the velocity correlation time does not play a role. However, for particles large enough, the approximation breaks down and the current theory must be generalized to incorporate a time-dependent diffusion coefficient.
Another assumption, made implicitly, is that there is no interaction between spheres, and we only consider the self-diffusion of particles. The particles must experience some repulsive force to prevent them from aggregation, or at least there has to be a hard-sphere interaction between spheres. In the experiment, we added 0.5% sodium dodecyl sulfate to the buffer to facilitate a monodisperse suspension of the sphere. Presumably the spheres are charged and there is Coulomb interaction between spheres. As mentioned above, our treatment neglects the interaction between spheres. It is possible to include such interactions in the theoretical treatment, which is of great interest by itself for research in colloidal systems. The validity of our model lies in the fact that the concentration of the sphere is very low, such that the average distance between particles is much larger than the size of the particle. The interaction contributes to the correlation function only when two particles collide with each other in the excitation beam. When the concentration is small, such events have very low probability and can be safely neglected.
In this article, we have not considered the effect of rotation on the correlation function. In addition, we restricted ourselves to the correlation function for circularly and spherically symmetric particles. These are mathematically the most simple to treat. Also, vesicles and many viruses exhibit spherical symmetry. Another advantage is that rotational dynamics does not play a role for a spherical object. For an arbitrary shaped particle, the current formulism must be modified to account for the effects of rotational diffusion.
Not only the size but also the distribution of fluorophores within the particle affects the shape of the autocorrelation function, as demonstrated in Fig. 4 for a surface- and internally labeled fluorescent sphere of equal diameter. Generally, the shape of autocorrelation function is not sufficiently different to distinguish particles with the same size but different fluorophore distributions. For example, both the shell and sphere model describe the correlation curves of Fig. 4 equally well. However, if it is possible to establish the size of the spherical particle independently, for example, by electron microscopy, then FCS provides information about the fluorophore distribution within a particle. This is illustrated in Fig. 4, where the shell and sphere model lead to distinct correlation curves for the same particle size.
Finally, techniques that reduce the observational volume as much as possible are developed to apply FCS to biological samples at very high concentrations (22,23). Thus, the effect of particle size will play an even more important aspect in such experiments. This article provides some of the foundation needed to extend FCS to finite-sized particles.
Acknowledgments
This work was supported by grants from the National Institutes of Health (GM64589) and the National Science Foundation (PHY-0346782).
APPENDIX A
For a stationary and homogenous system, the correlation of concentration fluctuations 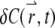 is translational invariant both temporally and spatially:
is translational invariant both temporally and spatially:
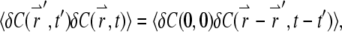 |
(A1) |
which implies
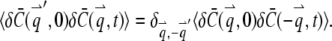 |
(A2) |
With the above equation, we obtain the correlation of fluorescence fluctuation from Eq. 3
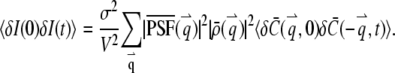 |
(A3) |
So far, the formulation is exact. Now we introduce an approximation by assuming that the concentration, 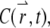 satisfies the diffusion equation with a constant diffusion coefficient, D:
satisfies the diffusion equation with a constant diffusion coefficient, D:
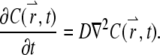 |
(A4) |
The validity of the above assumption is discussed in the text. For a spherical particle, D is given by the Stokes-Einstein relation:
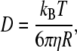 |
(A5) |
where kB is the Boltzmann constant, T is the temperature in Kelvin, 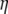 is the viscosity of the solvent, and R is the radius of the sphere. Taking the Fourier transform of Eq. A4, it is straightforward to verify that
is the viscosity of the solvent, and R is the radius of the sphere. Taking the Fourier transform of Eq. A4, it is straightforward to verify that
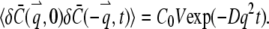 |
(A6) |
With the definition of the normalized form factor, 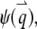 and the normalized PSF filter function,
and the normalized PSF filter function, 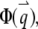 and by changing the summation of
and by changing the summation of  to integration, we obtain
to integration, we obtain
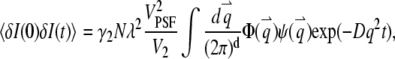 |
(A7) |
where d is the dimension of the space. The autocorrelation function of the fluorescence (Eq. 4) is directly determined from this equation.
APPENDIX B
In this appendix, we list the normalized form factor and the autocorrelation function for particles of different geometries.
1. Disk, a uniformly dye-labeled disk diffusing through a 2D Gaussian PSF:
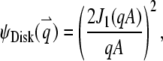 |
(B1a) |
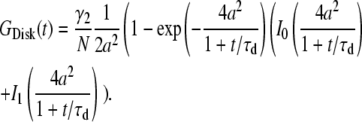 |
(B1b) |
When a ≪ 1, Eq. B1b can be expanded and written in the form of a point-particle correlation function (Eq. 8) with the apparent number of molecules and diffusion time defined by 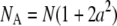 and
and 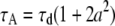 2. Shell, a uniformly surface-labeled sphere diffusing through a 3D Gaussian PSF (Eq. 5b):
2. Shell, a uniformly surface-labeled sphere diffusing through a 3D Gaussian PSF (Eq. 5b):
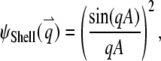 |
(B2a) |
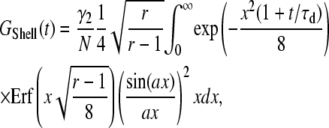 |
(B2b) |
where 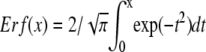 is the error function. When the particle is small, the correlation function reduces to the form of a point-particle correlation function:
is the error function. When the particle is small, the correlation function reduces to the form of a point-particle correlation function:
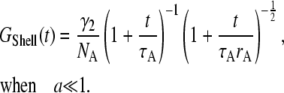 |
(B2c) |
The apparent parameters are 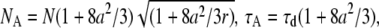 and
and 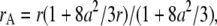 where
where 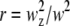 is the squared beam waist ratio
is the squared beam waist ratio
3. Sphere, a uniformly volume-labeled sphere diffusing through a 3D Gaussian PSF (Eq. 5b):
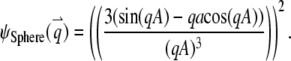 |
(B3a) |
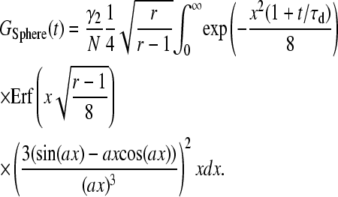 |
(B3b) |
The small-particle expansion for a sphere is given by Eq B2.c with apparent parameters of 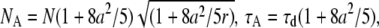 and
and
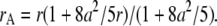 |
Editor: Elliot L. Elson.
References
- 1.Magde, D., E. Elson, and W. W. Webb. 1972. Thermodynamics fluctuations in a reacting system: measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29:705–708. [Google Scholar]
- 2.Widengren, J., U. Mets, and R. Rigler. 1999. Photodynamic properties of green fluorescent proteins investigated by fluorescence correlation spectroscopy. Chem. Phys. 250:171–186. [Google Scholar]
- 3.Walter, N. G., P. Schwille, and M. Eigen. 1996. Fluorescence correlation analysis of probe diffusion simplifies quantitative pathogen detection by PCR. Proc. Natl. Acad. Sci. USA. 93:12805–12810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Skinner, J., Y. Chen, and J. Mueller. 2005. Position-sensitive scanning fluorescence correlation spectroscopy. Biophys. J. 89:1288–1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen, Y., L. N. Wei, and J. D. Muller. 2003. Probing protein oligomerization in living cells with fluorescence fluctuation spectroscopy. Proc. Natl. Acad. Sci. USA. 100:15492–15497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chattopadhyay, K., E. L. Elson, and C. Frieden. 2005. The kinetics of conformational fluctuations in an unfolded protein measured by fluorescence methods. Proc. Natl. Acad. Sci. USA. 102:2385–2389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bahns, J., C. Liu, and L. Chen. 2004. Characterizing specific phage-protein interactions by fluorescence correlation spectroscopy. Protein Sci. 13:2578–2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rhoades, E., T. F. Ramlall, W. W. Webb, and D. Eliezer. 2006. Quantification of α-synuclein binding to lipid vesicles using fluorescence correlation spectroscopy. Biophys. J. 90:4692–4700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rusu, L., A. Gambhir, S. McLaughlin, and J. Radler. 2004. Fluorescence correlation spectroscopy studies of peptide and protein binding to phospholipid vesicles. Biophys. J. 87:1044–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ricka, J., and T. Binkert. 1989. Direct measurement of a distinct correlation-function by fluorescence cross-correlation. Phys. Rev. A. 39:2646–2652. [DOI] [PubMed] [Google Scholar]
- 11.Starchev, K., J. W. Zhang, and J. Buffle. 1998. Applications of fluorescence correlation spectroscopy: particle size effect. J. Colloid Interface Sci. 203:189–196. [Google Scholar]
- 12.Lumma, D., S. Keller, T. Vilgis, and J. O. Radler. 2003. Dynamics of large semiflexible chains probed by fluorescence correlation spectroscopy. Phys. Rev. Lett. 90:218301. [DOI] [PubMed] [Google Scholar]
- 13.Winkler, R. G., S. Keller, and J. O. Radler. 2006. Intramolecular dynamics of linear macromolecules by fluorescence correlation spectroscopy. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 73:041919. [DOI] [PubMed] [Google Scholar]
- 14.Hess, S. T., and W. W. Webb. 2002. Focal volume optics and experimental artifacts in confocal fluorescence correlation spectroscopy. Biophys. J. 83:2300–2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Berne, B. J., and R. Pecora. 1976. Dynamic Light Scattering. Wiley, New York.
- 16.Wu, B., and J. D. Müller. 2005. Time-integrated fluorescence cumulant analysis in fluorescence fluctuation spectroscopy. Biophys. J. 89:2721–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chen, Y., J. D. Müller, P. T. So, and E. Gratton. 1999. The photon counting histogram in fluorescence fluctuation spectroscopy. Biophys. J. 77:553–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen, Y., and J. D. Muller. 2007. Determining the stoichiometry of protein heterocomplexes in living cells with fluorescence fluctuation spectroscopy. Proc. Natl. Acad. Sci. USA. 104:3147–3152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zemanova, L., A. Schenk, N. Hunt, G. U. Nienhaus, and R. Heilker. 2004. Endothelin receptor in virus-like particles: ligand binding observed by fluorescence fluctuation spectroscopy. Biochemistry. 43:9021–9028. [DOI] [PubMed] [Google Scholar]
- 20.Palmer, A. G., and N. L. Thompson. 1987. Molecular aggregation characterized by high order autocorrelation in fluorescence correlation spectroscopy. Biophys. J. 52:257–270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Müller, J. D., Y. Chen, and E. Gratton. 2000. Resolving heterogeneity on the single molecular level with the photon-counting histogram. Biophys. J. 78:474–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Blom, H., L. Kastrup, and C. Eggeling. 2006. Fluorescence fluctuation spectroscopy in reduced detection volumes. Curr. Pharm. Biotechnol. 7:51–66. [DOI] [PubMed] [Google Scholar]
- 23.Kastrup, L., H. Blom, C. Eggeling, and S. W. Hell. 2005. Fluorescence fluctuation spectroscopy in subdiffraction focal volumes. Phys. Rev. Lett. 94:178104. [DOI] [PubMed] [Google Scholar]