Analyzing Forced Unfolding of Protein Tandems by Ordered Variates, 2: Dependent Unfolding Times

Abstract

Statistical analyses of forced unfolding data for protein tandems, i.e., unfolding forces (force-ramp) and unfolding times (force-clamp), used in single-molecule dynamic force spectroscopy rely on the assumption that the unfolding transitions of individual protein domains are independent (uncorrelated) and characterized, respectively, by identically distributed unfolding forces and unfolding times. In our previous work, we showed that in the experimentally accessible piconewton force range, this assumption, which holds at a lower constant force, may break at an elevated force level, i.e., the unfolding transitions may become correlated when force is increased. In this work, we develop much needed statistical tests for assessing the independence of the unobserved forced unfolding times for individual protein domains in the tandem and equality of their parent distributions, which are based solely on the observed ordered unfolding times. The use and performance of these tests are illustrated through the analysis of unfolding times for computer models of protein tandems. The proposed tests can be used in force-clamp atomic force microscopy experiments to obtain accurate information on protein forced unfolding and to probe data on the presence of interdomain interactions. The order statistics-based formalism is extended to cover the analysis of correlated unfolding transitions. The use of order statistics leads naturally to the development of new kinetic models, which describe the probabilities of ordered unfolding transitions rather than the populations of chemical species.

INTRODUCTION

Most of mechanically active proteins perform their biological function in linear tandems of “head-to-tail” connected repeats. For example, ubiquitin (Ub), a naturally occurring multimer of identical Ub repeats, is involved in protein degradation and several signaling pathways (1,2). A giant protein, titin plays a crucial role in muscle contraction and relaxation. Titin spans almost half of the muscle sacromer and consists of ∼300 domains and 30,000 amino acids (3,4). There are two types of titin domains, immunoglobulin (Ig) and fibronectin (Fn) modules, which are linked in a tandem. The number of Ig domains varies from 37 to 90 in different titin molecules (5,6). Fibronectin is composed of ∼20 distinct Fn domains of type FnI–FnIII. FnIII contains multiple binding sites for integrin receptors of the extracellular matrix (5). In ddFLN, a dimeric filamin from Dictyostelium discoideum, and in human filamin (A protein), a single chain is composed of a rod-like tandem of several Ig domains (6–8). Filamins, which also form multidomain tandems, play an important role in cellular locomotion (6,7).

In single-molecule atomic force microscopy (AFM) experiments, the consecutive unfolding transitions of protein domains in a tandem or a polyprotein are analyzed by applying constant mechanical force (force-clamp mode) or time-dependent force (force-ramp) (9–14). In force-ramp AFM experiments, the force-induced unraveling of protein tandems results in sawtooth profiles of the unfolding forces, {f₁, f₂, …, f_n}, which correspond to the unfolding of individual protein domains. In force-clamp AFM probes, the force-induced tension in the tandem chain results in the stepwise elongation of the tandem end-to-end distance, X. For the polyubiquitin chain (Ub_n, 3 < n < 12), elongation of X in steps of ΔX ≈ 20 nm was used to identify the unfolding transitions in the individual Ub domains (15,16).

Current statistical analyses of forced unfolding data for protein tandems ((D)_n) rely on the assumption that a), the forced unfolding transitions of individual domains (D) are mutually independent (uncorrelated), and that b), the recorded unfolding forces (force-ramp) and unfolding times (force-clamp) are realizations of the same probability density function (pdf) (13,14,16–18). Said differently, these analyses are based on the assumption that the unfolding times and forces form a set of independent identically distributed (iid) random variables. In our previous computer simulation studies of forced unfolding, hereafter referred to as Study 1 (19), we tested the validity of the “iid assumption” in an experimentally accessible piconewton range of applied constant force. We showed that the uncorrelated forced unfolding transitions, observed for the model tandem S2–S2–S2, become correlated when the applied force is increased (19).

In a typical force-clamp AFM experiment on a tandem D₁–D₂– … −D_n, the recorded first, second, etc. forced unfolding times, t_1:n, t_2:n, …, t_n:n, are ordered, i.e., t_1:n ≤ t_2:n ≤ …t_n:n (19). Because any domain D_i, i = 1, 2, …n, could have unfolded at any time, there is no direct correspondence between the observed ordered unfolding time data, {t_1:n, t_2:n, …, t_n:n}, and the unobserved parent unfolding times {t₁, t₂, …, t_n} for individual domains D₁ (t₁), D₂ (t₂), …, D_n (t_n). The main goal of unfolding time data analysis is to characterize the forced unfolding times of individual domains. This is equivalent to inferring the parent unfolding time distributions for individual domains, ψ₁(t) (D₁), ψ₂(t) (D₂), …, ψ_n(t) (D_n), from the distributions of ordered time variates, t_1:n, t_2:n, …, t_n:n. As we showed in Study 1 (19), only when the unfolding times are iid, which is the case for the uncorrelated unfolding times for a homogeneous tandem (D)_n, the connection between ordered unfolding times and the parent densities is direct, and ψ (t) = ψ₁(t) = ψ₂(t) = … = ψ_n(t) can be estimated by combining all ordered time variates into a single histogram. However, when the parent distributions are nonidentical, i.e., ψ₁(t) ≠ ψ₂(t) ≠ … ≠ ψ_n(t) (heterogeneous tandem D₁–D₂– … −D_n) and/or the unfolding times, t₁, t₂, …, t_n are correlated (dependent), the relationship between the observed ordered time data and the unobserved parent time data is more complex, and data analysis based on the iid assumption is inappropriate. We will show in this study that when the unfolding times are correlated, the use of the iid assumption could result in an inaccurate description of protein unfolding. Hence, statistical tools for testing whether the iid assumption holds are much needed.

In the case of noninteracting domains, such as domains S2 in tandem S2–S2–S2 (Study 1), the emergence of correlations among the unfolding transitions is due to dynamic competition between the unfolding kinetics and tension propagation along the tandem chain (19). However, in wild-type protein tandems, correlations can also build up due to interdomain interactions. Recent experiments on tandems of I27–I28 repeats showed enhanced domain stabilization against applied pulling force, which causes the increase of the average unfolding force from 260 pN (for the tandem of domains I27) to 300 pN (for the tandem of I27–I28 repeats) (20). Similar domain stabilization effect has been reported for the tandem of FnIII domains (21). Also, recent force-ramp AFM measurements on the homogeneous tandems of fibrinogen, performed at a pulling speed of 1 μm/s, revealed that the consecutive unfolding transitions are strongly correlated (A. Brown and J. Weisel, University of Pennsylvania Medical School, private communication, 2008). This behavior is most likely due to interaction between fibrinogen's αC-domains and its central region (22).

These experimental findings demonstrate the importance of the inter- and intramolecular protein-protein interactions and show that current AFM technology can be used to probe these interactions by analyzing correlated (dependent) forced unfolding transitions in protein tandems. In force-ramp AFM measurements on protein tandems, mutual independence between the unfolding transitions can be accessed by applying standard tests for independence, such as the Pearson correlation (23), Spearman rank correlation coefficient (23), or Hoeffding's D statistic- (24,25) based test to the recorded unfolding forces. In the case of force-clamp AFM measurements, however, the observed forced unfolding times are ordered. To assess independence of the parent unfolding times, one would have to use statistical tests designed to detect possible correlations of the unobserved unfolding time data by analyzing the observed ordered unfolding times. Yet such tests do not exist. Standard tests for independence can only be applied to the unobserved parent unfolding times. In this study, we develop statistical tools for assessing 1), independence of the forced unfolding times and 2), equality of their (parent) pdfs from observed ordered time data. We illustrate the use of these tests by analyzing the unfolding times for a model of the homogeneous dimer S2–S2 and the heterogeneous dimer S2–S1 of connected domains S2 and S1.

To model correlated unfolding transitions and interdomain interactions in protein tandems, novel theoretical approaches that go beyond the iid assumption are needed. In Study 1, we introduced an order statistics-based approach to analyze the ordered unfolding transitions in protein tandems (19). The key elements of the order statistics formalism are the cumulative distribution function (cdf) of the r-th order statistic (r = 1, …, n) in a tandem of length n, Φ_r:n(t) ≡ Prob(t_r:n ≤ t), and the corresponding probability density function (pdf), φ_r:n(t) = dΦ_r:n(t)/dt. Because the order statistics cdfs and pdfs, Φ_r:n(t) and φ_r:n(t), depend on the parent cdfs and pdfs, Ψ(t) and ψ (t), order statistics-based theory can be used to infer Ψ(t) and ψ (t) from the ordered time data. In this study, we extend the use of order statistics to analyzing correlated unfolding transitions in model tandems S2–S2 and S2–S1, characterized by dependent and identically distributed (did) and dependent and nonidentically distributed (dnid) unfolding times, respectively. In our test studies, we use single domains S2 and S1, and the dimers S2–S2 and S2–S1 to represent protein tandems of short and long length, respectively. The order statistics-based analysis, presented here, can be performed by using experimental unfolding time data for homogeneous as well as heterogeneous tandems of any length. In AFM experiments on a tandem (D)_N of length, say N = 12, the unfolding data for short (long) tandems can be obtained by grouping together and analyzing separately the unfolding times for tandems of length n = 1–3 (n = 9–12). Because in a typical AFM experiment the cantilever tip randomly picks up a tandem of any length n, 1 ≤ n ≤ N, this can always be done.

The rest of this study is organized as follows. First, we describe Langevin dynamics simulations of the forced unfolding for single domains S2 and S1, and tandems S2–S2 and S2–S1. Second, we model the unfolding time distributions for single domains S2 and S1. The models of forced unfolding for single domains are used to assess the prediction accuracy of the order statistics-based analysis. Third, we perform a preliminary analysis of the forced unfolding times for tandems S2–S2 and S2–S1. Because in computer simulations we can access the parent unfolding times, we use standard tests for independence, based on Spearman rank correlation coefficient and Hoeffding's D statistic, and the quantile-quantile (Q-Q) plots to probe, respectively, the independence of unfolding times and their distributional equality. This allows us to classify the forced unfolding times as iid, inid, did, and dnid random variables (Table 5, Study 1) (19). Next, we use these data to generate ordered time variates, as observed in force-clamp experiments. The ordered unfolding times are then used to assess the performance of proposed tests for independence of the unobserved (parent) unfolding times and equality of their (parent) distributions. Finally, the dependent (did and dnid) unfolding times are used to illustrate the order statistics-based analysis of correlated unfolding transitions in tandems S2–S2 and S2–S1.

METHODS

Langevin dynamics simulations of tandem S2–S2 and S2–S1

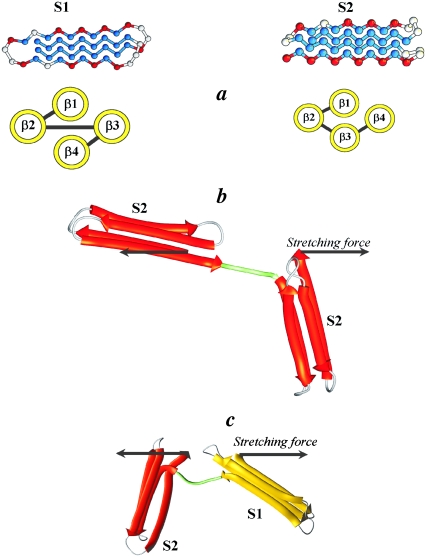
We performed Langevin simulations of forced unfolding using coarse-grained models of the homogeneous dimer S2–S2 and the heterogeneous dimer S2–S1, formed by domains S2 and S1 (Fig. 1) (26,27). The off-lattice C_α-based coarse-grained model of protein tandems serves as a conceptual representation of the wild-type multidomain proteins (27–30).

FIGURE 1.

(a) Model β-barrel proteins S1 (left) and S2 (right), formed by the hydrophobic (in blue), hydrophilic (in red), and neutral Gly residues (in gray). In the native state of S1, the terminal strands β1 and β4 (shown by yellow circles) form a rigid and highly stable native core; the native core of S2 involves the nonterminal strands β2 and β3, and the terminal strand β4 is flexible. (b and c) The homogeneous tandem S2–S2 (b) and the heterogeneous tandem S2–S1 (c) of S2 domain (shown in red) and S1 domain (yellow), connected “head-to-tail” by a flexible linker (shown in green). The linker is composed of five Gly residues. Constant mechanical force, f, is applied to the N-terminal of the first domain S2 and the C-terminal of the second domain S2 (S1) in the tandem S2–S2 (S2–S1). The arrow indicates the direction of applied force.

Tandem construction

The domains S2 and S1 consist of 46 hydrophobic (B), hydrophilic (L), and neutral (N) residues. Each bead is represented by a united atom at the position of the C_α atom (Fig. 1). The distance between C_α carbons is a = 3.8 Å. The tandems S2–S2 and S2–S1 are constructed by connecting domains S2 and S1 “head-to-tail” by a flexible linker of five Gly residues (Fig. 1) (19). The potential energy V = V_BL + V_BA + V_DIH + V_NB includes the bond-length potential V_BL, bond-angle potential V_BA, dihedral angle potential V_DIH, and nonbonded potential V_NB (26,30). The nonbonded distance R dependent interaction between a pair of B residues is given by 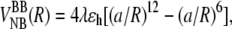where λ accounts for variation in the strength of hydrophobic interactions, and ɛ_h = 1.25 kcal/mol is the average strength of hydrophobic contacts. In the native state, S2 and S1 form four-stranded β-barrels, stabilized by Q₀ = 106 native contacts (6.8 Å cut-off), with the potential energies of −85.5 kcal/mol and −88.0 kcal/mol, respectively. Interdomain interactions are limited to steric repulsion.

Forced unfolding

The forced unfolding kinetics are obtained by integrating the Langevin equations for each residue coordinate x_j, subject to the total potential V_tot = V − fX, i.e., ηdx_j/dt = − ∂V_tot/∂x_j + g_j(t), where η is the friction coefficient and g_j is Gaussian white noise. The force f = fn of magnitude f is applied to C- and N-terminals of the tandem in the direction of the end-to-end vector X (Fig. 1). Numerical integration is performed with a step size δt = 0.05τ_L, where τ_L = (ma²/ɛ_h)^1/2 = 3 ps is the unit of time, and m ≈ 3 × 10⁻²² g is the residue mass. The simulation temperature T_s = 0.69ɛ_h /k_B < T_F ≈ 0.79ɛ_h /k_B, where T_F ≈ 0.79ɛ_h /k_B is the equilibrium folding temperature for S1 and S2, is defined as the temperature at which the average fraction of contacts 〈Q(T_s)〉 ≈ 0.7Q₀. The unfolding time for domain S2 (or S1) is defined as the time at which all contacts are disrupted. Throughout this study, the unfolding times and rates are expressed in terms of the number of integration steps N_tot (t = N_totδt).

Preliminary analysis of the unfolding times for S2–S2 and S2–S1

To prepare the stage for the use of order statistics, we analyze the forced unfolding times for single S2 and S1 domains, and characterize their parent pdfs, ψ_S2(t) and ψ_S1(t). We also analyze the parent unfolding times for first (S2₁) and second (S2₂) domain in tandem S2–S2, and first (S2₁) domain and second (S1₂) domain in tandem S2–S1 for independence and equality of their parent pdfs. The tests used in this section should not be confused with the statistical tests for independence and distributional equality for ordered unfolding times introduced in the following section.

Unfolding times for single domains S2 and S1

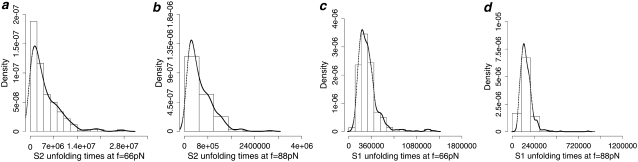
Histograms of the unfolding times for single S2 and S1 domains, obtained at constant force f = 66 pN and f = 88 pN, and corresponding nonparametric density estimates are presented in Fig. 2. A nonparametric density estimate provides a visual assessment of the distribution and fits the density by locally weighting the observations (19,31,32). In force-clamp AFM experiments on a protein tandem of length n, a suitable model for the parent unfolding time pdfs can be obtained by using trial densities for the distribution of the first unfolding times, φ_1:n(t), and fitting φ_1:n(t) to the histograms of the first unfolding times {t_1:n} (see Eqs. 7 and 8 in the next section). Here, as in Study 1, we used the Gamma density to describe the parent unfolding time pdfs for single domains S2 and S1,

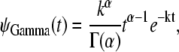(1)

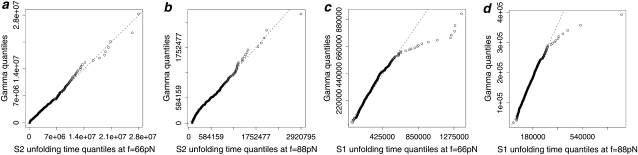
where α and k are the shape parameter and unfolding rate, respectively, and Γ(α) ≡ (α − 1)! (19). The Q-Q plots of the unfolding times for single domains S2 and S1 versus unfolding times for the Gamma distribution (Eq. 1) are displayed in Fig. 3. A Q-Q plot is a graphical technique for determining whether two data sets come from populations with common distribution (19). If the two sets have the same distribution, the points fall along the 45° reference line. Gamma provides a good fit to the unfolding times for S2 and S1 domains. The parameters of the Gamma distribution were computed using the maximum likelihood estimation method described in Study 1 (19). The maximum likelihood estimates of α and k for single S2 and S1 domains, which were used to compute the Gamma quantiles in the Q-Q plots, are reported in Table 1. The difference in the obtained parameter values shows clearly that the unfolding times for single S2 and S1 domains are nonidentically distributed.

FIGURE 2.

Histograms (bars) of the forced unfolding times for single S2 domain (a and b) and single S1 domain (c and d) obtained at constant force f = 66 pN (a and c) and f = 88 pN (b and d). The overlaid curves are the nonparametric density estimate (the bandwidth bw = 0.9 × min(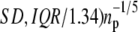 used in the calculations is the default value used in the R software for statistical computing (36), where SD is the standard deviation, and IQR is the interquantile range of the data (32)). In the histograms presented here and in Figs. 4 and 7, the number of bins n_b and the bandwidth bw are estimated as described above. In this figure and in Figs. 3–7, the time t is expressed in units of the number of integration steps N_tot (t = N_tot0.15 ps).

FIGURE 3.

Q-Q plots of the forced unfolding times for single S2 domain (a and b) and S1 domain (c and d), obtained at f = 66 pN (a and c) and f = 88 pN (b and d) versus quantiles of the Gamma density (Eq. (1)). The dashed line is the 45° reference line.

TABLE 1.

Maximum likelihood estimates and 95% standard errors for the dimensionless shape parameter α and unfolding rate k (in units of integration step) for single domains S2 and S1 obtained at f = 66 pN and f = 88 pN

Force, pN	αS2	αS1	kS2	kS1
66	0.98 ± 0.09	4.62 ± 0.18	(2.27 ± 0.26) × 10−7	(1.52 ± 0.06) × 10−5
88	2.02 ± 0.14	7.03 ± 0.23	(3.84 ± 0.31) × 10−6	(4.59 ± 0.16) × 10−5

Unfolding times for tandems S2–S2 and S2–S1

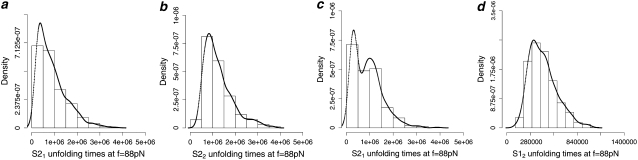
The unfolding time histograms for domains S2 and S1 are shown in Fig. 4. The parent unfolding times for the first S2₁ domain (t₁) and second S2₂ domain (t₂) in tandem S2–S2, and unfolding times for the first S2₁ domain (t₁), and second S1₂ domain (t₂) in tandem S2–S1, were analyzed for independence and equality of their parent distributions.

FIGURE 4.

Histograms (bars) and nonparametric density estimates (curves) of the unfolding times for the first S2₁ domain (a) and second S2₂ domain (b) in tandem S2–S2, and for the first S2₁ domain (c) and second S1₂ domain (d) in tandem S2–S1, obtained at f = 88 pN.

Test for independence of unfolding times

In Study 1, we used the Spearman rank correlation coefficient (23,33), a nonparametric and scale-invariant measure of dependence. This measure detects linear and some nonlinear yet always monotonic relationships between two data sets {t₁} and {t₂}, when the sets either change in the same or in the opposite direction, i.e., when the values {t₁} and {t₂} both increase or decrease, or when the values {t₁} always increase (decrease) while the values {t₂} decrease (increase). Hoeffding's nonparametric test for independence, described in Appendix A (24,25), and its asymptotic equivalent (34) detect all dependence alternatives, including highly nonmonotonic relationships. The values of D range from −0.5 to 1, with larger D(t₁, t₂) values signifying stronger dependence between t₁ and t₂. In statistical data analyses, both tests of independence are typically carried out so that monotonic as well as nonmonotonic associations between two variables can be detected.

The values of D(t₁, t₂) and the Spearman rank correlations for the unfolding times {t₁} and {t₂} obtained at f = 66 pN and f = 88 pN for tandems S2–S2 and S2–S1 are reported in Table 2. The associated p-values for testing independence are given in parentheses. The threshold p-value, which represents the level of tolerance for rejecting the independence hypothesis, was set to 0.01 (in statistical hypothesis testing, the null is rejected if the p-value does not exceed the threshold). At f = 66 pN, both dependence measures conclude that domains S2₁ and S2₂ in tandem S2–S2 and domains S2₁ and S1₂ in tandem S2–S1 unfold independently. In contrast, at f = 88 pN, Hoeffding's test for independence finds the forced unfolding times for the same domains in the tandems S2–S2 and S2–S1 to be dependent. The Spearman rank correlation coefficient test, on the other hand, is not significant at level 0.01 for either tandem and does not detect dependence. Since Hoeffding's test is significant, the dependence between the unfolding times for the two domains in both tandems, obtained at f = 88 pN, is nonmonotonic. This result supports our previous finding (Study 1) that increasing the magnitude of applied force, f, may result in dependent unfolding transitions (19).

TABLE 2.

Preliminary analysis of the forced unfolding times

	f = 66 pN		f = 88 pN
Tandem	Hoeffding's D	Spearman correlation	Hoeffding's D	Spearman correlation
S2–S2	0.0003 (0.25)	−0.06 (0.15)	0.0032 (0.01)	−0.03 (0.59)
S2–S1	−6.08291 × 10−6 (0.37)	−0.05 (0.26)	0.0043 (0.0052)	−0.10 (0.02)

Hoeffding's D statistics and Spearman rank correlation coefficients of the unfolding times for domains S2₁ and S2₂ in tandem S2–S2, and domains S2₁ and S1₂ in tandem S2–S1, obtained at f = 66 pN and f = 88 pN. The numbers in parentheses are the p-values for testing for independence of the two variables.

Test for equality of unfolding time pdfs

Q-Q plots were used for the empirical assessment of the equality of the unfolding time pdfs for domains S2 and S1 in tandems S2–S2 and S2–S1 (Fig. 5). The Q-Q plot for the first S2₁ domain against the second S2₂ domain in tandem S2–S2, obtained at f = 66 pN, shows that almost all data points fall on the reference line, indicating equality of the parent pdfs, i.e., 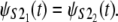A small parallel deviation of the time quantiles from the reference line for the same domains, obtained at increased force f = 88 pN, indicates only approximate distributional equality, i.e., 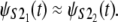Indeed, the unfolding times of the S2₁ domain are consistently shorter than the unfolding times of the S2₂ domain by a small time constant, Δt ≈ 0.4 × 10⁶. This can also be seen by comparing the unfolding time histograms (Fig. 4, a and b). This time difference (Δt) induces the dependence detected by Hoeffding's D statistic. The Q-Q plots for the first S2₁ domain against the second S1₂ domain in tandem S2–S1 strongly indicate lack of equality of the parent pdfs both at f = 66 pN and f = 88 pN, i.e., 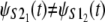(Fig. 5, c and d). This can also be seen from the bimodal shape of the unfolding time density for the S2 domain (Fig. 4 c).

FIGURE 5.

Q-Q plots of the unfolding times for the first domain S2₁ (t₁) versus the second domain S2₂ (t₂) in tandem S2–S2, obtained at f = 66 pN (a) and f = 88 pN (b), and for the first domain S2₁ (t₁) versus the second domain S1₂ (t₂) in tandem S2–S1, obtained at f = 66 pN (c) and f = 88 pN (d).

To summarize this section, we showed that the parent unfolding times for S2 domains in tandem S2–S2 are iid for f = 66 pN and did for f = 88 pN, whereas the parent unfolding times for S2 and S1 domains in tandem S2–S1 are inid for f = 66 pN and dnid for f = 88 pN.

RESULTS

We use simulated unfolding time data for model tandems S2–S2 and S2–S1 to assess the performance of the proposed tests for independence of the (parent) unfolding times and equality of the parent unfolding time pdfs from the ordered time data, t_1:n ≤ t_2:n ≤ … ≤ t_n:n. To generate ordered time variates as observed in force-clamp AFM experiments, the unfolding times {t₁} and {t₂} for domains S2₁ ({t₁}) and S2₂ ({t₂}) in tandem S2–S2, and domains S2₁ ({t₁}) and S1₂ ({t₂}) in tandem S2–S1 were rearranged in increasing time order. That is, t_min < t_max, where t_min = min(t₁, t₂) and t_max = max(t₁, t₂) are the minimum and maximum unfolding times, respectively. The ordered variates from 500 runs for each dimer were grouped into ordered sets of the first {t_min} = {t_1:2}, and second {t_max} = {t_2:2} unfolding times.

Testing equality of the parent unfolding time pdfs by analyzing ordered time data

A simple empirical test for assessing distributional equality of the parent unfolding time pdfs for individual domains in a tandem D₁–D₂– … −D_n can be based on a recurrence relation for order statistics (19). When the forced unfolding times are iid, the pdfs of the r-th and (r + 1)-st unfolding times (order statistics) in a tandem of length n are related to the pdf of the r-th unfolding times in a tandem of length n − 1 via the recurrence relation (34,35)

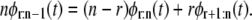(2)

Equation 2 also holds when the unfolding times are “exchangeable”, i.e., when they are identically distributed but could be dependent (did) (34,35), and when the parent unfolding time pdfs are identical in the sense that they have the same shape but may differ in the location of the peak, which quantifies the most probable unfolding time t*. This is the case for tandem S2–S2, at f = 88 pN. Hence, Eq. 2 applies both when the parent unfolding times for domains D_i and D_j are strictly identically distributed, and when the unfolding times for, say, domain D_j are “shifted” from the unfolding times for domain D_i by a time constant Δt = |t_j* − t_i*|.

By applying Eq. 2 recursively, we can obtain the parent unfolding time pdf for a single domain D, ψ (t) ≡ φ_1:1(t), i.e.,

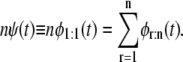(3)

Equation 3 provides a means to infer the parent distribution for a domain in a tandem from the order statistics pdfs φ_r:n, 1 ≤ r ≤ n, when the forced unfolding times are iid or did; that is, regardless of their dependence structure. In particular, Eq. 3 implies that when the unfolding times are identically distributed with common parent pdf ψ (t), then the latter can be obtained by “mixing” all the order statistics pdfs, φ_r:n, r = 1, 2, …, n, with equal weight 1/n, i.e.,

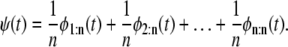(4)

A simple test for equality of the parent unfolding time pdfs for individual domains in a tandem can be constructed as follows. First, the ordered unfolding times, collected at a fixed force, are grouped into two time sets, one for unfolding times for a shorter tandem of length, say n₁ = 1–3, and the other for unfolding times for a longer tandem of length say, n₂ = 9–12. As noted in the introduction, in AFM experiments, the cantilever tip randomly picks up a tandem of any length, so that this separation is implementable in practice. The corresponding pdfs, 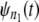and 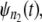are estimated by using Eq. 4. 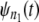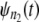Next, and are compared via a Q-Q plot. If the time quantiles for and 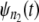fall close (far) to (from) the reference line, then the parent pdfs for individual domains in tandems of length n₁ and n₂ are identically (nonidentically) distributed. The difference between the time quantiles for 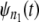and 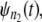if any, can be used as a signature of the distributional inequality of the parent pdfs.

Test for equality of parent pdfs

The above arguments lead us to the following computational algorithm:

• Step 1. Collect the forced unfolding times, for a tandem of shorter length n₁.

• Step 2. Generate a random number U in the interval (0, 1).

• Step 3. If U ∈ (0, 1/n₁), randomly select a point from the first order statistic, 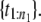If U ∈ (1/n₁, 2/n₁), randomly select a point from the second order statistic, 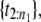and so on.

• Step 4. Repeat Steps 2 and 3 M times to obtain a sample of size M from 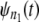(Eq. 4).

• Step 5. Collect the forced unfolding times, for a tandem of longer length n₂, and repeat Steps 2–4 to obtain a sample of size M from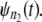

• Step 6. Draw the Q-Q plot for the time quantiles of 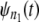against the time quantiles of 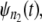and estimate the distance of the time quantiles from the reference line.

If the unfolding time quantiles fall close to the reference line, i.e., they are either aligned with or are parallel and close to the reference line, then Eq. 4 is satisfied and the parent unfolding times for individual domains (Ds) in a tandem D₁–D₂– … −D_n are identically distributed, regardless of whether they are dependent. Significant nonlinear divergence from the reference line would indicate their distributional inequality.

Application of the algorithm to the ordered unfolding times of S2–S2 and S2–S1

We tested the performance of the proposed algorithm by using ordered unfolding time data for tandems S2–S2 and S2–S1. For two-domain tandems, Eq. 4 becomes

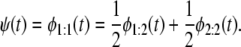(5)

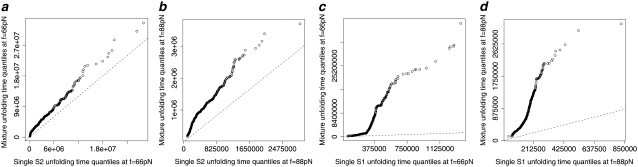
The Q-Q plots of the time quantiles for single domain S2 versus the quantiles for tandem S2–S2, sampled from the mixture of the order statistics pdfs (Eq. 5), are displayed in Fig. 6. At f = 66 pN, the unfolding time quantiles run almost parallel to the reference line, indicating an approximate distributional equality (up to the time shift Δt) of the parent unfolding times for the first S2₁ domain and the second S2₂ domain, i.e., 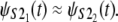The time shift at the median (50% quantile) from the reference line is ∼Δt ≈ 3 × 10⁶ integration steps (Fig. 7 a). At f = 88 pN, the time quantiles show a shorter time shift, Δt ≈ 0.5 × 10⁶ integration steps, still running almost parallel to the reference line, which indicates an approximate distributional equality (up to Δt) of the parent unfolding times for S2 domains in S2–S2, i.e., 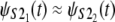(Fig. 6 b).

FIGURE 6.

(a and b) Q-Q plots of the unfolding times for single S2 domain versus the unfolding times for tandem S2–S2, generated by “mixing” the first and second order statistics pdfs via 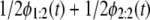(Eq. 5) for the ordered unfolding times t_1:2 and t_2:2, obtained at f = 66 pN (a) and f = 88 pN (b). (c and d) Q-Q plots of the unfolding times for single S1 domain versus the unfolding times for tandem S2–S1, generated by mixing the first and second order statistics pdfs for t_1:2 and t_2:2, obtained at f = 66 pN (c) and f = 88 pN (d).

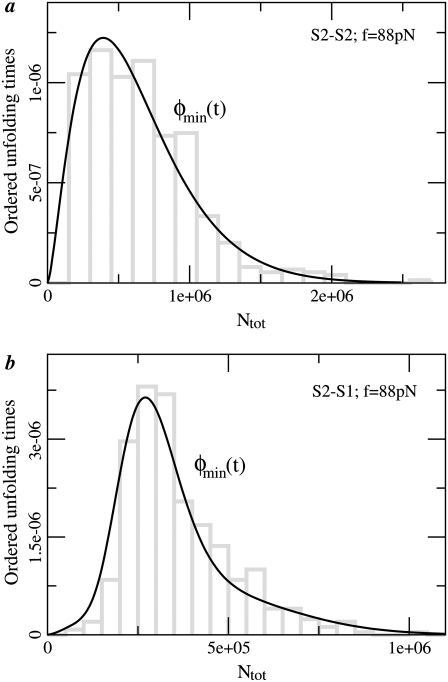
FIGURE 7.

Probability density functions for the first order (min) statistic, t_1:2 = t_min, for tandems S2–S2 (a) and S2–S1 (b), obtained at f = 88 pN. The histograms (bars) of t_min are superimposed with the theoretical pdfs, φ_min(t) ≡ φ_1:2(t) (Eqs. 7 and 8). The parameter values, obtained from the fit, are given in Table 4.

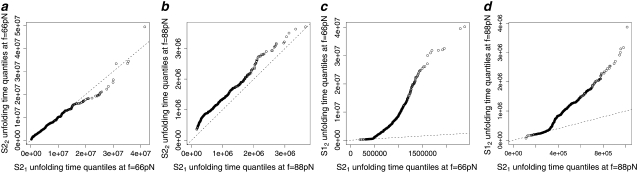
The observed time shift Δt is due to the tension drop in the tandem chain, which occurs after the first unfolding transition in one of the two domains at time t = t_1:2. The resulting chain elongation lowers the force-induced tension and the instantaneous force to a lower value, f′ < f = 66 pN, and hence it takes time Δt to ramp it up back to the initial level (f′ → f). As a result, the time quantiles obtained for the longer tandem (S2–S2) are above the reference line, indicating prolonged unfolding for S2 domains in the tandem compared to a single S2 domain. Although in our case study we used a single S2 domain and the dimer S2–S2 to represent, respectively, the tandems of shorter and longer length, this algorithm can be used to analyze protein tandems of any length n₁ and n₂ > n₁. The Q-Q plots of the time quantiles for single domain S1 versus the quantiles for tandem S2–S1, sampled from the mixture of the order statistics pdfs (Eq. 5), are also displayed in Fig. 6 for comparison. We observe much greater nonparallel divergence from the reference line with a larger time shift, Δt ≈ 8 × 10⁶ integration steps (f = 66 pN) and Δt ≈ 1 × 10⁶ integration steps (f = 88 pN), at the 50% quantile, compared with tandem S2–S2. Such strong nonlinear divergence is indicative of the fact that the forced unfolding times for domains S2 and S1 in tandem S2–S1 are differently distributed both at f = 66 pN and f = 88 pN.

The results of the proposed test for distributional equality of the parent unfolding time pdfs, applied to the ordered unfolding times, agree with the results of preliminary data analysis, and confirm that the parent unfolding times, obtained at f = 66 pN and f = 88 pN, are identically distributed for tandem S2–S2 and nonidentically distributed for tandem S2–S1. The proposed algorithm can be used in statistical analyses of unfolding data available from force-clamp AFM measurements. In addition, for homogeneous tandems, the difference between the unfolding time quantiles for tandems of short and long length, parameterized by Δt, can be used to estimate the timescale of force-induced tension propagation along the tandem chain, τ_f. Indeed, there are n − 1 intervals of dropped tension of duration Δt in a tandem of length n. 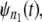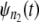When the pdfs for tandems of different length n₁ ≠ n₂, and are compared via Q-Q plots, τ_f can be estimated as τ_f ≈ Δt/|n₂ − n₁|.

Testing independence of the parent unfolding times by analyzing ordered time data

In this section, we propose a permutation test for iid versus did parent unfolding times and an overlap fraction test for inid versus dnid unfolding times using the ordered unfolding times for tandems S2–S2 and S2–S1.

Permutation test for iid versus did unfolding times

Let us assume that we record n ordered unfolding times sampled from the joint distribution Ψ(t₁, …, t_n) and joint pdf ψ (t₁, …, t_n), where as before t_i denotes the unfolding time of the ith domain (i = 1, …, n) in a tandem of length n. Suppose we observe the unfolding time order statistics, t_1:n ≤ t_2:n ≤ … ≤ t_n:n, sampled from the joint distribution Ψ(t₁, …, t_n). We want to infer if the (unobserved) parent data, t₁, t₂, …, t_n are uncorrelated from their order statistics, t_1:n ≤ t_2:n ≤ … ≤ t_n:n. Suppose now that the parent unfolding time data are indeed iid; that is, Ψ(T₁, …, T_n) = Ψ(T₁ ≤ t₁)Ψ(T₁ ≤ t₂)…Ψ(T₁ ≤ t_n), where Ψ(t) is their common cdf, and ψ (t₁, …, t_n) = ψ (t₁)ψ (t₂)…ψ (t_n), where ψ (t) = dΨ(t)/dt is their common pdf. This factorization implies that if the parent data were iid, then the order statistics, t_1:n ≤ t_2:n ≤ … ≤ t_n:n, could have had resulted from any permutation of the original data with equal probability. For example, the parent sample t₁, t₂, …, t_n could have resulted in t_1:n ≤ t_2:n ≤ … ≤ t_n:n with equal probability as the sample t₁, t₃, …, t_n or the sample t_n, t₃, …, t₁, and so on. The order in which the n-tuple (t₁, …, t_n) is arranged is irrelevant because all n! permutations of the n parent data points are equally likely to be observed, since they are independent realizations of the same distribution. Let us generalize the above arguments to M measurements. Suppose M ordered n-tuples, 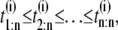are observed, i = 1, …, M. If the parent unfolding time data were iid, the unfolding time order statistics obtained in the ith experiment, 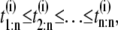could have had resulted from any permutation of the parent data with equal probability. For each i = 1, …, M, all n! permutations of the n data points are equally likely to be the parent sample of the observed order statistics. This leads to the following algorithm for testing pairwise independence:

• Step 1. For each experiment i = 1, …, M, randomly permute the n-tuples of the recorded unfolding time order statistics and let be the b-th permuted order statistics, where b is a permutation number. Store the result in matrix 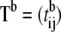of dimension M × n, where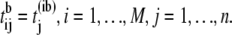

• Step 2. Repeat Step 1 B times, i.e., b = 1, …, B to obtain matrices T¹, …, T^B.

• Step 3. For b = 1, …, B, carry out 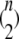pairwise tests for independence of all pairs of the n columns of T^b at a fixed significance level. Compute and store the fraction of rejections of the null hypothesis of independence.

In Step 3, both Spearman's rank correlation and Hoeffding's D statistic should be used so that most types of dependence are checked for (23–25). Both measures are based on test statistics with known asymptotic distributions, which allow the computation of the p-values for testing independence. If the parent unfolding time data are independent, the test for independence in Step 3 will not be significant. An illustration of the algorithm is given in Appendix B.

Application of the algorithm to the ordered unfolding times of S2–S2

Table 3 summarizes the results of the application of the permutation algorithm to the ordered unfolding times for tandem S2–S2. The entries are the fractions of p-values >0.05 over 500 replicates (B = 500). We used a 5% cutoff, i.e., we assumed that if the obtained p-value ≤ 0.05, then there exists statistically significant dependence among the parent unfolding times for domains S2. At f = 66 pN, Hoeffding's test rejected independence only 100 − 99.6 = 0.4% of the time, thus providing strong support for the independence of unfolding times for the first S2₁ domain (t₁) and second S2₂ domain (t₂) in tandem S2–S2. The Spearman rank correlation coefficient also detected independence 100% of the time (Table 3). At f = 88 pN, the fraction of the p-values exceeding 0.05 for the Hoeffding's test is 0. That is, all 500 p-values for testing independence were highly significant, i.e., below the 5% cutoff, providing strong evidence for lack of independence between the parent unfolding times for the first S2₁ domains (t₁) and the second S2₂ domain (t₁) in tandem S2–S2. Thus, the permutation test for independence, applied to iid and did unfolding times for tandem S2–S2, recovers the results of the preliminary data analysis.

TABLE 3.

Results of the permutation test for independence of the parent unfolding times for domains S2₁ (t₁) and S2₂ (t₂) in tandem S2–S2

f = 66 pN		f = 88 pN
Test	% of p-values >0.05	Test	% of p-values >0.05
Hoeffding's D	0.996	Hoeffding's D	0
Spearman correlation	1	Spearman correlation	0

An empirical test for inid versus dnid unfolding times

An empirical approach for deducing independence of the parent inid and dnid unfolding times can be based on the overlap fraction F(r, r + 1;n), r = 1, …, n − 1, defined as the fraction of values shared by the r-th order statistic, t_r:n, and the (r + 1)-st order statistic, t_r+1:n, in an heterogeneous tandem (D₁–D₂)_n/2 of length n. That is,

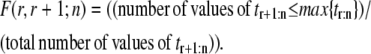(6)

If F(r, r + 1;n) is smaller than a threshold value F*, then the unfolding times for, say, domain D₁, differ from the unfolding times of domain D₂ in a consistent fashion. Since domains D₁ and D₂ have different (parent) pdfs, i.e., this would mean that unfolding of D₁ domains does not affect unfolding of D₂ domains, and that these domains unravel independently. For example, the forced unfolding of domain S1 occurs on a faster timescale compared to the unfolding of the S2 domain (Fig. 5). Hence, the first unfolding transitions (t_1:2) occur more frequently for domain S1 as compared to the S2 domain, and the consecutive unfolding transitions t_1:2 and t_2:2 are separated in time (uncorrelated). On the other hand, large values of F(r, r + 1;n), i.e., F(r, r + 1;n) > F* would indicate mixing among the unfolding times for domains D₁ and D₂ and signify their dependence.

Application of the overlap fraction test to the ordered unfolding times of S2–S1

We applied the overlap fraction test to assess independence of the parent unfolding times for S2₁ domain (t₁) and S1₂ domain (t₂) in tandem S2–S1. We set the threshold value for the overlap fraction to F* = 50%. For a heterogeneous tandem of length n = 2, the heuristic argument that led to this choice follows along these lines: if there were perfect mixing, that is the first order statistic originated with equal probability from both domains, then the ordered pair 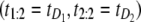would be observed 50% of the time, and the ordered pair 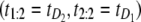would be observed 50% of the time as well, where 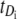denotes the unfolding time of domain D_i, i = 1, 2. This would lead to no separation between the values of the two order statistics (they would fall in the same range) and the overlap fraction would be close to one. Lack of mixing would mean that, say, the pair 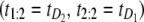would be observed nearly always and the complement pair 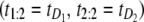would be observed almost never, so that the overlap fraction would be close to zero. Of course, because of sampling variability, the overlap fraction would never be exactly equal to zero or one but rather close to either value. The closeness would depend on the magnitude of correlations and the size of the sample. The cutoff of 50% is simply the midpoint of the unit interval. In principle, one can estimate the cutoff much more accurately using resampling methods; here we simply use this subjective cutoff. For this choice, values of F(1, 2;2) < 50% would imply that one of the two domains S2 and S1 unfolds on a faster timescale, compared to the other domain. In the opposite case, i.e., when F(1, 2;n) > 50%, we would conclude that S2 and S1 domains unfold on a similar timescale and that the unfolding times are correlated. We found that at f = 66 pN, F(1, 2;n) = 24% < 50%, and at f = 88 pN, F(1, 2;n) = 61% > 50%. Hence, we recover the results of the preliminary analysis for tandem S2–S1, namely that the parent unfolding times for S2 and S1 domains in the tandem are independent at f = 66 pN, but dependent at f = 88 pN.

For tandems of length larger than two, if the tandem is fully heterogeneous, i.e., all its domains are distinct, perfect mixing is equivalent to all permutations of the n-tuple (t_1:n, …, t_n:n) being equally likely, and the overlap fraction of any two order statistics would be close to one. In particular, the overlap fraction of any two consecutive order statistics, F(r, r + 1;n), would also be close to one. In the other extreme of no mixing, the overlap fraction would be close to zero. Thus, even when the tandem consists of more than two domains, the midpoint cutoff of 50% can also be used. To conclude independence, all overlap fractions F(r, r + 1;n), r = 1, …, n − 1, must be smaller than the cutoff. We plan to examine the more general case of tandems composed of a mix of the same and distinct domains in a separate study.

Order statistics-based analysis of did and dnid unfolding times

The application of the test for distributional equality to ordered unfolding times obtained at f = 88 pN revealed a pronounced time shift Δt ≈ 0.5 × 10⁶ integration steps for tandem S2–S2 and Δt ≈ 1 × 10⁶ integration steps for tandem S2–S1 (Fig. 6). As we argued before, the origin of Δt is a tension drop in the tandem chain, which accompanies each unfolding transition. As a result, every next unfolding transition (t_2:n, t_3:n, …, t_n:n) after the first transition (t_1:n) in a tandem of length n is delayed by Δt. This builds up correlations (dependence). However, the dependence structure, defined by the time shift Δt, is trivial and affects only the second (t_2:n), third (t_3:n), etc., unfolding transition, but does not affect the first transition (t_1:n). Therefore, for correlated unfolding events characterized by did and dnid unfolding times with such trivial dependence, the first order statistic t_1:n can be described by using the order statistics for iid and inid unfolding times (Study 1) (19).

To illustrate our approach, here we use previously generated ordered time variates, i.e., the first unfolding times, {t_min} = {t_1:2}, and second unfolding times, {t_max} = {t_2:2}, for tandems S2–S2 and S2–S1 of length n = 2, to analyze did and dnid unfolding times for these tandems. Clearly, this approach can be generalized to a homogeneous ((D)_n) and heterogeneous tandem ((D₁–D₂)_n/2) of any length n. The first order statistics pdfs, φ_1:2(t), for tandems S2–S2 and S2–S1 are given by

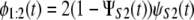(7)

and

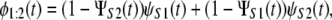(8)

respectively, where Ψ_S2(t) (ψ_S2(t)) and Ψ_S1(t) (ψ_S1(t)) represent the cdfs (pdfs) for domains S2 and S1 (19). To model φ_1:2(t), we used the Gamma density (Eq. 1) with shape parameter α and unfolding rate k, which determine the most probable unfolding time, t* = (α − 1)/k, and the unfolding timescale τ = Γ(α + 1)/(Γ(α)k) for protein domains (see below). We used Eqs. 7 and 8 to fit the theoretical pdf for the first (min) order statistics, φ_min(t) = φ_1:2(t), to the histograms of the first unfolding time, t_min = t_1:2, for tandems S2–S2 and S2–S1, obtained at f = 88 pN. The results of the fit are displayed in Fig. 7, and the obtained values of the model parameters are summarized in Table 4. In general, these agree with the maximum likelihood estimations of the same quantities for single domains S2 and S1 (Table 1). However, the values of α are slightly longer and the values of k are somewhat shorter for tandems S2–S2 and S2–S1, compared to the same quantities for single S2 and S1 domains. The same effect was observed in our previous study of forced unfolding in trimers S2–S2–S2 and S2–S1–S2 (Study 1) (19).

TABLE 4.

Numerical values of the shape parameter, α, and unfolding rate, k, (in units of integration steps) for domains S2₁ and S2₂ in tandem S2–S2, and domains S2₁ and S1₂ in tandem S2–S1

	Parameters
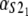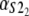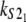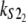S2–S2	2.5	2.6	2.8 × 10−6	2.9 × 10−6
	Parameters
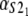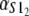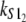S2–S1	2.6	9.4	2.9 × 10−6	3.3 × 10−5

Values are obtained from the fit of the first order (min) statistics pdf, φ_1:2(t) = φ_min(t) to the histograms of the ordered unfolding times, t_1:2, obtained at f = 88 pN (Fig. 7).

The increased (decreased) values of α (k), inferred from the order statistics pdf φ_1:2(t) for domains S2 and S1 in tandems S2–S2 and S2–S1 are due to the presence of a short linker, which tends to prolong the forced unfolding times of protein domains in tandems. We estimated the effect of linkers on the unfolding timescale for domains S2 in tandem S2–S2 by taking the difference between the average unfolding times 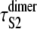for domain S2 in tandem S2–S2 and the average unfolding time τ_S2 for single S2 domain, i.e.,

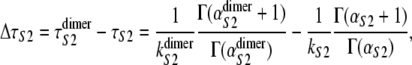(9)

where the values of k_S2 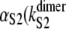and and 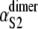) were taken from Table 1 (Table 4). Applying Eq. 9 yields Δτ_S2 ≈ 8.3 ns. Although for the models of protein dimers connected by a short linker of five Gly residues this time is negligible compared to the average unfolding time of S2 domain in the dimer 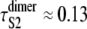μs and for a single S2 domain τ_S2 ≈ 0.08 μs, the effect of linkers may become more pronounced in long protein tandems, especially at a low force and/or for longer linkers. In force-clamp AFM experiments on a protein tandem of length n, the influence of linkers on the unfolding kinetics can be estimated by comparing the average first unfolding time (first order statistics) for a linker of a shorter length l₁, τ_1:n(l₁), and a longer length l₂ > l₁, τ_1:n(l₂). The ratio (τ_1:n(l₂) − τ_1:n(l₁))/(l₂ − l₁) can then be used as an estimate for the unfolding time delay per unit length of the linker.

Let us now calculate the error in the estimates of the shape parameter, α, and unfolding rate, k, we would make if we were using the iid assumption in the analysis of did unfolding times for tandem S2–S2 obtained at f = 88 pN. When the unfolding times are iid, the parent unfolding time pdf, ψ(t), is obtained by pulling all unfolding times into a single histogram, i.e., 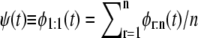(Eq. 6 in Study 1) (19). For n = 2, ψ(t) = φ_1:2(t)/2 + φ_2:2(t)/2. By fitting the Gamma density (Eq. 1) to the histogram of combined first and second unfolding times (t_1:2 and t_2:2), we obtain α_S2 = 2.4 and k_S2 = 2.2 × 10⁶. The relative difference in the shape parameter α_S2 and the unfolding rate k_S2 between the estimates, obtained by using order statistics (α_S2 = 2.55, k_S2 = 2.85 × 10⁻⁶ (Table 4)) and by using the iid assumption, is small, ∼6% for α_S2, but fairly large, ≈23%, for k_S2. This comparison indicates that employing the iid assumption when the data are not iid may result in substantial estimation error of the forced unfolding rate.

DISCUSSION AND CONCLUSION

In our previous work (Study 1) (19), we proposed what to our knowledge is a new theory for describing the forced unfolding transitions in wild-type protein tandems and engineered polyproteins, available from force-clamp AFM experiments. The theory is inspired by the experimental AFM setup, in which only the ordered, i.e., first, second, etc., unfolding times in a tandem D₁–D₂– … −D_n of length n are recorded. Given the stochastic nature of unfolding, it is not possible to tell which domain D_i (i = 1, 2, …, n) has unfolded at any given time, t_1:n, t_2:n, …, t_n:n. Order statistics overcomes this difficulty by analyzing ordered variates, and because the distributions of ordered unfolding times, φ_1:n, φ_2:n, …, φ_n:n, depend on the parent distributions for protein domains, 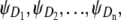the order statistics-based theory can be used to infer the parent pdfs (ψ) from the order statistics pdfs (φ).

We showed in Study 1 (19) that the iid assumption, that the (parent) unfolding times are independent (uncorrelated) and identically distributed (iid), may or may not hold depending on the tandem composition, the presence of interdomain interactions, and the magnitude of applied force. For example, in the heterogeneous tandems (D₁–D₂)_n the unfolding times of nonidentical domains D₁ and D₂ are expected to be nonidentically distributed. Also, the domain stabilization effect, observed in the heterogeneous tandems of I27–I28 repeats of titin, in tandems of FnIII domains (20,21), and in the homogeneous tandems of fibrinogen, makes the forced unfolding transitions strongly correlated. We showed that in tandems with no interdomain interactions, such as the model trimers S2–S2–S2 and S2–S1–S2 (Study 1, (19)) and dimers S2–S2 and S2–S1, analyzed here, the dynamic competition between tension propagation along the tandem chain and forced unfolding may couple the consecutive unfolding transitions at an elevated force level (f = 88 pN). As we argued in Study 1, in force-clamp AFM experiments on protein tandems, the forced unfolding transitions can be characterized by four different types of unfolding times, namely iid, inid, did, or dnid unfolding times (Table 5 in Study 1) (19). Only when the parent unfolding times are iid, which is not known a priori, can conventional unfolding data analyses, in which the unfolding times are pooled together into a single histogram, be used. However, when the parent unfolding times are correlated and/or nonidentically distributed, i.e., when the unfolding data are did, inid, or dnid, this approach is inappropriate. To illustrate the latter, we showed that the use of iid assumption in analyzing dependent unfolding times results in large estimation errors for the forced unfolding rate.

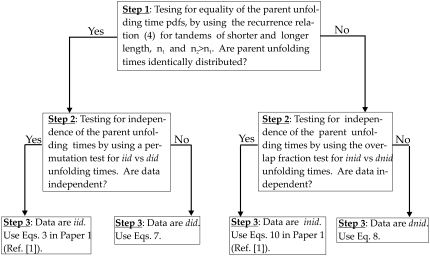
To take advantage of the proposed formalism, the unfolding times must be first classified as iid or inid or did or dnid unfolding times. In this study, we developed statistical tests for assessing the independence of parent unfolding times and their distributional equality. These tests allow one to gain information on the unobserved (parent) unfolding times for individual domains by analyzing the observed ordered unfolding times. The tests can be used in statistical analysis of unfolding data available from force-clamp AFM measurements to assess the validity of the iid assumption and to classify the forced unfolding transitions. We assessed the performance of these tests against the results of computer simulations of forced unfolding for the model dimers S2–S2 and S2–S1. We recovered the results of preliminary analysis, namely that the parent unfolding times for the homogeneous dimer S2–S2 are iid at f = 66 pN and did at f = 88 pN, whereas the parent unfolding times for the heterogeneous dimer S2–S1 are inid at f = 66 pN and dnid at f = 88 pN, which validates the order statistics-based theory. Although in our studies we employed the dimers (n₂ = 2) and single domains (n₁ = 1) to represent protein tandems of longer and shorter length, the tests can be used to assess the validity of the iid assumption and to classify the forced unfolding transitions for tandems of arbitrary lengths n₁ and n₂ > n₁. The monomers and dimers serve as prototypes for tandems of short and long lengths as observed in force-clamp AFM probes on a protein tandem, (D)_N, where unfolding data are available for tandems of different length, 1 < n < N. For the convenience of the reader, in Fig. 8 we outline the main steps for testing the distributional equality of the parent unfolding times and their mutual independence. We also give reference to the relevant Eqs. 3 and 10 presented in Study 1 (19), and Eqs. 7 and 8 in this study, which can be used to model the parent unfolding time distributions.

FIGURE 8.

Flowchart for characterization (Steps 1 and 2) and modeling (Step 3) of the forced unfolding times for a protein tandem.

In tandems formed by the noninteracting domains, such as domains S2 and S1 in dimers S2–S2 and S2–S1, the dependence among the consecutive unfolding transitions can be induced by the dynamic competition between the force-induced tension propagation along the tandem chain and the forced unfolding kinetics. It is likely that the dynamic coupling between tension propagation and unfolding kinetics occurs in wild-type tandems and engineered polyproteins as well. As we showed in this study, in such a case the dependence structure between the consecutive unfolding transitions is rather trivial, namely that every next unfolding transition after the first one in a tandem of length n, i.e., the second (t_2:n), third (t_3:n), etc., are delayed by constant time Δt of dropped tension. The test for distributional equality can be used to estimate the timescale for tension propagation, τ_f. This can be done, e.g., by comparing the parent unfolding time pdfs, 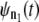and 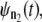generated by using recurrence relation (3) for tandems of different length n₁ and n₂ > n₁ via a Q-Q plot. Specifically, τ_f can be estimated from the time shift, Δt, as τ_f ≈ Δt/(n₂ − n₁). For the tandem S2–S2, we found that τ_f ≈ 0.5 μs for f = 66 pN and τ_f ≈ 0.07 μs for f = 88 pN. Hence, a moderate 33% change in applied force shifts τ_f by an order of magnitude.

We showed that in protein tandems with no interdomain interaction, yet characterized by the correlated unfolding transitions with the constant time shift, the first unfolding events (t_1:n) are unaffected by the tension drop. Because of this, the pdf of the first order statistic φ_1:n(t), can be still described by the order statistics for independent random variables (iid and inid, Study 1 (19)). To illustrate this point, we modeled φ_1:2(t), for tandems S2–S2 and S2–S1 by using Eqs. 3 and 10 of Study 1. The shape parameter, α, and unfolding rate, k, obtained from the fit of φ_1:2(t) to the histograms of the first unfolding times (t_1:2) for tandems S2–S2 and S2–S1 (Table 4) agree with the same quantities obtained for single domains S2 and S1 (Table 1), thus validating our theory. We also showed that due to the presence of flexible linkers, the unfolding times for domains S2 and S1 in the model tandems S2–S2 and S2–S1 are slightly longer, as compared to the unfolding times for single S2 and S1 domains. This result corroborates our previous findings for longer tandems S2–S2–S2 and S2–S1–S2 (Study 1) (19). In wild-type protein tandems, the tension drop in the tandem chain and the presence of flexible linkers could slow down the protein unfolding kinetics, especially for large proteins and/or long linkers at a low stretching force. Here, we showed how the order statistics-based approach can be used to access the dynamics of tension propagation in the tandem chain and to estimate the effect of linkers.

The advantage of the order statistics-based approach is that it can be used to describe correlated as well as uncorrelated unfolding transitions in both homogeneous tandems (D)_n of identical repeats (Ds) and heterogeneous tandems D₁–D₂– … −D_n formed by nonidentical domains (D₁, D₂, …, D_n). Hence, the proposed formalism offers a unified framework for analyzing the forced unfolding transitions in protein tandems and polyproteins probed in force-clamp AFM experiments. Recent AFM probes on tandems of immunoglobulin I27–I28 repeats (20), heterogeneous tandem of FnIII domains (21), and homogeneous tandems of fibrinogen domains (22) show enhanced domain stabilization possibly due to intra- and/or interdomain interactions. In these tandems, the unfolding transitions are strongly correlated and the dependence structure is most likely nonmonotonic. Development of the order statistics-based theory for analyzing intra- and interdomain interactions in protein tandems is under way.

APPENDIX A: HOEFFDING'S D STATISTIC

Hoeffding's D statistic is a measure of the distance between the joint cdf of the two variables, Ψ(t₁, t₂), and the product of their marginal cdfs, Ψ₁(t₁)Ψ₂(t₂). When t₁ and t₂ are independent, Ψ(t₁, t₂) = Ψ₁(t₁)Ψ₂(t₂). In practice, the test is implemented as follows. Let (x₁, y₁), …, (x_n, y_n) be a random sample from the joint pdf f (x, y), n ≥ 5. To test the hypothesis that X is independent of Y, let r_i denote the rank of x_i in the sample x₁, …, x_n, let s_i be the rank of y_i in the sample y₁, …, n, and let c_i denote the number of sample pairs (x_a, y_a) for which both x_a < x_i and y_a < y_i. That is,

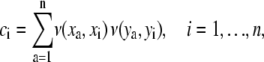where ν(a, b) = 1 if a < b; 0 otherwise. Hoeffding's D statistic is defined by

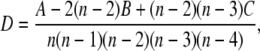(A1)

where 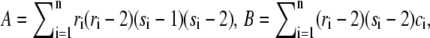and 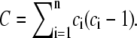If D ≥ d(α, n), X and Y are found to be statistically significantly dependent at level β. The critical values of d(α, n) can be obtained from Table A.25 in Hollander and Wolfe (25). In the free access statistical software R (36), the package Hmisc computes the test statistic and associated p-values for testing that two variables are independent.

APPENDIX B: ILLUSTRATION OF THE PERMUTATION TEST

Suppose we collect unfolding time data from a protein tandem of size n = 3 and repeat the experiment two times (M = 2). Suppose that the observed values of the first sample are 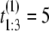μs, 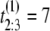μs, and 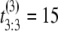μs. If the unfolding times were iid, the observed ordered times could have had originated from any of the following six observations with equal probability 1/6: (t₁ = 5 μs, t₂ = 7 μs, t₃ = 15 μs), or (t₁ = 7 μs, t₂ = 5 μs, t₃ = 15 μs), or (t₁ = 7 μs, t₂ = 15 μs, t₃ = 5 μs), or (t₁ = 15 μs, t₂ = 7 μs, t₃ = 5 μs), or (t₁ = 15 μs, t₂ = 5 μs, t₃ = 7 μs), or (t₁ = 5 μs, t₂ = 15 μs, t₃ = 7 μs). Suppose now that the observed ordered unfolding times of the second sample are 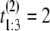μs, 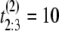μs and 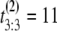μs. Similarly, they could have had originated from any of the following six observations with equal probability 1/6: (t₁ = 2 μs, t₂ = 10 μs, t₃ = 11 μs), or (t₁ = 10 μs, t₂ = 2 μs, t₃ = 11 μs), or (t₁ = 10 μs, t₂ = 11 μs, t₃ = 2 μs), or (t₁ = 11 μs, t₂ = 10 μs, t₃ = 2 μs), or (t₁ = 11 μs, t₂ = 2 μs, t₃ = 10 μs), or (t₁ = 2 μs, t₂ = 11 μs, t₃ = 10 μs). The permutation algorithm, applied to this example, would involve the following steps:

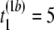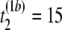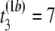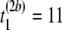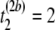• Step 1. Suppose the first permutation (b = 1) of the first and second samples resulted in the following observations, ( μs, μs, μs), and ( μs, μs, 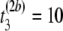μs), where b is the permutation number. Store the result in matrix T^b = T¹ of order M × n = 2 × 3 = 6,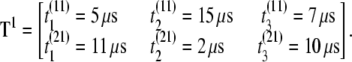

  

• Step 2. Repeat Step 1 B times, i.e., b = 1, …, B, to obtain matrices T¹, …, T^B.

• Step 3. For b = 1, …, B, carry out 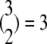pairwise tests for independence of all pairs of the three columns of matrix T^b at a fixed level β. For b = 1, compute Hoeffding's D statistic and Spearman's rank correlation for the unfolding time pairs (5 μs, 15 μs) and (15 μs, 2 μs), (5 μs, 15 μs) and (5 μs, 11 μs), and (15 μs, 2μs) and (5 μs, 11 μs), and record the p-values of the three tests for independence.