Paxillin Dynamics Measured during Adhesion Assembly and Disassembly by Correlation Spectroscopy

Abstract

Paxillin is an adaptor molecule involved in the assembly of focal adhesions. Using different fluorescence fluctuation approaches, we established that paxillin-EGFP is dynamic on many timescales within the cell, ranging from milliseconds to seconds. In the cytoplasmic regions, far from adhesions, paxillin is uniformly distributed and freely diffusing as a monomer, as determined by single-point fluctuation correlation spectroscopy and photon-counting histogram analysis. Near adhesions, paxillin dynamics are reduced drastically, presumably due to binding to protein partners within the adhesions. The photon-counting histogram analysis of the fluctuation amplitudes reveals that this binding equilibrium in new or assembling adhesions is due to paxillin monomers binding to quasi-immobile structures, whereas in disassembling adhesions or regions of adhesions, the equilibrium is due to exchange of large aggregates. Scanning fluctuation correlation spectroscopy and raster-scan image correlation spectroscopy analysis of laser confocal images show that the environments within adhesions are heterogeneous. Relatively large adhesions appear to slide transversally due to a treadmilling mechanism through the addition of monomeric paxillin at one side and removal of relatively large aggregates of proteins from the retracting edge. Total internal reflection microscopy performed with a fast acquisition EM-CCD camera completes the overall dynamic picture and adds details of the heterogeneous dynamics across single adhesions and simultaneous bursts of activity at many adhesions across the cell.

INTRODUCTION

The formation and disassembly of adhesions is central to cell migration. Adhesions form near the leading edge and stabilize the extending protrusion, form connections with the actin cytoskeleton to provide traction, and initiate a plethora of signals, including those that regulate migration-related processes (1,2). Some of these initial adhesions turn over rapidly in consort with the extension of the leading edge; others stabilize and mature into larger adhesions (3–5). In rapidly migrating cells, the rapid turnover of small adhesions in protrusions is highly prominent, whereas less motile cells are populated by larger, more stable adhesions (6). Adhesions also disassemble at the rear of migrating cells during tail retraction (1,7).

Although significant progress has been made in elucidating the signals that regulate adhesion dynamics, the mechanisms by which these signals affect the adhesions and control their assembly, maturation, and disassembly are not well understood. It appears that adhesion assembly is at least partially regulated and sequential and thus can result in a large number of different adhesion sizes and compositions. The adhesions in highly motile cells, for example, tend to be small, and in some cases, they are not readily visualized by conventional light microscopy (6). In contrast, adhesions in less motile cells are heterogeneous; smaller adhesions reside near the leading edge, and larger adhesions are more peripheral and at the rear of the cell (6). The stability and maturation of adhesions are regulated by a complex signaling network that includes kinases like Src, FAK, PAK, and Erk, adapters like paxillin, and regulatory nodes that include Rho-family GTPases, like Rac and Rho. Effectors include myosin II for inducing tension, calpain to cleave talin and other adhesion components, and phosphorylation events that alter the affinities of different adhesion components (8).

The assembly process is thought to begin with receptor ligation and a talin-induced increase in integrin activation (affinity) and/or the formation of small, submicroscopic clusters of adhesion receptors (9–14), although the presence of small preformed complexes, outside of adhesions, is also possible (14). Tension and posttranslational modifications of adhesion components appear to mediate adhesion growth (15). However, the critical posttranslational modifications have not yet been identified, and the mechanism by which tension mediates adhesion assembly is not known. Disassembly is thought to be mediated in several ways, including by changes in tension and posttranslational modifications or by proteolytic cleavage of critical adhesion components (16–18). In retracting regions of the cell, adhesions tend to move retrograde and then disperse and leave integrin (with a portion of the membrane) on the substratum, suggesting a disconnect between integrin and the bulk of the adhesion during disassembly (13).

Thus, changes in associations, i.e., altered affinity and/or organization (i.e., clustering), are likely critical elements in mediating the formation and disassembly of adhesions. The challenge, therefore, is to develop methods for measuring these parameters during adhesion formation and disassembly in migrating cells. To be useful, these measurements need to be made with a resolution that captures these highly localized and transient events, which occur in specific regions of the cell and at specific times during migration. The ideal technology would provide cellular maps of binding and interaction data at diffraction-limited resolution and over a wide range of dynamics using image sequences of migrating cells. Recent developments in correlation microscopy are beginning to approach this goal. Raster image correlation spectroscopy (RICS), for example, provides the needed data over a wide dynamic range with a spatial resolution of ∼2 μm² (13,19–23).

In this study, we develop and use several related and complementary intensity fluctuation modalities, e.g., point, line and orbit scanning fluctuation correlation spectroscopy (FCS), temporal ICS (TICS), photon-counting histograms (PCH), RICS, and camera based total internal reflection fluorescence (TIRF-TICS). These different methods allow us to capture diffusion and binding information at very high spatial resolution (diffraction-limited) and over a wide range of temporal dynamics, from microseconds to minutes. The methods we describe have complementary temporal and/or spatial resolution and thus provide information on different aspects of protein dynamics within and around adhesions during their assembly and disassembly.

We apply these technologies to study paxillin, an adhesion adaptor protein that plays a prominent role in regulating adhesion formation and turnover (24). We first measured paxillin dynamics in the cytoplasm, where it is present as single molecules or in very small aggregates, and then measured paxillin binding and unbinding to adhesions at various loci in the cell, including adhesions near the leading edge during their assembly and disassembly. The data reveal rapid binding dynamics of paxillin in newly forming and maturing regions of adhesions and high affinity and clustering in more mature or disassembling adhesions. The data also reveal dynamic differences among adhesions and a large gradient of binding interactions and clustering within individual adhesions. This latter observation leads to a model for the movement (sliding) of adhesions in which the leading and trailing ends of the adhesions are assembling and disassembling in concert with the addition of single paxillin molecules or small complexes to the assembling border and large aggregates leaving the disassembling end.

MATERIALS AND METHODS

Cell culture and transfection

Chinese hamster ovary (CHO-K1) cells stably transfected with paxillin-enhanced green fluorescent protein (EGFP) were cultured and maintained in a humidified, 8.5% CO₂ atmosphere at 37°C in Dulbecco's modified Eagle's medium (Gibco, Paisley, UK) supplemented with 10% fetal bovine serum, nonessential amino acids, glutamine, and 0.5 mg/mL geneticin (G418) (Invitrogen, Carlsbad, CA) to maintain selection of transfected cells.

Mouse embryo fibroblasts (MEFs) were cultured in high-glucose Dulbecco's modified Eagle's medium (Life Technologies, Rockville, MD) supplemented with 10% fetal bovine serum (FBS), 1% (v/v) nonessential amino acids, and penicillin/streptomycin (3). The cells were transfected using Lipofectamine according to the manufacturer's instructions (Life Technologies). Generally, 0.25 μg of plasmid (diluted with Dulbecco's phosphate-buffered saline) encoding paxillin-EGFP was incubated with 5 μl of Lipofectamine for 30 min. The diluted mixture was then added to 2 × 104 MEF cells prewashed with serum-free media and then incubated for 4 h. The medium was then changed to serum containing, and the cells were maintained in a humidified, 8.5% CO₂ atmosphere at 37°C and used within 48 h. In some cases, the MEFs were transfected with paxillin-EGFP. Cells were trypsinized and plated on 35-mm optic glass-bottom dishes (Matek, Tewksbury, MA) precoated with 2 μg/mL fibronectin 1 h before imaging. The cells were maintained in CCM1 medium (Hyclone, Logan, UT) at 37°C during the course of the experiments with a Warner Instruments heated stage insert (Warner Instruments, Hamden, CT).

Microscopy

Two-photon microscopy

Measurements with two-photon excitation used a scanning fluorescence microscope (M3) built at the Laboratory for Fluorescence Dynamics (University of Illinois at Urbana-Champaign, Urbana, IL) around a Zeiss M135 microscope body. For raster and circular scanning, the laser was guided into the microscope by xy galvanoscanner mirrors (6350, Cambridge Technology, Cambridge, MA). The mirrors are driven in a preset scanning path using the ISS 3-axis card (ISS, Champaign, IL) and synchronized with data acquisition using the ISS-FCS dual channel card (ISS). For scanning in a circular orbit, the x and y scan mirrors are driven by two identical sine waves with a 90° phase shift. The radius and frequency of the circular scan were controlled by the amplitude and frequency of the sine wave. For a raster scan, the x and y scanner mirrors were driven by two sawtooth signals at different frequencies. A photomultiplier tube (R7400, Hamamatsu Photonics, Bridgewater, NJ) was used for light detection in the photon-counting mode. Data were acquired and processed by the SimFCS software developed at the Laboratory for Fluorescence Dynamics. A mode-locked titanium-sapphire laser with 80-fs pulses (Tsunami, Spectra-Physics, Palo Alto, CA) coupled to the back port of the microscope was used for excitation. A BG39 optical filter was placed before the photomultiplier for efficient suppression of infrared used for excitation light. A 40× water immersion objective (Zeiss, Germany) with 1.2 NA was used for the measurements. The volume of the point spread function (PSF) was calibrated by measuring the autocorrelation curve for 20 nM fluorescein in 0.01 M NaOH, which was fit in turn with a diffusion coefficient of 300 μm²/s. Typical values of w₀ (that define the point spread function) were in the range 0.30–0.50 μm, depending on the laser wavelength and objective used. The average power at the sample was maintained at the milliwatt level. Under these circumstances, we have not observed appreciable blinking of the EGFP molecules, and photobleaching was minimized.

For two-photon excitation, scanning fluorescence imaging data were collected at the rate of 32 μs/pixel. The scan area for a full frame (256 × 256 pixels) corresponds to 32 × 32 μm. The average fluorescence intensity of the sample remained constant, indicating that the fluorophore was not photobleached significantly during the measurement.

Single-point and scanning FCS analysis

Single-point FCS data were analyzed using the autocorrelation function (ACF) fit to a three-dimensional Gaussian-Lorentzian beam profile as described previously (25). For scanning FCS, a point was selected as the center of the scanning orbit. The scanning diameters ranged between 1.6 and 8 μm. The period of the orbit was 1 ms and 64 points were sampled along the orbit. The data collected during the circular scanning are presented in a pseudoimage in which the intensity along one orbit is displayed in the horizontal axis and each subsequent orbit is displayed in the vertical axis starting at the top of the pseudoimage, also called the “carpet.” The temporal data were analyzed using either the ACF at each point along the orbit or the RICS equations as described in (19). For time correlation, each column of the carpet is analyzed as a sequence of data with a sampling time equal to the orbit time. In this way, the fluctuation dynamics at each point in the orbit are measured with the highest time resolution (i.e., the orbit time). Data were also analyzed using the RICS spatial correlation approach (19,20). Since two adjacent points in the orbit are acquired at very high speed (orbit period/number of points in orbit) using the RICS approach, the microseconds time range characteristic of diffusion times of small protein molecules in the cytoplasm is accessible. The intensity in a single column will vary as the immobile fraction at that location bleaches. Correction for bleaching (or increasing intensity at the assembling adhesions) was done by dividing the time trace from one column into segments of ∼20 s each and adding random uncorrelated counts in each segment to match the intensity of the segment with the most counts. The resulting detrended intensity versus time data are free of the bleaching component or any other slow-intensity variation; but they still contain all the rapid-correlated intensity fluctuations due to paxillin-EGFP dynamics up to a timescale of ∼10 s.

One-photon excitation line scanning and raster image correlation spectroscopy

Line scanning and raster scanning measurements were performed with the Olympus Fluoview 300 (Olympus, Melville, NY) confocal microscope attached to an IX71 microscope with a 60×, 1.4 NA PlanApo oil-immersion objective. Raster-scanned images were collected using a 256 × 256-pixel subregion at 1024 × 1024-pixel resolution and slow scan speed (pixel dwell time was 8 μs and interline time was 3.45 ms).

Data analysis

All FCS data were analyzed using the SimFCS program developed at the Laboratory for Fluorescence Dynamics and available at http://www.lfd.uci.edu. Briefly, the single-point FCS time series was autocorrelated using

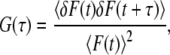(1)

where the brackets indicate time average and δF is the fluorescence intensity fluctuation or the difference between the fluorescence intensity at any given instant of time and the average fluorescence intensity.

The autocorrelation function was analyzed using

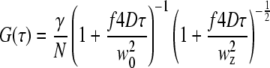(2)

to extract the diffusion coefficient. Here, γ, the illumination profile factor, was assumed to be 0.35 and 0.076 for one-photon and two-photon excitation setups, respectively; w₀ and w_z, the radial and axial 1/e² profiles, respectively, were independently calibrated every day using a solution of fluorescein molecules with a known diffusion coefficient of 300 μm²/s. The factor f is 2 for two-photon excitation and 1 for one-photon excitation. For the conversion between diffusion coefficients and correlation times,

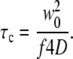(3)

For analysis of two diffusion components, we used

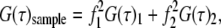(4)

where the fractional intensity contributions in terms of molecular brightness ɛ and number of molecules 〈N〉 in the excitation volume are given by

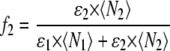(5)

and

(6)

For the scanning FCS and line-scanning experiments, the diffusion coefficients were determined by fitting the temporal ACF at each point along the orbit or line using Eq. 2.

Binding kinetics were modeled by a bimolecular reaction between a macromolecule (M) and a small ligand (L), assuming that the diffusion of the macromolecule is not altered by the binding of the ligand; there is an excess of ligand (i.e., the reaction is pseudo-first-order); and the binding occurs much faster than the diffusion of the macromolecule through the volume. Based on this model, the ACF can be calculated in closed form and is given by

(7)

where is the apparent rate coefficient, with and 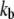the forward and backward reaction rates, respectively. f_M, f_ML, and f_L are the fractional fluorescence intensity contributions of the macromolecule alone, the macromolecule with the ligand, and the ligand alone, respectively. In our case, M (the adhesion) represents the site of attachment of the free paxillin molecule L (ligand). For our experimental conditions, assuming that the empty site of attachment is not fluorescent, the diffusion of the adhesion is negligible, and free paxillin moves fast (outside the range of the interorbit or interline time), Eq. 7 reduces to

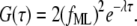(8)

The amplitude of intensity fluctuations is proportional to the square of the brightness of the molecule, whereas the correlation time depends both on the forward and backward binding rates.

For the RICS analysis, the raster scan data were first spatially autocorrelated using the 2D fast Fourier transform method (ξ and ψ indicate spatial increments in the x and y directions of the raster scan image):

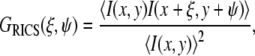(9)

and then fit to the diffusion model using the following set of equations:

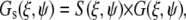(10)

where the S and G spatial correlation functions are given by

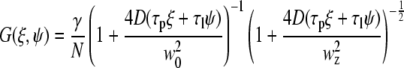(11)

and

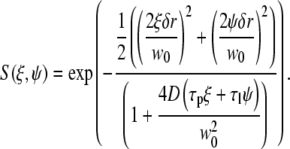(12)

In the above equations τ_p and τ_l are the pixel dwell time and the line repeat time, respectively, and δr is the pixel size. The pixel and line time, as well as the pixel size, were determined for each measurement according to the microscope scanning setup and the objective used. Removal of the immobile fraction was performed using the methods described in Digman et al. (19,20) based on the subtraction of slowly changing image features (seconds) as compared to fast diffusion of paxillin in the cytoplasm (submilliseconds) or fast binding kinetics at adhesions (subseconds). Briefly, the image sequence stack was divided into periods of ∼10–20 s. The average image was calculated for each time period and subtracted pixel by pixel from each image within the sequence during the same time period. A number equal to the average intensity of the image was then added back to avoid having negative intensities. This operation was then repeated for the entire image sequence, moving the time period one frame along the sequence in a moving average fashion. This operation of subtracting the moving part was used both for image correction and for line- or circular-scan operations.

For PCH analysis, the system was calibrated by measuring the average brightness of EGFP free in solution (26,27). If the fluorescent proteins are clustered, then the average brightness of a particle will increase, that is, for dimers the brightness would be double, for trimers it would be triple, etc. The PCH analysis was performed according to the equations reported by Chen et al. (26) using the Globals Unlimited software package (Globals Unlimited, Laboratory for Fluorescence Dynamics, University of California, Irvine).

Detrending was done by dividing the time trace from one column in segments of ∼20 s each and adding random uncorrelated counts in each segment to match the intensity of the segment with the most counts.

TIRF experiments were performed on an Olympus IX70 microscope equipped with a TIRF illumination attachment and using a 60× Planapo, NA 1.45, TIRF oil-immersion objective. Excitation was from the 488-nm line of a 200-mW laser attenuated with neutral-density filters and an acousto-optic tunable filter to ∼10% power. Images were collected with a Cascade 512 EM-CCD (Photometrics, Tucson, AZ) used at a frame rate of 90 frames/s using the stream acquisition feature in the MetaMorph software (Molecular Devices, Sunnyvale, CA). The TIRF data were analyzed using the temporal ACF method at each pixel.

The intensity derivative for the TIRF data at each point in the image was calculated by first averaging 128 frames (∼1.42 s) and then calculating the normalized derivative according to the expression

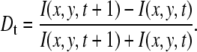(13)

RESULTS

Heterogeneous dynamics and clustering of paxillin across the cell

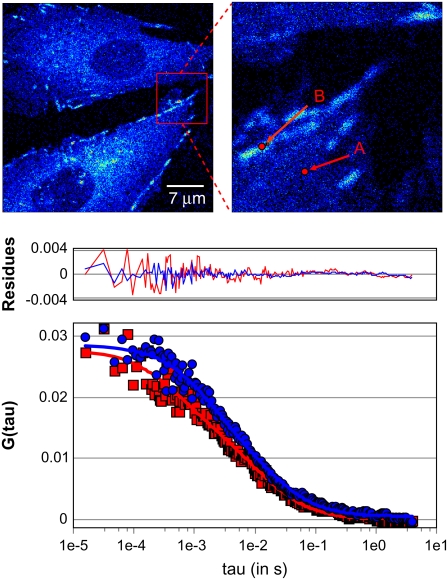
Two-photon FCS and PCH analysis of temporal intensity fluctuations within a single laser focal volume provide high-resolution data on molecular dynamics (FCS) and states of aggregation (PCH). The ACFs from cytosolic regions in CHO-K1 cells display variable shapes and correlation times, revealing heterogeneous dynamics of paxillin across the cytosol (Fig. 1, upper right, point A). Control experiments on cells that were not transfected with paxillin-EGFP showed negligible autofluorescence and no correlations were detected. Data from measurements on >30 cells were pooled and fit globally (i.e., simultaneously) to a two-component diffusion model, which gave correlation times of τ = 1.34 ms and τ = 18.1 ms. These correlation times correspond to apparent diffusion coefficients (D_app) of 19.6 μm²/s and 1.43 μm²/s (Table 1). The fast-diffusing component fits well with the measured diffusion coefficient for soluble cytosolic proteins in general (27). Since the dynamics of the slower component is ∼15-fold slower than that of the faster component, the Stokes-Einstein relationship (where D depends on the inverse cube of the molecular mass) predicts an effective molecular weight of ∼3200 times that of the free paxillin. A complex of this size would be visible and suggests that the slower-moving component does not likely correspond to simple diffusion, but rather to transient binding to immobile structures such as adhesions and/or steric hindrance within a crowded protein environment. This is supported by a scatter-plot analysis in which all of the data are presented with the mean value, the 5–95% percent intervals and the minimum and maximum values (Fig. 2); note that the variance of the data is larger for locations near adhesions.

FIGURE 1.

Single-point FCS data from CHO k1 cells expressing paxillin-EGFP in the cytosolic regions (A) and on the adhesions (B) were analyzed globally using a two-component fit (Table 1). Blue circles are the autocorrelation function at points selected on adhesions; red squares are the function at points selected in the cytosolic regions.

TABLE 1.

Two component diffusion analysis

Paxillin-EGFP	Diffusion (μm2/s)	Fractional Contribution Cytosol (%)	Fractional Contribution Adhesions (%)
D1	19.6	61	44
D2	1.43	39	56

The diffusion coefficients were fit using the Globals analysis software where the best fit averages for diffusion D1 and D2 were fixed both species and the G(0) values were allowed to vary. The fractional contributions were obtained from the G(0) values of more than 30 CHO-K1 cells.

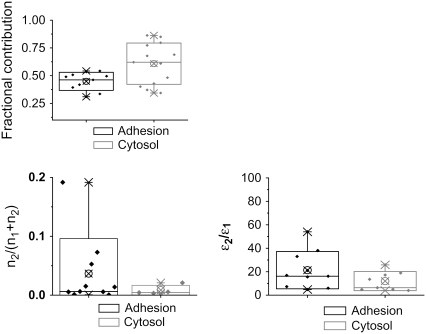
FIGURE 2.

Statistical representation of single-point FCS data. The minimum-maximum data (×); the mean, represented by a circled “×”; and the 5–95% data range (boxes) are shown. (Upper) Fractional contribution from the fast-diffusing component (D_app = 19.6 μm²/s) relative to the slower component from single-point FCS data. (Lower left) Fractional contribution of the aggregated protein (n₂) relative to the total protein (monomeric (n₁) plus aggregated (n₂)) determined from the G(0) correlation function amplitude. (Lower right) Ratio of the brightness of the aggregate protein (ɛ₂) to that of the monomer (ɛ₁).

The amplitude information from the ACF fitting reveals the relative contribution of the two components to the fit. In the cytosolic regions, 61% of the paxillin contributes to the fast component (Table 1, Fig. 2 A), whereas in regions containing adhesions (Fig. 1, upper right, point B) this contribution is only 44% (Table 1, Fig. 2 A).

The PCH analysis of the same temporal intensity fluctuation data also shows two different populations of paxillin-EGFP. One is monomeric and likely corresponds to the fast-diffusing component, and the other is ∼10- to 20-fold brighter (Table 2). We can estimate the fractions of molecules in each component in two ways. First, the apparent fractional intensities depend on the square of the molecular brightness (ɛ). Second, the number of particles in the excitation volume (n) can be measured from the extrapolated ACF amplitude (G(0)). Therefore, we can calculate the relative abundance of the monomeric (n₁) and the clustered (n₂) protein species using Eqs. 4–6 (see Materials and Methods). Alternatively, we can independently determine the number of molecules directly from the PCH analysis, as shown in Table 2. The data show that the fraction of the “clustered” component (n₂, Fig. 2 B) and the relative ratio of the clustered/monomeric protein brightness (Fig. 2 C) are higher for adhesive regions of the cell. Specifically, the clustered paxillin component represents ∼5% of the protein near adhesions, whereas it represents <1% in the cytosol (Table 2). Thus, both the correlation function amplitude and the PCH brightness analysis show that paxillin is more clustered in adhesive regions of the cell.

TABLE 2.

PCH analysis of Paxillin-EGFP

	Adhesion	Cytoplasm
ɛ1 (in c/s/m)	5,700	5,730
N1	4.57	5.61
ɛ2(in c/s/m)	122,240	68,480
N2	0.23	0.049
ɛ2/ɛ1	21.4	12
N2 (as % of total)	4.8	0.9

The PCH curves were Globally fitted to a two species model where the molecular brightness (ɛ) and number of molecules (N₁ and N₂) were allowed to vary. The percent number of molecules for the brighter species (N₂) shows to be more abundant in the adhesions versus the cytosol.

Taken together, these data show that paxillin dynamics in the cytosol and in proximity to adhesions is very heterogeneous. Paxillin within the cytosol is essentially monomeric, whereas near adhesions the dynamics are too slow to simply arise from protein aggregate diffusion and are likely the result of a binding equilibrium between protein complexes containing 10–20 paxillin proteins and immobile adhesion components (e.g., integrins, actin, and actin binding proteins). The slow dynamics of paxillin binding occurs with kinetics at ∼20 ms.

Paxillin dynamics is heterogeneous across adhesions

The single-point FCS offers high spatial and temporal resolution and a wide dynamic range but only provides information at one spatial location. However, the heterogeneity in paxillin dynamics across the cell point to the need for simultaneous measurements in different regions of the cell to determine and follow changes in protein dynamics during cellular processes. Therefore, we employed scanning-FCS (sFCS) (25), where the laser beam is scanned in a circular orbit, to investigate regional dynamics across adhesions. With this approach, many pixel locations can be sampled within one experiment at a high spatial resolution. The time resolution for sFCS is determined by the orbit period, which is 1 ms for these experiments. Although this timescale will not detect free diffusion in the cytosol, it will detect the slower dynamics characteristic of paxillin in the vicinity of adhesions.

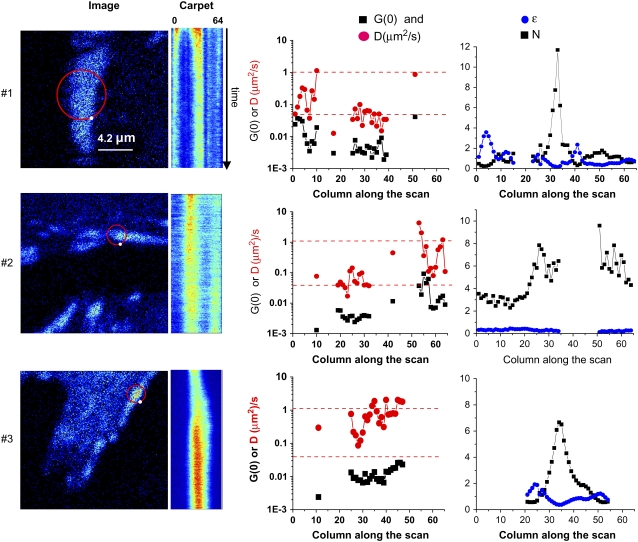
The intensity data captured by orbit scanning can be displayed in an intensity “carpet” (Fig. 3). The spatial information along each orbit is displayed along each row (the x axis, 64 pixels) and data from successive orbits is displayed along each column (y axis). Temporal autocorrelation functions are computed at each pixel location along the orbit, i.e., from the intensity data down each column of the intensity carpet. Three intensity carpets (representing >50 experiments) from different adhesions in different cells show that there is heterogeneity in the dynamics of paxillin both within a single adhesion and among different adhesions.

FIGURE 3.

sFCS of paxillin-EGFP in and around an adhesion. Data were sampled at 64 kHz (1 ms/orbit, 64 points/orbit). The circle on the images shows the center position of the laser scanning orbit. The white dot on the orbit path shows the beginning of the orbit. The orbit is scanned clockwise. Intensity carpets are an image generated using the intensity data along each orbit, the x axis, with each successive orbit displayed along the y axis. Plots are also shown for the ACF-extrapolated amplitude (G(0,0), solid squares), the apparent diffusion coefficient in μm²/s (D_app, red circles), PCH analysis of the molecular brightness in kHz/molecule, (ɛ, blue dots), and the number density (N, solid squares) along the scan orbit. The G(0) and diffusion coefficients were calculated with a one-species fit after detrending. Adhesion 1 (upper) is a relatively stationary adhesion in paxillin null MEFs (pax(−/−)). The region at position 35 corresponds to the bright intensity column in the carpet representation. The total time of this measurement was 240 s. Adhesion 2 (middle) is a growing adhesion in CHO-K1 cells stably expressing paxillin-EGFP. The orbit diameter was 0.85 μm, corresponding to a 0.04-μm pixel size, along the orbit. The total acquisition time for this experiment was 540 s. Adhesion 3 (lower) is a growing adhesion in CHO K1 cells stably expressing paxillin-EGFP. The orbit diameter was 0.85 μm, and the total measurement time was 540 s.

It can be seen in Fig. 3 that adhesion 1 (upper) was relatively stable during the course of the measurement, since the position and shape of the adhesion did not change significantly within 30 min. Although the adhesion does not appear to move, as an average it slightly widens and shrinks. The sFCS orbit (4 μm diameter) crossed the middle of the adhesion at two locations, positions 4–11 and 28–40, which are seen as two vertical stripes in the intensity carpet (Fig. 3, upper). Note that the orbit appears to go outside of the cell, but the lamellipodium actually extends outward past the brighter adhesion. The intensity carpet reveals an initial bleaching of the paxillin within the adhesion, with a characteristic bleaching time of ∼20 s (Fig. 3, upper). Bleaching contributes to the ACF as a slowly relaxing component that can completely mask other fast dynamic processes; therefore, the data were detrended to remove the bleaching component before analysis (see Materials and Methods).

ACFs were calculated for each column of the intensity carpet, i.e., each pixel location along the scan orbit. Initially, all of the ACFs along the orbit were globally fit by averaging. The analysis revealed at least two different paxillin populations with correlation times of τ = 20 ms and τ = 810 ms; these correspond to apparent diffusion coefficients of 1–2 μm²/s and ∼0.02 μm²/s, respectively. The faster component corresponds to the slower component measured by FCS, whereas the slower component corresponds to an even slower process than that measured on the timescale of the FCS experiments presented above. The ACF for each column was fit and the apparent diffusion (D, red circles) and the extrapolated correlation function amplitude (G(0), black squares) were plotted as a function of the position along the orbit (Fig. 3, upper). It is of interest that two regions within adhesion 1 have different dynamics. The first of these regions (columns 4–11, D_app = 0.2 ± 0.02 μm²/s) has faster dynamics than the second (columns 28–40, D_app = 0.05 ± 0.005 μm²/s). The data also suggest a gradient of dynamics within the first region, whereas the second region appears more homogeneous.

A PCH analysis of the same data in each column shows that part of the adhesion, near column 5 (Fig. 3, upper right) has a high molecular brightness (ɛ, blue circles), suggesting large intensity fluctuations in this region from paxillin aggregates. This part of the adhesion is moving slowly toward the left, as seen in the intensity carpet; the trailing part of the adhesion that is disassembling is around column 5, which corresponds to this widening and shrinking effect. In the region of the adhesion comprised by columns 28–40, the apparent number of molecules (N, black squares) increases as the brightness decreases (column 33). In this part of the adhesion, the average intensity is high, so that the relative fluctuation amplitude is small, and therefore, the PCH analysis cannot distinguish between brightness (clustering) and number of molecules. The average brightness for a monomer in these experiments was ∼3000 counts/s/molecule, different from the experiments using single-point FCS (Table 2) due to the different lower laser intensity in these experiments. Note that this part of the adhesion is moving slightly toward the right. The brightness analysis shows that paxillin proteins on the left border (the disassembling part) are brighter (more clustered) than at other points along the orbit. Note that there are no data for the cytosolic regions between adhesions because the dynamics are too fast to be measured with sFCS (Fig. 3, upper right, gaps in plots).

Adhesion 2 (Fig. 3, middle) is growing at one end, but is not “sliding.” The dynamics at the growing tip (columns 53–64, right end of adhesion) is more heterogeneous and faster than at other parts of the same adhesion (columns 19–32): D_app = ∼0.1–1 μm²/s and < 0.1 μm²/s, respectively (Fig. 3, middle, red dots). Note that the bleaching at the growing end is relatively modest. It is interesting that at all positions along the orbit, the molecular brightness (ɛ) is similar and corresponds to that of paxillin monomers (Fig. 3, middle). In general, the fluctuations near the growing or newly stabilized adhesions are mainly from monomers or small paxillin aggregates.

Adhesion 3 (Fig. 3, lower) shows a more rapidly growing adhesion. The more rapid fluctuations (<2 s) were analyzed by detrending the intensity data with a fast time window (2 s) to remove contributions to the ACF arising from the increasing intensity of the adhesion as it grew. The dynamics were rapid (D_app ≈ 1 μm²/s, red dots) and revealed a gradient in dynamics across the adhesion, with one side more dynamic than the other (Fig. 3, lower). This adhesion appears to be sliding toward the right (Fig. 3, lower, intensity carpet), with columns 22–27 corresponding to the trailing region. The PCH analysis in this region shows a high brightness (Fig. 3, lower, ɛ, blue dots), indicating the presence of large aggregates than are present in regions where adhesions are disassembling.

Overall, our data show that paxillin dynamics within adhesions are fast and that paxillin adds to the adhesions in monomers or small aggregates when adhesions are growing or are relatively stable in protrusive parts of the cell. In contrast, when adhesions are sliding or disassembling, the trailing region has slower dynamics and is more aggregated, e.g., ∼10 times brighter than the monomeric population. These examples and conclusions represent data from several different cells measured on different days.

Effective diffusion at adhesions is dominated by binding kinetics

To probe many adhesions at once, linear scanning (line sFCS) rather than circular scanning was done using a commercial Olympus FV300 confocal (Fig. 4). The main difference between the two scanning modalities is that there is a discontinuity in the data stream with line scanning, because the laser scanning mirrors move back from the end of one line to the starting position for the subsequent lines. In our measurements, the time between successive lines was 3.45 ms compared to 1 ms/circular orbit for the sFCS.

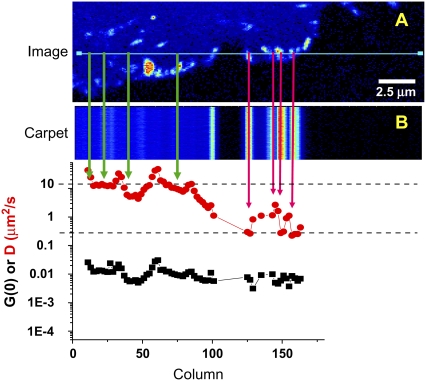
FIGURE 4.

Line scanning of paxillin-EGFP in CHO-K1 cells captured on an Olympus FV300 laser scanning confocal microscope. Two hundred fifty-six pixels were captured along the x axis with a pixel dwell time of 8 μs/pixel; there are 10,000 lines in the y axis. (A) The cell and scan line. (B) The intensity carpet of the line scan after detrending for photobleaching. The temporal autocorrelation function at each column was calculated from the detrended data, and the extrapolated amplitude (G(0), solid squares) and apparent diffusion coefficient (D_app, red circles) for each column were determined.

The line-scanning data were detrended and transposed into an intensity carpet analogous to that described for the orbital scanned data (Fig. 4 B). A time correlation analysis was performed for each pixel location along the scan axis, as in the circular-scanning data presented above. The apparent diffusion coefficients, D_app, were ∼10 μm²/s in cytosolic regions (Fig. 4, green arrows) and 0.05–0.1 μm²/s in adhesive regions (Fig. 4, pink arrows) and revealed heterogeneity among adhesions. In adhesive regions, the binding-kinetics model (Eqs. 7 and 8) consistently yielded a better fit of the autocorrelation functions than the diffusion model (χ² ∼30% smaller, Table 3), supporting the notion that the dynamics in adhesive regions is dominated by binding equilibria rather than diffusion. In addition, if paxillin were undergoing diffusion in a large, slowly moving complex, its dynamics would be on a timescale similar to that of the scan speed and would therefore be apparent in the intensity carpet. In other words, if large aggregates diffuse on a timescale similar to that of the line scanning, the intensity from the complex will propagate outside of the adhesions and appear in adjacent columns in the intensity carpet as an intensity streak (simulated data, not shown), which is not seen in the data (Figs. 3 and 4, intensity carpet).

TABLE 3.

Results of the line-scanning experiment

Line No.	G(0)	D	χ2	A	k (s−1)	χ2	χ2 ratio
101	0.0070	0.90	1.3	0.0057	13.7	0.9	1.4
127	0.0078	0.63	1.6	0.0065	11.6	1.1	1.4
143	0.0083	1.09	1.6	0.0061	16.3	1.4	1.2
151 (×2)	0.0108	0.82	2.4	0.0086	13.9	1.7	1.4
160 (×2)	0.0091	0.67	2.1	0.0073	11.6	1.5	1.4
Average	0.0086	0.82	1.8	0.0068	13.4	1.3	1.4

At lines 151 and 160, two adjacent lines were averaged. Fits were performed using either a diffusion term characterized by G(0) and D (in μm2/s) or an exponential term characterized by amplitude A and rate k (in s⁻¹). Each fit provides a χ² value. The ratio of the χ² values for the fit using the diffusion equation and the rate equation are reported in the last column.

Since the data obtained by line-scanning sFCS are limited because of the delay between successive lines (>1 ms), the fast protein dynamics in the cytosol are inaccessible using standard point-by-point time correlation. However, RICS (19), which is based on spatial correlations within the line-scanned images, can be used to determine the cytoplasmic dynamics. In the RICS analysis, the spatial ACF is calculated for images and the dynamics of the laser beam motion is separated from the dynamics due to molecular motion by fitting the ACF to Eqs. 10–12. This can be adapted to line-scanning data by analyzing in one dimension along the scan line. The immobile removal algorithm is applied using data from successive line scans to remove the large spatial features due to the shape of adhesions and other structures that would otherwise dominate the spatial ACF. RICS in the cytosolic regions of the line scan (Fig. 4, green arrows) yielded D_app = 20 ± 1 μm²/s, whereas in adhesive regions (Fig. 4, pink arrows) the dynamics were slower, with D_app = 0.1 ± 0.02 μm²/s. Therefore, the RICS analysis of the spatial-temporal line-scanning data provides information on fast diffusion dynamics, whereas the same data can be analyzed point by point (column by column) over time to obtain slower binding kinetic information.

Global maps of paxillin dynamics across the cell and adhesions

To ascertain the integrated spatial and temporal processes that underlie cell migration, it is critical to simultaneously measure protein dynamics across large regions of the cell. Therefore, we developed a high resolution modality consistent with the binding dynamics observed within adhesions using time correlation of TIRF image time series. To rapidly collect high-resolution images (pixel size ∼280 nm) with a sufficient signal/noise ratio, a high-sensitivity back-thinned EM-CCD camera was used at 90 frames/s (10-ms exposure time). Since the camera acquires the intensity of the pixels in parallel, the temporal autocorrelation of the intensity fluctuations can be calculated for each pixel in the image sequence (28). Intensity fluctuations within TIRF images are dominated by the movement of fluorescent molecules into and out of the 100-nm-deep evanescent wave at the basal surface of the cell. Therefore, only regions near the substratum, e.g., near adhesions, which correspond to binding interactions, should show dynamics on this timescale. Note that, due to limited sensitivity and speed of camera acquisition, the technique is not fast enough to detect movements of cytosolic paxillin, which are on the submillisecond timescale.

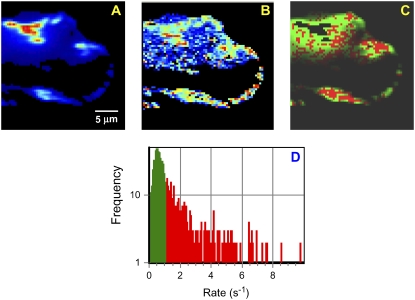
Images of paxillin-EGFP (Fig. 5 A) were collected at a rate of 11 ms/frame for 8192 frames. The temporal ACF was calculated at each pixel location and fit with a binding kinetic model (i.e., an exponential decay, Eqs. 7–9). When comparing the intensity (Fig. 5 A) and the ACF amplitude maps (Fig. 5 B), it is clear that the maximum fluctuation amplitudes do not necessarily coincide with adhesion size or brightness. In fact, there are many small adhesions (diffraction-limited spots) identified near the leading edge of the cell where there are fluctuations of significant amplitude (Fig. 5 B, red regions at the leading edge). The recovered rates span the range from 0.1 s⁻¹ to ∼10 s⁻¹, indicating that there are both fast and slow processes occurring across the cell. The rates are displayed pixel by pixel, with an arbitrary threshold (∼1 s⁻¹), showing green pixels as “slow” rates and red pixels as “fast” rates. Note that paxillin is very dynamic in the protrusions at the front of the cell (Fig. 5 B, red pixels).

FIGURE 5.

Temporal pixel correlation analysis of TIRF images. (A) Average intensity for the image time series. (B) Fluctuation amplitude of the autocorrelation function, G(0), at each pixel. The color scale for the G(0) map is from 0 to 0.00065. (C) Spatial plot of the rates obtained by fitting each temporal ACF to an exponential decay; the rates are color-coded, with those >1 s⁻¹ in red and those <1 s⁻¹ in green. (D) Histogram of rates determined from temporal correlation analysis. Scale bar, 5 μm.

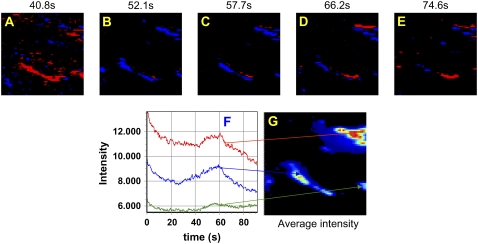
These image stacks contain an immense amount of information, but with so many frames it can be daunting to discern what is going on in the cell on longer timescales. To avoid this difficulty, we computed the intensity derivative at each pixel in the image (see Materials and Methods for details) to reveal which areas are showing positive changes in intensity, i.e., adhesion assembly, and negative changes in intensity, i.e., adhesion disassembly. The images were grouped into averages of 128 sequential frames, corresponding to ∼1.4 s in time. The changes in intensity between successive frames for each pixel within these average image frames were calculated according to Eq. 13. This analysis generates two new image time series, one in which the intensity map represents positive changes, or growth of paxillin-containing adhesions; and another representing the magnitude of negative changes, or disassembly of paxillin-containing adhesions.

Unexpectedly, these maps revealed synchronies in adhesion assembly and disassembly. The map of the intensity derivative in the small region (64 × 64 pixels) shown in Fig. 6 contains several areas with prominent, bright adhesions (Fig. 6 G). For two of the adhesions, the intensity increases at t = 41 s (Fig. 6 A, red), remains high for a few seconds, and then decreases suddenly. At t = 58 s, the intensity derivative has leveled off (Fig. 6 C). At other times, either the two adhesions do not change in intensity or the derivative map of only one of the adhesions changes (Fig. 6 E). For example, at t = 66 s only one of the adhesions is growing (Fig. 6 D, red), whereas at t = 75 s two new adhesions (or part of a large adhesion) are brightening (Fig. 6 E, red) while other parts of the same adhesion are disassembling (Fig. 6 E, blue). In fact, the intensity map at selected points in the image (Fig. 6 F) shows that some of the intensity changes occur at similar times. That is, they are synchronized on the seconds but not the milliseconds timescale, suggesting that adhesion assembly regulation may be controlled simultaneously for entire regions of the cell. However, not all adhesions participate in this quasisynchronous growth and disassembly: some are more stable. This timescale (seconds) is consistent with known rates of adhesion assembly and disassembly (3,4,6).

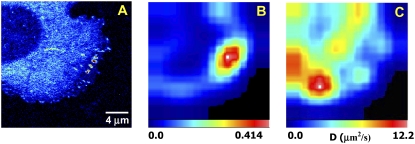
FIGURE 6.

RICS analysis of CHO K1 cells expressing EGFP-paxillin. (A) The image was analyzed using the RICS method. A small region of 32 × 32 points was sequentially analyzed and moved in the x and y direction by 16 pixels/step. For each step, the spatial ACF was fit to the RICS equations for one diffusion component. (B and C) Maps of the G(0) and apparent diffusion coefficient, respectively. Scale bar, 4 μm.

The RICS approach using LSCM images can complement the slower binding dynamics revealed by TIRF and map fast protein dynamics across the cell with 2- to 3-μm spatial resolution (19,20). Since many areas of the cell contain relatively immobile structures, e.g., cytoskeletal structures and adhesions (Fig. 7 A), that will dominate the spatial ACF in those areas, an immobile removal algorithm (see Materials and Methods) was applied (19). The RICS analysis is shown in Fig. 7, B and C, for the G(0) and the diffusion coefficient, respectively. In the G(0) map, the borders of the cell display larger fluctuations (red pixels). In cytosolic regions, D_app ≈ 10 μm²/s, in good agreement with single-point FCS, sFCS, and line RICS analysis (Fig. 7 C). These dynamics are somewhat slower than those measured for freely diffusing paxillin in the cytosol; this is likely due to the presence of slower-diffusing components that cannot be completely resolved. In the RICS analysis, the dynamics are averaged over a larger area so it can be difficult to separate the fast and slow components. Regions that include adhesions systematically show slower dynamics (D_app ≈ 1 μm²/s) than regions without visible adhesions (Fig. 7), in accord with Table 3 data obtained from the line-scanning experiment. It is interesting that the dynamics of paxillin near the leading edge are very slow (D_app ≈ 0.2 μm²/s), likely due to transient binding interactions with nascent adhesions known to be present in this region of the cell (6).

FIGURE 7.

(A–E) Negative (blue) and positive (red) pixel intensity derivatives at selected times; 128 frames were averaged to calculate the derivative at each time point from 41 to 75 s. (F) Intensity versus time traces at different pixel locations within the image time series. The red, blue, and green arrows identify the points in the image (G) corresponding to the intensity traces.

Adhesion sliding occurs through a treadmilling mechanism

The FCS and PCH data presented earlier show that the paxillin monomers exchange rapidly with the leading portion of sliding adhesions while the large aggregates are simultaneously exchanging more slowly in the trailing region. This suggests a treadmilling mechanism for adhesion sliding, in which the adhesion is assembling by the rapid addition of monomers at its leading edge while it is disassembling by a slow release of large aggregates at its trailing edge. This is supported by observations on the large row of adhesions shown in Fig. 5. Derivative intensity analysis and velocity maps show that these adhesions are moving up and to the right; this is not a continuous process, but occurs in starts and stops. The TIRF-FCS analyses show that the fastest exchange rates correspond to the growing region, and slower rates are found at the trailing edge. Analysis of brightness (cluster size) using the extrapolated G(0) and intensity (see Materials and Methods) shows that large clusters are exchanging at the trailing region, where the exchange rates are slower, whereas smaller clusters or monomers are exchanging with the leading edge. In addition, when nascent adhesions assemble, there is a continuous increase in intensity consistent with addition of paxillin monomers, whereas when the adhesions dissemble, the loss of intensity occurs in larger steps compatible with release of larger aggregates (E. Gratton and M. Digman, unpublished observation).

Data from fluorescence recovery after photobleaching also show dynamic heterogeneity in adhesions. In stable adhesions, ∼20% of the paxillin is immobile, whereas in nascent adhesions, 100% of the paxillin exchanges (unpublished observation). The analyses of data from fluorescence recovery after photobleaching show that the entire mobile component of paxillin can exchange in as little as 12 s (unpublished observation). These exchange rates are compatible with the TIRF time correlation measurements, which show exchange rates on the order of 1–10 s⁻¹. In translocating (“sliding”) adhesions, the distal part of the adhesion has a slower mobile fraction, whereas the proximal, assembling part shows complete recovery (8). The regions between the rear and the front show intermediate values of mobile fractions (8).

DISCUSSION

In this article, we implement a toolbox of complementary fluctuation methods for studying the dynamics of adhesion proteins during cell migration. Although the dynamics of proteins in adhesions are well suited to investigation by correlation approaches, the range of dynamics and their highly localized and transient nature present a considerable challenge. This requires significant modifications of existing methods and the development of some new approaches. We applied these modified methods to paxillin, an adaptor protein that resides in adhesions and regulates the formation and dynamics of protrusions and adhesions (29). Paxillin is one of a large number of molecules that populate adhesions, either permanently or transiently, and is a good marker for a variety of adhesion-related phenomena, including their assembly and disassembly (30).

In the cytoplasm, paxillin diffuses relatively freely; this conclusion is based on a comparison of the diffusion coefficients for EGFP alone (molecular mass 30 kDa) and paxillin-EGFP (molecular mass 98 kDa), which are similar, after scaling for the different molecular masses. In addition, a brightness analysis using PCH confirms that paxillin-EGFP is present as a monomer in these regions of the cytoplasm.

In contrast to the nearly free diffusion of paxillin in the cytoplasm, the motion of paxillin near adhesions is slower and dominated by binding kinetics rather than diffusion. The apparent affinity (avidity) increases in the proximity of the adhesion, probably due to the high concentration of appropriate partners for binding in these regions. Our analyses reveal that the motion of paxillin near and at the adhesions is too slow to represent “pure diffusion”; this is based on the following: 1), the Stokes-Einstein relationship, which assumes a viscosity similar to that found in other regions of the cytoplasm (three to five times the viscosity of water), predicts that the size of the diffusing object must be on the order of 10⁸ D, but still contain a few (∼10) paxillin molecules. 2), Only specific locations in the cell (adhesions and adhesion borders) have high amplitude fluctuations, suggesting the presence of large clusters in these regions. 3), The autocorrelation function is best fit using first-order binding kinetics at locations close to or at adhesion sites. 4), Different sides of the adhesions show different dynamics, probably due to a different affinity for paxillin or concentration of the partners with which paxillin interacts.

The binding rate obtained with this analysis is the residence time, or “exchange rate”, i.e., the sum of the “on” and “off” rates. To separate the two rates, we would need to either know one of the two rates (or the equilibrium constant), or use the analysis of the on/off statistics, similar to the occupation analysis performed in single-molecule experiments (31). Unfortunately, the S/N ratio is not yet sufficient for this type of analysis, since we cannot clearly distinguish the “on” from the “off” event for single sites from the traces we collected. However, the values that we obtain appear to be largely independent of expressed paxillin concentration, and therefore it appears that our measurements are dominated by the off-rate.

It is also interesting that the amplitude of the fluctuations increases in some adhesions, although the G(0) decreases due to the higher concentration of paxillin at these locations. Since we do not use the τ = 0 point of the autocorrelation function, which is strongly affected by the shot noise, the large fluctuation amplitude recovered by the PCH and by the binding rate analysis implies that aggregates containing, on average, 10 paxillin molecules (10 EGFP equivalents) are involved in the fluctuations at these locations. Thus, it appears that large proteins aggregates are exchanging within some adhesions or regions of adhesions.

Our analyses also point to significant differences in dynamics and aggregation of paxillin in different adhesions. The nascent adhesions that reside near the leading edge have short lifetimes, and bind relatively low-brightness particles, presumably monomers with relatively low affinity (faster fluctuations). In contrast, more centrally located adhesions, which are relatively stable and can last as long as 30 min, bind paxillin more strongly, presumably as part of a protein complex, and leave adhesions as large protein aggregates. Our analyses have also revealed an interesting heterogeneity in the dynamics within translocating or “sliding” adhesions. In the proximal (away from the leading edge) part of the adhesion intensity increases are seen, whereas in the distal part the intensity decreases. There is also heterogeneity in paxillin dynamics at the lateral edges of the adhesions. The sFCS and TIRF-FCS analyses show that these adhesions have two distinct regions with differential dynamics. In growing edges, paxillin molecules are accumulating and exchanging as monomers. In the retracting edges, paxillin leaves the adhesion in large complexes containing many paxillin molecules, as well as other molecules. The combination of these processes results in an apparent sliding of the whole adhesion, with the distal part of the adhesion disassembling. Although this kind of treadmilling has been proposed previously to explain the sliding of adhesions (9), our data provide direct evidence for this mechanism and extend it by revealing the large differences in the organization and dynamics of the leading and disassembling regions. They also suggest that adhesions assemble by the addition of monomers or very small aggregates rather than from preformed structures.

Our observations also bear on the interpretation of the effective diffusion coefficients obtained previously by single-point FCS applied to study the dynamics of proteins in the cell interior. These data were generally interpreted in the context of the rate of transit of the molecule or particle through the excitation volume. Here, we show that the permanence time in a specific location could also be due to transient binding interactions. The analysis of the fluctuation amplitude performed by the PCH, along with the model used to fit the correlation function, is crucial for distinguishing the diffusion of protein aggregates from single-molecule binding kinetics.

From a biological point of view, our observations begin to define the differences among adhesions. Our analyses clearly demonstrate heterogeneity in the organization, i.e., clustering, and strength of binding interactions among adhesions. In addition, there is also heterogeneity within adhesions. This extends a number of studies that point to compositional differences in adhesions. Although the origin of these differences remains to be uncovered, the degree of integrin clustering by the ECM, the organization of actin interacting with adhesions, and posttranslational modifications of adhesion components are all likely contributors. It is of interest that regions in which adhesions assemble, e.g., nascent adhesions near the leading edge, growing adhesions, and translocating (treadmilling adhesions) adhesions all show relatively weak binding equilibria and low clustering. In contrast, regions where adhesions are disassembling have higher affinities and are in equilibrium with large, highly clustered adhesion complexes.

In conclusion, this work has demonstrated the application of correlation methods for understanding adhesion dynamics in migrating cells. Paxillin-EGFP displays different dynamical behavior in different parts of the cell and different adhesions. In regions removed from adhesions, paxillin diffuses freely in the cytoplasm. At and around the adhesions, the translational dynamics is determined by binding interactions with partners that are concentrated in these regions. Close to the adhesion, paxillin interacts as a monomer with the other proteins. At the adhesion, large complexes containing several paxillin molecules associate with other molecules in the assembling or disassembling of the adhesions. The small, dynamic adhesions near the leading edge are highly dynamic and show rapid exchange rates, whereas the more peripheral adhesions are more stable and show slower exchange rates. Within a single adhesion, there also appears to be heterogeneity, revealing maturation as the adhesion forms. For translocating (“sliding”) adhesions, the newly forming part is highly dynamic, like the new adhesions at the front of the cell, whereas the “older”, more stable and disassembling regions are less dynamic.

Several fluctuation techniques were used to obtain this overall picture of paxillin dynamics, including single-point, circular and line scanning FCS, RICS, and temporal correlation using fast cameras. These methods have single-molecule sensitivity and can be implemented in the laser scanning microscope environment available in most cell biology laboratories. These methods cover a large range of temporal and spatial resolution. The very fast molecular dynamics observed with “freely” diffusing molecules in the cytoplasm are better visualized by either single-point FCS or by RICS, whereas the medium-speed (millisecond) dynamics seen for molecules interacting with adhesions are better detected using the line- or circle-scan correlation methods as well as with high-speed, high-sensitivity cameras exploiting TIRF methodology. All of these methods offer very high spatial resolution. At this point, no one approach is able to cover the spectrum of dynamics at high spatial resolution. As implemented here, these methods complement each other and together provide a coherent picture of the different molecular interactions of paxillin in the cell. When combined with the PCH analysis, they begin to provide a novel and useful picture of the organization and dynamics of adhesions.