Abstract
Escherichia coli requires an efficient transport and signaling system to successfully sequester iron from its environment. FecA, a TonB-dependent protein, serves a critical role in this process: first, it binds and transports iron in the form of ferric citrate, and second, it initiates a signaling cascade that results in the transcription of several iron transporter genes in interaction with inner membrane proteins. The structure of the plug and barrel domains and the periplasmic N-terminal domain (NTD) are separately available. However, the linker connecting the plug and barrel and the NTD domains is highly mobile, which may prevent the determination of the FecA structure as a whole assembly. Here, we reduce the conformation space of this linker into most probable structural models using the modeling tool CABS, then apply normal-mode analysis to investigate the motions of the whole structure of FecA by using elastic network models. We relate the FecA domain motions to the outer-inner membrane communication, which initiates transcription. We observe that the global motions of FecA assign flexibility to the TonB box and the NTD, and control the exposure of the TonB box for binding to the TonB inner membrane protein, suggesting how these motions relate to FecA function. Our simulations suggest the presence of a communication between the loops on both ends of the protein, a signaling mechanism by which a signal could be transmitted by conformational transitions in response to the binding of ferric citrate.
INTRODUCTION
Cellular intake of iron is essential for the survival of Escherichia coli (1,2). Iron is transported through the membrane in the form of ferric citrate by the FecA protein. FecA interacts with several intracellular membrane proteins to effect this intake. The ferric citrate is first transported to the periplasm by FecA, and then to the cytoplasm by the FecBCDE complex in the inner membrane. The TonB (3,4) protein provides energy required for the transportation of the ferric citrate into the cell (5).
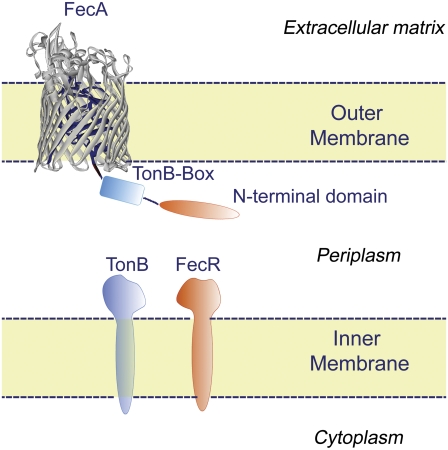
Besides acting simply as a transporter, FecA also plays other roles. When ferric citrate binds to FecA, located in the outer membrane of E. coli, the protein initiates a signaling cascade from the surface through its plug and barrel domains leading to the N-terminal domain (NTD) located in the periplasm (Fig. 1) (Ala1–Glu79). The signal transduction events continue through conformational changes when the NTD interacts with the FecR regulator in the inner membrane. The regulatory protein FecR transmits the signal further into the cell (5) by activating the sigma factor FecI in the cytoplasm. This activation leads to transcription initiation of the FecABCDE genes by RNA polymerase (6).
FIGURE 1.
The plug and barrel domains of the FecA transporter are shown embedded in the outer membrane. The barrel domain (gray) and the plug domain (blue) are highlighted here. The height of the FecA barrel domain is 65 Å, and its cross section is 35 Å × 47 Å. The NTD, TonB box, and the TonB and FecR proteins are shown schematically. The NTD extends from the plug domain into the periplasm. (This figure is adapted from Yue et al. (5).)
The energy required for this active transport system is purported to be provided by the TonB-ExbB-ExbD complex in the inner membrane. The TonB box, formed by residues D80-A81-L82-T83-V84, interacts with TonB. Deletion experiments (7) show that excision of this region stops both transcription initiation and the whole transport process of FecA.
FecA consists of three domains: the plug, the barrel, and the NTD (see Fig. 1, adapted from Yue, Grizot, and Buchanan (5)). The barrel domain forms an elliptical cylinder comprised primarily of β-sheets, typical for bacterial outer membrane proteins. The cross section of the barrel measures 35 × 47 Å and the height of the barrel is 65 Å. FecA crosses the outer membrane and extends ∼30 Å into the extracellular environment (8). The plug acts as a barrier between the environment outside the cell and the periplasm. It also serves as a binding site for ferric citrate. The NTD interacts with TonB and FecR proteins.
To elucidate the role of the interactions of FecA with TonB and with FecR for energy transduction and transcription signaling, the whole FecA structure is needed. However, x-ray crystallography has been able to determine only the plug and barrel domains of FecA, not its whole structure (the 80 N-terminal residues are missing in the pdb file 1kmo (5,8). The periplasmic domain structure has been determined separately by NMR (9,10). There has been one attempt to assemble FecA structure computationally. In their work, Garcia-Herrero and Vogel (10) proposed putative models of the entire FecA structure. These models are based on selected conformations of the linker from a large set of essentially randomly distributed conformations inferred from the NMR studies of the 96-residue construct containing the NTD. Thus, the proposed models (10) for the FecA complex are rather approximate. The models proposed in this work are results of extensive simulations that account for complex interactions between domains, and therefore are significantly more plausible. Based on our experience with hierarchical molecular docking using the CABS model (highly successful at CASP-6 (11)), the presented models and the mechanisms of assembly are likely to be correct (within the resolution of the modeled structure).
To analyze the domain motions and residue fluctuations of FecA, we use the Gaussian network model (GNM) (12) and the anisotropic network model (ANM) (13). Both of these elastic network models are based on the rubberlike elasticity theory of phantom polymer networks (14). The GNM considers a protein as a networked elastic body with residues as the nodes of the network. The coordinates of the nodes are usually given by the locations of the Cα atoms of amino acids. Additionally, it is assumed that all nodes interact with identical simple springlike harmonic potentials if the distance between two nodes falls within the cutoff distance, Rc; otherwise, the potential between nodes is zero. According to Tirion (15), all spring constants (and cutoffs, Rc) are assumed to have the same values, regardless of whether the pair is bonded or nonbonded. In addition to the residue-level coarse-grained models, atomic level (16), mixed coarse-grained models (17), and hierarchical coarse-graining methods (18) were developed by Bahar, Jernigan, and colleagues, and successfully applied to model proteins and other large biological structures, such as the ribosome (19,20). There are also elastic network models based on atomistic contacts with more detailed potentials (21,22). These approaches have now been widely applied by many groups to many problems (21,23–30).
The application of the GNM to biological structures is providing us with information and insights on global domain motions, which frequently relate to their biological function. For example, elastic network models are successful in capturing conformational changes upon binding (31). In our previous work, we used the GNM to explain the phenomenon of promiscuous protein binding, leading us to the general conclusion that both native and promiscuous functions can be comprehended as different combinations of the normal modes determined by protein shape and evolutionary constraints (32). The GNM is a simple model that captures the essential features of dense packing in proteins controlling their motions, and it is readily applicable to biological systems. The model allows us to calculate the mean-square fluctuations of residues, and therefore provides direct ways to compare its theoretical predictions with experimental data from x-ray crystallography (12), NMR (33,34), and hydrogen-exchange experiments (35). The GNM has also proved to be highly successful in prediction of the protein folding cores (36).
However, the GNM gives us only information for spherically symmetric fluctuations of residues about their equilibrium positions, with no directional information on domain motions. This limitation was overcome by the ANM, based on the second derivatives of the Hessian matrix. The ANM enables the calculation of the three-dimensional profile of residue fluctuations and yields direct information on the directions of global motions of biological structures.
In this article, we have applied these two elastic network models to the protein FecA to elucidate its domain dynamics and analyze how its NTD might interact with TonB and FecR. One advantage of using coarse-grained elastic network models for the analysis of NTD dynamics is their insensitivity to the protein resolution. As shown by Doruker and Jernigan (37), even highly coarse-grained protein models constructed on a lattice of varying resolution exhibit similar behavior of low-frequency normal modes that correspond to global motions (38,39).
METHODS
Gaussian network model
A detailed description of the Gaussian network model can be found elsewhere (12,41). Readers can refer to the following reviews (23,27,42) for further discussion. The underlying concept of the original GNM treatment is to represent a protein as a collection of springs (with a uniform value of the spring constant) between all geometrically close pairs of residues. In this treatment, each residue is represented as a point (node) positioned at its Cα atom. There are two parameters in the model: the cutoff distance, Rc, and the spring constant, γ. The cutoff distance, Rc, determines whether two residues will be connected by a spring, i.e., if they are in contact, not differentiating between bonded and nonbonded interactions. These contacts are expressed in the contact (Kirchhoff) matrix Γ with its elements Γij defined as
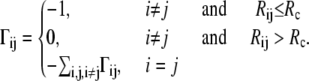 |
(1) |
Here, Rij is the distance between nodes i and j, and Rc is the cutoff distance. The matrix Γ is singular, because some of its eigenvalues are zero, and hence it has no proper inverse. However, the pseudoinverse of Γ can be obtained with singular value decomposition (SVD) by elimination of the zero eigenvalues. It can be shown that correlations between the fluctuations in positions,  of nodes from their mean positions
of nodes from their mean positions 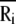 are
are
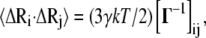 |
(2) |
where k is the Boltzmann constant, γ is the spring constant, and T is temperature. The diagonal of the pseudoinverse of the contact matrix provides information about the mean-square fluctuations for each node 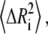 which in turn may be compared with the experimental crystallographic Debye-Waller temperature factors (B-factors), generally available in the PDB files. These are related to the mean-square atom fluctuations by
which in turn may be compared with the experimental crystallographic Debye-Waller temperature factors (B-factors), generally available in the PDB files. These are related to the mean-square atom fluctuations by
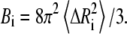 |
(3) |
The computed mean-square fluctuations can be decomposed into normal modes by using standard eigenvalue methods. The smallest eigenvalues corresponding to the global or collective motions are responsible for the largest-scale conformational rearrangements in proteins. On the other hand, the largest eigenvalues corresponding to noncollective modes represent mainly local dynamics. From the point of view of the overall protein motions, large-scale domain motions are significant, as they relate to protein functions (37,38). We used the Gaussian network model (GNM) with a cutoff radius to define contacts between residues. The cutoff radius is usually 7 Å for globular proteins. To compensate for the distance between the NTD and the plug and barrel domains, and to better capture the elastic dynamics of the FecA complex, we have used a slightly higher cutoff radius of 8 Å (16,43).
Anisotropic network models
Although the GNM has been highly successful in predicting the normal modes of proteins, it does not provide the directionalities of these modes, since it is a spherically symmetric model. To overcome these difficulties, the ANM has been proposed. In the ANM, the contact matrix is replaced by the Hessian matrix of size 3N × 3N, where N is the number of residues, formed by the second derivatives of the overall potential with respect to residue positions. The detailed theory of the ANM can be found in Atilgan et al. (13). Here, we used a cutoff value of 13 Å.
We applied the ANM to predict the domain motions of FecA corresponding to the slowest normal modes (the lowest-frequency large-scale domain motions). These global motions enable large conformational changes in the protein that are vital for the fulfillment of its function. Although the global domain motions are the most crucial for protein function, it is extremely difficult to study them by computer simulation methods such as molecular dynamics, because the required simulation times are usually beyond present-day computer capabilities, especially for larger structures. In that respect, the ANM is an important, simple, and highly useful tool to predict and visualize these domain motions, providing immediate insights into the mechanisms of protein function.
Modeling the N-terminal domain structure
Folding simulations of the entire Feca complex based on structural restraints for the N-terminal domain and the transmembrane domain are performed using the CABS method (44). The details and description of the force field can be found in Kolinski and Boniecki et al. (44,45). The docking of the N-terminal domain to the transmembrane fragment was done using the replica-exchange Monte Carlo sampling technique with unrestricted mutual orientation of the domains. The results of the CABS simulations were subjected to the average linkage hierarchical clustering (46), with the distance root mean-square separations being a measure of structural similarity. For each cluster, the centroid was calculated and a full atomic model rebuilt to provide the final model. The above-mentioned hybrid approach ranked among the best methods in the Sixth Critical Assessment of Techniques for Protein Structure Prediction (CASP-6) experiment (11) and has proven to predict appropriate protein models even in cases where no consensus fold was reported by the fold recognition servers (47,48). Several models of FecA were obtained, which differed in their relative orientation of the NTD with respect to the membrane.
Correlation coefficient
We calculate the linear correlation coefficient C,
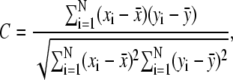 |
(4) |
where N is the number of residues, and xi and 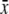 are, respectively, the mean-square residue fluctuations from the GNM computations and the average fluctuation over all residues. Similarly, yi and
are, respectively, the mean-square residue fluctuations from the GNM computations and the average fluctuation over all residues. Similarly, yi and 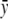 are the experimentally determined B-factors and their means. The linear correlation coefficient is a straightforward way to analyze the extent of linear dependence between two quantities. Its values range between 1 and −1, corresponding to perfect correlation and perfect anticorrelation, respectively. However, this coefficient has its limitations. The linear correlation coefficient shows only how two quantities deviate simultaneously from their means, without any reference to their relative amplitudes. Therefore, this parameter provides only information about the relative up-and-down patterns.
are the experimentally determined B-factors and their means. The linear correlation coefficient is a straightforward way to analyze the extent of linear dependence between two quantities. Its values range between 1 and −1, corresponding to perfect correlation and perfect anticorrelation, respectively. However, this coefficient has its limitations. The linear correlation coefficient shows only how two quantities deviate simultaneously from their means, without any reference to their relative amplitudes. Therefore, this parameter provides only information about the relative up-and-down patterns.
Overlap
Absolute overlap between two eigenvectors, each representing specific motions, is defined as
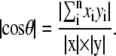 |
(5) |
In this equation, x and y are two eigenvectors, xi and yi denote their ith components, and θ is the angle between x and y. If two eigenvectors are exactly collinear, then their absolute overlap equals 1. If they are orthogonal to each other, then the absolute overlap is zero, and the angle between the two eigenvectors is 90°. This provides a measure of the extent of similarity in the directions of motions for different modes.
RESULTS AND DISCUSSION
Modeling of FecA complex
The FecA protein contains 741 residues and consists of three domains: the plug, the barrel, and the NTD. The crystallographic structure of the FecA plug and the barrel domains (residues 81–741) has been solved by x-ray crystallography (PDB code 1kmo (8)). The N-terminal fragment of the plug domain, containing 17 residues, is variable and changes upon binding the substrate.
Recently, the 79-residue-long fragment, the NTD, was the subject of an NMR study (10). The authors found that the NTD has a well-structured, 74-residue N-terminal fragment that forms a closely packed α + β fold. The C-terminus of the NTD (residues 75–96) was found to be unstructured. The analysis of the NMR data for this fragment shows a large number of alternative conformers. The structure of the NTD domain has also been determined by NMR by another group (9) (PDB code 1zzv). That structure is similar to the one found by Garcia-Herrera and Vogel (10) (root mean-square deviation (RMSD) = 2.3 Å (9)), with only slight differences between the two. One important feature of the second NMR structure is that the hydrophobic core is well protected from the solvent (9).
The most interesting questions are: 1), What is the orientation (and resulting interactions) of the NTD with respect to the main portion of FecA? and 2), What is the structure of the linker and how does it influence the mobility of the NTD? Due to lack of sufficient experimental data we must resort to molecular modeling to solve these problems.
Unfortunately, the large size of the molecular system makes molecular dynamics impractical. Therefore, we have applied a hierarchical modeling protocol based on CABS, our reduced conformational space modeling tool. CABS employs a simplified representation of protein conformations: the modeled polypeptide is reduced to an α-carbon trace, up to two united atoms representing the side chain and a virtual atom located in the center of each connecting Cα-Cα vector. These virtual atoms define the positions of the main chain hydrogen bonds. The CABS force field consists of a balanced set of knowledge-based statistical potentials. The conformational space is sampled via an efficient Monte Carlo algorithm. As a result, the simulations performed with CABS can cover a time interval by orders of magnitude larger than would be possible using classical molecular dynamics. Details of the CABS model and its force field can be found elsewhere (44). CABS has been effectively used for a variety of molecular modeling tasks: comparative modeling, de novo folding (11), the study of macromolecular assemblies (49), and protein-protein docking (50), and also to study long-time protein dynamics (51).
The modeling process consists of several steps. First, we generate an initial structure of the entire molecule. The coordinates of residues 81–741 were taken for the 1kmo PDB file and projected onto the lattice representation of CABS. Then the N-terminal portion of the FecA chain was added as an unstructured random coil. During simulations, residues 97–741 were kept frozen. For the structured 1–74 fragment, a set of weak distance restraints (a few hundred Cα-Cα distances, uniformly distributed) was derived from the NMR structure (PDB code 1zzv (9)). The strength of these restraints was set in such a way that the restrained residues were allowed to move 2–3 Å with respect to each other in a single Monte Carlo cycle. The linker (residues 75–96), including the TonB box, was not restrained in any way, and was allowed to move freely and to interact with the entire molecule. Two types of simulations were performed. In the first simulation, we employed replica-exchange Monte Carlo (REMC) to minimize the entire structure. The initial replicas have different, randomly generated conformations of the 96-residue N-terminus. During the simulations, the NTD fold assembled very rapidly. Due to the way the restraints were imposed, the NTD remained mobile during the rest of the simulation. The NTD structure fluctuated around the equilibrium internal coordinates of the NMR structure, and the entire domain rotated and translated with respect to the two C-terminal domains, stretching and folding the portions of the linker and adjusting interactions with the transmembrane cap and the plug domain. The structure of the NTD never departed by >2–2.5 Å from the NMR structure (cRMSD for the α-carbon traces).
After an initial equilibration (required for folding of the NTD), a large number of snapshots (a few thousand) were collected at equal intervals from a very long REMC simulation. These snapshots were subsequently subjected to hierarchical clustering (46). After this, atomic details for the cluster centroids were rebuilt (52) and the resulting all-atom structures were energy-minimized using an all-atom force field with an implicit solvent. In the all-atom minimization, the transmembrane barrel was frozen. Thus, no model of an implicit solvent was applied to this part of the assembly. The implicit solvent model was applied only to the NTD, and the membrane was treated as a nonpenetrable medium for the NTD. The changes of conformation for the NTD after the all-atom minimizations were small (essentially negligible), ranging from 0.2 Å to 0.4 Å (differing mainly in the orientations of the NTD with respect to the rest of the molecule). The all-atom energy was used to rank the models of the entire assembly. The minimization improved the packing of the side chains, allowing more exact analysis of the side-chain contacts. The use of all-atom energy has been shown to be highly effective in selecting the best models from the CABS simulations (53). Thus, we believe that the models presented are representative of the flexible orientations of the NTD with respect to the rest of the FecA structure.
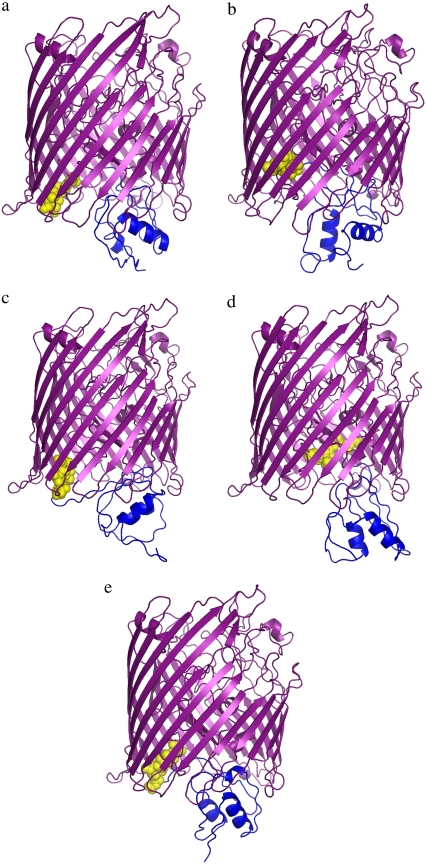
To further verify the model, we additionally performed a long isothermal simulation (using a single replica) at a temperature at which the NTD structure is well defined yet allowed to move with respect to the rest of the assembly. During the single-replica simulations, the transmembrane barrel was again kept frozen. The results were consistent with the REMC simulations. The NTD rotated and translated with respect to the rest of the FecA structure. Periods of highly local fluctuations near the structures identified in the two leading clusters from the REMC simulations, and fast transitions between these structures, were observed many times. Thus, the simulations indicate the existence of two dominant conformations of the complex, which (under the studied conditions) exchange their structures frequently. The three remaining clusters from the REMC simulations seem to correspond to shallow free-energy minima marking transition states between the two major minima. Here, we will call the first model FecA complex A, and the second FecA complex B (Fig. 2, a and b). The overall RMSD between the structures of these two leading clusters is 3.1 Å. This value reflects different orientations of the NTD domains.
FIGURE 2.
FecA complex structures obtained using hierarchical clustering from CABS simulations. The plug and barrel domains are shown in purple, the TonB-box in yellow, and the NTD domain in blue. FecA complex A (a) and FecA complex B (b) appear most frequently and the remaining conformations (c–e) appear less frequently in the CABS simulations (see Supplementary Materials for the coordinates of models).
The behavior of the linker is interesting. During the stretching phases, it was essentially unstructured. During the compacting phases, the residues on its C-terminus (85–96) frequently formed a β-strand (expanding the β-sheet of the plug domain) and a short flexible helix next to the β-sheet. The 75–84 fragment of the linker always remained essentially unstructured and highly flexible.
Ton-B box protection and exposure
The TonB box (D80–V84) is the interface where FecA interacts with the inner membrane protein TonB for energy transduction. The position of the TonB box differs in our two most reliable models of the FecA complex (Fig. 2, a and b). In the first model, FecA complex A, the TonB box is partially exposed to the periplasm in a conformation that allows the docking of TonB to FecA. In contrast, for FecA complex B, the TonB box is in a more protected conformation, shielded on the sides by the plug and barrel domains and at the bottom by the N-terminal of the plug domain. Our simulations capture these two essential conformations, which may play a part in various stages of the FecA-TonB interaction. These two different states suggest that when the FecA complex-TonB docking is initiated, the FecA conformation should switch from FecA complex B to complex A, exposing and aligning the TonB box for proper docking to TonB.
The fluctuations predicted with the Gaussian network model correlate well with experimental B-factors
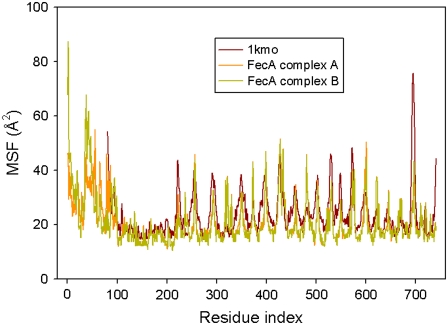
We analyzed the functional motions of the structures obtained in the modeling procedures using the elastic network models (12,13). These models (see Methods) can reproduce experimental data such as temperature factors (12,13), and provide the cooperative, global protein motions at low frequencies. A comparison of calculated and experimental fluctuations (Fig. 3) shows that the GNM is successful in reproducing the experimental results: the qualitative agreement between the predicted mean-square fluctuations and the experimental B-factors is strong. For a quantitative comparison, we calculated the correlation between experimental fluctuations and theoretical predictions using both FecA complex models, A and B. For residues 81–741, for which experimental B-factors are available, the correlation is 0.57 for both models. This value is close to the average value of correlations, 0.59, obtained by GNM (54). In the fluctuation plots, maxima correlate with protein residues of high flexibility, whereas minima correspond to regions of restricted flexibility. In the case of the FecA complex, the high-mobility regions generally coincide with the extracellular and periplasmic loops of the barrel domain, whereas the low-mobility regions correspond to residues in the β-sheets interacting with the cell membrane.
FIGURE 3.
Comparison of Cα mean-square fluctuations of the NTD (residues 1–86), plug domain (residues 87–223), and barrel domain (residues 224–741) of crystallized FecA, FecA complex A model, and FecA complex B model. The PDB code for the plug and barrel domains of FecA protein is 1kmo (8).
The global functional modes of the plug and barrel domains
To understand the functional motions of FecA embedded in the membrane, we applied the elastic network models to the plug and barrel domains to isolate the motions of these domains from the highly mobile NTD. Our elastic network analysis (see Methods) shows that in the slowest modes, FecA exhibits distinct motion patterns. The cross section of the plug and barrel domains noticeably opens and closes in a manner similar to a breathing motion. The most interesting observation is the high mobility of the periplasmic loops. The periplasmic loops swing as a result of the breathing motion of the plug and barrel domains. This high mobility suggests the functional importance of the periplasmic loops when FecA is interacting with the inner membrane proteins TonB and FecR. Both the extracellular and periplasmic loops are highly mobile in the slowest modes, but exhibit significantly correlated fluctuations (computed from Eq. 2). This is an interesting observation, as it implicitly suggests the presence of a communication between the loops on both ends of the protein, a signaling mechanism by which a signal could be transmitted by conformational transitions in response to the binding of ferric citrate.
Motion overlap between the two most probable conformations of the FecA complex
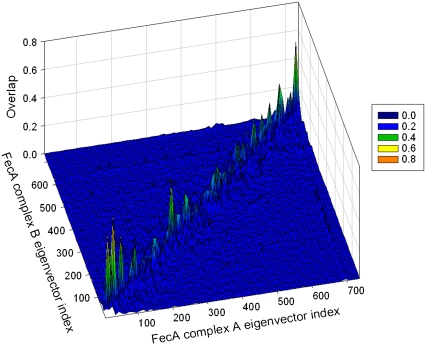
We analyzed the extent of similarity between the global motions of the two most probable computed conformations of the FecA complex (FecA complexes A and B.) Although FecA moves continuously during simulations and acquires various conformations, certain conformations are more preferred (Fig. 2). The main question, then, is, when FecA changes its conformation as a result of its dynamic nature, to what extent are the functional slow motions affected? A simple overlap between eigenvectors of the two preferred conformations can shed light on this issue. This overlap is shown in Fig. 4. Here, eigenvectors with smaller indexes refer to slower modes, and those with larger indexes to faster modes. In the 3D graph in Fig. 4, there are peaks and lighter colors when there is high overlap. The overlap is especially strong for the slowest modes along the diagonal.
FIGURE 4.
The overlap between the eigenvectors of FecA complexes A and B obtained using the GNM. Lighter colors represent higher overlap values.
Global modes of motion of the FecA complex
We used FecA complexes A and B to investigate global motions of FecA. Fig. 5 shows the cross-correlation between the residue fluctuations of these two conformations calculated using the following formula:
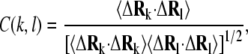 |
(6) |
where C(k,l) is the cross-correlation between the fluctuations of residues k and l. For the plug and barrel domains, the correlations between two conformations are highly similar; the major difference occurs for the NTD domain. To gain a visual understanding of the motions, we have performed further analysis and computed the flexibility of various parts of the FecA structure (Fig. 6). The most mobile regions are shown in red and green; and rigid regions are shown in blue. A striking feature in Fig. 6 is the presence of the rigid regions: although the membrane structure has not been included in the model, the membrane-bound plug and barrel domains still display comparatively high rigidity. This rigidity emphasizes that β-barrel arrangements are structurally stable and suggests that the shape of the β-barrel fold may not require the bilipid membrane for its structural integrity. However, as has been observed in several studies (55–58), the nonpolar side chains are exposed on the outside of the barrel and thus require the hydrophobic environment of the outer membrane. Thus, in the case of the FecA complex, the shape-dependent stability is enhanced by chemical specificity of binding to ensure structural integrity.
FIGURE 5.
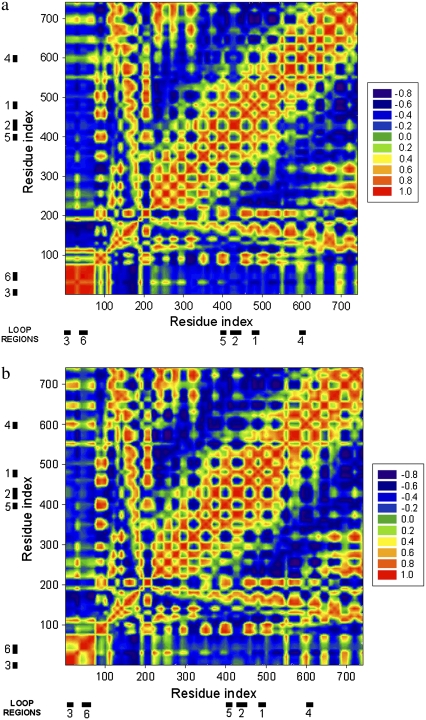
Cross-correlation map between the residue fluctuations for the cumulative first five slowest modes for (a) FecA complex A and (b) FecA complex B using GNM. The red color shows the perfect correlation and the blue color the perfect anticorrelation. The locations of the loops that show highly correlated, large motions are displayed with thick bars and numbered according to the following notation: Region 1, Asn477–Glu484; Region 2, Thr422–Arg438; Region 3, Ala1–Ile5; Region 4, Leu597–Asp602; Region 5, Ile397–Ala401; and Region 6, Asn38–Gly49. These regions are also shown in Fig. 6 on the FecA structure with the same numbering scheme.
FIGURE 6.
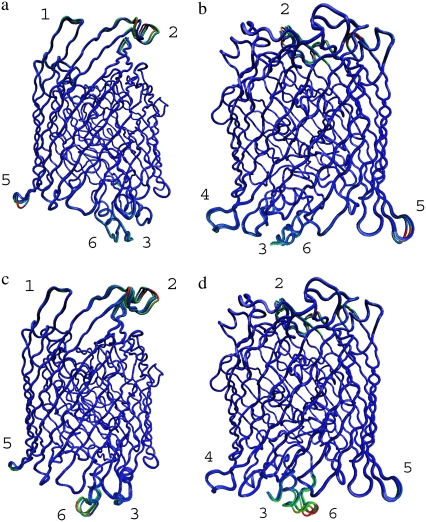
The mobile regions in FecA complex for the first four slowest modes using ANM. FecA is positioned in such a way that the top faces the extracellular matrix and the bottom faces the periplasm. The conformations are overlapped and colored according to the range of motions. Red and blue represent the most mobile and most rigid regions, respectively. (a and b) FecA complex A. (c and d) FecA complex B. Regions shown on the right are the 180° rotated views of a and c. The most mobile regions are identified with the same numbers in all figures for comparison. See text for detailed information on these regions.
The mobile regions are numbered in Fig. 5 for further analysis: Region 1, Asn477–Glu484; Region 2, Thr422–Arg438; Region 3, Ala1–Ile5; Region 4, Leu597–Asp602; Region 5, Ile397–Ala401; and Region 6, Asn38–Gly49. As Region 1 is the free chain end of the N-terminal, its mobility is not a consequence of cooperative motions, but originates as a result of the absence of structural constraints. Most of the other mobile regions are located on the loops connecting regular secondary structures. Because loops have a higher degree of freedom compared to the highly packed regions, their high mobility is usually expected. However, the slowest modes derived from elastic network models are highly specific: only certain loops—not all loops—show large correlated motions, which suggests that these mobile loops may have functional roles in the ferric citrate signaling and transfer. Directed single-site mutagenesis or deletion experiments may reveal details about which specific residue sites on the loops are essential.
Although the plug and barrel domains show less mobility, they do not stay entirely rigid, but rather show distinct motions: for example, the barrel cross section enlarges and contracts in a breathing motion, as discussed above. Through this mobility of the cross section, the plug and barrel domains serve as a connector between periplasmic and extracellular loops, transferring the mechanical energy in a collective manner.
Correlated motions between different parts of FecA have different characteristics at different slow modes. In some cases, they display “pinching motions,” such as between the periplasmic loops in Regions 5 and 6. In other cases, certain loops twist in coordination, such as the extracellular loops in Regions 1 and 2. However, the most striking feature in these correlations is not the type of motion they exhibit, but that in slow motions, at least one periplasmic and one extracellular loop move in coordination. This observation suggests the presence of allosteric communication between the extracellular and periplasmic sides of FecA. Such paths of communication are essential to relay the information of ferric citrate binding from the extracellular side to the periplasmic domain and, finally, to the cell interior.
One of the mobile regions that is particularly interesting is Region 6, as it has slightly different conformations in FecA complex models A and B. Region 6 (Fig. 6) is located at the periplasmic side of FecA and its mobility is not restricted to the loop, but extends to the helix structure. Although the helix orientation differs in both complex models, the helix-loop region moves in coordination with other mobile regions. This brings up the question of whether this region on the periplasmic side plays a critical role in docking to the inner membrane proteins.
Other slow modes show different combinations of coordinated movements of the periplasmic and extracellular loops, as well as other loops shown in Fig. 6. These examples support the point of view that, even for nonallosteric proteins (59), the protein shape is essential to allow for communication between distant sites executed through concerted motions.
CONCLUSION
The transmembrane protein FecA is located in the outer membrane of E. coli and is responsible for recognition and intake of ferric citrate, and transcription of the genes FecABCDE, which is required for ferric citrate transport to the cell cytoplasm. During this process, FecA interacts with inner membrane proteins and obtains its energy from the TonB-ExbB-ExbD complex. Although FecA plays a vital role in cellular fitness, its full structure is not completely known; the structures of the plug and barrel domains and the NTD are available separately. This structural information gap hinders our ability to fully elucidate the mechanism of ferric citrate transport in E. coli. To narrow this gap, we modeled the three-dimensional structure of the full FecA complex.
In our modeling, we carried out CABS folding simulations with a comprehensive force-field description, extracted several structures from multiple simulation samplings using hierarchical clustering, and validated plausible structures by checking interatomic distances to obtain the final model.
As the protein dynamics is inherently related to its function, we also applied elastic network models to probe FecA cooperative motions related to lowest normal modes. The NTD exhibits a range of motions, including swinging, twisting, and rotating, which harness the relative flexibility of the loop connecting the NTD to the plug domain. Such mobility is required for proper docking of the TonB protein to the TonB box, but the mechanistic details of this interaction are currently unknown. The two most striking features in the FecA global modes are 1), correlated motions of the NTD and the extracellular and periplasmic loops; and 2), the presence of two conformations that control the exposure of the TonB box to the periplasm, which may control TonB docking to FecA. These coupled motions may be useful in signal transduction associated with ferric citrate binding, as well as in ferric citrate transport. We expect that the structural models obtained in this study will stimulate more experiments and simulations for more detailed elucidation of these mechanisms in the future.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
T.Z.S. thanks Ozge Kurkcuoglu for her assistance with graphics. The authors also thank two anonymous reviewers for helpful suggestions that improved this article.
M.K. received a fellowship from the National Institutes of Health (NIH) National Science Foundation BBSI Summer Institute in Bioinformatics and Computational Biology. T.Z.S., A.Klo., and R.L.J. acknowledge financial support provided by NIH grants 1R01GM072014-01 and 1R01GM073095-02. A.Klo., R.L.J., A.Kol., and J.M.B. acknowledge financial support provided by NIH grant 1R01GM081680-01.
Margaret Kloster's present address is Dept. of Biostatistics, University of Washington, Seattle, WA 98195-7232.
Editor: Angel E. Garcia.
References
- 1.Braun, V. 2003. Iron uptake by Escherichia coli. Front. Biosci. 8:S1409–S1421. [DOI] [PubMed] [Google Scholar]
- 2.Braun, V., and M. Braun. 2002. Iron transport and signaling in Escherichia coli. FEBS Lett. 529:78–85. [DOI] [PubMed] [Google Scholar]
- 3.Wiener, M. C. 2005. TonB-dependent outer membrane transport: going for Baroque? Curr. Opin. Struct. Biol. 15:394–400. [DOI] [PubMed] [Google Scholar]
- 4.Pawelek, P. D., N. Croteau, C. Ng-Thow-Hing, C. M. Khursigara, N. Moiseeva, M. Allaire, and J. W. Coulton. 2006. Structure of TonB in complex with FhuA, E. coli outer membrane receptor. Science. 312:1399–1402. [DOI] [PubMed] [Google Scholar]
- 5.Yue, W. W., S. Grizot, and S. K. Buchanan. 2003. Structural evidence for iron-free citrate and ferric citrate binding to the TonB-dependent outer membrane transporter FecA. J. Mol. Biol. 332:353–368. [DOI] [PubMed] [Google Scholar]
- 6.Kim, I., A. Stiefel, S. Plantor, A. Angerer, and V. Braun. 1997. Transcription induction of the ferric citrate transport genes via the N-terminus of the FecA outer membrane protein, the Ton system and the electrochemical potential of the cytoplasmic membrane. Mol. Microbiol. 23:333–344. [DOI] [PubMed] [Google Scholar]
- 7.Ogierman, M., and V. Braun. 2003. Interactions between the outer membrane ferric citrate transporter FecA and TonB: studies of the FecA TonB box. J. Bacteriol. 185:1870–1885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ferguson, A. D., R. Chakraborty, B. S. Smith, L. Esser, D. van der Helm, and J. Deisenhofer. 2002. Structural basis of gating by the outer membrane transporter FecA. Science. 295:1715–1719. [DOI] [PubMed] [Google Scholar]
- 9.Ferguson, A. D., C. A. Amezcua, N. M. Halabi, Y. Chelliah, M. K. Rosen, R. Ranganathan, and J. Deisenhofer. 2007. Signal transduction pathway of TonB-dependent transporters. Proc. Natl. Acad. Sci. USA. 104:513–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Garcia-Herrero, A., and H. J. Vogel. 2005. Nuclear magnetic resonance solution structure of the periplasmic signalling domain of the TonB-dependent outer membrane transporter FecA from Escherichia coli. Mol. Microbiol. 58:1226–1237. [DOI] [PubMed] [Google Scholar]
- 11.Kolinski, A., and J. M. Bujnicki. 2005. Generalized protein structure prediction based on combination of fold-recognition with de novo folding and evaluation of models. Proteins. 61:84–90. [DOI] [PubMed] [Google Scholar]
- 12.Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
- 13.Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kloczkowski, A., J. E. Mark, and B. Erman. 1989. Chain dimensions and fluctuations in random elastomeric networks. 1. Phantom Gaussian networks in the undeformed state. Macromolecules. 22:1423–1432. [Google Scholar]
- 15.Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
- 16.Sen, T. Z., Y. P. Feng, J. V. Garcia, A. Kloczkowski, and R. L. Jernigan. 2006. The extent of cooperativity of protein motions observed with elastic network models is similar for atomic and coarser-grained models. J. Chem. Theory Comput. 2:696–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kurkcuoglu, O., R. L. Jernigan, and P. Doruker. 2005. Collective dynamics of large proteins from mixed coarse-grained elastic network model. QSAR Comb. Sci. 24:443–448. [Google Scholar]
- 18.Doruker, P., R. L. Jernigan, and I. Bahar. 2002. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem. 23:119–127. [DOI] [PubMed] [Google Scholar]
- 19.Wang, Y. M., A. J. Rader, I. Bahar, and R. L. Jernigan. 2004. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 147:302–314. [DOI] [PubMed] [Google Scholar]
- 20.Tama, F., M. Valle, J. Frank, and C. L. Brooks. 2003. Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proc. Natl. Acad. Sci. USA. 100:9319–9323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kondrashov, D. A., Q. A. Cui, and G. N. Phillips. 2006. Optimization and evaluation of a coarse-grained model of protein motion using x-ray crystal data. Biophys. J. 91:2760–2767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kondrashov, D. A., A. W. Van Wynsberghe, R. M. Bannen, Q. Cui, and G. N. Phillips. 2007. Protein structural variation in computational models and crystallographic data. Structure. 15:169–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chennubhotla, C., A. J. Rader, L. W. Yang, and I. Bahar. 2005. Elastic network models for understanding biomolecular machinery: from enzymes to supramolecular assemblies. Phys. Biol. 2:S173–S180. [DOI] [PubMed] [Google Scholar]
- 24.Ertekin, A., R. Nussinov, and T. Haliloglu. 2006. Association of putative concave protein-binding sites with the fluctuation behavior of residues. Protein Sci. 15:2265–2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Konuklar, F. A. S., V. Aviyente, and T. Haliloglu. 2006. Coupling of structural fluctuations to deamidation reaction in triosephosphate isomerase by Gaussian network model. Proteins. 62:715–727. [DOI] [PubMed] [Google Scholar]
- 26.Shrivastava, I. H., and I. Bahar. 2006. Common mechanism of pore opening shared by five different potassium channels. Biophys. J. 90:3929–3940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tama, F., and C. L. Brooks. 2006. Symmetry, form, and shape: guiding principles for robustness in macromolecular machines. Annu. Rev. Biophys. Biomol. Struct. 35:115–133. [DOI] [PubMed] [Google Scholar]
- 28.Tobi, D., and I. Bahar. 2005. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA. 102:18908–18913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Erman, B. 2006. The Gaussian network model: precise prediction of residue fluctuations and application to binding problems. Biophys. J. 91:3589–3599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Eyal, E., L. W. Yang, and I. Bahar. 2006. Anisotropic network model: systematic evaluation and a new web interface. Bioinformatics. 22:2619–2627. [DOI] [PubMed] [Google Scholar]
- 31.Keskin, O. 2007. Binding induced conformational changes of proteins correlate with their intrinsic fluctuations: a case study of antibodies. BMC Struct. Biol. 7:31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Fernandez, A., D. S. Tawfik, B. Berkhout, R. W. Sanders, A. Kloczkowski, T. Z. Sen, and R. L. Jernigan. 2005. Protein promiscuity: drug resistance and native functions—HIV-1 case. J. Biomol. Struct. Dyn. 22:615–624. [DOI] [PubMed] [Google Scholar]
- 33.Haliloglu, T., and I. Bahar. 1999. Structure-based analysis of protein dynamics: comparison of theoretical results for hen lysozyme with X-ray diffraction and NMR relaxation data. Proteins. 37:654–667. [DOI] [PubMed] [Google Scholar]
- 34.Temiz, N. A., E. Meirovitch, and I. Bahar. 2004. Escherichia coli adenylate kinase dynamics: comparison of elastic network model modes with mode-coupling N-15-NMR relaxation data. Proteins. 57:468–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bahar, I., A. Wallqvist, D. G. Covell, and R. L. Jernigan. 2006. Correlation between native-state hydrogen exchange and cooperative residue fluctuations from a simple model. Biochemistry. 37:1067–1075. [DOI] [PubMed] [Google Scholar]
- 36.Rader, A. J., and I. Bahar. 2004. Folding core predictions from network models of proteins. Polymer (Guildf.). 45:659–668. [Google Scholar]
- 37.Doruker, P., and R. L. Jernigan. 2003. Functional motions can be extracted from on-lattice construction of protein structures. Proteins. 53:174–181. [DOI] [PubMed] [Google Scholar]
- 38.Lu, M. Y., and J. P. Ma. 2005. The role of shape in determining molecular motions. Biophys. J. 89:2395–2401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ming, D., Y. F. Kong, M. A. Lambert, Z. Huang, and J. P. Ma. 2002. How to describe protein motion without amino acid sequence and atomic coordinates. Proc. Natl. Acad. Sci. USA. 99:8620–8625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Reference deleted in proof.
- 41.Haliloglu, T., I. Bahar, and B. Erman. 1997. Gaussian dynamics of folded proteins. Phys. Rev. Lett. 79:3090–3093. [Google Scholar]
- 42.Ma, J. P. 2005. Usefulness and limitations of normal mode analysis in modeling dynamics of biomolecular complexes. Structure. 13:373–380. [DOI] [PubMed] [Google Scholar]
- 43.Sen, T. Z., and R. L. Jernigan. 2005. Optimizing the parameters of Gaussian network model for ATP-binding proteins. In Normal Mode Analysis: Theory and Applications to Biological and Chemical Systems. Q. Cui and I. Bahar, editors. CRC, Boca Raton, FL. 171–186.
- 44.Kolinski, A. 2004. Protein modeling and structure prediction with a reduced representation. Acta Biochim. Pol. 51:349–371. [PubMed] [Google Scholar]
- 45.Boniecki, M., P. Rotkiewicz, J. Skolnick, and A. Kolinski. 2003. Protein fragment reconstruction using various modeling techniques. J. Comput. Aided Mol. Des. 17:725–738. [DOI] [PubMed] [Google Scholar]
- 46.Gront, D., and A. Kolinski. 2005. HCPM: program for hierarchical clustering of protein models. Bioinformatics. 21:3179–3180. [DOI] [PubMed] [Google Scholar]
- 47.Kurowski, M. A., and J. M. Bujnicki. 2003. GeneSilico protein structure prediction meta-server. Nucleic Acids Res. 31:3305–3307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kosinski, J., I. A. Cymerman, M. Feder, M. A. Kurowski, J. M. Sasin, and J. M. Bujnicki. 2003. A “Frankenstein's monster” approach to comparative modeling: merging the finest fragments of fold-recognition models and iterative model refinement aided by 3D structure evaluation. Proteins. 53:369–379. [DOI] [PubMed] [Google Scholar]
- 49.Kurcinski, M., and A. Kolinski. 2007. Steps towards flexible docking: modeling of three-dimensional structures of the nuclear receptors bound with peptide ligands mimicking co-activators' sequences. J. Steroid Biochem. Mol. Biol. 103:357–360. [DOI] [PubMed] [Google Scholar]
- 50.Kurcinski, M. and A. Kolinski. 2007. Hierarchical modeling of protein interactions. J. Mol. Model. 13:691–698. [DOI] [PubMed] [Google Scholar]
- 51.Kmiecik, S., M. Kurcinski, A. Rutkowska, D. Gront, and A. Kolinski. 2006. Denatured proteins and early folding intermediates simulated in a reduced conformational space. Acta Biochim. Pol. 53:131–143. [PubMed] [Google Scholar]
- 52.Gront, D., S. Kmiecik, and A. Kolinski. 2007. Backbone building from quadrilaterals: a fast and accurate algorithm for protein backbone reconstruction from α carbon coordinates. J. Comput. Chem. 28:1593–1597. [DOI] [PubMed] [Google Scholar]
- 53.Kmiecik, S., D. Gront, and A. Kolinski. 2007. Towards the high-resolution protein structure prediction. Fast refinement of reduced models with all-atom force field. BMC Struct. Biol. 7:43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Kundu, S., J. S. Melton, D. C. Sorensen, and G. N. Phillips. 2002. Dynamics of proteins in crystals: comparison of experiment with simple models. Biophys. J. 83:723–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Haltia, T., and E. Freire. 1995. Forces and factors that contribute to the structural stability of membrane proteins. Biochim. Biophys. Acta. 1228:1–27. [DOI] [PubMed] [Google Scholar]
- 56.Murzin, A. G., A. M. Lesk, and C. Chothia. 1994. Principles determining the structure of β-sheet barrels in proteins. 1. A theoretical analysis. J. Mol. Biol. 236:1369–1381. [DOI] [PubMed] [Google Scholar]
- 57.Murzin, A. G., A. M. Lesk, and C. Chothia. 1994. Principles determining the structure of β-sheet barrels in proteins. 2. The observed structures. J. Mol. Biol. 236:1382–1400. [DOI] [PubMed] [Google Scholar]
- 58.Wimley, W. C. 2003. The versatile β-barrel membrane protein. Curr. Opin. Struct. Biol. 13:404–411. [DOI] [PubMed] [Google Scholar]
- 59.Gunasekaran, K., B. Y. Ma, and R. Nussinov. 2004. Is allostery an intrinsic property of all dynamic proteins? Proteins. 57:433–443. [DOI] [PubMed] [Google Scholar]