Spatial Regulation Improves Antiparallel Microtubule Overlap during Mitotic Spindle Assembly

Abstract

The mitotic spindle plays an essential role in chromosome segregation during cell division. Spindle formation and proper function require that microtubules with opposite polarity overlap and interact. Previous computational simulations have demonstrated that these antiparallel interactions could be created by complexes combining plus- and minus-end-directed motors. The resulting spindles, however, exhibit sparse antiparallel microtubule overlap with motor complexes linking only a nominal number of antiparallel microtubules. Here we investigate the role that spatial differences in the regulation of microtubule interactions can have on spindle morphology. We show that the spatial regulation of microtubule catastrophe parameters can lead to significantly better spindle morphology and spindles with greater antiparallel MT overlap. We also demonstrate that antiparallel microtubule overlap can be increased by having new microtubules nucleated along the length of existing astral microtubules, but this increase negatively affects spindle morphology. Finally, we show that limiting the diffusion of motor complexes within the spindle region increases antiparallel microtubule interaction.

INTRODUCTION

During mitosis, microtubules (MTs) organize to produce the mitotic spindle, providing the necessary network for successful cell division. How MTs interact to form the mitotic spindle is not fully understood. Although many of the proteins involved in spindle formation have been identified, the dense MT network makes it difficult to visualize and measure their interactions and collective contributions to spindle formation. This compounds the difficulty of inferring an accurate model of spindle formation from experimental observations. Computer simulations allow us to approach the problem from the opposite direction; they allow us to specify a hypothesized model and let the simulation determine the form of the resulting spindle. Given the multitude of possible regulatory models governing spindle formation and the difficulty in isolating them experimentally, the simulation approach is a particularly useful means of testing the effects of each individually (1–5).

Computer simulations have shown that stable interactions between overlapping MTs of antiparallel orientation can be generated by heterocomplexes of motor proteins that consist of one plus-end- and one minus-end-directed motor (Fig. 1 A) (6). In contrast, the presence of homocomplexes consisting of two plus-end-directed motors makes the asters fuse, whereas that of two minus-end-directed motors makes the asters separate. Although motor heterocomplexes lead to spindles with antiparallel MT interaction, the number of interacting MTs is small. In addition, the presence of long astral MTs makes the morphology of these simulated spindles weakly reminiscent of that of real spindles. The differences in spindle morphology generated by the model and spindles observed experimentally suggest that mechanisms are absent from the model. We consider a number of hypothesized mechanisms in our model and evaluate how well they improve MT overlap and distribution within the spindle region. Principal among these mechanisms is spatial regulation of parameters governing MT dynamic instability. Although much of the experimental evidence for the putative schemes considered here comes from Xenopus extracts, we do not focus on any one organism but instead aim at studying general mechanisms. However, these simulations are more likely to represent spindle formation in systems undergoing an open mitosis.

FIGURE 1.

Computer simulations of interacting MTs give rise to spindles. (A) MTs interact through the action of heterodimer motors consisting of plus- and minus-end-directed motors. These motors can link two MTs in either parallel or antiparallel configuration, depending on the orientation of the two MTs' polarities. (B) Simulations start with two noninteracting asters. The combined effects of diffusion, MT dynamic instability, and motor activity give rise to spindles. The relative interaction is defined by the spindle quality measure (Materials and Methods), which fluctuates over time because of the stochastic nature of the simulations. Shown is the spindle quality measure over time for one control simulation as well as snapshots of the MTs at specific times, denoted by the lower-case letters. Each box in the insets is 30 μm × 30 μm. (C) Five different motor parameter sets (PS1–PS5) were considered, and baseline Spindle Quality (SQ) values for each were computed by repeated simulation. The bar graph shows the average SQ with error bars denoting the standard deviation. The insets show representative interactions for each parameter set. (D) For simulations involving spatial regulation, the kinetic parameters were varied spatially according to the profiles shown. For example, an eightfold increase in a dynamic instability parameter refers to the increase at the spindle center and decreases radially, reaching the basal level at the location of the asters and decreasing further out (green line). Spatial parameters that are down-regulated are similarly varied according to the red line, which is the reciprocal of the green line. The different colored dots in this panel represent the location and state of different motors: unattached (black), motors with only one hand attached (green), and motors linking parallel (red) or antiparallel (blue) oriented MTs.

Dynamic instability is a process under which MTs undergo cycles of growth and shrinkage at their ends (7). It has been suggested that cells may regulate the parameters dictating dynamic instability (catastrophe, rescue, growth, and shrinkage rates) spatially (8). Such spatial regulation could be accomplished by a concentration gradient of a morphogen diffusing away from a chromatin-associated source into the cytoplasm, where it is destroyed (9). An example is the RanGTP gradient that is produced by the nucleotide exchange factor RCC1, which localizes to chromosomes (10–13).

There is experimental evidence that is consistent with the hypothesized spatial regulation of dynamic instability parameters. The catastrophe promoter Stathmin Oncoprotein 18 (Op18) is deactivated by the chromosome-associated Aurora B kinase producing a chromosome-centered inactivation gradient (14,15). Aurora B kinase also inhibits the catastrophe promoter MCAK/XKCM1 (16,17). Thus, a spatial component in MCAK/XKCM1 activity may also be expected. Together, these data suggest that catastrophe frequency would be lower near the chromosomes. On the other hand, RanGTP enhances MT rescue frequency by up to eightfold in Xenopus egg extracts (18), and there is evidence, both theoretical and experimental, that RanGTP is found in a concentration gradient during mitosis based on the nucleotide exchange factor RCC1 being localized to chromosomes (10–13).

Evidence for spatial growth rate regulation is less certain. Experiments in vivo have shown larger growth rates than those in vitro, indicating that the cell has the ability to modulate growth rate (19). Measurements in Xenopus egg extracts found a large decrease in growth rate near the chromatin, almost to the extent of a pause (20).

Because spatial regulation of MT dynamic parameters is probably the most assured means of increasing antiparallel MT interactions and MT distribution within the spindle region while also being biologically supported, we explore the extent to which it does. Similar simulations have led to a model in which such spatial biasing, possibly by RanGTP gradients, provides improved chromosome capture efficiency during mitosis (21).

We also consider the effects of various MT nucleating schemes. Though centrosomes are the dominant microtubule organizing center, bipolar spindles can still form in their absence as observed in Xenopus egg extracts (22) and vertebrate somatic cells (23). In addition to MT nucleation on the centrosome, MTs have also been observed nucleating on kinetochores, chromosomes, and on the spindle itself (24). Simulations restricting MT nucleation to the centrosome (6) may inherently limit MT density within the spindle region compared with simulations in which MTs can be nucleated elsewhere (25,26). The orientation of the MT minus ends radiating from the centrosomes could also be a strong factor in spindle morphology and astral MT prominence. For example, maintaining a radially uniform distribution of MT minus ends at the centrosomes biases half of the MTs to point away from the spindle region and resists their bending toward the spindle region. We test the effects of nucleating MTs on astral MTs under various branching schemes and allow the orientation of the nucleated MTs to change according to motor-complex-induced forces in contrast to uniform radial orientation of the MT minus ends anchored to the centrosomes (6).

Although the nucleation mechanisms that underlie the phenotypes we explore are speculative, a wide variety of similar branching behaviors have been observed in various cells. Plant cells have been observed nucleating MTs at specific angles (40° angles in cortical MT arrays) (27). In Xenopus egg extracts, the orientation appears to be random in the absence of centrosomes (22). In fission yeast, MTs appear to nucleate in antiparallel bundles during interphase (28).

MATERIALS AND METHODS

Computational Model

Our starting point is the cytosim model of interacting MT asters via heteromotor complexes (6). The interactions of 5000 motor complexes and two asters (60 MTs each) are simulated for 1000 s with a 10-ms sampling time. Each microtubule is modeled as a sequence of 1-μm-long rods and is allowed to grow, shrink, bend, and diffuse. MTs stochastically change states between growing and shrinking according to their catastrophe and rescue frequencies. Initially, the asters are randomly placed within a two-dimensional 12 × 12 μm region but are allowed to move within a 60 × 60 μm region thereafter. The heteromotor complexes, consisting of one minus-end-directed motor and one plus-end-directed motor, were found to be the only arrangement that maintained stable antiparallel overlap between two asters (6) (plus-end-directed complexes and minus-end-directed complexes produced either aster fusion or aster separation without stable antiparallel overlap). Although such complexes do not specifically correspond to any that have yet been observed, the motors' properties were chosen to be similar to those of conventional kinesin (Table 1). The motor complexes are free to diffuse and stochastically bind and process along MTs that are within their reach. Motor complexes with both motors bound exert forces on the MTs according to Hooke's law, causing the MTs to bend and slide along one another. In linked motor complexes, one hand detaches stochastically if the Hookean spring force exceeds the motor's threshold.

TABLE 1.

Parameter sets differ only in the characteristics of their heteromotor complexes

Parameter set	Speed (μm/s)		Attach frequency (1/s)		Detach frequency (1/s)		Detach frequency at MT end (1/s)		Grab length (μm)		Maximum force (pN)		Motor link rigidity (pN/μm)
	+	−	+	−	+	−	+	−	+	−	+	−
1	0.31	–0.73	1.94	6.16	0.06	0.80	200	200	0.119	0.069	1.9	1.1	16.0
2	0.37	–0.55	0.05	36.68	0.07	0.12	0.1	100	0.146	0.046	1.9	0.6	13.0
3	0.43	–0.77	6.00	8.00	0.21	0.17	0.2	100	0.083	0.050	0.5	0.3	6.0
4	0.29	–0.87	9.09	3.39	0.87	0.05	200	0.1	0.113	0.188	0.9	1.5	8.0
5	0.38	–0.48	2.82	10.12	0.11	0.06	0.3	100	0.180	0.030	1.8	0.7	5.0
Avg	0.36	–0.68	3.98	12.87	0.26	0.24	80.1	100	0.128	0.076	1.4	0.8	9.6

Each heteromotor complex consists of one plus-end-directed hand (+) and one minus-end-directed hand (−).

At each time step, the MT positions are updated based on their mobility and the forces acting on them. Hookean spring forces from linked motor complexes cause their attached MTs to bend and slide relative to one another. Straightening forces are applied to bent MTs based on the radius of curvature. Forces from the static links holding each aster together are applied to the MT minus ends. Brownian motion forces are also applied. No other forces, such as steric forces resulting from MT collisions, are applied to the MTs.

The 10-ms sampling time was chosen to match the control simulations from Nedelec (6), and it is sufficiently small to model search and capture of MTs by diffusing motor complexes. With 100-nm-radius motor complexes and a viscosity of 50 mPa·s, the root mean-square diffusion distance of each motor complex during a time step of 10 ms is ∼30 nm. Each motor complex probabilistically binds to a MT when it is within its hand-grab length distance (∼100 nm), implying that as long as a motor complex does not diffuse beyond 200 nm each time step, it will have an opportunity to bind to neighboring MTs. We also ran control simulations with a 5-ms sampling time (rms diffusion distance of 21 nm) and obtained statistically similar results (not shown; average Students t-test value of 0.28).

Although this simulation is in two dimensions, the initial binding of a motor to a single MT corresponds to that in a three-dimensional simulation with a motor concentration of ∼30 nM. To obtain this correspondence, we solved for the number of motor complexes in a 60 × 60 × 60 μm volume required to generate an attachment probability equal to that used in our two-dimensional 60 × 60 μm simulations assuming a hand-grab length of 100 nm. Because this equivalent three-dimensional concentration is of the same order as motor concentrations that can be found in cells (Eg5 can be found at ∼100 nM), we would expect the corresponding simulations in three dimensions to produce consistent if not more pronounced results than those we found in our two-dimensional simulations. Furthermore, it is only the initial binding of a motor that would depend on three-dimensional diffusion, as subsequent linking of the other motor in the complex would no longer be diffusing, and its path would be restricted to the one-dimensional path of the MT to which the complex is bound. Also, the MTs are able to cross over each other, and motor complexes can diffuse past MTs if they do not bind as they would in a three-dimensional simulation.

Spatial regulation

Microtubule parameters are spatially regulated by multiplying by a factor whose value depends on a radially varying gradient. The gradient is determined by solving at equilibrium the one-dimensional reaction-diffusion equation, where c(x) is the concentration of a species (morphogen) that is created or activated at one end (for example, on the chromatin), diffuses a distance (x) from the spindle center (D is the diffusion coefficient), and is consumed or inactivated in the cytosol (with degradation constant k) (29). To solve the equation, we impose the following constraints: c(0) = G, c′(2R) = 0, and c(R) = 1. The first constraint specifies the speculative maximum concentration, G, at the center of the spindle. We locate the scaling factors' extrema at the spindle center based on the assumption that the putative regulators will have a peak concentration near the chromosomes (14–17). The second constraint causes the morphogen concentration to reach a constant value at twice the spindle radius, R. In our simulations, this concentration is used for distances farther than twice the spindle radius. This constraint is used to achieve faster execution time where the concentration would otherwise be approaching a constant value. The third constraint sets the parameter value at the spindle radius to that of the control so that the regulated parameters would be neither increased nor decreased at the boundary between the inside and the outside of the spindle region. The solution to the reaction diffusion is of the form c(x) = Ae^x/λ + Be^−x/λ, with 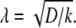Using the constraints to eliminate A and B, we obtain 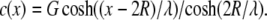Because we have not constrained D or k to be a particular value, λ is still an unknown. We solve for λ using the constraint c(0) = G and use the secant method to solve for for μ = 2R/λ.

For parameters that are up-regulated (e.g., rescue frequency), the scaling factor is greatest at the center of the spindle, equal to 1 at the spindle radius, and continues to decay radially out to twice the spindle radius, at which point it becomes constant (Fig. 1 D). For parameters that are down-regulated, the scaling factor is inversely proportional to those that are up-regulated, with the minimum found at the center of the spindle (Fig. 1 D). We tested a range of scaling factors between 2 and 20.

Nucleation

MTs are nucleated onto astral MTs under two different speculative branching angle schemes: one in which the initial branching angle is random and the other in which the angle is predetermined. Under both schemes, astral MTs and nucleated MTs are initially 1 μm long. Each astral MT has exactly one nucleated MT, with the minus end of the nucleated MTs anchored 0.1 μm from the plus end of the astral MTs when the astral MT lengths were only 1 μm. In these simulations, we decrease the number of astral MTs to 30 to keep the total initial polymerized tubulin length the same as in the control simulations. Under the random branching angle scheme, the angle was uniformly distributed from 0° to 360°, whereas for the predetermined scheme, we tested initial angles between 0° and 50° and allowed the branch to be placed randomly on the left or right side of the astral MT. As the simulation progressed, the branching angles varied according to the forces acting on the MTs. We also tested the effects of random nucleation anywhere along the length of existing astral MTs. The nucleation events were stochastic, averaging one nucleation event per second per aster (30), and the number of nucleated MTs was limited to 30 per aster to make the number of MTs per aster comparable to that in the other simulations.

Evaluating spindle quality

To obtain objective comparisons between spindles under differing assumptions, we define a quantitative measure of spindle quality as the fraction of motor complexes that are antiparallel-linked in the spindle region, divided by the sum of all microtubule lengths. This associates improved spindle appearance with the degree of antiparallel microtubule overlap, which we determine by the number of antiparallel-linked motor complexes. We choose this metric based on the conspicuously small amount of antiparallel overlap observed in nonspatially regulated simulations (6) in comparison to the abundance of antiparallel overlap in the spindle region observed experimentally (31). We take the fraction of motor complexes that are antiparallel-linked, as opposed to the absolute count, to measure the effect of our biological hypotheses rather than increased linking that can be attributed to varying the number of available motor complexes. Similarly, to avoid measuring linking increases caused by increased microtubule length, we divide by the sum of all microtubule lengths. This has the additional benefit of penalizing longer astral MTs that are not overlapping. The spindle quality measures are taken at 10-s intervals for the 1000 s that the simulation runs. The values corresponding to the last 500 s are then averaged to get a spindle quality measure representative of the entire simulation while ignoring initial transient effects (Fig. 1 B).

Choice of parameter sets

We ran our simulations for various sets (PS1–PS5) of motor complex parameters (e.g., attach and detach frequencies, motor speeds) (Table 1). These parameter sets were chosen based on their ability to produce spindles with a significant amount of MT interaction when simulated using the cytosim program (which has no spatial regulation or other biological assumption added) (6). Each of these five data sets selected was simulated 10 times with no spatial regulation to average over stochastic effects (Fig. 1 C). We ran over 1000 simulations on 10 Linux workstations with 3.06-GHz Xeon processors with 512 Mbytes of RAM; each simulation finished in ∼10 h.

RESULTS

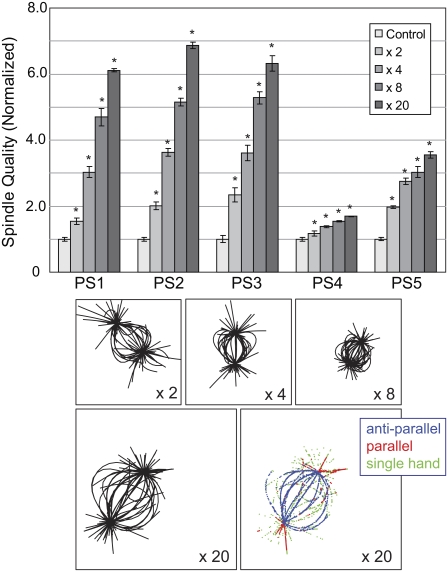
To establish a set of control spindle assembly conditions in the absence of spatial regulation, we considered five reference parameter sets (PS1–PS5) that appear to produce reasonably shaped spindles using the cytosim program (6) (see Materials and Methods). Each parameter set specifies different values for the motor complex attach and detach frequencies, hand speeds, maximum forces, and motor link rigidities (Table 1). For each parameter set, at least 10 simulations were run that assume no spatial heterogeneity in regulation to establish a baseline and to average over stochastic effects such as those arising from initial aster positions or MT dynamic instability. To enable quantitative comparisons, we defined a spindle quality measure indicative of the amount of antiparallel MT overlap based on the number of linked heteromotor complexes that link antiparallel MTs and the total length of all MTs (Materials and Methods). The observed spindle quality measures for the five parameter sets range from 0.020 ± 0.001 to 0.111 ± 0.0057 (mean ± SD) Arbitrary Units (Fig. 1 C), showing that the parameter sets chosen can cover quite a range of spindle quality measurements. Because the number of antiparallel-linked motor complexes is highly dependent on motor complex affinity to MTs, spindles with a higher spindle quality measurement may not necessarily look better, but they will have more antiparallel MT overlap. The degree of antiparallel overlap may not be visually apparent if the MTs collapse into an antiparallel bundle. The benefit of defining the spindle quality metric is more for comparison within a single parameter set where the motor complex affinity to MTs is constant, rather than comparison between or among different parameter sets.

We next determine the extent to which spindle morphology can improve by spatial regulation of the MT dynamic instability parameters. For each of the five parameter sets, we simulated spindle assembly under the assumption that one dynamic instability parameter was altered (Fig. 2). The degree to which these parameters were regulated was determined by a gradient that was maximal (for up-regulation but minimal for down-regulation) at the spindle center and decreased radially thereafter (Fig. 1 D; Materials and Methods). We applied gradients where the maximum regulation ranged from 2 to 20 times. The effect of this spatial regulation was measured by the percentage improvement in spindle quality over the control simulations.

FIGURE 2.

Spatial regulation of individual dynamic instability parameters can improve the spindle quality measures in the simulations. For each parameter set, the system was simulated as in Fig. 1, varying either rescue frequency (A), growth rate (B), shrinkage rate (C), or catastrophe frequency (D). Spatial variations considered were 2, 4, 8, or 20 times (or their reciprocals). Bar graphs are as in Fig. 1 C. Also shown are representative snapshots of the different simulations (from PS2, PS3, PS3, and PS2 in panels A–D, respectively). Asterisks denote statistically significant improvements over the respective control simulations to p < 0.01 using Student's t-test.

We up-regulated rescue frequency (Fig. 2 A) and growth rate (Fig. 2 B) and down-regulated shrinking rate (Fig. 2 C) and catastrophe frequency (Fig. 2 D). In most cases, spatial regulation of the dynamic instability parameters improved the spindle quality: these measures were significantly better (p < 0.01, Student's t-test) in 50/80 parameter set gradient combinations tested. On average, the improvement in spindle quality was 34%. As expected, higher gradients led to better improvements. When the gradient strengths were 2×, 4×, 8×, and 20×, the average improvements were 13%, 27%, 43%, and 55%, respectively, and the number of statistically significant improvements was 5/20, 13/20, 16/20, or 16/20, respectively. These numbers suggest that to make an important contribution, the gradient effect must be 5- to 10-fold, but the effect saturates at numbers higher than these, limiting further gain. Moreover, the beneficial effect of spatially regulating dynamic instability parameters is not uniform across parameter sets. In particular, PS1 and PS4 showed much smaller improvements than the other three parameter sets. The motor complexes in PS4 tended to move toward the minus ends of the MTs and decrease the number of motor complexes available to form antiparallel links at the spindle equator and thus not respond well to increased MT density there. The preference for the motor complexes to move toward the minus end, observed in the PS4 simulations, likely arises from the combined effects of several parameters. These motors have the fastest minus-end- and the slowest plus-end-directed hands of all the parameter sets. Moreover, the grab length of the minus end is longer than that of the plus end, so that the minus-end-directed hand is more likely to attach before the plus-end-directed hand. The weak improvements observed in PS1 are likely caused by the low ratio of attach to detach frequency in its minus-end-directed hand, resulting in the lowest affinity for MT attachment of all parameter sets.

Of the four dynamic instability parameters, the best improvements were obtained by down-regulating catastrophe frequency (54% improvement; 17/20 parameter set/gradient contributions being statistically significant). In addition to the gains in spindle quality, the morphology of the spindle improved with more MTs overlapping and shorter aster MTs (Fig. 2 D). The fraction of MTs inside the spindle region increased (see Fig. 5 B; 28% increase averaged over all gradient strengths; 19/20 parameter set-gradient strength combinations being statistically significant). The next highest gain in spindle quality was seen when the growth rate was regulated spatially (Fig. 2 B; 39% improvement). This regulation produced the next largest single gain in MT distribution within the spindle region (27% improvement on average; 18/20 parameter set-gradient strength combinations being statistically significant). Increasing the rescue frequency (Fig. 2 A) and decreasing the shrinking rate (Fig. 2 C) led to smaller spindle quality gains (26% and 18%, respectively). Moreover, both of these increased the fraction of MTs within the spindle region (10% and 9%, respectively).

FIGURE 5.

Overall improvements in spindle quality and fraction of total MTs inside the spindle for varying schemes. (A) These bar graphs summarize the data across different regulatory schemes averaged over all parameter sets. (B) Fraction of tubulin (total MT length) inside the spindle region as a function of total tubulin and normalized to the control simulations for the varying regulatory schemes. (C) Average length (normalized to control simulations) for MTs outside the spindle region. Legend in panel A applies to all three bar graphs.

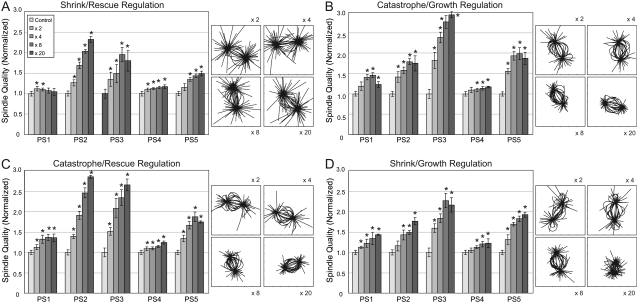
We next considered the effect of varying one pair (shrink/rescue, catastrophe/growth, catastrophe/rescue, and shrink/growth) of dynamic instability parameters at a time (Fig. 3). In all cases, the average improvement in spindle quality obtained by regulating pairs of parameters was higher than that achieved by regulating each of the two parameters individually. Combining catastrophe decrease with growth increase produced the largest spindle quality gain (64%, 18/20 simulation sets showed statistically significant improvements to p < 0.01) and produced the largest increase in MTs within the spindle region (see Fig. 5 B; 42%; 20/20 parameter set gradient combinations being statistically significant). Combining catastrophe decrease with rescue increase provided the next highest gain of 58% in spindle quality. These were followed by down-regulating shrink rate and up-regulating growth rate, which provided spindle quality gains of 45% and increases in MT density within the spindle region of 30%. Combining shrink rate decrease with rescue increase produced the lowest spindle quality gain of the parameter pairs tested with an improvement of 36%.

FIGURE 3.

Regulating two individual dynamic instability parameters simultaneously further improves spindle quality measures in the simulations. Simulations, as in Fig. 2, were repeated with two parameters varied simultaneously. Representative snapshots in the insets come from (A) PS2, (B) PS5, (C) PS5, and (D) PS4.

Dynamic instability parameters are natural candidates for studying the effect of spatial regulation on spindle formation, but we also investigated whether spatial regulation of other parameters affecting the system could have significant effects on spindle morphology. One hypothesis is that motor diffusion could be reduced inside the spindle region because of crowding effects or because of linking to other filaments (32). To test the effect of spatially reduced motor diffusion inside the spindle region on spindle formation, we simulated the system assuming that motor diffusion was down-regulated by factors ranging from 2 to 20 inside the spindle region (using the same profile as previously used) (Fig. 4 A). Remarkably, this spatial regulation had a considerably larger effect on spindle quality (25–191% depending on gradient strength, 17/20 are significant to p < 0.01) than regulating dynamic instability parameters. However, on average it decreased MT density within the spindle region by 7% (Fig. 5 B). Once again, we saw great variation in the performance of different parameter sets, with PS1 showing the greatest increase in spindle quality and PS4 demonstrating only marginal improvements. The substantially larger improvements in spindle quality for PS1 (33%, 117%, 222%, and 400% for gradient strengths of 2-, 4-, 8-, and 20-fold, respectively) observed by limiting diffusion regulation are likely a result of the high detach frequency at the ends of MTs in the plus-end-directed hand. Because its minus-end-directed hands have a low affinity for MT attachment, its motor complexes tend toward the plus ends of the MTs; once reaching the ends, they detach with a high probability. By limiting diffusion regulation, the motor complexes remain near the MTs from which they detached and increase their probability of reattachment.

FIGURE 4.

Effects of changing motor diffusion or sites of MT nucleation on spindle assembly. (A) Limiting motor diffusion inside the spindle greatly improves spindle quality. In these simulations, the motor diffusion was varied spatially as in Fig. 1 D. Representative snapshots in the insets come from PS5. (B) Simulations involving MT nucleation were also considered. Bar graphs represent random branching angles. The asters in these simulations had 30 MTs each. One MT was nucleated on each aster MT. (C) Snapshots of spindles formed under a nucleation scheme where the angle of MT branching was either fixed or randomly chosen.

We also tested the effects of motor-based MT regulation where motors at MT plus ends preferentially stabilize antiparallel-linked MTs or destabilize parallel MTs. By down-regulating catastrophe frequency by factors of 2, 4, 8, and 20, we found spindle quality increased by 13, 16, 23, and 22%, respectively, with only 6 of 20 parameter set regulation strength pairs being statistically significant to p < 0.01 (Fig. 6 A). In contrast, we found up-regulating catastrophe frequency to decrease the spindle quality by 24% on average, although the spindles appeared similar to those in controls (Fig. 6 B). Only 5 of 20 antiparallel stabilization pairs significantly improved the fraction of MTs within the spindle region (∼4% improvement), but none of the parallel destabilization pairs significantly improved the MT distribution (on average they decreased MT density within the spindle region by 11%).

FIGURE 6.

Spindle morphology for simulations involving motor-complex-based regulation. (A) In these simulations, MTs have a lower catastrophe frequency if a motor complex is bound near its plus end with one hand and bound to an antiparallel MT with the other. (B) Similar to A, except the catastrophe frequency is increased for parallel-linked MTs near their plus ends. Catastrophe frequencies were scaled by 2, 4, 8, or 20 times (or their reciprocals). Asterisks denote statistically significant improvements over the respective control simulations to p < 0.01 using Student's t-test. Also shown are snapshots from PS3 (A) and PS1 (B).

Although centrosomes contribute to establishing the mitotic spindle, there is ample experimental evidence that MTs are also nucleated at other sites (1,24,28,33,34). To test the role that acentrosomal MT nucleation has on spindle formation, we simulated a system in which new MTs are nucleated onto previously existing astral MTs at randomly selected angles (Fig. 4 B) (Materials and Methods). The spindles obtained in simulations where the MTs were nucleated at fixed lengths from the aster center showed moderate spindle quality gains with an average improvement of 32% (Fig. 4 B, 5 A). These simulations also produced a strong decrease in MT density within the spindle region (18%) (Fig. 5 B). To test whether the branching angle between the nucleated MTs and the astral MTs was important, we repeated the simulations assuming a range of predetermined branching angles (Fig. 4 C). Smaller branching angles (0° and 5°) produced MTs that were slightly more organized within the spindle, but the branching angles did not strongly affect spindle quality and for the most part produced disorganized spindles. By nucleating the MTs at random lengths along astral MTs, we found a smaller increase in the spindle quality measure of 14% and a larger decrease in the MT density within the spindle (28%).

Additionally, we considered the effect of MT nucleation away from the centrosome, either at sites of antiparallel MT overlap or unattached to existing MTs but in the spindle region. Neither of these schemes produced organized spindles; moreover, free-floating MTs tended to drift away from the spindle region (data not shown).

To determine which regulatory mechanism has the greatest effect on spindle quality independent of parameter set, we averaged the normalized spindle qualities for each regulatory mechanism over all five parameter sets (Fig. 5 A). Of all the schemes tested, decreasing diffusion had the largest improvement (2.9 ± 1.4 times larger than controls at a gradient strength of 20). Of the pairwise regulatory schemes, the catastrophe-growth pair and catastrophe-rescue pair performed similarly, with an increase of 1.7 times averaged over all gradient strengths. The catastrophe-rescue pair performed slightly better at larger gradient strengths (1.97 ± 0.74 times control at a gradient strength of 20) when compared with the catastrophe-growth pair (1.79 ± 0.71 times control), but the latter performed better at the lower gradient strengths (1.41 ± 0.29 versus 1.29 ± 0.18 for gradient strengths of 2). Of the single-parameter regulation schemes, decreasing catastrophe increased spindle quality the most (1.54 ± 0.27 times control averaged over all gradient strengths). Increasing MT growth produced the next highest gain at 1.39 ± 0.21-fold higher than control, followed by rescue regulation at 1.26 ± 0.16 and shrink-rate regulation at 1.18 ± 0.12.

To test which regulatory scheme had the greatest decrease in astral MT length, we calculated the average length of those MTs that had more than half of their length outside the spindle region and compared this average length to that of the controls. Decreasing the rescue frequency outside the spindle region produced average lengths of no less than 91% of controls (Fig. 5 C). Increasing shrink rate decreased astral MT length slightly more with an average length of 85% of control at a gradient strength of 20. Regulating catastrophe frequency or growth rate did substantially better, achieving average MT lengths as low as 48% and 61%, respectively, of the controls at the maximum gradients strengths of 20. Regulating diffusion or nucleating MTs on astral MTs did not produce any decrease in average astral MT length.

Finally, we tested the effects of combining all four MT dynamic instability regulatory schemes with motor complex diffusion regulation. The best of these simulations exhibited a strong contrast in MT density between inside and outside the spindle region (Fig. 7). Four of five parameters sets achieved gains in spindle quality greater than factors of three. At a gradient strength of 20, the astral MTs were 30% the length of those in control simulations. Under this regulation scheme, the fraction of MTs within the spindle region peaked at 56%, which is comparable to the 59% achieved when only the combined catastrophe and growth regulation was applied (Fig. 5 B).

FIGURE 7.

Spindle morphology for simulations involving multiple regulatory schemes. In these simulations, all four dynamic instability parameters, as well as the motor diffusion, were simultaneously regulated. In the bottom right-hand panel, we show the location and state of the hetero-motors that are bound to MTs. Motors that form antiparallel attachments are shown in blue, those connecting parallel-link MTs are shown in red, and motors in which only one hand is attached are shown in green. Note that the two 20× images are zoomed, so that the square is 20 × 20 μm. All images use PS5 parameters.

For any given regulation scheme, PS4 and PS5 have better spindle morphology than the other parameter sets. The motor complexes in PS5 tend to accumulate at the plus ends of MTs through the large grab lengths of their plus-end-directed hands and low detach frequencies at MT plus ends. The motor complexes also tend to stay linked longer as their maximum stretch length is longer than the others; moreover, when they do detach, the plus-end-directed hands often stay attached, whereas the minus-end-directed hands detach.

The minus-end-directed hands dominate the motor complexes of PS4 with larger grab lengths and faster hand speeds and tend to stay attached when motor complex links break. This causes motor complexes to accumulate at the poles with their minus-end-directed motors attached and their plus end hands free to attach to the plus ends of MTs radiating from the opposing aster. As astral MTs get pulled into the spindle and their plus ends reach the opposing pole, the abundance of plus-end-directed hands attach to these MT plus ends and cause the MT to be pushed back toward its own aster, forcing the MT to bulge outward at the equator, creating a spindle morphology similar to those seen experimentally. PS5, on the other hand, achieves MT bending through the accumulation of plus-end-directed hands at the tips of its astral MTs. As the MTs grow and cross over each other in the spindle region, the buildup of the motor complexes at the MT plus ends provides enough force to bend the MTs toward the opposing poles as guided by the associated MT asters.

DISCUSSION

Mitotic spindle formation involves the collective interactions among MTs, chromosomes, centrosomes, and their associated proteins (35–37). Although many of the components have been well characterized in isolation, their collective contributions to determining spindle morphology remain elusive. Because they allow easy manipulation of different parameters and incorporation of different hypotheses, computer simulations provide an excellent vehicle for testing how individual components work together to build effective structures during mitosis (1–4,6,25,26,38).

Previous simulations have demonstrated that a simple system that involves only interactions of dynamic MTs between two asters under the influence of diffusing motor complexes consisting of one plus-end directed motor and one minus-end directed motor can form spindle structures (6). Our results show that incorporating spatial heterogeneity in the parameters defining the MT dynamic instability leads to greater MT antiparallel overlap (Fig. 5 A) and spindles with more realistic morphologies (Figs. 2 and 3).

Two of the most salient features of spindles are the sharp drop in MT density outside the spindle and the high degree of MT interaction between the poles. To lessen the astral MT density, MTs outside the spindle region need to be less stable than those inside. In our simulations, the stability differential was accomplished by regulating catastrophe frequency, rescue frequency, and growth rate or shrink rate according to a spatial gradient of a putative morphogen concentration (Fig. 1 D). The catastrophe and growth rate regulation schemes increased MT polymerization inside the spindle region and decreased it outside, whereas the rescue and shrink rate regulation schemes decreased MT depolymerization inside the spindle and increased it outside (Fig. 2). Although astral MT prominence decreased in all four schemes, it was only under the regulation of catastrophe or growth rate regulation that substantial improvements were made (Fig. 5 C). These simulations also showed the best ratio of polymerized tubulin inside the spindle to total polymerized tubulin (Fig. 5 B; ∼47%). Such MT regulation may help more interpolar MTs stay in the growth state longer to achieve the poleward flux and subsequent spindle elongation in anaphase B as observed in Drosophila embryonic spindles (39), although our model does not address poleward flux or anaphase B spindle elongation.

Improved MT distribution as a result of catastrophe regulation or growth rate regulation over the regulation of rescue frequency or shrink rate may be a consequence of the increased time spent in the growth state relative to the shrinking state. To benefit from rescue or shrink rate regulation, the MTs must be depolymerizing. In our control simulations, MTs spend an average of 45 s growing but only 28 s shrinking (Table 2). Because the MTs spend less time depolymerizing, the regulation of rescue and shrink rate parameters has less of an effect on MT distribution.

TABLE 2.

MT dynamic instability parameters of control simulations

	Rescue (1/s)	Catastrophe (1/s)	Growth rate (μm/min)	Shrink rate (μm/min)	Avg. time to rescue (s)	Avg. time to catastrophe (s)
Control avg.	0.036	0.022	9.60	15.00	27.6	44.9

When two instability parameters were regulated simultaneously, the combinations with the most improved spindles were catastrophe down-regulation in combination with growth rate up-regulation, and catastrophe down-regulation combined with rescue frequency up-regulation (Fig. 3). These simulations performed better than those involving single-parameter regulations. At lower gradient strengths, the spindle quality improvements were often equal to or greater than the sum of their corresponding single regulation simulations, suggesting a cooperative mechanism. At higher gradient strengths, the improvements were mostly less than the sum, indicating that the number of motor complexes available for antiparallel linking was saturating. When all four dynamic instability parameters, as well as diffusion, were regulated, the corresponding improvements were considerable, and the same cooperative effects at lower gradient strengths and saturating effects at higher gradient strengths were observed (Fig. 7).

Most of the improvements obtained in our simulations were primarily observed for steep gradients in the parameters (eightfold or greater). Based on experimental evidence, the spatial variation in the dynamic instability parameters is likely no more than a factor of 10 (18,40,41). However, if complementary regulation is applied (e.g., MT polymerization is inhibited outside the spindle region and promoted inside), the overall difference can be much larger.

We also regulated motor complex diffusion and found greater improvements in spindle quality measure than by regulating dynamic instability parameters. By decreasing motor complex diffusion within the spindle region, motor complexes have a higher probability of reattachment after falling off MTs. Although the spindle quality measure did increase, the distribution of MTs was worse than the other types of MT regulation. Together with our previous simulations, this suggests that limiting motor complex diffusion needs to be incorporated with spatial regulation of dynamic instability parameters. Simulations of these combined effects led to realistic spindle morphologies (Fig. 7).

Stabilizing MT dynamics through antiparallel-linked motor complexes attached at the plus ends of MTs produced modest improvements in two of the five parameter sets but was not as effective as spatial regulation. Destabilizing MTs through parallel-linked motor complexes at MT plus ends reduced spindle quality on all of the parameter sets and decreased the fraction of MTs inside the spindle region. This suggests that parallel-linked MTs play an important role in forming antiparallel overlap, and destabilizing parallel-linked MTs would impair MT density within the spindle region. Those parameter sets that did improve spindle quality by stabilizing MTs with antiparallel-linked motors near their plus ends had lower motor detach frequencies at MT ends, thus allowing the motors to stay at the plus ends longer and exert MT stabilization for a longer period of time.

Because there is strong experimental evidence that MTs can be nucleated away from the centrosome (24,33,34), we also considered the effect of several acentrosomal MT nucleation schemes on spindle formation. Nucleating MTs onto existing astral MTs improved antiparallel overlap; however, the resulting spindles were considerably less organized than controls (Fig. 4, B and C). This was true even when the initial branching angle was small. When we allowed for nucleation of new MTs onto sites of existing antiparallel overlap, disorganized spindles were observed. We also allowed MT nucleation away from existing MTs but found that in this case, the free MTs tended to diffuse away from the spindle structure. Together, these simulations suggest that additional mechanisms beyond the heteromotor complexes are needed to organize MTs that are not nucleated on the centrosomes. A candidate is the chromokinesin-based MT organization in which chromatin-bound kinesins direct the plus end of MTs toward the chromatin-defined spindle center, whereas minus-end-directed dynein motors guide the MT minus ends toward spindle poles (26).

We observed a strong dependence of the spindle quality measure on motor complex parameters, as shown by the large variability in performance across various parameter sets (Figs. 2–4). Motor complexes with a greater affinity for MT binding and able to process for longer periods generally increased the spindle quality measure by increasing the number of antiparallel-linked motor complexes. The average MT length inside the spindle is also affected by motor complex parameters. Motor complexes that are able to capture MTs and bend them inside the spindle, where stabilization was greater, produce longer MTs. In contrast, MT lengths outside the spindle were less affected by motor complex parameters. This can be attributed to two factors. First, the spatial regulation far from the spindle has a smaller gradient (Fig. 1 D) so that motor complex-induced changes in MT position lead to only small changes in MT dynamics. Second, MTs outside the spindle region form fewer links with other MTs. Thus, the forces on each MT tend to be smaller, making them less motile.

Comparing the benefits of MT spatial regulation, motor complex diffusion reduction, and MT nucleation through simulation allows us to shed some light on the relative importance of these types of regulation in vivo. Though spatial regulation greatly improves the density and organization of MTs within the spindle, other regulatory mechanisms are likely present that improve MT density and organization within the spindle even further. Candidates include the underlying lamin meshwork (32), which could provide additional spatial cues for anchoring motor complexes or promoting MT nucleation within the spindle region and restricting their diffusion of the spindle region. Other mechanisms could depend on chromosome and kinetochore positioning in which MTs could be nucleated on them and guided toward the aster poles by MTs nucleated at the centrosomes, or spindle MTs might use the chromosomes to push up against to form their characteristic oval shape. Although simulations that produce high-fidelity spindles would not guarantee the necessity of their constituent mechanisms in vivo, the simulations can be used to measure whether a given set of mechanisms is sufficient to form realistic looking spindles, and where the simulations fall short of producing accurate spindles, we may find suggestions as to how to further refine our models.