Abstract
Sound stimuli excite cochlear hair cells by vibration of each hair bundle, which opens mechanotransducer (MT) channels. We have measured hair-bundle mechanics in isolated rat cochleas by stimulation with flexible glass fibers and simultaneous recording of the MT current. Both inner and outer hair-cell bundles exhibited force-displacement relationships with a nonlinearity that reflects a time-dependent reduction in stiffness. The nonlinearity was abolished, and hair-bundle stiffness increased, by maneuvers that diminished calcium influx through the MT channels: lowering extracellular calcium, blocking the MT current with dihydrostreptomycin, or depolarizing to positive potentials. To simulate the effects of Ca2+, we constructed a finite-element model of the outer hair cell bundle that incorporates the gating-spring hypothesis for MT channel activation. Four calcium ions were assumed to bind to the MT channel, making it harder to open, and, in addition, Ca2+ was posited to cause either a channel release or a decrease in the gating-spring stiffness. Both mechanisms produced Ca2+ effects on adaptation and bundle mechanics comparable to those measured experimentally. We suggest that fast adaptation and force generation by the hair bundle may stem from the action of Ca2+ on the channel complex and do not necessarily require the direct involvement of a myosin motor. The significance of these results for cochlear transduction and amplification are discussed.
INTRODUCTION
Sound stimuli are conveyed to the inner ear, where they vibrate the cochlear partition, an epithelium of hair cells and supporting cells born on the basilar membrane and overlain by an acellular tectorial membrane. The relative motion of the basilar and tectorial membranes is detected by rocking of the hair cell stereociliary (hair) bundles, which leads to opening of mechanotransducer (MT) channels. The MT channel is thought to be activated by tensioning tip links that extend from the top of one stereocilium to the side wall of its taller neighbor (1,2). The MT channel is preferentially selective for calcium (PCa/PNa ≈ 5:1 (3,4)) and, when open, permits calcium influx that is essential for triggering adaptation to optimize transducer sensitivity (5,6). There are two hypotheses about the role of calcium in adaptation: 1), it binds to the MT channel to make it more difficult to open (7,8); or 2), it acts on myosin molecules at the upper insertion point of the tip link, causing it to slip down the stereociliary wall and thus relieving force on the channel (9). The two mechanisms are not mutually exclusive but may be responsible for fast (channel) and slow (myosin) forms of adaptation, respectively (10,5,11). There have, however, been experimental and theoretical arguments that myosin motors may underlie both processes (12,13).
Mammalian cochlear hair bundles consist of 50–100 rigid stereocilia (14,4) interconnected by lateral extracellular links and tip links (15–17). During bundle deflection, the stereocilia pivot at their ankles (18). Defining the mechanical attributes of the hair bundle is central to understanding transduction and amplification in the vertebrate cochlea. These properties have been well documented in hair cells of nonmammalian vertebrates (19), from which has sprung the idea that hair-bundle mechanics are dictated not only by the passive structural elements (the flexibility of the stereociliary ankles, the interciliary connections, and the gating springs), but also by the opening and closing of the MT channels (20). Thus, mechanotransduction is reversible: force delivered via the tip links evokes a conformational change in the channel, culminating in opening; conversely, changes in channel conformation or location, such as those that occur during adaptation, are in turn transmitted via the tip links to elicit bundle motion. Both modeling and experiments have shown that MT channel activation and adaptation in nonmammals can give rise to active hair-bundle movements that amplify the extrinsic stimulus (21–23). Although there have been several studies of mammalian hair-bundle mechanics (24–26), the evidence for a component due to channel gating is much less complete. The faster kinetics of mammalian transduction (27), which is at the limits of existing measurement techniques, may partly explain the lack of evidence for active bundle motion. Nevertheless, it has been argued that active hair-bundle movements may also contribute to amplification in the mammalian cochlea (28,29).
The aim of this work was to document the time-dependent mechanics of mammalian cochlear hair bundles to address the following questions. Are the hair bundles purely passive mechanical elements or are their properties influenced by gating of the MT channels? Does calcium influx through the channels affect hair-bundle mechanics? Are there differences in hair-bundle mechanics between inner hair cells (IHCs) and outer hair cells (OHCs) that reflect their disparate functions in auditory transduction (30,31)? Finally, can the results be reproduced by a model of the hair bundle that incorporates channel gating?
MATERIALS AND METHODS
Preparation and recording
Experiments were performed on IHCs and OHCs in isolated cochlear coils of Sprague-Dawley rats using techniques reported previously (4,32). Neonatal animals 7–11 days old (P7–P11) were anesthetized with halothane and killed by decapitation using methods approved by the Institutional Animal Care and Use Committee of the University of Wisconsin. Cochlear coils were isolated after removing the bone from the apical and middle turns, unpeeling the stria vascularis, and lifting off the tectorial membrane. Excised apical or middle turns were fixed in the experimental chamber with strands of dental floss and viewed through a 40× long working distance water-immersion objective (numerical aperture 0.8) on a Zeiss (Jena, Germany) Axioskop FS microscope. The chamber was perfused with artificial perilymph of composition (in mM) 154 NaCl, 6 KCl, 1.5 CaCl2, 2 Na-pyruvate, 8 glucose, and 10 Na-HEPES, pH 7.4. The apical surface of the organ of Corti was separately superfused with one of several solutions: 1), a standard solution identical to the artificial perilymph containing 1.5 mM Ca2+; 2), a reduced calcium solution of (in mM) 150 NaCl, 6 KCl, 3.3 CaCl2, 4 NaHEDTA, 2 Na-pyruvate, 8 glucose, and 10 Na-HEPES, pH 7.4, which had an estimated free Ca2+ of 20 μM (buffered with HEDTA), similar to that in rat endolymph (33); 3), a normal saline with 1.5 mM Ca2+ containing 0.2 mM dihydrostreptomycin (DHS; Sigma Chemical, St Louis, MO) to block the MT channels; 4), a solution containing submicromolar calcium consisting of (in mM) 140 NaCl, 6 KCl, 1.8 mM CaCl2, 5 Cs4BAPTA, 8 glucose, and 10 Na-HEPES, pH 7.4; or 5), free Ca2+, 0.1 μM, which was pressure ejected onto the hair bundles for 1 to 3 s to sever the tip links and abolish transduction (34,35).
Borosilicate patch electrodes connected to an Axopatch 200A amplifier (Axon, Foster City, CA) were introduced through a small hole in the reticular lamina. Recordings were made from IHCs or first-row OHCs either at the beginning of the apical turn, ∼0.8 of the distance along the basilar membrane from the base, or in the middle turn, 0.5 of the distance from the base. From the place-frequency map in adult rats, the recording sites correspond to characteristic frequencies of ∼4 kHz and 14 kHz, respectively (36). Patch pipettes were filled with an intracellular solution of composition (in mM) 142 CsCl, 2 MgCl2, 1 EGTA, 3 Na2ATP, 0.5 Na2GTP, and 10 CsHEPES, pH 7.2. Patch pipettes had starting resistances of 3–6 MΩ and up to 70% series-resistance compensation was applied to yield recording-system time constants of 30–60 μs. MT currents were low-pass filtered at the output of the Axopatch 200A amplifier at 10 kHz. All membrane potentials were corrected off-line for the uncompensated series resistance and for the junction potential of the CsCl intracellular with respect to the apical perfusate. Hair cells were whole-cell voltage-clamped at holding potentials between −84 and +106 mV at room temperature (19–22°C). Mechanotransducer currents were digitized at 150 kHz with a Power1401 (CED, Cambridge, UK) and analyzed with IgorPro v4.00 (Lake Oswego, OR). All records are averages of 10 stimulus presentations and, unless otherwise noted, results are expressed as mean ± 1 SE. Statistical significance between control and test measurements was assessed by a paired t-test with p < 0.05. Reliable measurements were made on a total of 37 hair cells with maximum MT currents (IMAX) as follows: 22 apical turn OHCs (Imax = 619 ± 41 pA, range 300–866 pA), nine apical-turn IHCs (Imax = 673 ± 94 pA, range 333–1155 pA), and six middle-turn OHCs (Imax = 700 ± 84 pA, range 478–1000 pA). Peak MT current versus displacement (I-X) relationships were fitted with a single Boltzmann equation: I = IMAX/(1 + exp((X − XO)/XS)), where IMAX is the maximum current, XO is the displacement for half-maximal activation, and XS is the slope factor.
Mechanical stimulation
The mechanical properties of hair bundles were measured by stimulating with calibrated flexible glass fibers (∼30 μm in length, stiffness 1–3 mN·m−1), as previously described (18,22,29). The stiffness of each fiber was calibrated against a standard whose stiffness in turn had been determined from the displacement produced by spherical beads of polymethyl methacrylate of measured diameter and known density (1.185 kg m−3) attached to the tip. The proximal end of the experimental flexible fiber was cemented through the side of a nylon screw attached to a piezoelectric stack actuator (P-802, Physik Instrumente, Karlsruhe, Germany), the fiber thus being perpendicular to the axis of motion of the actuator. The fiber was introduced along the axis of the cochlea and its distal tip was coated with an ellipsoidal bead of Sylgard (Sylgard 184 elastomer, Dow Corning, Midland, MI) sized to snugly fit into the V-shaped hair bundle of the OHC (∼3 μm width (Fig. 1)) or the larger hair bundle of the IHC (∼6 μm width). The time course of motion of the fiber was monitored by projecting the image of the Sylgard bead onto a pair of photodiodes (LD 2-5, Centronics, Hudson, NH) at 300× total magnification. The differential photocurrent, which is assumed to be proportional to the motion of the fiber (18), was filtered at 10 kHz. The photodiodes were themselves mounted on a piezoelectric bimorph, displacements of which were used to calibrate the photodiode signals throughout the recording. The photodiode motion generated a calibration signal of 25 nm in the object plane. For each experiment, motion of the fiber when not attached to the hair bundle was also recorded for displacements up to 1 μm to calibrate the frequency response and linearity of the stimulator and detector. When the voltage step to the piezoelectric device was filtered at 1.5–2 kHz, the displacement of the tip of a fiber not on the bundle had a rise time of ∼200 μs. An experimental compromise was needed to obtain a flexible fiber with stiffness comparable to or less than that of the hair bundle but also fast enough to generate fast adaptation. Reducing the stiffness could only be done by lengthening the fiber, which increased the resistive drag and significantly slowed its response time course. To determine the mechanical properties of the hair bundle, the displacement signal was measured at the peak of the MT current to infer an instantaneous stiffness and, at later times, up to 1–3 ms after the onset of the command voltage to calculate the “steady-state” stiffness. The force delivered at any given point in time was calculated from the difference between the displacement of the piezoelectric actuator and the tip of the fiber attached to the bundle, this difference in motion (analogous to the compression in a spring) being scaled by the stiffness of the fiber.
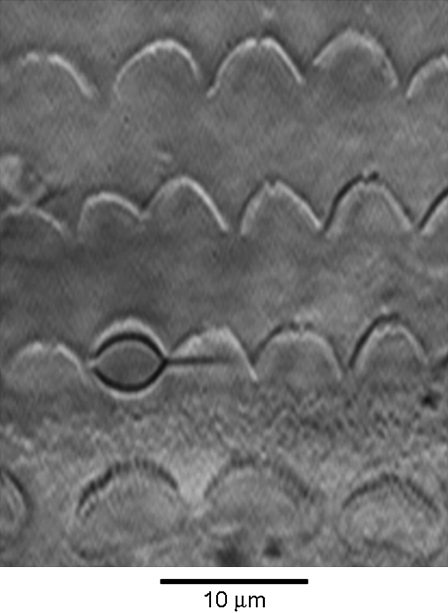
FIGURE 1.
Method of mechanical stimulation, showing four rows of hair bundles, one IHC at the bottom and three OHCs with the flexible fiber connected to a first-row OHC bundle by a Sylgard bead. The fiber is attached to a piezoelectric actuator and is introduced along the long axis of the cochlea, here from the right. P8 rat.
THEORY
Mechanical model of an OHC bundle
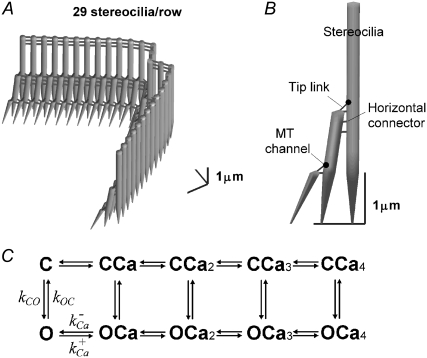
Hair-bundle mechanics and MT currents of a mammalian OHC were simulated with a three-dimensional finite-element (FE) model using the approach described previously (37,38), which in addition incorporated a kinetic scheme for MT channel gating and calcium binding. The model employed the known geometry of rat apical OHC bundles (4,39), with three rows of 29 stereocilia in a pseudohexagonal array, the two wings making an internal angle of 66° (Fig. 2 A). The stereocilia were interconnected by lateral links and by tip links that supplied force via a gating spring to an MT channel located at their upper end (Fig. 2 B). The heights of the stereociliary rows were 4.2, 2.2, and 1.1 μm, with the second and third rows tilted in toward the first row, and tensed in the resting state by myosin motors at the upper end of each tip link. Values for the mechanical parameters, the rotational stiffness of the stereociliary ankle region, and the stiffnesses of the tip link complex and horizontal connectors (Table 1) were adjusted to match the measurements. The stimulus consisted of a family of force steps shaped with a time constant of 33 μs and applied to the tallest row of stereocilia. The bundle motion was determined by the component stiffnesses, as well as a viscous drag force (38) experienced by each stereocilium.
FIGURE 2.
Model of an OHC bundle. (A) Geometry of a simulated hair bundle that contains three rows, with 29 stereocilia per row. The tallest stereocilia are nearly upright, whereas the shorter stereocilia are tilted toward the taller stereocilia. (B) There are three structural components: stereocilia, tip link (assembly), and horizontal connector. The channels are located at the upper end of each tip link. (C) The kinetic scheme used in the model for the MT channel has five closed (C) and five open (O) states, with the rate constants between C and O dependent on the mechanical stimulus and the transitions between each of the C (or O) states dependent on binding of one to four calcium ions. As Ca2+ binds to the channel, it requires an additional force, fCa, to open a channel, and the gating spring is released by the fixed amount, b2.
TABLE 1.
Model parameters
| Symbol | Value | Parameter |
|---|---|---|
| kP (N·m·rad−1) | 6.0 × 10−16 | Rotational stiffness of stereociliary rootlet |
| kGS,max (mN·m−1) | 4 | Stiffness of tip link complex (gating spring) |
| kSA (mN·m−1) | 0.2 | Stiffness of horizontal connectors |
| f0 (pN) | 25 | Intrinsic force difference between open and closed states |
| kb (ms−1μM−1) | 0.2 | Ca-binding coefficient |
| KD (μM) | 20 | Ca dissociation constant |
| kF (ms−1) | 12 | C→O rate constant |
| kR (ms−1) | 15 | O→C rate constant |
| η | 0.9 | Coefficient in Eqs. 3 and 4 |
| b1 (nm) | 1 | Gating swing |
| b2 (nm) | 5 | Channel release on binding Ca2+ |
| rK | 0 (0.8)* | Fraction of gating spring stiffness reduction as Ca2+ bound |
| fCa (pN) | 10 | Change in force to open channel on binding Ca2+ |
| FM (pN) | 20 | Maximal stalling force per channel by the adaptation motor |
| CFA (μM) | 0.1 (3–100) | [Ca2+] near the channel when a channel was closed (open) |
| r12 | 3 | [Ca2+] ratio between the two adaptation sites (CSA/CFA) |
| kA (nm·ms−1 pN−1) | 0.02 (0.05)† | Rate constant for myosin-driven adaptation |
| αM (μM−2) | 0.0125 | Constant in Eq. 9 |
| Q | 2 | Constant in Eq. 9 |
We used the finite-element model instead of the simpler lumped parallel model (8) (e.g., Fig. 1 D) for several reasons. First, it allows us to simulate the responses of individual transduction channels. Therefore, we could apply stochastic gating of multiple MT channels and their modulation by the instantaneous calcium concentration, rather than by an averaged calcium value (see below). It also treats the whole ensemble of stereocilia rather than assuming the bundle to be a parallel arrangement of identical pairs of stereocilia. Thus, it is a more descriptive mechanical model and does not simplify the geometry. One aspect of this treatment is that no approximation is required for the geometric gain between motion at the stereociliary tip and that at the channel. The value of the gain in the model was determined to be 0.11 for channels in both rows, with a tip link length of 180 nm and a tip link angle of 50° with respect to the apical surface of the cell. Finally (though not exploited here), the FE model can be used to compare hair bundles with different geometry under different forcing conditions, for example, driven by fluid motion or by point deflection of the stereocilia (40).
Channel kinetics
A new feature of the model was that the gating of each MT channel was treated as stochastic according to a kinetic scheme (Fig. 2 C) with four calcium-bound states and one calcium-free state for both open and closed configurations. Four calcium-binding sites, rather than one, were used to augment the sensitivity of adaptation to changes in extracellular calcium (10). The four sites may represent calcium binding on each of four subunits of a tetrameric channel. For simplicity, each of the calcium-binding sites was assumed to have identical affinity. Rate coefficients between the states were defined as follows. Two coefficients describe the calcium binding and unbinding rate.
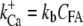 |
(1) |
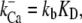 |
(2) |
where kb is the calcium binding coefficient, CFA is the calcium concentration at the binding site, and KD is the calcium dissociation constant (KD = 20 μM). The channel opened or closed according to another two rate coefficients, as follows.
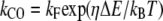 |
(3) |
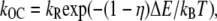 |
(4) |
where kB is the Boltzmann constant, T is the absolute temperature, and kF, kR, and η are constants. ΔE is defined by the tension, f, in the tip-link assembly, gating swing b1, and fCa, the change in force to open the channel on binding calcium multiplied by the number of bound calcium ions, nCa, given by
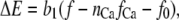 |
(5) |
where f0 is a constant that contributes to setting the resting open probability. When fCa > 0, calcium binding to the channel facilitates the channel closure and stabilizes the closed state (7,8). The definition of ΔE in Eq. 5 differs from the one more commonly used (20) in that it is expressed explicitly in terms of the tension in the gating spring, f, rather than the displacement.
The fCa stabilized the channel states, but had little effect on the bundle mechanics. To consider the calcium effect on bundle mechanics, we introduced, in addition to fCa, two alternative calcium-related mechanisms that affected bundle mechanics. In one, the unstrained length of the channel complex was increased by b2 as each calcium ion became bound. In the other, the stiffness of the channel complex was reduced by a factor rK as the calcium bound to the channel. Ideas similar to our formulation, represented by fCa, b2, and rK parameters, were suggested in previous studies and compared by Cheung and Corey (8). In hypothesizing b1 and b2, we assumed that the tip link is connected in series with the MT channel, which in turn is attached, directly or indirectly, to the actin cytoskeleton of the stereocilium (see Fig. 1 D in Holt and Corey (11) ). In the model, the unstrained length of the tip link assembly, xunstrained, is increased by b1 when the MT channel opens and by b2 when the channel binds a calcium ion:
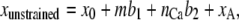 |
(6) |
where x0 is a constant, and m is the channel state (0 when closed, 1 when open). xA was added to describe the movement of the attachment point of the tip link caused by myosin-driven adaptation. This change in the unstrained length, whether due to b1 or b2, affects the tension, f, calculated in the finite-element analysis. Owing to the static equilibrium between the compliances in the tip-link assembly and stereociliary rootlets, the resultant change in length of the tip-link assembly due to channel opening or calcium binding is always less than b1 or b2, respectively. b1 and b2 may represent motion along the axis of the tip link due to conformational changes in the MT channel protein.
Calcium may also influence the effective stiffness of the channel complex (23). To consider the calcium-dependent stiffness change, we introduced a separate parameter rK, which indicates the stiffness reduction as calcium bound to the channel.
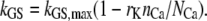 |
(7) |
Here, NCa is the number of calcium binding sites in a channel. A value of 0.8 for rK was used in the simulations, representing a maximal 80% reduction in stiffness. We considered that this calcium-dependent change occurs at the MT channel similar to the calcium-induced relaxation represented by the parameter b2.
Myosin-driven adaptation
Myosin motors are considered to provide force to maintain the resting tension in the gating spring, which sets the resting current (9). The extent of adaptation, xA, was governed by the equation
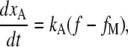 |
(8) |
where kA is the adaptation rate coefficient and fM is the stalling force of the myosin motors. The force of the myosin motors was inversely related to the calcium concentration (41):
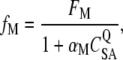 |
(9) |
where FM is the maximum stalling force of a pack of myosin motors per tip link and CSA is the calcium concentration at the slow-adaptation site. When Q > 0, greater CSA results in lower fM. We chose Q = 2. The value of αM = 1/80 was selected to activate <10% of channels at rest with high extracellular calcium (>1 mM) and >20% of channels at low calcium (<0.1 mM). Because the myosin-based slow-adaptation site (SA) may be farther from the pore than the channel-based fast-adaptation site (FA) (42), we assumed that CFA/CSA = 3.
The calcium near the MT channel (CFA) was assumed to cycle within 10 μs between a resting and elevated value in synchrony with the stochastic closing and opening of each of 58 channels. No calcium buffering or extrusion mechanisms were explicitly assumed. The calcium concentration CFA was 0.1 μM when the channel was closed and ranged from 3 to 300 μM when the channel was open, depending on the extracellular calcium concentration. According to the calcium buffering and diffusion theory (43), the internal calcium 30 nm from the pore in the presence of 1 mM EGTA is ∼130 μM for 1.5 mM extracellular calcium and ∼3 μM for 0.02 mM extracellular calcium. This calculation assumes a single channel current of 8 pA, of which 14% is carried by calcium in 1.5 mM extracellular calcium (4). In 0.02 mM calcium, the fraction of current carried by the ion was reduced in proportion to the extracellular concentration, but the channel conductance increased 1.5 times due to relief of calcium block (4).
Computation
The equations were integrated with a time step of 2 μs using an implicit integration method (38) in a computer program written in Matlab (Mathworks, Natick, MA). Values of the parameters are given in Table 1. Between 10 and 20 simulations were averaged to produce each record.
RESULTS
Hair-bundle mechanics in OHCs and IHCs
When the hair bundle was subjected to a force stimulus, the time course of its displacement had two kinetic components: a fast one with a time constant of 0.1 to 0.2 ms similar to that of the stimulus onset and a slower creep with a time constant in the range 0.4–3 ms, often comparable to the time constant of adaptation of the MT current (Fig. 3). As a consequence, the force-displacement relationship at short times was approximately linear but at later times became increasingly nonlinear, with a time-dependent increase in compliance. This type of behavior has been reported previously for OHCs (29) but is also seen in IHCs (Fig. 3 B). In this study, the majority of cells, both OHCs and IHCs, displayed these properties. The bundle stiffness, KHB, calculated from the slope of the steady-state chord force-displacement relationship around the origin, was ∼3 mN·m−1 for both apical IHCs and OHCs (Table 2). However, for middle-turn OHCs, the mean KHB was over twice that for apical-turn OHCs. Additionally, the 10–90% activation range of the MT channel in the middle-turn OHCs was about half the range of those in the apical turn (∼100 nm compared to 210 nm). These differences may largely reflect the smaller hair-bundle height, 3 μm in the middle turn compared to 5 μm in the apex (39), since the stiffness is inversely proportional to the square of the height (18,44). In neonatal rats, the cochlea is still developing over the period during which the experiments were performed (P7–P11) and the onset of hearing does not occur until P12. One developmental change is the loss of the kinocilium, which is present at P7 but has been reabsorbed by P10 (39). We had no evidence of a large change in stiffness over this period. The mean KHB was 3.2 ± 0.7 mN·m−1 (P7 + P8, N = 8) compared to 3.3 ± 0.9 mN·m−1 (P10 + P11, N = 9). We were unable to obtain reliable measurements after P11 and so cannot rule out changes in KHB later in development.
FIGURE 3.
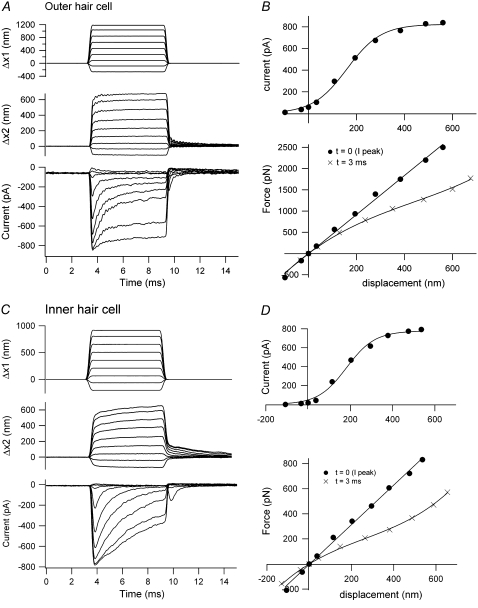
Hair-bundle displacements and MT currents in OHCs and IHCs. (A) OHC motion of the fixed end of the fiber cemented to the piezoelectric actuator (Δx1, upper), the end attached to an OHC bundle (Δx2, middle), and MT current (lower). The oscillations in the displacement and current records are attributable to slight underdamping of the stimulator. (B) MT current-displacement relationship (upper), with peak current plotted against instantaneous displacement measured at the peak of the current, and force-displacement relationships (lower) from records in A. The force is plotted against displacements measured 0.5 ms (instantaneous) and 3 ms (steady state) after stimulus onset. KHB = 5 mN·m−1, P7 rat. (C) IHC motion of the fixed end of a fiber (Δx1, upper), the end attached to the inner hair cell bundle (Δx2, middle) and MT current (lower). (D) MT current-displacement relationship (upper), with the peak current plotted against instantaneous displacement at the peak current, and force-displacement relationships (lower) from records in C. The force is plotted against displacements measured 0.6 ms (instantaneous) and 3 ms (steady state) after stimulus onset. KHB = 1.5 mN·m−1, P11 rat. Stiffness of flexible fiber: 1.6 mN·m−1 (A); 2.3 mN·m−1 (C).
TABLE 2.
Hair-bundle stiffness of inner hair cells and outer hair cells
| Hair cell | KHB (mN·m−1) (control) | KHB (mN·m−1) (test) | N | Condition |
|---|---|---|---|---|
| OHC (apex) | 3.1 ± 0.4 | — | 22 | 1.5 mM Ca |
| IHC (apex) | 3.0 ± 0.6 | — | 9 | 1.5 mM Ca |
| OHC (middle) | 6.8 ± 2.5 | — | 6 | 1.5 mM Ca |
| OHC (apex) | 3.1 ± 0.4 | 1.9 ± 0.4 | 5 | + BAPTA |
| IHC (apex) | 3.5 | 2.3 | 1 | + BAPTA |
| OHC (apex) | 2.6 ± 0.2 | 5.6 ± 1.3 | 5 | + 0.2 mM DHS |
| IHC (apex) | 2.5 | 3.6 | 1 | + 0.2 mM DHS |
| OHC (apex) | 2.5 ± 0.8 | 4.5 ± 1.0 | 8 | 0.02 mM Ca |
Mean ± SE of the hair-bundle stiffness (KHB) for small deflections about the resting position of the bundle for IHCs and OHCs under various conditions. For OHCs, measurements are given for two cochlear locations corresponding to a CF of 4 kHz (apex) and 14 kHz (middle). N = number of experiments
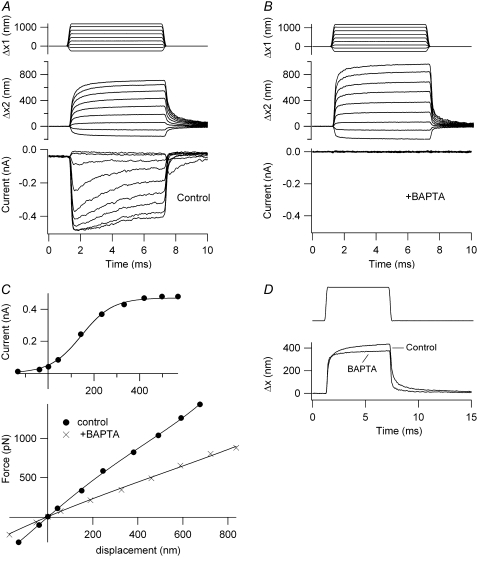
The time-dependent nonlinearity in the displacement response was largely eliminated and the stiffness reduced by brief treatment of the cell with submicromolar calcium buffered with BAPTA (Fig. 4). BAPTA treatment is thought to break the tip links and thereby abolish mechanotransduction in both nonmammals and mammals (34,45–47). In five OHCs, there was a 38% reduction in stiffness with BAPTA; for one IHC, the stiffness was reduced by 34%. These values are in reasonable agreement with the 43% reduction found in avian hair cells after BAPTA treatment (47). We reported previously that the time course of the slower component, the creep, in the bundle motion occurred synchronously with fast adaptation (29). In most of the cells in the study described here, this was also the case. For example, for the OHC in Fig. 3 A, the mean time constant of the secondary component for small displacements was 0.48 ms, compared to 0.43 ms for the fast adaptation. In the IHC in Fig. 3 B, the corresponding time constants were 0.8 ms for the displacement and 0.55 ms for fast adaptation. In the OHC of Fig. 5, the mechanical and electrical time constants for the low-level responses were 0.43 and 0.44 ms, respectively, under control conditions. After BAPTA treatment (Fig. 4 D), the slower component of the mechanical relaxation was lost. A similar acceleration of the onset and offsets after BAPTA treatment were seen in other cells. This is the opposite of what would be expected of a passive system where reduction in stiffness should slow the mechanical relaxation kinetics. It should be noted, however, that the time constant of fast adaptation, especially in OHCs, was slower with a stimulus delivered from a flexible probe than that measured previously by using a displacement step and a rigid probe (e.g., ∼0.2 ms (32)). This is most likely attributable to the slower stimulus onset achievable with the flexible fiber.
FIGURE 4.
Effects of BAPTA on hair-bundle stiffness of an OHC. (A) Control motion of the fixed end of the fiber (Δx1, upper), the end attached to the hair bundle (Δx2, middle), and MT current (lower). (B) Same measurements after a 2-s puff of a BAPTA-containing saline that abolished the MT current. (C) MT current plotted against instantaneous displacement (upper) and force plotted against steady-state displacement relationships (lower). The force-displacement plots are given before (solid circles, KHB = 2.5 mN·m−1) and after BAPTA application (crosses, KHB = 1.1 mN·m−1). P8 rat, IMAX = 490 pA. (D) Comparison of the two displacements of similar size shows the extra secondary component before BAPTA treatment. Stiffness of fiber, 1.9 mN·m−1.
FIGURE 5.
Effects of extracellular calcium on the hair-bundle mechanics in an OHC. (A) Motion of the fixed end of the fiber cemented to the piezoelectric actuator (Δx1, upper), the free end of the fiber attached to the hair bundle (Δx2, middle), and MT current (lower) in 1.5 mM extracellular calcium. (B) Motion of the fixed end of the fiber (Δx1, upper), the end attached to the hair bundle (Δx2, middle), and MT current (lower) in 0.02 mM extracellular calcium. (C, upper) Current-displacement relationships in 1.5 mM calcium (solid circles, prior control; open circles, wash) and in 0.02 mM calcium (crosses). (C, lower) Force-displacement relationships, with symbols the same as in upper. Fast-adaptation time constants (dashed lines): 0.44 ms for 1.5 mM calcium; 1.7 ms for 0.02 mM calcium. Secondary creep in displacement (dashed lines): 0.43 ms, 1.5 mM calcium; 0.70 ms; 0.02 mM calcium. P10 rat, IMAX = 800 pA, KHB = 8 mN·m−1 in 1.5 mM calcium. Stiffness of fiber, 2.4 mN·m−1.
Effects of calcium on hair-bundle stiffness
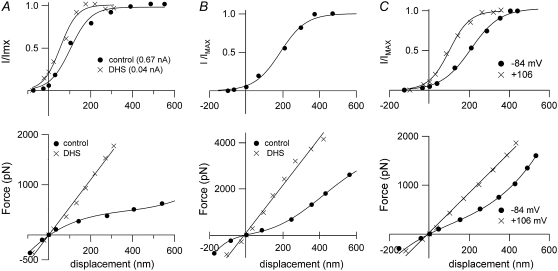
Fast adaptation is initiated by calcium entering through open MT channels (5,6,32). If there were a relationship between fast adaptation and hair-bundle mechanics, it might be expected that changes in calcium influx would affect the bundle response to a force stimulus. Three different experimental manipulations were performed to test this hypothesis. Reducing extracellular calcium concentration from 1.5 mM to 0.02 mM approximately doubled the stiffness (Table 2). In most of the cells, the secondary component in the displacement was also slowed in parallel with an increase in the adaptation time constant (29) (Fig. 5). A similar reversible increase in stiffness was also seen in five OHCs and one IHC on blocking the MT channels with 0.2 mM DHS (Fig. 6, A and B, Table 2). DHS at this concentration reduced the maximum MT current by over an order of magnitude, but it was still sometimes possible to construct a current-displacement plot that was shifted negative with respect to the control (Fig. 6 A), an effect similar to lowering the extracellular calcium concentration.
FIGURE 6.
Effects of DHS and depolarization on the hair-bundle mechanics. (A, upper) IHC, with MT current scaled to its maximum value, IMAX, plotted against displacement in control saline (solid circles, prior control) and in saline containing 0.2 mM DHS (crosses). (A, lower) Force-displacement relationships, with symbols the same as in A, upper. The current-displacement relationships have been fitted with single Boltzmann functions (see Methods), with IMAX = 655 pA (control) and 40 pA (DHS). Note that the DHS plot is shifted negative, which is consistent with a reduction in resting intracellular calcium due to channel block. KHB = 3.4 mN·m−1 in control and 4.9 mN·m−1 in DHS. P11 rat. (B, upper) OHC, with MT current scaled to its maximum value, IMAX, plotted against displacement in control saline. IMAX = 430 pA. (B, lower) Force-displacement relationships in control (solid circles) and in 0.2 mM DHS (crosses). The MT current in DHS was too small to be plotted. KHB = 4.2 mN·m−1 in control and 14.4 mN·m−1 in DHS. P11 rat. (C, upper) OHC, with MT current scaled to its maximum value, IMAX, plotted against displacement at −84 mV holding potential (solid circles) and at +106 mV (crosses). (C, lower) Force-displacement relationships with symbols the same as in C, upper. IMAX and KHB = 560 pA and 1.7 mN·m−1, respectively, at −84 mV, and 610 pA and 3.6 mN·m−1, respectively, at +106 mV. P11 rat. Stiffness of flexible fiber for all three cells, 1.6 mN·m−1.
A third manipulation to reduce calcium influx was depolarizing the hair cell to positive potential (Fig. 6 C). The mechanical stimulus was superimposed on a depolarizing voltage step to about +100 mV, the onset of the depolarization preceding that of the force by 7 ms. This experiment therefore differed from the other two maneuvers, where the calcium reduction occurred over a prolonged period of time and may have diminished the resting calcium level as well as that entering the bundle during deflection. In three cells (all recorded in 1.5 mM extracellular calcium), a 77% reversible increase in stiffness occurred during the depolarization, from a mean of 2.0 ± 0.6 mN·m−1 (−84 mV) to 3.5 ± 0.6 mN·m−1 (+106 mV).
Modeling the effects of calcium
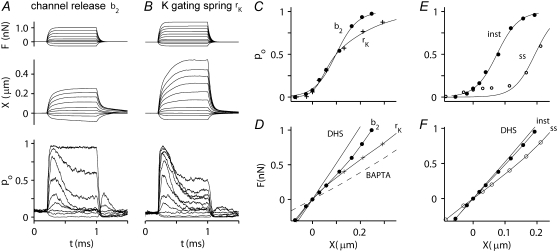
To account for the effects of calcium on hair-bundle stiffness, a finite-element model similar to that of Nam et al. (38) was developed for the OHC bundle incorporating the gating-spring theory of channel activation (20) and fast (channel-based) and slow (myosin-based) adaptation, both of which are assumed to be regulated by the local Ca2+ concentration. The model of channel gating in many respects resembles those described previously (8,23,48), but we assume four Ca2+ binding sites on the channel to augment the Ca2+ sensitivity. There are several differences from previous models. First, in stochastic channel gating, the consequent changes in calcium in each stereocilium are all-or-none, according to the stochastic activity of the channel, whether it is open or closed, as opposed to a smooth change in calcium paralleling the average change in open probability, as is usually assumed. Second, as Ca2+ binds to the channel, an extra force, fCa, is required to open a channel (8), and in addition, the gating spring is released by a fixed displacement, b2, here termed the channel release mechanism. A third action of Ca2+, to cause a reduction in the gating-spring stiffness, has been previously incorporated in some models of transduction (23) and was also examined here.
Force steps, delivered to the model bundle in an external calcium concentration comparable to the control experimental measurements, elicited a rapidly developing MT current that displayed fast adaptation with a submillisecond time constant and had a working range similar to those measured. The average time course and magnitude of the change in open probability for the channels in the first stereociliary row was identical to that for the channels in the second row (Fig. 7), as would occur if there were minimal splaying of the stereociliary ranks. Even though kinematic constraints were not imposed to enforce a coherent movement of the hair bundle (49), with only two MT channels along the excitatory-inhibitory axis, the channels in the two ranks responded in parallel. When examined in a Ca2+ concentration similar to that used experimentally (100 μM intracellularly at the channel mouth, equivalent to 1.2 mM Ca2+ extracellularly), the time course of the displacement for both mechanisms studied was slowed relative to the force and acquired a kinetic component comparable to adaptation (Fig. 8, A and B). On the channel release mechanism, the force-displacement relation displayed an inflection with a steady-state stiffness, KHB, for small displacements of 3.6 mN·m−1. For the mechanism in which calcium reduced the gating-spring stiffness, the force-displacement relationship was bilinear or curved, with the limiting stiffness being less for positive displacements than for negative ones. In this second model, KHB for small displacements was 3.9 mN·m−1. These two forms of theoretical force-displacement relationship, curved or with an inflection, represent two extremes. The shapes of the experimental force-displacement relationships (e.g., Figs. 3 and 6) fell in between these two extremes, suggesting that both theoretical mechanisms may operate in the OHC hair bundles. Two conditions in which the MT channel was inactive were also simulated. When the channel was blocked, as in the DHS experiments, bundle stiffness increased to 5.3 mN·m−1. To simulate channel block, the model channels were forced to remain in the closed state and, after a transient period during which calcium influx was abolished, all channels reverted to the calcium-unbound closed state (Fig. 2 C, C). When the tip links were removed, as in the BAPTA treatment, bundle stiffness decreased to 1.8 mN·m−1. The control values for KHB and those after treatment with DHS or BAPTA are close to the experimental measurements in rat cochlear hair cells (Table 2).
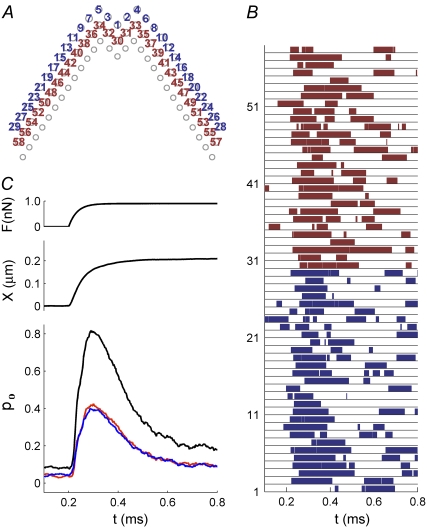
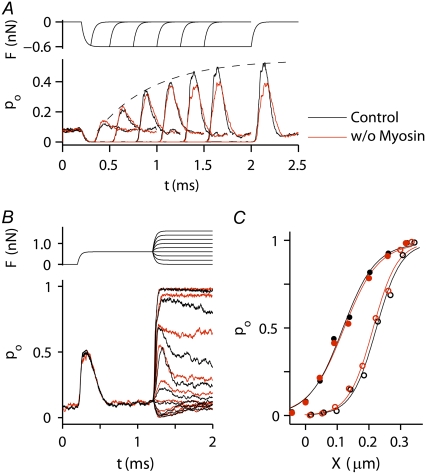
FIGURE 7.
Simulated responses of an OHC. (A) Top view of stereocilia showing numbering of MT channels in the first row (blue, 1–29) and second row (red, 30–58). MT channels are located solely at the top of each tip link, so the third row of stereocilia has no channels. (B) The channel numbers correspond to the numbers on the ordinate in the plot, showing the activity of each individual channel during a single force step of 0.9 nN, which was applied at t = 0.2 ms. The force was distributed equally to the tips of the tallest stereocilia. (C) Time course of the force step, F (upper curve), displacement, X (middle curve), and average probability of opening, pO (lower), computed from the individual responses in B. The average (pO) is identical for the first row (blue) and second row (red), the sum of the two responses shown in black.
FIGURE 8.
Simulated MT currents and hair-bundle mechanics on two different models. (A) Channel release model (b2): applied step force (F), bundle tip displacement (X), and the probability of MT channel opening (pO). The X and pO responses are averages of 10 simulations. Intracellular calcium at the fast-adaptation site with the MT channel open was 100 μM. (B) Calcium-induced reduction in the gating spring (rK): same simulations as in A. rK = 0.8 represents a maximal reduction in stiffness of 80%. (C) pO-X relationships of the channel on the “channel release” model (b2, solid circles) and on the “reduction in gating spring stiffness” model (rK, crosses). Results fitted with a single Boltzmann. (D) Force-displacement (F-X) relationships of the bundle for the two models. In addition, two passive conditions with no channel activity were also modeled. To simulate a hair cell treated with DHS, all the MT channels were blocked. To simulate a BAPTA-treated hair cell, the tip links were removed. KHB at X = 0 is 3.6 mN·m−1 (control; b2), 3.9 mN·m−1 (control; rk), 5.3 mN·m−1 (DHS), and 1.8 mN·m−1 (BAPTA). (E) pO-X relationships on the channel release model at the peak of the response (solid circles, inst) and after 1 ms (open circles, ss). (F) F-X relationships on the channel release model at the peak of the response (solid circles, inst) and after 1 ms (open circles, ss). Note that the instantaneous plot is close to that without channel activity in the presence of the blocker DHS.
The force generated by the calcium-dependent creep was estimated on the channel release mechanism from the “instantaneous” and “steady-state” force-displacement relationships (Fig. 8 F). Instantaneous measurements were taken at the peak of the MT current and steady-state ones at the end of the 1-ms bundle deflection. The instantaneous relationship was only slightly different from that measured in the presence of DHS, the small difference reflecting the instantaneous gating compliance (20). The force generated by the conformational change in the MT channel was determined from the maximum force difference between the instantaneous and steady-state curves at a fixed displacement. This value was 260 pN at 100 μM intracellular calcium. On the model in which calcium reduced the gating-spring stiffness, the maximum difference between the instantaneous and steady-state force-displacement relationships was 440 pN. On either model, the forces estimated are not far from those measured experimentally.
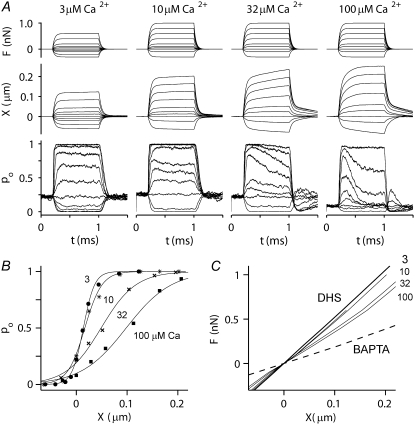
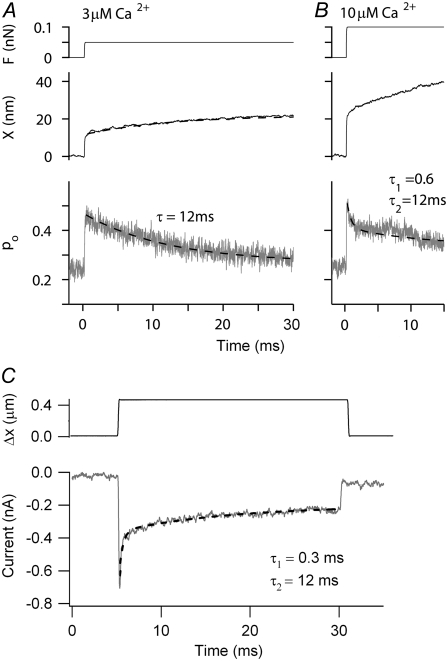
Simulated responses in different calcium concentrations
The consequences of altering extracellular calcium were also tested on the channel release (b2) mechanism (Fig. 9). For the MT current, the time constant of adaptation was slowed (from 0.12 ms to >1 ms) and the probability of channel opening at rest increased (from 0.07 to 0.26) as the internal calcium concentration when the channel was open (CFA) was lowered from 100 to 3 μM. These values of CFA correspond to external calcium concentrations of ∼1.2 mM and 30 μM, respectively, similar to the experimental range (see Methods). The model effects of calcium on the adaptation kinetics and probability of opening of the MT channel at rest resemble those found experimentally in auditory hair cells of both turtle (42) and rat (32). There was also a narrowing of the activation curve, the 10–90% operating range decreasing from 200 to 47 nm as CFA decreased from 100 to 3 μM. This effect may be explained by the fact that in a high calcium concentration, fast adaptation proceeds along with channel activation and thus broadens the current-displacement relationship. This implies that one should be cautious in deriving MT channel properties such as the gating-spring stiffness and gating swing by curve fitting the I-X curve with the two-state channel equation. The channel activation range on the gating-spring theory is best inferred from measurements in the absence of adaptation. With respect to the mechanical behavior of the hair bundle, there was a progressive rise in stiffness, with KHB increasing from 3.6 to 5.0 mN·m−1 as CFA decreased from 100 to 3 μM. At the lowest Ca2+ concentration, the force-displacement relationship converged on that in the presence of DHS. In addition, there was a slowing of the secondary creep in the displacement response and its eventual disappearance as CFA decreased and adaptation slowed and vanished. Simulations were also performed for CFA = 300 μM (results not shown), for which the force-displacement relationship was identical to that for 100 μM calcium but the time constant of adaptation was reduced further, to 0.06 ms (compared to 0.12 for 100 μM calcium).
FIGURE 9.
Simulated effect of calcium on MT channel and hair-bundle mechanics. (A) Probability of MT channel opening, pO (lower) and hair-bundle displacements, X (middle), for force steps (upper) at four different calcium concentrations: 3, 10, 32, and 100 μM at the fast-adaptation site (CFA) with the MT channel open. These calcium concentrations are approximately equivalent to 20 μM to 1.2 mM externally. Note the change in the speed of adaptation and of the secondary component of bundle displacement as the calcium increases. The adaptation time constants for small changes in pO for different values of CFA were 0.12 ms at 100 μM; 0.25 ms at 30 μM; 0.6 ms at 10 μM; and >1 ms at 3 μM calcium. (B) Effects of calcium on pO-X relationships for the four calcium concentrations. All relationships were fitted with a first-order Boltzmann equation. (Left to right) 3 μM (solid circles), 10 μM (asterisks), 32 μM (crosses), and 100 μM (solid squares) intracellular calcium. Note that the 10–90% operating range increased from 47 to 200 nm as CFA was increased from 3 to 100 μM. (C) F-X relationships for four different calcium concentrations (3, 10, 32, and 100 μM). Black lines are from the passive hair bundle with DHS (solid line) and BAPTA treatment (dashed line). With progressively increasing calcium concentration, the F-X relationship deviates further from the DHS curve. Simulations in this figure were performed only with the b2 model.
Contribution of the myosin motor
The channel release mechanism is similar to the idea of a calcium-induced release element in the myosin (12,50), in which a domain in myosin 1C was assumed to be the site of relaxation, regulated by the average calcium concentration. Although the kinetics of such a relaxation (e.g., the rocking of the myosin lever arm) are unknown, the speed of adaptation seems too fast to fit with a mechanism in which myosin dissociates from actin and goes through a full ATPase cycle. To investigate the latter possibility, the consequences of removing (locking) the myosin motor were examined in the channel release model by setting kA = 0 in Eq. 8. This is equivalent to maintaining the resting tension of the myosin motor but having it respond infinitely slowly. The myosin climbing speed in the previous simulations (Figs. 7–9) was ∼0.4 μm·s−1, comparable to that measured in vitro for myosin 1C (51). To look for any contribution of myosin to the response kinetics (and to shorten computation times), the climbing rate was increased to 1 μm s−1, still within the range reported experimentally for many myosin isoforms (51). The contribution of the myosin was assessed in two ways: first, by simulating the “rebound” at the end of a negative step due to recovery from adaptation (Fig. 10 A), sometimes referred to as negative adaptation (12); second, by examining the shift in the channel activation relationship after an adapting step (Fig. 10, B and C). The rebound was little affected without myosin and the adaptive shift was virtually identical in the presence and absence of myosin contribution. Lack of myosin also did not affect the time constant for fast adaptation for small stimuli (Fig. 10 B). Although in our model the myosin determined the resting tension, it did not significantly contribute to the response dynamics over the 2-ms simulation period. However, when the simulation period was extended, a slower component of adaptation with a time constant of 12 ms was evident (Figs. 11, A and B), which we attribute to the kinetics of myosin. Slower kinetic components of onset adaptation were also visible in the experimentally measured MT currents (Fig. 11 C). The slow time constant was somewhat variable between cells, ranging from 10 to 50 ms (mean ± SE = 25.9 ± 5.8 ms, n = 6).
FIGURE 10.
Theoretical contribution of the myosin motor on the channel release model. (A) Rebound of open probability after a negative step (pO) as a function of the duration of the step in the presence (black lines) and absence (red lines) of the myosin motor. The envelope of the rebound is an indicator of the adaptation process, which is little affected by removal of the myosin. (B) Effects of a positive 0.5-nN adapting step on the response onsets in the presence (black) and absence (red) of myosin. Note that lack of myosin does not affect the fast-adaptation time constant for small stimuli. The bundle displacement is 140 nm. (C) pO-X relationships under control conditions (solid circles) and after the 0.5-nN adapting step (open circles) in the presence (black) and absence (red) of myosin. The shift in the pO-X relationship is 110 nm. In these simulations, the rate constant for myosin-driven adaptation, kA, was 0.05 nm·ms−1·pN−1.
FIGURE 11.
Kinetic contribution of myosin to MT channel responses (A) Simulated probability of MT channel opening, pO (lower) and hair-bundle displacements, X (middle), for a force step (upper) for CFA = 3 μM calcium shown on a longer time scale. The size of the force step was chosen to evoke pO ≈ 0.5. Note the slow changes in pO and X that are fit with a time constant of 12 ms. No fast component attributable to channel adaptation was visible. (B) Simulated probability of MT channel opening, pO (lower) and hair-bundle displacements, X (middle), for a force step (upper) at CFA = 10 μM. In addition to the slow component of adaptation, the change in pO now had a fast component of time constant 0.6 ms due to the effects of calcium on the MT channel. In these simulations, the rate constant for myosin-driven adaptation, kA, was 0.05 nm·ms−1·pN−1. (C) Experimental response of an OHC to an extended displacement step. The adaptation was fitted with two components with time constants of 0.3 ms and 12 ms. P8 rat, 1.5 mM external calcium.
DISCUSSION
Hair-bundle stiffness and action of calcium
We have measured force-displacement relationships of both IHC and OHC hair bundles, mainly in the apical low-frequency region of the rat cochlea, and have shown that the relationship is altered by reducing calcium influx through the MT channels. The stiffness values of KHB, ∼3 mN·m−1, for small deflections about rest are toward the upper end of previous measurements on rodent hair cells, which in the low-frequency region of the cochlea ranged between 0.8 and 5.6 mN·m−1 (24–26). Both Strelioff and Flock (24) and Russell et al. (25) found little significant difference between IHC and first-row OHC bundles (e.g., OHC, 2.9 mN·m−1; IHC, 2.6 mN·m−1 (25)). Other things being equal, the stiffness should reflect the height and number of stereocilia in the bundle, which in the low-frequency region of the rat cochlea are comparable for both types of hair cell (4,39). Accurate values for hair-bundle stiffness are important in deciding whether the bundles contribute to the stiffness of the cochlear partition (52) and, therefore, whether vibrations of the partition can be influenced by MT channel gating. In a calcium concentration similar to endolymph (20 μM), the rat apical OHC bundles had KHB, of 5–6 mN·m−1 (Fig. 5). These values are about half those estimated indirectly from measurements in an intact organ of Corti, for which it was argued that they comprise a significant fraction of the stiffness of the cochlear partition (53).
The force-displacement plots of both inner and outer hair cells exhibited a time-dependent nonlinearity, showing an inflection or sometimes a curvature in which the stiffness for large positive displacements was less than that around the resting position of the hair bundle. The inflective nonlinearity has been previously observed in the force-displacement relationships of hair bundles of both nonmammals (20,54) and mammals (25,55). This nonlinearity is usually taken as an indication of the gating compliance as first reported in the frog saccule (20). However, with the stiffness values measured here, some an order of magnitude larger than in the frog saccule, the nonlinearity cannot be explained on the simple gating-spring hypothesis, as it requires a single channel gating forces much larger than those normally assumed (56). The single-channel gating force (equal to γb1kGS, where γ is the geometric gain, 0.11) was here ∼0.4 pN, which represents only a small contribution to the simulated force-displacement relationship. This contribution is evident as the difference between the instantaneous and DHS plots in Fig. 8 F. Furthermore, the nonlinearity reported here (and by Kennedy et al. (29)) was time-dependent and was diminished by procedures expected to reduce the calcium influx through open MT channels. These arguments imply a mechanism for the nonlinearity distinct from the gating compliance.
Model of the effects of calcium on MT channel gating and hair-bundle mechanics
The main conclusion from these experiments was that any manipulation that reduced calcium influx through the MT channels increased hair-bundle stiffness and diminished the nonlinearity in the force-displacement relationship. Two previous reports (on nonmammals) have hinted at a similar effect of calcium on bundle stiffness (54,57), but others have reached the opposite conclusion, that bundle stiffness was decreased rather than increased by lowering calcium (58,59). In neither of the latter two articles were MT currents recorded to confirm that the cells were transducing. Because we found similar stiffening with depolarization, channel block with DHS, and reduced external calcium, calcium must act at an intracellular location. To understand this effect of calcium, several sites of action should be considered, including the stereociliary rootlet, the horizontal connectors, and the MT channel complex, which includes the gating springs. Since calcium is known to promote fast adaptation with a submillisecond time course, the principal site of action of calcium is likely to be near the channel. Although we cannot rule out an additional effect of calcium at other structures such as the stereociliary rootlet, the diffusion distance along the stereocilium from the channel at the tip to the base seems too great for this to be the prime target for rapid calcium changes after channel opening.
To construct a unifying scheme, we chose a model in which the main site of calcium action is on the channel complex, in line with previous proposals (7,8,48). Four calcium-binding sites were assumed, because it was previously found that with a single binding site the dependence of the adaptation parameters on calcium was too weak (10). In the modeling described here, binding of calcium to a single site was investigated but found to be insufficient to achieve the extent of adaptation; an earlier model of channel-based adaptation invoked multiple calcium binding sites to produce bundle oscillations (48). Calcium binding increased the force to open the channel (8) and also caused a reduction in the stiffness of the gating spring or an increase in the unstrained length of the tip-link assembly by b2. A possible physical manifestation of the latter process would be a conformational change in the MT channel on calcium binding, similar to that occurring in the RCK gating ring of the BK channel when calcium binds (60). Both types of model reproduced the fast adaptation of the MT currents and, to a large extent, the form of the force-displacement relationship and its modification by calcium. In our channel release model, b2 is an important ingredient needed to predict the effects of calcium on hair-bundle stiffness and the secondary component of bundle displacement that parallels fast adaptation in response to a force step. Although fast channel adaptation is primarily attributable to stabilization of the channel state (fCa) increasing the force needed to open the channel, the b2 process also accentuates fast adaptation.
Although we have located the fast mechanical consequences of calcium binding solely to the channel, another recent approach has placed the mechanism entirely with the performance of the myosin motor (13). A strength of that approach was the ability to extend the model to multiple preparations, frog, turtle and rat. However, to account for the much greater speed of adaptation in the mammal, a maximal velocity of the myosin motor ∼100-fold larger in the mammal than in the nonmammals was assumed. Velocities up to 70 μm s−1 were invoked, much greater than those measured in vitro for myosin, most isoforms of which are <1 μm s−1 (see Table 13.1 in Howard (51)). For this reason, we chose to use the myosin to maintain the resting tension in the tip links but not to contribute to the fast submillisecond kinetics (Fig. 10). We should emphasize, however, that our description of the myosin activation is simplistic and does not take into account the more complex kinetics measured on single myosin 1C molecules in vitro (61). It is worth noting that, using a myosin climbing rate of 1 μm·s−1, the slow component of adaptation in our simulations had a time constant of 12 ms, which is almost identical to the time constant of the process referred to as “fast adaptation” by Stauffer et al. (see Fig. 2 K in Stauffer et al. (12)), but nearly 100-fold slower than the fast adaptation in rat OHCs.
Two features of the experimental responses were not predicted by our model: the extent of nonlinearity in some of the instantaneous force-displacement relationships, especially the negative slopes reported by Kennedy et al. (29); and the bundle recoil or twitch during a force stimulus observed in nonmammalian hair bundles (62,22,8) but not yet found in mammals. Owing to the complexity of the model and the time required for each computation, it was not feasible to explore the whole parameter space, so at this point we cannot rule out the possibility that one particular set of parameters not yet defined will generate the negative stiffness or the recoil. It is conceivable that differences between model and experimental results could be corrected by adjusting the relative sizes of b1 and b2, or by having b2 adopt different values for each of the four calcium binding sites. Increasing the gating swing, b1 (which at 1 nm is at the lower end of the range employed in other models) would augment the effect of the calcium-dependent channel reclosure on hair-bundle mechanics, but it would also diminish the operating range of the MT channel (20) to below the 200–300 nm observed experimentally. The value of b1 was chosen at least partly to match the working range of the model and experiment. It should be noted that values used in the model for b1 and b2 may still be considered large compared to the likely conformational movements to open an ion channel. The maximal channel deformation attributable to the effects of b1 and b2, taking into account the structural interactions in the model bundle, was <10 nm. Large values for the swing of the gate, b1 (up to 11 nm (13)) were used in previous gating-spring models, but those values have been justified by the possibility of a molecular lever working at a mechanical disadvantage (21).
Implications for amplification
Both a nonlinearity in the F-X relationship and a mechanical response synchronized with fast adaptation are central to high-frequency mechanical amplification in nonmammalian hair bundles. Whether they also provide a component of amplification in the mammalian cochlea is contentious. Nevertheless, evidence for both processes has been found in this study. Surprisingly, there was no major difference in the mechanical properties of hair bundles between IHCs and OHCs, even though amplification is normally ascribed solely to OHCs (30). In particular, nonlinearities in the force-displacement relation and in the time-dependent relaxation were evident in both cell types. There has been a recent proposal that IHCs may also exhibit bundle-based amplification to augment the motion near threshold (63). The amplification may be effective in vivo, since the IHC hair bundles are not directly attached to the tectorial membrane. We have previously argued that the time-dependent creep in hair-bundle displacement reflects force generation by the hair bundle linked to fast adaptation (29). This feature was also seen here and, indeed, was predicted by our model, though its magnitude was not enough to produce negative stiffness in the force-displacement relation. In the experiments presented here, we failed to observe the negative stiffness seen earlier (29). The reason for this discrepancy is unknown and warrants further investigation. Because displacement responses are most likely blunted by the slowness of our force stimuli, more accurate characterization of the time course of bundle motion, including searching for a recoil, will probably necessitate improved techniques for applying fast forces to the hair bundle.
Acknowledgments
This work was funded by a National Institutes on Deafness and other Communicative Disorders grant (RO1 DC 01362) to R.F.
Maryline Beurg and Jong-Hoon Nam contributed equally to this work.
Editor: E. Michael Ostap.
References
- 1.Pickles, J. O., S. D. Comis, and M. P. Osborne. 1984. Cross-links between stereocilia in the guinea pig organ of Corti, and their possible relation to sensory transduction. Hear. Res. 15:103–112. [DOI] [PubMed] [Google Scholar]
- 2.Hudspeth, A. J. 1989. How the ear's works work. Nature. 341:397–404. [DOI] [PubMed] [Google Scholar]
- 3.Ohmori, H. 1985. Mechano-electrical transduction currents in isolated vestibular hair cells of the chick. J. Physiol. 359:189–217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Beurg, M., M. G. Evans, C. M. Hackney, and R. Fettiplace. 2006. A large-conductance calcium-selective mechanotransducer channel in mammalian cochlear hair cells. J. Neurosci. 26:10992–11000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Eatock, R. A. 2000. Adaptation in hair cells. Annu. Rev. Neurosci. 23:285–314. [DOI] [PubMed] [Google Scholar]
- 6.Fettiplace, R., and A. J. Ricci. 2003. Adaptation in auditory hair cells. Curr. Opin. Neurobiol. 13:446–451. [DOI] [PubMed] [Google Scholar]
- 7.Crawford, A. C., M. G. Evans, and R. Fettiplace. 1989. Activation and adaptation of transducer currents in turtle hair cells. J. Physiol. 419:405–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cheung, E. L., and D. P. Corey. 2006. Ca2+ changes the force sensitivity of the hair-cell transduction channel. Biophys. J. 90:124–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gillespie, P. G., and J. L. Cyr. 2004. Myosin-1c, the hair cell's adaptation motor. Annu. Rev. Physiol. 66:521–545. [DOI] [PubMed] [Google Scholar]
- 10.Wu, Y. C., A. J. Ricci, and R. Fettiplace. 1999. Two components of transducer adaptation in auditory hair cells. J. Neurophysiol. 82:2171–2181. [DOI] [PubMed] [Google Scholar]
- 11.Holt, J. R., and D. P. Corey. 2000. Two mechanisms for transducer adaptation in vertebrate hair cells. Proc. Natl. Acad. Sci. USA. 97:11730–11735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stauffer, E. A., J. D. Scarborough, M. Hirono, E. D. Miller, K. Shah, J. A. Mercer, J. R. Holt, and P. G. Gillespie. 2005. Fast adaptation in vestibular hair cells requires myosin-1c activity. Neuron. 47:541–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tinevez, J. Y., F. Jülicher, and P. Martin. 2007. Unifying the various incarnations of active hair-bundle motility by the vertebrate hair cell. Biophys. J. 93:4053–4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lim, D. J. 1980. Cochlear anatomy related to cochlear micromechanics. A review. J. Acoust. Soc. Am. 67:1686–1695. [DOI] [PubMed] [Google Scholar]
- 15.Furness, D. N., and C. M. Hackney. 1985. Cross-links between stereocilia in the guinea pig cochlea. Hear. Res. 18:177–188. [DOI] [PubMed] [Google Scholar]
- 16.Tsuprun, V., and P. Santi. 1998. Structure of outer hair cell stereocilia links in the chinchilla. J. Neurocytol. 27:517–528. [DOI] [PubMed] [Google Scholar]
- 17.Tsuprun, V., P. A. Schachern, S. Cureoglu, and M. Paparella. 2003. Structure of the stereocilia side links and morphology of auditory hair bundle in relation to noise exposure in the chinchilla. J. Neurocytol. 32:1117–1128. [DOI] [PubMed] [Google Scholar]
- 18.Crawford, A. C., and R. Fettiplace. 1985. The mechanical properties of ciliary bundles of turtle cochlear hair cells. J. Physiol. 364:359–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fettiplace, R., and A. J. Ricci. 2006. Mechanoelectrical transduction in auditory hair cells. In Handbook of Auditory Research: Vertebrate Hair Cells. R. A. Eatock, R. R. Fay, and A. N. Popper, editors. Springer, New York. 154–203.
- 20.Howard, J., and A. J. Hudspeth. 1988. Compliance of the hair bundle associated with gating of mechanoelectrical transduction channels in the bullfrog's saccular hair cell. Neuron. 1:189–199. [DOI] [PubMed] [Google Scholar]
- 21.Martin, P., A. D. Mehta, and A. J. Hudspeth. 2000. Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell. Proc. Natl. Acad. Sci. USA. 97:12026–12031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ricci, A. J., A. C. Crawford, and R. Fettiplace. 2000. Active hair bundle motion linked to fast transducer adaptation in auditory hair cells. J. Neurosci. 20:7131–7142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Martin, P., D. Bozovic, Y. Choe, and A. J. Hudspeth. 2003. Spontaneous oscillation by hair bundles of the bullfrog's sacculus. J. Neurosci. 23:4533–4548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Strelioff, D., and A. Flock. 1984. Stiffness of sensory-cell hair bundles in the isolated guinea pig cochlea. Hear. Res. 15:19–28. [DOI] [PubMed] [Google Scholar]
- 25.Russell, I. J., M. Kossl, and G. P. Richardson. 1992. Nonlinear mechanical responses of mouse cochlear hair bundles. Proc. Roy. Soc. Lond. B. Biol. Sci. 250:217–227. [DOI] [PubMed] [Google Scholar]
- 26.Géléoc, G. S., G. W. Lennan, G. P. Richardson, and C. J. Kros. 1997. A quantitative comparison of mechanoelectrical transduction in vestibular and auditory hair cells of neonatal mice. Proc. Roy. Soc. Lond. B. Biol. Sci. 264:611–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ricci, A. J., H. J. Kennedy, A. C. Crawford, and R. Fettiplace. 2005. The transduction channel filter in auditory hair cells. J. Neurosci. 25:7831–7839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chan, D. K., and A. J. Hudspeth. 2005. Ca2+ current-driven nonlinear amplification by the mammalian cochlea in vitro. Nat. Neurosci. 8:149–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kennedy, H. J., A. C. Crawford, and R. Fettiplace. 2005. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 433:880–883. [DOI] [PubMed] [Google Scholar]
- 30.Dallos, P. 1992. The active cochlea. J. Neurosci. 12:4575–4585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Fettiplace, R., and C. M. Hackney. 2006. The sensory and motor roles of auditory hair cells. Nat. Rev. Neurosci. 7:19–29. [DOI] [PubMed] [Google Scholar]
- 32.Kennedy, H. J., M. G. Evans, A. C. Crawford, and R. Fettiplace. 2003. Fast adaptation of mechanoelectrical transducer channels in mammalian cochlear hair cells. Nat. Neurosci. 6:832–836. [DOI] [PubMed] [Google Scholar]
- 33.Bosher, S. K., and R. L. Warren. 1978. Very low calcium content of cochlear endolymph, an extracellular fluid. Nature. 273:377–378. [DOI] [PubMed] [Google Scholar]
- 34.Assad, J. A., G. M. Shepherd, and D. P. Corey. 1991. Tip-link integrity and mechanical transduction in vertebrate hair cells. Neuron. 7:985–994. [DOI] [PubMed] [Google Scholar]
- 35.Ricci, A. J., A. C. Crawford, and R. Fettiplace. 2003. Tonotopic variation in the conductance of the hair cell mechanotransducer channel. Neuron. 40:983–990. [DOI] [PubMed] [Google Scholar]
- 36.Müller, M. 1991. Frequency representation in the rat cochlea. Hear. Res. 51:247–254. [DOI] [PubMed] [Google Scholar]
- 37.Cotton, J. R., and J. W. Grant. 2000. A finite element method for mechanical response of hair cell ciliary bundles. J. Biomech. Eng. 122:44–50. [DOI] [PubMed] [Google Scholar]
- 38.Nam, J. H., J. R. Cotton, and W. Grant. 2007. A virtual hair cell, I: addition of gating spring theory into a 3-D bundle mechanical model. Biophys. J. 92:1918–1928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Roth, B., and V. Bruns. 1992. Postnatal development of the rat organ of Corti. II. Hair cell receptors and their supporting elements. Anat. Embryol. (Berl.). 185:571–581. [DOI] [PubMed] [Google Scholar]
- 40.Nam, J. H., J. R. Cotton, and J. W. Grant. 2005. Effect of fluid forcing on vestibular hair bundles. J. Vestib. Res. 15:263–278. [PubMed] [Google Scholar]
- 41.Vilfan, A., and T. Duke. 2003. Two adaptation processes in auditory hair cells together can provide an active amplifier. Biophys. J. 85:191–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ricci, A. J., Y. C. Wu, and R. Fettiplace. 1998. The endogenous calcium buffer and the time course of transducer adaptation in auditory hair cells. J. Neurosci. 18:8261–8277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Roberts, W. M. 1993. Spatial calcium buffering in saccular hair cells. Nature. 363:74–76. [DOI] [PubMed] [Google Scholar]
- 44.Howard, J., and J. F. Ashmore. 1986. Stiffness of sensory hair bundles in the sacculus of the frog. Hear. Res. 23:93–104. [DOI] [PubMed] [Google Scholar]
- 45.Crawford, A. C., M. G. Evans, and R. Fettiplace. 1991. The actions of calcium on the mechano-electrical transducer current of turtle hair cells. J. Physiol. 434:369–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Goodyear, R. J., W. Marcotti, C. J. Kros, and G. P. Richardson. 2005. Development and properties of stereociliary link types in hair cells of the mouse cochlea. J. Comp. Neurol. 485:75–85. [DOI] [PubMed] [Google Scholar]
- 47.Bashtanov, M. E., R. J. Goodyear, G. P. Richardson, and I. J. Russell. 2004. The mechanical properties of chick (Gallus domesticus) sensory hair bundles: relative contributions of structures sensitive to calcium chelation and subtilisin treatment. J. Physiol. 559:287–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Choe, Y., M. O. Magnasco, and A. J. Hudspeth. 1998. A model for amplification of hair-bundle motion by cyclical binding of Ca2+ to mechanoelectrical transduction channels. Proc. Natl. Acad. Sci. USA. 95:15321–15326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kozlov, A. S., T. Risler, and A. J. Hudspeth. 2007. Coherent motion of stereocilia assures the concerted gating of hair-cell transduction channels. Nat. Neurosci. 10:87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bozovic, D., and A. J. Hudspeth. 2003. Hair-bundle movements elicited by transepithelial electrical stimulation of hair cells in the sacculus of the bullfrog. Proc. Natl. Acad. Sci. USA. 100:958–963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Sunderland, MA.
- 52.Dallos, P. 2003. Organ of Corti kinematics. J. Assoc. Res. Otolaryngol. 4:416–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chan, D. K., and A. J. Hudspeth. 2005. Mechanical responses of the organ of Corti to acoustic and electrical stimulation in vitro. Biophys. J. 89:4382–4395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ricci, A. J., A. C. Crawford, and R. Fettiplace. 2002. Mechanisms of active hair bundle motion in auditory hair cells. J. Neurosci. 22:44–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.van Netten, S. M., and C. J. Kros. 2000. Gating energies and forces of the mammalian hair cell transducer channel and related hair bundle mechanics. Proc. Roy. Soc. Lond. B. Biol Sci. 267:1915–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Fettiplace, R. 2006. Active hair bundle movements in auditory hair cells. J. Physiol. 576:29–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Marquis, R. E., and A. J. Hudspeth. 1997. Effects of extracellular Ca2+ concentration on hair-bundle stiffness and gating-spring integrity in hair cells. Proc. Natl. Acad. Sci. USA. 94:11923–11928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Orman, S., and A. Flock. 1983. Active control of sensory hair mechanics implied by susceptibility to media that induce contraction in muscle. Hear. Res. 11:261–266. [DOI] [PubMed] [Google Scholar]
- 59.Pae, S. S., and J. C. Saunders. 1994. Intra- and extracellular calcium modulates stereocilia stiffness on chick cochlear hair cells. Proc. Natl. Acad. Sci. USA. 91:1153–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Niu, X., X. Qian, and K. L. Magleby. 2004. Linker-gating ring complex as passive spring and Ca2+-dependent machine for a voltage- and Ca2+-activated potassium channel. Neuron. 42:745–756. [DOI] [PubMed] [Google Scholar]
- 61.Batters, C., C. P. Arthur, A. Lin, J. Porter, M. A. Geeves, R. A. Milligan, J. E. Molloy, and L. M. Coluccio. 2004. Myo1c is designed for the adaptation response in the inner ear. EMBO J. 23:1433–1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Benser, M. E., R. E. Marquis, and A. J. Hudspeth. 1996. Rapid, active hair bundle movements in hair cells from the bullfrog's sacculus. J. Neurosci. 16:5629–5643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fridberger, A., I. Tomo, M. Ulfendahl, and J. Boutet de Monvel. 2006. Imaging hair cell transduction at the speed of sound: dynamic behavior of mammalian stereocilia. Proc. Natl. Acad. Sci. USA. 103:1918–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]