Abstract
Forced unbinding of complementary macromolecules such as ligand-receptor complexes can reveal energetic and kinetic details governing physiological processes ranging from cellular adhesion to drug metabolism. Although molecular-level experiments have enabled sampling of individual ligand-receptor complex dissociation events, disparities in measured unbinding force FR among these methods lead to marked variation in inferred binding energetics and kinetics at equilibrium. These discrepancies are documented for even the ubiquitous ligand-receptor pair, biotin-streptavidin. We investigated these disparities and examined atomic-level unbinding trajectories via steered molecular dynamics simulations, as well as via molecular force spectroscopy experiments on biotin-streptavidin. In addition to the well-known loading rate dependence of FR predicted by Bell's model, we find that experimentally accessible parameters such as the effective stiffness of the force transducer k can significantly perturb the energy landscape and the apparent unbinding force of the complex for sufficiently stiff force transducers. Additionally, at least 20% variation in unbinding force can be attributed to minute differences in initial atomic positions among energetically and structurally comparable complexes. For force transducers typical of molecular force spectroscopy experiments and atomistic simulations, this energy barrier perturbation results in extrapolated energetic and kinetic parameters of the complex that depend strongly on k. We present a model that explicitly includes the effect of k on apparent unbinding force of the ligand-receptor complex, and demonstrate that this correction enables prediction of unbinding distances and dissociation rates that are decoupled from the stiffness of actual or simulated molecular linkers.
INTRODUCTION
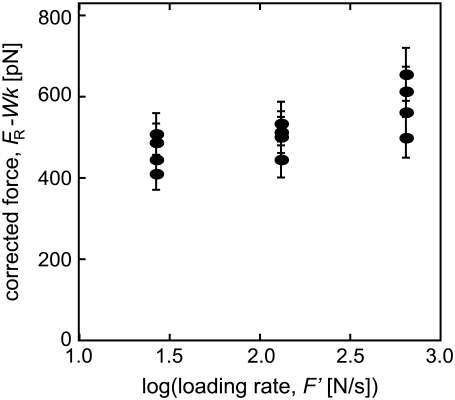
Ligand-receptor kinetics and energetics have been measured typically through experimental methods that quantify population-averaged responses (1), but a range of new experiments and simulations enables the probing of individual complexes to explore important variations in binding responses within and among ligand or cell populations (2–4). Biotin-streptavidin is among the strongest known ligand-receptor interactions and, as such, it has been widely studied as a model system (5–14) and utilized in biological experiments (15–23). Despite the ubiquitous application of the biotin-streptavidin complex in biotechnology and biophysics as a molecular glue capable of strong, specific interactions and long binding lifetime, there is considerable disagreement among experiments regarding the actual strength of this complex (24,25). Many studies of the dynamic strength of biotin-streptavidin have been reported, using diverse experimental tools such as optical traps (26), laminar flow chambers (27), electric fields (28), magnetic fields (29), the biomembrane force probe (30), and the atomic force microscope (31–39) to rupture the complex. Although these experimental methods differ from each other in many ways, they all aim to measure the unbinding force FR of the same molecular system. However, even among experiments at comparable loading rates—a known controlling factor of FR—the magnitude and rate dependence of FR can vary widely (24,25), as illustrated in Fig. 1. The dynamic strength of this complex has also been studied through various computational and analytical methods, such as steered molecular dynamics (40) and Langevin dynamics (41).
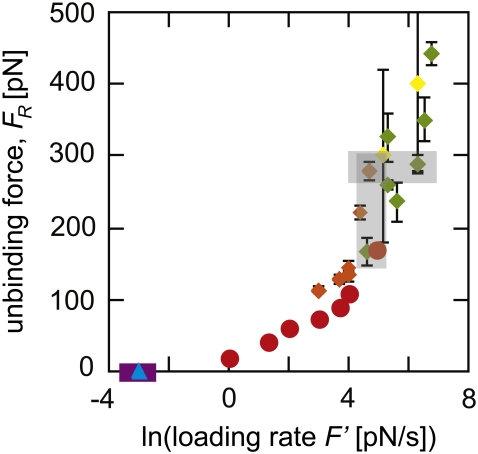
FIGURE 1.
Experiments to determine the unbinding force spectrum of biotin-streptavidin have not reached a consensus. Reported data on the unbinding force of biotin-streptavidin is shown as measured by AFM MFS (diamonds in green (35–37), orange (32), and yellow (38)), electric fields (blue triangles (28)), magnetic fields (purple squares (29), points overlap), and BFP (red circles (30)). Error bars indicating the standard deviation among experimental measurements are shown for all data points, but in some cases are smaller than the symbols. The shaded rectangles highlight measurements at similar loading rates where measured unbinding forces differ by a factor of two and measurements of similar unbinding forces where the loading rate differed by two orders of magnitude.
Accurate measurements of FR are necessary if experiments and simulations are to provide quantitative value to chemomechanical imaging of cell surfaces (42,43), biophysical studies of unbinding trajectories (4), and prediction of binding kinetics (42). Bell's model of specific adhesion under applied force (3,44,45) is commonly applied to such experiments to extract kinetic and energetic binding constants. For a monotonically increasing applied force, an adaptation of this model relates the unbinding force to experimental, kinetic, and energetic parameters as
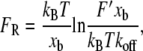 |
(1) |
where kB is Boltzmann's constant, T is absolute temperature, xb is the distance between the bound state, and the energetic maximum, F′ = kv is the loading rate (where k is the stiffness of the force transducer and v is the velocity), and koff is the kinetic rate of binding dissociation at equilibrium. From forced dissociation of molecules far from equilibrium, the extrapolated value of ln(F′) at FR = 0 and the slope of FR versus ln(F′) are critical for estimating both the kinetic (koff) and energetic (xb) parameters of the complex at equilibrium. To obtain accurate estimates of koff and xb, it is necessary to understand both the bandwidth of such measurements and the extent to which experimental or computational parameters perturb FR.
To the best of our knowledge, we have reviewed all reported studies of the forced unbinding of the biotin-streptavidin complex. Experiments in which the loading rate or the unbinding force could not be determined were excluded, and our focus was limited to studies utilizing methods that attempted to apply a monotonically increasing force to the ligand-receptor complex, including applied electric (28) and magnetic (29) fields, the biomembrane force probe (BFP) (30), the atomic force microscope (AFM) (31–39), and optical traps (26), as reviewed by Van Vliet et al. (46). We also excluded studies of slightly different molecules such as immunobiotin or avidin, to eliminate as many extraneous factors as possible.
After applying these criteria, eight experimental studies remained: Breisch et al.'s use of electric fields to apply force (28), Panhorst et al.'s use of magnetic fields (29), Merkel et al.'s use of the BFP (30), and five separate studies using the AFM to conduct molecular force spectroscopy (MFS) (32,35–38). Fig. 1 shows the unbinding or rupture forces FR reported in these studies as a function of the logarithm of the reported loading rate F′. It appears clear that the reported unbinding force FR is not a unique function of F′: experiments differing by more than an order of magnitude in F′ measured very similar unbinding force distributions, and unbinding forces measured at the same F′ differ by as much as 200%. One possible explanation is that discrepancies in reported unbinding forces could arise from subtle differences in experimental technique, such as the type of molecular linker utilized. However, this would not account for results reported by a single research group utilizing the same experimental approach that do not agree within the reported range of error, such as those of Lo et al. (35–37). Another rationale is that FR depends not just on loading rate, but also on the entire loading history of the complex; this is plausible yet difficult to quantify (24,25).
In light of these well-established discrepancies among experimental results for a model ligand-receptor complex, we performed new steered molecular dynamics (SMD) simulations (4) of forced unbinding of the biotin-streptavidin complex. These simulations allowed exploration of the effects of molecular structure, loading direction, and experimentally accessible parameters including force transducer stiffness k and velocity v on the observed unbinding force FR and inferred kinetic and energetic properties of the complex. The biotin-streptavidin pair was one of the first systems studied with SMD (40); while that report was groundbreaking in terms of technique, we performed new simulations because there were several aspects that would benefit from advances in computational resources and protocols over the past decade, including the current capacity to simulate the entirety of the streptavidin tetramer over nanosecond timescales. In both the experimental and simulated loading rate regimes, we find that several experimentally accessible factors other than loading rate significantly affect both the observed FR and the calculated binding parameters. Each of these factors can alter the ligand's exploration of the energy landscape presented by the receptor. In particular, an increase in the effective stiffness of the molecular force transducer k directly perturbs the energy landscape, leading to an increase in the observed FR and to wide variation in extrapolated binding parameters. A new model, which corrects for the effects of k on unbinding force and kinetic dissociation rates, is introduced.
METHODS
Steered molecular dynamics
Grubmüller et al. (40) have reported SMD simulations of the forced unbinding of biotin from the streptavidin monomer, a choice due in large part to limited computational resources. As the residues of the biotin binding pocket are located on two streptavidin subunits, our physics-based procedure for equilibration of simulation proteins (47) confirmed that the biotin-streptavidin monomer was an inherently poor representation of this complex. For detailed information on the SMD simulations performed on the biotin-streptavidin monomer, see Supplementary Material. We subsequently conducted SMD simulations of the full streptavidin tetramer, with biotin bound in all four binding sites. The biotin-streptavidin tetramer (PDB ID 1STP (13)) was simulated as described previously (47). Briefly, using the GROMACS molecular dynamics package, version 3.3 (48,49), the protein was solvated in a cubic box of edge length 8.59 nm with 18,533 simple-point charge (SPC216) water molecules: 50 sodium ions and 42 chlorine ions were added to provide charge neutrality and to mimic physiological conditions. Steepest-descent minimization of the x-ray diffraction structure was implemented to reduce the maximum force in the system to 2000 kJ mol−1 nm−1. After minimization, unconstrained molecular dynamics simulation over 100 ns was performed to equilibrate the system. This required one week on 12 dual-processor Intel Xeon 3.0 GHz cluster nodes. The initial position of the force transducer (spring) in all SMD simulations coincided with one of the terminal oxygen atoms of the biotin (designated O2 in the PDB structure), the atom at which intermediate linkers ostensibly bond in the molecular force spectroscopy experiments. The position of this atom in the structure of biotin is shown in Supplementary Material Fig. S2.
Using the protocol developed in Walton and Van Vliet (47), we determined that the complex had entered a local energy minimum within 15 ns of beginning the equilibration trajectory. Structures were taken from this trajectory at intervals of 10 ns from time 15 ns to 95 ns. These were used as initial configurations for subsequent, identical SMD simulations. One subunit of the tetramer was subjected to loading forces, although all four biotin binding sites were occupied. The tensile loading direction was defined as the vector between the initial center of mass of the streptavidin subunit and the O2 atom of the biotin bound to that subunit. The center of mass of the streptavidin tetramer was fixed, but the system was allowed to rotate about the center of mass. Transducer spring constants k ranged from 500 to 5000 kJ mol−1 nm−2 (0.83–8.3 N/m) while velocities v ranged from 0.4 to 10 m/s. Effective loading rates F′ ranged from 0.4 to 11 N/s.
We performed three sets of simulations on the biotin-streptavidin tetramer. In the first set, the loading conditions (velocity v and spring constant k) were maintained while the initial equilibrated structure was varied as above. This set of simulations was designed to test the effects of initial complex structure on the measured unbinding force. In the second set, the loading direction was varied by vector rotation of ±5° and ±10° around the x, y, and z directions. In the third set, the initial structure was maintained while the loading conditions were varied. The structure taken from the equilibration trajectory at 20 ns was used. This set of simulations was designed to test the effects of experimentally accessible parameters on the unbinding force measurement—that is, parameters that are amenable to intentional variation in physical experiments.
The resulting trajectories were analyzed to extract the force exerted by the spring and the reaction coordinate of the ligand as functions of simulation time. Here, the reaction coordinate χ is defined as the distance of the biotin O2 atom from its initial position, 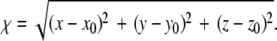 In analysis of the tetramer, we examined the forces at 200 fs intervals to investigate how the applied force varied with reaction coordinate χ. Other time intervals were also explored; 200 fs was selected because this interval allowed for examination of the trajectory without significant changes in the maximum unbinding force selected by visual inspection of force F versus reaction coordinate χ (ΔFR ∼1%). When the unbinding force FR is referenced, it is the maximum force recorded during a particular trajectory (e.g., see Supplementary Material Fig. S1 B). The energetic unbinding distance xb and kinetic dissociation rate koff were determined via a least-squares linear regression of FR versus lnF′ to obtain the slope (m) and x-intercept (b). From Bell's model, it is easily found that
In analysis of the tetramer, we examined the forces at 200 fs intervals to investigate how the applied force varied with reaction coordinate χ. Other time intervals were also explored; 200 fs was selected because this interval allowed for examination of the trajectory without significant changes in the maximum unbinding force selected by visual inspection of force F versus reaction coordinate χ (ΔFR ∼1%). When the unbinding force FR is referenced, it is the maximum force recorded during a particular trajectory (e.g., see Supplementary Material Fig. S1 B). The energetic unbinding distance xb and kinetic dissociation rate koff were determined via a least-squares linear regression of FR versus lnF′ to obtain the slope (m) and x-intercept (b). From Bell's model, it is easily found that 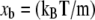 and koff = bxb/kBT.
and koff = bxb/kBT.
Experiments
AFM-enabled molecular force experiments on biotin-streptavidin were conducted to obtain FR, koff, and xb as a function of experimentally accessible variables such as loading rate and force transducer stiffness. Silicon nitride AFM cantilevers of varying nominal spring constant kc (11, 35, 58, and 121 pN/nm or mN/m) were used as force transducers (MLCT-AUHW, Veeco Instruments, Woodbury, NY; MAC-IV levers, Agilent/Molecular Imaging, Palo Alto, CA). These cantilevers were cleaned in piranha solution (30% hydrogen peroxide: 70% sulfuric acid) for 30 min, followed by rinsing in deionized water. Cantilevers were then dried in a stream of nitrogen. N,N-Di-isopropylethylamine (300 μL, Sigma-Aldrich, St. Louis, MO) and 3-aminopropyltriethoxysilane (900 μL, Sigma-Aldrich) were used for amine derivatization of cleaned cantilevers and freshly cleaved mica in a vacuum desiccator via chemical vapor deposition for 2 h. Biotinylated BSA (B-BSA, Pierce Biotechnology, Rockford, IL) in sodium bicarbonate (pH = 8.9, 0.5 mg/mL) was added to cantilevers and mica, and the adsorption reaction proceeded overnight at 37°C (50,51). Cantilevers and mica were rinsed with 150 mM NaCl phosphate-buffered saline (PBS) twice, followed by covalent attachment of B-BSA to the cantilevers and mica with 52 mM 1-Ethyl-3-[3-dimethylaminopropyl]carbodiimide hydrochloride (EDC, Pierce Biotechnology) for 2 h. After the covalent conjugation of B-BSA via EDC, cantilevers and mica were rinsed five times with PBS. B-BSA-conjugated mica was incubated with 100 μL of streptavidin (Pierce Biotechnology) in PBS (0.5 mg/mL) for 20 min, followed by rinsing 10 times with PBS.
Streptavidin-conjugated mica was imaged with biotin-functionalized cantilevers in contact mode and TopMAC mode within a fluid cell (PicoPlus AFM, Agilent/Molecular Imaging), using backside magnetically coated Si3N4 cantilevers. The tip was positioned for forced unbinding events based on this image (see Supplementary Material Fig. S3). The sensitivity of the photodetector (nm/V) was measured from the slope of force-displacement curves on bare mica. Cantilever spring constants (kc, mN/m) were measured via thermal fluctuations, as reported elsewhere (52,53). At least 50 replicate force-piezoactuator displacement (F–Δ) responses were acquired for each (kc, v) condition; retraction rate v of the piezoactuated cantilever was approximately constant for a given kc, ranging from 0.015 to 0.254 μm/s across this F′ range. Force-displacement responses were corrected for effects of hydrodynamic drag as described in the literature (54,55). Effective loading rate F′ (∼100, 300, and 2000 pN/s) was calculated as the product of v and the effective spring constant k = dF/dΔ just before unloading for each F–Δ curve (32,56). The average effective spring constants for the two cantilever types were k = 3.9 mN/m and 6.9 mN/m, respectively, but the value derived from each force-displacement slope was used to analyze the corresponding unbinding force and loading rate. Note that there exist commercially available AFM cantilevers of lower nominal stiffness than those used here, including kc = 11 pN/nm which we used to validate our predictions for these stiffer cantilevers. In this study, we primarily used these stiffer cantilevers for two reasons. First, we significantly increased the efficiency of acquiring force spectra by initially imaging the streptavidin-conjugated mica in TopMAC mode; this intermittent contact mode of imaging is not achievable in fluid for the most compliant cantilevers available. Second, in our experience with this AFM, more compliant cantilevers (kc < 30 mN/m) provide an insufficiently stable signal for a wide range of loading rates; and stiffer cantilevers (kc > 60 pN/nm) provide an insufficiently sensitive signal to detect pN-scale unbinding over these loading rates. These stabilities and sensitivities depend on the particular AFM laser-photodiode configuration. From these experimentally obtained spectra, xb and koff were determined as in Steered Molecular Dynamics, using the full distribution of unbinding forces in the linear regression. In short, more compliant cantilevers provide an insufficiently stable signal for a wide range of loading rates; and stiffer cantilevers provide an insufficiently sensitive signal to detect pN-scale unbinding.
In our AFM MFS experiments, we did not observe any loading rate dependence in effective spring constant k = dF/dΔ over the range of loading rates explored (100 to 50,000 pN/s). However, we did not use distensible linkers, which may be several nanometers in length (e.g., polyethylene glycol 800); such linkers may have an effective stiffness that depends on loading rate. Since unbinding force depends on both effective stiffness and loading rate, careful analysis of this loading rate dependence of effective k would be required to calculate accurate kinetic and energetic constants.
We note that in AFM MFS experiments, there are two potential definitions of the force transducer stiffness: cantilever stiffness kc, as measured by methods such as simple harmonic oscillator displacement at room temperature (52,53); and the effective stiffness of the cantilever-linker system k, as calculated from dF/dΔ just before each unbinding event. For typical bifunctional molecular linkers, k is smaller than kc by one order of magnitude (31,57). Therefore, when comparing results among experiments, it is important to consider whether a particular study defined the effective loading rate as kcv or kv.
RESULTS AND DISCUSSION
Effects of initial macromolecular structure
We simulated identical, forced unbinding experiments on a range of ostensibly equilibrated biotin-streptavidin tetramer structures to consider how slight variation of the initial atomic positions and velocities in the ligand-receptor complex affects the observed unbinding force and inferred unbinding kinetics. Rather than choosing a single structure from the equilibration trajectory as a starting point for the SMD simulations (see Methods), we selected nine distinct sets of atomic coordinates from that trajectory, spaced at 10-ns intervals. We used each of these sets of atomic coordinates as initial structures for separate SMD simulations with the same set of initial atomic velocities (as described in Methods). Additionally, we considered one of these structures (i.e., one set of atomic coordinates) with three different sets of initial atomic velocities in separate SMD simulations. These simulations were designed to probe the stochastic nature of individual ligand-receptor unbinding events by varying initial configurations (atomic positions and velocities) independently from loading conditions.
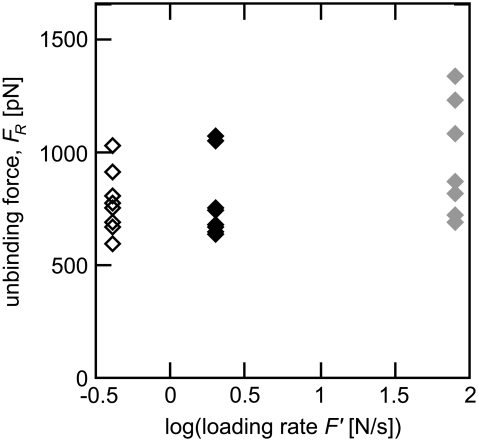
We found marked variation in the force-distance responses (e.g., Supplementary Material Fig. S1 B) among different equilibrated configurations (both initial atomic positions and initial atomic velocities) subjected to the same loading conditions. This distribution led to a range of ∼20% in observed unbinding forces, as shown in Fig. 2. We achieved this range whether we varied the initial atomic positions or the initial atomic velocities, indicating that either can be varied to enhance sampling in SMD simulations. Further, this range suggests the minimum variation in FR that corresponding experiments can be expected to achieve, independent of instrument precision.
FIGURE 2.
Steered molecular dynamics simulations were performed on nine different biotin-streptavidin complex configurations (some symbols overlap), with three sets of simulated experiments, differing in loading rate F′ (open, solid, shaded). Within each set of experiments the only difference among unbinding trajectories was the starting configuration of the atoms within the complex. Between each set of simulated experiments, the only difference is the velocity v, and therefore the loading rate F′ = kv (open, v = 0.4 m/s; solid, v = 0.8 m/s; and shaded, v = 4 m/s). The force transducer stiffness k was 2.8 N/m in all simulations. The large range in observed unbinding force (20%), based only on the initial configuration of the molecular complex, suggests a structural reason for the experimentally observed variation in unbinding force.
We also considered the effects of slight changes in the loading history of the ligand-receptor complex by changing loading vector orientation with respect to the binding pocket normal and also by varying the loading profile. Vector rotation by ±5° and ±10° around the x, y, and z axes led to variations in FR of ∼10%. We further found that changing the loading history of the complex by first pushing and then pulling along the loading vector (as would occur in AFM MFS experiments) had no effect on the measured unbinding force; the limited effect of loading history observed here was expected because the ligand was intentionally placed in the most energetically favorable bound state during the equilibration trajectory.
Effects of experimentally accessible parameters
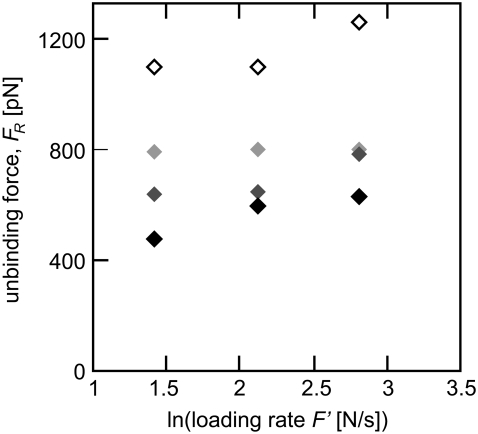
We designed a set of simulated experiments to investigate the effect of experimentally accessible parameters on the measured value of FR by systematically varying the force transducer spring constant k and the velocity v to produce three different effective loading rates F′, while maintaining the initial structure (atomic positions and velocities) of the complex constant. As shown in Fig. 3, we observe the expected loading rate dependence of FR for a given transducer stiffness k. These results also show that the magnitude of k strongly affects observed FR. At the same loading rate F′, simulations using larger values of k consistently exhibited higher unbinding forces FR. In contrast to these results, Bell's model implies that the loading rate is the controlling variable for the observed unbinding force (44,58).
FIGURE 3.
Testing the assumption that loading rate is the controlling variable for unbinding force, we systematically varied force transducer stiffness k (solid, 0.83 N/m; dark shaded, 1.66 N/m; light shaded, 4.15 N/m; open, 8.3 N/m) and velocity v to produce three different loading rates (F′ = 4.15 N/s, 8.3 N/s, and 16.6 N/s) in SMD simulations of biotin-streptavidin rupture. At the same loading rate, a stiffer force transducer correlated with a higher unbinding force (open points are the stiffest force transducers, shading to black, which are the most compliant).
In our simulations, the force transducer stiffness k increased by more than an order of magnitude, and correlating with an increase of ∼200% in observed unbinding forces. Consequently, the calculated dissociation rate koff of the biotin-streptavidin complex varied by more than an order of magnitude, from 1.32 × 10−8 s−1 for the stiffest force transducer (k = 8.3 N/m) to 5.3 × 10−9 s−1 for the most compliant force transducer (k = 0.83 N/m). In contrast, calculations of the location of the energetic barrier xb, which depend only on the slope of the linear fit to FR versus ln(F′), resulted in a range of xb between 0.05 and 0.06 nm. Estimates of xb from a combination of dynamic force spectroscopy experiments, flow chamber studies, and molecular dynamics simulations indicate an energetic barrier distance of ∼0.1 nm (25,30,41).
Comparison with experimental measurements
We performed AFM MFS experiments on the biotin-streptavidin system to consider whether our simulation predictions—that higher unbinding forces are measured with stiffer force transducers for a fixed loading rate—held true in the experimental loading-rate regime.
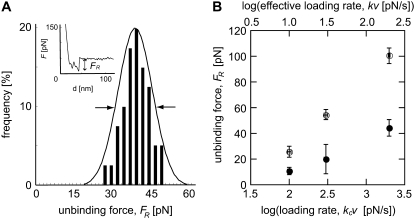
An initial investigation was carried out with two cantilevers of differing spring constants (kc = 35 mN/m and 58 mN/m), and the cantilever retraction velocity v was varied to measure unbinding forces at the same effective loading rates. The effective force transducer stiffness k was approximately one order-of-magnitude lower than kc for each biotin-functionalized cantilever, as expected (k = 3.9 mN/m and 6.9 mN/m, respectively); see Methods and the literature (32,56). The unbinding force FR, measured between a biotin-functionalized cantilever and a streptavidin-functionalized mica surface (Supplementary Material Fig. S3), was determined as the mean of a Gaussian fit to histograms constructed from at least 50 replicate single rupture events acquired under the same loading conditions (force transducer stiffness k and velocity v), as shown in Fig. 4 A. The resulting unbinding forces are presented in Fig. 4 B as a function of ln(F′), showing that the apparent strength of the complex increases as k increases—even if the loading rate F′ is maintained constant. That is, the correlation of stiffer cantilevers with higher measured unbinding forces continued in the experimental loading rate regime (on the order of nN/s). It is interesting to note that an equivalent effect was reported as an incidental observation for the biotin-streptavidin system, even before the appreciation that unbinding force depended on loading rate: for a fixed velocity (ranging from 1 to 50 μm/s) and unbinding force, a stiffer AFM cantilever yielded a shorter measured lifetime of the complex (38). In our experiments, the apparent strengthening effect of a stiffer cantilever had notable effects on calculated energetic and kinetic quantities, with an increase in effective k of 185% resulting in an increase in the measured unbinding force FR of ∼150%, a decrease in the calculated energetic unbinding length xb of ∼100% (0.15 nm to 0.07 nm), and an increase in the calculated dissociation rate koff of ∼250% (8.3 × 10−7 s−1 to 2.0 × 10−6 s−1). Here, koff and xb were calculated from a linear regression to the full distribution of unbinding forces, rather than the mean unbinding forces FR.
FIGURE 4.
(A) Experimental measurements of biotin-streptavidin unbinding force FR were performed via atomic-force microscope-enabled molecular force spectroscopy, utilizing cantilevers of two different spring constants. For each set of loading conditions (effective force transducer stiffness k and retraction rate v) at least 50 force-displacement (F − Δ) responses for single rupture events were recorded, with FR calculated as indicated. (Inset) A single rupture event of FR = 46 pN, under effective k = 4.12 mN/m and v = 0.073 μm/s. A Gaussian distribution was fit to the histogram of unbinding forces for each set of conditions (here, kc = 35 mN/m and v = 0.073 μm/s), and the distribution maximum was reported as FR. Arrows indicate the FWHM. (B) Unbinding force FR as a function of the logarithm of the loading rate F′, as measured by AFM using two different cantilevers: kc = 35 mN/m (solid circles) and kc = 58 mN/m (open circles); error bars represent one standard deviation in FR and effective F′, and may appear smaller than symbols. In all cases, the stiffer cantilevers measured higher unbinding forces than the more compliant cantilever, indicating that the dependence of measured FR on the stiffness of the force transducer k is not limited to the extreme loading rates achieved in simulation.
The unbinding force distribution can be expressed as full-width half maximum (FWHM) of the experimentally measured histograms of FR observed in replicate AFM MFS experiments at a given loading rate (see, e.g., Fig. 4 A). This FWHM corresponded well with the observed range in SMD-simulated unbinding forces among ostensibly equilibrated structures (∼20% of the mean FR). However, due to the computational resources required for SMD simulations of solvated proteins, it is currently not feasible to execute the large number of forced unbinding simulations for a given parameter set (structure, k, and v) that would be required to construct the histograms and probability density functions of FR attainable in experiments. Thus, simulations suggest but do not prove that the stochastic nature of forced unbinding of single ligand-receptor interactions is attributable in part to sampling small variations in atomic positions and velocities.
Due in part to the incomplete sampling of an ensemble response and the large difference in loading rates attainable in experiments (nN/s) and in simulations (N/s), it is not expected that the magnitude of FR or the extrapolated kinetic and energetic parameters will agree quantitatively (41). However, SMD simulations remain valuable tools for studying forced unbinding because they can reveal atomic-level detail of mechanisms and pathways not accessible by experiment (4). Here, both simulations and experiments on the biotin-streptavidin complex show clear effects of force transducer stiffness k on measured unbinding forces. One important implication of this effect is that two experiments performed over the same loading rate range and with different, single values of k would not necessarily obtain the same magnitude or loading rate-dependence of the unbinding forces. This has been noted recently for SMD simulations (59) and optical trap experiments (60) on the mechanically forced unfolding of biopolymers. Thus, both simulations and experiments suggest that the accuracy of ligand-receptor binding parameters extracted from analyses of single complexes will be significantly enhanced by consideration of a range of both F′ and k.
Effects of k on the energy landscape of the complex
Through SMD simulations and complementary AFM MFS experiments, we have shown that macromolecular structure, loading direction, and the loading conditions (k and v) can significantly affect the measured unbinding force FR and inferred unbinding kinetics. The commonality among these factors is that they all either perturb or alter exploration of the three-dimensional energy landscape E(x, y, z) of the complex.
The kinetics of any given reaction depends on the energetic barrier crossed during the reaction. The effects of applied force on the energy landscape (and, therefore, on koff and xb) have been well documented: applied force tilts the simplified one-dimensional energy landscape such that EF(χ) = E0(χ) − Fχ, where E0(χ) is the unperturbed energy landscape, leading to a reduction in energetic barrier height (3,45,61). This reduction increases the kinetic off-rate as 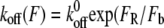 ), where
), where 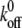 is the equilibrium kinetic off-rate and Fb is xb/kBT. However, the effect of the force transducer stiffness k on the observed unbinding force and kinetics has been neglected. Evans has noted that a stiffer force transducer leads to a higher energetic barrier at a given applied force, but did not include this effect explicitly in analytical predictions of koff under applied force (61). As we discuss below, this contribution can in fact be reasonably neglected for sufficiently compliant force transducers, such as the biomembrane force probe used in the experiments of Merkel et al. (30). Once the ligand is mechanically attached to the force transducer, the potential energy of the force transducer must be accounted for in the energy landscape as
is the equilibrium kinetic off-rate and Fb is xb/kBT. However, the effect of the force transducer stiffness k on the observed unbinding force and kinetics has been neglected. Evans has noted that a stiffer force transducer leads to a higher energetic barrier at a given applied force, but did not include this effect explicitly in analytical predictions of koff under applied force (61). As we discuss below, this contribution can in fact be reasonably neglected for sufficiently compliant force transducers, such as the biomembrane force probe used in the experiments of Merkel et al. (30). Once the ligand is mechanically attached to the force transducer, the potential energy of the force transducer must be accounted for in the energy landscape as
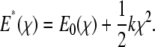 |
(2) |
Applying force to this perturbed energy landscape E* then tilts the energy landscape such that
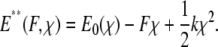 |
(3) |
As shown in Fig. 5, the barriers presented by the tilted landscape E**(F, χ) at a particular value of applied force also depend on k. When force is applied by an ideal spring (force = kχ), a stiffer force transducer leads to a higher energetic barrier to unbinding (and therefore a higher unbinding force) as shown by Eq. 3. The kinetic rate of dissociation is then
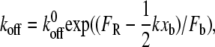 |
(4) |
where Fb is xb/kBT and 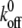 is the dissociation rate of the system at equilibrium (corresponding to E0(χ)). This implies that, rather than extracting the energetic and kinetic parameters of the complex from Eq. 1, xb and koff should be extrapolated from
is the dissociation rate of the system at equilibrium (corresponding to E0(χ)). This implies that, rather than extracting the energetic and kinetic parameters of the complex from Eq. 1, xb and koff should be extrapolated from
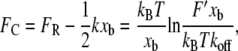 |
(5) |
where FC is the unbinding force at a particular loading rate F′ that has been corrected for the barrier perturbation due to k.
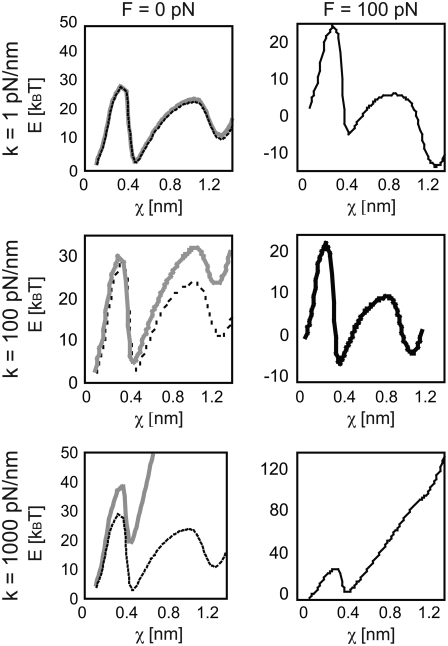
FIGURE 5.
The stiffness of the force transducer not only limits the exploration of the ligand in the energy landscape, but also changes the energy landscape the ligand traverses. Here, the effects of stiffness on the biotin-streptavidin energy landscape E**(F, χ) (adapted from (25,30,41)) are shown, both before pulling begins (F = 0, left column, gray solid line) and at an applied load of 100 pN (right column, black solid line). Compliant cantilevers of k < 1 pN/nm are typical of BFP and optical trap experiments (top row). For such small k, the perturbed energy landscape (E**(F, χ), solid) remains close to the equilibrium energy landscape (E0(χ), dashed) in the absence of applied force. Stiff cantilevers of k > 1000 pN/nm are typical of SMD simulations (bottom row). Even in the absence of significant applied force of the ligand, the perturbed energy landscape (E**(F, χ), solid) is far from the equilibrium landscape (E0(χ), dashed). AFM cantilevers of k ≈10–100 pN/nm are intermediate to these extremes (middle row). Since application of a nonzero force inherently implies a nonequilibrium state of the bound complex, no equilibrium landscape is depicted in the right column (F = 100 pN).
For some experimental approaches such as BFP and optical traps, the force transducer stiffness is typically small enough (k ≈ 1 pN/m) that the additional term 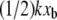 may be negligible. In fact, this contribution to the observed unbinding force has been reasonably neglected in such experiments thus far. However, in both AFM MFS and SMD measurements of the unbinding force, the opposing force contribution
may be negligible. In fact, this contribution to the observed unbinding force has been reasonably neglected in such experiments thus far. However, in both AFM MFS and SMD measurements of the unbinding force, the opposing force contribution 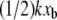 can be on the same order of magnitude as FR. It is important to note that the effective stiffness of the force transducer k may depend on loading rate as well as the mechanical compliance of any molecular linkers (see Methods). In Fig. 5, we demonstrate the effect of force transducer stiffness on the biotin-streptavidin energy landscape (25,30,41) for three different values of k (1 pN/nm, which corresponds to optical trap and BFP experiments; 100 pN/nm, which corresponds to AFM MFS; and 1000 pN/nm, which corresponds to SMD) and at two different instances of applied force (F = 0 pN, or before pulling begins, and F = 100 pN). Even before force is applied, the energy landscape is perturbed much more by the stiff force transducer than by more compliant force transducers. In the limit of an infinitely compliant force transducer (k = 0), the perturbed energy landscape E**(F, χ) is equal to the equilibrium energy landscape E0. In this case, E*(F, χ) and E**(F, χ) reduce to a single expression for the height of the energetic barrier at xb. Very compliant force transducers, such as those used in biomembrane force probe experiments (k ≈ 1 pN/nm for the strongly-bound biotin-streptavidin system (30)), may be considered to adhere to this compliant limit. However, as the force transducer stiffness increases, the perturbation of the energy landscape increases and the difference between E*(F, χ) and E**(F, χ) becomes significant. Next, we show that this correction of the observed unbinding force (Eq. 5) eliminates the apparent dependence of koff and xb on force transducer stiffness k for both simulations (Fig. 3) and experiments (Fig. 4 B).
can be on the same order of magnitude as FR. It is important to note that the effective stiffness of the force transducer k may depend on loading rate as well as the mechanical compliance of any molecular linkers (see Methods). In Fig. 5, we demonstrate the effect of force transducer stiffness on the biotin-streptavidin energy landscape (25,30,41) for three different values of k (1 pN/nm, which corresponds to optical trap and BFP experiments; 100 pN/nm, which corresponds to AFM MFS; and 1000 pN/nm, which corresponds to SMD) and at two different instances of applied force (F = 0 pN, or before pulling begins, and F = 100 pN). Even before force is applied, the energy landscape is perturbed much more by the stiff force transducer than by more compliant force transducers. In the limit of an infinitely compliant force transducer (k = 0), the perturbed energy landscape E**(F, χ) is equal to the equilibrium energy landscape E0. In this case, E*(F, χ) and E**(F, χ) reduce to a single expression for the height of the energetic barrier at xb. Very compliant force transducers, such as those used in biomembrane force probe experiments (k ≈ 1 pN/nm for the strongly-bound biotin-streptavidin system (30)), may be considered to adhere to this compliant limit. However, as the force transducer stiffness increases, the perturbation of the energy landscape increases and the difference between E*(F, χ) and E**(F, χ) becomes significant. Next, we show that this correction of the observed unbinding force (Eq. 5) eliminates the apparent dependence of koff and xb on force transducer stiffness k for both simulations (Fig. 3) and experiments (Fig. 4 B).
To determine xb from experiments using our corrected model, we fit the experimental unbinding forces FR from two cantilevers (kc = 35 and 58 mN/m) to Eq. 5, using least-mean-squares minimization of the residual defined as 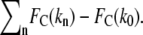 Here, n is the number of different transducer stiffnesses considered for a given loading rate (for our experiments, n = 2); and k0 is the stiffness of the most compliant transducer (for our experiments, k0 = 3.9 mN/m). To determine xb from the simulations, the identical procedure was performed with the simulated stiffnesses k and unbinding forces FR (for our simulations, n = 4 and k0 = 0.83 N/m). As shown in Fig. 6 for SMD simulations, correcting for the effects of k on the energy landscape as outlined above brings the corrected unbinding forces calculated with different force transducer stiffnesses k into agreement with each other, within the ±10% error attributable to the stochastic nature of ligand-receptor interactions. Corrections of the observed experimental unbinding forces FR yielded similar results. Both xb and koff can be extracted from the corrected data, resulting in values of 0.05 nm and 5.1 × 10−9 s−1, respectively, for the simulations; and 0.11 nm and 2.1 ± 0.5 × 10−7 s−1, respectively, for the AFM experiments. To validate this correction of effective force transducer stiffness on the energy landscape and inferred unbinding kinetics, we also repeated the calculation of koff after including unbinding forces obtained with both stiffer cantilevers (kc = 121 mN/m, FR = 112.0 ± 4.9 pN) and more compliant cantilevers (kc = 11 mN/m, FR = 38.7 ± 5.4 pN) at a loading rate of 2000 pN/s: koff calculated over this wider range of force transducer stiffness (2.7 ± 0.6 × 10−7 s−1 agreed within experimental error with that obtained over the narrower range of kc = 35 and 58 mN/m. Our values of xb from experiment and simulation agree well with previous experiments (25,30,41), which indicate that xb is ∼0.1 nm, the energetic distance of the innermost energy barrier accessible at these loading rates. The equilibrium dissociation rate of biotin-streptavidin as measured by competitive binding is 2.4 × 10−6 s−1 (62), which is within an order of magnitude of our experimental koff. Given our limited range of loading rates, we find this agreement to be reasonable. Although koff inferred from SMD simulations does not extrapolate well to equilibrium dissociation rates, as anticipated for such large F′ (4), it is notable that this correction of simulated FR by
Here, n is the number of different transducer stiffnesses considered for a given loading rate (for our experiments, n = 2); and k0 is the stiffness of the most compliant transducer (for our experiments, k0 = 3.9 mN/m). To determine xb from the simulations, the identical procedure was performed with the simulated stiffnesses k and unbinding forces FR (for our simulations, n = 4 and k0 = 0.83 N/m). As shown in Fig. 6 for SMD simulations, correcting for the effects of k on the energy landscape as outlined above brings the corrected unbinding forces calculated with different force transducer stiffnesses k into agreement with each other, within the ±10% error attributable to the stochastic nature of ligand-receptor interactions. Corrections of the observed experimental unbinding forces FR yielded similar results. Both xb and koff can be extracted from the corrected data, resulting in values of 0.05 nm and 5.1 × 10−9 s−1, respectively, for the simulations; and 0.11 nm and 2.1 ± 0.5 × 10−7 s−1, respectively, for the AFM experiments. To validate this correction of effective force transducer stiffness on the energy landscape and inferred unbinding kinetics, we also repeated the calculation of koff after including unbinding forces obtained with both stiffer cantilevers (kc = 121 mN/m, FR = 112.0 ± 4.9 pN) and more compliant cantilevers (kc = 11 mN/m, FR = 38.7 ± 5.4 pN) at a loading rate of 2000 pN/s: koff calculated over this wider range of force transducer stiffness (2.7 ± 0.6 × 10−7 s−1 agreed within experimental error with that obtained over the narrower range of kc = 35 and 58 mN/m. Our values of xb from experiment and simulation agree well with previous experiments (25,30,41), which indicate that xb is ∼0.1 nm, the energetic distance of the innermost energy barrier accessible at these loading rates. The equilibrium dissociation rate of biotin-streptavidin as measured by competitive binding is 2.4 × 10−6 s−1 (62), which is within an order of magnitude of our experimental koff. Given our limited range of loading rates, we find this agreement to be reasonable. Although koff inferred from SMD simulations does not extrapolate well to equilibrium dissociation rates, as anticipated for such large F′ (4), it is notable that this correction of simulated FR by 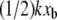 results in extracted energetic and kinetic parameters of the complex that agree much more closely with experimental estimates.
results in extracted energetic and kinetic parameters of the complex that agree much more closely with experimental estimates.
FIGURE 6.
After correcting biotin-streptavidin unbinding forces measured via SMD simulations according to Eq. 3, the corrected unbinding force FC for all for all values of k agree within estimated error ranges (error estimated as ±10%, based on 20% FWHM of force distribution in both simulations and experiments). Uncorrected unbinding forces FR are shown in Fig. 2.
Another interpretation of the experimentally observed stiffness dependence of the unbinding force is that, at a given loading rate, a stiffer cantilever will lead to the AFM probe being in contact with the surface for a longer period of time (at a given F′, a stiffer cantilever necessitates a slower v; total displacement remains constant). Although the contact times in the range of experimental loading rates we employed are well above the generally reported association time for biotin-streptavidin (∼1 μs (63)), with more time to interact, one could conjecture that biotin may have sufficient time to sample a lower energy minimum in the streptavidin binding pocket. Note that while the probability of the complex rebinding is also dependent on stiffness (61), rebinding is prohibited at the velocities employed in AFM MFS experiments and SMD simulations. As illustrated in Fig. 5, the biotin-streptavidin energy landscape has three major energy minima (25,30,41); the timescale of our AFM experiments (≈0.2–2 s) is such that it is theoretically possible for both the deepest and the second-deepest minima to be populated (25). However, this would suggest that a multimodal distribution of unbinding forces would be observed for a given k and F′. We did not observe such a distribution in our experiments, suggesting that our AFM MFS experiments consistently sampled a single energy minimum.
CONCLUSIONS
Our computational and experimental analyses of forced unbinding for the biotin-streptavidin complex demonstrate that loading rate is not the only controlling factor of the observed unbinding force FR and inferred unbinding kinetics. The effective stiffness k, which represents the mechanical resistance of the total force transducer inclusive of any molecular linkers, can lead to manifold changes in the magnitude and rate dependence of the observed FR. Further, our consideration of multiple structures of this complex demonstrates that a common assumption of SMD simulations—namely, that a single equilibrated structure will not explore enough of its phase space to impact simulation results—is not true for forced unbinding of ligand-receptor pairs. Even in consideration of an incomplete ensemble of ostensibly equilibrated initial configurations, we observed variations of >20% in FR attributable only to minute differences in atomic positions or velocities.
We have demonstrated that the measured unbinding force of a ligand-receptor complex depends on several experimentally accessible factors that perturb or limit exploration of the energy landscape. These factors are especially important in interpretation of results utilizing effective force transducer stiffness of k > 1 pN/nm, as is common in AFM MFS experiments and SMD simulations. Beyond the established dependence on F′, the magnitude of the force transducer k has the most dramatic effect on the inference of equilibrium behavior, as captured by the velocity of dissociation koff and the energetic distance xb. Consideration and quantification of these factors is necessary if forced unbinding experiments are used to infer the kinetics and energetics required for both predictive simulations and biomedical applications such as drug discovery. The demonstrated synergism between simulation and experiment elucidates several key parameters that affect the nature and interpretation of forced ligand-receptor unbinding. In particular, although it has been known that the magnitude of k effectively limits the exploration of the energy landscape of a ligand-receptor complex, these results show that this controllable parameter also directly perturbs that landscape to effect wide variations in FR, koff, and xb. We have demonstrated that this perturbation of the energy landscape via force transducer stiffness can be accounted for to obtain an effective unbinding force at each loading rate, and thus the equilibrium energetic and kinetic parameters of the complex. Beyond these model systems and experiments, our results suggest that the force required to dissociate molecular complexes can be altered by the mechanical compliance of the macromolecular structures to which the ligand (or receptor) is tethered, e.g., that of the extracellular matrix. Both experimental and computational analyses of biologically relevant ligand-receptor complexes under mechanical constraints or strain (64) will benefit from consideration of the sources and magnitude of variation in the observed unbinding forces and inferred kinetics.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
The authors thank R. Krishnan for assistance in performing the SMD simulations.
The authors thank the National Defense Science and Engineering Graduate Fellowship program (to E.B.W.), as well as the National Science Foundation Nanoscale Exploratory Research program and National Science Foundation CAREER Award, and the Arnold and Mabel Beckman Foundation Young Investigator Program (to K.J.V.V.). Computational support for this project was provided by the National Science Foundation though grant No. IMR-0414849.
Editor: Angel E. Garcia.
References
- 1.Scheidegger, P., W. G. Weiglhofer, S. Suarez, S. Console, J. Waltenberger, M. S. Pepper, R. Jaussi, and K. Ballmer-Hofer. 2001. Signaling properties of an HIV-encoded angiogenic peptide mimicking vascular endothelial growth factor activity. Biochem. J. 353:569–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Van Vliet, K. J., and P. Hinterdorfer. 2006. Probing drug-cell interactions. NanoToday. 1:18–25. [Google Scholar]
- 3.Evans, E. A., and D. A. Calderwood. 2007. Forces and bond dynamics in cell adhesion. Science. 316:1148–1153. [DOI] [PubMed] [Google Scholar]
- 4.Sotomayor, M., and K. Schulten. 2007. Single-molecule experiments in vitro and in silico. Science. 316:1144–1148. [DOI] [PubMed] [Google Scholar]
- 5.Chilkoti, A., and P. S. Stayton. 1995. Molecular-origins of the slow streptavidin-biotin dissociation kinetics. J. Am. Chem. Soc. 117:10622–10628. [Google Scholar]
- 6.Dixon, R. W., and P. Kollman. 1999. The free energies for mutating S27 and W79 to alanine in streptavidin and its biotin complex: the relative size of polar and nonpolar free energies on biotin binding. Proteins. 36:471–473. [PubMed] [Google Scholar]
- 7.Freitag, S., V. Chu, J. E. Penzotti, L. A. Klumb, R. To, D. Hyre, I. Le Trong, T. P. Lybrand, R. E. Stenkamp, and P. S. Stayton. 1999. A structural snapshot of an intermediate on the streptavidin-biotin dissociation pathway. Proc. Natl. Acad. Sci. USA. 96:8384–8389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hendrickson, W. A., A. Pahler, J. L. Smith, Y. Satow, E. A. Merritt, and R. P. Phizackerley. 1989. Crystal-structure of core streptavidin determined from multiwavelength anomalous diffraction of synchrotron radiation. Proc. Natl. Acad. Sci. USA. 86:2190–2194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hyre, D. E., I. Le Trong, S. Freitag, R. E. Stenkamp, and P. S. Stayton. 2000. Ser45 plays an important role in managing both the equilibrium and transition state energetics of the streptavidin-biotin system. Protein Sci. 9:878–885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hyre, D. E., L. M. Amon, J. E. Penzotti, I. L. Trong, R. E. Stenkamp, T. P. Lybrand, and P. S. Stayton. 2002. Early mechanistic events in biotin dissociation from streptavidin. Nat. Struct. Biol. 9:582–585. [DOI] [PubMed] [Google Scholar]
- 11.Klumb, L. A., V. Chu, and P. S. Stayton. 1998. Energetic roles of hydrogen bonds at the ureido oxygen binding pocket in the streptavidin-biotin complex. Biochemistry. 37:7657–7663. [DOI] [PubMed] [Google Scholar]
- 12.Lindqvist, Y., and G. Schneider. 1996. Protein-biotin interactions. Curr. Opin. Struct. Biol. 6:798–803. [DOI] [PubMed] [Google Scholar]
- 13.Weber, P. C., D. H. Ohlendorf, J. J. Wendoloski, and F. R. Salemme. 1989. Structural origins of high-affinity biotin binding to streptavidin. Science. 243:85–88. [DOI] [PubMed] [Google Scholar]
- 14.Weber, P. C., J. J. Wendoloski, M. W. Pantoliano, and F. R. Salemme. 1992. Crystallographic and thermodynamic comparison of natural and synthetic ligands bound to streptavidin. J. Am. Chem. Soc. 114:3197–3200. [Google Scholar]
- 15.Ewalt, K. L., R. W. Haigis, R. Rooney, D. Ackley, and M. Krihak. 2001. Detection of biological toxins on an active electronic microchip. Anal. Biochem. 289:162–172. [DOI] [PubMed] [Google Scholar]
- 16.Kurihara, A., Y. Deguchi, and W. M. Pardridge. 1999. Epidermal growth factor radiopharmaceuticals: in-111 chelation, conjugation to a blood-brain barrier delivery vector via a biotin-polyethylene linker, pharmacokinetics, and in vivo imaging of experimental brain tumors. Bioconjug. Chem. 10:502–511. [DOI] [PubMed] [Google Scholar]
- 17.Maraveyas, A., G. Rowlinson-Busza, S. Murray, and A. A. Epenetos. 1998. Improving tumor targeting and decreasing normal tissue uptake by optimizing the stoichiometry of a two-step biotinylated-antibody/streptavidin-based targeting strategy: studies in a nude mouse xenograft model. Int. J. Cancer. 78:610–617. [DOI] [PubMed] [Google Scholar]
- 18.Muzykantov, V. R., E. N. Atochina, V. Gavriljuk, S. M. Danilov, and A. B. Fisher. 1994. Immunotargeting of streptavidin to the pulmonary endothelium. J. Nucl. Med. 35:1358–1365. [PubMed] [Google Scholar]
- 19.Rosebrough, S. F., and M. Hashmi. 1996. Galactose-modified streptavidin-GCLC antifibrin monoclonal antibody conjugates: application for two-step thrombus embolus imaging. J. Pharmacol. Exp. Ther. 276:770–775. [PubMed] [Google Scholar]
- 20.Schechter, B., L. M. Chen, R. Arnon, and M. Wilchek. 1999. Organ selective delivery using a tissue-directed streptavidin-biotin system: targeting 5-fluorouridine via TNP-streptavidin. J. Drug Target. 6:337–348. [DOI] [PubMed] [Google Scholar]
- 21.Wilchek, M., and E. A. Bayer. 1988. The avidin biotin complex in bioanalytical applications. Anal. Biochem. 171:1–32. [DOI] [PubMed] [Google Scholar]
- 22.Yao, Z. S., M. L. Zhang, H. Kobayashi, H. Sakahara, H. Nakada, I. Yamashina, and J. Konishi. 1995. Improved targeting of radiolabeled streptavidin in tumors pretargeted with biotinylated monoclonal-antibodies through an avidin chase. J. Nucl. Med. 36:837–841. [PubMed] [Google Scholar]
- 23.Zhang, M. L., Z. S. Yao, H. Sakahara, T. Saga, Y. Nakamoto, N. Sato, S. J. Zhao, H. Nakada, I. Yamashina, and J. Konishi. 1998. Effect of administration route and dose of streptavidin or biotin on the tumor uptake of radioactivity in intraperitoneal tumor with multistep targeting. Nucl. Med. Biol. 25:101–105. [DOI] [PubMed] [Google Scholar]
- 24.Marshall, B. T., K. K. Sarangapani, J. Lou, R. P. McEver, and C. Zhu. 2005. Force history dependence of receptor-ligand dissociation. Biophys. J. 88:1458–1466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pincet, F., and J. Husson. 2005. The solution to the streptavidin-biotin paradox: the influence of history on the strength of single molecular bonds. Biophys. J. 89:4374–4381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ota, T., T. Sugiura, and S. Kawata. 2005. Rupture force measurement of biotin-streptavidin bonds using optical trapping. Appl. Phys. Lett. 87:043901. [Google Scholar]
- 27.Pierres, A., D. Touchard, A.-M. Benoliel, and P. Bongrand. 2002. Dissecting streptavidin-biotin interaction with a laminar flow chamber. Biophys. J. 82:3214–3223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Breisch, S., J. Gonska, H. Deissler, and M. Stelzle. 2005. Measuring single-bond rupture forces using high electric fields in microfluidic channels and DNA oligomers as force tags. Biophys. J. 89:L19–L21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Panhorst, M., P.-B. Kamp, G. Reiss, and H. Bruckl. 2005. Sensitive bond force measurements of ligand-receptor pairs with magnetic beads. Biosens. Bioelectron. 20:1685–1689. [DOI] [PubMed] [Google Scholar]
- 30.Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
- 31.Zhang, X., and V. T. Moy. 2003. Cooperative adhesion of ligand-receptor bonds. Biophys. Chem. 104:271–278. [DOI] [PubMed] [Google Scholar]
- 32.Yuan, C., A. Chen, P. Kolb, and V. T. Moy. 2000. Energy landscape of streptavidin-biotin complexes measured by atomic force microscopy. Biochemistry. 39:10219–10223. [DOI] [PubMed] [Google Scholar]
- 33.Wong, J., A. Chilkoti, and V. T. Moy. 1999. Direct force measurements of the streptavidin-biotin interaction. Biomol. Eng. 16:45–55. [DOI] [PubMed] [Google Scholar]
- 34.Moy, V. T., E.-L. Florin, and H. E. Gaub. 1994. Intermolecular forces and energies between ligands and receptors. Science. 266:257–259. [DOI] [PubMed] [Google Scholar]
- 35.Lo, Y.-S., J. Simons, and T. P. Beebe. 2002. Temperature dependence of the biotin-avidin bond-rupture force studied by atomic force microscopy. J. Phys. Chem. B. 106:9847–9852. [Google Scholar]
- 36.Lo, Y.-S., Y.-J. Zhu, and T. P. Beebe. 2001. Loading-rate dependence of individual ligand-receptor bond-rupture forces studied by atomic force microscopy. Langmuir. 17:3741–3748. [Google Scholar]
- 37.Lo, Y.-S., N. D. Huefner, W. S. Chan, F. Stevens, J. M. Harris, and T. P. Beebe. 1999. Specific interactions between biotin and avidin studied by atomic force microscopy using the Poisson statistical analysis method. Langmuir. 15:1373–1382. [Google Scholar]
- 38.Lee, G. U., D. A. Kidwell, and R. J. Colton. 1994. Sensing discrete streptavidin-biotin interactions with atomic force microscopy. Langmuir. 3:354–357. [Google Scholar]
- 39.Florin, E.-L., V. T. Moy, and H. E. Gaub. 1994. Adhesion forces between individual ligand-receptor pairs. Science. 264:415–417. [DOI] [PubMed] [Google Scholar]
- 40.Grubmüller, H., B. Heymann, and P. Tavan. 1996. Ligand binding: molecular mechanics calculation of the streptavidin-biotin rupture force. Science. 271:954–955. [DOI] [PubMed] [Google Scholar]
- 41.Izrailev, S., S. Stepaniants, M. Balsera, Y. Oona, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lee, S., J. Mandic, and K. J. VanVliet. 2007. Chemomechanical mapping of ligand-receptor binding kinetics on cells. Proc. Natl. Acad. Sci. USA. 104:9609–9614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chtcheglova, L. A., J. Waschke, L. Wildling, D. Drenckhahn, and P. Hinterdorfer. 2007. Nano-scale dynamic recognition imaging on vascular endothelial cells. Biophys. J. 93:L11–L13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 45.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.VanVliet, K. J., G. Bao, and S. Suresh. 2003. The biomechanics toolbox: experimental approaches for living cells and biomolecules. Acta Mater. 51:5881–5905. [Google Scholar]
- 47.Walton, E. B., and K. J. Van Vliet. 2006. Equilibration of experimentally determined protein structures for molecular dynamics simulation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 74:061901. [DOI] [PubMed] [Google Scholar]
- 48.Berendsen, H., D. van der Spoel, and R. van Drunen. 1995. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 91:43–56. [Google Scholar]
- 49.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. 7:306–317. [Google Scholar]
- 50.Chen, A., and V. T. Moy. 2000. Single molecule force measurements. Methods Cell Biol. 68:301–309. [DOI] [PubMed] [Google Scholar]
- 51.Stroh, C., H. Wang, R. Bash, B. Ashcroft, J. Nelson, H. Gruber, D. Lohr, S. Lindsay, and P. Hinterdorfer. 2004. Single-molecule recognition imaging microscopy. Proc. Natl. Acad. Sci. USA. 101:12503–12507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hutter, J. L., and J. Bechoefer. 1993. Calibration of atomic-force microscope tips. Rev. Sci. Instrum. 64:1868–1873. [Google Scholar]
- 53.Butt, H. J., and M. Jaschke. 1995. Calibration of thermal noise in atomic force microscopy. Nanotechnology. 6:1–7. [Google Scholar]
- 54.Janovjak, H., J. Struckmeier, and D. J. Muller. 2005. Hydrodynamic effects in fast AFM single-molecule force measurements. Eur. Biophys. J. 34:91–96. [DOI] [PubMed] [Google Scholar]
- 55.Alcaraz, J., L. Buscemi, M. P. de Morales, J. Colchero, A. Baro, and D. Navajas. 2002. Correction of microrheological measurements of soft samples with atomic force microscopy for the hydrodynamic drag on the cantilever. Langmuir. 18:716–721. [Google Scholar]
- 56.Puntheeranurak, T., L. Wildling, H. J. Gruber, R. K. Kinne, and P. Hinterdorfer. 2006. Ligands on the string: single-molecule AFM studies on the interaction of antibodies and substrates with the Na+-glucose co-transporter SGLT1 in living cells. J. Cell Sci. 119:2960–2967. [DOI] [PubMed] [Google Scholar]
- 57.Neuert, G., C. Albrecht, E. Pamir, and H. E. Gaub. 2006. Dynamic force spectroscopy of the digoxigenin-antibody complex. FEBS Lett. 580:505–509. [DOI] [PubMed] [Google Scholar]
- 58.Evans, E. 1999. Looking inside molecular bonds at biological interfaces with dynamic force spectroscopy. Biophys. Chem. 82:83–97. [DOI] [PubMed] [Google Scholar]
- 59.Karcher, H., S. E. Lee, M. R. Kaazempur-Mofrad, and R. D. Kamm. 2006. A coarse-grained model for force-induced protein deformation and kinetics. Biophys. J. 90:2686–2697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wen, J.-D., M. Manosas, P. T. X. Li, S. B. Smith, C. Bustamante, F. Ritort, and I. T. Jr. 2007. Force unfolding kinetics of RNA using optical tweezers. I. Effects of experimental variables on measured results. Biophys. J. 92:2996–3009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Evans, E. 2001. Probing the relation between force-lifetime and chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. 30:105–128. [DOI] [PubMed] [Google Scholar]
- 62.Piran, U., and W. Riordan. 1990. Dissociation rate constant of the biotin-streptavidin complex. J. Immunol. Methods. 133:141–143. [DOI] [PubMed] [Google Scholar]
- 63.Qureshi, M. H., J. C. Yeung, S.-C. Wu, and S.-L. Wong. 2001. Development and characterization of a series of soluble tetrameric and monomeric streptavidin muteins with differential biotin binding affinities. J. Biol. Chem. 276:46422–46428. [DOI] [PubMed] [Google Scholar]
- 64.Shenoy, V. B., and L. B. Freund. 2005. Growth and shape stability of a biological membrane adhesion complex in the diffusion-mediated regime. Proc. Natl. Acad. Sci. USA. 102:3213–3218. [DOI] [PMC free article] [PubMed] [Google Scholar]