Fuzzy Clustering Neural Networks for Real-Time Odor Recognition System

Abstract

The aim of this study is to develop a novel fuzzy clustering neural network (FCNN) algorithm as pattern classifiers for real-time odor recognition system. In this type of FCNN, the input neurons activations are derived through fuzzy c mean clustering of the input data, so that the neural system could deal with the statistics of the measurement error directly. Then the performance of FCNN network is compared with the other network which is well-known algorithm, named multilayer perceptron (MLP), for the same odor recognition system. Experimental results show that both FCNN and MLP provided high recognition probability in determining various learn categories of odors, however, the FCNN neural system has better ability to recognize odors more than the MLP network.

1. INTRODUCTION

Electronic/artificial noses are being developed as systems for the automated detection and classification of odors, vapors, and gases. The two main components of an electronic nose are the sensing system and the automated pattern recognition system. The sensing system can be an array of several different sensing elements (e.g., chemical sensors), where each element measures a different property of the sensed odor, or it can be a single sensing device (e.g., spectrometer) that produces an array of measurements for each odor, or it can be a combination. Each odor presented to the sensor array produces a signature or pattern characteristic of the odor. By presenting many different odors to the sensor array, a database of signatures is built up. This database of labeled odor signatures is used to train the pattern recognition system. The goal of this training process is to configure the recognition system to produce clustering of each odor so that an automated identification can be implemented [1–5].

The odor sensing system should be extended to new areas since its standard style, where the output pattern from multiple sensors with partially overlapped specificity, is recognized by a neural network [6–9]. In many practical pattern classification and recognition problems, the performance of a single classifier may not be satisfactory. This has raised awareness of the potential of multiple classifier systems. Indeed, different machine learning systems to solve more complex problems have became one of the main directions in machine learning research [10].

Zvi Boger has described some of his recent electronic nose-based ANN applications [11]. A specific example is the classification of the type of bacterial infection in intensive care unit patients. Gas samples were collected from the exhaled breath of patients connected to a respiration machine at oxygen concentrations of 30%, 50%, and 100%. Electrical conductance data of an array of 16 conductive polymers was used to train ANN model to predict the presence of the more prevalent bacteria species in 59 training examples; the ANN model gave 4 (6.8%) false positives, while 6 out of the 21 validation examples. Kusumoputro et al. have developed a new kind of hybrid neural learning system, combining unsupervised self-organizing maps (SOM) and supervised back-propagation (BP) learning rules [12]. This hybrid neural system could estimate the cluster distribution of given data, and direct it into a predefined number of cluster neurons through creation and deletion mechanism. Dutta et al. have presented comparative works to classify the six bacteria classes, using an unsupervised classifier named fuzzy c means (FCM) and SOM network, and three supervised classifiers, namely, multi layer perceptron (MLP), probabilistic neural network (PNN), and radial basis function (RBF) network, respectively [13]. Karlık and Bastaki have presented a higher-order MLP structure to diagnos bad breath of sugar diabetic illness taking the odor data from the patients [14]. The disadvantage of all these works given above is less recognition rate for more than ten different odor classes. Then, Temel and Karlık have proposed a learning vector quantization (LVQ) neural network to classify twenty different odor patterns of perfume [15]. The only disadvantage of this proposed algorithm is the need for storing class covariance matrices. Manipulation of a new data involves storage and retrieval of class covariance matrices, which in fact is a minor expense compared to bulky processing with other well-known methods.

In this study, we have developed-odor sensing system with the capability of the discrimination among closely similar 16 different odor patterns and proposed a real-time classification method, using a handheld odor meter (OMX-GR sensor) and fuzzy clustering neural networks. A high-performance biologically inspired odor-identification system is described. Due to a sample-based decision, the system can be reliably operated as a real-time odor recognition system (or electronic nose).

2. BACKGROUND

Artificial neural networks are often seen as black boxes which compute, in a mysterious way, one or more output values for a vector of input values. The impressive advantages of NNs are the capability of solving highly nonlinear and complex problems and the efficiency of processing imprecise and noisy data. The feedforward neural network is usually trained by a back-propagation training algorithm, which has generalized delta rule learning. This was the effective usage of it only after 1980s [16]. Furthermore, this training method requires a great deal of computational time. With the advantage of high-speed computational technology, NNs are more realistic, easily updateable, and implementable today. In the following sections, the high-order NN and the fuzzy clustering NN algorithms are summarized.

2.1. Multilayer perceptron (MLP)

The most common neural network model is the MLP. An MLP network is grouped in layers of neurons, that is, input layer, output layer, and hidden layers of neurons that can be seen as groups of parallel processing units. As illustrated by the example shown in Figure 1, each neuron of a layer is connected to all the neurons of the following layer (feedforward neural network). These connections are directed (from the input to the output layer) and have weights assigned to them. Associated with each connection is a numerical value, which is the strength or the weight of that connection: w_ij = strength of connection between units i and j [17].

Figure 1.

General architecture of MLP.

The connection strengths are developed during the training of neural network. When presented an input pattern, a feedforward network computation results in an output pattern that is the result of generalization and synthesis of what it has learned and stored in its connection strengths. This type of neural network is known as a supervised network because it requires a desired output in order to learn. Back-propagation algorithm was created by generalized delta learning rule to multiple-layer networks and nonlinear differentiable transfer functions [18].

A feedforward network computation with these back-propagation neural networks proceeds as follows.

1. The units in the input layer receive their activations in the form of an input pattern; this initiates the feed-forward process.

2. The processing units in each layer receive outputs from other units and perform the following computations.

   1. Compute their net input N_j as follows:

      $$N_j={\displaystyle \sum _{k=1}^M}{w}_{jk}{o}_k$$ (1)

      in which o_k = output from units impinging on unit j, and M = number of units impinging on unit j.
   2. Compute their activation values from their net input values:

      $$a_j=F_j(N_j)\mathrm{,}$$ (2)

      where F_j is usually a sigmoid function as follows:

      $$F_j=\frac{1}{1+e^{-(N_j-{\theta }_j)}}\mathrm{.}$$ (3)
   3. Compute their outputs from their activation values. In the neural network type used in this study, the output is the same as the activation value, that is,

      $$o_j=a_j\mathrm{.}$$ (4)

3. The output values are sent to other processing units along the outgoing connections.

4. This process continues until the processing units in the output layer compute their activation values. These activation values are the output of the neural computations.

The modification of the strengths of the connections in the generalized delta rule, described by Rumelhart et al. [16], is accomplished through the gradient descent on the total error in a given training case,

$$\mathrm{\Delta }{w}_{ij}=\eta {\delta }_j{o}_j\mathrm{,}$$ (5)

in which η = a learning constant called the learning rate; and δ_j = gradient of the total error with respect to the net input at unit j. At the output units, δ_j is determined from the difference between the expected activations t_j and the computed activations a_j:

$${\delta }_j=(t_j-a_j)F^{\prime }(N_j)\mathrm{,}$$ (6)

where F′ = a derivative of activation function. At the hidden units, the expected activations are not known a priori. The following equation gives a reasonable estimate of δ_j for the hidden units:

$${\delta }_j=\left({\displaystyle \sum _{k=1}^M}{\delta }_k{w}_{jk}\right)F^{\prime }(N_j)\mathrm{.}$$ (7)

In (7), the error attributed to a hidden unit depends on the error of the units that influence it. The amount of error from these units attributed to the hidden unit depends on the strength of connection from the hidden unit to those units; a hidden unit with a strong excitatory connection to a unit exhibiting error will be strongly “blamed” for this error, causing this connection strength to be reduced. The greatest disadvantage of this algorithm is that it does not even ensure convergence towards a local minimum.

2.2. Fuzzy clustering neural network (FCNN)

FCNN consists of combination of a fuzzy self-organizing layer and the MLP, which is connected in cascade, where the number of data points is reduced using fuzzy c-means clustering before inputs are presented to a neural network system. Therefore, the training period of the neural network is decreased. The self-organizing layer is responsible for the clustering of the input data. The outputs of all self-organizing neurons (the cluster centers) form the input vector to the second MLP subnetwork [19–22]. The number of data points is reduced using fuzzy c-means clustering before inputs are presented to a neural network system. The idea of fuzzy clustering is to divide the data into fuzzy partitions, which overlap with each other. Therefore, the containment of each data to each cluster is defined by a membership grade in (0,1). In formal words, clustering in unlabeled data X = {x₁, x₂, …, x_N} ⊂ ℜ^h, where N is the number of data networks and h is the dimension of each data vector, is the assignment of c number of partition labels to the vectors in X. The c-partition of X are sets of (c · N) membership values {u_ik} that can be conveniently arrayed as a (c × N) matrix U = [u_ik]. The problem of fuzzy clustering is to find the optimum membership matrix U. The most widely used objective function for fuzzy clustering in X is the weighted within-groups sum of the squared-errors objective function J_m.[23]:

$$\underset{¯}{\underset{U,V}{\min }}\{J_m(U,V;X)={\displaystyle \sum _{k=1}^N}{\displaystyle \sum _{i=1}^c}{(u_{ik})}^m||x_k-v_i{||}_A^2\}\mathrm{,}$$ (8)

where

$$\begin{array}{c}U\end{array}\in \begin{array}{c}{M}_{\text{fcn}}\hfill \end{array}\begin{array}{c}=\left\{U\in {\Re }^{cN}\mid \begin{array}{l}0\le u_{ik}\le 1\forall ik\&\forall k,u_{ik}>0\exists i\hfill \\ 0<{\displaystyle \sum _{k=1}^N}{u}_{ik}<n{\forall }_i\&{\displaystyle {\displaystyle \sum }_{i=1}^c}{u}_{ik}=1\forall k\hfill \end{array}\right\}\mathrm{.}\hfill \end{array}$$ (9)

V = {v₁, v₂, …, vc} is a vector of (unknown) cluster centers, and ${||x||}_A=\sqrt{x^{T}Ax}$ is an inner product norm. A is an hxh positive definite matrix, which specifies the shape of the clusters. Fuzzy partitions are carried out by the fuzzy C-means (FCM) algorithm through an iterative optimization of equation according to the following steps.

Step 1 —

Choose the number of clusters (c), weighting exponent (m), iteration limit (iter), termination criterion (ε > 0), and the norm for error = ||V_t − V_t−1||.

Step 2 —

Guess the initial position of the cluster centers: V₀ = {v_1,0, v_2,0, …, v_c,0} ⊂ ℜ^ch.

Step 3 —

Iterate for t = 1 iteration; calculate

$$\begin{array}{c}{u}_{ik,t}={\left[{\displaystyle \sum _{j=1}^c}{\left(\frac{||X_k-V_{i,t-1}{||}_A}{||X_k-V_{j,t-1}{||}_A}\right)}^{2/(m-1)}\right]}^{-1}\mathrm{,}\\ V_{i,t}=\frac{{\sum }_{k=1}^N{(u_{ik,t})}^m{x}_k}{{\sum }_{k=1}^N{(u_{ik,t})}^m}\mathrm{.}\end{array}$$ (10)

If error = ||V_t − V_t−1|| ≤ ε, then stop and put (U_f, V_f) = (U_t, V_t) next to t.

3. MATERIALS AND METHODS

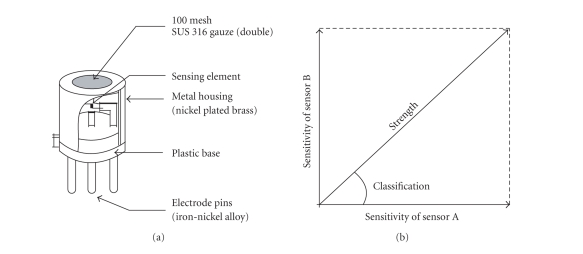
In this study a “handheld odor meter, OMX-GR” is used to obtain odor data. This is completely manufactured by FiS as an OEM product. The OMX-GR sensor indicates two factors of odor, “strength” and “classification”, with numeric values. This is very useful for various applications related to odor detection and measurement. Also, real-time continuous data can be stored into a personal computer through RS-232C interface. As it can be seen in Figure 2, the strength and classification of odor can be identified by using two different gas sensors: one has a specific sensitivity to a light and fresh smell and the other has a specific sensitivity to a heavy and bad smell. Memory sampling of this odor meter is suitable to store 16 different patterns of odor sampling.

Figure 2.

Sensor configuration and measurement principle.

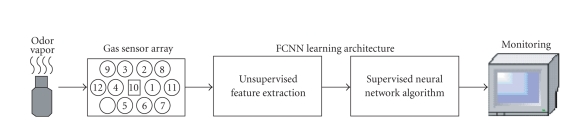
The schematic diagram of the whole system is illustrated in Figure 3. The multiple (consisting of two semiconductor gas sensors) OMX-GR odor sensor signals are simultaneously measured, using the strength of odor concentration. Both of these gas sensors (OMX-GR) operate in the real-time sampling mode. The samples were delivered to a fuzzy c mean (FCM) clustering algorithm to obtain unsupervised feature extraction. FCM is a fuzzy data clustering and partitioning algorithm in which each data point belongs to a cluster according to its degree of membership. With FCM, an initial estimate of the number of clusters is needed so that the data set is split into C fuzzy groups. A cluster center is found for each group by minimizing a dissimilarity function. Fuzzy clustering, essentially, deals with the task of splitting a set of patterns into a number of more or less homogeneous classes (clusters) with respect to a suitable similarity measure such that the patterns belonging to any one of the clusters are similar and the patterns of different clusters are as dissimilar as possible. The similarity measure used has an important effect on the clustering results since it indicates which mathematical properties of the data set should be used in order to identify the clusters. Fuzzy clustering provides partitioning results with additional information supplied by the cluster membership values, indicating different degrees of belongingness [15]. Then the multiplexed time-series data, which belongs to 16 different odors of perfumes, are clustered and are inputs to the supervised neural network algorithm. This neural network trained BP algorithm classifies the sensor-array output patterns into odor categories. The system was trained to identify odors of 16 different perfumes with 20 samples for each.

Figure 3.

A prototype of a real-time odor recognition system.

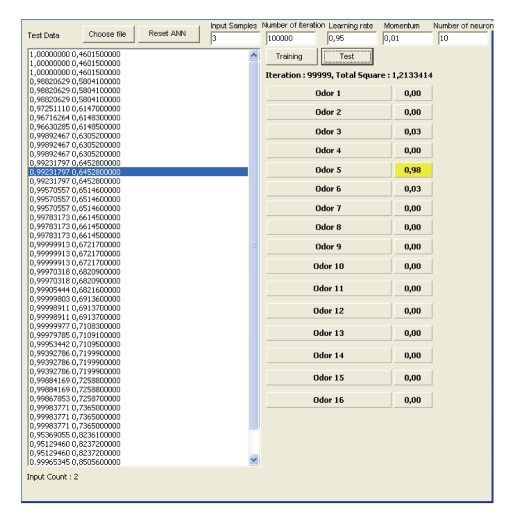
This system allows users to obtain the desired data from a particular odorant (perfume). There are two ways to obtain data by using a handheld odor meter. These are real-time sampling data and memory sampling data. The sensor output voltages (raw data) were sampled approximately every one second. The last form is ANN System, which classifies the training and test data of odor samples (see Figure 4). The number of features in each input pattern, in our case, is 16 × 20 (each odor contains 20 samples). The numbers of output units are 16 outputs for 16 different classes of odor samples.

Figure 4.

The recognition form.

4. EVALUATION OF NEURAL NETWORK-CLASSIFICATION PERFORMANCE

The sixteen different odors of perfume dataset were analyzed using two types ANN classifiers, namely the multilayer perceptron (MLP) and the proposed fuzzy clustering neural network (FCNN) structures. The training of both ANN structures was performed with half of the whole data set. The other half was used for testing both structures of neural networks. These percentages were selected arbitrarily and were applied for all datasets (see Figure 4).

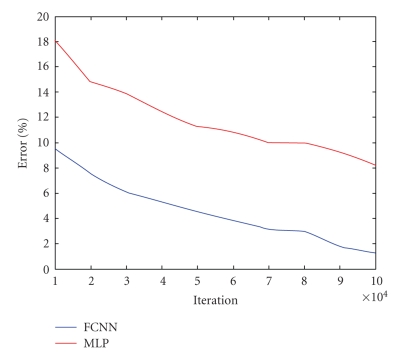
Figure 5 describes the comparing results between high-order MLP (it consists of 2 hidden layers) and FCNN algorithms for 100 000 iterations. As noted, the average mean square error (MSE) of FCNN is less than the MLP structure. In other word, we can say that an average recognition

Figure 5.

Training error results for both architectures of neural networks.

accuracy of FCNN is better than MLP. Moreover, it is noted, in the results above, that the FCNN converges to a determined error goal faster than the MLP. By the way, we tried to recognize these data by using a 3-layered perceptron, which has only one hidden layer, but it could not classify the whole dataset. It was able to recognize only 9 different odors out of 16.

FCNN was able to correctly classify 93.75% of the response vectors whereas the HO-MLP neural network's level of correct classification was up to 62.6875% of accuracy for whole normalized data set of 16 different odors. Depending on using both ANN architectures, optimum learning rate and momentum coefficient were found as 0.95 and 0.01, respectively.

It can be seen in Figure 6, the number of hidden layers was fixed to one hidden layer for ANN structures, and the number of nodes (or units) in that hidden layer was changed several times. Also, the iteration number was fixed to 100 000 iterations. These results (of the output error) were drawn together with the number of nodes in the hidden layer in a curve.

Figure 6.

Error according to number of nodes for one hidden layer of FCNN.

The artificial neural networks were coded in Delphi, and the back-propagation algorithm was employed for network training. Networks with different numbers of hidden units and initial weights were experimented and optimized.

5. CONCLUSIONS

In this works, a real-time odor recognition system, employing two classifiers, is described. It contains two phases for training and testing phases. The training phase aims at localizing samples in their respective classes. It was shown that odors are identified very reliably and faster with FCNN than MLP. These systems are designed for specific applications with a limited range of odors. Training the ANN system, using the data we have collected during our study of the electronic nose, resulted in the following output of error. Another advantage of the parallel processing nature of the ANN is the speed performance. During development, ANNs are configured in a training mode. This involves a repetitive process of presenting data from known diagnoses to the training algorithm. This training mode often takes many hours using, especially, ordinary MLP. The payback occurs in the field, where the actual odor identification is accomplished by propagating the data through the system which takes only a fraction of a second. This proposed ANN program, named FCNN, is very useful for real-time odor record and odor recognition system, which has a various types of odor samples.