Robustness of neural codes and its implication on natural image processing

Abstract

In this study, based on the view of statistical inference, we investigate the robustness of neural codes, i.e., the sensitivity of neural responses to noise, and its implication on the construction of neural coding. We first identify the key factors that influence the sensitivity of neural responses, and find that the overlap between neural receptive fields plays a critical role. We then construct a robust coding scheme, which enforces the neural responses not only to encode external inputs well, but also to have small variability. Based on this scheme, we find that the optimal basis functions for encoding natural images resemble the receptive fields of simple cells in the striate cortex. We also apply this scheme to identify the important features in the representation of face images and Chinese characters.

Introduction

In natural environments, variations on the view angle, distance and background, and deformations of images, mean that the external inputs from the same object to neural systems are highly fluctuated. In order to recognize objects reliably, it is important for neural systems to extract the important features of external inputs. Mathematically this is expressed as statistical inference.

We write down the external inputs to a neural system as 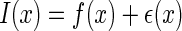, with x denoting the spatial location of the data points in the image and 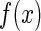the important features of external inputs which are necessary to define the stimulus and 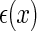representing those un-important components which are regarded as noise. We consider that 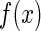is encoded as an activity pattern a in the neural system. The goal of a neural estimator is to infer the value of a based on the noisy input 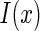. Because of noise, the inferred result 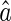is in general different from the true value a. Robustness, or sensitivity, of neural coding refers to the discrepancy between 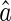and a due to noise. Low robustness, or large sensitivity, implies that neural responses to the same object corrupted with different kinds of noise are dramatically different. Clearly, in order to recognize objects reliably, it is desired that neural coding is robust against noise.

Two issues concerning the robustness of neural codes are explored in the present study. Firstly, we identify what are the key factors influencing the robustness of neural coding, and find that the overlap between neural receptive fields plays a critical role, i.e., the larger the overlap, the more susceptive to noise the neural responses are. This property implies that for achieving robust coding, neural systems should use receptive fields having as small as possible overlap (under the proviso that external objects are adequately encoded).

Secondly, we investigate, under the requirement of robustness, how neuronal receptive fields are shaped in order to encode natural images accurately. It turns out that the obtained results resemble the localized and oriented receptive fields of simple cells in the striate cortex (Hubel and Wiesel 1968; Palmer 1999). This finding is very interesting, which provides a novel justification for the receptive field properties of simple cells, different from those in the literature (see, e.g., Olshausen and Field 1996; Bell and Sejnowski 1997; van Hateren and van der Schaaf 1998; Lewicki and Olshausen 1999; Simoncelli and Olshausen 2001; Hurri and Hyvärinen 2003; Vincent and Baddeley 2003). The robust coding algorithm we formulate is quite close to the well-known sparse coding approach (Olshausen and Field 1996). The main difference is that rather than restricting the sparseness of neural activities, we minimize the total variability of neural responses. It turns out that apart from predicting the similar basis functions, our method makes the neural system being more robust to external noise.

The organization of the paper is as follows. In Section “Statistical inferential sensitivity”, we first study a simple statistical inference model and elucidate the factors which influence the sensitivity of neural responses. In Section “Robust coding for natural images”, a robust coding scheme which minimizes the sensitivity of neural responses to noise is proposed. This scheme enforces the neural responses not only to encode external inputs well, but also to have small variability. Based on this scheme, we optimize the basis functions for encoding natural images, and compare the results with the receptive fields of simple cells. In Section “Discussions”, robust coding is compared with other efficient coding schemes, such as sparse coding (Olshausen and Field 1996, 1997; Simoncelli and Olshausen 2001) and temporal coherence (Földiák, 1991; Becker 1993; Stone 1996; Wiskott and Sejnowski 2002; Hurri and Hyvärinen 2003). Its implications on our understanding of neural information processing are discussed. Finally, in Section “Conclusion”, the overall conclusion of this work is given.

Statistical inferential sensitivity

Our study on the robustness of neural codes is based on a simple model of neural encoding. It assumes that external stimuli 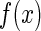is represented as a linear superposition of a set of basis functions (Olshausen and Field 1996; Bell and Sejnowski, 1997)

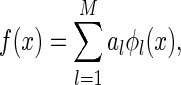1

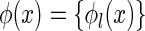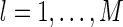where , for , represent the basis functions, and the coefficients 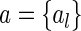, for 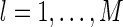, the representation of the stimulus 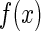in the basis set 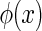. It is known that the basis functions can be associated with neuronal receptive fields, and the variable a to neural activities (Olshausen and Field 1996; Bell and Sejnowski, 1997).

We first study a simple toy model, which allows us to analytically quantify the sensitivity of estimating a due to noise.

A toy model study

Consider an extremely simple case, in which there are only two coding units and the basis functions are fixed to be Gaussian. The noises in external inputs are also assumed to be independent Gaussian, which are written as

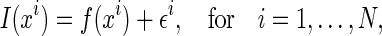2

where 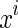represents the ith sampling point of the stimulus, and 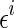a Gaussian random number of zero mean and variance σ². N is the number of data points sampled from the stimulus.

We consider a simple inference method, called Least Square Error (LSE), whose estimate for 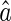is given by

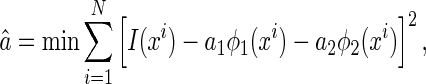3

that is, the inferred result is the one that has the minimum reconstruction error for the external inputs.

It can be proved that for the above simple model, when N is sufficiently large, the LSE satisfies a normal distribution (see Appendix A),

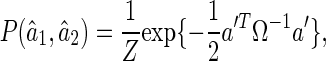4

where the vector, 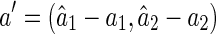, denotes the decoding errors. The matrix Ω is the covariance matrix, whose inverse is given by

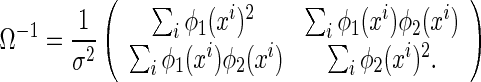5

It can be checked that Ω is the inverse of the Fisher information (see Appendix A). This implies that the inferential sensitivity of LSE with respect to noise has reached the minimum possible value. This is because, according to the Cramér-Rao bound, the inverse of the Fisher information is the lower bound for decoding errors of un-biased estimators.1 Thus, our discussion below on the statistical inferential sensitivity is independent of the decoding method used.

The sensitivity of decoding can be described by the marginal distribution of 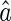, which is calculated as (see Appendix A),

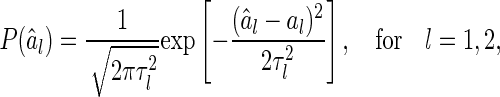6

where the variance 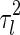is given by (only 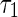is shown, the result for 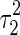is similar)

7

The magnitude of , i.e., the broadness of the marginal distribution, quantifies the sensitivity of decoding. Intuitively, the broader the distribution, the more the estimate can be expected to deviate from the true value. Large sensitivity implies that inferred results for the same stimulus corrupted with different instantiations of noise can be dramatically different.

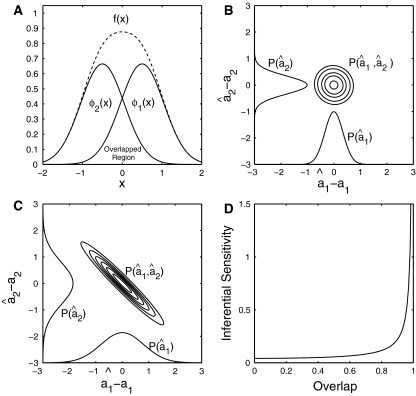
From Eq. (7), we see that the sensitivity of decoding is determined by several factors, namely, the noise strength (), the number of data points (N) and the overlap between basis functions.

The overlap between basis functions is measured by (see the denominator of Eq. (7))

8

Figure 1 illustrates that inferential sensitivity increases with the amount of overlap. This effect is intuitively understandable. In the overlapping region, the contributions from the two basis functions (i.e., the two statistical components) on generating the stimulus are mixed. As a result, data points in this region are less informative for ‘distinguishing’ the activities of the two encoding units. More overlap leads to more ambiguity in inference. Consider the extreme case when the two basis functions are completely overlapping, there exists an infinite number of pairs of 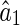and 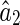, with 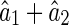a constant, that can equally interpret the stimulus, and the inferential sensitivity is infinitely large.

Fig. 1.

The results of the toy model study. (A) An illustration of the stimulus and two overlapped basis functions; (B) In the case of small overlap, the joint and marginal distributions of the estimation are narrow; (C) In the case of large overlap, the joint and marginal distributions are broad; (D) The inferential sensitivity (measured by 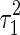) vs. the amount of overlap

The moral of the toy model study

The model studied above is quite simple, but the moral it reveals to us is profound, which has at least two important implications:

• First, it tells us that if neural receptive fields are overlapped, then neural responses are inevitably sensitive to noise.

• Second, it tells us that if robustness is desired for neural responses, then neural systems should choose those basis functions having as small as possible overlap (under the proviso that objects can be adequately encoded).

These two issues will be further explored in the study below.

Robust coding for natural images

Our hypothesis is that to recognize objects reliably, neural coding should be constructed to be as robust as possible against noise. As shown above, this requires neural receptive fields to have small overlap. To test this idea, we carry out the following experiment. Firstly, we construct a coding scheme, which not only encodes external inputs well, but also suppress the sensitivity of neural responses to noise. Based on this scheme, we optimize the basis functions to encode natural images, and compare the result with the receptive fields of simple cells. This is motivated by that the optimal basis functions for encoding natural images under the linear framework of Eq. (1) and proper constraints tend to resemble the receptive fields of simple cells (Olshausen and Field 1996; Bell and Sejnowski 1997; van Hateren and van der Schaaf 1998; Lewicki and Olshausen 1999; Simoncelli and Olshausen 2001; Hurri and Hyvärinen 2003; Vincent and Baddeley 2003).

The coding scheme

The coding scheme we consider minimizes the following cost function,

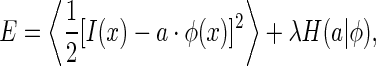9

where 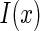represents a natural image. The term 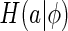is a measure about the variability of neural responses given the basis functions ϕ. The bracket 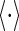denotes averaging over the set of natural images. The parameter λ controls the balance between the reconstruction error and the variability of neural responses.

The choice of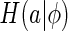

To quantify the inferential sensitivity of neural code, ideally, we should set 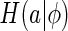to be the summation of the marginal entropy of neural responses when a fixed stimulus is presented, for instance,

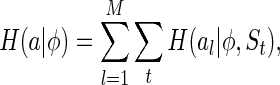10

where 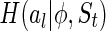is the marginal entropy of the lth neuron’s responses given a particular stimulus 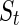, and the summations are over all neurons and the stimuli to be encoded. But unlike the above toy model (where the stimulus is fixed), here for encoding natural images, we do not know in advance what are the important features and what should be regarded as noise2. Thus, the measure Eq. (10) cannot be used.

To overcome this difficulty, our strategy is to choose 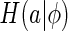to be the summation of the marginal entropy of neural responses given the set of natural images, rather than a particular important feature, i.e.,

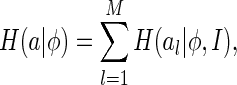11

where 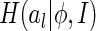is the marginal entropy of the lth neuron’s responses given the set of natural images I. 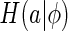therefore measures the total variability of neural responses for representing a set of external inputs. Our expectation is that through properly combining the neural response variability and the reconstruction error, the neural system will, on one hand, learn to encode the important features of external inputs, as this is most effective for decreasing the reconstruction error, and on the other hand, become insensitive to those un-important components, as a consequence of restricting the total variability of neural responses (since in this case the variability of neural responses is mainly used for the encoding of important features). Therefore, minimizing the cost function Eq. (9) can indirectly achieve our goal of implementing robust coding. This idea is confirmed by the simulation result in Section “Sensitivity of robust coding”.

Furthermore, we choose the Renyi’s quadratic entropy to quantify 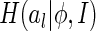(Renyi 1976), which is defined as

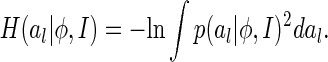12

The good point of this measure is that although we do not know the analytic form of 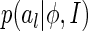, the Renyi’s quadratic entropy allows us to approximate 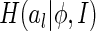in a data-dependent way, i.e., by using sampled values of a_l when a number of images are presented.

Let us denote 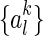, for 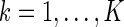, as the sampled values of a_l after K natural images are presented and the basis functions are ϕ. According to the Parzen window approximation (Parzen 1962), the distribution 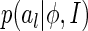can be approximated as

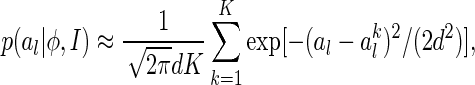13

where the Gaussian kernel has been used in the Parzen window approximation with d the width of the kernel.

Substituting Eq. (13) in (12), we obtain (see Appendix B)

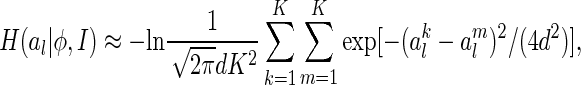14

which now fully depends on sampled values of a_l.

In practice, sampled values of {a_l}, for 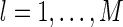, are easily obtained. We use the gradient descent method to minimize the function E (for detail, see Appendix B). At each step of updating 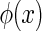, we present K≫ 1 training examples, which automatically generates K sampled values for each a_l.

Finally, combining Eqs. (9) and (14), we get the cost function

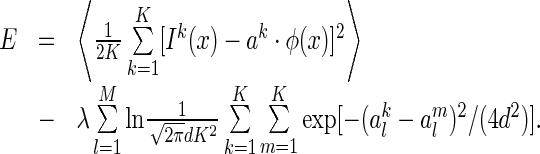15

Here, for clarity, we have written down explicitly the batch of images, denoted as 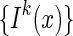, for 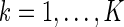, presented at each step of training. The detail of the training procedure is presented in Appendix B.

Simulation results

For natural scenes

We first choose natural scenes, such as leaves, trees, rocks and river etc., as external inputs. They are constructed as follows. First, we select ten, 480 × 480 pixels, pre-whitened natural scenes as the repository of training examples (for examples of natural scenes and their whiten images, see Fig. 2A, B). Then, at each step of training, we randomly choose 100 (i.e., the sampling size K = 100) 20 × 20 image patches from the repository as inputs. The neural system consists of 400 neurons. Initially, all basis functions are randomly initialized in the 20 × 20 image space. After training, these basis functions are optimized, as shown in Fig. 2C.

Fig. 2.

Simulation on natural images. (A) Two examples of natural scenes. (B) Whitened images of (A). (C) The obtained optimal basis functions. The parameters used are ,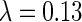

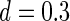
We see that the optimal basis functions are oriented and localized in the space, resembling the properties of receptive fields of simple cells in the striate cortex (Hubel and Wiesel 1968; Palmer 1999). How should we interpret this result in the view of robustness? From Eq. (9), we see that optimal basis functions need to satisfy two conditions, namely, to encode natural scenes well and to maintain small variability in neural responses. First, to encode external inputs well, from the theory of function approximation (Bishop 1996; Schölkopf and Smola 2001), this requires basis functions to ‘match’ the structures of the external inputs. Second, to maintain small variability in neural responses, this requires basis functions to have a small overlap. It is straightforward to see that the above localized and oriented basis functions best meet these two requirements. Firstly, they have the same shapes as the oriented lines and edges, the salient features in natural scenes. Secondly, they are dispersed in the space and have a relatively small extent of overlap.

For human faces

To validate further our analysis, we use parts of human faces as external inputs. The advantage of these inputs is that they have some new localized features, such as the shapes of eye, nose or mouth, which provides us an opportunity to check whether our coding scheme works consistently.

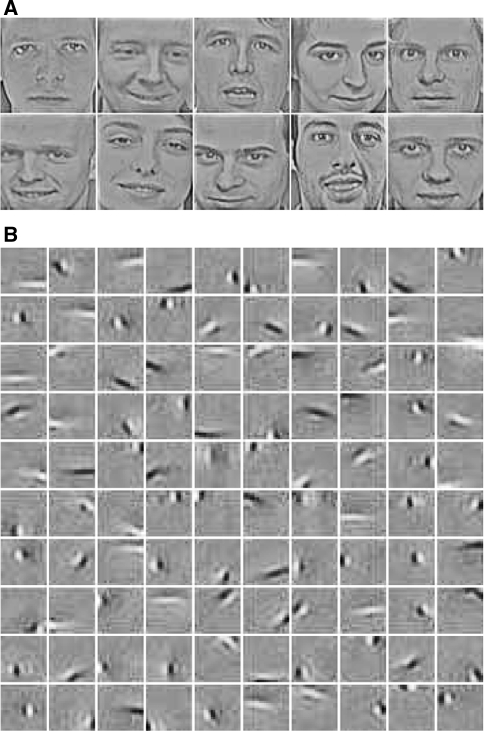
The face images are taken from the ORL face database (Olivetti Research Laboratory in Cambridge, UK), and they are properly re-scale into a size of 70 × 70 pixels (for examples, see Fig. 3A). Again, we first select 117 face images as the repository, and then, at each step of training, we randomly choose 100, 20 × 20 image patches as training examples. The training results are shown in Fig. 3B. We see that, apart from the shapes of localized lines and edges, some basis functions display curved or round shapes.

Fig. 3.

Simulation on face images. (A) Examples of face images from ORL database, the size of the images is 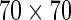pixels. (B) The obtained optimal basis functions. The parameters used are 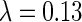, d = 0.3

For Chinese characters

Essentially, the coding scheme Eq. (9) can also be used as a general method for feature extraction: It selects those important features so that the coding system non only encodes external inputs but also has small entropy. To test this idea, we apply this method to the representation of Chinese characters.

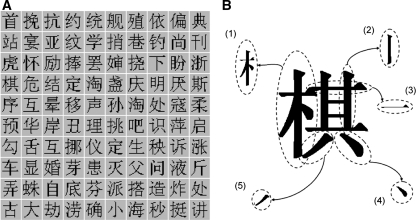
Chinese characters, whose history can be tracked back to thousands of years ago, appear to be very complicated in terms of recognition (see, e.g., examples in Fig. 4). In fact, however, they are composed of some simple pictographs and ideographs in a logical way that can be easily remembered. The most elementary component of the Chinese character is strokes, which further compose radicals or other structured components. A radical may be shared by characters having the same category meaning. An example of such a Chinese character, which means “chess” in Chinese, is illustrated in Fig. 4B. This character is left and right structured. The left part (indicated as part 1 in the figure) is a radical, which is shared by many characters having a meaning related to wood. The right part is actually another character that points out the pronunciation of this character but is meaningless in the structure, being just composed of a few strokes. Many research work including psychophysical and functional Magnetic Resonance Imaging (fMRI) studies have revealed that strokes and radicals play important roles in Chinese character recognition (Hildebrandt and Liu 1993; Peng et al. 2004). They are the salient features for Chinese characters, like lines and edges for natural scenes.

Fig. 4.

Chinese characters. (A) Examples of Chinese character images, the dataset is the most frequently used 2,500 Chinese characters, the size of the images is 25 × 25 pixels. (B) Decomposition of a typical Chinese character, which means “chess”. This left and right structured character is composed of a radical (part 1) at the left side and another character at the right side. For the right component, it is composed of four kinds of strokes (parts 2–5)

We choose some of the most frequently used Chinese characters as the training dataset, which consists 2,500 words.3. Each character is presented as a 25 × 25 pixels image, see Fig. 4A for example. During the training, the number of basis functions was set to 100, and at each step of updating, 200 character images were randomly chosen as inputs.

The training results are shown in Fig. 5, which demonstrate that the optimal basis functions resemble the shapes of strokes, the salient features of Chinese characters, supporting that our method can extract the important features of external inputs.

Fig. 5.

Simulation results on Chinese character images. The training set is chosen as the most frequently used 2,500 Chinese characters, the size of the images is 25 × 25 pixels. The obtained optimal basis functions are shown here with the parameter setting 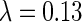and d = 0.3

Discussions

Relationship with other efficient coding schemes

The idea of assuming neural codes are designed to satisfy certain efficient criteria is a valuable top–down method for us to explore the properties of neural information processing (see, e.g., Attneave 1954; Barlow 1961; Laughlin 1981; Atick 1992; Field 1994; Li and Atick 1994; Lewicki and Olshausen 1999). This kind of method is of particular importance at the current stage since we do not have much knowledge about the detail of neural systems. In this study, we assume that neural codes are constructed to be as robust as possible against noise. Based on this hypothesis, we show that the receptive fields of simple cells may be justified as the consequence of encoding natural images optimally. We should point out that our work is neither the only one nor the first that predicts these simple-cell like basis functions. Indeed, quite a few methods based on different efficiency criteria have successfully achieved this, which particularly include sparse coding (Olshausen and Field 1996, 1997), independent component analysis (ICA) (Bell and Sejnowski 1997; van Hateren and van der Schaaf 1998), temporal coherence (Hurri and Hyvärinen 2003) and energy-efficient coding (Vincent and Baddeley 2003).

Sparse coding was the first approach to make this breakthrough, whose fundamental assumption is that the neural system interprets external stimuli by using very few statistically independent components, and hence neural responses should be sparse. For natural images, these statistically independent components happen to be the oriented lines and edges. ICA, when applied to analyze natural images, has a similar spirit to sparse coding.

Temporal coherence, on the other hand, has the same origin as robust coding, in the sense of that it also assumes the robustness of neural codes. But, unlike the formulation here which restricts the variability of neural responses, temporal coherence imposes the robustness constraint in a different way, which takes into account that in natural environments, temporal sequences of images, such as videos, vary slowly. It is therefore reasonable to assume that the variations between two temporally consecutive inputs are mainly due to noise, and enforce neural systems to respond least to such changes. Temporal coherence and robust coding can be seen as two complementary approaches demonstrating that robustness is important in the construction of neural coding.

It is worth further clarifying the difference between robust and sparse coding. Although both schemes predict the same, or similar, basis functions for encoding natural images, their natures are different. In the formulation of sparse coding, the cost function is set to be

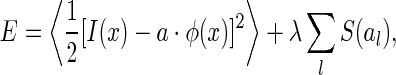16

where S(a_l) is the sparseness constraint, which can be chosen to be, e.g., 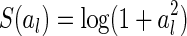. S(a_l) takes small value when the neural activity a_l are small. Thus, sparse coding tends to restrict the total activity of neurons (under the proper forms). This is different to robust coding, where the total variability of neurons is restricted (see Eq. (14), robust coding tends to minimize the difference between the activities of individual neurons when different inputs are presented, i.e., it is to minimize 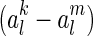rather than the absolute value of a_l.). This difference will be confirmed by the simulation in Section ”“Sensitivity of robust coding”.

In some sense, the coding scheme Eq. (9) is to implement the minimum entropy code under the constraint that external inputs are adequately encoded (Barlow 1989). Sparse coding can be also interpreted equally, but it evaluates the entropy based on a specific assumption about the distribution of neural responses, that is, this distribution is peaked at zero and has heavy tails (Lewicki and Olshausen 1999). Here, for robust coding Eq. (9), the entropy is evaluated based on the sampled data when a set of images are presented. We should point out that the idea of using the Renyi’s formula to estimate entropy in a data-dependent way has been used in other places, for instance, Principle et al. use this strategy to solve the blind source separation problem (Principe et al. 2000). But here, it is the first time this strategy is used to impose a robustness constraint for investigating the encoding of natural image.

All the above coding schemes we discussed focus on exploring how the input statistics determine the coding properties of neurons. In reality, however, the neural coding strategies are also strongly influenced by the tasks the neural systems aim to perform. In a recent work (Salinas 2006), Salinas has shown how the output statistics may shape the neuronal tuning curves. It will be interesting in our future to combine the robustness constraint and the specific task requirements.

We should also note that the coding model we consider is different from the de-noising method in image processing (e.g., Hyvärinen 1999). Here, we do not care about how to remove noise in external inputs (although the scheme can have this effect), but instead how to construct a code so that the responses of coding units are robust against input noise.

Sensitivity of robust coding

To confirm that the coding scheme Eq. (9) indeed suppresses the sensitivity of neural responses to noise, we carry out the following experiment.

The noisy inputs to the neural system are generated as follows (Li and Wu 2005). First, we choose a large-size natural image as a seed, and randomly down-sample this image 100 times with a rate of 25% (this can be done, for instance, by randomly and uniformly choosing 25% data points from the seed image). These down-sampled images are almost visually indistinguishable, and can be regarded as noisy inputs from the same object (for examples of down-sampled images, see Fig. 6A, B). Then, we calculate the neural responses to these noisy inputs, which are obtained by minimizing E with the basis functions fixed to be optimal. The sensitivity of coding is measured by the variance of the neural responses.

Fig. 6.

(A) & (B) Two down-sampled images at the rate of 25% from the same seed. (C) Examples of basis functions in three coding schemes: (1) robust code, (2) sparse code, and (3) Gaussian

For comparison, we also calculate the sensitivity of sparse coding and a scheme using Gaussian functions as the basis. The Gaussian basis functions are chosen to be 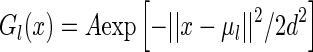, for 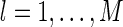, with the center μ_l being at each pixel in the image space. To ensure that the comparison is fair, we normalize all basis functions, including the optimal and the Gaussian ones, i.e., 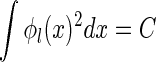, for 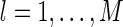and C a constant. 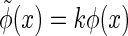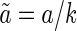This is to avoid the problem that under the transformations of and , the reconstruction error is invariant, but the variance of a decreases 1/k² times. Also, for the coding scheme using Gaussian basis functions, we set the width d of Gaussian functions to be the value, such that it has the same reconstruction error as robust coding. The basis functions used in the three coding schemes are illustrated in Fig. 6C.

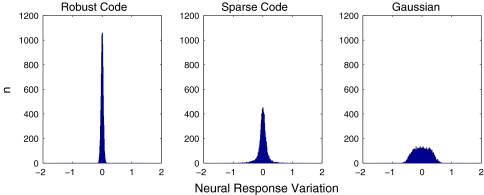
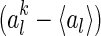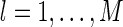Figure 7 shows the distribution of the variation of neuronal responses to their mean values, i.e., , for and 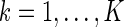, where 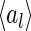is the mean activity of the lth neuron. We observe that: (1) The scheme using Gaussian basis functions has the broadest distribution, indicating that in this scheme neural response is most sensitive to noise. This is understandable, since its basis functions are not optimized and have the largest overlap. (2) The neural response variation in robust coding is much more sharply distributed than that in sparse coding, although they have the similar basis functions. This indicates that in robust coding neural responses are much more robust to noise, confirming our analysis. The sensitivities of the three schemes, measured by 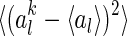, are calculated to be 0.0021, 0.025 and 0.076 for robust coding, sparse coding and Gaussian basis functions, respectively.

Fig. 7.

The distribution of the variation of neuronal responses for three coding schemes. The variation of the lth neuron is calculated to be 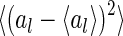, where the symbol 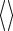denotes the average over all stimuli. The figure shows the distribution of the variances of all neurons

How robust can neural coding be?

We argue that neural codes are constructed to be robust against noise and also show that the overlap between receptive fields critically determines the sensitivity of neural responses. Then, an interesting question is: how robust can neural codes be? This turns out that the robustness of neural codes depends on the statistical property of external inputs to be encoded. Let us consider first an extreme case where a coding system only needs to encode a single object, then we can easily construct a set of non-overlapping basis functions with the minimum sensitivity to represent the object well, e.g., by simply dividing the image space into N non-overlapping pieces. In practice, however, the task the neural system faces is to use a single set of basis functions to encode a large number of objects with varied structures. In such a case, in order to achieve high encoding accuracy, it is important for the basis functions to match the coherent structures of external inputs, and the overlap between basis functions becomes inevitable.4. That is, there is in general a trade-off between encoding accuracy and inferential sensitivity. The situation for natural images seems to be a little bit special, where the external inputs happen to have some salient features which are oriented and localized in the space, and this property enables the neural system to encode natural images well at a cost of relatively low statistical inferential sensitivity.

Conclusion

The present study investigates the robustness of neural codes, an issue of critical importance for our understanding of neural information processing. Based on the view of statistical inference, we show that the overlap between neural receptive fields critically determines the sensitivity of neural responses. We then investigate the optimal basis functions for encoding natural images under the requirement of robust coding, and find that they resemble the receptive fields of simple cells. This provides a new justification for the receptive fields of simple cells. Interestingly, we find that that although both robust and sparse coding predict the same, or similar, optimal basis functions for encoding natural images, the neural response’s variabilities the two scheme are different. This may provide a clue for future research to clarify which one is more biologically plausible. Through investigating the encoding of Chinese characters, we also show that the coding scheme we propose may serve as a general method for feature extraction. This issue will be studied in the future work.

Appendix A: The Fisher information and the performance of LSE

The Fisher information

Since noise is independent Gaussian, the conditional probability of observing data I(x) given a is written as

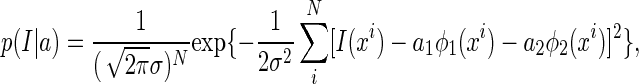17

where N is the number of data points and σ² the noise strength.

The Fisher information matrix F is calculated to be

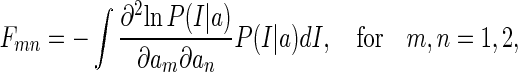18

where F_mn is the element in the mth row and nth column of F.

It is straightforward to check that

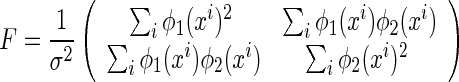19

According to the Cramér-Rao bound, the inverse of the Fisher information defines the lower bound for decoding errors of un-biased estimators. Consider the covariance matrix for estimation errors of an un-biased estimator is given by 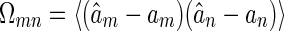. The Cramér-Rao bound states that 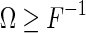, or more exactly, the matrix 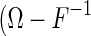) is semi-positive definite. Intuitively, this means that the inverse of the Fisher information quantifies the minimum inferential sensitivity of un-biased estimators.

The asymptotical performance of LSE

It is straightforward to check that for independent Gaussian noise, LSE is equivalent to maximum likelihood inference, i.e., its solution is obtained through maximizing the log likelihood, 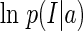(comparing Eq. (3) with Eq. (17)). This implies the solution of LSE satisfies the condition,

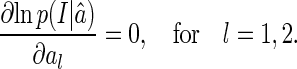20

Consider 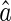is sufficiently close to the true value a, the above equations can be approximated as (the first-order Taylor expansion at the point a)

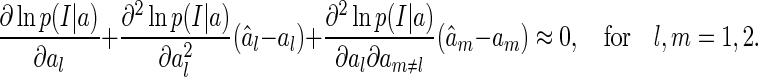21

By using Eq. (17), the above equations can be simplified as

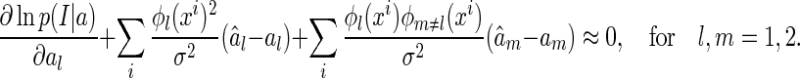22

Since noise are independent Gaussian, we have

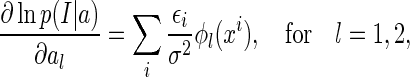23

where 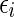, for i = 1,...,N, are independent Gaussian random numbers of zero mean and variance σ².

Combining Eqs. (22) and (23), we obtain the estimation error of LSE. Here, we only show the result for 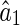(the case for 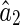is similar), which is given by,

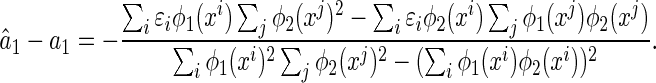24

It is easy to check LSE is un-biased, i.e.,

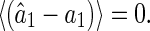25

The variance of 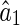is calculated to be

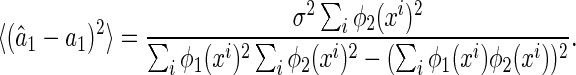26

According to the Central Limiting Theorem, when the number of data points N is sufficiently large, the random variable will satisfy a normal distribution with the variance given by Eq. (26).

The covariance between the estimation errors of the two components can also be calculated, which is given by

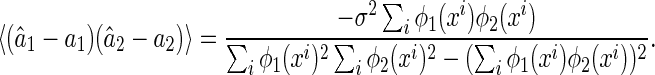27

It is straightforward to check that the covariance matrix of estimation errors of LSE, given by 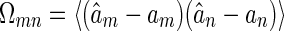, for m,n = 1,2, is the inverse of the Fisher information matrix F, i.e., . This implies LSE is asymptotically efficient.

Appendix B: Optimizing the basis functions of robust coding

The sensitivity measure H(a)

We choose the Renyi’s quadratic entropy to measure the variability of neural responses when natural images are presented, which is given by

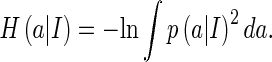28

Here for simplicity, we use a to replace a_l, for .

Suppose we have K sampled values of a which are obtained when K natural images are presented, then according to the Parzen window approximation (with the Gaussian kernel), 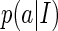can be approximated as

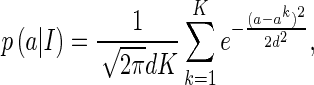29

where 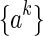, for k = 1,...,K, represents the sampled values, and d is the width of Gaussian kernel.

Note that

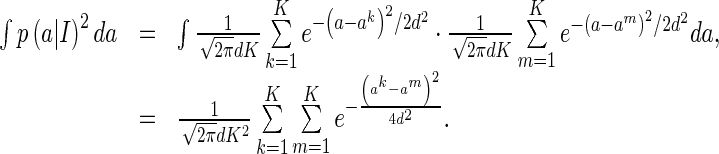30

Thus, we have

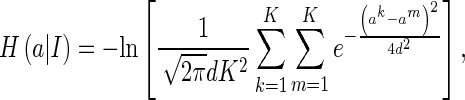31

which fully depends on the sampled values.

The training procedure

Minimizing Eq. (15) is carried out by using the gradient descent method in two alternative steps, namely, (1) updating a while fixing ϕ and (2) updating ϕ while fixing a.

(1) Updating a

To apply the gradient descent method, the key is to calculate the gradient of E with respect to 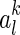, for 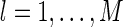and k = 1,...,K.

For the first term in Eq. (15), we have

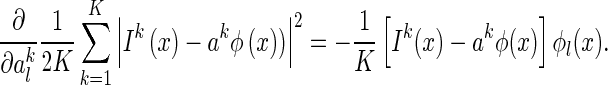32

For the second term, we have

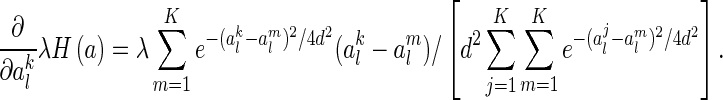33

Combining Eqs. (32) and (33), we obtain the update rule for a:

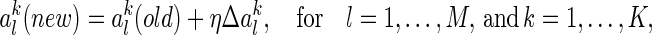34

where η is the learning rate, and 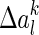is given by

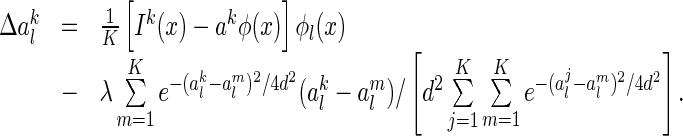35

(2) Updating ϕ

Similarly, the update rule for ϕ is given by

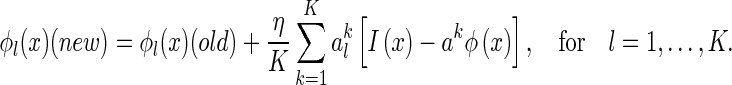36