Skip to main content
PMC home page
Cognitive Neurodynamics logoLink to Cognitive Neurodynamics
. 2007 Apr 12;1(3):237–248. doi: 10.1007/s11571-007-9018-9

Theta phase precession emerges from a hybrid computational model of a CA3 place cell

John L Baker 1,2, James L Olds 2,✉
PMCID: PMC2267674  PMID: 19003516

Abstract

The origins and functional significance of theta phase precession in the hippocampus remain obscure, in part, because of the difficulty of reproducing hippocampal place cell firing in experimental settings where the biophysical underpinnings can be examined in detail. The present study concerns a neurobiologically based computational model of the emergence of theta phase precession in which the responses of a single model CA3 pyramidal cell are examined in the context of stimulation by realistic afferent spike trains including those of place cells in entorhinal cortex, dentate gyrus, and other CA3 pyramidal cells. Spike-timing dependent plasticity in the model CA3 pyramidal cell leads to a spatially correlated associational synaptic drive that subsequently creates a spatially asymmetric expansion of the model cell’s place field. Following an initial training period, theta phase precession can be seen in the firing patterns of the model CA3 pyramidal cell. Through selective manipulations of the model it is possible to decompose theta phase precession in CA3 into the separate contributing factors of inheritance from upstream afferents in the dentate gyrus and entorhinal cortex, the interaction of synaptically controlled increasing afferent drive with phasic inhibition, and the theta phase difference between dentate gyrus granule cell and CA3 pyramidal cell activity. In the context of a single CA3 pyramidal cell, the model shows that each of these factors plays a role in theta phase precession within CA3 and suggests that no one single factor offers a complete explanation of the phenomenon. The model also shows parallels between theta phase encoding and pattern completion within the CA3 autoassociative network.

Electronic supplementary material

The online version of this article (doi:10.1007/s11571-007-9018-9) contains supplementary material, which is available to authorized users.

Keywords: Theta rhythm, Hippocampus, Pyramidal cell, Computer simulation, Learning and memory

Introduction

The discovery of place cells in the rat hippocampus by O’Keefe and Dostrovsky (1971) demonstrated a direct linkage between the activity of single cells in the mammalian brain and high-level cognitive processes involving spatial orientation and learning. Experimentally, each place cell fires over a spatially limited area in the animal’s environment, the place field. Place cells are found in the CA1 and CA3 portions of the hippocampus, and similar spatially tuned cells are found as well in the entorhinal cortex and dentate gyrus (Muller 1996; Best et al. 2001). Simultaneous experimental recordings made from only a few CA1 place cells have allowed accurate reconstruction of an animal’s movements over time (Wilson and McNaughton 1993). CA3 place cells have place fields without any apparent topographical relationship between the place field location in the animal’s environment and place cell location in the hippocampus (Muller 1996) with only a small proportion of CA3 place cells active in any given spatial context (Vazdarjanova and Guzowski 2004). Because the hippocampus also plays a key role in memory formation (Gluck and Myers 2001), it seems plausible that a detailed mechanistic understanding of place field formation might shed light on other aspects of mnemonic function as well.

The hippocampus has been extensively studied by neuroscientists. An early theory of memory (Marr 1971) identified the extensive recurrent connection pattern among pyramidal cells in CA3 as a putative locus for simple memories, that is, uncategorized sensory patterns. More sophisticated formulations of this theory identify CA3 as an autoassociative memory system relying on sparse representations and attractor states to store and retrieve memories even when prompting cues are noisy or incomplete (Rolls and Treeves 1998). Such a system can be extended to the storage of information about multiple independent spatial contexts in the form of multichart attractor maps (Samsonovich and McNaughton 1997).

CA3 place cell firing has been studied in the context of computational models based on biophysically motivated neuronal network simulations (Wallenstein and Hasselmo 1997; Káli and Dayan 2000). A limitation in existing work is that it is difficult to relate the extensive collections of in vivo and in vitro experimental findings with assumptions in the various models. In vitro studies have yielded results concerning the physiology of hippocampal cells and the neuronal networks they form (Johnston and Amaral 1998), while in vivo studies have been able to show the effects of spatial learning but still have limited ability to selectively probe the biophysical mechanisms involved (Muller 1996; Best et al. 2001). It is suggested here that a computational model based on detailed neurophysiology could offer a useful link for connecting in vitro and in vivo experimental results in the hippocampus.

Theta phase precession is an example of a phenomenon that is difficult to interpret without a model of some form. Rhythmic field potentials in the 4–12 Hz theta frequency range can be found in the hippocampus during exploratory locomotion and rapid eye movement (REM) sleep (Buzsáki 2002). Preferred firing times of many cell types in the hippocampus, including place cells, are phase-locked to this theta rhythm. A surprising finding in this regard is the phenomenon of theta phase precession, in which place cell firing comes progressively earlier in the theta cycle as the animal moves through the cell’s place field (O’Keefe and Recce 1993; Skaggs et al. 1996). A number of different proposals have been made as to the origins of theta phase precession. These have been reviewed by Wagatsuma and Yamaguchi (2007). Briefly, the proposals include an interference effect among oscillators of different frequencies (O’Keefe and Recce 1993; Bose et al. 2001; Bose and Recce 2001), an encoding of afferent excitation resulting from out-of-phase dendritic excitation and somatic inhibition (Kamondi et al. 1998; Harris et al. 2002; Mehta et al. 2002), inheritance of phase precession present in afferent cell groups (Skaggs et al. 1996; Yamaguchi 2003; Jones and Wilson 2005), an independent encoding of salient behavioral or sensory information (Huxter et al. 2003), and, in CA3, the effect of activity spread through associative synaptic connections (Jensen and Lisman 1996; Tsodyks et al. 1996; Wallenstein and Hasselmo 1997). Because there can be multiple interacting sources of theta precession, quantitative modeling should facilitate examination of the various contributing factors.

Although the computational model used in the present study was not specifically created with the intention of studying theta phase precession, it has provided a platform for addressing the question of theta phase precession within CA3. Within this context, a plausible question to ask is whether, in the model, theta phase precession will emerge in a simulated CA3 pyramidal cell and under what circumstances. By using manipulations that could be performed only in a model, the various sources of theta phase precession can be selectively suppressed showing the significance of each individually. In addition to causal factors most commonly proposed, the current model suggests that the theta phase offset between dentate gyrus activity and corresponding activity in CA3 place cells provides a significant contribution to theta phase precession within CA3. The model also suggests that theta phase precession may have a functional interpretation in non-spatial contexts.

Methods

Computational model

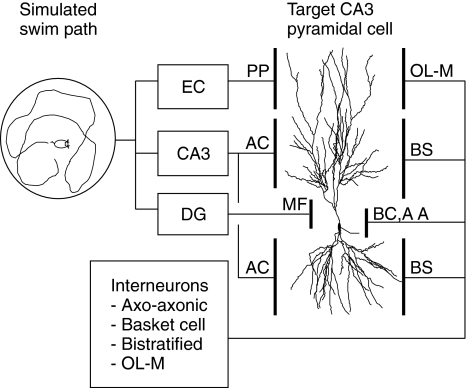
The present study used a model intermediate in approach between a detailed biophysical simulation of the entire hippocampus and a theoretical analysis of populations of idealized cells. The current work aimed to reproduce the responses of a single “target” CA3 pyramidal cell by modeling the cell at an anatomically derived, highly detailed level. At the same time, the cell model was provided with neurophysiologically realistic afferent spike trains derived from the movements of a simulated mouse (Fig. 1). Neurons that would normally be afferent to the target cell throughout the hippocampus are represented in the model (Table 1; Amaral et al. 1990).

Fig. 1.

Fig. 1

Open in a new tab

General model schematic showing afferent cell groups and target cell relationships. Place cell firing is determined by the location of a simulated animal moving within a maze. Afferent cell groups are found in the entorhinal cortex (EC), which provides perforant path (PP) inputs, CA3 peer pyramidal cells, which provide associational connection (AC) inputs, and dentate gyrus (DG) granule cells, which provide mossy fiber (MF) inputs. Interneurons are divided into four separate population subgroups: axo-axonic cells (AA), basket cells (BC), bistratified cells (BS), and cells with soma in the stratum oriens and axons in strata lacunosum-moleculare (OL-M)

Table 1.

Afferent cell group network parameters

Afferent cell group Group pop. size Active freq. (Hz) Peak theta phase TPP rate (°/cm) Target cell synapses (typical) Synapse laminar extent (μm) Synapse receptor types
EC II–III 2,000 2 5° 10 1,348 350–500 apical AMPA, NMDA
DG 4,000 1 296° 10 43 0–100 apical AMPA, NMDA
CA3 Peer 12,000 2 19° 10 5,362 100–350 apical AMPA, NMDA
4,622 0–300 basal AMPA, NMDA
Axo-axonic 100 17 185° 0 200 IS GABAA
Basket Cell 100 8 271° 0 200 soma GABAA
Bistratified 500 6 359° 0 2,565 all dendrites GABAA, GABAB
OL-M 100 5 19° 0 335 350–500 apical GABAAS, GABAB
Open in a new tab

Laminar extent is measured from the target cell soma in apical or basal directions. Active frequency is approximate, depending on maze and path. The number of target cells synapses varies based on random assignments. Abbreviations: theta phase precession (TPP), modulation (mod), initial segment (IS), GABAA slow (GABAAS)

The target cell is a compartmental model (Segev and Burke 1998) based on a previously published description of a morphologically reconstructed CA3b pyramidal cell (Turner et al. 1995). The current model represented the CA3 pyramidal cell and a portion of its axon using 368 discrete spatial compartments. The model incorporated a variety of ion channel models that were adjusted to conform with recent experimental data. The target cell model also included models of excitatory glutamatergic synapses containing α-amino-3-hydroxy-5-methyl-4-isoxalone propionic acid (AMPA) and N-methyl-d-aspartate (NMDA) receptors as well as inhibitory synapses with types A and B γ-aminobutyric acid (GABA) receptors. Neuromodulatory affects of acetylcholine (ACh) were represented in the target cell model.

Synaptic plasticity in glutamatergic synapses was modeled using a Markov model formulation that phenomenologically describes spike-timing dependent plasticity (STDP) with characteristics found in hippocampal pyramidal cells (Debanne et al. 1998; Bi and Poo 1998) and other cells showing similar synaptic plasticity properties (Sjöström et al. 2001). Short-term plasticity was modeled using a previously published model of spike-train dependent facilitation and depression in glutamatergic synapses (Dittman et al. 2000).

Afferent spike trains were generated using phenomenological models of place cells in the entorhinal cortex (EC), dentate gyrus (DG), and peer cells in CA3 with associated synaptic connections through the perforant path (PP), mossy fibers (MF), and associational connections (AC), respectively. Interneuron spike trains were derived from phenomenological models based on recent experimental measurements of interneuron activity in CA1 (Klausberger et al. 2003, 2004) under the assumption that a similar pattern holds in CA3. Cell firing in each afferent place cell population are also phase-locked to the theta rhythm with properties dependent on the population group (Fox et al. 1986; Stewart et al. 1992; Skaggs et al. 1996).

Medial EC place cells have previously been characterized as having large, relatively unselective place fields (Quirk et al. 1992), but more recent measurements of dorsal EC layer II and III cells show more spatially selective place cells with multiple activity peaks arranged in a grid-like pattern (Fyhn et al. 2004; Hafting et al. 2005). These cells have also been shown to exhibit theta phase precession (Hafting et al. 2006). For the current model, EC place cells are treated as having place fields and theta phase precession similar to those of CA3 pyramidal cells. Because of the limited range of motion simulated in the current model, multiple activity peaks would have little effect and are not included in the model.

Supplementary materials contain a more detailed description of the computational model and its rationale. Results of simulations validating conformance of the model to basic properties of CA3 pyramidal cell electrophysiology and synaptic plasticity are also in the supplementary materials.

Data analysis

During simulations, all afferent cell spikes as well as spikes of the target cell were recorded in external files. As needed, membrane potential and calcium concentration were recorded from each compartment of the target cell. Special events including local dendritic spiking were also separately recorded. Data analysis was subsequently performed off-line following the simulation.

Firing rates were computed using a spatial grid made up of 5 cm square bins. Simulated mouse position was recorded every 25 ms of simulated time and correlated with simultaneous firing activities. Bins that were visited for less than 0.5 s were not included in firing rate estimates. Otherwise, the firing rate in the spatial bin was estimated as the total number of spikes occurring within the bin divided by the simulated time within the bin.

Total afferent synaptic drive provides a measure of the spatial pattern imposed on synaptic weights through the process of synaptic plasticity. It is defined as

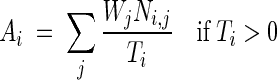graphic file with name M1.gif 1

where Ai is the total afferent synaptic drive at spatial bin i, Ni,j is the number of spikes generated by afferent cell j while the simulated mouse is in spatial bin i, Ti is the occupancy time in spatial bin i, and Wj is the synaptic weight of the synapse associated with afferent cell j. Total afferent synaptic drive was computed separately for each group of afferent cells whose synapses exhibit synaptic plasticity, that is, EC and peer CA3 pyramidal cells, using the same spatial grid used for computing firing rates.

Theta phase precession was computed along a straight-line path parallel to the lower boundary of a square maze. Theta phase for each target cell spike was initially determined on the basis of a theta cycle of 125 ms, the period of an 8 Hz theta frequency. This initial theta phase was then “unwrapped” by performing a circular fit using a “barber pole” model of the form assumed by O’Keefe and Recce (1993):

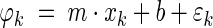graphic file with name M2.gif 2

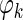where Inline graphic is the theta phase of spike k, xk is the location at which the spike occurred, m is the estimated phase precession rate, b is the phase at location x = 0, and εk is a random phase error. Values of m and b are found that yield a zero circular mean for the εk while minimizing the circular variance (Fisher 1995). A range of −30 to +30°/cm was exhaustively searched in determining an optimal value of m. The circular model was converted to a linear model by adjusting values of the 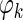Inline graphic by integer multiples of 360° such that error variance in the corresponding linear model was minimized. A standard linear regression was then used to refine the values of m and b and to derive the sample correlation coefficient and t-statistic.

Student’s t-test was used for testing statistical significance of theta phase precession. Tests for differences between samples were performed using a two-sample Wilcoxon rank sum test.

Implementation

The computational model was implemented in C++ (Microsoft, Redmond, WA) as a portable generalized object-oriented framework for defining neuronal models. Random number generation was performed using the Mersenne Twister algorithm of Matsumoto and Nishimura (1998). Numerical integration was performed using an adaptive semi-implicit form of the Crank-Nicolson method (Mascagni and Sherman 1998) in combination with Richardson extrapolation (Press et al. 1992). Data analysis and visualization were performed using MATLAB (The MathWorks, Natick, MA) and R (The R Foundation for Statistical Computing, http://www.r-project.org).

Results

Afferent phenomenological place cell spike trains

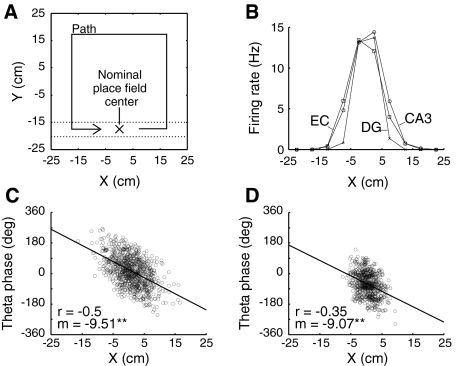
The “maze” used for the simulations is shown here in Fig. 3A along with the path followed by a simulated mouse. A wall-following algorithm maintains an approximate simulated distance of 7.5 cm from the maze boundary. A single afferent DG granule cell with a place field center location of (0, −17.5) was used as a “teacher cell” to establish the nominal place field center of the emergent place field in the target cell. The teacher cell is provided with sufficiently large synaptic efficacy to independently fire the target CA3 pyramidal cell, as has found to be the case for in vivo preparations (Henze et al. 2002).

Fig. 3.

Fig. 3

Open in a new tab

Phenomenological afferent place cell model. (A) Simulated mouse movements in a square maze. The simulated mouse maintains a fixed distance from the maze boundary moving in a counterclockwise direction at a speed of 10 cm/s. Relevant spikes occur when the simulated mouse is in the region between the dotted lines. The nominal target place field center is located at maze coordinates (0, −17.5). (B) Firing rate by location along the X coordinate for representative phenomenological afferent EC, CA3, and DG place cells whose place fields are located near the target place field center. Rates are determined over a 9-min interval. (C) Spikes generated by the representative CA3 place cell. Theta phase is “unwrapped” (see Methods) to show phase precession. The sample correlation coefficient (r) and precession rate in degrees/cm (m) are determined from a linear fit. The representative EC place field has similar properties. Circular mean of spike theta phase is 17° for the cell shown. (D) Theta phase precession in the representative DG place cell. Note reduced place field size and earlier firing in the theta phase compared with the CA3 place cell. Circular mean of spike theta phase is −62° or, equivalently, 298° for the cell shown

Figure 3B shows firing rates of representative peer CA3, EC, and DG place cells with place fields centered near (0, −17.5). Panels C and D show the pattern of theta phase precession for the corresponding CA3 and DG cells. The DG cell shown is the teacher cell. DG cells afferent to the target cell, other than the teacher cell, have very low-firing rates throughout the simulation and have a minor effect on target cell firing. Note that the mean theta phase of DG cell activity occurs earlier in the theta cycle than mean activity of the CA3 population whole (Fox et al. 1986), as can be seen by comparing the absolute theta phase of firing of the respective cells in Fig. 3C and D as well as the histograms in Fig. 2. In the phenomenological model of place cell firing, theta phase precession in afferent place cells occurs at a fixed rate of 10°/cm as found experimentally in rat CA3 complex-spike (presumed pyramidal) cells (O’Keefe and Recce 1993). Random variability in spike generation accounts for the differences between this value and the estimated values shown in Fig. 3. The representative model EC place cell has similar place field and theta phase precession to that of a CA3 place cell and is not shown.

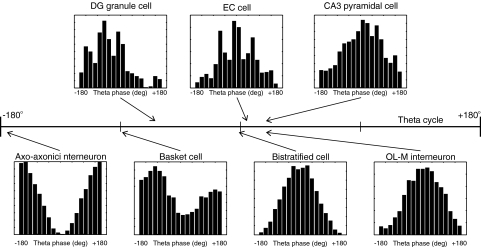
Fig. 2.

Fig. 2

Open in a new tab

Theta phase of phenomenological afferent cell activity. Activities of representative model cells from each population group of afferent place cells and interneurons are summarized as theta phase firing histograms. Arrows indicated the theta phase (−180° to 180°) at which the corresponding population activity is maximal. For basket cell interneurons, maximal and minimal activity theta phase are −89° and 0°, respectively. For other cell populations, minimal activity is offset 180° from the maximal activity theta phase

Emergence of target cell place field and theta phase precession

A simulated training period of nine minutes (0–540 s) was used for the initial formation of the target cell place field. Synaptic weights for AC and PP synapses were set to zero at the beginning of the simulation and then were modified according to STDP rules during the training period. For the first 6 min of the training interval, the simulated extracellular ACh concentration was initially set to a value of 50 μM and then decreased linearly to 20 μM at the end of the 6-min period. This decrease corresponds to a reported novelty response in which ACh is elevated when an animal initially explores a novel environment (Giovannini et al. 2001). Following the training period, synaptic weights were frozen at their then current values, and an additional simulated period of 3 min (540–720 s) was used to probe target cell firing rates and theta phase precession. In the final simulated 3 min (720–900 s), the DG teacher cell was rendered inactive, and target cell firing arose solely in response to stimulation through AC and PP synapses. Pattern completion in the target cell was shown by spatially relevant activity during this final period.

As shown in Fig. 4A, early in the training period when AC and PP synaptic weights had low values, target cell firing was reduced compared with rates attained during the later firing rate probe interval. Following the training interval, firing rates increased and the place field center shifted opposite the direction of travel and became spatially asymmetric such that as the simulated mouse approached the place field, rates were higher than when the place field was exited. This effect is similar to one found in recordings of CA1 place cells (Mehta et al. 1997, 2000). In Fig. 4A, a pronounced shift in the place field center but greater spatial symmetry can also be seen in the pattern completion probe interval. Figure 4B shows the contribution of associational CA3 and EC synapses to target cell firing measured in terms of total weighted afferent firing rates. Afferent synaptic drive from CA3 and EC was more spatially symmetric than the overall firing pattern of the target cell and, unlike the afferent DG synaptic drive, was displaced opposite the direction of motion. In this instance, spatial asymmetry in target cell firing can been seen as primarily a consequence of a spatial displacement in different afferent synaptic drives.

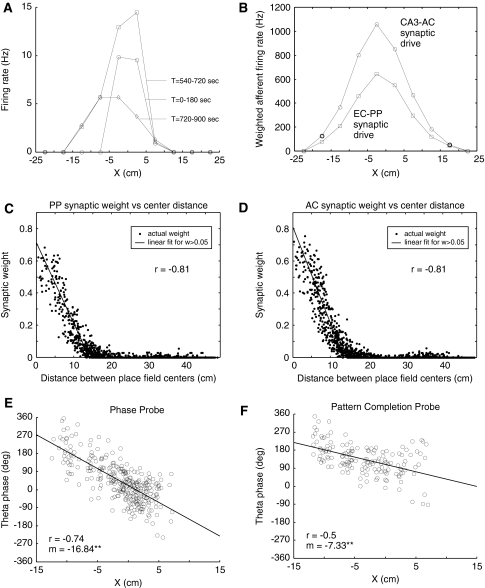
Fig. 4.

Fig. 4

Open in a new tab

Simulated place field and theta phase precession emergence. Synaptic weights for perforant path (PP) and associational connection (AC) synapses are allowed to vary based on plasticity rules during the first 9 min (0–540 s) of the simulated experiment after which weights are frozen and an additional 3 min (540–720 s) are simulated to probe the target cell place field firing pattern and theta phase. In the final 3-min interval (720–900 s), dentate gyrus (DG) input is suppressed to probe pattern completion responses by the target cell. Representative results are shown. (A) Target cell place field firing rates by location along the X coordinate axis. Firing rates are determined in 5 cm bins. Rates in the 0–180 s interval primarily reflect DG input because other synaptic weights have values near zero during this interval. (B) Total weighted afferent synaptic drive (see Methods) as of the end of the training interval for PP and AC synapses associated with afferent place cells in EC and CA3, respectively. (C, D) Synapse weights for PP and AC synapses by the distance between afferent cell place field centers and the nominal target place field center. Synapse weights for inactive afferent place cells are not shown. The sample correlation coefficient (r) is derived from a linear fit with distance as the response variable and near-zero synaptic weights removed from the sample. (E, F) Target cell firing theta phase by location during the phase and rate probe interval (540–720 s) and pattern completion probe interval (720–900 s), respectively. A circular “unwrapping” process is used to determine the theta phase of target cell spikes after which a sample correlation coefficient (r) and precession rate (m) in degrees/cm are derived using a linear regression (see Methods). ** indicates statistically significant non-zero theta phase precession (P < 0.01)

Figure 4C and D show the spatial pattern of synaptic weights at the end of the training interval. Both CA3 AC and EC PP synapses show distance-correlated synaptic weights indicating that STDP provided an effective learning rule for creating a pattern of synaptic weights leading to spatially relevant pattern completion in the target cell. In general, weights attained by AC and PP synapses in the model increase over the 9-min training interval without reaching equilibrium values (data not shown). Maximum synaptic weights would ultimately be constrained by limits imposed by assumptions of the STDP model. For CA3 pyramidal cell associational synapses, simultaneous pre- and postsynaptic spike pairings lead to LTD rather than LTP (Debanne et al. 1998), suggesting that locally generated dendritic spikes could provide a constraint on maximum synaptic weights. Note that the spatial symmetry of the weighted afferent synaptic drive and the closeness of the fit between synaptic weight and absolute distance between place field centers both suggest that synaptic weights would not develop in the asymmetric fashion sometimes assumed. That is to say, the efficacy of synaptic connections between pairs of CA3 place cells with place fields adjacent along a path could be both non-zero and of comparable magnitude.

Figure 4E and F examines theta phase precession in target cell firing during the rate and phase probe (540–720 s), and during the pattern completion probe (720–900 s). Theta phase precession was evident in each of these intervals, though to different degrees. Target cell firing circular mean theta phase shifted from 18° in the phase probe interval to 136° in the pattern completion probe interval, indicating that dentate gyrus input played a significant role in both the rate of theta phase precession and the mean phase of target cell firing. The theta phase at which target cell firing is initiated as the place field is entered can be seen as being approximately the same in the phase probe and the pattern completion probe, indicating that this early firing is independent of activity in the dentate gyrus teacher cell associated with the target CA3 pyramidal cell.

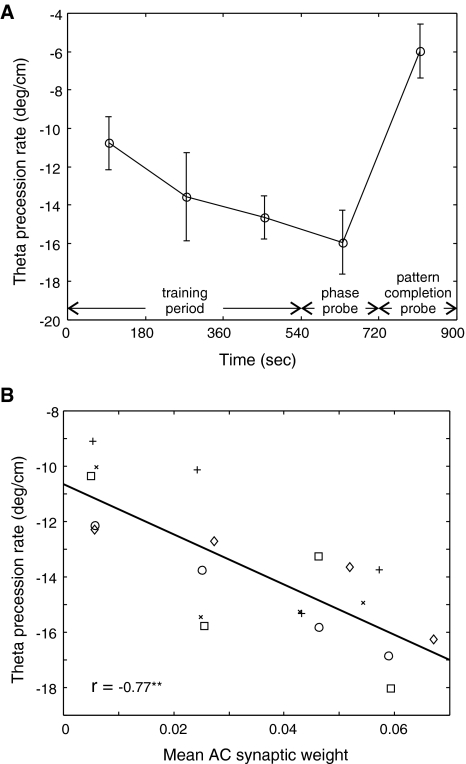
In simulating random processes, an algorithm was used to generate pseudo-random numbers. The stream of pseudo-random numbers generated in each simulation run was controlled by initial seed values supplied to the random number generator as a parameter of the test. To address the question of whether a specific random number stream influenced the results obtained, different seed values were used to produce different streams of random numbers. These seed values themselves were selected from consecutive entries in a previously published table of random values (Weast 1964). Figure 5A shows the effect of using five different random number seeds on the rate of theta phase precession that emerges in the current model. The phase precession rate shown is the mean of the rates over comparable intervals generated when different random number seeds were used. Although the different random number seeds clearly have an effect, the overall trends emergent in the model appear robust.

Fig. 5.

Fig. 5

Open in a new tab

Evolution of theta phase precession over time. Afferent spike trains and neurotransmitter release are modeled using a random number generator that is seeded to produce repeatable results. Multiple simulations with different random number seed values were used to create additional results and the resulting theta phase precession rates, including those shown in Fig. 4, are summarized here. (A) Mean theta phase precession rates found are shown with standard error of measurement as indicated (N = 5). (B) Mean theta phase precession rate is fitted as a function of mean AC weight in the corresponding time period with individual data points shown in a scatter plot

As a necessary computational simplification, the current model discounts the effects of attractor dynamics within the CA3 network. For this and a variety of other reasons, the current model cannot provide a reliable estimate of the absolute rate at which theta phase precession would develop over time. Even so, the different precession rates derived from different test runs provide a way to test the relationship between changes in synaptic plasticity and the rate of emergence of theta phase precession in target cell firing.

Mean AC synaptic weight was used as a measure of the change in synaptic weights overall. A mean weight value was derived at the end of the second minute in each of the 3 min periods in the training and phase probe intervals. The theta phase precession rate found in the corresponding time period was then fit as a dependent variable of the mean synaptic weight. As shown in Fig. 5B, there is a strong relationship between synaptic weights and theta phase precession. However, even with a mean synaptic weight value of zero, corresponding to all silent synapses, these results suggest that theta phase precession would still be present in the target CA3 pyramidal cell, as might be expected on the basis of inheritance of theta phase precession from dentate gyrus input.

Contributing factors in theta phase precession

Within the current model, only a single CA3 pyramidal cell is simulated in detail, and because of this, theta phase precession is assumed a priori as a property of afferent DG, EC, and CA3 place cells. To test whether the target cell’s theta phase precession is more than simply inherited from its afferents, theta phase precession in afferent place cells was suppressed without otherwise altering the spatial firing properties of afferent place cells. This is a manipulation that can be accomplished in the model, but for which there are no available experimental counterparts. An emergence of theta phase precession in the target cell under these conditions indicates that such precession can arise in CA3 independent of any inheritance of theta phase precession from afferents and can arise as an independent network property within CA3.

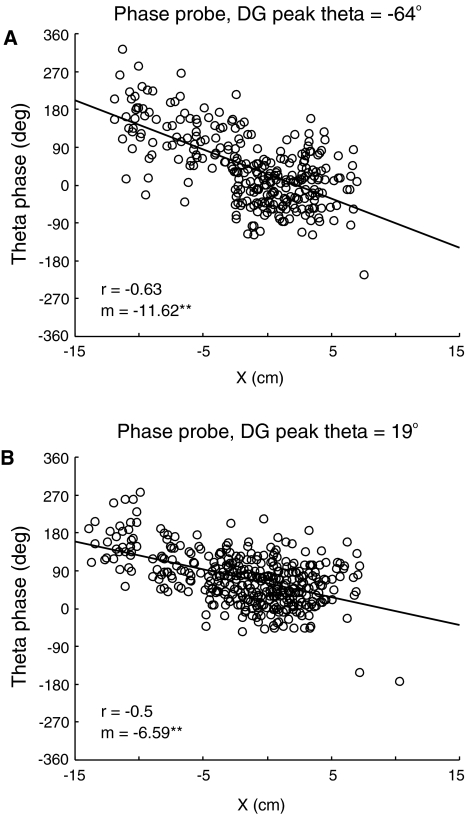
In addition to validating the assumptions of the model, suppressing afferent theta phase precession allows a selective examination of the sources of theta phase precession in the simulated target cell. Figure 6A shows the pattern of theta phase precession in target cell firing that emerged when all afferent theta phase precession was suppressed in the model. There was strong afferent synaptic drive during the phase probe interval (540–720 s) and robust theta phase precession is evident in target cell firing, as would be expected from the combination of increasing afferent excitation and phasic inhibition. Note, however, that because multiple inhibitory cell populations are included in the model and because these populations are active at different points in the theta cycle, the theta phase at which target cell firing was initiated on entry to the place field does not coincide with minimal somatic inhibition and represents a more complex interaction than might otherwise be expected.

Fig. 6.

Fig. 6

Open in a new tab

Effects of afferent theta phase on target cell theta phase precession. Representative results are shown using theta phase “unwrapping” of target cell spikes as in Fig. 4E. (A) Target cell firing during a phase probe interval (540–720 s) following a training interval (0–540 s). During both intervals, afferent place cell theta phase precession is suppressed by setting the theta phase precession rates (ρtpp) to zero for all afferent phenomenological place cells. Theta phase of simulated DG granule cell activity is unchanged from the pattern shown in Fig. 3D. (B) Target cell firing during a phase probe interval (540–720 s) in which afferent theta phase precession remains suppressed and the theta phase of peak DG granule cell firing is altered to coincide with peak CA3 pyramidal cell activity. Spatial properties of afferent place cells and synaptic connections with the target cell are otherwise unaffected in this simulation

DG population activity peaks prior to corresponding activity in CA3. The significance of this relationship for theta phase precession can be seen by comparing the pattern of target cell firing in Fig. 6A and B. In Fig. 6B, the relationship has been changed such that peak activity of the DG teacher cell coincides with that of the CA3 place cell population without otherwise altering the spatial firing properties of afferent place cells or altering the pattern of synaptic connections with the target cell. As in Fig. 6A, all afferent theta phase precession remains suppressed. With this change, peak afferent excitatory population activities are nearly coincident, as might be assumed in a model that considered only aggregate synaptic drive as a source of theta phase precession. The change in DG activity phase means that DG inputs to the target cell are moved from a period of high somatic inhibition to one of lower somatic inhibition. Compared with activity shown in Fig. 6A, peak place field firing rate has increased slightly from 13.7 Hz to 14.6 Hz, and the circular mean theta phase of target cell firing changed from 22° to 69°, indicating that the target cell no longer fires in the same part of the theta cycle as the afferent CA3 place cell population as a whole. Although the spatial extent of the place field in Fig. 6A and B are comparable, the total phase shift over the extent of the field is reduced when the phase of peak DG activity is altered in this fashion.

Simulations using different random number seeds (N = 5) were used to evaluate the change in both theta phase precession rate and mean theta phase of target cell firing associated with suppressing afferent theta phase precession and with changing DG peak activity theta phase. Suppressing theta phase precession in afferents resulted in a change in the average magnitude of the theta phase precession rate by −6.2 ± 1.7°/cm and a change in average circular mean theta phase of 12.0 ± 6.0°. Both changes are statistically significant (P < 0.05). Further changing the theta phase of peak DG activity to 19° resulted in a change of −4.5 ± 1.0°/cm in the average theta phase precession rate and of 40.1 ± 8.2 degrees in the circular mean theta phase, both of which are statistically significant (P < 0.01). As compared with the normal case illustrated in Fig. 4, when afferent theta phase precession is suppressed, the precession rate near the center of the place field, that is, for X between −5 and 5 cm, changes by −8.30 ± 3.77°/cm, indicating that inheritance of theta phase precession is significant in this region (P < 0.01). Changes in average peak firing rate were not statistically significant across these samples.

Discussion

Results from simulations show that for a model CA3 pyramidal cell, theta phase precession of firing can emerge from the interaction of synaptic plasticity and network properties of CA3 under the assumptions of the hybrid biophysical–phenomenological model used here. Theta phase precession arises in the simulated target CA3 pyramidal cell regardless of whether or not theta phase precession is present in the firing of afferent dentate gyrus cells, entorhinal cortex cells, or even other CA3 pyramidal cells. Because the target cell is similar to other pyramidal cells found in CA3, the emergence of theta phase precession in this cell is indicative of the ability of theta phase precession to arise autonomously throughout CA3.

In spite of the apparent complexity of the model, the origins of theta phase precession within it can be described qualitatively. The description is generally consistent with prior models of theta phase precession with the addition of a factor associated with early theta phase activity in the dentate gyrus. Figures 4 and 6 together show how different types of afferent stimulation affect target cell firing within the theta cycle, as follows:

  1. As the simulated mouse approaches the place field, late-phase target cell firing results from associational and perforant path synaptic drive conditioned by spatially correlated synaptic weights in combination with phasic inhibition. Dentate gyrus input is not initially a factor because of the smaller size of the corresponding dentate gyrus place field. Of particular note, firing at this stage is the same as that seen during pattern completion, as suggested in an earlier biophysically based model (Wallenstein and Hasselmo 1997).

  2. Excitatory synaptic drive increases as the mouse further approaches the place field center. This results in a progressively earlier target cell firing, still with minimal contribution from dentate gyrus input, consistent with models that emphasize the effect of increasing excitatory synaptic drive (Kamondi et al. 1998; Harris et al. 2002; Mehta et al. 2002). At the same time, theta phase precession in afferent spike trains, both from entorhinal cortex and peer CA3 pyramidal cells, contributes to progressively earlier target cell firing, consistent with models that emphasize this source (Skaggs et al 1996; Yamaguchi 2003; Jones and Wilson 2005). In this stage the primary source of afferent synaptic drive and consequently inherited theta phase precession in the current model arises from peer CA3 pyramidal cells rather than directly from EC or DG inputs.

  3. Dentate gyrus place cell activity increases near the center of the place field, giving rise to strong excitatory stimulation of the target cell earlier in the theta cycle. This results in a location-dependent shift in target cell firing to earlier in the theta cycle and a somewhat more random theta phase of target cell firing in this region because of the limited number of active dentate gyrus granule cells afferent to the target CA3 place cell. Inheritance of afferent theta phase precession from DG inputs also plays a significant role in this stage.

Although the current model does not specifically address theta phase precession in CA1 or other brain regions, the sequence of events described above may have parallels in CA1, though perhaps with somewhat different mechanisms involved. A detailed model including CA1 would be needed for a more complete and detailed analysis. For example, the current model might be extended to include a target CA1 pyramidal cell. Interconnections among EC, DG, CA3, CA2, CA1, and other cell populations associated with the hippocampus, however, suggest that theta phase precession may be a widespread system property without a single locus of origin.

The proposed relationship between pattern completion and theta phase precession may yield insights into the independence of theta phase precession from firing rate that has been observed experimentally (Huxter et al. 2003; O’Keefe and Burgess 2005). Furthermore, theta phase precession may have a more general role outside the phenomenon as currently understood. Firing late in the theta cycle as the simulated mouse approaches the place field can be interpreted either as sequence learning or as pattern completion. Pattern completion within an autoassociative network in the context of rhythmic activity such as the theta rhythm would result in some cells firing earlier and others later, with firing phase encoding a “certainty” factor allowing elements that are inferred via pattern completion to be distinguished from others. When paired with phase-coupled modulation of synaptic plasticity, something not included in the current model for lack of supporting experimental data, this could serve to resolve a potential conflict previously identified via theoretical analysis that arises when training of the CA3 network overlaps with retrieval (O’Reilly and McClelland 1994; Hasselmo et al. 1995; Hasselmo 2005). Such a “certainty” encoding could also play a role in spatial navigation downstream of CA3.

A primary component of the current model is the biophysical model of the target pyramidal cell. The target cell model reproduced key properties needed to simulate place cell responses. These include passive properties, bursting patterns, and active dendrites. Passive properties of the model cell resulted in a high input resistance and a relatively long time constant, properties needed for synaptic integration over the time frame of the theta cycle. Ion channels included in cell model dendrites led to small enhancements to distal EPSPs that result in rough parity between proximal and distal dendrites. Long-term synaptic plasticity was modeled based on properties of NMDA receptors and was dependent upon postsynaptic depolarization at the site of the synapse as a predicate for plasticity changes. Active backpropagation of somatic action potentials by a common set of dendritic ion channels that also scale EPSPs thus forms an essential component of synaptic plasticity.

While the current model is based on experimental findings, there are numerous areas in which approximations and estimations were required in the formulation of the model because of limitations in the currently available experimental data. Of particular interest, the model of spike-timing synaptic plasticity used here is limited in that it does not attempt to fully reflect underlying biochemical pathways that are still under active investigation. The quantitative nature of the current model, however, lends itself to successive refinements in the model as new experimental findings become available.

A realistic bottom-up biophysical model of a single CA3 pyramidal cell in combination with phenomenological models of afferent cell spike patterns results in autonomously generated theta phase precession as an emergent property. In the model, theta phase precession is caused within a theta cycle by the overlap of early CA3 pyramidal cell firing resulting from strong dentate gyrus stimulation and later firing resulting from pattern completion firing stimulated primarily by associational connections from other CA3 pyramidal cells. Theta phase precession may be at least partially an intrinsic property of CA3 and may be functionally related to an encoding of “certainty” as well as location. Based on the generality of the conditions needed for emergence, the current model suggests that theta phase precession or similar phase-related encoding might also be found in brain regions outside the hippocampus.

Electronic supplementary material

Below is the link to the electronic supplementary material.

(PDF 721 kb) (721.8KB, pdf)

Acknowledgments

We would like to thank Professors Kim Blackwell, Giorgio Ascoli, and James Gentle for the advice they generously provided during the conduct of this research. We also gratefully acknowledge the suggestions of multiple anonymous reviewers. JLB was supported by a fellowship from the Krasnow Institute of Advanced Study.

Footnotes

Electronic supplementary material

The online version of this article (doi:10.1007/s11571-007-9018-9) contains supplementary material, which is available to authorized users.

Contributor Information

John L. Baker, Email: jbakerb@gmu.edu

James L. Olds, Email: jolds@gmu.edu

References

  1. Amaral DG, Ishizuka N, Claiborne B (1990) Neurons, numbers and the hippocampal network. Prog Brain Res 83:1–11 [DOI] [PubMed]
  2. Best PJ, White AM, Minai A (2001) Spatial processing in the brain: the activity of hippocampal place cells. Annu Rev Neurosci 24:459–486 [DOI] [PubMed]
  3. Bi GQ, Poo MM (1998) Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci 18:10464–10472 [DOI] [PMC free article] [PubMed]
  4. Bose A, Booth V, Recce M (2001) A temporal mechanism for generating the phase precession of hippocampal place cells. J Comput Neurosci 5:9–30 [DOI] [PubMed]
  5. Bose A, Reece M (2001) Phase precession and phase-locking of hippocampal pyramidal cells. Hippocampus 11:204–215 [DOI] [PubMed]
  6. Buzsáki G (2002) Theta oscillations in the hippocampus. Neuron 33:325–340 [DOI] [PubMed]
  7. Debanne D, Gähwiler BH, Thompson SM (1998) Long-term synaptic plasticity between pairs of individual CA3 pyramidal cells in rat hippocampal slice cultures. J Physiol 507:237–247 [DOI] [PMC free article] [PubMed]
  8. Dittman JS, Kreitzer AC, Regehr WG (2000). Interplay between facilitation, depression, and residual calcium at three presynaptic terminals. J Neurosci 20:1374–1385 [DOI] [PMC free article] [PubMed]
  9. Fisher NI (1995) Statistical analysis of circular data. Cambridge University Press, New York
  10. Fox SE, Wolfson S, Ranck JB Jr (1986) Hippocampal theta rhythm and firing of neurons in walking and urethane anesthetized rats. Exp Brain Res 62:495–508 [DOI] [PubMed]
  11. Fyhn M, Molden S, Witter MP, Moser EI, Moser MB (2004) Spatial representation in the entorhinal cortex. Science 305:1258–1264 [DOI] [PubMed]
  12. Giovannini MG, Rakovska A, Benton RS, Pazzagli M, Bianchi L, Pepeu G (2001) Effects of novelty and habituation on acetylcholine, GABA, and glutamate release from the frontal cortex and hippocampus of freely moving rats. Neuroscience 106(1):43–53 [DOI] [PubMed]
  13. Gluck MA, Myers CE (2001) Gateway to memory. MIT Press, Cambridge, MA
  14. Hafting T, Fyhn M, Molden S, Moser MB, Moser EI (2005). Microstructure of a spatial map in the entorhinal cortex. Nature 436:801–806 [DOI] [PubMed]
  15. Hafting T, Fyhn MH, Moser M, Moser EI (2006) Phase precession and phase locking in entorhinal grid cells. Program No. 68.8. 2006 Neuroscience Meeting Planner. Society for Neuroscience, Atlanta, GA
  16. Harris KD, Henze DA, Hirase H, Leinekugel X, Dragoi G, Czurkó A, Buzsáki G (2002) Spike train dyamics predicts theta-related phase precession in hippocampal pyramidal cells. Nature 417:738–741 [DOI] [PubMed]
  17. Hasselmo ME (2005) What is the function of the hippocampal theta rhythm?—Linking behavioral data to phasic properties of field potential and unit recording data. Hippocampus 15:936–949 [DOI] [PubMed]
  18. Hasselmo ME, Schnell E, Barkai E (1995) Dynamics of learning and recall at excitatory recurrent synapses and cholinergic modulation in rat hippocampal region CA3. J Neurosci 15:5249–5262 [DOI] [PMC free article] [PubMed]
  19. Henze DA, Wittner L, Buzsáki G (2002) Single granule cell reliably discharge targets in the CA3 hippocampal network in vivo. Nat Neurosci 5(8):790–795 [DOI] [PubMed]
  20. Huxter J, Burgess N, O’Keefe J (2003) Independent rate and temporal coding in hippocampal pyramidal cells. Nature 425:828–832 [DOI] [PMC free article] [PubMed]
  21. Jensen O, Lisman JE (1996) Hippocampal CA3 region predicts memory sequences: accounting for the phase precession of place cells. Learn Mem 3:279–287 [DOI] [PubMed]
  22. Johnston D, Amaral DG (1998) Hippocampus. In: Shepherd GM (ed) The synaptic organization of the brain, 4th edn. Oxford University Press, New York
  23. Jones MW, Wilson MA (2005) Phase precession of medial prefrontal cortical activity relative to the hippocampal theta rhythm. Hippocampus 15:867–873 [DOI] [PubMed]
  24. Káli S, Dayan P (2000) The involvement of recurrent connections in area CA3 in establishing the properties of place fields: a model. J Neurosci 20:7463–7477 [DOI] [PMC free article] [PubMed]
  25. Kamondi A, Ascády L, Wang XJ, Buzsáki G (1998) Theta oscillations in somata and dendrites of hippocampal pyramidal cells in vivo: activity-dependent phase-precession of action potentials. Hippocampus 8:244–261 [DOI] [PubMed]
  26. Klausberger T, Magill PJ, Márton LF, Roberts JDB, Cobden PM, Buzsáki G, Somogyi P (2003) Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature 421:844–848 [DOI] [PubMed]
  27. Klausberger T, Márton LF, Baude A, Roberts JDB, Magill PJ, Somogyi P (2004) Spike timing of dendrite-targeting bistratified cells during hippocampal network oscillations in vivo. Nat Neurosci 7:41–47 [DOI] [PubMed]
  28. Marr D (1971) Simple memory: a theory for archicortex. Philos Trans R Soc Lond B Biol Sci 262(841):23–81 [DOI] [PubMed]
  29. Mascagni MV, Sherman AS (1998) Numerical methods in neuronal modeling. In: Koch C, Segev I (eds) Methods in neuron modeling: from ions to networks, 2nd edn. MIT Press, Cambridge, MA
  30. Matsumoto M, Nishimura T (1998) Mersenne twister: a 623-dimensionally equidistributed uniform pseudorandom number generator. ACM Trans. Model Comput Simulat 8:3–30. http://www.math.sci.hiroshima-u.ac.jp/∼m-mat/MT/emt.html. Cited 23 July 2004
  31. Mehta MR, Barnes CA, McNaughton BL (1997) Experience-dependent, asymmetric expansion of hippocampal place fields. Proc Natl Acad Sci USA 94:8918–8921 [DOI] [PMC free article] [PubMed]
  32. Mehta MR, Lee AK, Wilson MA (2002) Role of experience and oscillations in transforming a rate code into a temporal code. Nature 417:741–746 [DOI] [PubMed]
  33. Mehta MR, Quirk MC, Wilson MA (2000) Experience-dependent asymmetric shape of hippocampal receptive fields. Neuron 25:707–715 [DOI] [PubMed]
  34. Muller R (1996) A quarter of a century of place cells. Neuron 17:813–822 [DOI] [PubMed]
  35. O’Keefe J, Burgess N (2005) Dual phase and rate coding in hippocampal place cells: theoretical significance and relationship to entorhinal grid cells. Hippocampus 15:853–866 [DOI] [PMC free article] [PubMed]
  36. O’Keefe J, Dostrovsky J (1971) The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res 34:171–175 [DOI] [PubMed]
  37. O’Keefe J, Recce ML (1993) Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3(3):317–330 [DOI] [PubMed]
  38. O’Reilly RC, McClelland JL (1994) Hippocampal conjunctive encoding, storage and recall: avoiding a trade-off. Hippocampus 4:661–682 [DOI] [PubMed]
  39. Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in C. 2nd edn. Cambridge University Press, New York
  40. Quirk GJ, Muller RU, Kubie JL, Ranck JB Jr (1992) The positional firing properties of medial entorhinal neurons: description and comparison with hippocampal place cells. J Neurosci 12:1945–1963 [DOI] [PMC free article] [PubMed]
  41. Rolls ET, Treves A (1998) Neural networks and brain function. Oxford University Press, New York
  42. Samsonovich A, McNaughton BL (1997) Path integration and cognitive mapping in a continuous attractor neural network model. J Neurosci 17:5900–5920 [DOI] [PMC free article] [PubMed]
  43. Segev I, Burke RE (1998) Compartmental models of complex neurons. In: Koch C, Segev I (eds) Methods in neuron modeling: from ions to networks, 2nd edn. MIT Press, Cambridge, MA
  44. Sjöström PJ, Turrigiano GG, Nelson SB (2001) Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32:1149–1164 [DOI] [PubMed]
  45. Skaggs WE, McNaughton BL, Wilson MA, Barnes CA (1996) Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6:149–172 [DOI] [PubMed]
  46. Stewart M, Quirk GJ, Barry M, Fox SE (1992) Firing relations of medial entorhinal neurons to the hippocampal theta rhythm in urethane anesthetized and walking rats. Exp Brain Res 90:21–28 [DOI] [PubMed]
  47. Tsodyks MV, Skaggs WE, Sejnowski TJ, McNaughton BL (1996) Population dynamics and theta rhythm phase precession of hippocampal place cell firing: a spiking neuron model. Hippocampus 6:271–280 [DOI] [PubMed]
  48. Turner DA, Li XG, Pyapali GK, Ylinen A, Buzsáki G (1995) Morphometric and electrical properties of reconstructed hippocampal CA3 neurons recorded in vivo. J Comp Neurol 356:580–594. http://neuron.duke.edu/cells/. Cited 7 April 2004 [DOI] [PubMed]
  49. Vazdarjanova A, Guzowski JF (2004) Differences in hippocampal neuronal population responses to modifications of an environmental context: evidence for distinct, yet complementary, functions of CA3 and CA1 ensembles. J Neurosci 24:6489–6496 [DOI] [PMC free article] [PubMed]
  50. Wagatsuma H, Yamaguchi Y (2007) Neural dynamics of the cognitive map in the hippocampus. Cogn Neurodyn (in press) DOI 10.1007/s11571-006-9013-6 [DOI] [PMC free article] [PubMed]
  51. Wallenstein GV, Hasselmo ME (1997) GABAergic modulation of hippocampal population activity: sequence learning, place field development, and the phase precession effect. J Neurophysiol 78:393–408 [DOI] [PubMed]
  52. Weast RC (ed.) (1964) C.R.C. Standard mathematical tables, 13th edn. The Chemical Rubber Co., Cleveland, OH
  53. Wilson MA, McNaughton BL (1993) Dynamics of the hippocampal ensemble code for space. Science 261(5124):1055–1058 [DOI] [PubMed]
  54. Yamaguchi Y (2003) A theory of hippocampal memory based on theta phase precession. Biol Cybern 89:1–9 [DOI] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Below is the link to the electronic supplementary material.

(PDF 721 kb) (721.8KB, pdf)

Articles from Cognitive Neurodynamics are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES