A new adaptive grid-size algorithm for the simulation of sedimentation velocity profiles in analytical ultracentrifugation

Abstract

Analytical ultracentrifugation allows one to measure in real-time the concentration gradients arising from the application of a centrifugal force to macromolecular mixtures in solution. In the last decade, the ability to efficiently solve the partial differential equation governing the ultracentrifugal sedimentation and diffusion process, the Lamm equation, has spawned significant progress in the application of sedimentation velocity analytical ultracentrifugation for the study of biological macromolecules, for example, the characterization of protein oligomeric states and the study of reversible multi-protein complexes in solution. The present work describes a numerical algorithm that can provide an improvement in accuracy or efficiency over existing algorithms by more than one order of magnitude, and thereby greatly facilitate the practical application of sedimentation velocity analysis, in particular, for the study of multi-component macromolecular mixtures. It is implemented in the public domain software SEDFIT for the analysis of experimental data.

Introduction

Analytical ultracentrifugation is one of the classic techniques of biophysics and physical biochemistry. It derives its potential from the conceptual simplicity and from its firm theoretical thermodynamic basis. In sedimentation velocity analytical ultracentrifugation (SV), an optical system allows monitoring the evolution of macromolecular concentration gradients in free solution caused by the application of a gravitational force. In the eight decades following Svedberg's Nobel prize in 1926, it found wide-spread applications and is still an important today tool in many traditional areas of protein biochemistry [1-3], synthetic polymer chemistry [4], molecular biology [5], protein interactions [6], as well as more recently emerging fields such as supramolecular chemistry [7], dendritic polymers [8, 9], the characterization of nanoparticles for drug or gene delivery and biomaterials [10-13], amyloid formation of proteins [14], and the development of formulation conditions for protein therapeutics in pharmaceutical industry [15-18]. In the last decade, the increasing potential for computational data analysis, in particular, the highly detailed mathematical analysis of the sedimentation boundary shape has spawned a resurgence of interest and the development of many new applications. For recent reviews and introductions, see [19-23 ].

In 1929, Lamm derived the partial differential equation (eq. 1) for the evolution of the macromolecular concentration distribution in a sector-shaped solution column in the centrifugal field: for an ideally sedimenting, non-interacting macromolecular component, the concentration profile χ(r,t) as a function of distance from the center of rotation, r, and time, t, follows

$$\frac{\partial \chi }{\partial t}=\frac{1}{r}\frac{\partial }{\partial r}\left[rD\frac{\partial \chi }{\partial r}-s{\omega }^2{r}^2\chi \right]$$ (1)

where s and D denote the macromolecular sedimentation and diffusion coefficient, respectively, and ω is the rotor speed [24]. In the following decades, approximate analytical solutions for several special cases that were of practical importance in the experimental study of SV of macromolecular samples were found by Archibald [25], Faxen [26], Fujita [27], and others [3, 28-30]. In the 1960s, the advent of computers allowed the prediction of concentration profiles in the general case including the description of sedimentation, diffusion, and chemical reactions. Several groups used this tool to explore a variety of topics important in biochemical applications, such as hydrodynamic non-ideality [31], effects of hydrostatic pressure [32], density gradients [33], coupled sedimentation and chemical reaction for proteins with rapid self- and hetero-association [34-36], and enzymatic activity [37].

At this time, also the modeling of experimental data with Lamm equation (LE) solutions was envisioned and addressed to the extent possible [36]. With the resurging interest in analytical ultracentrifugation since the 1990s, more approximate analytical [38-40] and numerical [41-43] solutions of the LE were developed, and several software packages are currently available that embed different approaches to the modeling of experimental SV data, including BCPFIT [44, 45], LAMM [39], SEDANAL [46], SVEDBERG [38], ULTRASCAN [47], and from our own laboratory SEDFIT [41, 48] and the multi-method global analysis platform SEDPHAT [49, 50]. The latter two are based on the concept of directly fitting (single or multiple) data sets from the entire sedimentation process(es) in the original data space, accounting explicitly for the characteristic systematic signal offsets of SV data acquisition by algebraic separation of variables [51].

Recently, increasing computational power readily available in desktop computers enabled more complex applications, some of which are currently widely used [21, 52]. It allowed, for example, using LE solutions to be used as the kernel in Fredholm integral equations, such as in the sedimentation coefficient distribution c(s)

$$a(r,t)\cong \int c\left(s\right){\chi }_1(s,D\left(s\right),r,t)ds$$ (2)

(where a(r,t) is the measured concentration evolution) [53-55], and multidimensional extensions such as the two-dimensional size-and-shape distributions [56], and multi-component sedimentation coefficient distributions for multi-protein complexes [57]. Fitting these models to experimental data gives high-resolution, diffusion-deconvoluted macromolecular size-distributions. This approach has been extended to the description of macromolecular sedimentation in density gradients from sedimenting co-solutes [58], which are frequently an obligate sample component, for example, to achieve sufficient protein stability, or to study proteins stability in pharmaceutical formulation conditions. Computationally, this latter case requires the kernel of integral equations to be a set of coupled LEs with a cross-term describing the time-varying macromolecular buoyancy [58]. Further, sets of coupled LEs are required to model sedimentation of multiple macromolecular components that exhibit chemical reactions on the time-scale of the experiment [46, 59]. Clearly, the ability to very efficiently solve the LE is a key factor in these approaches, and can still be limiting in some practical applications. Therefore, algorithms for solving the LE is an important topic that directly relates to the biophysical study of macromolecules by sedimentation velocity. It provides tools that are unique for studying interacting multi-component mixtures in free solution [21 , 57].

The development of algorithms for the LE has been an active field for several decades. Solving the LE is not trivial due to the large concentration range that is spanned by LE solutions (see Figure 1), the steep gradients at the distal end (or ‘bottom’) of the solution column, and the necessity for an accuracy sufficient to fully exploit the high experimental signal/noise ratio of up to 1000:1. Numerical approaches currently appear to be advantageous compared to approximate analytical solutions mainly due to their flexibility, which allows features like non-uniform loading concentrations [41, 60], density gradients [58, 61], the acceleration phase of the rotor [62], and – importantly – chemical reactions [34-37, 46, 59] to be incorporated naturally into the model. Several different finite difference and finite element approaches have been described. Finite difference approaches with fixed spatial grids were used in [41, 63], but due to effects of ‘numerical diffusion’ or ‘numerical dispersion’ [35, 64, 65] (graphically illustrated in [65] and [66]), they are only applicable for conditions of small molecule sedimentation with small sedimentation coefficient [41]. Alleviating this problem, time-dependent grids were developed, either with regions of different grid intervals periodically remapped to maintain fine grids at the position of the boundary [67], or by continuously adjusting the grid points such as to provide a moving frame of reference [35, 65].

Figure 1.

Example for the shape of sedimentation velocity profiles of large macromolecules. The curves shown are calculated for a large protein complex (1 MDa and 30 S) at unit concentration sedimenting at 50,000 rpm. Steep slopes can be discerned in the sedimentation boundary, in particular, at early times close to the meniscus at 6.2 cm (1), and close to the distal end (bottom) of the solution column (2). The latter steep increase close to the end of the solution column is referred to as back-diffusion region. It cannot be experimentally reliably imaged, and is therefore customarily excluded from the data analysis (but until recently not from the computed LE solutions). The inset shows the increase in concentration with time at the end of the solution column (3), reaching concentrations > 100-fold the loading concentration, in the experiment frequently leading to phase transitions and surface film formation. This back-diffusion region can be excluded from the LE solution by using the boundary conditions for a semi-infinite column (or permeable bottom). Except for very early and very late time-points, the boundary enclosed by regions of the solvent plateau (4) and solution plateau (5). The concentration in the solvent plateau is negligible (for example, < 10⁻³⁰ from 6.2 to 6.3 cm at times > 600 sec), and in good approximation is constant at zero. The concentration in the solution plateau is also virtually constant, but decreasing with time due to the effect of radial dilution in the sector-shaped solution column (see Eq. 4). Also shown are examples for the location of the fitting limits r₁* and r₂* that exclude the regions of experimental optical artifacts and describe the radial range of reliable data acquisition.

Claverie has introduced the first finite element approach to solve the LE on a fixed set of equidistant radial grid points [68]. It avoids the problem of ‘numerical diffusion’ due to the higher-order approximation of spatial derivatives inherent in the finite difference method, and provides very precise concentration profiles when applied with sufficiently fine spatial and temporal discretization. Later, we have described an extension of the finite element method on a grid with moving frame of reference, similar to the grid described in [65]. Translating the grid points in time like sedimenting point particles generates a moving frame of reference on which the LE reduces to an easier to solve diffusion problem [42]. This method naturally imposes a logarithmically spaced grid with higher density closer to the meniscus [42, 65]. Recently, in their adaptive space-time finite element algorithm (ASTFEM), Cao & Demeler have combined the moving frame of reference approach with a region of stationary grid points at high density close to the bottom of the cell, in order to permit the use of sparser grids without compromising the numerical stability [43] (see below).

To our knowledge, all previous approaches used reflective boundary conditions at the meniscus and the bottom of the solution column as suggested by the physical setup of the experiment (with the exception of the algorithms by Cox and co-workers [36], which were not suitable for incorporating boundary conditions and therefore simulated sedimentation starting from a synthetic boundary on an infinite column). Also, to our knowledge, in all approaches the choice of the total number (and average density) of grid points, which scales the computational effort and the accuracy, was empirically chosen. Finally, in none of the computational methods was use made of the trivial analytical solutions for the regions outside the sedimentation boundary. These issues were examined in more detail in the present work, which, as will be shown, precipitated the development of a novel algorithm that is far superior in accuracy or speed.

The difficulty of solving the LE is exacerbated for large macromolecules at high rotor speeds, where the low diffusion coefficient also increases the steepness of the migrating sedimentation boundaries (Figure 1). This makes it necessary to use a high density of radial grid points, which, in turn, increase the computational cost. However, In SV experiments of large macromolecules, the region of back-diffusion from the bottom of the solution column is customarily excluded from consideration in the data analysis for several experimental reasons: (1) the inability to faithfully measure the steep concentration gradients with existing detection systems (chiefly due to refractive index gradients); (2) the common observation of a phase transition of materials at the high concentration in contact with the surface, leading to the formation of poorly reversible surface films, which will substantially alter or even eliminate back-diffusion; (3) the expectation that strong repulsive non-ideality will occur at the high concentrations close to the bottom, making models of ‘ideally sedimenting’ interacting or non-interacting species models inappropriate for this region, even when the ideal models apply at the significantly lower concentration range observed throughout the rest of the solution column. In order to exploit this observation, we have introduced recently the concept of solving the LE for a semi-infinite solution column by implementing permeable boundary conditions at the bottom of the physical solution column [56, 59]. This eliminates entirely the back-diffusion gradients, and thereby greatly simplifies and improves the stability and computational cost of solving the LE, in particular for the more difficult cases of large macromolecule SV at high rotor speeds [56]. Despite the unphysical boundary condition at the bottom, it can be applied to the analysis of experimental data from the region ‘above’ (i.e. at lower radii than) the back-diffusion range without compromising accuracy [56].

In the current work, we reappraise the accuracy of the finite element algorithms for solving the LE under these simplified boundary conditions of a semi-infinite solution column. We demonstrate that, surprisingly, the dominant factor for the remaining numerical errors is caused simply by the approximation of the curved concentration profiles as a sequence of linear segments on a limited number of spatial grid points, and that this error scales with the ratio of the local grid density and the width of the sedimentation boundary. Because the sedimentation boundaries are steeper in the beginning and then continuously broaden due to diffusion, this error is largest close to the meniscus. Based on this observation and from physical considerations, we describe a new finite element approach with spatially varying grid density that minimizes the discretization error throughout the solution column, and thereby significantly improves the accuracy of the LE solution. A rational expression is given that allows to determine the minimal grid necessary to achieve a pre-set accuracy, adaptively adjusting according to the macromolecular sedimentation and diffusion coefficients, and also considering the specific experimental conditions and fitting limits. Further, we introduce a new concept of a dynamic division of the grid into active and inactive points, which eliminates numerical computation for the regions of the solvent and solution plateaus (Figure 1) where accurate analytical expressions are available. We describe results from this new algorithm, which, in comparison to existing algorithms, we found to reduce by more than one order of magnitude the computational cost for solving LE solutions.

Methods

Solutions of the Lamm equation

As initial condition for solving the LE, we assume uniform loading throughout the solution column with the concentration c₀. Unless noted otherwise, we assume an ideally sedimenting, non-interacting macromolecule in a solution of constant density. The modifications to account for chemical reactions or density gradients reported in [58, 59] can be applied to the algorithm described in the following without further complications. First, we recapitulate two important special cases with relatively simple solutions:

(1) At infinite time, the distribution attains sedimentation equilibrium, which follows the well-known Boltzmann exponential

$$c_{eq}\left(r\right)=c_0\frac{M_b(\xi \left(b\right)-\xi \left(m\right))}{\exp \left(M_b\xi \left(b\right)\right)-\exp \left(M_b\xi \left(m\right)\right)}\times \exp \left(M_b\xi \left(r\right)\right)$$ (3)

(with the abbreviation ξ(r)=ω²r² / 2RT , the buoyant molar mass M_b = sRT/D , the gas constant R and the absolute temperature T) [1]. For standard experimental configurations of uniform initial loading (and also excluding flotation), at radii larger than the hinge-point of the distribution [3], it is c_eq(r) > χ(r,t) at all times, such that c_eq(r) can be used as an upper limit for the extent of back-diffusion encountered in a solution column for the sedimentation of particles with given s and D [56].

(2) For finite times but in the limit of very large, non-diffusing particles (D = 0), Eq. 1 has the simple analytical solution

$$\begin{array}{cc}\hfill & \chi (r,t)=c_p\left(t\right)\times \{\begin{array}{cc}0for\hfill & r<m{e}^{{\omega }^{2}st}\hfill \\ c_0\hfill & else\hfill \end{array}\phantom{\}}\hfill \\ \hfill & c_p\left(t\right)=e^{-2{\omega }^{2}st}\hfill \end{array}$$ (4)

This expression has been used, for example, in the apparent sedimentation coefficient distribution ls-g*(s) [69], and can be generalized to account for solvent compressibility [61]. Eq. 4 describes the sedimentation boundary as a step-function. For D > 0, at any given time, Eq. 4 is still an excellent approximation for the plateau regions where the concentrations are radially constant (regions 4 and 5 in Figure 1).

In the general case, the finite element solution of the LE follows the methods by Claverie and Schuck that were described earlier [42, 59, 68], as briefly outlined in the following. The boundary shape is approximated as a linear combination

$$\chi (r,t)\approx \sum _{i=1}^N{c}_i{P}_i(r,t)$$ (5)

of basis functions

$$P_i(r,t)=\{\begin{array}{cc}\frac{r-r_{i-1}}{r_i-r_{i-1}}\hfill & r_{i-1}\le r\le r_i\hfill \\ \frac{r_{i+1}-r}{r_{i+1}-r_i}\hfill & r_i<r\le r_{i+1}\hfill \\ 0\hfill & else\hfill \end{array}\phantom{\}}$$ (6a)

for i = 2,...,N-1, and

$$\begin{array}{cc}\hfill P_1(r,t)& =\{\begin{array}{cc}\frac{r_2-r}{r_2-r_1}\hfill & r_1\le r\le r_2\hfill \\ 0\hfill & else\hfill \end{array}\phantom{\}}\hfill \\ \hfill P_N(r,t)& =\{\begin{array}{cc}\frac{r-r_{N-1}}{r_N-r_{N-1}}\hfill & r_{N-1}\le r\le r_N\hfill \\ 0\hfill & else\hfill \end{array}\phantom{\}}\hfill \end{array}$$ (6b)

(termed chapeau- or hat-functions) with an underlying grid of radial points r₁...r_N , starting at the meniscus (r₁ = m) and ending at the bottom (r_N = b) of the solution column. Because P_i(r,t) are triangular, the concentration distribution χ(r,t) in Eq. 5 is approximated by piece-wise linear segments. Inserting Eq. 5 into Eq. 1, multiplication with P_j and radial integration leads to a matrix equation for the evolution of the coefficients c_i(t).

$$\begin{array}{cc}\hfill & \sum _j\frac{\partial c_j}{\partial t}{\mathbf{B}}_{\mathrm{kj}}\left(\mathrm{t}\right)=\hfill \\ \hfill & \sum _j\left[{\omega }^2(s{\mathbf{A}}_{\mathrm{kj}}^{\left(2\right)}\left(\mathrm{t}\right)-s_G{\mathbf{A}}_{\mathrm{kj}}^{\left(3\right)}\left(\mathrm{t}\right))-D\alpha {(t-t_0)}^{-2}{\mathbf{A}}_{\mathrm{kj}}^{\left(1\right)}\left(\mathrm{t}\right)\right]c_j\hfill \end{array}$$ (7a)

with the tridiagonal matrices

$$\begin{array}{cc}\hfill {\mathbf{B}}_{\mathrm{kj}}& ={\int }_m^b{P}_j{P}_{k}rdr\hfill \\ \hfill {\mathbf{A}}_{\mathrm{kj}}^{\left(1\right)}& ={\int }_m^b(\partial P_j∕\partial r)(\partial P_k∕\partial r)rdr\hfill \\ \hfill {\mathbf{A}}_{\mathrm{kj}}^{\left(2\right)}& ={\int }_m^b{P}_j(\partial P_k∕\partial r)rdr\hfill \\ \hfill {\mathbf{A}}_{\mathrm{kj}}^{\left(3\right)}& ={\int }_m^b(\partial P_j∕\partial t)P_{k}rdr\hfill \end{array}$$ (7b)

The values of the matrix elements depend on the boundary conditions and on the grid. Claverie has used a static, equidistant grid, and the boundary condition of a vanishing transport flux (j = sω²rc – D(dc/dr)) at the beginning and end of the solution column, leading to the conventional LE solution for a finite solution column [68]. Cox and Dale have given expressions for B, A⁽¹⁾, and A⁽²⁾ for this case [36]. When a time-varying grid is used with grid-points that sediment like point particles r_i(t) = r_i(0)exp{ω²s(t-t₀)}, a moving frame of reference is established so that simulation of sedimentation reduces to a diffusion problem, which can be solved with greater stability for large particles [42]. The logarithmically spaced grid

$$r_i\left(0\right)=m{(b∕m)}^{(i-3∕2)∕(N-1)}$$ (8)

(for k = 2,...,N-2) is unique in that the grid maps onto itself after time-intervals Δt = 1/[ω²s(N-1)]×log(b/m), such that the evolution from sedimentation collapses into a simple renumbering of indices. This makes this approach more stable and accurate for cases of high sedimentation and low diffusion constants [42]. With the spacing Eq. 8, the density of grid points increases from meniscus to bottom approximately by the factor b/m, i.e. for practical conditions of analytical ultracentrifugation typically on the order of 15%. Values for B, A⁽¹⁾, A⁽²⁾, and A⁽³⁾ for the case of non-equidistant, time-dependent grids are given in [42]. Recently, a modification of the moving frame of reference method was described by Cao & Demeler [43], where the grid points do not follow the spacing Eq. 8, but are chosen to strongly increase in density towards the bottom of the cell (see discussion below).

We have shown recently that the boundary condition of a non-vanishing transport flux at the bottom leads to slightly modified matrix elements, and allows the simulation of sedimentation on a semi-infinite solution column [59]. As indicated above, the equilibrium expression Eq. 3 was used to judge for any given set of parameters, whether or not back-diffusion can be safely excluded, considering the distance between the highest experimentally observed data point and the bottom of the solution column [56, 59]. This approach has been combined with the Claverie and the moving hat finite element algorithm.

In the implementation in SEDFIT and SEDPHAT, an adaptive time increment was chosen, and propagation was computed according to the second-order Crank-Nicholson scheme [42, 70]. This greatly stabilizes oscillations that otherwise may occur, in particular at coarse grids at the bottom of the solution column. For considering the rotor acceleration, the rotor speed was considered a linear function of time ω(t), with a slope $\stackrel{.}{\omega }$ of 200 rpm/sec, and updated in 10 sec intervals [62]. (When modeling experimental data, $\stackrel{.}{\omega }$ can be taken from the entries of t and ∫ω²dt of the experimental data file.)

Estimating the maximal observed boundary spread

From fundamental considerations, we can expect that the diffusional spread of the sedimentation boundary will be time-dependent, and approximately follow $\sigma \sim \sqrt{D\tau }$ (with τ denoting the diffusion time). Of interest is the boundary spread at a radial point r₁* adjacent to the optical artifacts that arise when imaging the meniscus (Figure 1). r₁* is usually removed from the meniscus by a few tenth of a millimeter, as judged from visual inspection of the superposition of scans. As implemented in SEDFIT, r₁* is the smaller of the two fitting limits. At a given sedimentation coefficient, the boundary will have the velocity dr/dt = sω²r, such that the time required for the boundary to arrive at a given radial point r₁* is on the order of τ∼(r₁*-m)/sω²r* (neglecting the small radial-dependence of the force and velocity). It follows that when the boundary has reached a radius r₁*, the spread is approximately

$$\sigma \sim \frac{1}{\omega }\sqrt{\frac{D}{s}\times \frac{({r_1}^{\ast }-m)}{{r_1}^{\ast }}}=\frac{1}{\omega }\sqrt{\frac{RT}{M_b}\times \frac{({r_1}^{\ast }-m)}{{r_1}^{\ast }}}$$ (9)

, with the identity on the right-hand side using the Svedberg relationship [1] between s, D, and the buoyant molar mass M_b. Straightforward corrections can be applied to account for the slightly increased extent of diffusion arising from the time lag caused by the acceleration phase of the rotor.

Estimating the minimum obligate error from the representation of a smooth boundary with piece-wise linear segments

In the numerical solution of the LE, the continuous function χ(r,t) is represented by a piece-wise linear function. If we take the maximum absolute deviation from the true, smoothly curved χ(r,t) as a measure for the goodness of the approximation, the obligate minimal error that must occur is that from linear segmentation, i.e. the deviation

$${\delta }_o=\underset{c_i,r_0}{\min }\left\{\underset{{r_1}^{\ast }<r<{r_2}^{\ast }}{\max }\mid \chi (r,t)-\sum _{i=1}^N{c}_i{P}_i\left(r\right)\mid \right\}$$ (10)

(with r₁* and r₂* denoting again the radial fitting limits, and the radial grid given by r_i = r₀ + (m – b) × (i – 1) /(N – 1) ). We expect this error to depend only on the relative dimensions of the grid density and the boundary spread. In δ_o the amplitudes c_i at the grid points may partially compensate the error from linearization, as well as the relative location r₀ relative to the boundary midpoint. In practice, somewhat larger errors may be encountered since the c_i are computed by the propagation scheme for the LE solution (see above), and not by the optimization problem Eq. 10. Therefore, we also estimated the following quantities δ₁ and δ₂

$$\begin{array}{cc}\hfill {\delta }_1\left(N\right)& =\underset{r_0}{\max }\left\{\underset{{r_1}^{\ast }<r<{r_2}^{\ast }}{\max }\mid {\chi }_F\left(r\right)-\sum _{i=1}^N{\chi }_F(r_i,t)P_i\left(r\right)\mid \right\}\hfill \\ \hfill {\delta }_2\left(N\right)& =\underset{r_0}{\max }\left\{\underset{{r_1}^{\ast }<r<{r_2}^{\ast }}{\max }\mid {\chi }_F\left(r\right)-\sum _{i=1}^N{\chi }_F(r_i,t)P_i\left(r\right)\mid \right\}\hfill \end{array}$$ (11)

, i.e., we assume that the concentration values of the approximations at the grid points are identical to the LE solution. For computational purpose, we calculate these quantities for LE solutions χ_F(x,t) either based on a numerical solution with a very fine grid or on the Faxen analytical approximation [29]. δ₁ and δ₂ reflect the worst and best location of the grid relative to the boundary. They will be slightly larger than the obligate minimal error δ_o, because of the missing flexibilities to freely adjust each individual amplitude c_i. δ_o, δ₁, and δ₂ were evaluated using MATLAB (The Mathworks Inc., Nantucket, MA).

Generalization of the Claverie approach to spatially non-uniform grids

We examined a generalization of the Claverie approach with static, but non-equidistant grid. We focused on the case with high ratio s/D (high molar mass) that is numerically more difficult and time-consuming to solve, but for which in practice back-diffusion can usually be safely neglected (and reliably predicted). We considered the notion that the obligate minimum discretization errors Eqs. 10 and 11 will depend on the relative boundary spread, which takes the form Eq. 9. The steepest boundary possibly encountered in the data analysis occurs when the sedimentation boundary is at the left fitting limit r₁*. We determined the spacing between neighboring points at this point to be Δr₀(r₁*) = σ/α, where the σ is the boundary width calculated by Eq. 9, and α is a factor that determines the number of grid points per boundary width. (We note that a constant value of α, the obligate segmentation error will remain approximately constant independent of the experimental configuration: for example, values of α = 5 provide ∼ 25 points across the central 90% of the boundary height, which can describe boundaries usually with a relative accuracy on the order of ∼ 0.001, see below). At radial points above r₁*, in order to provide a constant ratio σ/α as the boundary moves through the solution column, we chose the interval between neighboring points Δr_i to increase after that according to

$$\Delta r_i=\Delta r_0\{\begin{array}{cc}1\hfill & forr\le {r_1}^{\ast }\hfill \\ \sqrt{\frac{{r_1}^{\ast }(r_i-m)}{r_i({r_1}^{\ast }-m)}}\hfill & else\hfill \end{array}\phantom{\}}$$ (12a)

with

$$\Delta r_0=\frac{\sigma }{\alpha }=\frac{1}{\alpha \omega }\sqrt{\frac{RT}{M_b}\times \frac{({r_1}^{\ast }-m)}{{r_1}^{\ast }}}$$ (12b)

It follows that the grid positions are determined by

$$r_i=\{\begin{array}{cc}m\hfill & fori=1\hfill \\ b\hfill & fori=N\hfill \\ m+\sum _{j=2}^i\Delta r_i\hfill & else\hfill \end{array}\phantom{\}}$$ (12c)

and this recipe then determines the total number of grid-points N needed, based on the pre-set choice of α. An example for the radial distribution of grid points generated by Eq. 12 can be discerned from the pattern of vertical lines in Figure 2. The matrix elements B, A⁽¹⁾, A⁽²⁾ required for this choice of grid can be calculated with the expressions we reported previously for nonuniform grids and the adjustments for semi-infinite solution columns [42, 59].

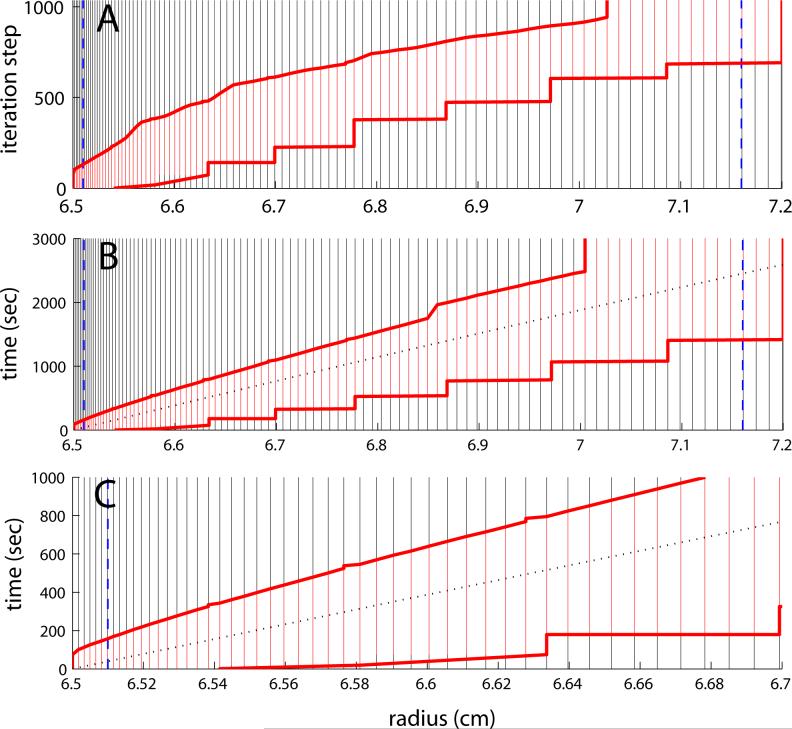
Figure 2.

Spatial distribution of the radial grid and the evolution of active and inactive grid points. The grid is taken from the example discussed in Figure 7, where N = 100 points are used to describe sedimentation of a 10 S, 450 kDa protein in a solution column from 6.5 to 7.2 cm. For the data analysis limits at 6.51 cm and 7.165 cm (blue dashed lines), Eq. 12 results in grid points indicated by the vertical lines. Dependent on the position of the sedimentation boundary, grid points that are active (differing by more than 10⁻⁴ from both solvent and solution plateaus) are shown in red. The inactive grid points, shown in black, do not require numerical computation. The evolution of the concentration profile is indicated by the vertical axis, which denotes the iteration steps (A) or time (B and C), respectively. The division of active and inactive is dynamically adjusted (bold red lines), leaving less than half of the points active throughout the simulation. In Panels B and C, the dotted line indicates the boundary midpoint. Panel C provides an expanded view for early times and radii close to the meniscus. It should be noted that the grid spacing between 6.5 cm and 6.51 cm is constant at Δr₀ (Eq. 12b), before increasing in a manner following diffusional broadening (Eq. 12a).

Dynamic division of active and inactive grid points

With the grid according to Eq. 12, for experimental configurations commonly encountered in practice, the increase in grid spacing can be ∼ 10-fold. Thus, once the sedimentation boundary has moved further into the solution and has depleted the meniscus region, the majority of grid points would remain at locations with negligible solute concentrations. The following strategy can alleviate this computational inefficiency: We note that χ(r,t) without back-diffusion is monotonically decreasing with time at all radius values, and at any point in time χ(r,t) is monotonically increasing in radius. At a time-point t’, we search for the highest radial point r’ where the concentration values has fallen below a threshold value that can be safely considered to be zero without significant impact on accuracy (safely below the required accuracy, e.g. c(r’) < c₀×ε, with ε = 10⁻⁴ − 10⁻⁶). Because χ(r<r’,t>t’) < χ(r’,t’) all concentration values at smaller radii and later times will be negligible. The range of radius values r’ for which this condition is true will start near the meniscus and continuously grow to higher radius values.

To take advantage of this, we devised modifications of the standard algorithms for the tridiagonal matrix operations for the case that only the elements between N’ and N of the concentration vectors are nonzero. This allows to eliminate most (though not all) of the matrix operations for all grid points within r_i < r’(t). Essentially, in this way, the computationally utilized portion of the grid shrinks with time as the boundary moves away and leaves the region close to the meniscus behind in the solvent plateau.

Analogously, it is possible to utilize the analytically trivial concentration value of the solution plateau (Eq. 4): First, a consequence of the absence of back-diffusion is that for any radius values r’’ where the concentration is within a pre-set accuracy from the solution plateau (i.e., c_p(t) – χ(r’’,t) < c₀×ε) it is χ(r>r’’,t) > χ(r’’,t) and therefore any radius value higher than r’’ will be even closer to the plateau (i.e., c_p(t) – χ(r>r’’,t) < c₀×ε). Second, we note that with the boundary condition for the semi-infinite solution column it is in fact irrelevant where the simulated bottom position is located, as long as it is within the plateau region. Therefore, we can shorten the simulation to the grid points at radii smaller than r’’ , i.e. to points r_i with i < N’’, by modification of the propagation matrix to permeable boundary conditions at N’’. This eliminates all operations for i > N’’. Within the pre-set accuracy, the concentration values at r > r’’ (i > N’’) can be substituted by the analytically calculated plateau value. With the progress of sedimentation, this upper limit N’’ should be moved to larger values. This was implemented so that once less than 10% of the solution column are within ε of the plateau value, N’’ will be increased by 0.1×N. When time-dependent rotor speeds occur, due to the consideration of rotor acceleration, the expression Eq. 4 for the solution plateau can be replaced by a differential form for radial dilution per time-increment. Eq. 4 does also not apply for pressure-dependent sedimentation in compressible solvents, but the analytic expressions for the solution ‘plateau’ in [61] could be used for the analytic extension of the dynamic grid.

As a consequence of the dynamic adjustment, only the portion of the grid will be computationally utilized that is required for the non-trivial portion of the concentration profile. This is illustrated in Figure 2. Initially, when the boundary is close to the meniscus and small time-steps are required for stable solutions, most of the grid throughout the solution column is switched off and only the high-density portion needed for precise simulation is active. As the boundary migrates away from the meniscus, this region containing the density of grid points will be continuously deactivated, and new points will be activated in a density such that the broadened boundary encounters just sufficient grid points to maintain the preset accuracy of simulation. Synchronized with the boundary movement, the computational limit of the semi-infinite column will move ahead until the data analysis limit (or the real bottom of the cell) is reached.

Results

It is helpful to clarify first the measure of accuracy in the simulations to be used, as well as the accuracy and useful radial range in the experimental data. The goal of modern sedimentation velocity analysis by direct modeling of LE solution is not merely to determine the average sedimentation rate and boundary midpoint, but to extract detailed information on the sedimenting solutes from the shape of the sedimentation boundary. As a consequence, our measure of goodness for the numerical approximation of the LE solutions will be the maximum deviation from the true solution in the sedimentation boundary. This is superior as a measure of error to the root-mean-square deviation (rmsd) across the whole concentration profile: The latter can exhibit more than 90% of data points in the solvent and solution plateaus (Figure 1), which are trivial to predict (Eq. 4), and therefore the rmsd value can be misleadingly low, even though the errors in representing the boundary shape may be unacceptably far above the experimental error (see also the discussion).

In typical SV experiments, the noise in the data acquisition is between 0.003 − 0.01 (OD units for absorbance optical data, or fringe shift units for interference optical data), such that a benchmark for the maximum deviation to remain below 0.001 seems to be a necessary conservative criterion. The radial increments of digitally stored data points are > 0.0007 cm (< 1,500 data points per scan for a 10 mm solution column), which sets an upper limit for the smoothness in the curvature of the fitting functions required in the data analysis.

From the point of view having practical data analysis in mind, it is important to consider the radial range for which reliable experimental data are available. Obviously, the theoretical errors of the LE solutions will be irrelevant outside this radial range. Because of optical artifacts close to the meniscus, the data analysis typically cannot start at values smaller than r* = m + 0.01 cm, a value assumed in the following (see discussion below). For the maximum radius, following common practice in sedimentation analysis we concentrated on the case where back-diffusion is absent within the radial range of data analysis (except when dealing with very small molecules), and chose the maximum radius accordingly. For medium and large proteins, the extent of back-diffusion decays rapidly with increasing distance from the bottom of the solution column. For example, in the configuration in Figure 4A below, the amplitude of signal arising from back-diffusion at a radius b – 0.5 mm is 0.003, and it is below 0.001 at b – 0.6 mm. (As described previously, the sedimentation equilibrium profiles Eq. 3 are upper limits for χ_F(r,t) and can therefore be used to predict whether, at the maximum radius considered in the data analysis, back-diffusion may need to be considered or the LE can be solved for a semi-infinite solution column.)

Figure 4.

(A) Concentration profiles calculated for a 100 kDa protein with a sedimentation coefficient of 6 S sedimenting at ω = 50,000 rpm in a 10 mm solution column (m = 6.2 cm, b = 7.2 cm). Under these conditions, back-diffusion does not extend into the data range shown. In order to serve as a reference solution, the LE was solved on a fine grid with N = 10,000 using the standard Claverie algorithm without consideration of rotor acceleration. The time-intervals between the boundaries shown are 300 sec, mimicking experimental data acquisition of scans at discrete times. For clarity, the concentration profiles at selected times are highlighted: 300 sec (red), 600 sec (blue), 4500 sec (cyan), and 7800 sec (green). (B) Difference to the reference solution when the LE solution is calculated on a coarse grid with N = 100, using the standard Claverie algorithm. The maximum deviation of ∼ 0.0085 occurs for the first ‘scan’ (red line), the boundary with the highest slope. For comparison, the bold black lines show the theoretical deviations from the representation of the boundaries as piece-wise linear segments, requiring the concentrations at the grid points to be identical to the true solution (δ₂ in Eq. 11, dotted line), or to be freely optimized (δ₀ in Eq. 10, dashed line). (C) On the same scale, the difference to the reference solution when the LE solution is calculated with the new algorithm using the placement of grid-points according to Eq. 12, at the same total number of initial grid points N = 100. (With α = 3.63, this resolution does not quite at the more conservative goal of α = 5, which would require N = 137 points and have a maximum deviation of 0.00065.) The dynamic reduction of grid points in the solvent plateau leads to the use of only 31 grid points at the time of the latest scan shown.

A premise of all currently used numerical solutions of the LE is the approximation of the concentration profiles by piece-wise linear segments. This is accomplished through the approximation by piece-wise linear elements (e.g., triangular hat function, Eq. 5). This motivated us to examine the error incurred with this segmented representation when applied to a curve shaped like a sedimentation boundary. As a reference curve, we chose a smooth boundary taken from the simulated sedimentation of a 100 kDa protein at t = 1770 sec (Figure 3A). Figure 3B shows the maximum error from a piece-wise linear approximation dependent on the density of grid points. For convenience, we scaled the grid point density relative to our measure of the boundary width σ defined in Eq. 9. The red lines in Figures 3A and B were calculated allowing the concentration values at each grid point to freely minimize the maximum deviation δ₀ (Eq. 10), i.e. without any constraints from any context with LE solutions. The solid red line shows the error encountered with the best relative lateral shift of the grid relative to the boundary, and the dotted line represents the worst-case relative position of grid to boundary. In order to explore what might happen if the concentration values at the grid points are constrained to be computed from LE algorithm, we also calculated the analogous quantities δ₁ and δ₂ encountered when the concentration values fall exactly on the ‘true’ curve (blue lines in Figures 3A and 3B). Clearly, for a coarse grid, the errors are very significant and above the noise in the ultracentrifugal data acquisition, while for finer grids with α-values greater than approximately 5, the errors are below our threshold.

Figure 3.

Theoretical deviation of a segmented piece-wise linear approximation to a smooth sedimentation boundary. (A) As a reference boundary, the concentration profile of a 100 kDa, 6 S – species sedimenting for 1770 sec at a rotor speed of 50,000 rpm was computed with a very fine grid (black line). Assuming a constant distance between neighboring grid points given by the expression σ (Eq. 9) (which corresponds to value of α = 1, or approximately 6 points available to describe the transition from solvent to solution plateau), the best possible boundary approximation with piece-wise linear segments is shown as red dotted line (optimizing the concentration values at each grid point to minimize the largest vertical deviation). The maximum deviation at the most favorable lateral offset of the grid relative to the boundary is termed δ₀ (Eq. 10), and represents the obligate error, a lower limit that any numerical LE solution will have to exceed. The blue line shows the segmented boundary representation when the concentration values at the grid points are constrained to the true values at these grid points. This deviation is δ₁ or δ₂ (Eq. 11), and is larger than δ₀. The inset shows an expanded view of the leading edge of the boundary. (B) The deviations from the smooth boundary change as a function of grid interval, plotted in units of α. Shown are the maximum deviations when the concentration values at the grid points are held at the ‘true’ value of the smooth curve, for the best and worst possible relative position of grid and boundary midpoint (δ₂ and δ₁, blue solid and dotted lines), respectively. The obligate error δ₀, when the concentration values are not held to the smooth curve, is shown as red solid line. For comparison, also shown is this error at the worst possible relative position of grid to boundary midpoint (dotted red line).

In order to examine the discretization error when solving the LE, we generated first a reference solution with very fine grid (total number of grid points N = 10,000), using sedimentation parameters and sample geometry as could be encountered in practice for the 100 kDa protein (Figure 4A). Next, we examined the accuracy of the LE solution obtained at different time-points with different grid spacings. Figure 4B shows the residuals to the reference solution obtained when using a grid of N = 100. Very similar patterns are observed when using either the Claverie or the moving hat method. It can be discerned that the largest deviations occur closer to the meniscus and for scans that are earlier in time, i.e. scans exhibiting steeper sedimentation boundaries. This observation holds true for all cases, except for very high N where the maximum errors are < 0.001 throughout. Further, a scalloped pattern can be discerned, suggesting the residuals to arise from the approximation of a curved line by piece-wise linear segments. This suggests that the simple geometric constraints introduced when using coarse grids may be a significant contributor to the observed deviations. To this end, we calculated the obligate error from discretization δ₀, as well as δ₁ and δ₂, for each time-point. The bold dotted and dashed lines in Figure 4B show these errors across the boundaries when plotted as a function of boundary midpoint. The close correspondence further supports that the simple discretization errors may be the dominant limitations in the accuracy of the LE solution at coarse grids.

We examined how the maximum deviation changes for different grids and different sedimentation parameters. For the sedimentation parameters of Figure 4, the green dotted line in Figure 5A shows the observed values as a function of grid density. In order to maintain the required accuracy indicated by the black dotted horizontal line, a grid interval of less than 0.004 cm (or a total grid number of N = 250 for the 10 mm column, see top axis) is required. A slightly finer grid is required when sedimentation is simulated (for both the reference and the coarse grid) considering the acceleration of the rotor (green solid and dashed lines). The Claverie algorithm using the equidistant grid (solid line) and the moving hat algorithm with the logarithmically spaced grid (dashed line) show very similar results. Analogously, we examined the maximum deviations for a range of sedimentation parameters, mimicking particles of increasing size and boundary steepness. For very small, rapidly diffusing particles, coarse grids are sufficient (e.g., 0.016 cm for the 1 kDa particle), while for very large, slowly diffusing particles that form steep boundaries, very fine grids are required (e.g., 0.0008 cm for the 1 MDa particle). In practice, this poses the difficulty of automatically choosing an appropriate discretization that neither is wasteful in computation time, nor leads to unacceptably large errors.

Figure 5.

Errors of numerical LE solution for different sedimentation parameters and grids. (A) Maximum deviation as a function of grid interval, or total grid size N for a 10 mm column, respectively. Shown are simulations based on the Claverie algorithm with equidistant grid (solid lines) and/or moving hat algorithm with logarithmically spaced grid following Eq. 8 (dashed lines) for particles with: 1 kDa, 0.3 S, 50,000 rpm (black); 10 kDa, 1.5 S, 50,000 rpm (blue); 100 kDa, 6S, 50,000 rpm (green), 450 kDa, 10 S, 60,000 rpm (magenta), and 1 MDa, 30 S, 50,000 rpm (cyan). The simulated sedimentation included a rotor acceleration phase with dω/dt = 200 rpm/sec, except for one comparison with the 100 kDa species indicated as thin green dotted line, which did not include rotor acceleration. In all calculations, a LE solution was calculated as a reference, with the same parameters on a very fine grid with N = 10,000. The maximum deviation from coarse-grid simulation was observed in the radial range excluding the 0.01 cm closest to the meniscus, and excluding the back-diffusion region (except for the smallest species). The benchmark of the desired maximum error of 0.001 is indicated as black dotted line. (B) The same data plotted as a function of α, the ratio between minimum boundary width σ and grid interval. σ was determined as described in Eq. 9. The colors and linetypes are unchanged. Additionally, the bold dash-dotted lines are the maximum deviations observed using the new algorithm with optimized non-equidistant grid Eq. 12.

Based on the hypothesis developed above that the major contributing factor to the deviations are the obligate errors arising from the segmented piece-wise linear approximation, we plotted the observed deviations from Figure 4A as a function of α, i.e. the ratio of smallest boundary width (as determined from the fitting limit close to the meniscus, see Eq. 9 above) to the grid interval, which determines the number of points available to describe the curvature of the boundary. This is shown in Figure 4B. Consistent with our hypothesis, and remarkably similar to the theoretical obligate error without solving the LE, for all sedimentation processes simulated the deviation scales in a very similar way, with an acceptable maximum deviation of 0.001 for values of α between 4 − 6. This corresponds to between 24 − 36 discrete points that are required to describe the transition between the solvent and solution plateaus of the smooth sedimentation boundary with sufficient accuracy. This observation can be used to provide a rational prediction of the most efficient, yet still acceptable grid density. As implemented in the program SEDFIT, the default value is α = 5.¹

Since the major limiting factor for the accuracy of the numerical LE solution appears to be the spatial discretization relative to the boundary width, we attempted to exploit this observation to construct an optimal grid with a density that is adequate for the steepest boundary close to the meniscus, and then continually decreases in density such that the diffusing boundary will be modeled by approximately a constant number of grid points. The scheme Eq. 12 outlined above has these properties. As can be anticipated from the significant drop in the obligate error as a function of radius (dotted lines in Figure 4B), assuming an optical artifact close to the meniscus covering 0.01 cm, in this scheme the grid spacing at the end of a 10 mm solution column is 9.3-fold larger than in the beginning. This translates into a grid that for the same α-value requires approximately fivefold fewer grid points. In combination with the scheme described above to inactivate grid points once the boundary has migrated across and they are not needed anymore, this algorithm will be more than fivefold faster. Conversely, when using the same total number of grid points N, the improved spacing of the grid points provides an increase in the α-value by a factor of five.

In order to establish the correct implementation of this algorithm, we first verified that for all simulations the results correctly converged to the previously calculated fine-grid reference solutions when using a very high number of grid points (data not shown). Next, we tested its performance by applying it to our reference sedimentation in Figure 4, using the same number of total grid points (N = 100). While the traditional equidistant grid provides an α-value of 0.73 and the residuals in Figure 4B, the optimized grid at N = 100 corresponds to α = 3.63 and provides the residuals shown in Figure 4C. It can be discerned that the magnitude of the residuals is much smaller. Whereas the standard Claverie algorithm has a maximum error ∼ 0.0085, the new algorithm has a maximum error of ∼ 0.001. Interestingly, the residuals show a more uniform distribution across the cell, with the scalloped residual pattern increasing in distance but not in height (Figure 4C). This shows the grid design was successful in providing constant discretization relative to the diffusionally broadened boundary. For the time range shown in Figure 4, the simulation starts with 8% of the grid points active, never exceeding 70%, and for last concentration profile only 31% of the grid points remain active, which shows that the dynamic reduction of grid size is also highly effective. This gain is independent of the α-value.

We re-analyzed the sedimentation of different size particles using the new algorithm at different α-values. For small particles, where back-diffusion is shallow and cannot be excluded, the new algorithm performed slightly worse than the standard Claverie algorithm with equidistant grid. (For example, for the 10 kDa particle, a grid with total size N = 145 provides a maximum deviation of 0.0024 with the new algorithm, but 0.0018 with the equidistant grid.) The lack of gain in accuracy is due to presence of back-diffusion, which produces similarly steep boundaries close to the bottom as are encountered close to the meniscus, and this cannot be appropriately matched by the continuously sparser grid in the new algorithm. Further, the ability to scale the discretization according to α breaks down in the presence of back-diffusion. This is a reminder that the error analysis and the grid design described in the present paper was based on the absence of back-diffusion. However, the gradients in the sedimentation profiles of small particles are relatively shallow throughout, and the standard algorithms pose no difficulty and are already highly efficient (see the black and blue lines in Figure 5A).

In contrast, when back-diffusion is localized to the bottom of the cell and the boundary conditions for semi-infinite column can be used, the theoretical predictions on which the new algorithm is based hold true. As shown by the dash-dotted lines in Figure 5B, despite the approximately fivefold reduction of grid size N throughout, for a given α value the accuracy is similar to that with the larger equidistant grid, and the maximum deviation follows the predicted values. When comparing grids of similar size N, again, the gain in accuracy is very significant. For example, for the 1 MDa particle the simulated sedimentation with N = 269 using the new algorithm provides a maximum deviation of 0.001 (α = 5), whereas with the moving hat algorithm a maximum deviation of 0.12 is obtained (α ∼ 1). At a slightly finer grid with N = 385, the new algorithm generates a maximum deviation of 0.0007 (α = 7) versus 0.011 (α ∼ 1.5) with the standard moving algorithm. We conclude that the new optimized grid eliminates the need for computationally very costly high total number of grid points, while providing a predictably high accuracy.

Finally, we compared the results with the ASTFEM finite element approach proposed by Cao & Demeler [43]. Instead of eliminating the steep back-diffusion region exhibited by large macomolecules, Cao & Demeler placed a higher density of grid points into the back-diffusion region. They observed that the ASTFEM method is stable for sedimentation of very large particles even when using very coarse grids, such as N = 100 – numerical discretization parameters for which both the standard Claverie and the moving hat methods are not designed and show instabilities – while reporting only minor differences between the algorithms when using larger grid sizes for the same sedimentation parameters. Because Cao & Demeler did not consider the regions of steepest gradients in their measure of goodness of fit (excluding both the 5 % of data points closest to the meniscus and the 5% closest to the bottom), we re-examined their results in the light of the criteria developed in the present study and compared them to the results with the new method proposed in the present study.

As one benchmark model system, Cao & Demeler used a model system of a particle with s = 10 S and D = 2×10⁻⁷ cm²/sec sedimenting at 60,000 rpm, for which the sedimentation boundaries at different grid sizes are shown in Figure 6 (which is reproduced from Figure 8B in [43]). Although the ASTFEM approach provides stability at coarse grids, very large errors are encountered (e.g. red line in Figure 6 for N = 101). Despite the exclusion of the first 0.035 cm from consideration, the maximum error at N = 101 was ∼0.03, dropping to ∼0.01 at N = 201 [43]. In none of the examples shown in [43] was the maximum error below our threshold of acceptable accuracy. This result is consistent with our predictions on the obligate errors at grids as coarse as those in [43].

Figure 6.

Accuracy of simulated sedimentation obtained with Cao & Demeler's ASTFEM method for a model system of a particle with s = 10 S, D = 2×10⁻⁷ cm²/sec (corresponding, for example, to an elongated 450 kDa protein with f/f₀ ∼ 2.0) sedimenting at 60,000 rpm in a 7 mm solution column from 6.5 cm to 7.2 cm. This is Figure 8B from Cao & Demeler [43], reproduced with permission. It shows the boundary approximations with the ASTFEM method at different grid size values N for the same sedimentation parameters. The red line is the simulated boundary at a value of N = 100. For comparison, the calculated sedimentation boundaries with the same parameters using the new non-equidistant static grid finite element algorithm are shown in Figure 6B.

Figure 7 shows the concentration profiles encountered for the same sedimentation parameters using the new generalized dynamic Claverie method for semi-infinite solution column with static, non-equidistant grid, with the left and right analysis limits r₁* and r₂* placed at 6.51 cm and 7.165 cm, respectively. For this system, the standard accuracy of 0.001 (α = 5) for modeling experimental data would require approximately N = 300 initial grid points. However, for comparison with Figure 6B, we calculated the concentration profiles when the grid size was constrained to the same N = 100 total points (red dotted line in Figure 7A and solid red line in Figure 7B). This corresponds to α = 1.7, and resulted in a maximum error of 0.0043. From visual comparison of Figure 6 and 7B over the same radial range, an improved accuracy by more than an order of magnitude can be easily discerned. At the same time, the dynamic reduction of grid points leads to the elimination of 80% of the grid points at the time point of the last scan shown in Figure 7A, and the elimination of greater than 50% of the grid points at any time-point.

Figure 7.

Sedimentation profiles calculated for the same parameters as in Figure 6. (A) Reference concentration profiles were computed with a very fine grid (N = 10,000) , shown in time-intervals of 100 sec (black line). The concentration scale is truncated, and reaches values > 900 at the bottom, but quickly decays with increasing distance from the bottom, e.g. 1000-fold within 0.01 cm of the bottom. Also shown as dashed red line is the LE solution with the new non-equidistant, static grid algorithm with N = 100 (corresponding to α = 1.7) eliminating back-diffusion by placing the left and right analysis limits r₁* and r₂* at 6.51 cm and 7.165 cm, respectively. Over this radial range, the maximum error to the data shown is 0.0043. The dynamic reduction of grid points in the solvent plateau leads to the use of only 20 points at the time of the last scan shown. (B) Focusing on selected early time-points, this plot is showing the ‘true’ boundary (bold black line) and the same LE solution at N = 100 and N = 200 with the non-equidistant grid (red line and thin white line within the red, respectively). The segmentation of even the red N = 100 line cannot be easily discerned visually (e.g. from the uneven thickness of the black rim in the leading shoulders caused by the piece-wise linear red line within the black, and by the red rim caused by the thin white N = 200 line within the red line). Nevertheless, as expected, for N = 100 at α = 1.7 the discretization is not yet regarded sufficient as judged by the maximum deviation of 0.0043 between r₁* and r₂*. The standard accuracy of 0.001 for modeling experimental data requires approximately N = 300 grid points. The errors at N = 100 are approximately 20fold smaller at r₁* than those seen in Figure 6 at the same grid size with Cao & Demeler's ASTFEM method. The difference is due to the placement of the highest density of the radial grid points in the latter method close to the bottom to stabilize computation of the back-diffusion region, whereas in the generalized Claverie method with non-equidistant grid the highest density is found where the steepest sedimentation boundaries occur. For comparison, the step-functions Eq. 4 are shown as gray lines. These have a maximum deviation of 0.49, but an rmsd of only 0.041.

Discussion

In the last decade, the ability to solve efficiently the partial differential equation for sedimentation, diffusion, and chemical reactions in the centrifugal field has transformed experimental approaches and the data analysis in analytical ultracentrifugation. It has significantly improved detection limits and resolution, and our ability to quantitatively describe complex sedimentation processes of macromolecular mixtures. In particular, the convenient use of LE solutions as model function in non-linear regression and/or as kernels in Fredholm integral equations enabled many new techniques, including direct boundary modeling with distributions of LE solutions, and direct boundary modeling with systems of LEs with chemically reacting species, which found wide-spread application in physical biochemistry, for example, in the study of protein-protein interactions [46, 49, 59, 71], the detection of immunogenic oligomeric species of protein pharmaceuticals [10-13], global multi-signal sedimentation velocity analysis of reversible multi-protein complexes [23, 57, 72-74], and other applications [52].

Many different algorithms for numerically solving the LE have been described over four decades [34, 36, 41-43, 46, 59, 63, 75, 76], and their further development is still a topic of active investigation since it is critical for many practical applications [21]. Recently, we have noted that the boundary conditions for a permeable bottom (leading to the model of a semi-infinite solution column) can facilitate significantly the LE solution by removing numerical instabilities in the steep gradient of the back-diffusion region. This was introduced first as a tool to stabilize the system of LEs describing the sedimentation of chemically reacting mixtures of macromolecules [59], but later also applied to simplify the LE solution of non-interacting, ideally sedimenting species [56]. Clearly, back-diffusion cannot be excluded when describing the sedimentation of small molecules, where the radial range of back-diffusion is broad and extends significantly into the solution column. However, in this case the gradients are shallow and pose no difficulty experimentally or computationally. For large particles, however, the extent of back-diffusion is confined to a narrow region close to the bottom of the cell and has to be excluded from consideration in the practical data analysis, because: (1) it cannot be imaged reliably due to the refractive index gradients; (2) the high concentrations encountered would make the consideration of repulsive forces between macromolecules indispensable; and (3) the solubility limit of many proteins is exceeded, leading to a phase transition and generation of surface films that will substantially alter the back-diffusion. The decision whether or not to exclude back-diffusion is usually not further problematic, since its extent can be visually discerned from the experimental traces, and in theory it can be easily predicted for any set of sedimentation parameters and automatically compared to the radial range of experimental data to be considered [56].²

Having eliminated one of the numerically problematic features of sedimentation profiles for large macromolecules using the permeable boundary conditions, in the current paper we have reappraised the accuracy of different finite element algorithms for the remaining problem of simulating sedimentation in the semi-infinite column. Based on the findings, we propose a series of modifications of the original Claverie approach that leads to approximately an order of magnitude or more improved accuracy and efficiency for solving the LE in the absence of back-diffusion.

Perhaps the most striking observation was that for the semi-infinite solution column, both finite element models predict surprisingly accurate concentration values at the spatial grid points. For the parameter range tested with particles up to 30 S (and with at least several grid points available for the steepest boundary) few differences were observed between the performance of the moving hat and the Claverie approach. This suggests that, at least for ideally sedimenting non-interacting species, the advantage of the moving hat algorithm reported previously [42, 43] may be due to improved stability in the back-diffusion region, a factor removed in the current study (see above).

Cao & Demeler have suggested that the Claverie finite element approach suffers from the problem of ‘numerical diffusion’ [43]. This is in conflict with the results presented here. We believe Cao & Demeler have misinterpreted their findings: Numerical diffusion is an effect that occurs in finite difference schemes due to the combination of fast translation of the boundary described with large spatial increments (i.e. high Péclet numbers) [41, 64]. It is noteworthy that the errors observed by Cao & Demeler were strongly dependent on the time step Δt [43]. However, a hallmark of numerical diffusion is that it cannot be eliminated by reducing the time-step. Indeed, an analytical expression for the excess ‘numerical diffusion’ ΔD = sωrΔr/2 encountered in naïve finite difference schemes has been given already by Goad & Cann [35] (consistent with our observation ΔD ∼ sωΔr reported in [41]). Goad & Cann also gave a prescription to minimize it either by diminishing the radial grid interval Δr, using higher-order accuracy schemes for the gradients determining the fluxes, or using grids with moving frame of reference [35]. We do see numerical diffusion with simple finite difference approaches because of the low approximation of the spatial derivatives of the concentration profile [35, 41, 64], however, this effect is absent in the finite element approach using hat functions, because the latter naturally can describe the spatial derivatives much better, equivalent to a forth-order compact finite difference approximation [64]. We believe the poor numerical results observed by Cao & Demeler were caused by a poor choice of large time-steps causing negative concentrations, an effect which we can reproduce (data not shown) but is easily eliminated by appropriate adaptive time-step management.³

In fact, we found the accuracy of the Claverie finite element propagation scheme is so high that, for obtaining the accuracy required in experimental data analysis, the chief limitation arises not from the properties of the LE, but rather from the simple error of approximating the smooth boundary by piece-wise linear functions! This error is not at all dependent on the algorithm for computing the evolution of concentration values at the grid points, but is an obligate geometric consequence of using linear basis elements. Although it seems an obvious concern in retrospect, to our knowledge, this source of error has previously not been systematically appreciated in the LE literature, possibly because it has been masked by larger numerical errors in the back-diffusion region – which are now removed in the semi-infinite column. However, even in the study by Cao & Demeler where numerical errors in the back-diffusion region were minimized [43], the large obligate errors obtained from too coarse grids (e.g, Figure 6) were not recognized or addressed. It should be noted that this error is not artificially introduced in this theoretical study but highly relevant in practice, since the typical grid density used to compute the LE solutions are lower than the density of experimental data points, and also lower than the radial resolution of the optical systems, and therefore are of concern when the experiment involves conditions that lead to the observation of steep concentration gradients. In regard to the latter, the new algorithm described in the present paper adaptively adjusts the prediction of maximum concentration gradients that need to be considered according to the relative location of meniscus and first data point r₁* to be modeled.

In examining this obligate error of LE solutions from linear segmentation, we find it most instructive to focus on the maximum deviation incurred in the sedimentation boundary, as opposed to the overall rmsd, since the data points in the solvent and solution plateau are trivial, and their contribution confounds the analysis and provides misleadingly low error values (see below). This also corresponds well to the judgment of the quality of fit in practice, where the bitmap representation of the residuals [55] has proven to be a highly useful tool to emphasize the quality of fit at each time-point in the sedimentation boundaries. Clearly, computed LE solutions that show excellent accuracy in the solvent and solution plateau, but exhibit large numerical inaccuracies just in the representation of the boundary shape, will not be suitable for use in detailed data analysis in practice. When analyzing experimental data, the accuracy in the boundary shape is indispensable, for example, when deconvoluting diffusion in order to achieve higher resolution sedimentation coefficient distributions [53, 54], characterizing trace species [15-18, 77], determining molar masses and size-and-shape distributions [56], or when studying chemically reacting species and their equilibria and kinetics [46, 49, 59, 71].⁴

Our observation that the largest errors occur with the steepest boundaries near the meniscus close to the beginning of the sedimentation seems to coincide with occasional reports of large deviations in the fit of experimental scans from the beginning of the run close to the meniscus. Whether or not the latter can be attributed to errors in the LE solution certainly depends on the grid size used in the computation. While some of the grid sizes suggested recently by Cao & Demeler [43] are too coarse for large macromolecules (Figure 6, see Results section above), the default settings in SEDFIT are conservatively designed to lead to grid size that warrant a default numerical accuracy in the sedimentation boundary better than the noise of data acquisition. Considering that the steepest boundaries in the beginning of a run are also most susceptible to experimental imperfections, chiefly convection, we believe experimental factors to be usually limiting. This is corroborated by the observation that with SEDFIT fits within the noise of data acquisition can be routinely achieved.

Recognizing that, for the semi-infinite solution column, the grid density relative to the boundary width (the α-value) is a factor that can scale uniformly the maximum errors involved in the discretization, we have used simple physical considerations to rationally predict the computationally most parsimonious grid size required to ensure a pre-set accuracy. We found that for a given geometry of the solution column the product $\omega \times \sqrt{M}$ or $\omega \times \sqrt{s∕D}$ scales the total number of grid points required. This is different from the empirical scaling relationships described by Cao & Demeler, suggesting that N be largely independent of s, but N ∼ D^−1/4 [43]. The different observations may be due to the problematic choice of the rmsd (or more precisely the L² –norm over the central 90% of the solution column) as a measure of error, and perhaps due to the effects that back-diffusion has on the numerical accuracy in their algorithm.

Although the finite element method as introduced by Claverie was described with equidistant grid points, it can be naturally extended to arbitrarily placed spatial grid points, when the general expressions for the matrix elements given in [42] are used. We have exploited this possibility to generate a grid that has the highest density where the steepest gradients in the semi-infinite column are encountered, following the expressions for the estimated increase in boundary width as a function of radius. It is implemented in SEDFIT adaptively adjusting to the given sedimentation and diffusion coefficients, rotor speed and acceleration, and radial range to be modeled. Even though the moving hat method also exhibits a slightly higher density closer to the meniscus, imposed by its inherent symmetry requirements, the change across the solution column is much stronger in the new method, which uses the considerations of obligate error from the approximation with piece-wise linear elements to predict the optimal grid spacing. An alternative approach to strongly diminish the obligate error while maintaining coarse grids would be the use of quadratic, or other curved, elements replacing the hat functions. However, this would lead to more complicated band matrices to be solved at each time step, offsetting some of the advantage [64].

Following the idea of Cao & Demeler [43], with the static non-equidistant grid approach one could also place more grid points in the region close to the bottom region. However, we did not pursue this since for the configurations exhibiting shallow back-diffusion, when a description of back-diffusion is needed, the standard Claverie algorithm works very efficiently and accurately in our hands, and for configurations exhibiting steep back-diffusion the permeable boundary condition eliminates numerical problems in this region without extra computational cost. In fact, the dynamic inactivation of grid points permits the entire leading solution plateau to be dynamically eliminated from the computation and replaced by the trivial analytical computation of solution plateaus.

We also did not further explore the application of more complex time-dependent grids. The continuous dynamic inactivation of the higher density portion of the grid once the boundary has passed is a new approach that has little computational overhead and provides very satisfactory results. Similarly, the inactivation of points in the solution plateau facilitated by the boundary condition for the semi-infinite solution column is straightforward, and in combination, the two approaches generate a dynamically changing active set of grid points that maintains an optimal density of points while co-migrating with the sedimentation boundary.

In conclusion, based on a detailed error analysis and simple physical principles, we have developed a new finite element method for solving the LE on a semi-infinite solution column, using a static, non-equidistant grid optimized for achieving a uniform pre-set accuracy, in conjunction with adaptive time-steps in Crank-Nicholson scheme and in combination with a novel approach for dynamic inactivation of grid points in the trivial regions of the solvent and solution plateau. From our experience so far, we believe it outperforms existing algorithms by approximately an order of magnitude or more in computation time or accuracy, not in the least because it can estimate the minimal grid size necessary to achieve a preset accuracy, if measured by the maximum deviation in the sedimentation boundary. This can benefit several areas where the computation of LE solutions is still posing constraints. For example, this principle can be applied to systems of coupled LEs for chemically reacting species [46, 49, 59, 71], which are significantly more difficult to compute, and where the large computation time for the LE solutions is currently still affecting practical non-linear regression in global modeling. For using LE solutions as kernels in integral equations for sedimentation coefficient distributions [53, 54] and size-and-shape distributions [56], the operations connected to the handling of the typically very large number of experimental data points are frequently the most time consuming [53]. However, when radial pre-averaging is applied to reduce the number of experimental data points, fast and precise LE solutions can become limiting. This is important, for example, for embedding sedimentation coefficient distributions into non-linear regression of additional parameters, such as one or more scaling parameters for the frictional ratio f/f₀ for mixtures of globular macromolecules, or the persistence length for distributions of linear macromolecules, and/or geometric parameters of the solution column [54]. Other applications where the calculation of LE solutions are still the limiting factor are the modeling of macromolecular sedimentation in the presence of dynamic density gradients formed by sedimenting co-solutes [58], and the modeling of sedimentation of macromolecular distributions at high concentrations under non-ideal conditions (P. Brown and P. Schuck, manuscript in preparation). The latter topics are of increasing interest in the characterization by sedimentation velocity of protein therapeutics and their formulations with regard to trace contents of immunogenic aggregates, which is an area of emerging importance [15-18, 78]. They are of importance also, for example, for the detailed analysis of proteins in the presence of high concentrations of co-solvents stabilizing or de-stabilizing the conformation. Since the LE solutions are the key to the detailed quantitative interpretation of sedimentation velocity experiments, their more efficient and accurate calculation may also facilitate other more advanced applications of analytical ultracentrifugation to the study or macromolecules in solution and their interactions.