Dosimetric impact of motion in free-breathing and gated lung radiotherapy: A 4D Monte Carlo study of intrafraction and interfraction effects

Abstract

The purpose of this study was to investigate if interfraction and intrafraction motion in free-breathing and gated lung IMRT can lead to systematic dose differences between 3DCT and 4DCT. Dosimetric effects were studied considering the breathing pattern of three patients monitored during the course of their treatment and an in-house developed 4D Monte Carlo framework. Imaging data were taken in free-breathing and in cine mode for both 3D and 4D acquisition. Treatment planning for IMRT delivery was done based on the free-breathing data with the corvus (North American Scientific, Chatsworth, CA) planning system. The dose distributions as a function of phase in the breathing cycle were combined using deformable image registration. The study focused on (a) assessing the accuracy of the corvus pencil beam algorithm with Monte Carlo dose calculation in the lung, (b) evaluating the dosimetric effect of motion on the individual breathing phases of the respiratory cycle, and (c) assessing intrafraction and interfraction motion effects during free-breathing or gated radiotherapy. The comparison between (a) the planning system and the Monte Carlo system shows that the pencil beam algorithm underestimates the dose in low-density regions, such as lung tissue, and overestimates the dose in high-density regions, such as bone, by 5% or more of the prescribed dose (corresponding to approximately 3–5 Gy for the cases considered). For the patients studied this could have a significant impact on the dose volume histograms for the target structures depending on the margin added to the clinical target volume (CTV) to produce either the planning target (PTV) or internal target volume (ITV). The dose differences between (b) phases in the breathing cycle and the free-breathing case were shown to be negligible for all phases except for the inhale phase, where an underdosage of the tumor by as much as 9.3 Gy relative to the free-breathing was observed. The large difference was due to breathing-induced motion/deformation affecting the soft/lung tissue density and motion of the bone structures (such as the rib cage) in and out of the beam. Intrafraction and interfraction dosimetric differences between (c) free-breathing and gated delivery were found to be small. However, more significant dosimetric differences, of the order of 3%–5%, were observed between the dose calculations based on static CT (3DCT) and the ones based on time-resolved CT (4DCT). These differences are a consequence of the larger contribution of the inhale phase in the 3DCT data than in the 4DCT.

I. INTRODUCTION

The development of 4DCT scanning technology allows the acquisition of multiple image-sets of the breathing cycle.^1–3 Several groups pioneered 4D image-guided radiotherapy by incorporating the concepts of 4DCT into radiotherapy.^4–6 With this information, tumor motion can be tracked in real time, and radiation treatment planning or delivery strategies can be adjusted to account for tumor motion by applying an internal target margin (ITV) or by gated and tracking delivery techniques.

Tumor motion is of particular interest for intrathoracic tumors. It is here where respiratory (diaphragm) or cardiac motion presumably causes the biggest displacement. The size of displacement depends considerably on the patient and the location of the tumor. Variations are due to tumor position in the lung, patient breathing pattern, lung capacity, etc. Organs in the thorax and abdomen move approximately periodically along the cranio-caudal and anterior-posterior axes during respiration with a period of about 4 s.^7,8

In the case of lung cancer, low local tumor-control and poor long-term survival have been observed when using radiation therapy. The difficulties with trying to cure lung cancer by radiation therapy are caused by insufficient tumor coverage (geographical failures) or by the inability to escalate dose to a level needed for successful treatment.⁹ Intensity modulated radiation therapy (IMRT) allows improvements in dose conformality. However, organ motion can negate some of the advantages of IMRT because of the need for large margins or interplay effects between tumor motion and leaf motion in the case of small segment delivery.¹⁰

Although technology might still be in the development stage for treatment delivery,¹¹ sophisticated dose calculation methods can be used to investigate motion effects. Monte Carlo methods have been used in lung and head-and-neck regions where they are believed to be more accurate than conventional pencil beam and collapsed cone methods.^12–15 The evaluation of breathing motion effects in lung cancer treatment planning has indicated that between two and five breathing phases are required to accurately predict the total dose delivered to the lung.^16,17 These studies did not account for the variation of the delivered doses due to intrafraction or interfraction effects that occur during or between treatment fractions due to coughing, breath hold, sneezing, etc.

For this study, dosimetric effects in IMRT due to patient breathing during treatment were investigated with an image-guided 4D Monte Carlo (4D MC) framework developed in-house. The results were compared with predictions made by the commercial treatment planning system corvus (North American Scientific, Chatsworth, CA). The dosimetric analysis was done for three patients for whom the Varian real-time position management system [(RPM) Varian Medical Systems, Palo Alto CA] was used during radiation treatment to identify the breathing phase to which the delivered dose was given. Interfraction and intrafraction variations of the delivered dose were studied considering free-breathing and gated treatments. Combining the doses from various breathing phases generated composite dose distributions.

The present work is divided into three studies:

1. Comparison of dose predictions based on the corvus pencil beam and Monte Carlo calculations for lung IMRT using free-breathing CT scans;

2. Assessing dosimetric effects of organ motion by considering individual breathing phases and the free-breathing case for IMRT fields; and

3. Assessing interfrcation and intrafraction motion effects in free-breathing and gated radiotherapy combining the dose distributions from each of the breathing phases to generate a “composite” plan.

The novelty of this work is that interfraction and intrafraction variations of the delivered dose are studied for free-breathing and gated radiotherapy with a 4D MC toolkit using real patient RPM trace signals measured during treatment. Radiotherapy treatment planning is typically based on 3D helical CT. However, during dose delivery, the patient is typically either treated under free-breathing or restricted free-breathing (gating). The 4DCT data combined with an on-line RPM trace signal can be used to characterize the patient’s breathing pattern during treatment. In this study we investigated if (a) 3D helical CT and (b) 4DCT scans can lead to differences in the planned and delivered dose. In previous studies equal weightings were given to breathing phases when combining them to produce composite conformal dose maps, while in the present article individual patient weightings were applied. In addition, differences between dose distributions (i.e., such as between Monte Carlo and pencil beam, or between inhale and exhale dose distributions) were analyzed as a function of the tissue density within a specific volume of interest, i.e., clinical target volume (CTV) or ITV.

II. METHODS AND MATERIALS

II.A. Patient imaging and motion analysis

Three patients with lung cancer were used in this study and will be referred to as Patient 1, 2, or 3. All patients had two sets of pretreatment CT scans taken a using helical CT: (a) a “free-breathing” (FB) scan and (b) an axial cine-mode scan. The 4DCT data were acquired on a GE Lightspeed Qx/I 4-slice CT scanner. For thorax scans a current of 170 mA was used for the 140 kV tube potential with a CT slice thickness of 2.5 mm, helical pitch of 7.5 mm per rotation, and gantry rotation speed of 0.8 s per rotation. The total 3D helical scan was approximately 20 s.

Respiratory motion was recorded by the RPM system in the axial cine mode. Reconstructed CT images were retrospectively sorted into spatiotemporally coherent volumes with phase information of the breathing pattern. For the three patients considered, tumor motion was observed to have amplitudes of the order 1.5–2.5 cm and was mainly in the superior-inferior direction. In the present study the 4DCT images were sorted into ten phases. We denote these phases by SE0%, SE10%, SE20%, SE30%, SE40%, SE50%, SE60%, SE70%, SE80%, and SE90%, where SE0% and SE50% are the inhale and the exhale position in the breathing cycle, respectively. Correspondingly, SE10% to SE40% are phases leading from inhale to exhale, and SE60% to SE90% are phases leading from exhale to inhale.

In addition to collecting motion information in the pre-treatment CT scans, RPM data were recorded during treatment, on a daily basis. The RPM signal was then used to generate a probability density function (PDF) to describe the various phases of the breathing cycle for each treatment day. As an example, the RPM signals for day 1 and day 6 (first day of the second week of treatment) are presented in Fig. 1. In addition, in Fig. 1 the PDF of the breathing period and phase for day 1 and day 6 of treatment of Patient 1 is presented for free-breathing and gated deliveries. For both RPM signals the mean value of the amplitude was subtracted from the measured amplitude to correct for baseline drifts. The part shown in red represents the gated-treatment situation. The RPM signal shows a significant variation in amplitude from week 1 to week 2 of the treatment. Figure 1(b) illustrates that the breathing period also changes between the two consecutive weeks of treatment, where for days 1 and 6 the breathing period is approximately 4 and 3 s, respectively. Figures 1(c) and 1(d) show the PDF of the breathing phase for the free-breathing and gated treatment, respectively, where the phase varies from 0 to 1, representing respectively, 0 and 2π rad (the sampling bin size was 0.02). The gated treatments were performed for the exhale phase, where the radiation beam was active whenever the amplitude of the RPM trace signal was within 10%–15% of the maximum exhale amplitude. Inhale and exhale phases correspond respectively to the 0.0 and 0.5 values (i.e., 0% and 50% of the breathing cycle). The free-breathing PDF is more or less constant, except for a peak around 0.8 in the transition between exhale and inhale corresponding to shallow inhales by the patient. In the case of the gated PDF, the distribution is different from day 1 to day 6, indicating that possibly day-today variations of the breathing may affect the dose delivered to the tumor.

Fig. 1.

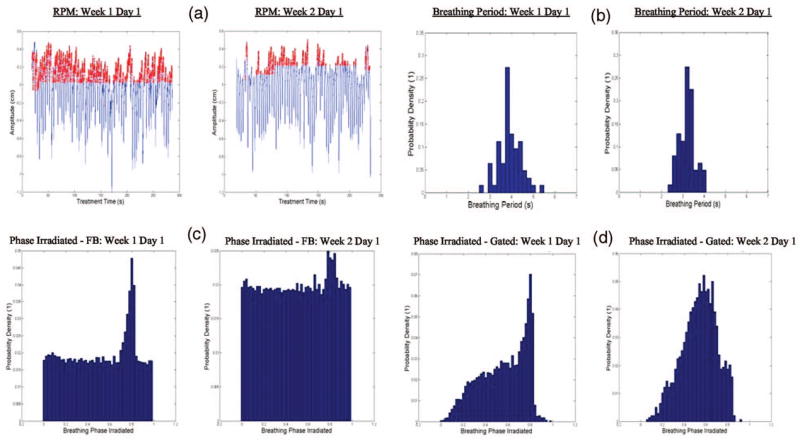
(a) Breathing amplitude as a function of treatment time is shown as an example to illustrate the variation between treatment fractions considering the RPM signals for free-breathing (in blue) and the gated treatment (in red); (b) PDF for the breathing period on days 1 and 6; (c) PDF for the breathing phase irradiated in free-breathing for a single day (days 1 and 6); (d) PDF for the breathing phase irradiated for gated treatment for a single day (days 1 and 6).

For treatment planning purposes, the gross target volume (GTV) and CTV were contoured for Patient 3 only, while for all patients the ITV was contoured (for Patient 1 three distinct volumes—ITV1, ITV2, and ITV3—were identified by the physician for the primary/secondary tumors volumes). The ITV is created by a visual inspection of the tumor motion on all the breathing phases and then contouring a region on the free-breathing CT that encompasses all tumor motion. In order to account for random and setup errors, a margin was added to the GTV, CTV, or ITV to generate the PTV. The margins were 8, 5, and 7 mm for Patients 1, 2, and 3, respectively. The margins were added to account for random and setup uncertainties during treatment. Special attention was given to avoiding irradiating the heart and the spinal cord. In Fig. 2, a CT slice obtained for each patient is given as an example, where tumor volumes are represented. In addition for each patient, the distributions of tissue density within the volume of interest are shown.

Fig. 2.

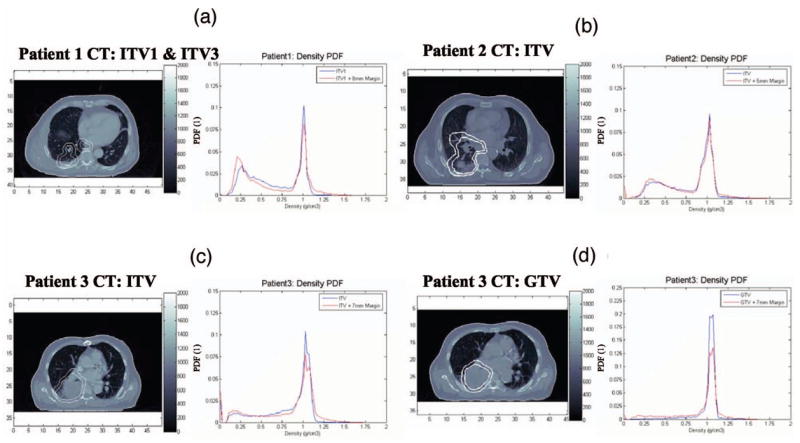
The distribution of tissue densities for all patients within ITV and GTV volumes obtained for the free-breathing static CT. (a) ITVs for Patient 1, (b) ITV for Patient 2, (c) ITVs for Patient 3, and (d) GTVs for Patient 3.

The probability tissue-density functions (PTDFs) peak around the density of 1.0 g/cm³ representing the tumor. In addition, the ITV regions contain significant volumes of lung tissue mostly in the range of 0.25–0.3 g/cm³. For Patient 3, the GTV contains the tumor with very little lung within the planning target volume. However, this GTV does not account for possible motion due to respiration, while the ITV approach accounts for motion of the tumor during respiration and therefore has both regions of tumor and lung.

Figure 3 shows a comparison of the PTDF within the PTV regions of Patients 1 and 2 (Patient 3 has values similar to Patient 1), for the FB and inhale breathing phases. The FBCT has a PTDF tissue distribution within the PTV volumes that is approximately equal to that of the exhale phase. However, this tissue distribution is different from that present in the PTV volume represented on the inhale phase. These differences between FB and the inhale phases occur in the lung and in the tumor volume for Patient 1, where both show significant changes in the respective density distribution. For Patient 2, less pronounced density variations were observed in the lung and tumor volume.

Fig. 3.

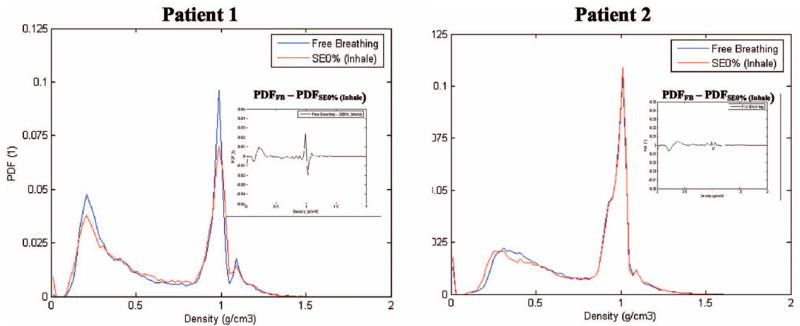
Comparison of the probability tissue-density function in the PTV for Patients 1 and 2 comparing CT scanning methods: (a) Helical 3DCT scan with patient under free-breathing and (b) 4DCT scanning with the SE0% (inhale phase) represented in the figure. This illustrates density variations due to patient breathing.

II.B. Treatment planning

IMRT treatment planning and volume of interest contouring were performed with the corvus planning system on the FBCT. The prescribed dose for each patient was 63 Gy for ITV1/2/3 of Patient 1 and 45 Gy for Patients 2 and 3, where the organs at risk were the heart, lungs, esophagus, and spinal cord. The tumors were irradiated with approximately uniformly distributed beams around the tumor with either five, seven, or four beams, respectively, for Patients 1, 2, and 3. The corvus pencil beam (PB) algorithm was used for dose calculation and inverse planning.

II.C. Image registration

To include nonrigid motion, i.e., organ deformation, in the dose calculation, the static results are combined using deformable image registration. A B-spline deformable registration method¹⁸ based on the Insight Segmentation and Registration Toolkit (ITK), was used. We registered all breathing phases to the end-of-exhale (EEH) volume.

The deformation vectors are computed using B-spline interpolation from the deformation values of points located in a coarse grid, which is usually referred to as the B-spline grid. The parameter space of the B-spline deformation is composed by the set of all the deformations associated with the nodes of the B-spline grid.²⁷ The B-spline grid used was a 50 mm cube. Based on expert identified homologous points in both end of inhale and EEH phases were represented and matched with B-spline. The method achieved an accuracy of 4.21±2.42 mm in the lungs for these points.

II.D. Monte Carlo dose calculation

For phase space fluence calculation for the VARIAN 2100C/D photon linear accelerator we used EGSnrc¹⁹ and for patient dose calculation we used DPM²⁰ (ECUT and PCUT were 700 and 50 keV, respectively) Monte Carlo (MC) commissioning involved matching calculated and experimental results for both percentage depth dose (PDD) and off-axis ratios (OAR) obtained from standard open fields adopting the method described elsewhere¹⁵ (see Fig. 4).

Fig. 4.

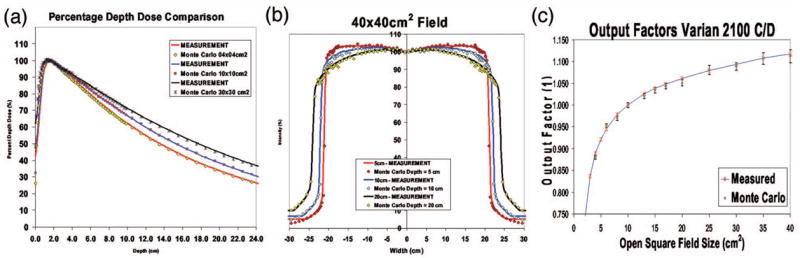
Comparison of Monte Carlo predictions with measured data from the Varian 2100C/D linac: (a) percentage depth doses for 4 × 4 cm², , and 30 × 30 cm² fields; (b) profiles in 40 × 40 cm² field at depths of 5, 10, and 20 cm; (c) output factors for all open fields.

The PDD and OAR match to within 2 mm/2% and the open fields output factors match to within 0.6% of the measured values after the appropriate backscatter correction due to the X and Y jaws to the ionization chamber.²¹ A calibration factor was obtained for 10 × 10 cm² field to convert MC units of dose per unit incident particle into dose per monitor unit.

In simulating patient geometry, mass density and atomic composition at each point of the CT, a Hounsfield unit (HU) conversion to electron density was used based on the Schneider et al.²² method. In this method, HUs for 71 human tissues, whose characteristics were taken from the literature, were calculated. Mass density and elemental weights of any HU were obtained via linear interpolation. The HU conversion used a total of 14 materials according to Vanderstraeten et al.²³ All MC results were converted from dose-to-medium to dose-to-water for comparison with the planning system.

Leaf geometry was incorporated into photon MC with the use of the Siebers et al. method.²⁴ This method describes an efficient and accurate method of transporting photons through MLCs and accounts for beam hardening and tongue-and-groove effect by using first Compton scatter in the MLC medium. The method was extended to allow photon transport through the JAWS and MLC using multiple Compton scatter. To incorporate temporal changes in the leaf position, different incidences in time were combined based on the prescribed monitor units.

II.E. Dose analysis and motion study

For all studies we used either free-breathing CT generated images or RPM sorted CT images on which to perform dose calculations. In the case of the RPM sorted CT data, the dose cubes from the ten breathing phases were combined based on the daily RPM signal taken during treatment to generate either a free-breathing or a gated treatment. Table I gives an overview over the treatment/dose calculation options used in the studies.

Table I.

Imaging, motion assessment, and motion mitigation methods considered in this study.

Reference name adopted	CT image used for dose calculation	Daily method used to account for breathing
3DCT/FB	Free-breathing	Free-breathing
4DCT/FB	RPM sorted CT	Free-breathing
4DCT/GATED	RPM sorted CT	Gated

The first analysis dealt with the comparison of MC and pencil beam for dose delivered in lung cancer under FB. The dose volume histograms (DVH) and the 3D dose maps obtained with each dose algorithm for tumor volumes and organs at risk were compared using the gamma index. In order to analyze the spatial differences between corvus and MC as a function of the density, we define a new parameter called omega index, Ω(ρ) or Ω(ρ; f, VOI), where the density, ρ, is the independent variable, and f is a dose or dose difference distribution and VOI is the volume of interest for which the omega index is calculated:

$$\mathrm{\Omega }(\rho ;f,\text{VOI})=\frac{\int f{(x)}^{\ast }\delta (\rho (x)-\rho )dx}{\int \delta (\rho (x)-\rho )dx}.$$ (1)

The parameter f can either be a 3D dose cube or a dose difference between two 3D cubes, i.e., f =D_CORVUS –D_MC or f =D_MCϕ1 –D_MCϕ2 for any breathing phases ϕ₁ and ϕ₂.

The second study dealt with the dosimetric effect of motion on the individual breathing-phases of the respiration cycle based on 4DCT information. Dose volume histograms obtained for different phases were compared. Finally, the impact of intrafraction and interfraction motion effects on FB and gated delivery was studied. The dose distributions calculated based on the ten phases of the 4DCT breathing cycle were resorted based on the breathing pattern measured during treatment.

III. RESULTS AND DISCUSSION

III.A. Monte Carlo versus pencil beam in predicting dose in IMRT for lung cancer

The study was performed for the FBCT data. In Fig. 5 and Table II the DVH results of all three patients are shown.

Fig. 5.

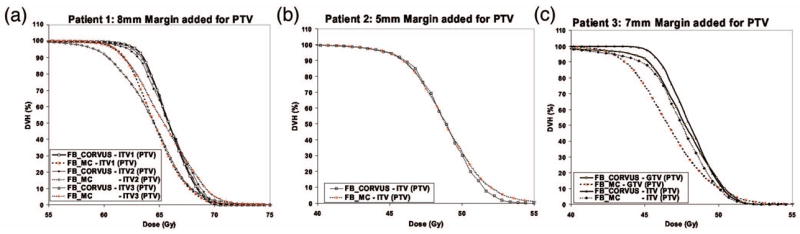
Dose volume histograms for (a) Patient 1, (b) Patient 2, and (c) Patient 3 based on dose calculations with corvus and Monte Carlo using free-breathing 3DCT.

Table II.

Comparison of the corvus and Monte Carlo based dose distributions based on free-breathing 3DCT at 50% and 95% of the tumor volume.

	FBCORVUS-FBMC (50% volume)	FBCORVUS-FBMC (95% volume)
Patient 1	1.1 Gy (1.9%)	2.1 Gy (3.8%)
Patient 2	0.1 Gy (0.2%)	−0.1 Gy(−0.2%)
Patient 3	0.5 Gy (1.1%)	2.7 Gy (5.8%)
Average	0.6 Gy (1.1%)	1.6 Gy (3.1%)

The MC predicts overall lower doses than does corvus in Patients 1 and 3, while there is an agreement for Patient 2. The differences are 0.6 Gy (1.1%) and 1.6 Gy (3.1%), on average, respectively, for 50% and 95% of the ITV tumor volumes (GTV value was not included). These results indicate that for the three patients studied, the corvus pencil beam algorithm performed reasonably well and is approximately, within 3% of MC predictions.

A dosimetric analysis based on Ω(ρ) is shown in Fig. 6. The data illustrate the difference between the corvus pencil beam and the MC dose prediction (D_CORVUS–D_MC) as a function of the tissue density in each voxel of the ITV and GTV volume [cf. Eq. (1)]. For all three patients, the corvus PB algorithm overestimates the dose in lung or low-density regions (density <0.7 g/cm³) and underestimates the dose in the tissues structures density higher than 1.1 g/cm³) relative to the MC predictions. The higher lung dose estimates by the corvus pencil beam is the reason why in the case of Patients 1 and 3, corvus estimated 1–2 Gy higher doses in the PTV (see Fig. 5). For Patient 2, an approximately equal lung dose between corvus and MC has lead to approximately equal DVH values. In addition, the large differences in the dose values in bone (density >1.1 g/cm³) have had a small impact for Patient 2.

Fig. 6.

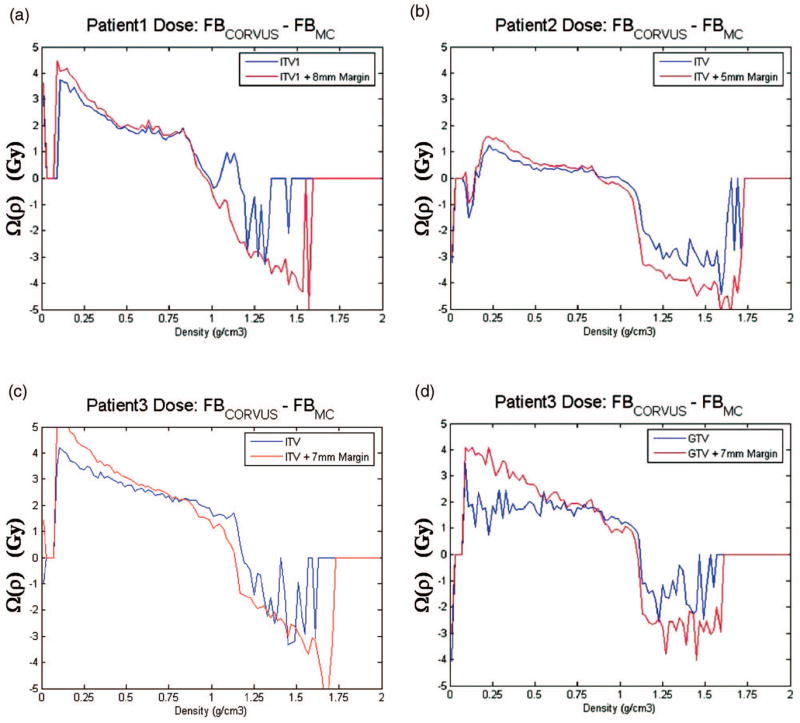
Omega index prediction for ITV1 of (a) Patient 1, (b) ITV of Patient 2, (c) ITV of Patient 3, and (d) GTV of Patient 3.

The MC DVH results presented in Fig. 5 have a higher (by approximately 3–5 Gy) maximum dose to the tumor volume than the corvus predictions, for all patients. As may be observed from Fig. 6, this is a consequence of the bone and cartilage regions of the rib cage and spine within the ITV and PTV volumes, which have higher density than 1.1 g/cm³. In these regions MC predicts a 3–4 Gy higher dose than the corvus pencil beam for all patients. Obviously, while such information can be obtained using tissue-density information, it cannot be deduced based on a DVH analysis alone. Other published studies have also yielded dose differences of a few Gy between MC, pencil, and collapsed cone,^14,15,25,26 where these studies focused on comparing DVHs and gamma indices. In the present study, the comparison MC versus pencil beam was performed using the Ω(ρ) index to investigate the tissue-density dependence of the dose differences. Our results indicate that conventional algorithms, e.g., pencil beam algorithms, do not appropriately account for density effects in tumor sites. In our case, this led to overestimating lung doses by up to 4–5 Gy and underestimating bone doses by up 3–4 Gy. As pointed out in Refs. ²⁸ and ²⁹ these differences are the consequence of incorrect modeling of the lateral scatter in photon beams and the use of mass-density radiation path length instead of electron-density radiation path length. Electron-density radiation path length should be used to accurately model photon beam attenuation through lung and bone regions within the patient.

Because of the impact of lung and bone tissue, the width of margin added to the CTV to produce either the ITV or/and PTV can significantly change the dosimetric interpretation of results based on pencil beam algorithms. Care is therefore needed in the margin added to produce either the ITV or/and PTV.

III.B. Dosimetric effect of motion on the individual breathing-phases of the respiration cycle

In evaluating the effect of heterogeneities and motion-induced deformations on the various breathing phases, we compared the DVH and Ω(ρ) index for the FB with several of the individual breathing phases (cf. Fig. 7).

Fig. 7.

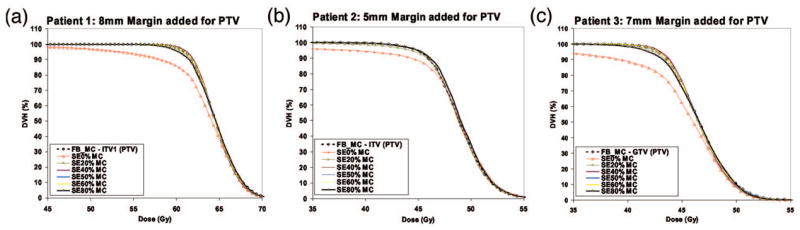
Dose volume histograms for (a) Patient 1, (b) Patient 2, and (c) Patient 3 from Monte Carlo dose predictions for the various breathing phases in the 4DCT data set.

The largest dose differences were observed between inhale (SE0%) and FB, where the DVH for inhale indicates large cold regions within the tumor volume. In the inhale phase, 95% of the tumor volume is receiving 9.3 Gy (averaged over all patients) less than the FB value. This corresponds to an underdosage of 20.7% of the inhale phase relative to the FB case. The remaining breathing phases show small or negligible dosimetric differences relative to the FB prediction. In Fig. 3, we had shown that the FB and inhale phases had different PTDF distributions primarily within the lung. Due to motion and deformation, the lung density changed between inhale and the FB phases.

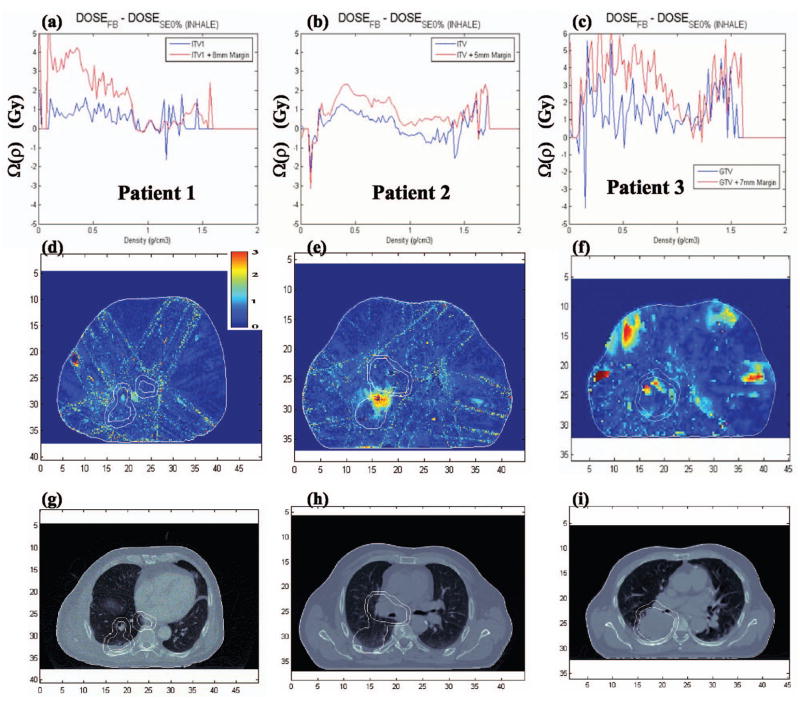
As was the case for the differences in the static case, also the dose discrepancies in the dynamic cases can be, at least in part, understood by looking at tissue-density differences. Density variations between FB and inhale significantly affect the dose within the tumor volume. The Ω(ρ;Dose_FB–Dose_SE0%, VOI=ITV or GTV) results for all three patients are given in Fig. 8 and indicate that the large dose differences between inhale and FB phases are primarily due to dose differences in lung and bone structures within the contoured tumor region. Dose differences between FB and inhale are of the order of 4–5 Gy for lung and 3–4 Gy for bone.

Fig. 8.

(a)–(c) Omega index prediction, (d)–(f) gamma index predictions, and (g)–(i) an example CT slice for Patients 1–3 (gamma values γ>3 are represented as red, the maximum gamma value of the color scale).

Figure 8 also shows the gamma index plots for all patients, where 3%/2 mm represents γ=1. Large differences in the gamma index appear within the tumor volume in the low-density regions (gamma values γ>3 are represented as red, the maximum gamma value of the color scale). Further, the large dose differences that exist outside the tumor volume and near the surface of the patient [cf. Fig. 8(f)]were due to motion of the rib cage, which may move in or out of the radiation beam.

The dose differences between the various phases of the breathing cycle illustrate how breathing-induced motion/deformation affects IMRT treatment planning, on a breathing phase-by-phase basis comparing DVH, gamma, and omega indices. The largest differences were observed between then inhale (SE0%) and the FB phase for all three patients studied, due to tumor motion of the order of 2–3 cm in the superior-inferior direction. The 95% tumor volume was significantly underdosed in the inhale phase relative to the FB case, while the remaining phases had their dose distributions approximately equal to the FB case. The large differences between inhale and the remaining phases were shown in Fig. 8 to be a consequence of differences in tissue density within the tumor and motion of bone structures (such as the rib cage) in and out of the beams, affecting the primary photon beam attenuation.

In Rosu et al.,^17,30 the authors also investigated the difference in the dose distributions in the various breathing phases and found significantly smaller differences between inhale and other breathing phases. In their study, no RPM or external marker was used to generate the 4DCT images. The CT scans were obtained during coached voluntary breath holds at either inhale or exhale breathing points. No dynamic or breathing pattern information of the patient was obtained and the amplitude of the tumor motion was found to be around a maximum of 2 cm. The authors concluded that the average phase of the respiratory cycle could be used to describe fairly well the dose distribution within the tumor and organs at risk. Flampouri et al.¹⁶ also investigated the variation of the delivered dose with the breathing phases. They assessed how the final dose plan depended on the number of phases required to generate a dose distribution that was within 3% of the ten-phase composite plan. All phases were combined with equal weighting and no account was made of intrafraction and interfraction breathing motion. The authors concluded they required at least three phases to achieve better than 3% agreement with the ten-phase composite plan. In the present study, we see that one phase might not be enough to accurately predict the dose within the tumor, but maybe two or three phases are required to account for differences between inhale and exhale.

In both publications mentioned above the dose distributions from each of the phases were combined using equal weighting. This is only approximately valid for the FB type as may be seen in Fig. 1(c) where a peak around 0.8 in the transition between exhale and inhale corresponding to shallow inhales by the patient and not for by previous studies.^16,17,30 Since most lung treatments are gated, the composite plan should account for different weightings of each phase in the final composite dose plan as indicated in Fig. 1(d).

III.C. Intrafraction and interfraction motion effects

In Fig. 9 and Table III the DVH results of all three patients are presented for the cases 3DCT/FB, 4DCT/FB, and 4DCT/GATED. The 3DCT/FB case is used as reference since the majority of the radiotherapy clinics still do not have 4DCT capabilities and radiotherapy planning is still largely performed using 3DCT FB data.

Fig. 9.

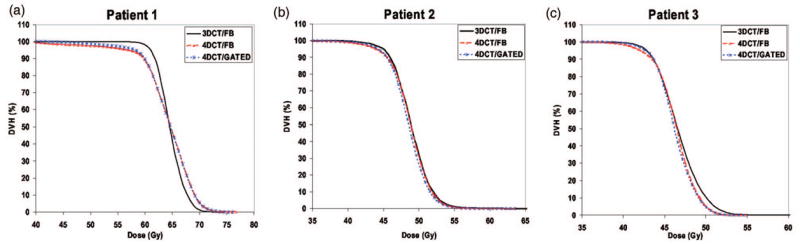
Dose volume histograms for (a) Patient 1, (b) Patient 2, and (c) Patient 3 from Monte Carlo dose predictions for the 3DCT/FB, 4DCT/FB, and 4DCT/gated data sets.

Table III.

Comparison of the 3DCT/FB with 4DCT/FB and 4DCT/gated dose results for (a) 5%, (b) 50%, and (c) 95% of the tumor volume.

	5% volume		50% volume		95% volume
	a	b	a	b	a	b
Patient 1	2.24	2.30	1.15	1.18	−5.90	−3.92
Patient 2	−0.57	−0.49	−0.04	−0.02	−1.93	−0.50
Patient 3	−2.29	−1.76	−0.54	−0.34	−1.88	0.36
Average	−0.21	0.01	0.19	0.27	−3.24	−1.35

^a[4DCT/FB-3DCT/FB/(3DCT/FB)]*100.

^b[4DCT/GATED-3DCT/FB/(3DCT/FB)]*100.

III.C.1. Comparison of 3DCT/FB with the 4DCT FB and gated treatments

Differences of the order of 3% exist between the 3D and the 4D dose results for the dose coverage of 95% of the tumor volume. These differences exist because 3DCT data have a significantly larger contribution to the inhale phase than the 4DCT/FB and 4DCT/gated cases. This is because a helical scan, performed in 10–20 s, is very sensitive to the initial breathing phase in which the image acquisition started or to breath holds or coughing during scanning. The three patients used in this study represent a small population sample. However, treatment planning on FB 3DCT data and delivery to the patient using either the FB or gated method has shown a systematic underdosage of 95% of the tumor by 3%–5% of the prescribed dose. In the case of the 5% and 50% tumor volume, differences between 3D and 4D dose results are significantly smaller.³⁰

Not surprisingly, the present results indicate that radiotherapy planning for lung cases should be performed using 4DCT generated data, i.e., the exhale phase or the midventilation reconstructed phase.³¹ The midventilation method is more representative of the 4D behavior of the lung; in addition it also significantly reduces the dosimetric effect of the inhale phase in the final delivered dose, relative to the FBCT.

III.C.2. Comparison of 4DCT/FB with 4DCT/gated results

In this case the dose differences are significantly smaller and of the order of 1% on average for 5%, 50%, and 95% of the tumor volume (cf. Table III). Therefore interfraction dose variations are very small, as may be seen from Table III when comparing 4DCT/FB with 4DCT/gated results. In the case of intrafraction motion, we assessed the standard deviation of the daily dose variations and found that the dose varies daily by less than 1%. In addition, the delivered dose to organs at risk (i.e., lung and heart) were found to vary little between 4DCT/FB and 4DCT/gated. However, this study did not account for interplay or small MU effects,¹⁰ where a fraction of the IMRT segment can be delivered to one phase of the breathing cycle in one treatment fraction.

IV. CONCLUSION

The corvus pencil beam algorithm seems to underestimate the dose in low-density regions in the tumor, such as lung, and overestimate for high-density regions such as bone. The differences between pencil beam and MC predictions were 4–5 and 3–4 Gy, for lung and bone tissues, respectively, within the contour tumor volumes (corresponding to approximately 5% or more of the planned dose). Consequently, the width of margin added to the CTV to produce either the ITV or/and PTV can significantly change the dosimetric accuracy of the pencil beam algorithm. This is a consequence of the increased amount of lung tissue within the planning volume and that will change the final dose. Care is therefore needed in the margin added to produce either the ITV or/and PTV.

The MC dose differences between the various phases of the breathing cycle and the free-breathing case were shown to be negligible for all phases except for the inhale phase (SE0%). In the case of the inhale phase, an underdosage of the tumor by as much as 9.3 Gy relative to the free-breathing dose prediction, corresponding to 20.7% less dose, was observed. This large difference was due to breathing-induced motion/deformation affecting the soft/lung tissue density within the contour tumor volume and due to motion of the bone structures (such as the rib cage) in and out of the field irradiating the tumor volume.

Small intra/interfraction dosimetric differences were observed between FB and gated delivery for the 4DCT data, representing the delivered dose to the patient under dynamic conditions representing patient breathing during radiation. Larger dosimetric differences, of the order of 3%–5%, were observed between the 3D and the 4D data sets, because of the larger contribution of the inhale phase in the 3DCT data than in the 4DCT. The three patients analyzed in this study suggest that radiotherapy planning for lung cases should be performed using 4DCT generated data, i.e., the exhale phase or the midventilation reconstructed phase.³¹ The systematic difference between 3DCT planning and 4DCT delivery (representing the patient motion during delivery) can lead to underdosage of 95% of the tumor volume.