Abstract
To better understand the role of surface chemical heterogeneity in natural nanoscale hydration, we study via molecular dynamics simulation the structure and thermodynamics of water confined between two protein-like surfaces. Each surface is constructed to have interactions with water corresponding to those of the putative hydrophobic surface of a melittin dimer, but is flattened rather than having its native “cupped” configuration. Furthermore, peripheral charged groups are removed. Thus, the role of a rough surface topography is removed, and results can be productively compared with those previously observed for idealized, atomically smooth hydrophilic and hydrophobic flat surfaces. The results indicate that the protein surface is less hydrophobic than the idealized counterpart. The density and compressibility of water adjacent to a melittin dimer is intermediate between that observed adjacent to idealized hydrophobic or hydrophilic surfaces. We find that solvent evacuation of the hydrophobic gap (cavitation) between dimers is observed when the gap has closed to sterically permit a single water layer. This cavitation occurs at smaller pressures and separations than in the case of idealized hydrophobic flat surfaces. The vapor phase between the melittin dimers occupies a much smaller lateral region than in the case of the idealized surfaces; cavitation is localized in a narrow central region between the dimers, where an apolar amino acid is located. When that amino acid is replaced by a polar residue, cavitation is no longer observed.
Keywords: confinement, water, biopolymer, compressibility, cavitation
It has long been accepted that the hydrophobic effect plays a key role in the stability of compact native protein structures (1–3). The protein contains hydrophobic regions which associate, at least in part, due to the favorable solvent-mediated free energy of aggregation of nonpolar moieties in an aqueous environment (2, 4, 5). Although experimental studies (6) suggest that this rationalization is valid, and theoretical work using model systems and realistic protein structures (7) confirms such observations, much is still unknown about the role and behavior of water near proteins and how the aqueous solvent contributes to protein structural stability at the molecular level. The main focus of the present work is to contribute to the understanding of water near, and between, nominally hydrophobic, but realistic, protein surfaces.
When one turns to the molecular details of the mechanism of nonpolar aggregation in water, the picture is still not completely clear. The two limiting scenarios for events such as protein folding and directed self-assembly are summarized well in ref. 8, in the context of protein folding. The basic feature distinguishing these scenarios is the relationship between solute dehydration and solute spatial approach. In the traditional view, water is gradually reduced within and between the associating regions in a manner that is concerted with their spatial approach. In an alternative cavitation scenario, a thermodynamic instability leads to water evacuation from the intervening space between hydrophobic regions, and the “hydrophobic collapse” to contact then follows; the processes are sequential. Illustrative examples summarized from available protein folding studies (8) suggest that a path involving cavitation is not the norm, but rather that the water plays a critical role in the folding landscape at all stages.
Theoretical studies show clearly that, on thermodynamic grounds, water films embedded between planar hydrophobic surfaces will undergo cavitation at some critical intersurface separation, which depends on the degree of hydrophobicity (9–15). Experimental evidence of the long range attractions (e.g., 10–100 nm) between hydrophobic surfaces has been known for several years (16–20). Although the interpretation of the origin of the long range attraction has been somewhat controversial, this phenomenon has been attributed, at least in part, to a theoretically predicted cavitation between hydrophobic surfaces.
Fundamental studies of the rates of cavitation focus on the free-energy barrier to cavitation between finite hydrophobic surfaces. The barrier increases with separation and with the size of the contacting surface (13). Studies using a coarse-grained model for water have been used to provide quantitative estimates (21), with the conclusion that the barrier to cavitation only becomes thermally accessible at ambient conditions for molecular-scale contact areas and surface separations. Hence, the study of solvation and cavitation, including metastable states, for realistic models of solvent and solute are timely.
Although several studies of the role of water in protein folding have been undertaken (7) and this role has been shown to be important (22), the prevalence of cavitation in the process remains an open question (8). Numerous studies have shown, however, that the details of the water-surface interaction are critical in determining the observation of cavitation (see, e.g., ref. 23). Heterogeneity in the chemical character (hydrophobic and hydrophilic) of nanoscale surfaces has a profound effect on their wetting behavior (24–26). Given that the interfaces of a nominally hydrophobic contact region in a native protein are both topologically and chemically heterogeneous, an understanding of the impact of such effects on hydration is of great interest. Recent work (26) has addressed some of these issues in the framework of a systematic approach whereby chemical heterogeneity is introduced into initially homogeneous nonpolar planar surfaces. Here, we extend this line of study to a surface that is explicitly based on a protein interface, but retains a planar surface topology.
Of special interest for the present work are the recent simulations by Liu et al. (27) and Zhou et al. (28), which have provided direct observations of solvent-mediated hydrophobic protein-protein interactions. Zhou et al. investigated the BphC homodimer protein assembly, whereas Liu et al. studied the interaction between a pair of melittin dimers that assemble crystallographically as a tetramer. In the work of Zhou et al., the dimer contact surface between the BphC monomers is relatively flat and composed mainly of hydrophobic residues (28). Varying the distance between BphC monomers in a bulk water bath, cavitation was not manifest at any distance where solvent could sterically access the gap. Removing all electrostatic interactions between the monomer surfaces and water did result in the observation of cavitation, suggesting that chemical heterogeneity of the native surface is critical to the behavior of confined water. In Liu et al.'s study, the separate melittin dimers associate through the contact between a pair of slightly curved, concave hydrophobic contact regions (27). This study reported two key results. First, cavitation was observed between the two largely hydrophobic contact regions, even with native electrostatic interactions. Second, after altering the geometry of the tetramer via specific mutations at the periphery of the dimer contact region, cavitation was no longer observed. These mutations removed protruding hydrophobic side chains specifically affecting the topology of the surface, so that water between the surfaces at close approach could be described roughly as a droplet in the native case and as a slab between flatter surfaces, connected to the bulk, in the mutated case.
The demonstration that both the electrostatic and topological heterogeneity of the interface apparently contribute significantly to the hydration structure motivates us to study the hydration properties of a planar but otherwise intrinsically protein-like interface. We thus consider here a systematic separation of the topology and electrostatic character of the interfaces to better understand the effect of each of these on the hydration properties of a chemically heterogeneous protein-like system. To this end, we have developed a planar surface construct using the atomic characteristics of a melittin dimer as a template, thereby essentially decoupling the topology variable from the chemical characteristics. This protein surface is one that is generally accepted as typically hydrophobic, yet chemically heterogeneous, allowing us to better address the role of protein-like surface character on hydration. In this work, a flattened surface of the crystallographic nonpolar melittin dimer contact region is constructed as described below. We then use these coordinates to compose a tetramer with the same relative dimer orientation as that of the crystallographic structure tetramer used in the earlier study of Liu et al. (27). We follow by considering the hydration of the tetramer as a function of distance between the dimer surfaces and pressure. To further understand the effect of electrostatic interactions, we introduce a polar mutation in the center of the planar protein surfaces and carry out additional simulations.
This paper is organized as follows. In the next section, we describe the subject protein and the structural modifications. We then describe our results for fluid phase and hydration structure as a function of surface separation and pressure, and compare these to our recent studies of idealized surfaces (24, 26). Finally, we present our conclusions. The technical details and simulation protocols are included in supporting information (SI) Appendix.
Construction of the Hydrated Protein System
Melittin.
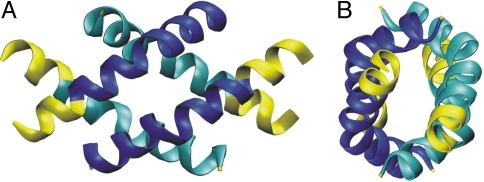
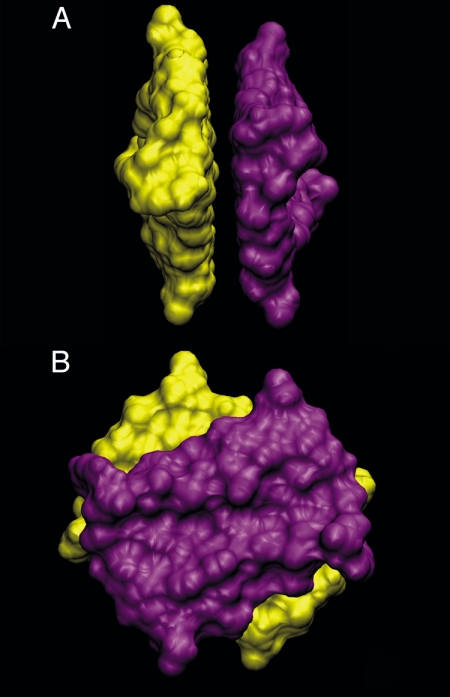
Melittin is a bee venom protein that has been shown to exhibit membrane activity, possibly by forming transmembrane pores (29). It is a relatively small polypeptide (27 residues) and is one of the few membrane-active peptides that have been crystallized. It consists of a kinked helical secondary structure throughout the protein, and a characteristic amphiphilic amino acid distribution along the helical axis, with easily recognized hydrophilic and hydrophobic sides. In the crystal, two monomers align in an antiparallel fashion forming crystallographic dimers in the unit cell. The dimer possesses a quite clear and relatively large hydrophobic patch that comes into contact with another pair of dimers, forming an “X” type of configuration, and thus a tetrameric unit (Fig. 1). The tetramer's well-defined hydrophobic contact region makes it an ideal model system for the investigation of protein-protein contacts in a well understood and relatively simple protein environment (25, 27).
Fig. 1.
Front (A) and side (B) view of the melittin tetramer from the x-ray crystal structure (30). The residues that are truncated for our simulation purposes are shown in yellow. Each dimer pair is shown in light (dark) blue.
Melittin Modifications
Truncation.
We aim to construct, to the extent possible, a planar nanoscale interface preserving the chemical heterogeneity of the native protein hydrophobic patch. The structure of choice for the present study is the crystal structure of the Melittin dimer (30) from the protein data bank (PDB ID code 2MLT). The terminal polar groups from each monomer in 2MLT, located at the periphery of the dimer (shown in yellow in Fig. 1 A and B) are removed from the original crystal structure as these regions contain potentially confounding charged residues that we wish to avoid in this study of the hydrophobic contact region. This modification preserves residues 2–20 from each monomer in the tetramer and the complete contact region between the dimer pairs. The resulting chain terminating amino acids (2, 20) are left in the resulting neutral charge state after truncation. The remaining charge due to the Lys7 residue of each monomer (also lying outside the contact region) is modified by setting the charge of the ammonium group to zero. Thus each protein monomer and the overall tetramer possess a neutral charge, but the individual atoms preserve their normal partial charges, except as described.
Planar Surface.
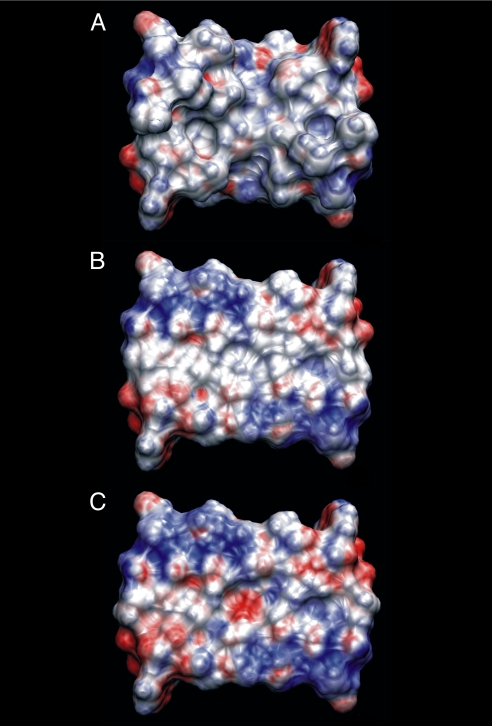
To obtain a surface that is planar but preserves chemical heterogeneity, we have used the electrostatic potential at the solvent accessible surface area (SASA) as a guiding criterion for success (31, 32). The electrostatic potential, calculated with the APBS program (33), on the SASA of the truncated crystal geometry is shown in Fig. 2A. To obtain an essentially planar surface, the truncated peptide dimers that compose the tetramer are distorted as follows: the coordinates from the crystallographic dimer are oriented such that the dimer hydrophobic patch is approximately parallel to the xy-plane of the coordinate system, which we set as the reference plane. We identify in each residue that atomic coordinate which is closest to the reference plane along the z-axis and calculate the distance from this coordinate to the reference plane. All atoms within a residue are then shifted by this distance; the atom originally closest to the reference plane now lies on the plane. Performing this procedure for each residue results in the flattened surface shown in Fig. 2B. In carrying out this procedure, some atoms from different residues are brought into regions where their repulsive potentials would overlap. The protein is rigid in all calculations so that causes no fundamental problem. The overlap might produce a slightly stronger dispersive attractive contribution from the surface, but the electrostatic potential (see below) is much like the original. It is important to note here that the surface is only approximately planar, but the method used maintains the magnitude of the group polarities of the chemical entities. We perform the same procedure for the complementary dimer in the tetramer. As seen in Fig. 2B, each flattened dimer is nonpolar to a similar degree as the native structure. The blue regions located in the second and fourth quadrant of the planar surface indicate a slightly polar surface. However, the area along the diagonal that goes from the first to the third quadrant is mostly colorless indicating a lack of polarity of the atoms in this region. This region is also the contact area for the complementary dimer.
Fig. 2.
Solvent accessible surface area colored by electrostatic potential for the truncated melittin dimer (A), flattened, truncated melittin dimer (B), and mutated, flattened, and truncated melittin dimer (C). The coloring gradient ranges from −5kBT/e (red) to 5kBT/e (blue)
Mutation.
To further elucidate the role of electrostatics in the hydration of the planar surfaces, a mutation was introduced into the system to replace a nonpolar residue in the center of the contact region with a polar residue. We chose to mutate residue Leu13 to the nearly geometrically equivalent Asn13 (L13N) in each monomer. The field of electrostatic potential values on the SASA of the mutated tetramer is depicted in Fig. 2C. As shown, the region near the center of the plane contains red coloration, indicating the presence of polarity and introducing a hydrophilic hot spot in the otherwise hydrophobic contact area.
Results
We consider first the phase behavior of the fluid, and compare to our earlier results for idealized surfaces (24, 26). We then describe the water structure and focus particularly on the role of pressure. The way in which both water structure and phase behavior reflect the degree of hydrophobicity of the surface is of particular interest and is emphasized. It should be pointed out that we use the term “phase behavior” to denote the identification of fluid phases that are stable within the time span of the simulations, with the understanding that some of these states may be metastable (34, 35), as discussed in the Introduction.
Phase Diagram.
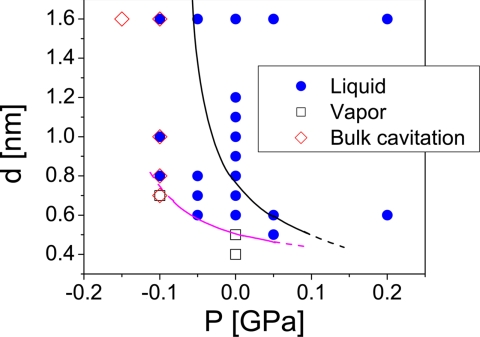
Fig. 3 summarizes the results of our simulations for the state points studied. In agreement with ref. 24, we find that cavitation occurs outside the confined space at P ≤ −0.1 GPa, i.e., bulk liquid water becomes unstable. The simulation at P = −0.15 GPa and d = 1.6 nm lasts for only ≈15 ps before cavitation occurs throughout the system. At P = −0.1 GPa, we observe that for d ≥ 0.8 nm the confined space remains wetted during the entire simulation, until bulk water cavitates. In contrast, the gap also cavitates for d = 0.7 nm. For P ≥ −0.05 GPa, there is no bulk cavitation, and the confined water remains either in the liquid or vapor phase, depending on the separation between the plates. In fact, inspection of Fig. 3 indicates that at P ≥ −0.05 GPa, when bulk cavitation does not occur, localized loss of hydration is found only at separations d ≤ 0.5 nm, which present significant steric hindrance to the presence of confined water. The data shown in Fig. 3 also suggest that cavitation is suppressed at approximately P = 0.15–0.2 GPa. This value is in agreement with experiments (36, 37), indicating that hydrophobic protein cavities can be filled by water molecules if the pressure is increased above ≈0.15 GPa.
Fig. 3.
Phase diagram. Magenta line separates approximately the state points at which water confined by the melittin dimers remains in the liquid (blue points) or vapor (open squares) phase. The black line, included for comparison, is from ref. 24, for water confined between hydrophobic atomically flat nanoscale walls.
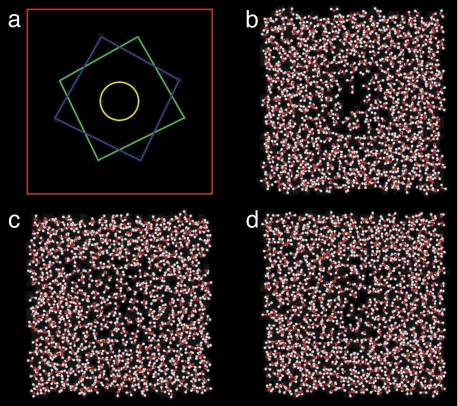
A typical snapshot of the system in the vapor case is shown in Fig. 4b. Only a slab of the whole system which contains the confined space is shown. The area covered by the water molecules in the figure corresponds to the simulation box cross-section. This cross-section is indicated by the red square in Fig. 4a; the two melittin dimers are also represented schematically in the figure by the green and blue squares. The melittin dimers in Fig. 4b are located below and above the water slab shown in the figure, but are not included for clarity. The yellow circle in Fig. 4a indicates approximately the region of cavitation between the dimers. The size of this region is comparable to that of nonpolar protein cavities found in experiments (36, 37). Fig. 4 c and d are typical snapshots of the confined space where water remains in the liquid phase at somewhat higher pressure or dimer separation. Examples showing the time dependence of the number of water molecules in the confined space are given in SI Appendix.
Fig. 4.
Snapshots of confined water. (a) Scheme showing the simulation box cross section (red square, side length, L ≈ 4.75 nm), and the two melittin dimers (green and blue squares), one on top of the other. The yellow circle (with a radius of 0.5 nm), centered along the axis connecting both dimers, corresponds to the base area of the cylindrical volume used for the calculation in Fig. 5. Snapshots obtained from simulations at: P = 0, d = 0.5 nm, 500 ps (b); P = 0.05GPa, d = 0.5 nm, 900 ps (c); P = 0, d = 0.6 nm, 500 ps (d). Only b shows clear cavitation which is reversed by small increases in pressure in c. Increasing the separation between the melittin dimers results in a thicker water layer between the surfaces (d).
In ref. 24, we performed MD simulations of water confined by silica-based structured nanoscale hydrophobic (apolar) surfaces and found that confined water can also remain in the liquid or vapor phase depending on the separation between the surfaces and pressure. Our present results can be directly compared with those for hydrophobic silica of ref. 24. The black line in Fig. 3 is reproduced from ref. 24. Values of P-d above this line are state points where water confined by the hydrophobic silica walls remains in the liquid phase; below this line a vapor phase (cavitation) is observed. Fig. 3 clearly shows that when the hydrophobic walls are replaced by melittin dimers, the phase boundary shifts to smaller d and smaller P; confined water is relatively more stabilized in the liquid state (see magenta line). This is evident, for example, at P = 0 and d = 0.6 nm (below the black line in Fig. 3). Therefore, although a vapor phase can occur between both flat melittin dimers and idealized hydrophobic silica surfaces, cavitation occurs only at smaller pressures and smaller separations between the heterogeneous hydrophobic protein surfaces. This is clear evidence that the protein surface is less hydrophobic than the hydrophobic (Lennard–Jones) silica surface.
A comparison of Fig. 4b with figure 3d of ref. 24 also shows that the vapor phase region is smaller and much more localized in the case of water confined by the melittin dimers (the areas covered by the water molecules in both figures are comparable). Although the whole wall area is contacted by a vapor phase in figure 3d of ref. 24, only the central region between the dimers in Fig. 4b is dry (this area is comparable to the yellow circle of radius 0.5 nm shown in Fig. 4a). Therefore, this also indicates that the formation of a vapor phase in the confined space is weaker for the melittin dimers. The explanation for this is almost certainly the presence of weak hydrophilic sites in the melittin surface, as reported by the red and blue regions in Fig. 2b. This observation mirrors our previous finding for patterned surfaces that the degree of hydrophobicity of hydrophobic patches is reduced by the presence of adjacent hydrophilic regions (26) (see also the next section). We note that our observations are completely consistent with those of Liu et al. (27) and confirm that the cavitation that is seen in the native structure is induced by the topology of the confinement, absent for flat surfaces.
The cavitation observed in Fig. 4b occurs at the center of the dimer surface, where the central hydrophobic residue, Leu13, is located. To explore the response of the vapor phase to the local hydrophobicity, we performed a simulation at P = 0 and d = 0.5 nm using the flattened, truncated, and mutated melittin dimers shown in Fig. 2c (see Melittin Modifications). At these conditions, the flattened and truncated melittin dimers induce the formation of a vapor phase (see Fig. 3). We start our simulation with a dry initial condition. Only the single residue is mutated, although it is to a rather polar Asn. We find that, by 360 ps, the gap has wetted, and confined water remains thereafter in the liquid phase. A typical snapshot of the system resembles Fig. 4c. The behavior between the dimers is reminiscent of the results reported in ref. 28, where hydration between the two domains of BphC protein was studied. In that work, it was found that there was no cavitation when the two domains of the BphC protein approached each other, although a vapor phase occurred in the confined space when the protein-water electrostatic interactions were artificially eliminated.
Water Structure: Effect of Pressure.
Here, we discuss the effect of pressure on water confined by the melittin dimers of Fig. 2b and compare the findings to our earlier results for hydrophobic (apolar) and hydrophilic (polar) silica-based walls (24). There, we found that the response of the fluid density profile to pressure had a characteristic signature for hydrophobic, compared with hydrophilic, surfaces. Water in hydrophobic confinement was found to behave as a “soft,” highly compressible material (34), whereas hydrophilically confined water behaved as a “hard,” incompressible material. Here, “hard” and “soft” refers to the compressibility of confined water and not to any mechanical property of melittin, which is implemented as rigid in the simulation.
The analysis here needs to account for the fact that the vapor phase observed at small dimer separation occurs only next to a localized region of the dimer flat surface. To compare the effect of pressure on water confined by the hydrophobic dimers, we focus on the properties of water only in the small volume within the confined space where cavitation occurs. We define a cylindrical volume parallel to the z-axis, extending between the flat surfaces of both dimers. The base of this cylindrical volume has a radius of 0.5 nm and is indicated by the yellow circle in Fig. 4a. All of the water properties discussed below are obtained by averaging over molecules within this cylindrical volume.§
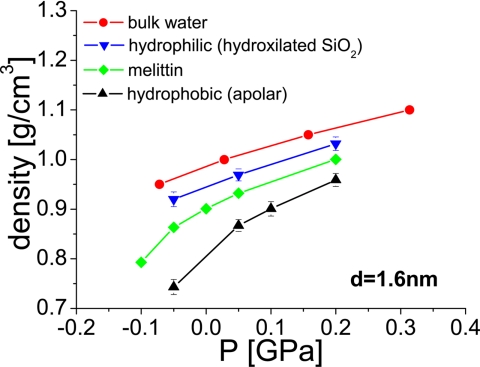
Fig. 5 shows the average density as a function of the applied pressure for water confined by the melittin dimers (see Fig. 6). The distance between the surfaces is d = 1.6 nm; at this separation, no vapor phase occurs. We also include the results obtained for bulk water reported in ref. 38 (see ref. 24), and for water confined by the hydrophobic and hydrophilic silica-based structured walls from ref. 24.
Fig. 5.
Density of water in the confined volume as a function of the applied pressure for different surfaces. Data for bulk water are from ref. 38. Data for water confined by hydrophobic and hydrophilic surfaces is from ref. 24. In the melittin case (green; this work), the density was computed in a cylindrical region, as shown in Fig. 4a. The density calculated at P = −0.01 GPa with the melittin dimers is obtained before bulk cavitation occurs.
Fig. 6.
Side (A) and (B) top view of the melittin dimers in the configuration implemented in our simulations (see also Fig. 1).
It can be seen that even though the flat melittin surface is hydrophobic, in this case the density of water falls between that computed by using the hydrophilic and hydrophobic walls (24). Similarly, the value of the compressibility of water confined by the melittin dimers (which is closely related to the slope of the curves shown in Fig. 5) is intermediate between that obtained for the hydrophobic and hydrophilic walls: at 0 GPa, the compressibility values obtained by polynomial fit of the ρ(P) data (P ≥ −0.05 GPa) are 0.52, 0.76, and 1.47 GPa−1 for hydrophilically confined water (24), water confined by melittin (this work), and water in hydrophobic confinement (24), respectively. It can be seen, then, that the values of the density and compressibility of water confined by the melittin dimers appear somewhat closer to those obtained in the presence of confining hydrophilic surfaces than to the numbers observed in the presence of hydrophobic (apolar) walls. Simulations performed at d = 0.8 nm show stronger similarities in density and compressibility between water confined by melittin and water confined by hydrophilic surfaces than those observed at d = 1.6 nm (see SI Appendix).
We include within SI Appendix figures showing density, ρ(z), and coordination number, CN(z),¶ profiles at different pressures for a separation of d = 1.6 nm. These calculations can be directly compared with the corresponding results of ref. 24, given there in figure 8 a and b for water confined by hydrophobic walls, and figure 12 a and b for water confined by hydrophilic walls. In agreement with the results of Fig. 5, the amplitude of the first maximum of ρ(z) is found to be intermediate between those obtained when using the hydrophobic and hydrophilic confining walls of ref. 24. The first peak of ρ(z) does not shift with pressure (although it increases in height). In contrast, when confined by hydrophobic walls, the first peak shifts toward the wall upon application of pressure (24). However, other properties are typical of the density profiles obtained for water confined between the hydrophobic walls. For example, there is no clear structure beyond the first peak of ρ(z). A very distinct second maximum next to the surface is observed in the hydrophilic walls case, whereas such a maximum is absent in the case of hydrophobic walls (24). Possible reasons for the mixed properties shown by ρ(z) (i.e., hydrophobic- and hydrophilic-like) are, on one hand, the lack in melittin of the periodic atomic scale roughness that characterizes the silica-based walls (24). The silica-based hydrophobic walls offer interstitial sites between the surface silica tetrahedra that can be increasingly accessed by water as P increases. This results in a shift of the first peak in ρ(z) with P for the hydrophobic case, a manifestation of a “soft,” pressure-responsive surface. Further, it is possible that the periodic polarity of the hydrophilic hydroxylated silica may play a role. Additional studies of aperiodic but otherwise ideal surfaces will be required to establish these answers.
The coordination number profile of water confined by the melittin dimers resembles closely that obtained under confinement using hydrophobic walls (see figure 8b of ref. 24). In both cases, the amplitude of CN(z) at z = 0 increases from ≈3.5 at P = −0.05 GPa to ≈3.9 at P = 0.05GPa. Instead, in the hydrophilic walls case (see figure 12b of ref. 24), CN(z) decreases with pressure. The coordination number decreases monotonically as the melittin surface is approached, with no peaks next to the surface.
Finally, we note that the water molecule orientation distribution next to the melittin surfaces does not resemble any of the orientation distributions characterizing the truly flat hydrophobic and hydrophilic walls (39). A similar result was found for water next to native melittin surfaces (25).
Conclusions
In this work, we have studied the behavior of water confined by flat and hydrophobic proteinaceous surfaces constructed from flat and truncated melittin dimers (see Fig. 6). By this construction, we are able to study the behavior of water confined by protein-like hydrophobic surfaces, without the additional effects produced by the native surface topology. The present simulations can be directly compared with our previous simulations (24) of water confined by hydrophobic and hydrophilic silica-based structured walls.
In comparison with the simulations using hydrophobic silica-based structured walls (24), melittin is less hydrophobic than a nonpolar purely dispersive Lennard–Jones representation of silica. Water is more resistant to cavitation when it is confined by the flat and truncated melittin dimers. In the melittin dimers case, the vapor phase occurs only at more extreme (i.e., smaller) values of P-d than required to obtain cavitation in the presence of the ideal hydrophobic surfaces. Even when there is a vapor phase between the melittin dimers, that region is confined to the most central region of the dimers surface, which is substantially smaller than the whole confined space. The central region of the melittin surface corresponds to the location of the Leu13 residue, where earlier studies of a single native dimer (25) indicated that the water structure most resembled that at an ideal hydrophobic surface. When this residue is replaced by a polar residue, the vapor phase does not occur. This indicates a high sensitivity of cavitation to the local hydrophobicity of the surface, consistent with earlier studies of hydrophilic patterning (26). The results we have obtained are consistent with those obtained by Liu et al. (27) for the native dimer geometry, and reinforce the conclusion that the cavitation observed there results from the concave nature of the approaching native protein structure.
We also studied the behavior of liquid water confined by melittin dimers at large separations, where no cavitation is observed, and the hydration of the individual surfaces is the point of focus. We found that the proximal water shows an intermediate behavior between that observed adjacent to structured hydrophobic or hydrophilic silica-based walls. The mechanical response of the hydration surface is hydrophilic-like, in that the interface is quite insensitive to changes in pressure. However, water shows no structure beyond the first maximum of the density profile, similar to the behavior observed for the hydrophobic wall case. Taken as a whole, our results indicate that the inherent hydrophobicity of the flat melittin dimer surface is intermediate between that of idealized hydrophobic and hydrophilic silica-based structured walls of ref. 24.
The results obtained here suggest that a prototypical hydrophobic protein surface behaves in a manner intermediate between an idealized hydrophobic solid surface and a strongly hydrophilic surface. Correspondingly, cavitation is only seen in a very local region of the interface and at short separations approaching the limit of steric accessibility to solvent. These results are consistent with expectations based on coarse grained models (21). At the same time, the potential to exploit surface topology to influence hydrophobicity is reinforced. Whether these observations are generalizable to other protein surfaces will require additional comparative studies. These will be of great interest in expanding our knowledge of the hydrophobic interaction.
Supplementary Material
ACKNOWLEDGMENTS.
P.G.D. gratefully acknowledges support by Unilever Research U.S. P.J.R. gratefully acknowledges support by the R. A. Welch Foundation (F-0019). P.G.D. and P.J.R. gratefully acknowledge the support of National Science Foundation Collaborative Research in Chemistry Grants CHE0404699 and CHE0404695.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0708088105/DC1.
We obtain similar results if we define a cylindrical volume with radius of 0.7 nm or if we use a “cylinder” with an ellipsoidal base of radii a = 0.3 nm and b = 0.7 nm. A cylindrical volume with radius 1nm results in a sampling space that is too large and molecules from “bulk” water confound the statistics.
The CN of a given molecule is defined as the number of neighbor oxygen atoms within a sphere of radius 0.32 nm centered at the oxygen atom of a central molecule. Oxygen atoms of the melittin dimers are also included in the calculations.
References
- 1.Hummer G, Garde S, Garcia AE, Pratt LR. Chem Phys. 2000;258:349–370. [Google Scholar]
- 2.Dill KA. Biochemistry. 1990;29:7133–7155. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- 3.Guo WH, Lampoudi S, Shea JE. Biophys J. 2003;85:61–69. doi: 10.1016/S0006-3495(03)74454-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sharp KA, Nicholls A, Fine RF, Honig B. Science. 1991;252:106–109. doi: 10.1126/science.2011744. [DOI] [PubMed] [Google Scholar]
- 5.Harano Y, Kinoshita M. Chem Phys Lett. 2004;399:342–348. [Google Scholar]
- 6.Sadqi M, Lapidus LJ, Munoz V. Proc Natl Acad Sci USA. 2003;100:12117–12122. doi: 10.1073/pnas.2033863100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cheung MS, Garcia AE, Onuchic JN. Proc Natl Acad Sci USA. 2002;99:685–690. doi: 10.1073/pnas.022387699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Levy Y, Onuchic JN. Annu Rev Biophys Biomol Struct. 2006;35:389–415. doi: 10.1146/annurev.biophys.35.040405.102134. [DOI] [PubMed] [Google Scholar]
- 9.Lum K, Chandler D, Weeks JD. J Phys Chem B. 1999;103:4570–4577. [Google Scholar]
- 10.Huang X, Zhou R, Berne BJ. J Phys Chem B. 2005;109:3546–3552. doi: 10.1021/jp045520l. [DOI] [PubMed] [Google Scholar]
- 11.Huang X, Margulis CJ, Berne BJ. Proc Natl Acad Sci USA. 2003;100:11953–11958. doi: 10.1073/pnas.1934837100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Truskett TM, Debenedetti PG, Torquato S. J Chem Phys. 2001;114:2401–2418. [Google Scholar]
- 13.Lum K, Luzar A. Phys Rev E. 1997;56:6283–6286. [Google Scholar]
- 14.Choudhury N, Pettitt BM. J Am Chem Soc. 2005;127:3556–3567. doi: 10.1021/ja0441817. [DOI] [PubMed] [Google Scholar]
- 15.Rajamani S, Truskett TM, Garde S. Proc Natl Acad Sci USA. 2005;102:9475–9480. doi: 10.1073/pnas.0504089102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Parker JL, Claesson PM, Attard P. J Phys Chem. 1994;98:8468–8480. [Google Scholar]
- 17.Tsao Y-H, Yang SX, Evans DF, Wennerstroem H. Langmuir. 1991;7:3154–3159. [Google Scholar]
- 18.Pashley RM, McGuiggan PM, Ninham BW. Science. 1985;229:1088–1089. doi: 10.1126/science.4035349. [DOI] [PubMed] [Google Scholar]
- 19.Cristenson HK, Claesson PM. Science. 1988;239:390–392. doi: 10.1126/science.239.4838.390. [DOI] [PubMed] [Google Scholar]
- 20.Singh S, Houston J, van Swol F, Brinker CF. Nature. 2006;442:526. doi: 10.1038/442526a. [DOI] [PubMed] [Google Scholar]
- 21.Luzar A. J Phys Chem B. 2004;108:19859–19866. [Google Scholar]
- 22.Papoian GA, Ulander J, Eastwood ME, Wolynes PG. Proc Natl Acad Sci USA. 2004;101:3352–3357. doi: 10.1073/pnas.0307851100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hua L, Huang X, Liu P, Zhou R, Berne BJ. J Phys Chem B. 2007;111:9069–9077. doi: 10.1021/jp0704923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Giovambattista N, Rossky PJ, Debenedetti PG. Phys Rev E. 2006;73:041604/1–041604/14. doi: 10.1103/PhysRevE.73.041604. [DOI] [PubMed] [Google Scholar]
- 25.Cheng YK, Rossky PJ. Nature. 1998;392:696–699. doi: 10.1038/33653. [DOI] [PubMed] [Google Scholar]
- 26.Giovambattista N, Debenedetti PG, Rossky PJ. J Chem Phys C. 2007;111:1323–1332. doi: 10.1021/jp071957s. [DOI] [PubMed] [Google Scholar]
- 27.Liu P, Huang X, Zhou R, Berne BJ. Nature. 2005;437:159–162. doi: 10.1038/nature03926. [DOI] [PubMed] [Google Scholar]
- 28.Zhou R, Huang X, Margulis CJ, Berne BJ. Science. 2004;305:1605–1609. doi: 10.1126/science.1101176. [DOI] [PubMed] [Google Scholar]
- 29.Yang L, Harroun TA, Weiss TM, Ding L, Huang HW. Biophys J. 2001;81:1475–1485. doi: 10.1016/S0006-3495(01)75802-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Terwilliger TC, Eisenberg D. J Biol Chem. 1982;257:6010–6015. doi: 10.2210/pdb1mlt/pdb. [DOI] [PubMed] [Google Scholar]
- 31.Varshney A, Brooks FP, Jr, Richardson DC, Wright WV, Manocha D. Proceedings of the IEEE Visualization '95; Oct 29–Nov 3, 1995; Atlanta GA. New York: IEEE Press; 1995. pp. 36–43. [Google Scholar]
- 32.Humphrey W, Dalke A, Schulten K. J Mol Graphics. 1996;14.1:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 33.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Proc Natl Acad Sci USA. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bratko D, Curtis RA, Blanch HW, Prusnitz JM. J Chem Phys. 2001;115:3873–3877. [Google Scholar]
- 35.Leung K, Luzar A, Bratko D. Phys Rev Lett. 2003;90:065502/1–065502/4. doi: 10.1103/PhysRevLett.90.065502. [DOI] [PubMed] [Google Scholar]
- 36.Collins MD, Hummer G, Quillin ML, Matthews BW, Gruner SM. Proc Natl Acad Sci USA. 2005;102:16668–16671. doi: 10.1073/pnas.0508224102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Collins MD, Quillin ML, Hummer G, Matthews BW, Gruner SM. J Mol Biol. 2007;367:752–763. doi: 10.1016/j.jmb.2006.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Starr FW, Sciortino F, Stanley HE. Phys Rev E. 1999;60:6757–6768. doi: 10.1103/physreve.60.6757. [DOI] [PubMed] [Google Scholar]
- 39.Giovambattista N, Debenedetti PG, Rossky PJ. J Chem Phys B. 2007;111:9581–9587. doi: 10.1021/jp071957s. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.