A multimetric approach to analysis of genome-wide association by single markers and composite likelihood

Abstract

Two case/control studies with different phenotypes, marker densities, and microarrays were examined for the most significant single markers in defined regions. They show a pronounced bias toward exaggerated significance that increases with the number of observed markers and would increase further with imputed markers. This bias is eliminated by Bonferroni adjustment, thereby allowing combination by principal component analysis with a Malecot model composite likelihood evaluated by a permutation procedure to allow for multiple dependent markers. This intermediate value identifies the only demonstrated causal locus as most significant even in the preliminary analysis and clearly recognizes the strongest candidate in the other sample. Because the three metrics (most significant single marker, composite likelihood, and their principal component) are correlated, choice of the n smallest P values by each test gives <3n regions for follow-up in the next stage. In this way, methods with different response to marker selection and density are given approximately equal weight and economically compared, without expressing an untested prejudice or sacrificing the most significant results for any of them. Large numbers of cases, controls, and markers are by themselves insufficient to control type 1 and 2 errors, and so efficient use of multiple metrics with Bonferroni adjustment promises to be valuable in identifying causal variants and optimal design simultaneously.

The last century provided a leapfrog from linkage in Drosophila to its slow development in human genetics, then to acceleration as blood groups and isozymes were replaced by DNA markers. This progress stimulated the Human Genome Project that provided a physical reference, which led in turn to the HapMap Project and endless diversity (1). Two milestones in this progression were recognition of DNA block and step structure (2) and advocacy of genome-wide association (GWA) to identify common causes of disease (3). These developments were dramatically capped by success in six of seven common diseases (4), with most significant single markers (msSNPs) localized in the physical map in base pairs without reference to neighboring markers or a map in linkage or linkage disequilibrium (LDU). However, power to detect small effects, epistasis, rare causal genes, and disease determinants other than SNPs is low (5, 6). Will this simple method suffice if the numbers of cases, controls, and markers are greatly increased? Should other methods that may be more efficient be examined? It will be some time before such uncertainties are resolved, but a beginning can be made.

At this point it may seem that the many GWA studies now being conducted offer an embarras de choix. However, public tests are delayed necessarily by consortium agreements and unnecessarily by the assumption that only consortium members may be trusted to behave ethically (7). One way of filling this gap is to analyze simulated data that mimic some of the important features of real data. We evade the limitations of this approach to an unknown world by collaborating with two research groups on large sets of single nucleotide polymorphisms (SNPs) genotyped in a substantial number of cases and controls, with the understanding that the origin, disease, SNPs, locations, and other confidential information not be divulged before publication by the consortia (sample A), whereas after publication, the information is no longer confidential (sample B). In this way, some of the many questions raised by advances in association mapping can be realistically addressed before the expected flood of association data requiring GWA mapping and meta-analysis, without compromising anonymity of participants, data access agreements, the authorship rights of consortia to first publication, and other ethical constraints. However, the scope of this approach is presently limited to the first phase of GWA and is therefore heuristic rather than decisive. Only the importance of these issues justifies their examination at this time.

Stage 1 is typically a genome scan of nonoverlapping regions with the object of identifying the regional msSNP in the physical map or the maximum likelihood point estimate in a linkage or LDU map with multiple markers specified by a commercial gene chip, using conventional formula (8). Markers with rare minor allele frequencies or violating Hardy–Weinberg proportions are conventionally discarded. The most significant regions however defined are then submitted to phase 2 analysis in a different and preferably larger sample with more markers in the region of interest. Typically, the selected set is <1% of the number of regions in phase 1 and therefore can be studied in greater detail, although absence of an appropriate gene chip increases effort. More versatile phase 2 strategies that rely on sequencing are being developed with potential to detect rare causal genes not limited to SNPs (9). Limitations of any approach include choice of markers, sample selection and size, and methods of analysis. If msSNPs are used, regional significance is exaggerated relative to composite likelihood unless a Bonferroni adjustment or other appropriate correction is made as described in Materials and Methods, which also gives the way in which composite likelihood and the adjusted msSNP are combined by principal component analysis to yield three metrics. A unique feature of our algorithm is selection of the n most significant regions for each of the metrics, which generates <3n regions for phase 2. The msSNP is most sensitive to omission of a causal SNP, whereas composite likelihood is most sensitive to omission of neighboring SNPs. These metrics are given approximately equal weight and may be economically compared without expressing an untested prejudice or sacrificing the most significant result for any of them. Given adequate allowance for N regions (for example by setting P < 0.05/N), phase 3 may turn to sequence analysis with reasonable assurance both of a causal locus in the region and little probability of omitting an equally strong signal elsewhere.

Results

Composite Likelihood.

Sample A with 5,387 regions gave 53 nominal P values <0.01 for composite likelihood under H₁. Sample B with 3,078 regions gave similar results, with 28 regions having nominal P values <0.01. The number of permutation replicates in these subsets was raised from 1,000 to 50,000 to assure reliable estimates of variance and therefore P. The smallest P value in sample A increased 10-fold from the initial value with 1,000 replicates, but there was no systematic effect on larger P values, which supports the conjecture that a number of replicates >10/P assures a reliable estimate of P (9). Taking χ₂² = −2lnP for sample A, the estimates of its mean and variance over all regions are μ = 2.0 and V = 4.2. Constraining V to its expected value of 4 under H₀, the estimate of μ remains 2.0. For sample B, the variance did not require adjustment because the values were μ = 2 and V = 4. Regression analyses with P values from composite likelihood as the dependent variable revealed no significant effect of either regional LDU length or SNP number for sample A or B.

Bonferroni Adjustment for msSNPs.

Evidence from msSNPs is very different. The value of nominal P falls far short of 1 in every region. In both samples, the maximum P value is near 0.3, showing the bias in selecting the msSNP from at least 30 SNPs in each region. We therefore assigned regions to subsets with limited SNP number diversity and determined R by regula falsi, where R is the effective number of independent SNPs in a given subset, and S is the weighted mean number of SNPs in a region. Table 1 shows these values for each of the subsets for the two samples. Sample A has more subsets and a more even distribution of regions per subset. Sample B has lower SNP density and therefore often requires >10 LDU to have at least 30 SNPs. Not surprisingly, regression on LD length is significant only in sample B.

Table 1.

Number of regions (m) within a SNP range, with mean S and Bonferroni correction (R)

SNP range	Sample A		Sample B
	m	R	S	m	R	S
30	1,536	27.10	30.00		2,014	20.42	30.00
31–35	638	26.55	33.12		294	23.50	32.80
36–40	712	32.86	37.96		205	27.51	37.86
41–45	650	35.76	42.87		165	24.63	42.89
46–50	508	35.99	47.89		137	28.28	47.90
51–55	421	41.73	52.93		90	23.48	52.64
56–60	280	37.66	57.91		63	29.89	57.94
61–65	221	44.89	62.77		110	35.09	71.83
66–70	163	67.41	67.82
71–75	109	63.89	72.83
76+	149	71.06	84.63
Total	5,387	—	—	3,078	—	—

Brace indicates a grouped range of 61+ for sample B. Dashes indicate values not given.

The highly significant relationship between S and R was investigated by regression in each sample. Weighting by m, the regional number of markers, sample A gives a good fit to the linear model R = aS. Sample B does not fit a linear model, the quadratic term being significant (P = 0.0035). The best fit with two parameters is to the model R = a(1 − e^−bS) (Table 2). Compared with sample A, the lower SNP density in sample B has a more variable distribution on the LD map. The relation between R and S must vary among msSNP samples, just as the error variance for composite likelihood does, but the Bonferroni correction is easily made. By using these relationships, a value of R can be calculated for each region based on the number of SNPs in the region (S). Then R is used to correct the P value, P_ci = 1 − (1 − P_ni)^R. Taking χ₂² = −2lnP_c, for sample A, the estimates of mean and variance over all regions are μ = 2.0 and V = 5.2. Constraining V to its expected value of 4 under H₀, the estimate of μ becomes 1.8, corresponding to β = 1.1 (see Materials and Methods). For sample B, the values are μ = 2 and V = 4 as before.

Table 2.

msSNP fit of R by aS, aS + bS², and a(1 − e^−bS)

Sample	Model	A	SE(a)	P for b = 0	F2,6
A	aS	0.818	0.027	0.80	—
B	aS + bS2	0.622	0.034	0.0035	660.82
B	a(1 − e−bS)	41.02	7.21	—	717.96

Dashes indicate values not given.

Combination of Evidence.

We applied principal component analysis to all regions for the χ² values of composite likelihood and msSNPs, calculated as −2lnP_c and adjusted to V = 4 where necessary. The first principal component was converted to a rank, which was then transformed (10) to P and χ₂². For sample A, the largest combined χ² (2 df) is 17.2, and the top 50 are all >9.3. For sample B the largest χ₂² is 16.1, and the top 50 are all >8.2. As with composite likelihood and msSNPs examined separately, no region met the critical significance level of 0.05/N, corresponding to χ₂² of 23.17 for sample A and 22.06 for sample B.

Among the 100 most significant regions (50 from each sample) identified by combination of the two χ² values, 4 had a second principal component with value >4, indicating substantially greater significance for the msSNP than for composite likelihood. In no instance was the converse observed (second principal component less than −4). Local LDU maps for these outlier regions were constructed from control data, and the derived composite likelihoods were compared with initial results from the cosmopolitan HapMap. There was little difference between the LDU maps in terms of the fit to the data and the structure and length of the maps. The composite likelihood χ² values were also very similar (Table 3). These 4 cases had the largest difference in χ² between the msSNP and the next most significant SNP in their respective samples, as expected for an LDU subregion with low SNP density.

Table 3.

Outliers favoring evidence from msSNPs

Sample	msSNP χ21	HapMap χ32*	Local map χ32*	Local map ε	Composite likelihood rank	msSNP rank	Combined PC1 rank
A	19.20	6.33	5.20	1.11	569	4	16
A	23.06	1.49	0.96	1.07	3,695	1	19
A	21.15	0.68	0.45	1.12	4,731	3	29
B	15.19	0.71	1.19	1.12	2,660	3	47
Total		9.21	7.80

*Composite likelihood.

The high rank of the 4 msSNPs even after Bonferroni correction is not paralleled by composite likelihood, the rank of which exceeds 500 and shows no suggestion of association even in local LDU maps constructed from control data that give slightly larger estimates of ε for the rate of LDU decline. This inconsistency cannot be resolved until meta-analysis of multiple samples has determined the error rate of the two methods. Provisionally, the first principal component PC1 is favored because it combines the evidence, providing an intermediate P value that lies within the top regions without competing with the most significant ones. Absence of a standard error for the msSNP complicates meta-analysis, whether or not the PC1 is used.

Tables 4 and 5 summarize all regions within the 10 most significant by composite likelihood, msSNP, or combined rank (PC1). The last is most significant in sample A for one region and least significant for another, whereas in sample B the distribution is 1 most significant and 2 least significant. All five differences are small and occur among the combined ranks of 10 or less. Sample A has greater variability than sample B in composite likelihood rank, despite its greater number of individuals. This variability may well be an artifact of the greater number of regions in sample A generated by more SNPs and the convention of at least 30 SNPs per region. Instead of the 30 tests expected if the three metrics were independent, there are 20 tests for sample A, in 8 of which χ₂² is greater for composite likelihood than for the Bonferroni-adjusted msSNP. In sample B, there are 16 tests, in 9 of which χ₂² for composite likelihood is greater. The most powerful test has yet to be determined, but prejudice in phase 2 can be avoided by selecting regions with the smallest P values for any metric. If a large number of cases, controls, and markers is used, we conjecture that minimal rank need not exceed 10 as in Tables 4 and 5.

Table 4.

Comparison of association tests (sample A)

Combined metrics		PC1	PC2	MsSNP		Composite likelihood		Difference*	SNPs†
Rank	χ22			Rank	χ22	Rank	χ22
1	17.18	11.17	1.37	2	22.19	1	16.30	0.00	75
2	15.80	8.37	1.06	7	17.18	17	12.67	0.04	60
3	14.99	8.19	0.21	9	15.53	7	13.64	0.09	37
4	14.41	7.68	0.00	12	14.37	13	13.20	0.36	55
5	13.97	7.49	−1.63	37	11.44	3	15.31	0.16	45
6	13.60	7.32	−1.51	38	11.36	4	14.87	0.23	44
7	13.29	7.15	−2.13	54	10.09	2	15.53	0.00	30
8	13.03	7.13	2.39	5	17.34	64	8.94	0.00	37
9	12.79	7.11	−0.80	23	12.16	8	13.54	0.52	32
10	12.58	6.99	−0.27	19	12.83	18	12.59	0.00	31
11	12.39	6.95	−1.05	35	11.52	6	13.68	0.24	38
13	12.05	6.66	−2.11	75	9.33	5	14.78	0.83	34
16	11.64	6.25	4.44	4	19.20	569	4.68	0.00	30
19	11.30	6.10	6.98	1	23.06	3,695	0.76	7.51	51
20	11.19	6.04	3.45	6	17.29	325	5.82	0.00	55
22	11.00	5.92	−1.92	115	8.45	9	13.43	0.11	55
23	10.91	5.84	3.16	8	16.48	307	5.94	0.00	30
29	10.45	5.33	6.56	3	21.15	4,731	0.26	1.33	30
45	9.57	4.81	−2.94	520	5.03	10	13.31	1.24	30
126	7.51	3.50	4.75	10	15.30	4,798	0.23	4.90	35

*Difference in LDU between estimates from the msSNP and composite likelihood.

^†Number of SNPs in the region.

Table 5.

Comparison of association tests (sample B)

rs	Combined metrics		PC1	PC2	msSNPs		Composite likelihood		Difference	SNPs
	Rank	χ22			Rank	χ22	Rank	χ22
6683968	1	16.06	10.29	3.15	1	20.91	8	12.08	1.14	30
242596	2	14.68	9.30	−0.26	4	14.72	1	15.50	0.01	31
2328529	3	13.87	8.94	−0.44	5	13.95	2	15.25	0.00	30
10496704	4	13.29	7.14	−0.17	9	11.81	6	12.32	0.40	30
2037028	5	12.85	7.02	2.56	2	15.47	48	8.28	0.00	31
10495719	6	12.48	6.82	−1.15	20	9.98	3	13.25	0.01	30
1895684	7	12.17	6.40	−0.89	22	9.75	7	12.29	0.26	56
1113314	8	11.91	6.34	−1.60	41	8.67	4	13.22	0.21	40
714048	9	11.67	6.20	1.62	6	13.00	44	8.45	0.51	30
6766101	10	11.46	6.12	1.46	7	12.66	40	8.56	0.18	30
1190281	14	10.79	5.22	−2.51	167	5.80	5	12.91	1.21	30
240431	18	10.28	4.88	−1.84	121	6.27	10	11.49	0.13	31
17190837	19	10.18	4.81	1.93	10	11.49	155	6.06	0.06	30
10513645	34	9.01	4.43	−2.56	303	4.63	9	11.87	1.12	30
7748118	47	8.36	4.09	5.29	3	15.19	2,660	0.28	1.62	30
10485218	62	7.81	3.77	3.42	8	12.11	855	2.48	0.01	30

Discussion

“Classical genetics emerged in 1900 with the rediscovery of Mendelism and ended in 1953 with the publication of the double-helical structure of DNA” (11). Its definitive characteristic was experimental as anticipated by Mendel (12), and therefore the observational priority of de Maupertuis (13) in deducing dominant inheritance from a human pedigree of polydactyly is seldom recognized, although the decisive role of cytogenetic observation in the emergence of classical genetics is generally acknowledged. Human genetics (despite continued reliance more on observation than experimentation) played an increasing role in science during the postclassical half century, culminating in the Human Genome Project and its HapMap successor. For the first time, tests of the assumptions underlying evolutionary genetics were becoming feasible, although not probative. Genetic epidemiology has become less family-oriented in rising to a new challenge: “The success of the HapMap will be measured in terms of the genetic discoveries enabled, and improved knowledge of disease etiology” (1). As the unit in all branches of genetics shrinks from the species to the cell, distinction between observation and experimentation becomes fastidious. However designated, the challenge will be to determine how to exploit the massive accumulation of genomic data soon to be released.

Many of our initial results in GWA tests were not anticipated. It proved surprisingly easy to obtain a Bonferroni adjustment for msSNPs, despite the diversity of their regional lengths and SNP densities, but as shown in Table 2, the two samples conform to different two-parameter models. We conjecture that this represents different sampling rules. When evidence was combined in the PC1, the most significant region in sample B gave a point location that coincided with a gene identified in multiple samples as causal. Its region ranked 8 for composite likelihood and 1 for msSNP and PC1. However, when the 50 most significant regions in each sample were examined, none met the conservative Bonferroni level of 0.05/N, where N is the number of regions in a given genome scan. Of the 100 most significant regions when the two samples were pooled, 4 gave evidence only from the msSNP, with no support from composite likelihood. Were those msSNPs type 1 errors or wrongly placed? When the cosmopolitan HapMap was replaced by the local map, evidence from composite likelihood became even weaker. Was SNP coverage inadequate in those regions? At present, there can be no objective recognition of the more reliable test, and so we include PC1 that places the 4 outliers among the most significant regions, but far from the top. The second principal component was used only to detect discrepancies between evidence from msSNPs and composite likelihood and thereby to retain for meta-analysis the 4 outliers that were not identified by composite likelihood.

During the past year much has been learned about association mapping, but the field is still in its infancy compared with a century for linkage. Whereas composite likelihood has proved its utility in regional studies, reliance on msSNPs in genome-wide tests has produced some notable successes that account for a small fraction of disease association. Many causal markers must remain to be identified (5, 6). Very large numbers of cases and controls have been invoked as a panacea, either for a single incisive study or meta-analysis of multiple smaller studies that by luck or design use the same most predictive SNP. One alternative is to infer SNPs that may exist and if so may be correctly imputed (14). The authors of that approach note that “the optimal way to combine called genotypes with imputed data is not clear.” A valid analysis requires Bonferroni correction of significance attributed to the inferred msSNP based on both observed and imputed SNPs. The type 1 and 2 errors of these alternatives have not yet been examined. If association mapping is approached as carefully and from as many directions as linkage analysis of major loci in the last century, high power and reliability will be attained.

Materials and Methods

Samples and Regions.

Sample A is composed of affected and normal subsamples, termed case and control, respectively. It has >200,000 SNPs typed in 403 cases and 395 controls, analyzed on an Illumina 300M gel. Because no results have yet been published, we are committed in this work to minimal description. Sample B dichotomizes the 7.5% tails of a quantitative trait: for our present purpose we classify high values as cases and low values as controls. This German sample is part of the material that led to recognition of the NOS1 regulator NOS1AP as a modulator of cardiac repolarization. The quantitative trait is the electrocardiographic (ECG) QT interval with ≈30% heritability. Typing was by Affymetrix oligonucleotide arrays containing 115,571 SNPs as described in detail (15). Our sample differs from these data only by inclusion of males and females, both corrected for heart rate, age, and sex as published and giving 208 cases and 201 controls. Hardy–Weinberg tests were conducted on controls in both samples A and B, excluding SNPs with χ₁² >10. The remaining SNP data in each sample were split into nonoverlapping regions, each of which covers at least 10 LDU and contains a minimum of 30 SNPs without breaking blocks of LD. Because of differences in SNP density, doing so gives 5,387 regions in sample A and 3,078 regions in sample B.

LDU Maps and CHROMSCAN.

Genomic patterns of LD are informative for locating disease genes, and power increases when a causal marker is typed. LDU maps describe these patterns more accurately than kilobase maps (16). Physical locations were taken from build 35 of the human genome sequence (University of California, Santa Clara, May 2004). Unlike physical maps, study-specific and various genome-wide LDU maps are available corresponding to the four HapMap samples separately and combined (17). The LDU map with the highest SNP density, largest sample size, and closest to the experimental data should be optimal. We therefore use the cosmopolitan LDU maps constructed from Phase II HapMap data (release no. 20, January 2006) and available at www.som.soton.ac.uk/research/geneticsdiv/epidemiology/LDMAP/map2.htm.

The advent of GWA analysis led to dramatic increase in the computation time of CHROMSCAN, which analyses regions sequentially. Therefore, a parallel version (CHROMSCAN-cluster) has been developed to analyze multiple regions simultaneously (18; www.som.soton.ac.uk/research/geneticsdiv/epidemiology/chromscan/). In this way, large datasets can be studied without difficulty. These and earlier applications of composite likelihood are based on the Malecot model, two subhypotheses of which are used to test for a causal polymorphism within each region. Model A, which assumes no association between affection status and SNPs, is taken as the null hypothesis and compared with model D, which estimates disease location (S), its intercept under complex inheritance (M), and residual association (L). The test statistic depends on the composite likelihoods of these two models. To account for autocorrelation between SNPs as a result of LD, significance is determined empirically by a rank-based permutation test. To determine accurate levels of significance, the number of permutation replicates must approach 10/P. We therefore use 1,000 replicates to perform preliminary screens and, where necessary, increase this number to 50,000. The only deviation from the recent description of CHROMSCAN (9) is that P values are now taken from Ewens (10) instead of Tukey (19) because the former more closely approximates a uniform distribution (last section). CHROMSCAN assumes allelic additivity because a causal SNP may well not have been tested and nonadditivity degrades with recombination.

msSNPs.

To compare evidence from composite likelihood and single SNPs, we identify the msSNP for each region. Selecting the msSNP from such a large number of SNPs (30 or more) biases the nominal χ₁² and conventional P value computed on the null hypothesis. This bias was confirmed by regressing msSNP P values on LDU length and SNP number. Under H₀, the P values for random SNPs should correspond to χ₂² = −2lnP (20), with variance V = 4 and mean μ = 2. If selection of msSNPs were unbiased, adjustment of V would give an estimate of μ near 2, whereas μ is less sensitive to small values of P and therefore would not provide a good estimate of V. We must reduce the bias in μ before adjusting V.

Step 1.

Because regions defined above vary in the number of SNPs, our first problem is to select subsets with limited diversity but including a large number of regions so that estimates of the Bonferroni parameter R will be accurate. For a given subset, the weighted mean number of SNPs is S = Σf_im_i/Σf_i, where f_i is the number of regions with m_i SNPs.

Step 2.

Let R be the effective number of independent SNPs in a subset assigned S SNPs. The Bonferroni model assumes a corrected P value of P_ci = 1 − (1 − P_ni)^R. To obtain a mean of χ_2c² = 2 when χ_2cⁱ² = −2lnP_ci, we take

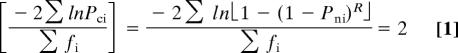and solve the equation

by regula falsi to give the Bonferroni P_ci with the desired mean χ_2c² of 2. This method requires two estimates of R flanking the final estimate so that one gives a negative solution and the other gives a positive solution. These values of R are then iterated until a solution sufficiently close to 0, in this case to five decimal places, is obtained (Table 1). The relationship between R and S was then determined by regression so that a value of R could be assigned to each region given S. Corrected P values for msSNPs are then given by 1 − (1 − P_ni)^R.

Step 3.

To set the variance of χ_2c² to 4 requires dividing both χ_2c² and μ by

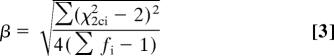to give the desired variance with mean 2/β, which is acceptable only if β ≈ 1.

This calculation greatly reduces the significance of msSNPs but conserves the order of the nominal P values without consideration of smaller effects of numbers of SNPs tested in the region and length of the region in kilobases or LDU. Analysis of composite likelihood is simpler because steps 1 and 2 are not required. Whereas the power of an msSNP depends on its inclusion in a sample that is a small fraction of all SNPs in the genome, composite likelihood does not require inclusion of a causal SNP. Instead of a single P value, composite likelihood gives a point estimate, standard error, and information that allow inference of confidence intervals and efficient meta-analysis.

Combination of Evidence.

The relationship between the corrected msSNP χ₂² and composite likelihood converted to χ₂² was determined by using correlation analysis. A principal component analysis based on this correlation matrix gives a PC1 with positive coefficients and a second principal component (PC2) that is negative when the msSNP has a lower rank than composite likelihood. PC1 was used to order and rank all N regions. Following Ewens (10), this was converted to a P value by rank/IN to give χ₂² = −2lnP for each region based on the combination of evidence. For each sample, the regions with the highest χ₂² defined in this way were examined further.

Calculation of Empirical P Values from Composite Likelihood.

Association mapping of a gene contributing to complex phenotypes requires an efficient estimate of genomic location and its standard error, derived from autocorrelated markers whose complex relationships must be parsimoniously approximated. This is a classical problem for composite likelihood formed by adding together individual component log likelihoods, each of which corresponds to a marginal or conditional event (21). Composite likelihood is often used in statistical genetics to make inferences about current or ancestral populations. It invariably encounters the problem that its component log likelihoods are not independent, and so conventional estimates of P values and standard errors are approximate. However, reliable values can be obtained by simulation of n replicates. Under H₀, the rank-based distribution of P is uniform with mean 1/2 and variance 1/12 in the limit as n → ∞. Many recipes have been proposed for reliability with smaller values of n, all of the form P_i = (i − A)/(n + B) for the ith value of P, where A and B are constants. Because the mean of the arithmetic progression from i = 1, … ., n is ı̄ = (n + 1)/2, the mean of P_i is (n + 1 − 2A)/2(n + B), which equals ½ only if B = 1 − 2A or n → ∞. Two suggestions for Monte Carlo methods, A = B = 0 and A = −1, B = 1, are biased in opposite directions with finite n. Because the mean is specified without error, the variance is computed with df = n.

This is shown in Table 6 for n = 10, which is unrealistically small but shows how different values of A and B behave. Taking A = B = 0, the mean for a uniform distribution is exceeded and the variance is underestimated, but the smallest P value (P₁) is uniquely 1/n. This is critical because P for single samples under H₁ is estimated by interpolation from replicates under H₀, requiring higher accuracy for the smallest values that are of greatest interest. All models that give the expected mean of 0.5 underestimate P₁, most grossly when A is set at 0.525 to recover the correct variance, by using regula falsi to estimate A so that the variance is correct to five decimal places (i.e., 0.08333). Progress with increasing n is shown in Table 7. The estimate of skewness γ₁ is 0 and of excess γ₂ is −1.2, as expected for a uniform distribution. The variance approaches 1/12 in the last three models for n = 100 but more slowly as B increases. The ad hoc fit of the variance by the last model for n = 10 deviates for n = 100 and 1,000. Even at n = 100,000 (data not shown), A = B = 0 is the only model that gives P₁ = 1/n, although A = 0, B = 1 converges quickly. The latter has the advantage of giving a correct mean but at the cost of a more conspicuous underestimate of the variance. All of the other models give misleading estimates of P₁ unless n is substantially >10,000.

Table 6.

Mean and variance of P_i for n = 10 under H₀ (df = n)

Ref.	A	B	Mean	Variance	P1
22	−1	1	0.5909	0.06818	0.18182
10	0	0	0.5500	0.08250	0.10000
23	0	1	0.5000	0.06818	0.09091
24	0.3	0.4	0.5000	0.07628	0.06731
19	1/3	1/3	0.5000	0.07726	0.06452
25	3/8	1/4	0.5000	0.07852	0.06098
24	0.5	0	0.5000	0.08250	0.05000
Adjusted*	0.525	−0.050	0.5000	0.08333	0.04774

Skewness (γ₁) = 0, Excess (γ₂) = −1.22.

*See Results.

Table 7.

Moments of P distribution for increasing n

Ref.	n = 100			n = 1,000			n = 10,000
	Mean	Variance	P1	Mean	Variance	P1	Mean	Variance	P1
22	0.5099	0.08168	0.0198	0.5010	0.08317	0.0020	0.5001	0.08332	0.00020
10	0.5050	0.08332	0.0100	0.5005	0.08333	0.0010	0.5001	0.08333	0.00010
23	0.5000	0.08168	0.0099	0.5000	0.08317	0.0010	0.5000	0.08332	0.00010
24	0.5000	0.08266	0.0070	0.5000	0.08327	0.0007	0.5000	0.08333	0.00007
19	0.5000	0.08277	0.0066	0.5000	0.08328	0.0007	0.5000	0.08333	0.00007
25	0.5000	0.08291	0.0062	0.5000	0.08329	0.0006	0.5000	0.08333	0.00006
24	0.5000	0.08332	0.0050	0.5000	0.08333	0.0005	0.5000	0.08333	0.00005
Adjusted*	0.5000	0.08341	0.0048	0.5000	0.08334	0.0005	0.5000	0.08333	0.00005

*As for n = 10.

Our role has been to determine the properties of different models that until now have been considered competitive to estimate significance levels for composite likelihood by Monte Carlo methods, widely used for association mapping and other applications of population genetics. This evidence demonstrates that the model of Ewens is best among the several alternatives that have been disputed and the infinite number that could be proposed. Alternatives should be abandoned.