Modelling the current distribution across the depth electrode-brain interface in deep brain stimulation

Abstract

The mismatch between the extensive clinical use of deep brain stimulation (DBS), which is being used to treat an increasing number of neurological disorders, and the lack of understanding of the underlying mechanisms, is confounded by the difficulty of measuring the spread of electric current in the brain in vivo. Here we present a brief review of the recent computational models which simulate the electric current and field distribution in the three-dimensional space, and consequently make estimations of the brain volume being modulated by therapeutic DBS. Such structural modelling work can be categorised into three main approaches: 1) Target specific modelling; 2) Models of instrumentation; 3) Modelling the electrode-brain interface (EBI). Comments are made for each of these approaches with emphasis on our EBI modelling, since the stimulating current must travel across the EBI in order to reach the surrounding brain tissue, and modulate the pathological neural activity. For future modelling work, a combined approach needs to be taken for revealing the underlying mechanisms, and both structural and dynamic models need to be clinically validated to make reliable predictions about the therapeutic effect of DBS in order to assist clinical practice.

DEEP BRAIN STIMULATION

There has been a sharp rise over the last twenty years in the use of deep brain stimulation (DBS), from a therapy used for a number of medically intractable neurological disorders [1-5] to various psychiatric disorders [6-8]. This procedure entails modulating the pathological neural activity by injecting electrical current into a condition-specific target deep in the brain via surgically implanted electrodes. Great efforts have been made to determine the appropriate selection of patients and brain targets, and the use of imaging and stereotactic surgical techniques helps to improve electrode placement within the brain. However, it remains unclear how the injected current alters neuronal activity and achieves the desired therapeutic effect [9-11], as DBS has mainly evolved from ablative procedures and not from systemic laboratory-based investigation. The setting of current parameters [12-14] and the electrode contact configurations [15-18] for achieving the desired neuromodulation are crucially important at the post-implantation stage, and these parameters must be uniquely tuned for each patient, a time-consuming process between clinicians and patients. If the biophysical mechanism of electric current distribution in the brain was better understood, adjustment of stimulation parameters could be predicatively determined, rather than chosen by trial and error, so that the therapeutic benefits and side-effects of DBS could be optimised.

STRUCTURAL MODELLING

One of the main obstacles to understanding more about the mechanisms of DBS is that it remains impossible to visualise in situ how the current injected into patients’ brains is spreading through the surrounding neural tissue, and how it is interacting with the pathologically synchronised neural activity, despite the increasing resolution of anatomical imaging techniques which can provide visualisation of the electrode placement with millimetre accuracy [19]. Therefore, in order to compensate for the lack of such quantitative investigations, we can utilise computational modelling. In particular by constructing a biologically-based three-dimensional structural model of the implanted electrodes and the surrounding brain tissue using the finite element method (FEM), in which the geometry and the biophysical properties of the electrode and the surrounding brain tissue are persevered. FEM models [20] are primarily based on the geometry of the system in question, and this approach was previously used to model chronically implanted cortical microelectrodes used in animal experiments [21], and was adapted soon after to study the macroelectrodes used in human DBS [22]. The aim is to ultimately use such models to estimate the electric field induced by DBS and visualise how the injected current spreads within the brain, which in turn will help clinicians to optimise the therapeutic effects in patients.

The estimation of the electric potential distribution using FEM models is primarily based on the geometry of the system in question. These three-dimensional geometries provide the domain over which to solve Laplace’s equation:

$$\nabla .\sigma \nabla V=0$$

where V is the induced potential (measured in Volts), and σ is the conductivity (measured in Siemens per metre). This equation follows from the full set of Maxwell’s equations for electromagnetics, under the condition that all time-derivatives are zero; therefore this approach only accounts for the electrostatic case.

The solution of this equation over the specified domain (the three-dimensional geometry) yields the potential distribution induced by DBS. We can further calculate (1) the electric field by using the relationship E = -∇V ; (2) the activation function, which is calculated as the second spatial derivative of the potential, and is a measure of how effective the stimulation is at exciting neurons in the surrounding tissue [23]. Note that the activation function is one of the approaches used to analyse the effects of stimulation, however as discussed previously it has significant short comings, such as only giving an accurate representation at pulse-widths of a few micro-seconds [24] and that it does not represent the neural processes being activated only the source stimulus [25]. Another method of estimating the activation of the neural tissue, is by coupling the results from the FEM model to compartmental cable models of single neurons or portions of neurons (most commonly of axons). Previous work has assessed how this analysis compares to the activation function, in determining the influence of the stimulation on the nearby neurons [26].

The structural models of DBS reported so far can be categorised into three main approaches: 1) Target specific modelling, which focuses on the region of tissue activated when an electrode is implanted in a specific brain region for treating a specific neurological disorder; 2) Models of instrumentation, which study the spread of current induced by different electrode designs; and 3) Modelling the electrode-brain interface (EBI), which focuses on the generic properties of the interface which are independent of the disorder being treated or of the target being stimulated.

Models of specific brain targets

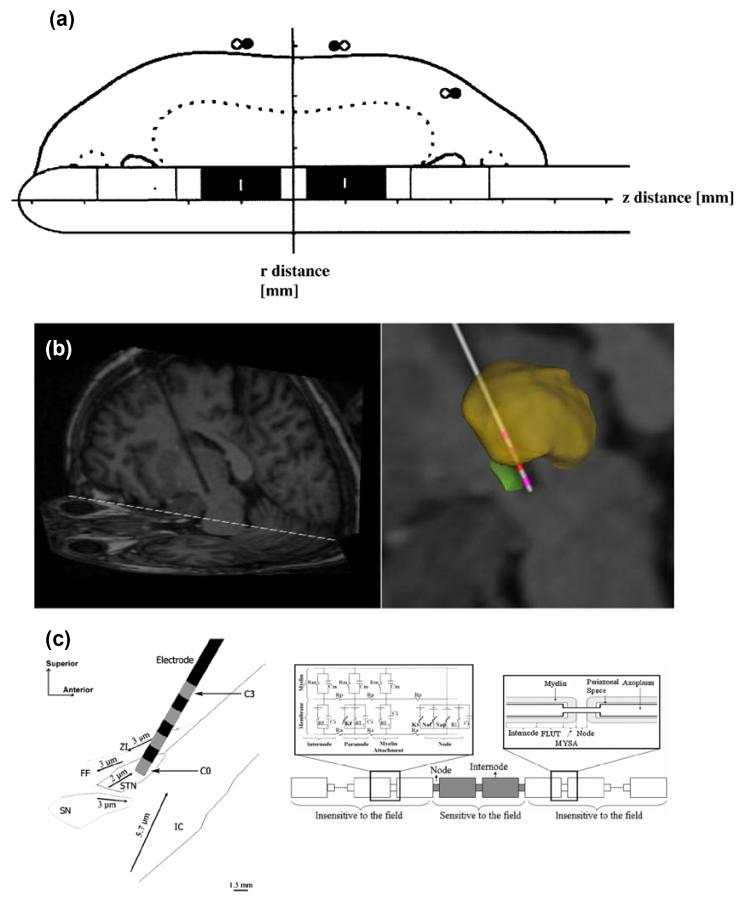
In order to understand the effect of DBS on a particular target nucleus, FEM models can be constructed to represent a specific brain region. One study of this type was based on DBS of the globus pallidus interna (GPi), which is a target used in the treatment of dystonia [27]. This study developed a model for visualising the electric field around the implanted DBS electrode using FEM, and co-registered the calculated electric field with the precise anatomy of the GPi obtained from a patient’s post-operative MRI scan, in order to assist the process of localisation and parameter selection by matching the field to the target in size and shape (Fig. 1a). In this way, Hemm et al were able to show how the modelling of the electric field, correlated with patient-specific anatomical information (via individual MRI images) could be useful for the routine determination of current parameters. However this model did not take the 3-D geometry of the brain into account when creating the model, but simply super-imposed the calculated electric field onto the MRI. Therefore this model does not account for the inhomogeneity of the three-dimensional surrounding brain tissue.

Figure 1.

Previous FEM models studying DBS. (a) Hemm et al [16] modelled the field surrounding a DBS electrode and co-registered the results to a MRI, in order to appreciate how the field spreads in and around the GPi. (b) Butson et al [28] model the STN using a standard brain atlas and a patient’s MRI (left) to obtain a patient-specific model (right). (c) Sotiropoulos & Steinmetz [29] also model an electrode implanted in the STN (left), and couple the results to compartmental models of axons (right).

Recently the McIntyre group took this approach further and initially defined the three-dimensional geometry of the FEM model by including the specific neuroanatomy details obtained from a brain atlas [28] (Fig. 1b). Therefore the effect of nucleus boundaries and fibre tracts on the electric field distribution could be more accurately visualised. They took this a step further and “warped” the geometry of the model to fit the precise STN geometry and electrode location of an individual patient, via the anatomical detail contained within the patient’s MRI scan. Note that image artefact introduced by the metal contacts of the electrode [19] may compromise the accuracy of localising the electrode in situ. Using this approach the specific structure of a patients’ brain can be taken into account when predicting the effect of stimulation, making the estimate of the volume of tissue activated more accurate. Therefore, natural variations in the size and shape of nuclei can be taken into account when selecting parameter values for that patient. This modelling approach needs to be systematically tested, via validation of the predictions made with the models in large-scale clinical trials.

A recent paper also took this target specific approach [29], and defined the geometry of their FEM model based on the STN and surrounding structures, which Sotiropoulos and Steinmetz obtained from digitised sagital sections from a stereotaxic brain atlas. Although they did not “personalise” the model to fit a specific patient’s MRI, and idealised the electrode localisation, they coupled the model to a large number of axon cable models (Fig. 1c). This step is one method of quantifying the effect of the induced electric field on the surrounding neural tissue. They went on to systematically vary fibre diameter, orientation, degree of anisotropy and homogeneity of the tissue, etc in order to fully characterise how these factors influence the results from their model. The combination of a target specific model, and an exhaustive parameter search in cable models representing the surrounding neural tissue, is an important step to validate their modelling approach towards making predictions about outcomes of neural activation. This paper demonstrates the dependence of these models on tissue properties, and the fragility of the predictions made under parameter changes, which must be highlighted if these models can be useful in a clinical setting.

Models of DBS electrodes

An alternative approach taken by a number of models is to focus on the implantable electrode used in the DBS procedure. There are two types of electrodes currently used for the DBS procedure (produced by Medtronic, MN). Both of these electrodes are cylindrical (diameter of 1.27mm), with an array of 4 platinum/iridium contacts (1.5mm in length), and they differ only in the degree of insulated (80A Urethane) spacing (0.5mm in model 3389 and 1.5mm in 3387). The use of an array of electrodes on a single probe is crucial for the existing procedure for the following reasons: 1) the ability to selectively activate a particular contact allows the optimisation of electrode placement relative to the target after implantation without having to move the electrode, and 2) this allows different configurations of the active electrode contacts in order to direct the current flow. To investigate whether the current electrode design is optimal for maximising the therapeutic effect, while minimising battery consumption, and chemical reactions at the electrode surface, a recent modelling study from the Grill group looked at potential alternative electrode designs, with either more or less than four contacts, in order to see how this influences the shape of the electric field induced [30]. The geometry of the model is based on the electrode surrounded by a cylinder of homogenous neuronal tissue. Therefore this study develops a FEM solution over a geometry for which Laplace’s equation could have been solved analytically. They showed that compared to solid electrodes (i.e. a single long contact), segmented electrodes generate larger magnitudes of the second spatial difference of the extracellular potentials, which is a good measure of neuronal activation, for the same stimulation intensity. Therefore such electrodes need less energy to achieve the same level of neuronal activation, which is desirable in order to reduce the number of surgeries to replace stimulator batteries.

Further results from a study by Butson et al., show that an increase in electrode contact height causes a linear increase in the volume of tissue activated [31], while increases in electrode contact diameter caused a decrease in this volume. This study focused on stimulation of the ventral intermediate nucleus (VIM) of the thalamus, which is a long and narrow nucleus with approximate dimensions of 8mm by 3mm by 12mm. By modelling the VIM using data from a brain atlas, they find that the Medtronic electrodes which are currently available for use in DBS procedures are only able to activate 26% of the VIM. They go on to predict that an electrode contact of different dimensions would achieve a better match with the VIM, and would stimulate 7% more of the nucleus, without increasing the current spread into neighbouring brain areas. Consequently, such studies suggest that the use of a specific electrode for individual brain targets may better localise the electric field, achieve better therapeutic outcome, and reduce undesirable side effects. As for previous approaches, the predictions of this model need to be validated and translated into clinical practice.

Another issue related to chronically implanted electrodes, is that of chemical reactions occurring at the surface of the electrode. An experimental study by Gimsa et al, showed that with the micro-electrodes used for chronic implantation in animal studies, high-frequency stimulation caused non-linearities in the current-voltage relationship, and furthermore that corrosion due to electro-chemical reactions, as well as dissolution of electrode material occurred after only 8 hours [32]. The micro-electrodes used in animal studies differ from those used for DBS in material (often including stainless steel) as well as shape. A later study by this group used the finite integration technique (an alternative method for solving the Laplace equation over a three-dimensional domain) to show that the areas of greatest metal curvature of depth electrodes caused the highest current density, which is related to tissue damage, and concluded that the electrode material and design must be chosen to avoid this [33]. However, a similar experimental study showed that stainless steel micro-electrodes caused tissue damage in rats following high-frequency stimulation, while platinum/iridium micro-electrodes did not [34].Therefore these studies showed that reactions occurring at the electrode surface are an important factor to take account of in the study of DBS.

Models of the depth electrode brain interface

The influence of the electrode-brain interface (EBI) on the currents crossing the interface has been considered in previous modelling work [35], but only recently has the EBI been a focus of DBS research [36-38]. Studies from our own group have observed dynamic changes occurring at the EBI, both in vitro and in vivo. In one study [36], electrodes which had been explanted from DBS patients were studied using electron microscopy. It was reported that in all cases, which included patients treated for different disorders and electrodes explanted from different brain regions, there was evidence that giant-cell (multi-nucleate body produced by cells fused together) type reactions had occurred at the surface of the DBS electrodes. This reaction was present irrespective of the duration of implantation, observed as early as two weeks post-implantation, and may be a response to either the metal contact or the polyurethane component of the electrode’s surface coat. In a similar study it was shown that the implanted silicon microelectrode arrays caused a chronic inflammatory reaction at the microelectrode brain tissue interface [39]. In another study [37], by recording in vivo through the implanted DBS electrode, it was demonstrated that the EBI could be modulated by physiological factors such as brain pulsation. A modulated electrode potential with a mean amplitude of approximately 7μV was detected a few days after implantation with a mean positive detection rate of 77.5%, across four different brain regions, and four neurological conditions. This electrode potential was correlated in frequency and amplitude to the simultaneously recorded blood pressure signal. This strongly indicates that this low-frequency component of the LFP, and therefore the EBI, is modulated by brain-pulsation.

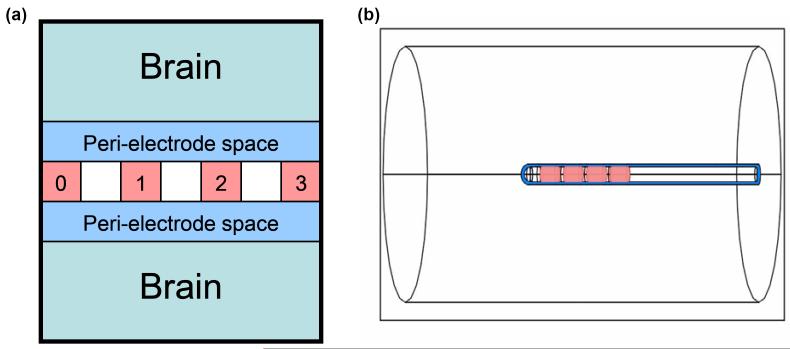
In order to investigate the changes occurring in both the acute and the chronic post-implantation stages and to simulate our previous pathological examination [36] of the explanted electrodes and our physiological study [37] of the acute EBI in situ, a three-dimensional model of the EBI has recently been established. This model focuses on the depth EBI, which we have defined as consisting of three components (Fig. 2): 1) the implanted DBS electrode; 2) the surrounding brain tissue; 3) a peri-electrode space, which is created by the mechanical force of implantation. In the acute stage the peri-electrode space is filled by extracellular fluid (ECF), and in the chronic stage by the growth of giant cells [36]. The model was created using FEMLAB 3.3, and meshed into tetrahedral elements. This 3-dimensional geometry is used to solve Laplace’s equation, using conductivity values as follows: σ _tissue = 0.2 S/m [40], σ _ECF = 1.7 S/m [41] and σ _{Giant Cell} = 0.125 S/m which is equivalent to the reported values for white matter, and is comparable with values used for the encapsulation layer in previous modelling studies [26]. Dirchilet boundary conditions are used to define the stimulating potential at the electrode contact(s). Note that solution of the electrostatic case neglects an important feature of a dynamic EBI, in which the impedance of the interface elements is time/frequency-dependent. This needs to be developed in future work. However, the electrostatic model does allow the investigation of the relative effects that changes at the interface have on the induced potential distribution, and serves as a natural comparison to the dynamic solution. Furthermore, the geometry of the EBI model could allow an analytical solution of Laplace’s equation, however this would require further simplification of the geometry.

Figure 2.

(a) The depth EBI consists of 3 essential components: (i) the implanted DBS electrode, which has an array of 4 metal contacts (pink, numbered here 0 to 3); (ii) the surrounding brain tissue (light blue); (iii) a peri-electrode space (dark blue), which is filled with extracellular fluid in the acute case, and reactive giant cells in the chronic case. (b) This description is modelled as a three-dimensional geometry using the software COMSOL Multiphysics 3.3. The dimensions of the electrode match those of the actual DBS electrode used (Medtronic model 3389), the peri-electrode space is arbitrarily defined to have a thickness of 0.25mm, and the surrounding brain tissue is modelled as a homogenous cylinder of 10mm radius.

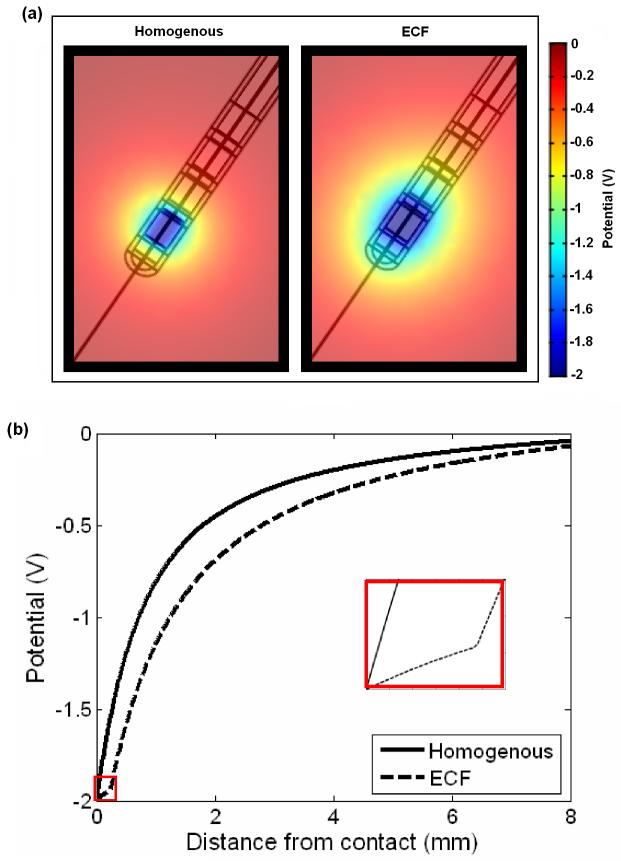
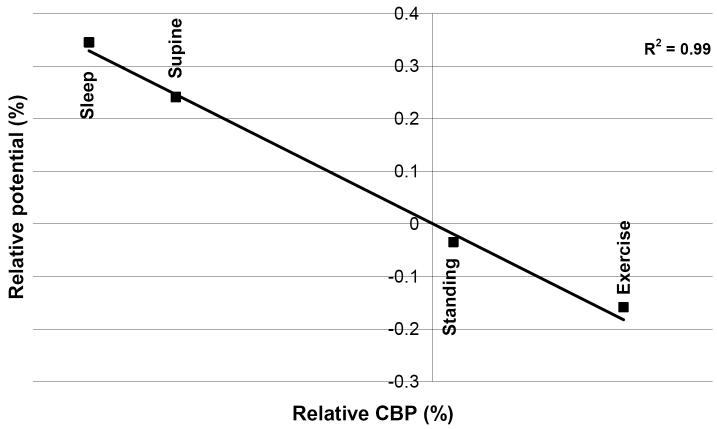
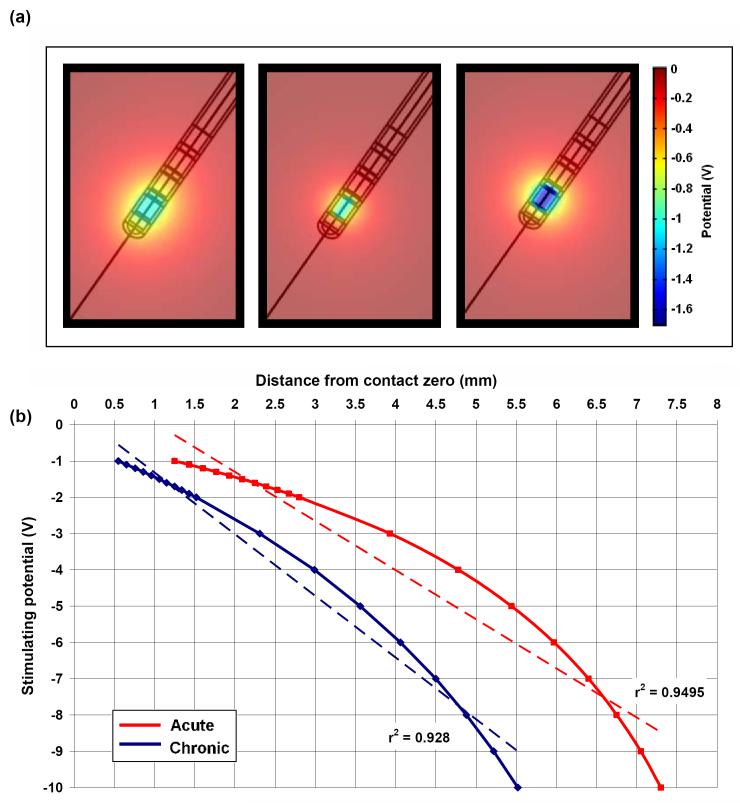
Using this model, we showed that acutely, the induced electric potential is able to spread further into the surrounding tissue (Fig. 3a), due to the presence of the high conductivity ECF layer, which creates a path of low resistance through which the current travels. This can be further demonstrated by the cross-section curves in Figure 3b, which show this shunting effect through the ECF layer, indicating that neglecting this peri-electrode layer in structural DBS models will result in a large underestimation in the predicted field strength during the acute stage. Furthermore, we assumed that as the EBI is dynamically modulated by the brain pulsation due to cerebral blood perfusion (CBP) [37], as (1) blood perfusion into the brain would increase pressure on the electrode surface; and (2) blood has a higher conductivity than brain tissue, therefore blood perfusion would also cause an increase in the conductivity of the surrounding brain tissue. We modelled these effects of brain pulsation at different physiological conditions, which differ in rate of CBF, by decreasing the thickness of the peri-electrode space, and increasing the tissue conductivity. We found a significant inverse linear correlation between CBP and potential distribution over different physiological conditions, suggesting that as CBP increases, there is a decrease in the amount of potential delivered to the surrounding tissue (Fig. 4). These percentage changes are too small to cause a clinically observable effect in stimulation of a few Volts in intensity. Nevertheless, the dynamic changes at the EBI may have a more profound effect on recording brain activity of a few microvolts in magnitude.

Figure 3.

(a) The potential distribution spreads further when the peri-electrode space surrounding the implanted electrode is filled with fluid (left) than surrounded by the homogenous brain tissue (right). (b) The cross-section measured radially outwards from the centre of contact zero through the potential distribution in the ECF (dashed line) and homogenous tissue (solid line) cases. The ‘shutting effect’ of the fluid filled peri-electrode space is highlighted in the inset.

Figure 4.

The mean percentage change in the spatial potential distribution in the four physiological conditions (four points) relative to sitting significantly correlates with the change in CBP.

In contrast, giant cells of low conductivity, which start to grow as early as two weeks post-implantation, produced a ‘shielding effect’ on the induced potential distribution in the model, by restricting the spread of current in the surrounding tissue (Fig. 5a). To compensate for giant cell growth, the stimulating intensity needed to be increased from -1.0V to -1.7V (70%) to maintain the same level of electric potential (Fig.5a right). These results have a clear implication for clinical applications, as they indicate that the stimulation intensity used acutely can be lower compared with during chronic stages. The activation distance/stimulation intensity curve for both ECF and giant cells conditions was plotted for a range of stimulating potentials (Fig. 5b), which highlights how stimulation efficacy is reduced in the initial weeks post-implantation by as much as 50%. In summary, our EBI modelling work has shown that the interface between the brain and the implanted depth electrode is dynamic and modulated by physiological and pathological factors, and has an impact on the current crossing from the electrode into the human brain during stimulation and on the current crossing in the opposite direction during recording. Therefore, the peri-electrode space and its modulation is a crucial component when modelling DBS and making predictions about the effects of stimulation on surrounding tissue.

Figure 5.

(a) Potential distribution when the peri-electrode space is filled with ECF (left, -1.0V) and giant cells (centre, -1.0V), and compensatory increase in stimulating intensity of -1.7V in the giant cell case (right, -1.7V) to maintain the same level of stimulation as the ECF case. (b) Comparison of the estimated intensity-distance curves with an assumed activation threshold of 0.5V between ECF and the giant cell cases, with lines of best fit (dashed). In order to compensate for the layer of low conductivity giant cells, the stimulating potential must be topped-up by between 70% and 100%.

To investigate how the electric field can be shaped by different electrode contact settings, we simulated these different settings of the quadripolar electrode within our EBI model. Simulating -2V monopolar stimulation at contact 0, the electric field spreads radially outwards from the active contact, which is the standard view of a ‘far-field dipole’ (Fig. 6a). For bipolar stimulation, we set ±1V at contacts 0 and 1 as the control case. The field surrounding the electrode forms a typical ‘near-field dipole’ with the electric field centred around contacts 0 and 1 (Fig. 6b). These results indicate that the range of stimulation is greater in the monopolar than in the bipolar setting with a comparable intensity. Furthermore, notice that the size of the bipolar near-field dipole increases as the active contacts move apart, i.e. when stimulating via contacts 0 and 2 (Fig. 6c) or 0 and 3 (Fig. 6d). These studies suggest that to fully explore the capabilities of the currently available DBS electrodes can be useful in order to optimise the outcome of DBS.

Figure 6.

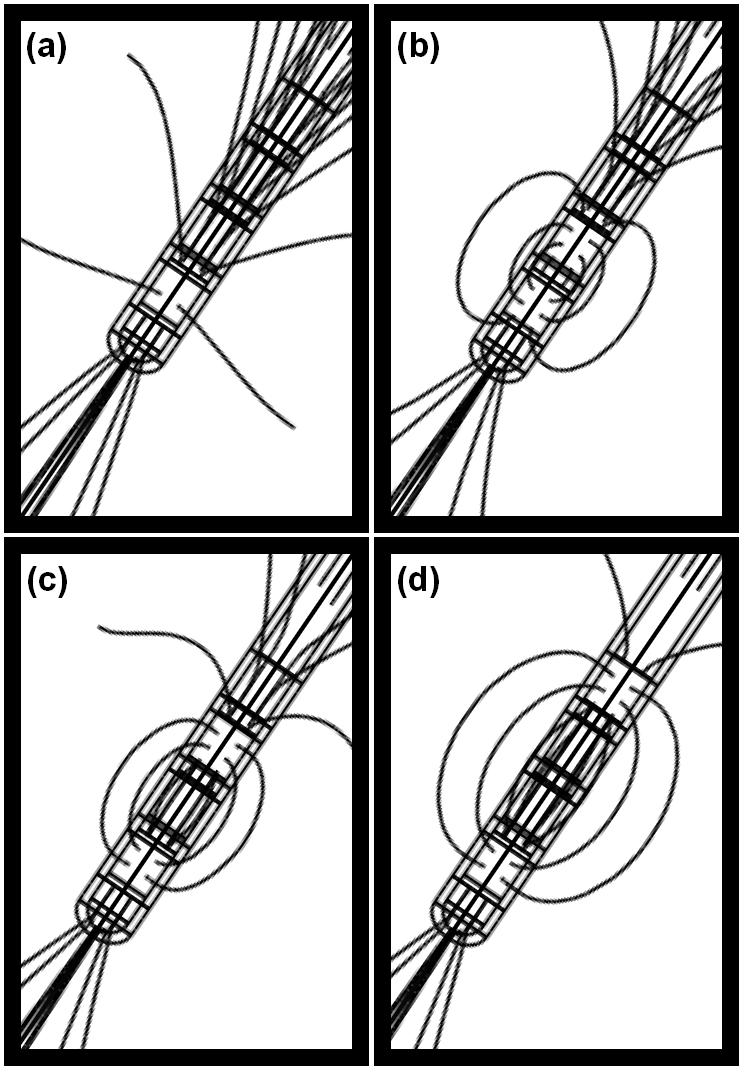
These figures show the field lines for (a) monopolar stimulation of -2V via contact 0; (b) bipolar stimulation of ±1V at contacts 0 and 1, (c) bipolar stimulation of ±1V at contacts 0 and 2, and (d) bipolar stimulation of ±1V at contacts 0 and 3.

Expert commentary

The models presented and described here are useful for visualising the spread of current in the human brain, which is impossible to do experimentally, and each approach has made numerous invaluable contributions to the study of DBS and the underlying mechanisms. A clear example comes from McIntyre and colleagues [42] on identifying the neural element activated by the extracellular stimulation. By coupling the results from a FEM model of DBS to multi-compartmental models of single neurons, they have shown that it is more likely the axons rather than the soma of neurons are activated. The significance of their work is reflected by the use of compartmental models of axon segments to estimate the activation of surrounding tissue so that the cellular mechanisms of DBS can be investigated at the systemic level [28,29,31,35,43]. Our own modelling of the depth EBI by focusing on the dynamic features of the peri-electrode space over the acute, transitional and stabilised chronic post-implantation stages quantitatively highlighted the significance of the peri-electrode space, its modulation over time and interaction with monopolar and bipolar stimulation settings on the DBS outcomes. Arguably the most enticing feature of FEM models is that they allow us the ability to visualise the induced electric field in co-registration with high-resolution images of individual patient. This allows us to make possible theoretically based prediction on parameter settings on the given information including clinical data, electrode placement and current distribution.

However, this approach also has a number of limitations, which must be taken into consideration when using this tool, and the predictions made in this way. For example, the finite element method is by definition an approximation of the analytical solution of Laplace’s equation over the specified three-dimensional geometry. However, analytical solutions for Laplace’s equation on any geometry which is more complex than spherically symmetric volumes, such as spheres, cylinders etc. are extremely complicated, if not impossible. Therefore it is reasonable to use such an approximation, particularly if the accuracy of the solution obtained with increasing mesh density is considered.

Another important consideration is how we can measure what effect the predicted induced electric field will have on the neurons surrounding the implanted electrode. Current studies often use compartmental models of axons and apply the calculated potential distribution as an extracellular stimulus, but this assumes that DBS mainly activates nerve fibres [28,29]. Therefore this approach does not allow for any degree of somatic or dendritic activation. To overcome this issue, another option is to look at the relative field (or potential strengths) induced by different conditions. However, the latter approach cannot give a quantitative estimate of the range of activation. This limitation requires a great deal of thought, if we are to be able to use such models to directly make predictions which can be used to guide the clinical use of DBS. One option is to test the predictions made from FEM models in focussed clinical trials. However, we must be mindful of ethical issues, and be sure that the patients’ welfare and best interests take precedence over research aims.

Finally, here we have discussed the spatial approach of FEM modelling, but other computational modelling approaches also consider the temporal properties of the stimulating current, and in particular how the current can desynchronise the pathologically synchronised activity [44]. This temporal approach concentrates on the patterns of electrical pulses which can effectively desynchronise the network, and is an important accompanying tool to FEM models. However, these two approaches have thus far advanced independently from one another, whereas the combination of these techniques is likely to immeasurably advance our understanding of the mechanisms underlying DBS.

Five year view

As the use of DBS spreads to new ailments such as epilepsy, depression, and obsessive compulsive disorder, the number of patients who may benefit from this surgical intervention will increase. The ultimate challenge for computational modelling will be to use such computer models within routine clinical practice in order to predict the best settings for the current applied to each individual patient, as and when they require the intervention. This has already commenced with patient specific models having been established, however, such models do not take into account the changes occurring at the interface between the brain and the electrode on both short and long timescales, nor the effect of stimulation on the network activity. Therefore in the next stages, a combined approach will be necessary to obtain an accurate picture of what is happening and better target the pathological neural activity.

Key issues.

• Why there is a need for structural modelling: The lack of technology which allows the visualisation of the spatial and temporal spread of the injected current in DBS makes computational modelling an important tool for understanding the mechanism through which DBS achieves the therapeutic benefit to patients.

• Validation: These FEM models and simulations based on them need to be validated on their accuracy and reliability. Correlation between the modelling work and clinical outcomes may be the only way forward.

• Clinical implications: To use the anatomical specificity revealed by imaging and form a patient specific model may be used to assist stimulation parameter settings for individual patients, to allow repetitive simulations within limited time frame for investigating possible reason if stimulation does not work well, and to predict clinical outcomes.