Characterization of the effect of high molecular weight hyaluronan on trans-synovial flow in rabbit knees

Abstract

1. The effect of a rooster comb hyaluronan (3.6–4.0 g l⁻¹) of similar chain length to rabbit synovial fluid hyaluronan, on the trans-synovial escape of fluid from the joint cavity in the steady state (Q̇_s) was studied in 29 rabbit knees at controlled intra-articular pressures (P_j).

2. Rooster hyaluronan caused the pressure-flow relation to flatten out as pressure was raised. At 10–20 cmH₂O the slope of the quasi-plateau, 0.05 ± 0.01 μl min⁻¹ cmH₂O⁻¹ (mean ±s.e.m.), was 1/39th that for Ringer solution (1.94 ± 0.01 μl min⁻¹ cmH₂O⁻¹).

3. Bovine synovial fluid had a similar effect to hyaluronan in Ringer solution.

4. The quasi-plateau was caused by increasing opposition to outflow; the pressure required to drive unit outflow increased 4.4-fold between 5 and 20 cmH₂O. The increased opposition to outflow at 20 cmH₂O was equivalent to an effective osmotic pressure of 13–17 cmH₂O at the interface. Since the infusate's osmotic pressure was only 0.9 cmH₂O, this implied concentration polarization to 15–18 g l⁻¹ hyaluronan at the interface.

5. Mechanical perforation of the lining, or enzymatic degradation of the interstitial matrix by chymopapain, abolished the quasi-plateau. Hydrational expansion of the matrix by /2-fold did not. The increased opposition to outflow was reversible by washing out the hyaluronan, or by reducing P_j. It was unaffected by interruption of tissue blood flow or synoviocyte oxidative metabolism. These properties are compatible with a concentration polarization mechanism, i.e. flow-induced concentration of hyaluronan at the synovial interface due to molecular reflection.

6. A concentration polarization theory was developed for a partially reflected solute. Numerical solutions supported the feasibility of this osmotic explanation of the quasi-plateau. Additional mechanisms may also be involved.

7. It is concluded that native-size hyaluronan helps to retain synovial fluid in the joint cavity when pressure is raised and acts, at least in part, by exerting osmotic pressure at the interface between synovial matrix and a concentration polarization layer.

Synovial fluid lubricates joints and tendon sheaths, and carries metabolites to and from the avascular articular cartilage. The fluid is generated primarily by ultrafiltration of synovial microvascular plasma into the joint cavity when intra-articular pressure is low, as in extension. Hyaluronan is added to the fluid by actively secreting synoviocytes in the lining. The role of hyaluronan as a hydrodynamic lubricant has long been recognized. A second hydraulic role was suggested recently, namely the conservation of intra-articular fluid during joint flexion. This idea arose from the observation that, as intra-articular pressure is raised, the opposition to fluid drainage from the joint cavity increases if hyaluronan is present, but not when it is absent (McDonald & Levick, 1995). The present study explores new facets of this action and its mechanism.

Hyaluronan is a non-sulphated glycosaminoglycan chain of variable length. Native chains in synovial fluid have a molecular mass of (2–7) × 10⁶ Da. In some commercial preparations, however, the molecular mass can be an order of magnitude smaller, and this was the case with the umbilical cord hyaluronan studied previously (McDonald & Levick, 1995). Despite this, umbilical hyaluronan greatly reduces the trans-synovial escape of fluid from the joint cavity in rabbit knees, and alters the fundamental shape of the pressure-flow relation. In the absence of hyaluronan, the relation between intra-articular pressure and trans-synovial outflow is concave towards the flow axis (steepens as pressure is raised), because the lining's conductance increases when pressure is raised. In the presence of 3–6 g l⁻¹ umbilical hyaluronan, however, the relation becomes convex, and at high pressures the trans-synovial outflow is almost independent of pressure, creating a ‘quasi-plateau’ region. This indicates that umbilical hyaluronan creates an opposition to fluid outflow that increases each time pressure is raised. The effect bears no simple relation to viscosity (McDonald & Levick, 1994, 1995), and was interpreted at the time of its discovery in terms of increased outflow resistance (but see below). Since convex pressure-flow relations with plateaux develop when macromolecular solutions are ultrafiltered across semipermeable membranes (Blatt et al. 1970; Kozinski & Lightfoot, 1972; Wijmans et al. 1985; Tarbell et al. 1988), it was suggested that the synovial lining partially sieves out hyaluronan molecules from the solution filtering across it. The local accumulation of hyaluronan chains would then increase outflow ‘resistance’ (Johnson et al. 1987).

Two additional findings support the hypothesis that the synovial surface can partially reflect hyaluronan molecules. (1) In rabbit shoulder, elbow and knee joints, the intra-articular residence time for native hyaluronan is an order of magnitude longer than that for albumin (Knox et al. 1988; Coleman et al. 1997). (2) When a hyaluronan solution is filtered across the synovial lining in vivo, 48–95 % of the hyaluronan molecules in the filtrand are retained within the joint cavity (Scott et al. 1998a). Synovial reflection is only partial, because labelled intra-articular hyaluronan permeates slowly into lymph (Brown et al. 1991). The estimated mean hydraulic radius of the pores through synovial interstitial matrix is 15–45 nm (Levick et al. 1998), while the radius of gyration of hyaluronan is larger, ∼100 nm. This is in keeping with the fact that a flexible polymer can permeate pores of much smaller radius than that of the solute's hydrated domain (Munch et al. 1979).

The initial study by McDonald & Levick (1995) suffered from certain experimental and interpretational limitations, as follows. (1) The umbilical hyaluronan was of sub-physiological molecular size, namely (0.55–0.77) × 10⁶ Da. By contrast the molecular mass of native rabbit knee hyaluronan is between 2.9 × 10⁶ Da by size-exclusion chromatography (Coleman et al. 1997) and (2.4–2.7) × 10⁶ Da by viscometry (intrinsic viscosity, 3740–4060 ml g⁻¹; Sunblad, 1953; Denlinger, 1982). Although the effect of shortened hyaluronan is of clinical interest, chain length being reduced in inflammatory arthritis, it is clearly important to evaluate also the effect of hyaluronan of physiological chain length. (2) In interpreting their results in terms of a ‘filtercake’, McDonald & Levick (1995) did not take into account the substantial osmotic pressure that hyaluronan can exert in a concentrated layer.

The objectives of the present investigation were, therefore, to evaluate the effect of normal sized hyaluronan chains (> 10⁶ Da) on trans-synovial flow; to measure the concentration-osmotic pressure relation; and to explore the phenomenological characteristics of the hyaluronan-related increased opposition to outflow. The explored factors included (1) a comparison of the effects of a simple hyaluronan solution and normal synovial fluid, (2) assessment of the effects of perforation of the synovial lining, enzymatic disruption of the interstitial matrix and dilution of the matrix upon the quasi-plateau, (3) the effect of intra-articular stirring by joint movement, (4) assessment of the reversibility of hyaluronan-induced rises in the opposition to outflow, and (5) the independence of hyaluronan's effect from synoviocyte metabolic activity or microvascular perfusion. In addition, a simple analysis of the concentration polarization layer generated by a partially reflected solute is presented, and the effect of this layer is interpreted using the osmotic (cf. resistance) form of the boundary layer hypothesis (Wijmans et al. 1985).

METHODS

Biochemical methods and materials

Materials

Rooster comb sodium hyaluronate (Sigma Chemical Co.; >10⁶ Da) was dissolved in sterile Baxter Ringer solution, a pyrogen-free intravenous fluid containing 147 mM Na⁺, 4 mM K⁺, 2 mM Ca²⁺ and 156 mM Cl⁻, pH 7.2 (Baxter Healthcare Ltd, Thetford, UK). The solution was adjusted to pH 7.4 with NaOH. Bovine synovial fluid was aspirated from the metatarso-phalangeal joints of 20-month-old steers recently slaughtered at a local abbatoir (Farnham, UK) and stored at -80°C until use. Sufficient bovine fluid was accumulated for a single experiment by pooling many aspirates. Chymopapain was from Sigma.

Hyaluronan analysis by high performance liquid chromatography (HPLC)

Hyaluronan concentrations and molecular weights were analysed with a HPLC system (Waters Ltd, Watford, UK) fitted with a size-exclusion TosoHaas TSK G6000 PW_XL column (Anachem Ltd, Luton, UK). Elution profiles were measured by a Waters 486 programmable ultraviolet absorbance detector at 206 nm. Hyaluronan standards of molecular mass 210, 790, 900, 1200, 2000, 3900 and 5500 kDa were generously donated by Dr O. Wik (New Pharmacia, Uppsala, Sweden). Their molecular masses had been determined by laser light scattering. The HPLC system, the molecular discrimination range (0.21 × 10⁶ Da to 3.90 × 10⁶ Da) and the calibration curves were described by Coleman et al. (1997).

Endotoxin assay

Because some joints/species are very sensitive to endotoxin, and this contaminates some biochemical products (Bassett et al. 1992), rooster comb hyaluronan was analysed for endotoxin, using the Limulus amoebocyte lysate assay (E-Toxate, Sigma). The lysate of the circulating amoebocytes of the horseshoe crab Limulus polyphemus increases in opacity and viscosity in the presence of very small quantities of endotoxin, a reaction that closely parallels the biological and pyrogenic activities of the molecule. All glassware was soaked overnight in cleaning agent, E-Toxa-Clean (Sigma), rinsed in pyrogen-free water (Baxter Healthcare) and oven dried at 300°C. Negative results were obtained with 0.2 ml standards at <1.2 pg endotoxin, which indicates that the assay's detection limit in our hands was 6 pg ml⁻¹.

Biophysical methods

Viscosity of rooster comb hyaluronan solutions

Intrinsic viscosity, [η], is a sensitive index of molecular chain length. To evaluate [η], the relative viscosities of solutions of rooster comb hyaluronan in Baxter Ringer solution were measured with a cylinder-in-cup, rotational torque viscometer (Contraves Low-Shear 30 Viscometer, Contraves AG, Zürich, Switzerland). Viscosities were measured at concentrations 0.25–4.00 g l⁻¹ and shear rates 2.4–128 s⁻¹ at 35°C, the normal intra-articular temperature. Intrinsic viscosity, which is a measure of the volume occupied by 1 g of solute at infinite dilution, was evaluated at zero shear rate by Haug-Smidsrød plots as described by McDonald & Levick (1995). Molecular mass M was calculated from the intrinsic viscosity, in millilitres per gram, using the Mark-Houwink equation, [η]=kM^a, where k is 0.0228 and a is 0.816 for hyaluronan (Cleland & Wang, 1970).

Chain length and radius of molecular domain

The radius of gyration (R_g) of a neutral flexible polymer at infinite dilution can be related to its molecular mass by the self-avoiding, random-walk model of Flory (1971), leading to the expression R_g³=M[η]/8.84N_A, where N_A is Avogadro's number. An expression for the ionic polymer hyaluronan in an electrolyte solution of defined molarity (salinity S), namely R_g= 0.025M^3/5S^−0.08, summarizes the results of Johnson et al. (1987).

Critical concentration for overlap of molecular domains

Because the solvated domain of a hyaluronan molecule is very large, adjacent molecular domains begin to touch each and interact strongly at a certain critical concentration, C*. This critical concentration can be calculated by de Gennes's formula, C*=n/(4/3)πR_g³ where n is the number of monomers per molecule and C* here is expressed as number of monomers per unit volume (de Gennes, 1979). Onset of molecular coupling can also be related directly to intrinsic viscosity, using the expression C*= 2.5/[η] (Morris et al. 1980).

Osmotic pressure of rooster comb hyaluronan solutions

The reduction in flow caused by a concentration polarization layer adjacent to a sieving membrane can be interpreted either in terms of the resistance of the layer to flow or, equivalently with respect to the thermodynamic activity of the solvent, in terms of increased colloid osmotic pressure at the interface (Wijmans et al. 1985; see below). The colloid osmotic pressures of 0.5–20.0 g l⁻¹ rooster comb hyaluronan solutions were therefore measured. Measurements were made at room temperature with an electronic osmometer fitted with an Amicon PM10 membrane of nominal exclusion ≥ 10000 Da (Amicon, Lexington, USA) (McDonald & Levick, 1995).

Physiological methods

Net bulk flow out the joint cavity across the synovial lining was measured at controlled intra-articular pressures over the range 2–24 cmH₂O in the presence of infused rooster comb hyaluronan at concentrations of 3.6 g l⁻¹ (12 rabbits) or 4.0 g l⁻¹ (17 rabbits). The hyaluronan concentrations were within the normal range found in synovial fluid aspirated from rabbit knees (3.00–4.02 g l⁻¹; mean, 3.6 g l⁻¹).

Animal preparation and modified infusion system

New Zealand White rabbits weighing 2–3 kg were anaesthetized by 30 mg kg⁻¹ sodium pentobarbitone plus 500 mg kg⁻¹ urethane i.v., tracheostomized and maintained by smaller half-hourly doses. Core temperature was monitored by a rectal thermistor and controlled by an electrically heated animal blanket. With the animal supine the hindlimbs were secured with the knees at an unforced angle, namely 100–130 deg extension. Two cannulae were inserted into the suprapatellar joint space (Fig. 1). One, a 21-gauge hypodermic needle with lateral perforations drilled near the tip, was connected to one port of a water-calibrated Validyne CD 15 differential pressure transducer (Linton Instruments, Palgrave, UK) to measure intra-articular fluid pressure (P_j, ± 0.1 cmH₂O). The transducer was zeroed by adjustment of the height of a water column connected to the opposite port, until level with the joint. The other intra-articular cannula was a sterile, 20 gauge polypropylene Medicut (Argyle-Sherwood, Tullamore, Ireland) with a lateral aperture cut just proximal to the tip to facilitate flow. This cannula was connected to a saline-filled infusion reservoir, the vertical height of which controlled intra-articular pressure. Flow of solution into the joint cavity (Q̇_in) was recorded by a photoelectric drop counter whose drop size was 8 μl over the range of flows observed. Conversion of Q̇_in to net trans-synovial flow is described later. Pressures and flows were recorded on a chart recorder.

Figure 1. Schematic diagram of method for studying trans-synovial flow in presence of hyaluronan.

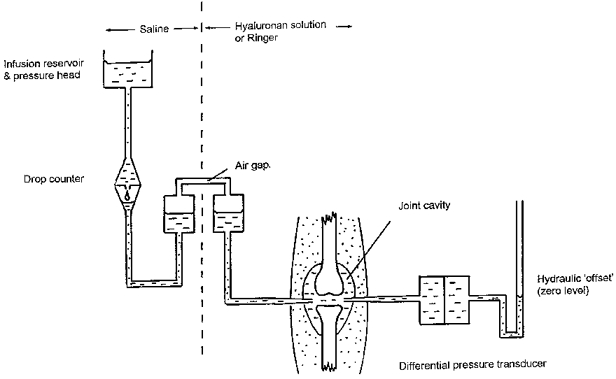
The saline pressure head was used to infuse hyaluronan solution and to control intra-articular pressure in the knee of an anaesthetized rabbit. For details, see text.

Because rooster comb hyaluronan is more viscous and more expensive than umbilical hyaluronan, the infusion apparatus was modified to reduce its hydraulic resistance and priming cost. An air gap was introduced into a vertical, wide-diameter chamber, which was pressurized by the infusion reservoir (Fig. 1). The pressurized chamber was connected to the synovial cannula by a short, wide bore tube to minimize hydraulic resistance. The system contained hyaluronan downstream of the air gap, and saline upstream of the air gap. Droplet formation was thus unaffected by hyaluronan, the hydraulic resistance and priming cost were minimized, and dilution of infused hyaluronan by saline was prevented. The infusate was not pre-warmed, because intra-articular heat transfer is rapid and efficient.

Procedures conformed to UK legislation and animals were killed by an overdose of i.v. sodium pentobarbitone at the end of the experiment.

Protocol for determining pressure-flow relations

An initial infusion of ∼500 μl hyaluronan solution or Ringer solution raised P_j from the endogenous, subatmospheric pressure in extension to the lowest pressure that generates a measurable absorption rate, namely between 0 and 2.5 cmH₂O above atmospheric pressure. Endogenous fluid (volume ≤ 50 μl) was diluted ≥10 times, so endogenous hyaluronan did not significantly influence intra-articular fluid composition. Control experiments have shown that a preceding washout of the endogenous synovial fluid does not significantly alter the control pressure-flow relation for Ringer solution. The rate of secretion of endogenous hyaluronan, namely (5–6) × 10⁻³ mg h⁻¹ per joint (Coleman et al. 1997), is too slow to alter the intra-articular hyaluronan concentration significantly over the 3–5 h duration of the experiment.

Intra-articular pressure was increased in steps of ∼2-4 cmH₂O by raising the infusion reservoir 2–4 cm at 30–60 min intervals. The time interval was selected after subsidiary studies of the time course of flow (see below). Net trans-synovial flow was calculated at the end of each interval. Experiments continued until P_j had been raised to ∼24 cmH₂O, which is well into the pathological range found in joint effusions. At the end of the experiment, samples of intra-articular fluid were taken in five cases for molecular weight determination by HPLC to check for any chain degradation during the 3–5 h experiment. In this laboratory's previous work with umbilical hyaluronan, there was evidence of depolymerization during the experiment.

With Ringer solution in the infusion line, a step elevation of the infusion reservoir produces a brisk rise in P_j, which reaches a new equilibrium in 1–2 min. With the very viscous hyaluronan solution in the infusion line, however, the filling of the synovial cavity is intrinsically slow. To counteract this, and attain a stable P_j within 1–2 min, the infusion reservoir was over-elevated by ∼10 cm initially, then gradually lowered to its final setting as P_j approached its intended level. In this way intra-articular filling with hyaluronan solution was achieved rapidly, and without the large swings in P_j generated in a previous study by manual injections (McDonald & Levick, 1995).

Subsidiary studies of time course of hyaluronan flows

Prior to the main study, experiments were carried out to establish the time required for stabilization of trans-synovial flow in the presence of rooster comb hyaluronan. Hyaluronan solution was infused at constant pressure for 100 min, either at a low P_j (<10 cmH₂O, n= 5) or a high P_j (>10 cmH₂O, n= 5). A non-absorbed oil was infused at the same intra-articular pressure for 100 min into the contralateral joint, as a control for creep of the cavity wall (see below). On the basis of these experiments (see Results), a 60 min infusion interval was adopted for the main pressure-flow study at low pressures (<10 cmH₂O). At higher pressures stable flows were achieved by 30 min, which allowed the interval at each pressure to be shortened. This reduced the duration of these long experiments and did not affect the outcome.

Calculation of net trans-synovial flow (Q̇_s) by correction for viscous creep (Q̇_creep): oil studies

When a step rise in infusion pressure is imposed, infusate flows into the joint cavity in two phases. There is an initial, fast inflow caused by elastic expansion of the cavity. This filling flow declines rapidly as P_j approaches its new, equilibrium level. After P_j has stabilized (∼2 min), a slow inflow persists, due in part to trans-synovial absorption of the infusate and in part to a slight, outward creep of the cavity walls with time (viscous creep). A correction is required for the latter component.

The volumetric creep rate (Q̇_creep) can be measured by infusing a non-absorbed oil instead of an aqueous solution into the joint cavity. Creep rates have been measured previously by this method at 15–20 min intervals after step increases in P_j, leading to the result Q̇_creep= 0.23P_j+ 0.4 (Levick, 1979). Creep rate at a given P_j decays slowly with time, however (Knight & Levick, 1983), so new creep measurements were needed here, corresponding to 30–60 min intervals after a pressure rise. The procedure was the same as that used to measure the inflow of hyaluronan solution, except that the aqueous solution in the post-airgap tube was replaced by a low viscosity, non-absorbable oil consisting of 25 % liquid paraffin and 75 % 200/0.65 cS Dow Corning silicone oil (BDH Laboratory Supplies, Poole, UK). The oil was stained with Sudan Black and the joint was dissected post mortem to check that the oil remained within the joint cavity (10 joints of 8 rabbits). Q̇_creep at the appropriate pressure and time interval was then subtracted from Q̇_in for the aqueous infusates to give trans-synovial flow (Q̇_s), i.e:

The creep correction (see Results) was proportionately small when Ringer solution was infused. For example, for Q̇_in= 60 μl min⁻¹ at P_j= 20 cmH₂O the volumetric creep rate was 8 % of Q̇_in, i.e. trans-synovial flow accounted for 92 % of Q̇_in at 15 min. Creep accounted for a bigger fraction of the inflow in the presence of hyaluronan, because the hyaluronan inflows were very small. For a hyaluronan inflow of 8 μl min⁻¹ at 20 cmH₂O and 30 min, the creep rate of 3 μl min⁻¹ accounted for 38 % of Q̇_in and trans-synovial flow accounted for 62 %.

Measurement of reverse creep rates on reducing pressure

In some experiments the effect of reducing intra-articular pressure, following elevation to 20–25 cmH₂O, upon trans-synovial flow was studied. This required a different creep correction because, following a step reduction in intra-articular pressure, the direction of viscous creep reverses; there is a slow inward creep of the cavity walls under constant pressure. This is equivalent to the tension recovery at constant volume described by Knight & Levick (1983) and is due to the visco-elastic nature of the tissue. Reverse creep rates were measured as follows. Oil was infused and the usual series of step increments in intra-articular pressure imposed until pressure reached 20–25 cmH₂O. The connections of the drop counter to the infusion reservoir and infusion cannula were then switched, so that the drop counter could record ouflow of oil from the joint cavity. The infusion pressure was then reduced by several centimetres of water to a new fixed level, resulting in a partial emptying of the joint through the drop counter. Oil outflow was noted when intra-articular pressure had been stable for 30 min. This value was given a negative sign to denote reversed, inward creep, and trans-synovial flows of aqueous solutions were again calculated as Q̇_s=Q̇_in - Q̇_creep.

Analysis of the pressure-flow relation and other statistical methods

In the absence of hyaluronan the P_j-Q̇_s relation commonly shows a marked steepening at about 7–14 cmH₂O (‘yield pressure’), with little or inconsistent curvature above or below this. To facilitate quantitative comparisons between experiments, the relation is usually represented empirically by two linear regressions, one fitted below the yield point and the other above it (Edlund, 1949; Levick, 1979). The yield point is determined by inspection. Regression slopes were compared by Student's paired t test, with P < 0.05 accepted as a significant difference. The pressure-flow relation in the presence of hyaluronan had a different shape from that for Ringer solution, and the infusion-driven intra-articular pressures varied a little between experiments. Therefore, in order to compare flows at identical pressures between experiments, the flows were interpolated when necessary to standard values at 2.5 cmH₂O intervals (2.5, 5.0, 7.5 cmH₂O, etc.), using linear interpolation between the two bounding measurements. Curvilinear relations between concentration and oncotic pressure or viscosity were fitted by non-linear regression analysis (Graphpad Prism, GraphPad Software, Inc., San Diego, CA, USA). Means are followed by the standard error of the mean (s.e.m.) throughout.

Theory of pressure-flow relation acoss an unstirred boundary layer and sieving membrane

In view of the evidence for partial reflection of hyaluronan by the synovial lining (see Introduction), it is useful at this point to introduce the formalism used in ‘Results’ to analyse the pressure- flow relation in the presence of hyaluronan.

When a solution of bulk concentration C_in and osmotic pressure π_in is ultrafiltered across a perfect semipermeable membrane (solute reflection coefficient, σ= 1) or a leaky one (0 < σ < 1), solute rejection at the filtering surface creates a steep, local concentration gradient. The solute concentration at the membrane surface (C_m), and its osmotic pressure (π_m) now exceed the input C_in and π_in (see Appendix). This has been confirmed experimentally for hyaluronan in vitro (Parker & Winlove, 1984; Barry et al. 1996). Even when the upstream compartment is stirred, an unstirred boundary layer always exists close to the surface, its thickness δ depending on stirring conditions (Dainty, 1963; Pedley, 1983; Johnson et al. 1987). In the steady state, convection of solute molecules into the boundary layer is offset wholly (in the case of σ= 1) or partially (σ < 1) by back-diffusion down the concentration gradient in the boundary layer.

For filtrate of concentration C_out and osmotic pressure π_out, the osmotic pressure drop across the membrane, Δπ_m, is π_m - π_out. This is greater than the osmotic pressure difference between the two bulk phases, Δπ_b, namely π_in - π_out, which is commonly negligible for polymer solutions. Filtration rates are therefore lower than would be predicted from the bulk osmotic pressures. For flow across a leaky semipermeable membrane, thermodynamic considerations lead to the well known expression:

(1)

where Q̇ is flow, ΔP is the pressure drop across the membrane, R_m is the hydraulic resistance of the membrane and η is the viscosity of the permeating fluid (Curry, 1984). Equation (1), for the case σ= 1, was called the ‘osmotic pressure model’ of flow reduction by Wijmans et al. (1985), in order to distinguish it from a resistance model (see below). From eqn (1) it follows that the opposition to flow, defined as the hydraulic pressure drop required to generate unit flow, is:

(2)

This describes observed ultrafiltration rate-pressure curves for albumin solutions very well (Kozinski & Lightfoot, 1972; Tarbell et al. 1988).

Wijmans et al. (1985) evaluated the relationship between the above ‘osmotic model’ of flow reduction and another common model, the ‘boundary layer resistance model’. In the latter the boundary layer is ascribed a hydraulic resistance, R_bl, in series with R_m, and only bulk phase osmotic pressures are considered. This leads to the expression:

(3)

Since π_in is usually trivial for polymer solutions (e.g. 0.8 cmH₂O for 3.6 g l⁻¹ hyaluronan), eqn (3) approximates to the form used in a previous study of trans-synovial flow of hyaluronan solution (McDonald & Levick, 1995):

(4)

From this the opposition to flow is:

(5)

The value of R_bl for hyaluronan concentration polarization layers formed in vitro can greatly exceed R_m (Nettelbladt & Sunblad, 1967; Parker & Winlove, 1984).

There are reasons for believing that subsynovial pressure is close to ‘zero’, i.e. atmospheric pressure, as discussed by McDonald & Levick (1995) and Price et al. (1996a). Thus the synovial opposition to outflow, ΔP/Q̇, can be estimated in practice by the ratio of the two measured terms, P_j/Q̇:

(6)

The osmotic model, eqn (2), and resistance model, eqn (5), are thermodynamically equivalent treatments of the boundary layer effect for the case of a non-gelling concentration polarization layer, both in theory and in practice (Wijmans et al. 1985). From eqns (1)–(6) it follows that, across the boundary layer:

(7)

A theory that relates membrane concentration C_m, and hence Δπ_m and Δπ_bl, to the diffusion coefficient, flow and boundary layer thickness for a membrane of σ < 1 is presented in the Appendix.

RESULTS

Biochemical and biophysical findings

Molecular size of rooster comb hyaluronan by HPLC

The HPLC retention times for rooster comb hyaluronan averaged 7.24 ± 0.01 min (n= 60), corresponding to an average molecular mass of 2.1 × 10⁶ Da (95 % confidence intervals (c.i.), (2.0–2.3) × 10⁶ Da). This is similar to native rabbit hyaluronan, namely (2.4–2.9) × 10⁻⁶ Da (see Introduction). A sample of umbilical cord hyaluronan (Sigma) had a lower mass, 1.3 × 10⁶ Da (n= 5). Rooster comb hyaluronan was thus the preparation of choice as bulk substitute for native rabbit hyaluronan.

Viscosity of rooster comb hyaluronan

The high viscosity of rooster comb hyaluronan solution is shown in Fig. 2A. From viscosity-concentration plots over a range of shear rates, intrinsic viscosity was evaluated as 2953 ml g⁻¹ (95 % c.i., 2465–3537 ml g⁻¹). This is twice the intrinsic viscosity of the umbilical hyaluronan used by McDonald & Levick (1995), namely 1456 ml g⁻¹ (95 % c.i., 1242–1707 ml g⁻¹), thus confirming the greater chain length of rooster comb hyaluronan (Fig. 2B). Substitution into the Mark-Houwink equation (see Methods) gave a viscometric molecular mass of 1.84 × 10⁶ Da for rooster comb hyaluronan.

Figure 2. Viscous and osmotic properties of rooster comb hyaluronan in Ringer solution.

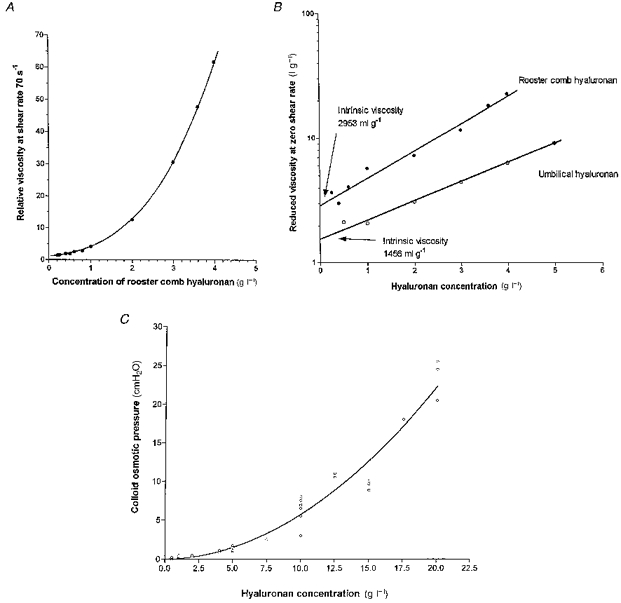
A, viscosity-concentration, measured at fixed shear rate (70 s⁻¹). B, regression of semi-logarithmic plot of reduced viscosities (extrapolated to zero shear rate) versus concentration to evaluate intrinsic viscosity (intercept), an index of molecular domain volume. Reduced viscosity is (relative viscosity - 1)/concentration. •, rooster comb hyaluronan. ^, umbilical hyaluronan (McDonald & Levick, 1995). C, colloid osmotic pressure of rooster comb hyaluronan solutions, π_HA (cmH₂O), at room temperature, fitted by the polynomial π_HA= 0.0257C+ 0.0545C² (correlation coefficient, r²= 0.944), where C is concentration in grams per litre.

Chain length and radius of molecular domain

Given a molecular mass of (1.84–2.1) × 10⁻⁶ Da, a known dissaccharide mass of 379 Da and disaccharide length of 0.95 nm, rooster comb hyaluronan comprises 4855–5541 disaccharides with a net chain length of 4.61–5.26 μm. The radius of gyration R_g was 101–105 nm by Flory's model (see Methods), and 167–181 nm by the expression of Johnson et al. (1987).

Critical concentration for overlap of molecular domains

The critical overlap concentration was ≤0.71 g l⁻¹ by de Gennes's formula (see Methods) and 0.85 g l⁻¹ from the intrinsic viscosity (Morris et al. 1980). Hyaluronan concentrations in vivo and in the experiments exceeded C*, so the intra-articular fluid was in the ‘semi-dilute regime’. The semi-dilute regime is one in which the entire body of solvent is spanned by a quasi-continous net of hyaluronan chains due to entanglements or other forms of transient, strong interactions between contiguous hyaluronan molecules (Welsh et al. 1980).

Osmotic pressure of rooster comb hyaluronan

The relation between the osmotic pressure (π_HA, cmH₂O) and concentration of rooster comb hyaluronan (C, g l⁻¹) was highly non-linear (Fig. 2C). Colloid osmotic pressure was trivial at physiological concentrations, viz. 1.00 ± 0.07 cmH₂O at 4 g l⁻¹, but increased steeply with concentration to 23.5 ± 1.5 cmH₂O at 20 g l⁻¹. The relation was well described by the second-order polynomial:

(8)

(correlation coefficient, r²= 0.944). The second virial coefficient arises from molecular interactions and was close to the value reported by Laurent & Ogston (1963), namely 0.062 in the present units. The first virial coefficient, 0.0257 here, was smaller than their value of 0.058 for a preparation of lower molecular weight (1.5 × 10⁶). The first virial coefficient is given by RT/M_n, where M_n is the number average molecular mass and RT is the gas constant × absolute temperature (24 atm l mol⁻¹ at 20°C). From this, M_n for rooster comb hyaluronan was calculated to be 0.97 × 10⁶ Da. This is, as expected, smaller than the viscometric or HPLC-derived average molecular mass, indicating a heterodispersity of chain lengths in the preparation. Osmotic pressure is strongly influenced by the number of shorter chains in a sample, while viscosity and exclusion are more strongly influenced by the longer chains.

Endotoxin assays

The endotoxin assay results for sterile saline (Baxter Healthcare), Baxter Ringer solution, rooster comb hyaluronan (0.2 ml at 2 g l⁻¹) and bovine serum albumin (Sigma fraction V; 0.2 ml at 20 g l⁻¹) were negative. Thus the albumin preparation contained <0.3 pg endotoxin per milligram albumin, and the rooster comb preparation contained <3 pg per milligram hyaluronan. A sample of human umbilical cord hyaluronan assayed marginally positively at 3 pg endotoxin per milligram hyaluronan. All materials were negative for endotoxin inhibitor, which the commercial kit also assayed.

Physiological results

Time course of flows after elevation of intra-articular pressure

The inflow of 3.6–4.0 g l⁻¹ rooster comb hyaluronan into the joint cavity after a step rise in infusion pressure is shown in Fig. 3A. Trans-synovial flow was effectively stable by 40–60 min at low intra-articular pressures (4.6–10 cmH₂O, 5 rabbits) and ∼30 min at higher pressures (>10 cmH₂O, 5 rabbits). Late-phase oil flow into the contralateral joint, which reflects the volumetric rate of creep of the cavity walls under constant intra-articular pressure (delayed compliance), occurred at a lower rate (Fig. 3A). Dissection post mortem showed that the Sudan Black-stained oil remained within the joint cavity. The difference between oil inflow and hyaluronan inflow at a given intra-articular pressure was, therefore, taken to represent net trans-synovial flow (see Methods).

Figure 3. Contribution of viscous creep to fluid uptake into joint cavity.

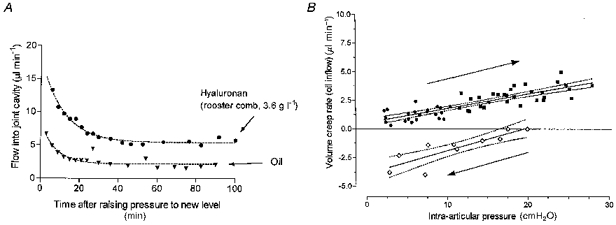
A, time course of flow of hyaluronan solution (upper curve) and oil (lower curve) into the synovial cavity in contralateral joints of same animal, after raising intra-articular pressure to a constant value of 8 cmH₂O. B, Effect of an incrementing series of sustained intra-articular pressures (rightward arrow) on late-phase viscous creep of the cavity walls (oil inflow, 10 rabbits). Oil inflow was measured at 30 min (▪) or 60 min (•) after each pressure rise. Results obtained when intra-articular pressure was subsequently reduced (leftward arrow) are shown as open symbols; the negative flow values denote reversed, inward creep of the cavity walls, i.e. mechanical recovery. Results are fitted by regression lines with 95 % confidence boundaries; see text.

Effect of intra-articular pressure on outward creep of cavity walls

Oil inflows after intra-articular pressure stabilization showed that the rate of creep of the cavity walls increased as a function of intra-articular pressure (10 joints; Fig. 3B). The regression equation fitted to 23 measurements at 60 min was:

while for 29 measurements at 30 min it was:

where Q̇_creep is in microlitres per minute and P_j is in centimetres of water. Neither the slopes nor the intercepts were significantly different between the 30 min and 60 min data, and the relation for the pooled set of 52 measurements in 10 joints was given by:

(correlation coefficient, 0.71; P < 0.0001).

Reverse creep after pressure reduction

Reversed, inward creep occurred when intra-articular pressure was held constant for 30–60 min after a reduction from a higher value (Fig. 3B). Starting from 20–25 cmH₂O, the relation between reversed creep rate and reduced intra-articular pressure was given by:

(correlation coefficient, 0.77; P < 0.001, 11 measurements in 2 joints). Q̇_creep evaluates with a negative sign here, denoting reversal from outward to inward creep. An improved correlation was noted between creep rate and change in pressure, ΔP_j, namely:

(correlation coefficient, 0.87; P < 0.0001, n= 11). ΔP_j here is intra-articular pressure minus starting pressure (20–25 cmH₂O), and so has an increasingly negative sign as pressure is reduced.

Effect of rooster comb hyaluronan and bovine synovial fluid on trans-synovial flow

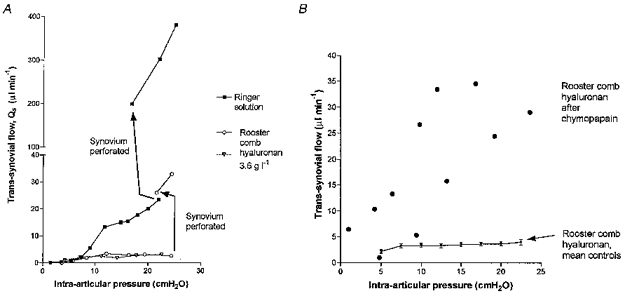
Rooster comb hyaluronan greatly reduced the trans-synovial flows compared with Ringer solution. It also altered the shape of the pressure- flow relation. When Ringer solution is infused, the relation steepens as pressure is raised (Edlund, 1949). When hyaluronan solution was infused, the relation flattened as pressure was raised, and the trans-synovial flows approached a near plateau (Fig. 4A). In this quasi-plateau region, a step elevation of intra-articular pressure produced a transient increase in flow but the flow then settled back, in the steady state, to a value close to that before the pressure rise.

Figure 4. Effect of intra-articular hyaluronan on trans-synovial flow.

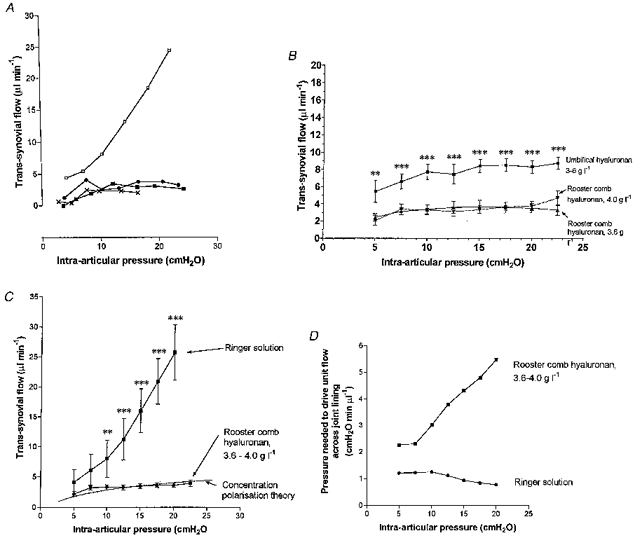
A, relation betwee intra-articular pressure and trans-synovial flow in the presence (bottom three curves) or absence (top curve) of hyaluronan in 4 individual rabbit knees. •, 4 g l⁻¹ rooster comb hyaluronan; ▪, 3.6 g l⁻¹ rooster comb hyaluronan in Ringer solution; ×, bovine synovial fluid. B, trans-synovial flows in presence of 3.6 g l⁻¹ (12 joints) or 4.0 g l⁻¹ rooster comb hyaluronan (17 joints) compared with 3.0–6.0 g l⁻¹ umbilical hyaluronan of lower molecular weight (10 joints; McDonald & Levick, 1995). Mean ±s.e.m. of flows interpolated to standard pressures. Differences between 3.6 g l⁻¹ and 4.0 g l⁻¹ are not significant. Asterisks refer to a comparison of pooled rooster comb hyaluronan with pooled umbilical results at same pressure; **P≤ 0.01, ***P≤ 0.001 (unpaired t test). C, mean trans-synovial flows for 29 joints infused with 3.6–4.0 g l⁻¹ rooster comb hyaluronan solution compared with Ringer solution. Asterisks refer to a comparison of pooled rooster comb hyaluronan with pooled Ringer solution at the same pressure; **P≤ 0.01, ***P≤ 0.001 (unpaired t test); P at 5 and 7.5 cmH₂O was 0.131 and 0.056, respectively. Dashed line describes theoretical flow across a hyaluronan concentration polarization layer in series with a membrane of fixed resistance, for δ/D= 3.25 × 10⁵ s cm⁻¹ (see Appendix). The theoretical curve passes within the standard error bars of all results except that at 7.5 cmH₂O, indicating an approximate fit overall. D, intra-articular pressure required to drive unit trans-synovial flow in the presence (top) or absence (bottom) of rooster comb hyaluronan, calculated from average flows. This is a measure of the opposition to outflow at each pressure; see text.

A similar pressure-flow relation was observed when a joint was infused with pooled bovine synovial fluid (Fig. 4A). Work with natural synovial fluid was limited to a single joint due to the difficulty of accumulating enough synovial fluid to prime the infusion system. The results with rooster comb hyaluronan at 3.6 g l⁻¹ (12 joints) and at 4.0 g l⁻¹ (17 joints) were not significantly different (Fig. 4B), and are therefore pooled in the following sections.

The flow-depressant effect of hyaluronan was quantified by calculating the ratio of interpolated trans-synovial flows during hyaluronan and Ringer infusions at the same pressure. Flow reduction was relatively modest at low pressures and became progressively more marked as intra-articular pressure was increased (Fig. 4C). At 5 cmH₂O, for example, the mean trans-synovial flow in the presence of 3.6–4.0 g l⁻¹ hyaluronan was 53.3 % of the Ringer value, whereas by 20 cmH₂O the trans-synovial flow in the presence of hyaluronan was only 14.1 % of the Ringer value.

The effect of hyaluronan on slope d Q̇_s/dP_j was also analysed. At low pressures, 5.0–7.5 cmH₂O, where the hyaluronan pressure-flow relation was steepest, the average slope d Q̇_s/dP_j for rooster comb hyaluronan solutions, 0.40 ± 0.11 μl min⁻¹ cmH₂O⁻¹ (n= 28), was 51 % of the slope for Ringer solution below yield pressure (0.78 ± 0.01 μl min⁻¹ cmH₂O⁻¹). By contrast, on the quasi-plateau section of the hyaluronan relation above 10 cmH₂O the ratio fell to 2.6 %, because d Q̇_s/dP_j for the pooled hyaluronan results decreased to 0.050 ± 0.01 μl min⁻¹ cmH₂O⁻¹ while d Q̇_s/dP_j for Ringer solution in the same pressure range increased to 1.94 ± 0.01 μl min⁻¹ cmH₂O⁻¹ (Fig. 4C). The hyaluronan quasi-plateau was not completely flat, unlike a true plateau, because the regression slope was significantly positive (P= 0.004).

After the last flows were recorded, samples of intra-articular hyaluronan were aspirated in five experiments for molecular size assessment by HPLC. The column retention time for rooster comb hyaluronan taken from the infusion line at the start of the experiment was 7.19 ± 0.06 min (mean ±s.d.) and the retention time for hyaluronan in joint aspirates after an experiment was 7.17 ± 0.04 min (n= 5; difference not significant). There was thus no evidence of depolymerization of rooster comb hyaluronan over these 3–5 h experiments, in contrast to the experience of McDonald & Levick (1995) with umbilical hyaluronan.

Effect of hyaluronan on opposition to outflow

‘Opposition to outflow’ is defined as the pressure drop required to generate unit flow (see Methods) and is estimated by P_j/Q̇_s (eqn (6)). In the presence of hyaluronan the opposition to outflow increased progressively with pressure, from 2.26 cmH₂O min μl⁻¹ at 5 cmH₂O to 5.48 cmH₂O min μl⁻¹ at 20 cmH₂O (Fig. 4D, upper curve), despite the fact that the intrinsic hydraulic resistance of synovium, R_m, decreases with pressure beyond a certain point (Edlund, 1949; Levick et al. 1998). In the absence of hyaluronan, P_j/Q̇_s is simply an estimate of membrane resistance, R_m. This changed little between 5 cmH₂O (resistance, 1.21 cmH₂O min μl⁻¹) and 10 cmH₂O (1.24 cmH₂O min μl⁻¹), then fell progressively with pressure, reaching 0.78 cmH₂O min μl⁻¹ at 20 cmH₂O (Fig. 4D, lower curve). The difference between the hyaluronan and Ringer solution values in Fig. 4D represents the combined effects of changes in membrane resistance, osmotic pressure at the interface and permeant viscosity (eqn (6)), and this increased from 1.06 cmH₂O min μl⁻¹ at 5 cmH₂O to 4.71 cmH₂O min μl⁻¹ at 20 cmH₂O.

Comparison of outflow buffering by rooster comb and umbilical hyaluronans

Pooled results from 29 knees infused with 3.6–4.0 g l⁻¹ rooster comb hyaluronan were compared with pooled results from 10 rabbit knees infused with 3.0–6.0 g l⁻¹ umbilical hyaluronan of subphysiological molecular weight (McDonald & Levick, 1995); it was established previously that the results for 3 g l⁻¹ and 6 g l⁻¹ umbilical hyaluronan were not significantly different. As shown in Fig. 4B, the curve for umbilical hyaluronan flattened as pressure increased, with a slope of 0.09 ± 0.03 μl min⁻¹ cmH₂O⁻¹ at 10–20 cmH₂O (cf. 0.05 ± 0.01 μl min⁻¹ cmH₂O⁻¹ for rooster comb hyaluronan; difference in slopes was not statistically significant). Rooster comb hyaluronan reduced flows to even lower levels than did umbilical hyaluronan (significant at all pressures, P < 0.005). The opposition to outflow, P_j/Q̇_s, increased monotonically with pressure in the presence of umbilical hyaluronan, reaching 2.41 cmH₂O min μl⁻¹ at 20 cmH₂O, which is a smaller opposition than that generated by rooster comb hyaluronan at the same pressure, namely 5.48 cmH₂O min μl⁻¹.

Effect of interference with synovial barrier properties on quasi-plateau flows

The flattening of the pressure- flow relation by hyaluronan is attributed primarily to partial reflection of hyaluronan by synovium (see Introduction). In order to test further the proposed barrier role of the synovial lining, flow measurements were made before and after synovial permeability had been deliberately increased by a variety of interventions.

Effect of mechanical perforation of synovium

The intra-articular steel cannula was over-advanced so as to perforate the synovial lining in the suprapatellar region of the cavity, and was then drawn back into the cavity. This increased the trans-synovial flow of Ringer solution by 5–14 times control flow at the same pressure (two joints), and greatly steepened the pressure-flow relation (Fig. 5A, upper curve). This confirmed that the synovial lining is a high-resistance barrier to fluid egress, and that the barrier can be greatly reduced by mechanical perforation. The needle track is assumed to create a channel of low outflow resistance due to rupture of cells and interstitial matrix components. In four other joints a solution of rooster comb hyaluronan was infused to establish a flow plateau, and then the joint lining was perforated. Perforation increased the trans-synovial flow to 3–13 times the control flows in the same joint at the same pressure (Fig. 5A, lower curve). Trans-synovial flow of hyaluronan solution after perforation averaged 21.4 ± 2.3 μl min⁻¹ at 20 cmH₂O, in contrast to 3.65 ± 0.37 μl min⁻¹ in intact joints. Also, in perforated joints the net trans-synovial flow of hyaluronan solution increased steeply with pressure, in contrast to the quasi-plateau for intact synovium.

Figure 5. Effect of interference with synovial barrier property on quasi-plateau flow.

A, effects of increasing hydraulic conductance of synovial lining by (1) mechanical perforation and (2) increased matrix hydration. In the Ringer experiment (▪) and one of the hyaluronan infusions (^), synovial conductance was increased by mechanical perforation of the lining (arrows). In the third joint (▿, hyaluronan infusion), hydraulic conductance was increased prior to hyaluronan infusion by Ringer infusion over 2.5 h to 20 cmH₂O (see text). This milder method of conductance elevation had no discernible effect on the curve. B, hyaluronan infusions after prior digestion of synovial matrix by the collagen-sparing protease chymopapain (2 joints). The quasi-plateau (control curve, bottom) is abolished.

Effect of enzymatic digestion of synovial extrafibrillar matrix

Since the intercellular matrix is thought to be crucial for hyaluronan reflection and plateau generation, the effects of two forms of matrix manipulation were studied. Chymopapain is a collagen-sparing protease that depletes the matrix of structural glycoproteins and proteoglycans, causing large increases in hydraulic permeability (Scott et al. 1998b). Treatment of two joints by 0.2 units activated chymopapain in 0.5 ml injectate for 40 min was followed by washouts with hyaluronan solution and determination of the hyaluronan pressure-flow relation. Chymopapain treatment increased the trans-synovial flow of hyaluronan solution to ∼10 times normal at >20 cmH₂O, steepened the relation and abolished the quasi-plateau (Fig. 5B). This confirmed the importance of the interstitial matrix for plateau generation.

Effect of dilution of synovial extrafibrillar matrix

Synovial hydraulic conductance increases when pressure is raised to >7-14 cmH₂O in Ringer-infused joints (Fig. 4C-D). The pressure-induced rise in conductance is not fully reversible upon lowering the intra-articular pressure in the short term (Edlund, 1949; Levick, 1979) and quantitative biochemical analyses show that this is due in part to increased matrix hydration, which reduces the interstitial biopolymer concentration (Price et al. 1996b). This offers a less destructive way to raise membrane permeability than mechanical perforation of synovium or enzymatic digestion of synovial extrafibrillar matrix. In two joints the intra-articular pressure was raised to 20–25 cmH₂O by Ringer infusion, and then the joint was drained and flushed four times with a 3.6 g l⁻¹ solution of rooster comb hyaluronan, mixing the intra-articular fluid by five flexion-extension cycles each time. The pressure-flow relation was then determined for 3.6 g l⁻¹ hyaluronan solution. The results were indistinguishable from those in normal joints infused with 3.6 g l⁻¹ hyaluronan solution (Fig. 5A, open triangles). Flow changed little with pressure above 10 cmH₂O, and the quasi-plateau flows were in the range 2–5 μl min⁻¹ as in control joints.

Effect of passive joint movement on plateau flow

Since the quasi-plateau in the stationary joint (Fig. 4C) is attributed primarily to hyaluronan accumulation near the synovial surface, the effect of joint movement was of interest, because this stirs the intra-articular fluid (Delecrins et al. 1992). In two joints infused with 4.0 g l⁻¹ rooster comb hyaluronan solution, trans-synovial flows were measured in the quasi-plateau region, namely 4.4 μl min⁻¹ at 19.8 cmH₂O in one joint and 2.8 μl min⁻¹ at 25.2 cmH₂O in the other. The intra-articular fluid was then stirred by alternately flexing and extending the joint five times, after which intra-articular pressure was restored to its former level as quickly as possible. This took ∼10 min, because flexion-extension in the presence of effusions produce large pressure oscillations. Trans-synovial flows were then 2.8 μl min⁻¹ at 19.8 cmH₂O and 2.9 μl min⁻¹ at 25.6 cmH₂O in the two joints. Thus, trans-synovial flows were not increased significantly at 10 min after intra-articular ‘stirring’.

Reversal of effect of hyaluronan

The above result might indicate either that the effect of hyaluronan is not reversible or that the effect, though reversible, is soon restored when intra-articular stirring stops. To discover whether the increased opposition to outflow is reversible, three different protocols were used.

Joint washout. Joints were infused with rooster comb hyaluronan solution to approximately 20 cmH₂O, generating low flows and high outflow resistances, then the hyaluronan was washed out of the joint cavity by flushing with Ringer solution, and the pressure-flow relation was re-determined with Ringer solution as infusate (8 joints). It was found that normal synovial conductance to Ringer solution was restored after thorough washout of the hyaluronan(Fig. 6A). The effect of hyaluronan was thus reversible by washout.

Figure 6. Reversal of effect on hyaluronan on opposition to outflow.

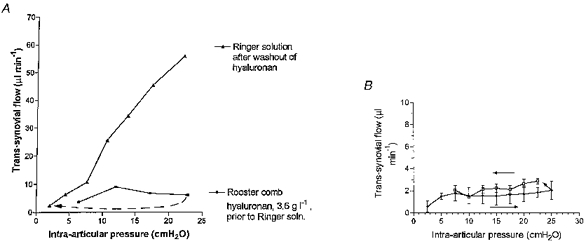
A, the joint was first infused with 3.6 g l⁻¹ rooster comb hyaluronan solution (bottom curve), then washed out (5 flexion-extension cycles per wash, 20 washes), and reinfused with Ringer solution (upper curve). Hyaluronan has not irreversibly raised outflow resistance. B, comparison of trans-synovial flows during ascending pressure steps followed by descending pressure steps, in the presence of rooster comb hyaluronan (mean ±s.e.m., 3 joints). Arrows indicate sequence. Flows at a given pressure in the pressure reduction phase are no smaller than in the pressure increment phase (paired t test). The increased opposition to fluid outflow following pressure increments is thus reversed by lowering pressure.

Effect of hyaluronidase

In one joint, 4.0 g l⁻¹ rooster comb hyaluronan solution was infused to ∼16 cmH₂O, generating low flows and high outflow resistances, and then a small volume of the intra-articular fluid was aspirated and replaced by an equal volume containing 500 U of Streptomyces hyaluronidase. Trans-synovial flow, measured at the same intra-articular pressure after 60 min, was 11.7 times the flow prior to hyaluronidase injection. Like the joint washout experiment above, this showed that exogenous hyaluronan does not irreversibley alter synovial matrix resistance.

Effect of pressure reduction

During joint usage intra-articular pressure rises with joint flexion and falls with joint extension. This raises an important physiological question: can the increased outflow resistance created by pressure elevation be reversed simply by lowering the pressure? The effect of reducing intra-articular pressure on trans-synovial flow was studied in three joints in which outflow opposition had already been raised by infusing hyaluronan to ∼20 cmH₂O. Flows after pressure reductions were corrected for reversed, inward creep; see Methods. Trans-synovial flows at a given pressure during pressure reduction were not significantly different from those during pressure elevation (Fig. 6B). This contrasts with a prediction of reduced flows if the increased opposition to outflow at higher pressures had been irreversible. From the pooled results for the three joints, the opposition to outflow P_j/Q̇_s increased from 9.3 ± 3.0 cmH₂O min μl⁻¹ at 10 cmH₂O to 16.5 ± 5.3 cmH₂O min μl⁻¹ at 25 cmH₂O as pressure was raised, and then decreased again as pressure was reduced, falling to 7.0 ± 0.4 cmH₂O min μl⁻¹ at 10 cmH₂O, a value not significantly different from that at the same pressure during pressure elevation. It is concluded that the hyaluronan-related increasing opposition to outflow during pressure elevation is reversed by lowering the pressure.

Lack of dependence on synoviocyte metabolic activity or microvascular perfusion

The interpretation of the flattened pressure-flow relation advanced by McDonald & Levick (1995) was entirely biophysical, being based on interactions between intercellular matrix, hyaluronan chains and solvent flow. The implicit assumption that cellular activity and blood supply play no part was tested here by infusing 3.6–4.0 g l⁻¹ hyaluronan solutions into joints (1) immediately post mortem (4 joints) or (2) after blocking synoviocyte oxidative metabolism by intra-articular 2 mM sodium azide solution in vivo (1 joint). The effect of hyaluronan on the pressure-flow relation post mortem closely mirrored the effect in vivo (Fig. 7). Similarly, the flows after intra-articular azide treatment in vivo were within the range recorded in normal joints, rising from 0.8 μl min⁻¹ at 2 cmH₂O to 3.0 μl min⁻¹ at 10 cmH₂O and then only slightly, to 4.4 μl min⁻¹ at 16 cmH₂O.

Figure 7. Effect of hyaluronan on trans-synovial flow post mortem.

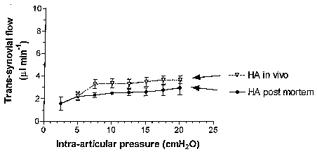
•, mean trans-synovial flow (±s.e.m.) in 4 knees post mortem. The pressure-flow relation post mortem is not significantly different from that in vivo (▿, n= 29; P≥ 0.38).

DISCUSSION

Hyaluronan of physiological chain length greatly attenuates the loss of fluid from a joint cavity when pressure is raised (Fig. 4), thereby conserving intra-articular lubricant. Normal bovine synovial fluid, though more complex in composition, had a very similar effect to plain hyaluronan solution, indicating that hyaluronan is the chief component buffering the outflow of native synovial fluid. The comparison of rooster comb hyaluronan (2.1 × 10⁶ Da) and umbilical hyaluronan ((0.55–0.77) × 10⁶ Da) indicated that chain length may influence trans-synovial flow: the larger molecules buffered outflow to a greater extent than the smaller molecules (Fig. 4B). Unpublished studies by the authors using shorter, sonicated chains support this inference.

Since mechanical perforation and enzymatic degradation of the lining both abolished the buffering of outflow by hyaluronan (Fig. 5), the effect is attributed to an interaction with the synovial lining. The interaction appears to be a biophysical process, since it is independent of metabolic energy (Fig. 7). Biophysical evidence indicates that synovial interstitial matrix is sufficiently dense to reflect, partially, the hyaluronan chains (see Introduction), and the matrix reflection coefficient is ≥0.79–0.95 for rooster comb hyaluronan at >C* (Scott et al. 1998a). Even when the concentration of the synovial interstitial matrix constituents was reduced here by ∼50 % via prior infusion of Ringer solution at raised pressures (Price et al. 1996b), outflow buffering persisted (Fig. 5, open triangles).

It is argued in detail later that partial reflection of hyaluronan at the synovial surface creates a concentration polarization layer that buffers outflow osmotically. Flexion- extension cycles should partially disrupt such a layer by intra-articular shearing, and thus increase outflow. Owing to the slow time course of measurements, however, the earliest flow measurements after movement were at 10 min, and trans-synovial flows were then back to pre-movement levels. The concentration polarization layer can thus reform within 10 min. Reduction of intra-articular pressure reverses the increased opposition to outflow (Fig. 6B), in keeping with partial dissipation of a concentration polarization layer by diffusion. The washout experiment (Fig. 6A) confirmed that hyaluronan caused no irreversible change in membrane structure, again in keeping with the proposed biophysical mechanism.

Physiological significance

Increased opposition to outflow with increased intra-articular pressure, and its reversal with pressure reduction, may be functionally significant in vivo because, as joints flex, intra-articular pressure rises, and as they extend towards the ‘angle of ease’, pressure falls (review, Levick et al. 1998). It is envisaged that opposition to outflow increases during periods of sustained flexion and decreases again during intervals of sustained relaxation, though not during rapid, oscillatory movement. In this way synovial fluid volume is preserved when threatened by sustained flexion, yet fluid balance, which depends on outflow matching inflow in the long term, is not imperilled by an irreversible increase in outflow resistance.

Differences must be noted between the closed system that exists in vivo and the open-ended experimental system. A boundary layer of thickness >220 μm, as inferred below, could develop in a joint effusion but not in a normal joint, because the mean thickness of the endogenous fluid layer is normally ≤ 100 μm, albeit uneven (Henderson & Edwards, 1987). Nevertheless, a net trans-synovial outflow of ∼3 μl min⁻¹ from the endogenous volume of 24–50 μl synovial fluid in vivo (Coleman et al. 1997) represents the ultrafiltration of 6-12.5 % of the native volume per minute. This will quickly cause a substantial rise in hyaluronan concentration at the membrane surface, and thus oppose outflow in vivo in an analogous fashion to that observed here using an open system.

Bulk viscosity: lack of correlation with trans-synovial flow

The lack of relation between the bulk viscosity of the intra-articular fluid and the reduction in trans-synovial flow, noted by McDonald & Levick (1994, 1995), was confirmed here. Trans-synovial flow in the presence of hyaluronan at 5 cmH₂O was 53 % of that for Ringer solution, whereas at 20 cmH₂O it was only 14 % even though infusate viscosity was the same. Similarly, the slope d Q̇_s/dP_j was 51 % of the Ringer slope at low pressures but 2.6 % in the quasi-plateau region. Thus outflow reduction was not related directly to the bulk viscosity of the infused solution.

Concentration polarization, ultrafiltration and membrane pore size

Increasing opposition to fluid outflow with pressure, as in Fig. 4D, is characteristic of an ultrafiltration/concentration polarization process at the surface of a molecular-sieving membrane, both experimentally (see Introduction) and theoretically (see Appendix). Hyaluronan concentration, measured by refractometry, increases steeply towards a membrane surface during ultrafiltration in vitro (Barry et al. 1996). The mean hydraulic radius of synovial matrix pores (r_H) calculated as the ratio of void volume to solid surface area, is 15–45 nm (Levick et al. 1998); and hyaluronan ultrafiltration has been observed in vitro with pores as wide as 200–450 nm (Nettelbladt & Sunblad, 1967; Parker & Winlove, 1984).

The radius of gyration (R_g) of hyaluronan molecules, 100–200 nm, exceeds synovial pore size r_H, 15–45 nm, yet there is a finite permeation of hyaluronan across synovium (Brown et al. 1991) and a reflection coefficient of <1 (Scott et al. 1998a). Similarly, Munch et al. (1979) showed that polyacrylamide can permeate pores that are narrower than the unconfined polymer, because the polymer is flexible and is aligned along the pore axis by local shear stresses during filtration. From their plot of σ in the dilute regime versusr_se/r_p (ratio of Stokes-Einstein radius of solute to radius of cylindrical pore), a second estimate can be made of synovial matrix pore size, assuming similar polymer flexibilities. Taking σ for hyaluronan in the dilute regime as ≥0.48 (Scott et al. 1998a), interpolation from the plot of Munch et al. (1979) gives r_se/r_p≥ 2. Since r_se for rooster comb hyaluronan is 82–139 nm (0.8 ×R_g), the inferred r_p for synovium is ≤41-70 nm. This is consistent with our previous estimate of r_H, 15–45 nm, because r_H is defined as void volume/surface area, and for a cylindrical pore this equals r_p/2.

Reflection of hyaluronan, leading to concentration polarization, is thus very likely in the present experiments. Equation (2) shows that, when concentration polarization is present, two factors can contribute to the increase in apparent resistance to outflow. They are (1) the osmotic pressure at membrane surface, π_m, and (2) the viscosity, η, of the permeating solution derived from the concentrated boundary layer when σ is <1. These factors are discussed next.

Estimation of hyaluronan concentration and osmotic pressure at synovial surface (upper limit)

The values for opposition to outflow for hyaluronan solution, (P_j/Q̇)_hyaluron, and for Ringer solution, (P_j/Q̇)_Ringer (Fig. 4D), enable estimation of the osmotic pressure at the membrane surface that would account fully for the low outflow at a given pressure (π_m‘), neglecting any contribution from mechanism (2), intramembrane viscosity, for the moment. For Ringer solution the relative viscosity is 1 and R_bl= 0, so from eqn (6):

(9)

To estimate π_m′ the relative viscosity of the permeating fluid η is set to 1 (but see below). Also, since the permeant has an even lower osmotic pressure than the feeding solution (∼0.9 cmH₂O), the magnitude of π_out is negligible relative to π_m. Equation (9) thus simplifies to:

(10)

Substituting the experimental results, σπ_m′ is found to increase progressively from 2.3 cmH₂O at P_j= 5 cmH₂O (flow 2.2 μl min⁻¹) to 17.2 cmH₂O at P_j= 20 cmH₂O (flow 3.65 μl min⁻¹). The corresponding surface concentrations, C_m, calculated from the osmotic pressure polynomial (eqn (8)) and reflection coefficient 0.95 at >C*, increased to 6.5 g l⁻¹ at 5 cmH₂O and 18.0 g l⁻¹ at 20 cmH₂O. Thus the observed buffering of outflow requires at most a fivefold rise in hyaluronan concentration at the synovial surface. It is relevant to note that at 18 g l⁻¹ the hyaluronan solution was a viscous fluid, not a gel that could support a pressure gradient.

Role of intra-membrane viscosity, η

A rise in the viscosity of the permeating fluid (η) could also contribute to the opposition to outflow (see eqn (2); also Tarbell et al. 1988; Levick & McDonald, 1994; Levick, 1994), and this would reduce the estimate of hyaluronan concentration at the surface, C_m. The size of this effect was assessed using the Appendix theory of concentration polarization. For the middle curve of Fig. 9A, which fits the data approximately, C_m is 15.1 g l⁻¹ at 3.65 μl min⁻¹, the highest mean filtration rate, and surface osmotic pressure is 12.7 cmH₂O. The corresponding filtrate concentration, C_out, is 0.76 g l⁻¹ (Fig. 9B) and its bulk phase viscosity, η_out, is 2.8 (see Fig. 2A).

Figure 9. Molecular sieving and pressure-flow relations predicted by osmosis/concentration polarization theory.

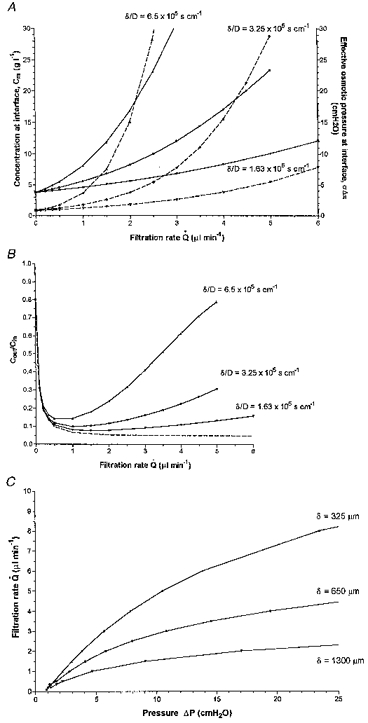
A, rise in concentration and osmotic pressure of hyaluronan at membrane surface during ultrafiltration across a membrane of reflection coefficient 0.95, for three values of δ/D, corresponding to δ= 0.13, 0.065, 0.0325 cm and D= 2× 10⁻⁷ cm² s⁻¹. For other calculation parameters, see text. B, hyaluronan sieving ratio C_out/C_in, i.e. concentration in filtrate/concentration in feeder solution, versus filtration rate for reflection coefficient 0.95. Dashed line shows equation of Patlack et al. (1963) for zero concentration polarization. C, pressure-flow relations across membrane in the presence of hyaluronan concentration polarization layers. The middle curve is a reasonable approximation to the experimental results in Fig. 4C.

Since the effective viscosity of permeant within an excluding matrix, η, is less than the bulk phase viscosity, η_out (Levick & McDonald, 1994; Levick, 1994), and since the surface osmotic pressure of 12.7 cmH₂O is substantial, it is inferred that raised intra-membrane viscosity is unlikely to account for most of the opposition to fluid outflow. In the above example, increased osmotic pressure at the membrane surface accounts for ≥70 % of the increased opposition to outflow, and intramembrane viscosity for ≤30 %.

Estimation of boundary layer thickness, δ, from results

The order of magnitude of boundary layer thickness, δ, can be assessed roughly from the above estimates of C_m, by noting that as σ→1, so C_m→C_inexp(Q̇/k), where transport coefficient k equals DA/δ (Dainty, 1963 and eqn (A9)). Substituting C_m= 15.1–18.0 g l⁻¹ (see above), C_in= 3.8 g l⁻¹, Q̇= 3.65 μl min⁻¹, D≡ 2 × 10⁻⁷ cm² s⁻¹ at 4 g l⁻¹ (Wik & Comper, 1982), and A≡ 17.4 cm² at 18 cmH₂O (Levick, 1994), the estimated boundary layer thickness was ∼790-890 μm at 20 cmH₂O. The calculated thickness at 5 cmH₂O was less, namely 220 μm, and increased monotonically with intra-articular volume and pressure. These estimates are within the physical constraint set by the ratio of cavity volume to synovial surface area: for example, for volume 1.8 cm³ and area ∼17.4 cm² at 18 cmH₂O the mean half-thickness of the fluid layer is 1034 μm.

Theoretical predictions of partial sieving from a concentration polarization layer

An expression is derived in the Appendix for the concentration profile across a boundary layer of known thickness, δ, generated by ultrafiltration across a membrane of σ < 1. This extends the analyses by Dainty (1963), Pedley (1983), Johnson et al. (1987) and Tarbell et al. (1988) for σ= 1. The surface concentration C_m is described as a function of flow and δ/D in eqn (A9), and solutions of the equation are shown in Fig. 9A. If certain conditions are fulfilled (see below), a pressure-flow relation can then be calculated, using eqn (1) to calculate the ΔP value that corresponds to a given flow and C_m or π_m value. Such curves are shown in Fig. 9C for values of δ/D in the range of interest. The middle curve, for δ= 650 μm and D= 2× 10⁻⁷ cm² s⁻¹, is superimposed on the experimental results in Fig. 4C.

Pressure-flow relations calculated as above assume that (1) membrane conductance and area and (2) permeant viscosity are independent of pressure, and (3) that no gel layer forms. A gel layer would act as a mechanical resistance between membrane and concentration polarization layer, reducing ΔP across the membrane (Blatt et al. 1970; Kozinski & Lightfoot, 1972). Gel formation was unlikely here, because C_m was <20 g l⁻¹, and hyaluronan solutions remain liquid at such concentrations. However, synovial conductance and area are undoubtedly a function of pressure (see Ringer curve, Fig. 4D), and permeant viscosity may increase modestly as C_m rises (see above). For these and other reasons, the polarization theory developed in the Appendix does not constitute a full model of synovial pressure-flow relations in vivo.

Other potential influences on the pressure-flow quasi-plateau

Although we have argued that π_m is an important factor shaping the pressure-flow curve in the presence of hyaluronan, a number of other factors not included in the Appendix theory, and arising from the complexity of biological materials, may modify the curve in vivo, as discussed briefly below.

(1) Interstitial matrix is less uniform than a synthetic membrane and has a compositional gradient normal to the flow axis (Levick et al. 1998). Reversible impaction or entanglement of hyaluronan within the superficial microfibrillar zone as a function of flow could increase R_m and possibly σ.

(2) The reflection coefficient of a flexible polymer could, in principle, decrease as fluid velocity increases, due to shear-induced deformation (Munch et al. 1979).

(3) The diffusion coefficient of hyaluronan increases with concentration between 0.6 and 4.0 g l⁻¹ (Wik & Comper, 1982), whereas the Appendix integral is derived for constant D. The problem becomes mathematically non-linear if D is a function of C. The dependence of D on C under the conditions of interest here, viz. 4–20 g l⁻¹ in 0.15 M Ringer solution, is unknown. In 10 mM NaCl a sharp reduction in concentration dependence was observed at ≥6 g l⁻¹ in a preparation of weight average molecular mass (M_w) 0.6 × 10⁶ Da (Barry et al. 1996). An approximate solution to the non-linear equation arising from D= f(C) (unpublished result of Dr J. Carling, St George's Hospital Medical School, London, cited with permission) predicts a lower C_m value and hence an increase in boundary layer thickness needed to explain the results.

(4) Local regions of capillary filtration into the joint cavity may occur even when the observed net fluid transfer is outward (Levick & McDonald, 1994). This would locally disrupt the concentration polarization layer. This appears to be of minor significance in the present experiments, however, because the relation was essentially unaffected by circulatory arrest (Fig. 7).

(5) Boundary conditions are less well defined in vivo than in the Appendix model. Fluid from the cannula dissipates through the cavity by flow along a plane parallel to the surface. This cross-flow may establish the boundary layer thickness over much of the surface, as in the model. As the joint recesses are approached, however, dead-end filtration must supervene, so a uniform boundary layer is unlikely to exist in vivo. Dead-end filtration does not reach a steady state; C_m increases non-linearly with time. Since a steady state was approached in vivo, cross-flow filtration with a finite boundary layer may nevertheless be a reasonable approximation for the experiment.

In conclusion, the study showed that, at physiological concentration and molecular weight, both synovial fluid and hyaluronan solutions conserve intra-articular lubricant by increasing the opposition to outflow when pressure is increased. The phenomenon is reversible The mechanism appears to arise, at least in part, from the partial reflection of hyaluronan by the synovial lining. Reflection creates a concentration polarization layer at the surface, where the osmotic pressure can be more than an order of magnitude higher than in the bulk phase. This ‘boosted’ osmotic pressure is a major factor, though probably not the sole one, in buffering fluid outflow.

APPENDIX

Theory of molecular sieving across a leaky membrane from a concentration polarization layer in the steady state

A simple analytical solution for concentration at the membrane surface, C_m, is readily reached for the case of a boundary layer adjacent to a stirred compartment of fixed concentration C_in when diffusion coefficient D is a constant. From C_m, the interface osmotic pressure and pressure-flow relation can be calculated. This approach, although only an approximation to the more complex situation in experiments on joints (see Discussion), is of heuristic value.

Concentration at the membrane surface

Figure 8 depicts, schematically, the osmotic and concentration profiles across a boundary layer of thickness δ, for a membrane of reflection coefficient 0 < σ < 1, diffusional permeability P and area A, during ultrafiltration at volume flow Q̇. Concentration C_in and osmotic pressure π_in are uniform and time independent in the bulk phase of the stirred, upstream compartment. This is achieved, ideally, by cross-perfusing the compartment (true steady state). In the case of an infused (cf. cross-perfused) compartment, bulk C_in will increase with time if σ > 0, but the increase will be negligible over the period of interest if the stirred compartment is made sufficiently large (quasi-steady state).

Figure 8. Concentration and osmotic profiles during steady state ultrafiltration across a boundary layer (concentration polarization layer) in series with a membrane of reflection coefficient < 1.

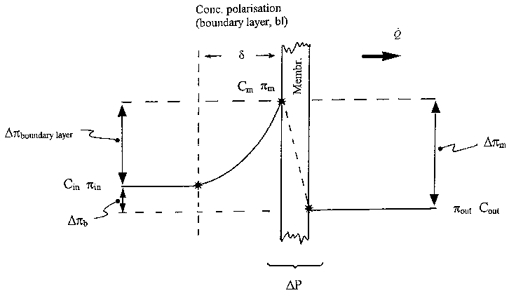
Gradient profiles are schematic. Non-linear gradients within the membrane itself (Curry, 1984) are not shown. For symbol definitions, see text.

Concentration and osmotic pressure increase across the boundary layer reach peaks of C_m and π_m at the membrane surface, and fall to C_out and π_out in the filtrate. Considering any plane of the boundary layer normal to the x-axis, of thickness dx, the convective transport of solute in direction 1→2 is Q̇C(x) and diffusive transport in direction 2→1 is, by Fick's law, DAdC/dx. In the steady state, net solute flux J_s,x through any such plane is given by the imbalance between the above two processes, i.e:

(A1)

The solute flux in the outflow, J_s,out, is:

(A2)

By the law of conservation of mass, J_s in the steady state has the same value for any plane at right angles to the x-axis, i.e. J_s,x=J_s,out. Thus eqns (A1) and (A2) can be equated to give:

(A3)

The relation between C_out and C_m for a partially reflective membrane is well known (Patlack et al. 1963; Curry, 1984), namely:

(A4)

where the Peclet transport number, Pe, equals Q̇(1 - σ)/PA. Pe represents the ratio of convective to diffusional transport capacity. Denoting the term (1 - σ)/(1 - σe^-Pe) in eqn (A4) by β, then substituting eqn (A4) into eqn (A3) and re-arranging:

(A5)

If D is constant with respect to x the solution is:

(A6)

For x= 0, C_x=C_in, giving the integration factor I:

(A7)

Also, for x=δ, C_x=C_m, from which, taking antilogarithms:

(A8)

Rearrangement gives the solution for concentration at the membrane surface:

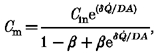(A9)

where β= (1 - σ)/(1 - σe^-Pe). Some numerical solutions of eqn (A9), based on values in the range of interest here, are presented in Fig. 9A.

Sieving ratios

The sieving ratio, C_out/C_in, is obtained by solving the simultaneous eqns (A4) and (A9), which leads to:

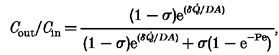(A10)

where Pe =Q̇(1 - σ)/PA. It is noted that the Patlack expression, eqn (A4), for sieving from a well stirred compartment, predicts that C_out/C_in= 1 at zero filtration rate and decreases monotonically towards the limit 1 - σ as Q̇ increases (see dashed line, Fig. 9B). This has been verified experimentally (Curry, 1984). In the case of sieving from a boundary layer, eqn (A10) shows that C_out/C_in= 1 at zero filtration rate, decreases at first as Q̇ increases, but then rises towards the limit 1 at very high filtration rates (Fig. 9B). In other words, rejection attains a maximum at a certain flow, after which the rise in concentration C_m at the membrane surface progressively reduces the rejected fraction, 1 - C_out/C_in. This has been observed experimentally when polymer solutions are ultrafiltered at increasing rates (Blatt et al. 1970; Munch et al. 1979).

Pressure-flow curves

Derivation of ΔP from π_m, Q̇_s and R_m (see eqn (1)) is described in the Discussion. Some numerical solutions are shown in Fig. 9C. The curve for δ= 0.065 cm and D= 2× 10⁻⁷ cm² s⁻¹ provides an approximate fit to the synovial results (see Results Fig. 4C).

Other values used to calculate the theoretical curves in Fig. 9 were σ= 0.95 (based on measured rejected fractions of 0.79–0.95 for 2–4 g l⁻¹ hyaluronan; Scott et al. 1998a), A≡ 12.7 cm² (average from Levick, 1994) and an estimated PA≡ 3.8× 10⁻³μl min⁻¹ (since hyaluronan rejection is 94–95 %in vivo (Coleman et al. 1997), which requires a Peclet number of 5 or more (eqn (A4))); for Pe = 5 and fluid turnover rate in vivoQ̇= 0.472 μl min⁻¹ (Coleman et al. 1997), PA= 3.8× 10⁻³μl min⁻¹.