GABA_A receptor subunit γ2 and δ subtypes confer unique kinetic properties on recombinant GABA_A receptor currents in mouse fibroblasts

Abstract

1. To determine their contributions to the rapid kinetic properties of GABA_A receptor (GABAR) currents, α1 and β3 subunit subtypes without or with δ or γ2L subtypes were transiently coexpressed in mouse L929 fibroblasts to produce α1β3, α1β3δ, or α1β3γ2L GABAR isoforms.

2. Brief (2–3 ms) applications of 1 mM GABA to outside-out membrane patches containing α1β3, α1β3δ, or α1β3γ2L isoforms elicited currents that activated rapidly with monophasic time courses and deactivated rapidly with biphasic time courses. α1β3γ2L currents exhibited a slower mean deactivation rate (76.1 ms) than α1β3 (34.1 ms) or α1β3δ currents (42.8 ms).

3. During 1 mM GABA applications, α1β3γ2L currents activated more rapidly (0.46 ms) than α1β3 currents (1.7 ms) or α1β3δ currents (2.4 ms). During 4000 ms GABA applications, α1β3 and α1β3γ2L currents desensitized with triphasic time courses to similar extents (α1β3, 94.6%; α1β3γ2L, 92.4%) and with similar mean rates (α1β3, 352 ms; α1β3γ2L, 462 ms). In contrast, α1β3δ currents desensitized only 55.6% with a biphasic time course and slower mean rate (1260 ms).

4. These experiments demonstrated that the α1β3 heterodimer formed a GABAR channel with rapid deactivation and rapid and nearly complete desensitization. Addition of the δ subunit did not alter the activation rate, but produced a receptor with slower and less complete desensitization. Addition of the γ2L subtype increased activation rate, prolonged deactivation and changed the pattern of rapid desensitization.

5. Rapid kinetic and steady-state single-channel data were used to construct kinetic models that predicted the behaviour of the α1β3γ2L and α1β3δ currents. These models represent a reconciliation of macroscopic and steady-state single-channel data for GABARs and provide a framework for systematically assessing the functional significance of different GABAR isoforms.

GABA_A receptors (GABARs) mediate the majority of fast inhibitory neurotransmission in the mammalian brain. Functional GABARs are ligand-gated chloride ion channels composed of five individual subunits. These subunits derive from six identified families, many with multiple subtypes (α1-6, β1-3, γ1-3, δ, ε and π). When expressed in Xenopus oocytes or mammalian cells, different GABAR subunit combinations form receptors with unique pharmacological and biophysical properties (Macdonald & Olsen, 1994). These subunits do not assemble randomly, however, for while αβ subunit combinations readily express in mammalian cells, addition of a γ subunit drives expression of αβγ isoforms (Angelotti & Macdonald, 1993). The majority of native receptors are believed to be formed by combinations of αβγ and αβδ subunits (McKernan & Whiting, 1996), although the recently characterized ε and π subunits may substitute for γ or δ subunits in some instances (Hedblom & Kirkness, 1997; Davies et al. 1997). In the rat, the γ2 subtype becomes the dominant γ subunit expressed at later developmental stages, and mRNA and membrane protein for this subtype are expressed in most brain regions. In contrast, the δ subunit is restricted only to a few cell populations in the postnatal rat that include thalamic relay neurons, cerebellar granule neurons and dentate granule neurons of the hippocampus (Laurie et al. 1992a,b; Wisden et al. 1992; Sperk et al. 1997). While the δ subunit has been shown to combine preferentially with the α6 subtype in cerebellar granule neurons (Jones et al. 1997), the GABAR subtypes that it combines with in dentate granule neurons remain unknown. The potential importance of hippocampal δ subunit-containing GABARs is underscored, however, by δ subunit knockout mice that exhibit spontaneous seizures (Olsen et al. 1997). For this investigation, we chose the α1β3γ2L and α1β3δ GABAR isoforms to determine the roles of γ and δ subunits in shaping GABAR currents.

α1β3γ2L and α1β3δ GABAR whole-cell currents have been characterized previously in L929 fibroblasts, where incorporation of the δ subunit resulted in higher apparent GABA affinity, slower and less complete whole-cell current desensitization, and smaller whole-cell currents compared with receptors containing the γ2 subtype (Saxena & Macdonald, 1994). α1β3 currents also desensitized more rapidly than α1β3δ currents, although both faster (Fisher & Macdonald, 1997) and slower desensitization (Dominguez-Perrot et al. 1996) relative to α1β3γ2L currents have been reported. In addition, α1β3 single channels had a smaller main channel conductance level (13 pS), while α1β3γ2L and α1β3δ channels had a similar larger main conductance level (27 pS). The γ2L subtype, however, conferred a change on the open and closed properties of the receptor, leading to a tendency for longer duration openings and longer bursts of openings (Fisher & Macdonald, 1997). While suggesting major differences in channel gating and desensitization, these analyses did not resolve the rapid phases of activation, desensitization and deactivation of GABAR currents.

These rapid kinetic properties are critical to understanding the potential synaptic roles of the α1β3γ2L and α1β3δ GABAR isoforms. In previous studies of native receptors, rapid application of GABA to outside-out membrane patches containing many GABARs reproduced the rapid activation and deactivation of IPSCs (Maconochie et al. 1994; Jones & Westbrook, 1995; Tia et al. 1996; Galaretta & Hestrin, 1997; Mellor & Randall, 1997, 1998). Also, with this rapid application protocol, it was demonstrated that GABAR desensitization was an important factor in shaping the deactivation time course of macropatch responses (Jones & Westbrook, 1995, 1996). In addition, macropatch deactivation kinetics were altered by allosteric modulators of GABARs such as benzodiazepines (Lavoie & Twyman, 1996; Mellor & Randall, 1997) and the anaesthetic propofol (Zhu & Vicini, 1997), as well as by intracellular phosphatase activity (Jones & Westbrook, 1997). Moreover, different recombinant GABAR isoforms displayed unique rapid kinetic properties (Verdoorn, 1994; Tia et al. 1996; Lavoie et al. 1997) that probably contribute to the diversity in GABAergic synaptic responses.

In addition to predicting the synaptic behaviour of recombinant GABAR isoforms, rapid kinetic analysis of macroscopic currents may serve as a bridge between single-channel and whole-cell analysis, allowing for the development of more comprehensive kinetic models of GABAR behaviour that incorporate desensitization (Macdonald & Twyman, 1992). For this study, we implemented a GABA application system that allowed very rapid solution exchange (10–90 % rise time < 400 μs) during electrophysiological recordings from outside-out membrane patches containing multiple receptor channels. Using this technique, we determined the rapid activation, desensitization and deactivation kinetics of α1β3γ2L and α1β3δ GABAR currents and used these kinetic data in combination with steady-state single-channel analysis to develop comprehensive models of GABAR kinetic behaviour for these isoforms. In some instances, the α1β3 isoform was examined so that contributions of the γ and δ subunits could be more thoroughly assessed.

METHODS

Expression of recombinant GABARs

The cDNAs encoding rat α1, β3, γ2L and δ GABAR subunit subtypes were individually subcloned into the plasmid expression vector pCMVNeo (Huggenvik et al. 1997). Mouse L929 fibroblasts (American Type Culture Collection, Rockville, MD, USA) were maintained in Dulbecco's Modified Eagle's medium supplemented with 10 % horse serum at 37°C in 5 % CO₂-95 % air and passaged prior to confluent growth. Cells were transfected with 4–8 μg of each subtype plasmid along with a plasmid (pEGFP; Clontech, Palo Alto, CA, USA) encoding for green fluorescent protein (GFP), in a 1:1:1:1 ratio using a modified calcium phosphate co-precipitation technique (Chen & Okayama, 1987) as previously described (Angelotti et al. 1993). The next day, cells were replated onto Mecanex gridded 35 mm culture dishes. Twenty-four hours after replating, electrophysiological recordings were performed on GFP-positive cells.

Electrophysiology

Patch-clamp recordings were performed on outside-out membrane patches pulled from L929 fibroblasts bathed in an external solution consisting of (mM): NaCl, 142; CsCl, 8; MgCl₂, 6; CaCl₂, 1; Hepes, 10; glucose, 10 (pH 7.4, 320 mosmol l⁻¹). Glass microelectrodes were formed from thick-walled borosilicate glass (World Precision Instruments, Pittsburgh, PA, USA) with a Flaming Brown electrode puller (Sutter Instrument Co., San Rafael, CA, USA), fire-polished to tip resistances of 10–20 MΩ, then coated with Q-dope (GC Electronics, Rockford, IL, USA). Patch electrodes were filled with an internal solution consisting of (mM): CsCl, 153; MgCl₂, 1; MgATP, 2; Hepes, 10; EGTA, 5 (pH 7.3, 300 mosmol l⁻¹). This combination of internal and external solutions produced a chloride equilibrium potential of 0 mV. Outside-out membrane patches were pulled from positively transfected L929 cells and voltage-clamped at -75 mV using an EPC-7 amplifier (List). The intensity of GFP fluorescence was used to identify cells with relatively high or low expression to use for macropatch or single-channel recordings, respectively.

GABA was applied to outside-out membrane patches using a rapid application system (Franke et al. 1987) consisting of a double-barrelled theta tube (FHC, Brunswick, ME, USA) connected to a piezoelectric translator (Burleigh Instruments, Fishers, NY, USA). One barrel was perfused with the external recording solution and the other was perfused with a GABA-containing external solution. Activation of the translator drove the solution interface rapidly across the patch surface. The solution exchange time was monitored at the end of each recording by blowing out the patch and stepping a dilute (90 %) external solution across the open electrode tip to measure a liquid junction current. The 10–90 % rise times for solution exchange were consistently less than 400 μs. The recording chamber was continuously perfused with external solution to prevent accumulation of GABA in the bath. All experiments were performed at room temperature (22–23°C).

Rapid kinetic analysis

Outside-out patch data were low-pass filtered at 3 kHz, digitized at 10 kHz and analysed using the pCLAMP6 software suite (Axon Instruments) and Origin 4.1 (Microcal, Northampton, MA, USA). Multiple GABA-elicited responses (5–20) were acquired for each GABA concentration at 30 s intervals, then were averaged to form ensemble currents for analysis. Deactivation of ensemble currents was measured as the current decay after the removal of GABA. Activation was measured as the 10–90 % rise time to the peak current and desensitization as the decline from peak current in the continuing presence of GABA. The deactivation and desensitization time courses of ensemble GABAR currents were fitted using the Levenberg-Marquardt least squares method with one-, two-, or three-component exponential functions. The number of exponential components was incremented until the addition of another component did not significantly improve the fit (P < 0.01) as determined by an F test on the sum of squared residuals. For comparison of deactivation and desensitization time courses among currents from different isoforms, mean deactivation and desensitization rates were calculated using a weighted summation of the fitted exponential components. For a triphasic decay, this equation was (A₁τ₁+A₂τ₂+A₃τ₃), where τ₁, τ₂ and τ₃ were the fitted time constants and A₁, A₂ and A₃ were the fitted component proportions. The extent of desensitization after 4000 ms GABA applications was measured as (peak current - fitted steady-state current)/(peak current). Numerical data were expressed as means ±s.e.m. Statistical significance was determined using Student's unpaired two-tailed t tests and ANOVAs (Student- Newman-Keuls test) where appropriate.

Single-channel analysis

Single-channel recordings were filtered at 2 kHz with an 8-pole Bessel filter (3 dB at 2 kHz), digitized at 20 kHz through a Digidata 2000 A/D converter (Axon Instruments) and acquired into Axoscope (Axon Instruments). Single-channel data were analysed using pCLAMP6 (Axon Instruments) and Interval5 (Dr Barry S. Pallotta, University of North Carolina, Chapel Hill, NC, USA). Single-channel events were identified with a 50 % threshold detection method. Subconductance levels were rarely observed (< 5 % of openings) but were included in the analysis if they reached the 50 % threshold. Recordings were only included in the kinetic analysis if overlaps of simultaneous openings occurred for less than 1 % of the openings. Overlapped openings and bursts were not included in the kinetic analysis. The presence of multiple channels would decrease the apparent duration of the longer closed components, but would have no effect on the open state properties. Duration histograms were constructed as described by Sigworth & Sine (1987) and fitted by a maximum likelihood method. The number of exponential functions required to fit the distribution was increased until additional components did not significantly improve the fit as determined by the log-likelihood ratio test (Horn, 1987; McManus & Magleby, 1988). Durations less than 1.5 times the system dead time (150 μs) including the 8-pole Bessel filter (3 dB cut-off at 2 kHz) were displayed in the histograms but were not included in the fit. For the definition of bursts, the two shortest closed components were considered as intraburst closures. A critical gap for each patch was calculated from the closed interval distribution to equalize the proportion of misclassfied events (Colquhoun & Sakmann, 1985).

Kinetic modelling

Modelling of the macroscopic currents was performed using SCoP (Berrien Springs, MI, USA). The models for α1β3γ2L and α1β3δ isoforms were based on a model developed to predict the steady-state single-channel kinetics of mouse spinal cord neurons (Macdonald et al. 1989; Twyman et al. 1990). This model incorporated two GABA binding steps of equal GABA affinity. The two shortest closed states were concentration-independent and fixed as the distal closed states emerging from the open states. To confirm the validity of this model for the application conditions of this study, we performed steady-state single-channel analysis at 1 mM GABA. For the α1β3δ isoform, only two open states were identified. These were both modelled as doubly liganded open states. A single slow desensitized state was added to account for the longest closed duration. For the α1β3γ2L isoform, we observed three open states and five closed states. Three desensitized states were included to explain the triphasic desensitization pattern. The sum of the closing rates from the open states was then fixed by the inverse of the mean open durations. Similarly, the inverses of the two briefest closed durations set the opening rates from the distal closed states (C₅-C₁₀). The remaining parameters were adjusted to fit best the macroscopic deactivation and desensitization rates and the single-channel open, closed and burst properties. Simulations of single-channel data using the models were performed with the Interval5 analysis software.

RESULTS

Macropatch α1β3, α1β3δ and α1β3γ2L currents at high GABA concentrations

Within the synaptic cleft, it has been predicted that GABA concentrations of 500 μm to 1 mM are reached within 100 μs, which decline rapidly over the course of a few milliseconds (Maconochie et al. 1994; Clements, 1996). To approximate a synaptic GABA time course, brief pulses of 1 mM GABA (2–3 ms) were applied to outside-out membrane patches pulled from L929 fibroblasts expressing α1β3, α1β3δ, or α1β3γ2L GABAR channels. Changing application durations over this range did not measurably alter the deactivation kinetics of the currents. Longer (400–4000 ms) GABA applications were used to evaluate activation and desensitization kinetics. GABA application elicited currents that activated and deactivated rapidly, but each isoform exhibited distinct rapid kinetic properties.

Deactivation

Representative current traces for each isoform are shown in Fig. 1A with 2 ms applications of 1 mM GABA denoted by open-tip liquid junction currents. This example illustrates that currents from all three isoforms deactivated with similar fast components ranging from 11.1–18.5 ms. The slow deactivation component was variable, ranging from 73.1 ms for the α1β3δ current to 182 ms for the α1β3γ2L current. To compare the deactivation rates of the currents among isoforms, we utilized a weighted sum of the fitted deactivation time constants to calculate a mean deactivation rate (see Methods). The α1β3 currents deactivated most rapidly with a mean of 34.1 ms (n= 5 patches) followed by α1β3δ currents at 42.8 ms (n= 4). The α1β3γ2L current deactivated significantly more slowly at 76.1 ms (n= 6) (Fig. 1B). The slower deactivation of α1β3γ2L currents was due to a significantly longer slow decay component (209 ms) than α1β3 (144 ms) and α1β3δ currents (82.4 ms) (P < 0.05). In addition, for α1β3γ2L currents, a significantly greater percentage of the decay was attributed to the slow component (32.0 %) than that for α1β3 currents (16.8 %) (P < 0.05) (Table 1).

Figure 1. Current deactivation following brief applications of 1 mM GABA.

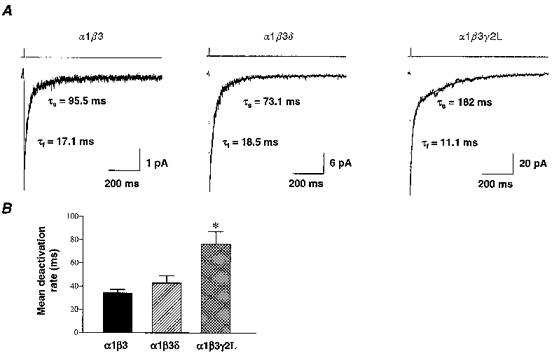
A, outside-out membrane patches were pulled from L929 fibroblasts expressing α1β3, α1β3δ and α1β3γ2L GABAR isoforms. In patches voltage-clamped at -75 mV, brief pulses (2–3 ms) of rapidly applied 1 mM GABA elicited inward GABAR currents that deactivated with biphasic time courses. Ensemble currents for α1β3 (n= 20 applications), α1β3δ (n= 12) and α1β3γ2L (n= 10) were shown. These deactivation time courses were fitted best with a two component exponential equation. The duration of GABA application was denoted by liquid junction currents above the traces. B, deactivation rates were compared by using a weighted sum of the fitted components ((proportion fast ×τ_f) + (proportion slow ×τ_s)) to obtain a mean deactivation rate. α1β3 currents deactivated with a mean of 34.1 ± 3.4 ms (n= 5 patches), similar to α1β3δ currents at 42.8 ± 6.3 ms (n= 5). α1β3γ2L currents deactivated significantly more slowly (*P < 0.05) at 76.1 ± 11.0 ms (n= 6).

Table 1.

Rapid kinetic properties of GABARs

	α1β3	α1β3δ	α1β3δ2L
Deactivation (2–3 ms)
n	5	4	6
τf (ms)	14.5 ± 2.2	17.1 ± 4.2	12.4 ± 1.3
τs (ms)	144 ± 18	82.4 ± 20	209 ± 21*
Percentage fast	83.2 ± 3.3*	57.3 ± 4.7	68.0 ± 2.9
Percentage slow	16.8 ± 3.3*	42.7 ± 4.7	32.0 ± 2.9
Activation (400 ms)
n	5	5	8
10-90% rise time (ms)	1.7 ± 0.40	2.4 ± 0.27	0.46 ± 0.04*
Deactivation (400 ms)
n	—	5	7
τf (ms)	—	14.7 ± 4.2†	33.4 ± 2.9
τs (ms)	—	79.7 ± 7.3†	193 ± 31
Percentage fast	—	45.8 ± 15†	10.5 ± 2.6
Percentage slow	—	54.1 ± 15†	89.5 ± 2.6
Desensitization (4000 ms)
n	6	4	6
τf (ms)	24.6 ± 3.2	75.7 ± 37.4	7.9 ± 1.5*
τi (ms)	200 ± 9.9	—	129 ± 26.4
τs (ms)	1570 ± 149	2190 ± 311	1540 ± 135
Percentage fast	61.1 ± 7.0	48.0 ± 9.2	50.2 ± 4.6
Percentage intermediate	20.1 ± 6.8	—	21.8 ± 2.4
Percentage slow	18.8 ± 2.3	52.0 ± 9.2*	28.1 ± 2.9
Extent (%)	94.5 ± 1.3	55.4 ± 3.6*	92.4 ± 1.4

n, number of patches. τ_f, τ_s and τ_i, fast slow and intermediate time constants, respectively.

^*Significant difference from all other isoforms, P < 0.05, Student-Newman-Keuls test.

^†Significant difference from α1β3γ2L isoform, P < 0.05, Student's two-tailed t test.

Activation

Since 2–3 ms GABA applications were too short to assess current activation accurately, 400 ms applications were used to compare the activation rates of the three GABAR isoforms (Fig. 2, Table 1). The average rate of activation for each isoform was measured as the 10–90 % rise time of currents elicited by 1 mM GABA. The whole-cell GABA EC₅₀ for these isoforms was previously determined to be 2.1 μm for the α1β3 isoform, 2.8 μm for the α1β3δ isoform, and 11.5 μm for the α1β3γ2L isoform (Fisher & Macdonald, 1997). We predicted that activation rates would correlate with EC₅₀ values and that the α1β3γ2L GABARs would activate relatively slowly compared with α1β3 and α1β3δ GABARs. Yet, when currents from each isoform were normalized and overlaid (Fig. 2A), α1β3 and α1β3δ currents activated relatively slowly compared with α1β3γ2L currents. The mean 10–90 % rise time to peak current was 1.7 ms (n= 5) for the α1β3 isoform and 2.4 ms (n= 5) for the α1β3δ isoform, but only 0.46 ms (n= 8) for the α1β3γ2L isoform (Fig. 2B, Table 1). Thus, the γ2L subtype conferred a more rapid rate of activation. A similar slower rise time of α1β3 currents in relation to α1β3γ2L currents has also been demonstrated in whole-cell recordings with slower application of lower GABA concentrations (Dominguez-Perrot et al. 1996).

Figure 2. Activation.

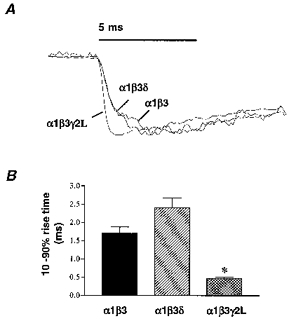
A, GABAR outside-out patch currents from α1β3, α1β3δ and α1β3γ2L isoforms were normalized and overlaid to compare the activation rates of currents evoked by rapid application of 1 mM GABA. B, α1β3 GABAR currents activated rapidly with a mean 10–90 % rise time to peak current of 1.7 ± 0.40 ms (n= 5), similar to the α1β3δ activation rate (2.4 ± 0.27 ms, n= 5). α1β3γ2L currents activated significantly more rapidly (*P < 0.05) with an mean 10–90 % rise time of 0.46 ± 0.04 ms (n= 8).

Desensitization

Previous whole-cell studies demonstrated that α1β_xγ2L currents desensitized more rapidly and completely than α1β_xδ currents (Saxena & Macdonald, 1994; Fisher & Macdonald, 1997). Long pulses (4000 ms) of rapidly applied GABA (1 mM) were used to examine the rapid desensitization of α1β3, α1β3δ and α1β3γ2L currents (Fig. 3). Peak currents varied with isoform, with the α1β3γ2L isoform producing the largest currents (143.7 ± 44.6 pA, n= 12), followed by the α1β3 (48.7 ± 17.4 pA, n= 9) and α1β3δ (11.9 ± 4.4 pA, n= 8) isoforms. During 4000 ms GABA applications, α1β3 and α1β3γ2L current desensitization time courses were fitted best by the sum of three exponential functions, but α1β3δ current desensitization was fitted best with only two exponential functions (Fig. 3A). α1β3 currents desensitized with a mean rate of 352 ± 43.7 ms, derived from fast, intermediate and slow time constants: τ_f= 24.6 ± 3.2 ms (61.1 ± 7.0 %), τ_i= 200 ± 9.9 ms (20.1 ± 6.8 %) and τ_s= 1570 ± 149 ms (18.8 ± 2.3 %) (n= 5). α1β3γ2L currents desensitized with a similar mean rate of 461 ± 56.0 ms with τ_f= 7.9 ± 1.5 ms (50.2 ± 4.6 %), τ_i= 129 ± 26.4 ms (21.8 ± 2.4 %) and τ_s= 1540 ± 135 ms (28.1 ± 2.9 %) (n= 6). α1β3δ currents desensitized with a significantly slower mean rate of 1260 ± 362 ms with τ_f= 75.7 ± 37.4 ms (48.0 ± 9.2 %) and τ_s= 2190 ± 311 ms (52.0 ± 9.2 %) (n= 5) (Fig. 3B, Table 1). The extent of desensitization was similar for α1β3 and α1β3γ2L currents, being 94.5 ± 1.3 and 92.4 ± 1.4 %, respectively, but significantly less for α1β3δ current at 55.4 ± 3.6 % (Table 1). While the desensitization time courses were similar for α1β3 and α1β3γ2L currents, there were subtle differences. α1β3γ2L currents showed a significantly more rapid fast component than α1β3 currents (P < 0.001), but a greater proportion of desensitization was concentrated in the slowest component (P < 0.05). Thus, addition of the δ subunit to α1 and β3 subtypes significantly reduced both the rate and the extent of desensitization, while addition of the γ2L subtype to α1 and β3 subtypes changed the pattern of desensitization.

Figure 3. Rapid phases of desensitization.

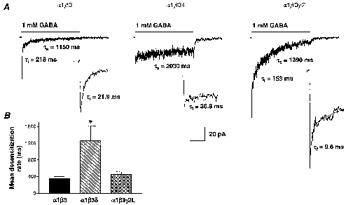
A, 1 mM GABA was rapidly applied for 4000 ms to outside-out membrane patches containing α1β3, α1β3δ and α1β3γ2L isoforms. For the representative traces shown, current desensitization was fitted with multicomponent exponential equations with time constants of 21.9 ms (τ_f, inset), 218 ms and 1150 ms for the α1β3 current (n= 6), 36.8 ms (τ_f, inset) and 2030 ms for the α1β3δ current (n= 5), and 9.6 ms (τ_f, inset), 153 ms and 1390 ms for the α1β3γ2L current (n= 5). Time calibration for A and insets is 1000 ms and 150 ms, respectively. B, α1β3 and α1β3γ2L currents desensitized with similar mean rates (352 ± 43.7 ms (n= 5) and 461 ± 56.0 ms (n= 6), respectively). α1β3δ currents desensitized with a mean rate of 1260 ± 362 ms (n= 4) that was significantly slower (*P < 0.01) than α1β3 and α1β3γ2L currents.

We examined the concentration dependence of desensitization by rapidly applying multiple concentrations of GABA for 4000 ms to outside-out patches containing the α1β3δ or α1β3γ2L isoforms (Fig. 4A). The α1β3δ isoform desensitized minimally at 3 μm GABA and exhibited biphasic desensitization at 1 mM GABA. For α1β3δ currents, due to the small current size and relatively low extent of desensitization, consistent fits of desensitization at GABA concentrations lower than 1 mM could not be obtained. For the α1β3γ2L isoform, 1 μm GABA currents did not desensitize. At higher GABA concentrations, the desensitization time course was concentration dependent, with slower phases appearing at 10 μm GABA and the most rapid phase only appearing at high concentrations of GABA (Fig. 4A and B). At 10 μm GABA, a small-amplitude faster component of desensitization (τ= 205 ± 47.7 ms, 16.9 ± 3.9 %; n= 6) was revealed, in addition to a predominant slow component (τ= 1960 ± 289 ms, 83.1 ± 3.9 %; n= 6). At 100 μm GABA, a third fast component of desensitization was revealed (τ_f= 16.1 ± 5.3 ms, 23.7 ± 6.8 %; n= 5) in addition to the intermediate (τ_i= 147 ± 44.1 ms, 23.3 ± 4.6 %; n= 5) and slow (τ_s= 1710 ± 177 ms, 52.4 ± 5.5 %; n= 5) components. At 1 mM GABA desensitization was also triphasic (Table 1). There was not a significant change in the desensitization rates of these components as GABA concentration was increased (Fig. 4B), but instead there was a shift towards a greater proportion of fast desensitization at higher GABA concentrations (Fig. 4C). This concentration independence of desensitization rates was similar to the desensitization pattern of cultured hippocampal neuron GABAR outside-out patch currents (Celentano & Wong, 1994) and to α1β3γ2L whole-cell currents (Dominguez-Perrot et al. 1997). This suggested that entry into desensitized conformations did not require additional GABA binding

Figure 4. Concentration dependence of desensitization.

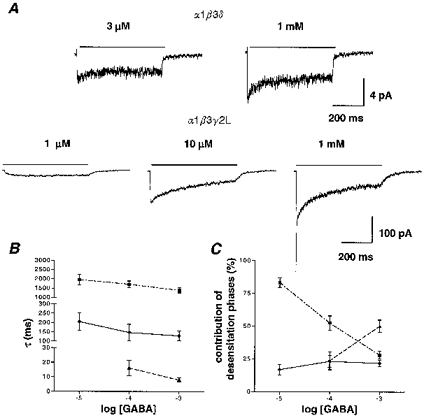
A, multiple GABA concentrations were applied to patches (α1β3δ: 3 μm and 1 mM; α1β3γ2L: 1, 10 and 100 μm and 1 mM) to examine the concentration dependence of desensitization. At 3 μm GABA, α1β3δ ensemble currents (n= 15) exhibited minimal desensitization during a 4000 ms GABA application while ensemble currents elicited by 1 mM GABA (n= 12) exhibited more pronounced desensitization. For the α1β3γ2L isoform, 1 μm GABA currents (n= 10) did not desensitize. At higher GABA concentrations, desensitization was concentration dependent, with slower phases of desensitization that appeared at 10 μm (n= 6) and a rapid phase of desensitization that appeared at higher GABA concentrations (1 mM shown; n= 5). B, for α1β3γ2L currents, the desensitization rates (τ values) for the slow (▪), intermediate (•) and fast phases (▴) of desensitization were plotted as a function of GABA concentration, showing their nearly flat concentration dependence. C, the percentage contributions of the slow (▪), intermediate (•) and fast (▴) desensitization phases to the total desensitization were plotted as a function of GABA concentration. The contribution of the slow phase decreased with increasing GABA concentration while the contribution of the fast phase increased after its appearance at 100 μm GABA.

We used 400 ms GABA applications to evaluate the effect of desensitization on current deactivation for α1β3γ2L and α1β3δ currents. Due to the relatively small size of α1β3 currents and their high extent of desensitization after 400 ms, we were unable to assess their deactivation following desensitization. Desensitization should prolong deactivation as more of the receptors equilibrate into desensitized states (Jones & Westbrook, 1995). This occurred with α1β3γ2L currents, which deactivated predominantly with the slow component (193 ± 31 ms, 89.5 ± 2.6 %) following 400 ms applications of 1 mM GABA rather than predominantly with the fast component (12.4 ± 1.3 ms, 68.0 ± 2.9 %) following brief GABA applications (Table 1). Moreover, a receptor that minimally desensitized should deactivate at nearly the same rate following short and long GABA applications. This was true of the α1β3δ currents, which deactivated with nearly identical rate constants and proportions following brief and prolonged GABA applications (Table 1).

Single-channel properties

We were interested in reconciling previous models of receptor function based on single-channel or whole-cell data for these isoforms. While previous studies examined single-channel properties of these isoforms at lower GABA concentrations, we were interested in the pattern of activity at predicted synaptic GABA concentrations. Thus, steady-state single-channel data at 1 mM GABA, the same concentration used to examine rapid macroscopic current properties, were obtained for the α1β3γ2L and α1β3δ isoforms. Representative single-channel traces illustrated that α1β3δ single channels had a main conductance level (23.8 ± 0.37 pS; n= 4) similar to α1β3γ2L channels (25.9 ± 0.60 pS; n= 4) (Table 2), but opened less frequently and for shorter durations (Fig. 5A). The open probability (NP_o) was significantly lower for α1β3δ (2.27 ± 0.57 %) channels than for α1β3γ2L (10.5 ± 1.5 %) channels (P < 0.05). Open interval analysis demonstrated at least three open states for α1β3γ2L receptors and at least two open states for α1β3δ receptors. Closed interval histograms were fitted best by five closed states for each isoform (Fig. 5B, Table 2). The number of open and closed states and their durations corroborated previous findings from these isoforms obtained at lower GABA concentrations (Fisher & Macdonald, 1997).

Table 2.

Single-channel properties of GABARs

	α1β3δ		α1β3γ2L
	Measured	Simulated	Measured	Simulated
Number of patches	4	—	4	—
Number of openings	7565	10000	10535	10000
Conductance (pS)	23.8 ± 0.37	—	25.9 ± 0.60	—
NPn± 100 (%)	2.27 ± 0.57*	1.40	10.5 ± 1.5	3.68
Mean open time (ms)	0.74 ± 0.11*	—	2.14 ± 0.07	—
Mean shut time (ms)	35.6 ± 8.1	—	21.0 ± 3.4	—
Open intervals
τ1 (ms)	0.33	0.34	0.30	—
	(0.31–0.34)	(0.31–0.36)	(0.22–0.35)	—
Area1 (%)	79.2	86.2	23.6	—
	(78.0–79.9)	(79.8–87.5)	(18.0–25.8)	—
τ2 (ms)	0.98	1.01	1.92	1.87
	(0.95–0.98)	(0.83–1.25)	(1.03–2.20)	(1.29–2.16)
Area2 (%)	20.8	13.9	48.0	67.1
	(20.6–21.0)	(13.5–14.3)	(45.5–51.0)	(63.5–68.5)
τ3 (ms)	—	—	3.47	3.62
	—	—	(2.86–4.49)	(2.90–4.84)
Area3 (%)	—	—	28.4	32.9
	—	—	(22.9–33.2)	(32.3–34.1)
Closed intervals
τ1 (ms)	0.27	0.27	0.20	0.21
	(0.22–0.30)	(0.23–0.32)	(0.17–0.22)	(0.19–0.23)
Area1 (%)	12.2	14.0	38.0	48.1
	(10.6–13.4)	(12.7–16.0)	(35.8–39.3)	(44.4–50.0)
τ2 (ms)	3.50	2.24	1.64	1.35
	(2.20–5.66)	(1.23–4.00)	(1.44–1.80)	(0.97–1.83)
Area2 (%)	20.9	9.0	35.7	15.9
	(18.2–22.2)	(8.4–9.8)	(33.1–37.0)	(13.9–17.6)
τ3 (ms)	15.2	10.5	8.89	8.21
	(12.3–37.9)	(9.3–12.2)	(7.81–9.89)	(6.89–9.85)
Area3 (%)	50.1	54.6	21.3	21.9
	(45.4–55.4)	(50.2–58.7)	(19.6–23.8)	(20.0–23.8)
τ4 (ms)	68.8	55.8	95.5	72.6
	(57.6–78.3)	(50.9–62.1)	(86.2–103)	(64.5–81.8)
Area4 (%)	15.8	22.2	4.0	12.7
	(13.6–19.2)	(19.1–25.2)	(3.8–4.4)	(11.5–14.2)
τ5 (ms)	1630	3990	990	4200
	(1470–1760)	(3720–4250)	(949–1030)	(3890–4530)
Area5 (%)	1.0	0.56	1.0	1.2
	(0.8–1.1)	—	(0.95–1.4)	(1.15–1.25)
Mean burst duration (ms)	1.51*	0.94	6.35	6.39
	(1.31–1.72)	(0.80–1.07)	(5.95–6.79)	(6.08–6.71)

^*Significant difference from α1β3γ2L, P < 0.05, Student's two-tailed t test.

Figure 5. Single-channel characteristics.

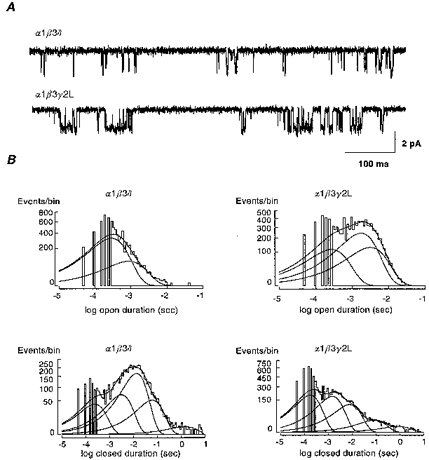
A, single-channel GABAR currents from outside-out membrane patches were voltage-clamped at -75 mV. Traces shown were continuous 700 ms recordings in response to 1 mM GABA. Channel openings are downwards. B, duration histograms of open and closed intervals were formed from steady-state single-channel data. Open duration histograms for α1β3γ2L GABARs were fitted best with three components, while the α1β3δ open duration histogram was fitted best with only two components. Closed interval histograms were fitted best by five components. For a summary of steady-state single-channel properties see Table 2.

GABAR kinetic modelling

Previous investigations of the steady-state single-channel properties of mouse spinal cord neuron GABARs led to the development of a working kinetic model (Macdonald et al. 1989; Twyman et al. 1990). This model incorporated two GABA binding steps and three open states (O) with interconnected concentration-dependent and concentration-independent (distal) closed states (C). Subsequent investigations of recombinant α1β1γ2L and α1β3γ2L GABARs demonstrated similar single-channel main conductances and open and closed properties (Angelotti & Macdonald, 1993; Fisher & Macdonald, 1997). This model was incomplete, however, as it did not adequately explain GABAR desensitization. Also, this model did not address the single-channel properties of the α1β3δ isoform, which exhibited only two resolvable open states with brief durations, leading to a low open probability. Taking this model as a framework, we used macroscopic rapid kinetic data and steady-state single-channel data to construct more comprehensive models to describe the kinetic behaviour of the α1β3δ (Fig. 6A) and α1β3γ2L isoforms (Fig. 7A). For the α1β3δ isoform (Fig. 6A), only two open states were identified. These were both modelled as doubly liganded open states. A single slow desensitized state (D_s) was added to account for the longest closed duration. For the α1β3γ2L isoform (Fig. 7A), we observed three open states. Three desensitized states were needed to explain the triphasic desensitization pattern. Desensitized states were entered only from doubly liganded states, as no concentration dependence of desensitization rates was found. The sum of the closing rates from the open states was then fixed by the inverse of the mean open durations. Similarly, the inverses of the two briefest closed durations set the opening rates from the distal closed states (C₅ - C₁₀). Another important constraint was to have the model generate a P_o lower than the measured NP_o for single channels. The remaining model parameters were optimized to fit the macroscopic activation, desensitization and deactivation rates of outside-out patch currents (Figs 6B and 7B). These optimized parameters were then used to generate simulated single-channel data, and the optimization process was continued until the models best predicted both the macroscopic rapid kinetic and steady-state single-channel open, closed and burst properties.

Figure 6. Kinetic model for the α1β3δ isoform.

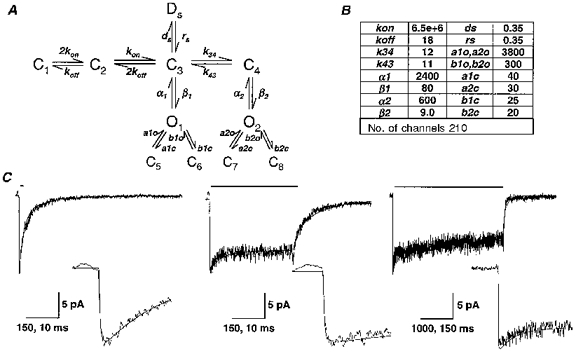
A, a kinetic model for the α1β3δ isoform was derived from steady-state single-channel analysis and rapid kinetic analysis of currents from outside-out membrane patches. B, the rate constants in the model were optimized to best fit the time course of the α1β3δ macroscopic currents and the single-channel open, closed and burst properties (see Methods). O, open state; C, closed state; D, desensitized state. Units for all rate constants were s⁻¹ except for k_on (m⁻¹ s⁻¹). C, the optimized model currents were superimposed on averaged α1β3δ data traces for 2 ms (n= 4), 400 ms (n= 5) and 4000 ms (n= 4) applications of 1 mM GABA (application bars above traces). The same currents are depicted on an expanded time scale in the insets. Time calibrations for 2 and 400 ms applications and insets are 150 and 10 ms, respectively. Time calibrations for 4000 ms and inset are 1000 and 150 ms, respectively.

Figure 7. Kinetic model for the α1β3γ2L isoform.

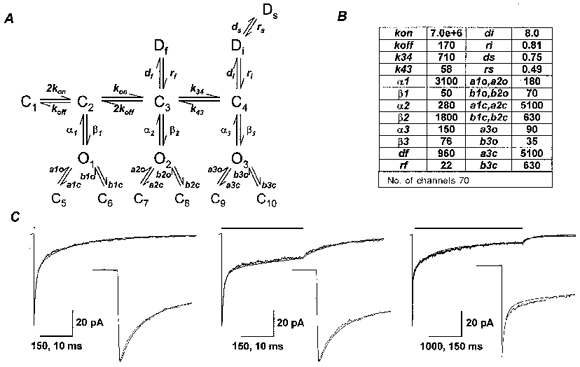
A, a kinetic model for the α1β3γ2L isoform was derived from steady-state single-channel analysis and rapid kinetic analysis of currents from outside-out membrane patches. B, the rate constants in the model were optimized to best fit the time course of the α1β3δ macroscopic currents and the single-channel open, closed and burst properties (see Methods). Units for all rate constants were s⁻¹ except for k_on (m⁻¹ s⁻¹). C, the optimized model currents were superimposed on averaged α1β3γ2L data traces for 2 ms (n= 6), 400 ms (n= 8), and 4000 ms (n= 6) applications of 1 mM GABA (application bars above traces). The same currents are depicted on an expanded time scale in the insets. Time calibrations for 2 and 400 ms applications and insets are 150 and 10 ms, respectively. Time calibrations for 4000 ms application and inset are 1000 and 150 ms, respectively.

The desensitization seen in macroscopic currents could have resulted from a redistribution of chloride ions during the course of the recordings, a redistribution of receptor conformations among relatively less stable short bound closed states, or the entrance of the receptor into more stable long-lived bound closed (desensitized) states. We examined the possibility of chloride ion redistribution by rapidly stepping a desensitizing current between -75 and 75 mV (reversal potental for Cl⁻, E_Cl= 0 mV) and found symmetrical currents even after several seconds of GABA application (K. F. Haas & R. L. Macdonald, unpublished observations), ruling out chloride ion redistribution as an explanation.

In the α1β3δ isoform model, the initial peak current was due primarily to initial synchronous brief O₁ openings, while the rapid phase of desensitization was caused by a rapid redistribution of receptors into the remaining doubly liganded states. To accurately reflect the slow macroscopic desensitization and the long closed periods seen in single-channel recordings, a desensitized state with very slow entry and exit rates was needed (D_s, Fig. 6A). Kinetic rate constants were optimized to best fit averaged current traces for the brief (2 ms) and prolonged (400 or 4000 ms) 1 mM GABA applications and the steady-state single-channel properties (Table 2). Traces simulated from the optimized model parameters (Fig. 6B) were overlaid on averaged current traces for the α1β3δ isoform (Fig. 6C).

For the α1β3γ2L isoform, the initial current peak was primarily due to synchronous intermediate O₂ openings. Three desensitized states (D_f, D_i and D_s; Fig. 7A) were needed to account for the triphasic desensitization during 4000 ms applications. Kinetic rate constants were optimized to fit best averaged current traces for the brief and prolonged 1 mM GABA applications and the steady-state single-channel properties (Table 2). Traces simulated from the optimized model parameters (Fig. 7B) were overlaid on averaged current traces for the α1β3γ2L isoform (Fig. 7C). When the desensitized states were altered in placement, other configurations such as entry into desensitization from an open state, or alternating the positions of fast and slow desensitized states did not reproduce the measured pattern of desensitization.

Based on these kinetic models for the α1β3δ and α1β3γ2L isoforms, simulated single-channel data were generated (Table 2). For the α1β3δ isoform, the model predicted similar open, closed and burst properties to those measured for α1β3δ channels. The simulated P_o of 1.40 % was less than the measured NP_o of 2.27 %. The low P_o was achieved by relatively slow opening rates (β values), meaning that a large number of channels (210) were needed to produce a small macroscopic current (14 pA) (Fig. 6B and C). The single desensitized state (D_s) accounted for the slow macroscopic desensitization and for the infrequent long duration closings present in single-channel recordings. The longest closed duration for measured single-channel data would have been shortened by the presence of multiple channels, which probably explained the shorter measured (1630 ms) than simulated (3990 ms) mean duration for this long closed state.

For the α1β3γ2L isoform, in most cases, the model predicted similar single-channel properties to those measured from α1β3γ2L channels. The model accounted for the intermediate (O₂) and long duration (O₃) open states and their relative proportions (Table 2). Similar to the α1β3δ isoform model, the simulated P_o (3.68 %) was lower than the measured NP_o (10.5 %). While the α1β3γ2L model accounted for the durations and proportions of longer duration (O₂ and O₃) openings at 1 mM GABA, it could not account well for the number of brief (O₁) openings recorded at high GABA concentration. The simulated closed interval data were also fitted best by five closed states, for at high GABA concentrations, relatively minimal time was spent in the unbound or monoliganded states (C₁ and C₂), which could not be resolved from the brief distal closed states (C₅-C₁₀). The predicted mean burst duration (6.39 ms) was nearly identical to the measured mean burst duration (6.35 ms).

To illustrate the similarity in measured and simulated single-channel properties, several seconds of measured and simulated single-channel traces were juxtaposed (Fig. 8). These traces illustrated the relatively low open probability at high GABA concentrations for both measured and simulated single-channel currents. At these high GABA concentrations, unbound closed states would probably have been very brief, so that any long closed states most probably represented entry into a desensitized conformation (Fig. 8). The several second duration closures (**) most probably included a visit into D_i and D_s, while other more frequent intraburst long closures (*) most probably included entry into D_f (mean duration = 45.4 ms). Thus, desensitization probably produced the characteristic pattern of clusters of openings separated by long closed periods.

Figure 8. Comparison of desensitization in measured and simulated single-channel currents.

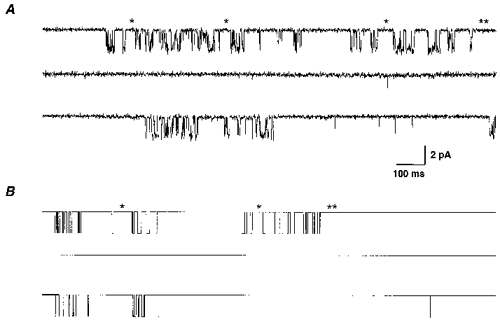
A, single-channel GABAR currents during application of 1 mM GABA to an outside membrane patch containing α1β3γ2L GABARs. The trace shown was a continuous 4.5 s recording filtered at 1 kHz for display. B, simulated single-channel currents at 1 mM GABA from the α1β3γ2L isoform model. The trace shown was a continuous 4.5 s simulation. For both A and B, single asterisks denoted some of the closed states that probably involved entry into D_f and the double asterisks denoted a long closed state that probably involved entry into D_i and D_s.

These models should also explain the concentration-dependent changes in the current time course (Fig. 3). Simulated currents were generated at 3 μm and 1 mM GABA from the α1β3δ kinetic model, and at 1 μm, 10 μm and 1 mM GABA from the α1β3γ2L kinetic model (Fig. 9). These simulated currents were overlaid on normalized averaged currents from α1β3δ (n= 4) and α1β3γ2L (n= 6) isoforms, where multiple GABA concentrations were applied to the same patch. While developed and optimized for macroscopic kinetic and steady-state single-channel data evoked by 1 mM GABA, the model predicted the time courses of GABAR currents evoked by lower GABA concentrations. For the α1β3δ currents, the simulated activation rate was somewhat slower than that measured at 3 μm GABA, but the comparison was difficult to make as only small currents were obtained at this concentration. For the α1β3γ2L currents, the measured and simulated activation rates were nearly identical (Fig. 9, insets). Also, the nearly flat concentration dependence of desensitization rates for α1β3γ2L currents was predicted by the model.

Figure 9. Model predictions at different GABA concentrations.

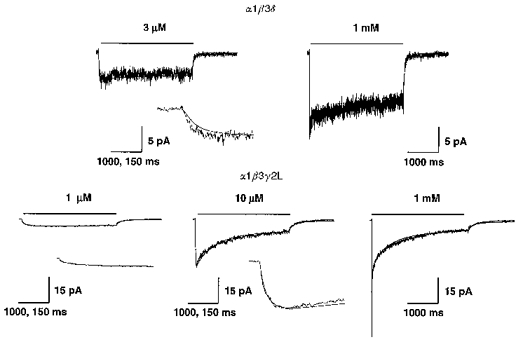
A, the kinetic model developed for the α1β3δ isoform was used to generate simulated currents for 4000 ms applications of 3 μm and 1 mM GABA. The simulated currents were overlaid on measured current responses at these same GABA concentrations. The measured current traces shown were averaged responses from three patches (3 μm) and four patches (1 mM) normalized to the 1 mM peak current values. B, the kinetic model developed for the α1β3γ2L isoform was used to generate simulated currents for 4000 ms applications of 1 μm, 10 μm and 1 mM GABA. The simulated currents were overlaid on measured current responses at these same GABA concentrations. The current traces shown were normalized averaged responses from six patches where multiple GABA concentrations were applied to the same patch. A small increase (<10 %) in the peak amplitude of simulated current at lower GABA concentrations (3 μm for the α1β3δ model; 1 and 10 μm for the α1β3γ2L model) was needed to reproduce the amplitude of the measured currents. This was probably due to rundown during recordings. Insets show the same currents on an expanded time scale for comparison of activation rates at low GABA concentrations. Time calibrations for normal and expanded current traces are 1000 and 150 ms, respectively.

Model simulations

One important issue was whether the brief GABA applications used in this study could accurately mimic synaptic conditions. While the time course of GABA in the synaptic cleft has not been measured, predictions were made based on models of the time course of the glutamate at some excitatory central synapses (Clements, 1996). In a simple model, this transmitter time course has been predicted to rise to a peak concentration around 1 mM within 100 μs and decay with a monoexponential time course over several milliseconds. We generated simulated currents elicited by GABA with this predicted synaptic time course and compared the deactivation time course for α1β3δ and α1β3γ2L currents (Fig. 10). This comparison demonstrated only small differences between the deactivation with the synaptic time course and that with a 2 ms square pulse, although the difference was greater for the α1β3δ currents. Nonetheless, the fitted deactivation rates and proportions were maintained, suggesting that the square pulse application protocol provided a good model for predicting the synaptic time course of recombinant GABAR currents.

Figure 10. Simulated synaptic currents.

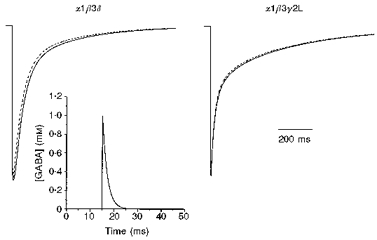
A simulated exponentially rising and decaying GABA time course (inset) was used to elicit simulated currents in the α1β3δ and α1β3γ2L kinetic models. The GABA time course was based on the predicted time course of GABA in the synaptic cleft with a peak concentration of 1 mM reached within 100 μs and a monoexponential decay with a time constant of 2 ms. These currents (dotted lines) were compared with currents elicited by a 2 ms square pulse 1 mM GABA application (continuous lines), illustrating the nearly identical current time courses with these modelled and simulated currents.

Another important issue was the role that desensitization played in shaping the deactivation of GABAR currents. For the α1β3γ2L model, we compared the time course of deactivation with and without both fast and slow desensitization and also with varying rates of desensitization (Fig. 11). Even without desensitization, the decay of current following a brief pulse of GABA was biexponential (Fig. 11B). Fast desensitization (D_f) acted to blunt the peak current achieved and had an important role in prolonging the current decay, similar to the model presented by Jones & Westbrook (1995) for GABARs from cultured hippocampal neurons (Fig. 11C). Slow desensitization (D_i and D_s) acted as a current sink over this time course, blunting the degree of the slow component of decay (Fig. 11D). Varying the rate of entry into or exit from D_f also dramatically altered the rate of deactivation (Fig. 11E and F).

Figure 11. Simulations addressing the role of desensitization.

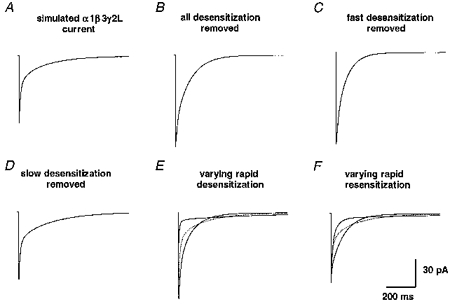
For the α1β3γ2L isoform, the role of fast and slow desensitization in shaping the current time course was assessed. A, using the optimized α1β3γ2L kinetic model, a simulated current was generated by a 2 ms application of 1 mM GABA. B, a non-desensitizing current exhibited a larger peak amplitude and deactivated with a biexponential time course. C, the removal of fast desensitization (D_f) increased the peak current amplitude and shortened the slow phase of deactivation. D, the removal of slow phases of desensitization (D_i and D_s) increased the magnitude and duration of the slow phase of deactivation. E and F, varying the rate of entry into and exit from D_f by 5-fold altered the shape of the deactivation time course. The original current time course is also shown (dotted line).

DISCUSSION

We used rapid GABA application to outside-out membrane patches containing α1β3, α1β3δ and α1β3γ2L GABAR isoforms to evaluate the contributions of the γ2L and δ subunits to the rapid activation, deactivation and desensitization of recombinant GABARs. The α1β3 currents activated relatively slowly, but exhibited rapid and nearly complete desensitization. Addition of the δ subunit substantially decreased the rate and extent of desensitization. In contrast, addition of the γ2L subtype increased activation rate and changed the pattern of desensitization. For the α1β3δ and α1β3γ2L isoforms, steady-state single-channel and rapid kinetic data were used to develop more comprehensive models of GABAR kinetic behaviour that began to reconcile microscopic and macroscopic kinetics.

Effect of receptor composition on deactivation

The net rate of deactivation was isoform dependent, with both α1β3 and α1β3δ currents deactivating more rapidly than α1β3γ2L currents. This result was primarily due to a longer, more pronounced slow deactivation component to α1β3γ2L currents. The deactivation kinetics of α1β3δ currents were very similar to those of recombinant α6β3γ2L currents that did not show any rapid desensitization in HEK 293 cells (Tia et al. 1996). This corroborated the finding that a homogeneous population of non-desensitizing receptors still deactivated with a biphasic time course. Moreover, the more rapid deactivation of α1β3 relative to α1β3γ2L currents was similar to that reported for recombinant α1β2 vs.α1β2γ2L receptors expressed in HEK 293 cells (Tia et al. 1996). Our findings demonstrated that the γ2L and δ subunit subtypes conferred unique biophysical properties on GABARs which were evident over a synaptically relevant time course.

Effect of receptor composition on activation rate

The more rapid activation of the α1β3γ2L currents initially seemed paradoxical as this isoform had a higher whole-cell GABA EC₅₀ than the α1β3δ and α1β3 isoforms. However, at the microscopic kinetic level, models of the α1β3δ and α1β3γ2L currents readily explained this activation rate difference on the basis of GABA binding and gating rates. The predominant determinant of activation rate differences was a slower opening rate for α1β3δ receptors since the modelled binding (k_on) rates were nearly identical.

As neurons integrate many inputs over time, the rapidity with which maximum inhibitory drive is achieved following GABA release could potentially be an important receptor property (Maconochie et al. 1994). If the GABA time course at the synapse was prolonged, the more than 3-fold faster activation rate conferred by the introduction of the γ2L subtype could be important in determining the extent and type of inhibition achieved.

Effect of receptor composition on desensitization

The rate and extent of rapid desensitization showed isoform dependency. Our finding of minimal desensitization of α1β3δ currents was similar to that described for recombinant α6β3γ2L GABAR currents in HEK 293 cells (Tia et al. 1996). While we have been unable to duplicate these findings with α6β3γ2L receptors in our cell system (K. F. Haas & R. L. Macdonald, unpublished observations), the implications of a non-desensitizing receptor remain the same. Desensitization could play a critical role in the repetitive activation of postsynaptic GABARs, where repetitive high frequency inhibitory responses would be attenuated for desensitizing receptor combinations, but not for non-desensitizing receptors.

Recent evidence suggested, however, that δ subunit-containing receptors may be primarily extrasynaptic on the soma of cerebellar granule neurons (Nusser et al. 1998). While the δ subunit-containing isoform present in hippocampal dentate granule neurons remains unknown, it most probably is not an α1β3δ combination (Jones et al. 1997). It remains to be demonstrated whether all δ subunit-containing combinations exhibit similar rapid desensitization kinetics, but a non-desensitizing extrasynaptic receptor with high GABA affinity would be ideally suited for providing tonic inhibition.

The more rapid fast phase of desensitization in α1β3γ2L currents than in α1β3 currents was qualitatively similar to that seen when the same isoforms were studied in HEK 293 cells (Dominguez-Perrot et al. 1997). The more prominent slow phase of desensitization in α1β3γ2L currents, however, contributed to the trend towards a slower mean desensitization rate for α1β3γ2L currents and may explain their slower desensitization rate in other whole-cell studies (Fisher & Macdonald, 1997).

Many studies have demonstrated that desensitization plays a critical role in shaping the deactivation time course of native GABAR responses in outside-out patch currents and neuronal IPSCs (Jones & Westbrook, 1995; Galarreta & Hestrin, 1997; Mellor & Randall, 1997). Moreover, a greater degree of fast desensitization has been linked to a prolonged slow phase of deactivation in cultured hippocampal neurons (Jones & Westbrook, 1995). This finding is supported by our results showing slower deactivation of the more rapidly desensitizing α1β3γ2L currents relative to the less desensitizing α1β3δ currents. However, this did not explain the more rapidly deactivating, yet highly desensitizing α1β3 currents. α1β3 currents may recover more rapidly from desensitization, leading to a more rapid deactivation rate, but this would need to be confirmed by paired-pulse experiments to examine recovery from desensitization.

γ2L and δ subunit structural determinants of rapid kinetic properties

The more rapid activation rate conferred by the γ2L subtype could have been due to more rapid binding of GABA to the receptor, more rapid coupling of binding to gating, and/or to a more rapid gating rate. The GABA binding pocket has been suggested to be on the β subunit, but EC₅₀ differences between isoforms have demonstrated that binding, coupling, and/or gating are influenced by other subunit families. Our models predicted similar binding rates (k_on) for α1β3δ and α1β3γ2L GABARs, and the activation rates were relatively insensitive to the unbinding (k_off) rates. The opening rate to the predominant open state for the α1β3γ2L isoform (1800 s⁻¹), however, was much faster than that for the α1β3δ isoform (80 s⁻¹). Thus, the models we developed for the α1β3δ and α1β3γ2L isoforms predicted that gating played the definitive role in the activation rate differences.

The structural determinants of activation and desensitization gating seem likely to be found in the subunit region spanning the first and second transmembrane domains (TM1 and TM2), which includes a short cytoplasmic loop linking TM1 and TM2. Previous studies have identified residues at M2 positions 5′, 9′ and 12′ that influence macroscopic desensitization rates of recombinant α1β1 GABAR currents (Tierney et al. 1996; Birnir et al. 1997a,b), but amino acids at these positions are conserved between δ and γ2L subtypes. Sequence alignments of δ and γ2L subtypes revealed differences in multiple amino acids toward the extracellular end of the M1 domain and differences in one neutral and two charged residues in the TM1-TM2 linker (Tyndale et al. 1995). The M2 domains were relatively similar except for substitution of a threonine for a valine at the 1′ position and a region of variability towards the extracellular end of the M2 domain. While speculation about the role of these differences would be premature, the domains of the δ and γ subunits that confer the binding and gating differences should be further tested with δ/γ subunit chimeras and site-specific mutagenesis.

Reconciling whole-cell and outside-out patch macroscopic data

For meaningful interpretation of both whole-cell and macroscopic outside-out patch data, the correlation of the two must be understood. For both α1β3δ and α1β3γ2L currents, the slow phases of desensitization revealed by 4000 ms GABA applications were similar in duration to the most prominent phase of desensitization in whole-cell studies, lending credence to the comparison between macropatch and whole-cell macroscopic kinetics for these recombinant GABARs. The rapid desensitization of α1β3 and α1β3γ2L currents predicted that desensitization attenuated up to 60 % of the true peak current during the 50–100 ms needed for GABA to reach its peak concentration in whole-cell studies of the same isoforms (Fisher & Macdonald, 1997). Even more rapid whole-cell applications (Gingrich et al. 1995; Dominguez-Perrot et al. 1996) probably were not fast enough to resolve the most rapid phase of desensitization found here in α1β3γ2L currents. Rapid application studies, however, predicted that this rapid phase of desensitization was probably the most important factor in shaping the synaptic time course of synaptic GABAR currents (Jones & Westbrook, 1995; Tia et al. 1996; Mellor & Randall, 1998; current study). Thus, the outside-out patch desensitization kinetics correlated with whole-cell desensitization kinetics, but, with the more rapid application, synaptically relevant faster phases of desensitization were resolved.

Reconciling macroscopic and single-channel data

Since any macroscopic current was simply the result of the underlying activity of many single channels, a valid GABAR kinetic model should predict macroscopic and single-channel current properties. Our models for the α1β3δ and α1β3γ2L isoforms predicted the concentration dependence of activation and desensitization, and they predicted the differences in the macroscopic rapid kinetic properties of these two isoforms. Furthermore, they were constrained by steady-state single-channel data that identified unique open, closed and burst properties for both isoforms (Fisher & Macdonald, 1997; current study). The simulated results predicted the low open probability for α1β3γ2L currents and even lower open probability for α1β3δ currents. This suggested that smaller macroscopic peak current amplitudes were primarily due to a lower channel open probability and slower activation gating, rather than to a difference in expression. The models also accounted for the relatively larger number of concentration-independent brief closings for the α1β3γ2L channels that constituted the intraburst closings, contributing to a longer mean burst duration for the α1β3γ2L channels than for the α1β3δ channels. Finally, the models accounted for the long duration closings that probably represented entry into desensitized states for both isoforms.

One difficulty encountered in the modelling was accounting for a relatively high proportion of brief openings. The briefest openings for both GABAR and nicotinic ACh receptors have been modelled as arising from the monoliganded state of the receptor (Colquhoun & Sakmann, 1985; Macdonald et al. 1989). Yet, as we increased the GABA concentration in our models, the k_on increased proportionally, and the models predicted many fewer of these brief openings than actually occurred. Single-channel recordings from the α1β3δ isoform exhibited predominantly brief openings. This was the basis for proposing that the brief open state of the α1β3δ isoform was doubly liganded. While previous single-channel data from this isoform suggested some concentration dependence for this open state (Fisher & Macdonald, 1997), modelling showed the prediction that the brief duration openings were monoliganded to be highly unlikely. For the α1β3γ2L isoform, there was a much clearer concentration dependence of the brief openings (Fisher & Macdonald, 1997). They were less prominent (23 %) at 1 mM GABA than the α1β3δ brief openings, but still much more frequent than the < 1 % predicted by the model. While alternate gating schemes to explain this discrepancy may be possible, it may also be due to open channel block, leading to a misclassification of O₂ and O₃ openings as O₁ openings at this high GABA concentration. To investigate this further would require a detailed single-channel kinetic analysis to determine the blocking rate of GABA as an open channel blocker. Nevertheless, at high GABA concentrations, these brief openings accounted for only 0.35 % of the total current, so they had little influence on the macroscopic current kinetics.

Comparison with other kinetic models

Other GABAR kinetic models have been suggested. Using macropatch recordings from cultured hippocampal neurons, Jones & Westbrook (1995) proposed a model that has proved very useful in predicting the contribution of fast desensitization to the GABAR current time course. Their model utilized an opening rate and fast desensitization rate that were similar in magnitude to those we associated with the O₂ open state in our model for the α1β3γ2L isoform. Their model also sought to reconcile macroscopic and single-channel GABAR behaviour. This effort, however, was made using relatively few openings from non-steady-state single-channel data collected at 10 μm GABA. Single-channel data were used to predict the closing rates (α values) of the channel, but the model predicted only two open states, most probably due to the small number of openings examined. This model incorporated two desensitized states, with the receptor entering D_s from its monoliganded form. With this configuration, high GABA concentrations would effectively bypass the transitions into the brief open state and D_s. The consequence of this would be a receptor that only opened to a single state and exhibited monophasic desensitization at high GABA concentrations. Our data did not support this kinetic scheme, since, during 4000 ms applications, currents elicited by 1 mM GABA still showed biphasic desensitization and single-channel recordings revealed multiple open states. Furthermore, at 1 mM GABA, their model predicted only two resolvable closed states of mean duration 0.29 s (73.5 %) and 67.3 s (26.5 %), which also did not accurately predict the multiple closed states we identified in steady-state single-channel data.

The α1β3γ2L kinetic scheme we proposed was very similar to that proposed to explain macroscopic kinetic differences in activation, desensitization and deactivation of recombinant α1β2γ2L and α3β2γ2L GABAR currents (Gingrich et al. 1995). The similarity of these models arose from their origin from the single-channel kinetic model derived by Twyman et al. (1990) from mouse spinal cord neurons. Gingrich et al. included two connected desensitized states in their α1β2γ2S model with entry rates of 30 and 0.4 s⁻¹ for the fast and slow desensitized states, respectively. We found the best model optimization occurred with a similar placement of D_i and D_s with our entry rates into these states of 8.0 and 0.75 s⁻¹ on the same order of magnitude as in their study. The fast desensitization rate we described was probably not resolvable in their whole-cell study with an application solution exchange time near 30 ms. This most rapid desensitized state was extremely important as it was predicted to have the greatest impact in shaping the time course of IPSCs.

Other studies have suggested that the second GABA binding step is of lower (Maconochie et al. 1994) or higher affinity (Lavoie & Twyman, 1996) than the initial binding step. We experimented with these model parameters and found that the essential predictions of the model could be achieved while incorporating unequal GABA binding affinities. Since there was no strong evidence concerning the magnitude of the affinity differences, however, we used the simpler assumption of equal GABA binding affinities for both steps.

While our α1β3δ and α1β3γ2L kinetic models cannot predict all of the complex kinetic properties of GABARs, their synthesis of macroscopic and single-channel kinetic data provided unique insights into GABAR function. In particular, the role of desensitization in shaping macroscopic currents was combined with an understanding of desensitization at the single-channel level. In steady-state single-channel records at high GABA concentrations, the long closed durations provided by entry into D_i and D_s accounted for the pattern of openings in desensitizing bursts. The development of comprehensive models is a necessary step in synthesizing information acquired about GABARs in single-channel and whole-cell studies and in predicting the role of subunit composition in shaping the time course of synaptic GABARs. In this instance, our models lead to a better general understanding of how activation and desensitization gating differences conferred by δ and γ2L GABAR subtypes would contribute to shaping the time course of GABAR currents on a rapid, more physiologically relevant time scale. More generally, these models should prove useful in reconciling the actions of allosteric modulators on the single-channel and macroscopic kinetic properties of GABARs, allowing for more accurate predictions about their physiological mechanism of action.

Importance of activation and desensitization kinetic differences for synaptic function

The rapid kinetic properties of the α1β3γ2L currents suggested that rapid activation and prolonged deactivation may be critical in the timing of neuronal inhibition. In some cases, inhibitory postsynaptic currents (IPSCs) have been shown to have more rapid decay times than membrane patch currents. One possibility may be subunit composition, but, as many of the neuronal receptors are predicted to be αβγ combinations, this is unlikely to provide the entire explanation. It is possible that the receptors in a patch are regulated differently from those at the synapse or that there is a difference between synaptic and extrasynaptic receptor properties. Alternatively, if the subunit composition is similar, modulators such as phosphorylation (Jones & Westbrook, 1997) or cytoskeletal coupling may be responsible for modulating the binding or gating kinetics of GABARs to produce relatively faster or slower decaying IPSCs. For instance, our model simulations demonstrated that a 5-fold increase in fast desensitization, resensitization, or the GABA unbinding rate would all dramatically accelerate the current decay.

Rapid application techniques permitted predictions about the potential synaptic role of the γ2L and δ subunits. When the γ2L subtype is present, rapid GABAR activation would produce a larger peak current with a prolonged decay produced by desensitized states. Thus, the γ2L subtype potentially plays an important role in both the magnitude and timing of the inhibition achieved. Isoforms that incorporate the δ subunit would probably produce smaller peak currents and decay more rapidly following brief application. Yet, they would desensitize slowly under the conditions of prolonged or repetitive application that may be more applicable to extrasynaptic receptors. Moreover, the combination of rapid kinetic and steady-state single-channel properties has led to the development of more comprehensive models of GABAR behaviour, which will lead to more accurate predictions about structural and allosteric determinants of GABAR function.