Divalent cation permeability and blockade of Ca²⁺-permeant non-selective cation channels in rat adrenal zona glomerulosa cells

Abstract

1. The effects of the divalent cations Ca²⁺, Mg²⁺ and Ni²⁺ on unitary Na⁺ currents through receptor-regulated non-selective cation channels were studied in inside-out and cell-attached patches from rat adrenal zona glomerulosa cells.

2. External Ca²⁺ caused a concentration-dependent and voltage-independent inhibition of inward Na⁺ current, exhibiting an IC₅₀ of 1.4 mm. The channel was also Ca²⁺ permeant and external Ca²⁺ shifted the reversal potential as expected for a channel exhibiting a constant Ca²⁺:Na⁺ permeability ratio near to 4.

3. External and internal 2 mm Mg²⁺ caused voltage-dependent inhibition of inward and outward Na⁺ current, respectively. Modelling Mg²⁺ as an impermeant fast open channel blocker indicated that external Mg²⁺ blocked the pore at a single site exhibiting a zero voltage K_d of 5.1 mm for Mg²⁺ and located 19% of the distance through the transmembrane electric field from the external surface. Internal Mg²⁺ blocked the pore at a second site exhibiting a K_d of 1.7 mm for Mg²⁺ and located 36% of the distance through the transmembrane electric field from the cytosolic surface.

4. External Ni²⁺ caused a voltage- and concentration-dependent slow blockade of inward Na⁺ current. Modelling Ni²⁺ as an impermeant slow open channel blocker indicated that Ni²⁺ blocked the pore at a single site exhibiting a K_d of 1.09 mm for Ni²⁺ and located 13.7% of the distance through the transmembrane electric field from the external surface.

5. External 2 mm Mg²⁺ increased the K_d for external Ni²⁺ binding to 1.27 mm, consistent with competition for a single binding site. Changing ionic strength did not substantially affect Ni²⁺ blockade indicating the absence of surface potential under physiological ionic conditions.

6. It is concluded that at least two divalent cation binding sites, separated by a high free energy barrier (the selectivity filter), are located in the pore and contribute to Ca²⁺ selectivity and permeability of the channel.

Non-selective cation channels are involved in a multiplicity of cellular functions including control of membrane excitability, synaptic transmission, sensory transduction and receptor-mediated signal transduction (Seimen, 1993). These channels share the common feature of non-selective permeation by monovalent cations but differ widely in divalent cation permeability, unitary conductance and regulation of gating behaviour. In a wide variety of cell types, receptor-activated Ca²⁺ influx may involve second messenger-mediated activation of non-selective cation channels (Tsien & Tsien, 1990; Fasolato et al. 1994). These channels may be Ca²⁺ permeant and mediate Ca²⁺ influx directly as well as indirectly by causing membrane depolarization and activation of voltage-dependent Ca²⁺ channels. In some cell types capacitative Ca²⁺ influx induced by depletion of intracellular Ca²⁺ stores (Putney, 1986) may involve activation of non-selective cation channels (for review, see Parekh & Penner, 1997).

We previously described a Ca²⁺-permeant non-selective cation channel activated by angiotensin II stimulation in rat adrenal glomerulosa cells (Lotshaw & Li, 1996). Stimulation of Ca²⁺ influx is essential for angiotensin II or elevated extracellular K⁺ stimulation of aldosterone secretion in these cells (Ganguly & Davis, 1994). Angiotensin II was observed to increase single channel open probability and this effect may contribute to stimulation of aldosterone secretion by directly mediating Ca²⁺ influx as well as by mediating membrane depolarization and activation of voltage-dependent Ca²⁺ channels. Single channel conductance, permeability and gating behaviour of this channel were very similar to that of a histamine-activated Ca²⁺-permeant non-selective cation channel in pulmonary arterial endothelial cells (Yamamoto et al. 1992) and endocardial endothelial cells (Manabe et al. 1995). Channel gating did not require cytosolic Ca²⁺ in either cell type and consisted of relatively voltage-independent long duration open and closed states. Furthermore, single channel current-voltage (I-V) relationships were non-linear in both glomerulosa and endothelial cell channels, apparently due to voltage-dependent Mg²⁺ block.

The divalent cation selectivity and permeability of second messenger-operated non-selective cation channels will be important determinants of their contribution to cellular function. Mechanisms that determine divalent cation permeability are largely unknown for this channel class; however, divalent cation permeation has been extensively studied in neurotransmitter- and cyclic nucleotide-gated (CNG) non-selective cation channels (Changeux et al. 1992; Hollman & Heinemann, 1994; Zagotta & Siegelbaum, 1996) as well as in the highly Ca²⁺-selective voltage-dependent Ca²⁺ channels (VDCC) (Tsien et al. 1987). Biophysical studies of ion permeation/blockade and site-directed mutagenesis of channel proteins have been utilized to predict the locations and features of pore structures that contribute to divalent cation selectivity and permeation in these channels. These channels are reported to possess multiple divalent cation binding sites within the channel pore that facilitate divalent cation permeation and/or blockade in the presence of much higher concentrations of monovalent cations. All of these channels conduct monovalent cations in the absence of divalent cations, and addition of Ca²⁺ reduces monovalent cation conductance due to its higher affinity for the binding sites and slower permeation through the channel. In general Mg²⁺ is much less permeable than Ca²⁺; this difference has been attributed to its slow dehydration which is necessary for permeation (Hille, 1992). These channels differ widely in their Ca²⁺ permeability and in their susceptibility to Mg²⁺ blockade, even within a single channel class (Frings et al. 1995). The high Ca²⁺ selectivity of VDCC appears to require the presence of only a single high affinity Ca²⁺ binding site within the pore (Ellinor et al. 1995); neighbouring lower affinity sites together with multi-ion occupancy of the channel are hypothesized to facilitate Ca²⁺ permeation (Carbone et al. 1997; Dang & McCleskey, 1998).

In the present study divalent cation permeation and blockade of the angiotensin II-regulated non-selective cation channel were examined using permeant Ca²⁺ and impermeant Mg²⁺ and Ni²⁺ cations. The location of divalent cation binding sites was determined from voltage-dependent blockade by Mg²⁺ and Ni²⁺. The results of these experiments demonstrated the presence of two divalent cation binding sites within the pore, one near the external mouth of the pore and one deeper within the pore separated from the other by an apparently insurmountable free energy barrier for Mg²⁺ and Ni²⁺ permeation. Differences in the characteristics of channel blockade by Ca²⁺, Mg²⁺ and Ni²⁺ suggested that divalent cation association with the external-most site involves partial dehydration of the blocker. These divalent cation binding sites impart ion conductance properties similar to those of the NMDA receptor and CNG channels. Voltage-dependent inhibition of inward conductance is attributable to fast open channel blockade by external Mg²⁺ binding to the external-most site and inward rectification is attributable to fast open channel blockade at the innermost site by internal Mg²⁺ and/or other cytosolic cations. These divalent cation binding sites are also postulated to facilitate Ca²⁺ selectivity and permeation of the channel.

METHODS

Cell culture

Primary cultures of rat adrenal glomerulosa cells were prepared as previously described (Lotshaw & Li, 1986) using female Sprague- Dawley rats weighing 150-200 g (Harlan, Indianapolis, IN, USA). All procedures involving the use and treatment of animals were in accordance with NIH guidelines and approved by the institutional IACUC committee. Animals were anaesthetized by CO₂ inhalation and subsequently killed by decapitation prior to surgical removal of adrenal glands. Isolated glomerulosa cells were plated on fibronectin-treated glass coverslip chips and maintained in culture medium at 37°C in a humidified atmosphere of 5 % CO₂-95 % air. Culture medium consisted of a mixture of Ham's F-12 and Dulbecco's modified Eagle's medium (1:1 by volume) supplemented to contain 2 % fetal calf serum, 8 % horse serum, 0.1 mM ascorbic acid, 1 μg ml⁻¹ insulin, 50 u ml⁻¹ penicillin G and 50 μg ml⁻¹ streptomycin, and 1 μm tocopherol. Sera were obtained from Gibco-BRL, collagenase from Worthington Biochemical Corp., and all other reagents from Sigma. Experiments were performed using cells maintained in primary culture from 12 to 48 h.

Patch clamp recording

Single glomerulosa cells were identified by visual appearance under phase-contrast microscopy as previously described (Lotshaw & Li, 1996). Single channel patch clamp recordings were performed in the cell-attached and inside-out patch configurations (Hamill et al. 1981). Glass coverslip chips containing adherent cells were transferred from culture dishes to a recording chamber (0.5 ml volume) and continuously superfused at 1 ml min⁻¹ with a modified Hanks’ saline equilibrated with 100 % O₂ (solution 1, Table 1). In cell-attached patch clamp recordings, a high K⁺ saline was used to zero the resting membrane potential (solution 3, Table 1). All experiments were performed at room temperature (23-26°C). In some inside-out patch experiments, a perfusion pipette was placed in the recording chamber to facilitate rapid changes in the saline on the cytoplasmic face of the patch membrane.

Table 1.

Composition of salines, pipette and bath solutions for cell-attached and inside-out patches

Salines
Solution	NaCl	KCl	CaCl2	MgCl2	NaHCO3	Hepes	Glucose
1	140	4	1.25	1.2	4.2	10	5.5
2	140	4	—	2.45	4.2	10	5.5
3	—	140	—	2.45	4.2	10	5.5
Pipette and bath solutions
Solution	NaCl	CaCl2	MgCl2	Hepes	EGTA	Glucose	NMDG
4	145	—	—	10	5	—	—
5	150	0.1	—	10	—	—	—
6	150	0.2	—	10	—	—	—
7	150	1.0	—	10	—	—	—
8	146	2.5	—	10	—	—	—
9	135.5	13.75	—	10	—	—	—
10	116	27.5	—	10	—	—	—
11	77	55	—	10	—	—	—
12	—	110	—	10	—	—	—
13	150	—	—	10	—	—	—
14	145	0.1	2.0	10	—	—	—
15	145	—	2.0	10	—	—	—
16	225	0.1	—	10	—	—	—
17	225	—	2.0	10	—	—	—
18	—	0.1	—	10	—	268	—
19	—	0.1	—	10	—	—	150

Solution compositions listed are millimolar. All solutions adjusted to pH 7.4 using NaOH except solutions 3 and 19 which were adjusted using KOH and HCl, respectively.

Patch pipettes were constructed from borosilicate glass capillary tubes (TW 150-4 glass, World Precision Instruments). Pipettes were pulled to give resistances of 5-6 MΩ when filled with 150 mM NaCl pipette saline and were coated with Sylgard (Dow-Corning) to within 100 μm of the pipette tip.

Membrane currents were measured with an Axopatch 200A amplifier (Axon Instruments). Current was low-pass filtered at 2 or 5 kHz (-3 dB) using a four-pole Bessel filter and recorded using a digital audio tape recorder (Sony, Tokyo, Japan) for later analysis. For computer analysis of recorded data, records were sampled at 10 kHz during playback using a TL-1-125 analog-to-digital converter (Axon Instruments) and analysed using pCLAMP software (Axon Instruments).

The compositions of pipette and bath solutions for cell-attached and inside-out patch clamp experiments are listed in Table 1. In most experiments 0.1 mM Ca²⁺ was included in the external (pipette) solution to block monovalent cation currents through voltage-dependent Ca²⁺ channels (Lux et al. 1990). Membrane voltages were corrected for liquid junction potentials caused by the composition of the pipette solution as described (Neher, 1992). Pipette solutions exhibiting liquid junction potentials greater than 2 mV were (normal bath saline with respect to pipette saline): -6.5 mV for 110 mM CaCl₂ (solution 12), -3.6 mV for 77 mM NaCl-55 mM CaCl₂ (solution 11), -1.9 mV for 116 mM NaCl-27.5 mM CaCl₂ (solution 10), 2.8 mV for 75 mM NaCl-134 mM glucose, and 6.0 mV for 37.5 mM NaCl-201 mM glucose. For calculations involving ionic activities, the ionic strengths of the solutions were calculated and appropriate activity coefficients used to convert molarities to activities. Activity coefficients for NaCl were taken from Robinson & Stokes (1960) and CaCl₂ activity coefficients were interpolated from Table 1 of Butler (1968). Ca²⁺ activity coefficients were estimated from that for CaCl₂ using the Guggenheim convention: γCa = (γ± CaCl₂)².

Data analysis

The effects of permeant and impermeant divalent ions were measured on unitary Na⁺ currents conducted through the Ca²⁺-permeant non-selective cation channels. Single channel events were detected for analysis using the 50 % of threshold criterion. Ca²⁺ permeation was characterized by measuring the effects of increasing external Ca²⁺ concentration on single channel conductance and reversal potential (V_rev). The predicted effect of increasing extracellular Ca²⁺ concentration on the reversal potential of unitary currents was calculated using the Goldman-Hodgkin- Katz (GHK) equation modified for mixtures of monovalent and divalent ions (extracellular Na⁺ and Ca²⁺:cytosolic Na⁺) (Iino et al. 1997):

(1)

where a^o and aⁱ represent the extracellular and intracellular activities of the indicated ions, P_Ca and P_Na represent the ionic permeabilities of Ca²⁺ and Na⁺, respectively, and R, T and F have their usual thermodynamic meanings. The cytosolic Ca²⁺ concentration was assumed to be zero for this calculation although the experimental cytosolic solution was only nominally Ca²⁺ free (solution 15, Table 1).

Voltage-dependent inhibition of unitary Na⁺ currents by Mg²⁺ and Ni²⁺ was modelled as a simple open channel block mechanism (Scheme 1). Transitions between the closed (C) and open (O) channel states are described by the opening and closing rate constants β and α, respectively. Transitions between the open and blocked states (B) are described by the association and dissociation rate constants, k₁ and k_-1, respectively. Unitary current amplitude is assumed to be zero in the blocked state.

Scheme 1.

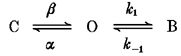
Open channel blockade by Mg²⁺ was described in terms of a fast block mechanism in which blocking events were too fast to resolve by the recording system and resulted in a decrease in average open channel current amplitude (Hille, 1992). The location of the blocker binding site within the transmembrane electric field and its affinity for Mg²⁺ were calculated by fitting the voltage-dependent inhibition of current amplitude to a linearized Langmuir isotherm which incorporated a Boltzmann relationship to account for the effect of voltage on blocker concentration (Woodhull, 1973; Coronado & Miller, 1979; Moczydlowski, 1992):

(2)

where i_o is the unitary current amplitude in the absence of blocking ion, i is the unitary current amplitude in the presence of blocker, [B] is the blocker concentration, K_d(0) is the apparent dissociation constant for blocker binding at 0 mV membrane potential, z is the valence of the blocking ion, δ is the fractional distance across the transmembrane electric field to the blocking site, V is the membrane potential, and F, R and T have their usual thermodynamic meanings. The fractional electrical distance (δ) and K_d(0) were determined from the slope and Y-axis intercept of the linear regression fit to the data, respectively.

Open channel blockade by Ni²⁺ was analysed in terms of a slow block mechanism in which blocking events were sufficiently long to be resolved and measured (Hille, 1992). In order to distinguish blocking events from open channel current noise and transitions to subconductance substates, a 75 % threshold criterion was adopted for detection of transitions from the open to closed state. The 50 % threshold criterion was retained for detection of channel openings (Colquhoun & Sigworth, 1995). The mean blocked and open times were determined from exponential fits of open and closed dwell time distributions using the method of maximum likelihood. Mean blocked times approached the resolution of the recording system and therefore mean open times were biased by missed blocking events due to the limited bandwidth of the recording system. Mean open times, τ_o, were adjusted for missed blocking events using a one step correction procedure previously described (Kuo & Hess, 1993a). The dead time of the recording system was approximately 0.15 ms at a cut-off filter setting of 2 kHz.

Analysis of slow open channel blockade required that blocked states be distinguishable from closed states. Current amplitude is zero in both states requiring that states be distinguished by dwell time analysis. At high blocker concentrations, blocking events were much more frequent than closing events, and the distribution of shut (closed and blocked state) dwell time became dominated by the blocker dissociation rate constant (k_-1) (Neher & Steinbach, 1978; Lansman et al. 1986). Ni²⁺ was found to induce a blocked state of much shorter mean duration than the closed state observed in the absence of Ni²⁺ (Lotshaw & Li, 1996), thus blocked and closed states were readily separated on the basis of shut dwell time.

The voltage-dependent dissociation constant for Ni²⁺, K_d(V), was calculated as the voltage-dependent dissociation rate constant, k_-1(V), divided by the association rate constant, k₁(V), after correction for missed blocking events (Neher & Steinbach, 1978). The Ni²⁺ dissociation constant was used to calculate the fractional distance (δ) across the transmembrane electric field to the blocking site based on a Boltzmann distribution for the concentration of a charged blocker within the transmembrane electric field (Woodhull, 1973; Neher & Steinbach, 1978; Moczydlowski, 1992):

(3)

where K_d(0) is the dissociation constant for blocker binding at 0 mV membrane potential, and the remaining variables are as defined above.

The expected shift in K_d(0) for Ni²⁺ binding caused by the presence of a competitive inhibitor, Mg²⁺, was predicted by:

(4)

where K_app is the K_d(0) for Ni²⁺ in the presence of a competitive inhibitor, K_dNi is the K_d(0) for Ni²⁺ in the absence of the competitive inhibitor, [I] is the concentration of the competitive inhibitor, and K_i the dissociation constant of the competitive inhibitor.

RESULTS

Ca²⁺ permeation and blockade

The effects of extracellular Ca²⁺ on unitary Na⁺ currents through non-selective cation channels were studied using inside-out patches. Spontaneously active channels were identified on the basis of their characteristic long open and closed times, relatively voltage-independent gating, single channel conductance, large open channel current noise, and inward rectification in the presence of cytosolic Mg²⁺ (Lotshaw & Li, 1996). Omission of external (pipette) divalent cations, Mg²⁺ and Ca²⁺ (pipette solution 4 and bath solution 15, Table 1) substantially increased inward current amplitude relative to that previously reported with 2 mM Mg²⁺ and 0.1 mM Ca²⁺ in the pipette solution (Lotshaw & Li, 1996). The observed increase in current amplitude was primarily attributable to removal of voltage-dependent inhibition by Mg²⁺ (see Mg²⁺ block below). Other channel characteristics such as the large open channel current noise, V_rev and inward rectification were unchanged by omission of extracellular divalent cations.

Increasing external Ca²⁺ caused a concentration-dependent inhibition of inward conductance (Fig. 1). Inhibition appeared to be voltage independent as illustrated by the nearly linear I-V relationships obtained below -20 mV (Fig. 1B). In the absence of external Ca²⁺ and Mg²⁺ (solution 4), the I-V relationship for inward current exhibited a nearly linear slope conductance of 37.9 ± 4.5 pS (mean ±s.d., n= 3). Inhibition by external Ca²⁺ became apparent at concentrations above 0.2 mM and was nearly maximal at 13.75 mM Ca²⁺. Inward slope conductance was reduced to 10.5 ± 2.6 pS (n= 3, where n is the number of patches) at 13.75 mM Ca²⁺ compared with 7.5 ± 0.8 pS (n= 3) with 110 mM Ca²⁺. Plotting the concentration-dependent Ca²⁺ inhibition of slope conductance as a fraction of maximal conductance and fitting the data to a Langmuir isotherm between the maximum (1.0) and minimum (0.2) fractional conductances yielded an IC₅₀ of 1.4 mM Ca²⁺ (Fig. 1C).

Figure 1. Effects of extracellular Ca²⁺ on unitary Na⁺ currents.

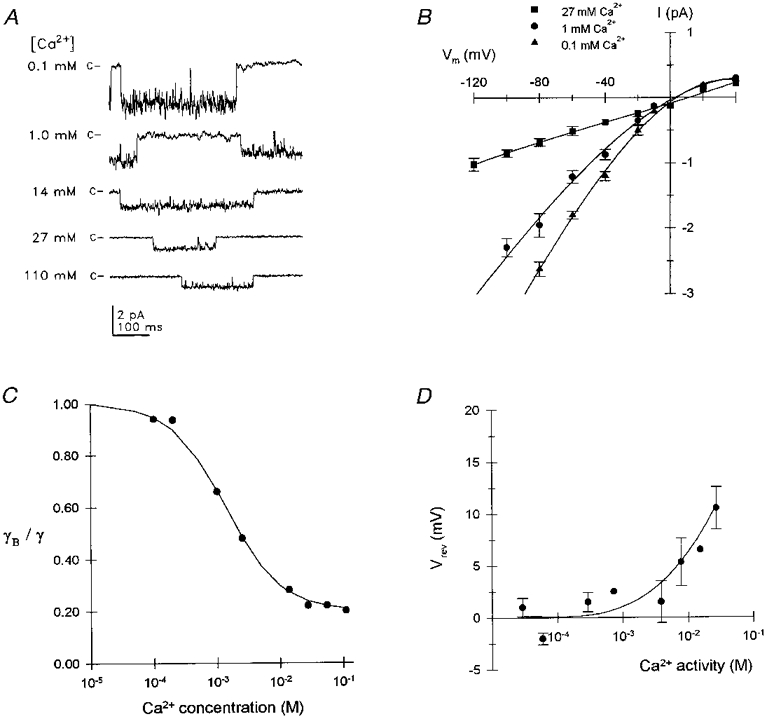
A, current traces illustrating representative single channel events measured at -80 mV for several Ca²⁺ concentrations (indicated at the left of each trace). The closed channel current level is indicated by c at the left of the traces; each trace was taken from a different patch. The external (pipette) solution composition for each Ca²⁺ concentration is described in Table 1; the bath (cytosolic face) saline was nominally Ca²⁺ free (solution 15). Current records were low-pass filtered at 500 Hz for display. B, I-V relationships are plotted from data obtained with 0.1 mM Ca²⁺ (▴, n= 5), 1.0 mM Ca²⁺ (•, n= 5) and 27 mM Ca²⁺ (▪, n= 3) pipette solutions. Symbols indicate the mean (±s.e.m.) unitary current amplitude; error bars are not shown for errors less than symbol size. Smooth curves represent polynomial regression fits to each data set. C, fractional inward slope conductance is plotted as a function of Ca²⁺ concentration: γ_B represents mean conductance at each Ca²⁺ concentration and γ the mean maximal conductance in the absence of external Ca²⁺. The smooth curve represents the best fit to a Langmuir isotherm, indicating an IC₅₀ of 1.4 mM for Ca²⁺ inhibition. D, V_rev of unitary currents is plotted as a function of external Ca²⁺ activity. Symbols represent the mean (±s.e.m.) of 3-5 determinations at each concentration; symbols lacking error bars represent the means of 2 determinations. The smooth curve represents the change in V_rev predicted from the modified GHK equation (eqn (1)) assuming a constant Ca²⁺:Na⁺ permeability ratio of 4.

Ca²⁺ inhibition of inward Na⁺ current may be attributed to multiple effects, such as blockade of the pore during Ca²⁺ permeation and/or surface charge screening. This channel was previously reported to be Ca²⁺ permeable based on V_rev measurements from inside-out patches under biionic conditions (Lotshaw & Li, 1996). The effect of increasing extracellular Ca²⁺ concentration (activity) on V_rev is shown in Fig. 1D. V_rev was determined from the voltage axis intercept of either a straight line drawn between the nearest inward and outward mean current amplitude or from polynomial regression fits of the I-V relationship from each patch examined. V_rev shifted in a positive direction as external Ca²⁺ concentration was increased. These data could be approximated by the GHK equation (eqn (1)) for a channel exhibiting a constant Ca²⁺:Na⁺ permeability ratio of 4, in agreement with our previous data (Lotshaw & Li, 1996). These results provide further documentation of the permeability of the channel to Ca²⁺ and indicate that Ca²⁺ inhibited Na⁺ conductance by binding to one or more sites in the pore during permeation. The IC₅₀ for Ca²⁺ inhibition is within the physiological range of Ca²⁺ concentrations, indicating that Ca²⁺ permeation is expected to occur under physiological ionic conditions. These data further suggested the absence of substantial negative surface charge at the external mouth of the pore. If a significant surface charge existed then low Ca²⁺ concentrations may have been expected to screen surface charge, reducing Na⁺ concentration at the mouth of the pore, and shifting V_rev as previously described for the nicotinic acetylcholine receptor (Lewis, 1979).

Mg²⁺ blockade

Cytosolic Mg²⁺ was previously shown to block outward unitary Na⁺ current, resulting in inward rectification of the I-V relationship (Lotshaw and Li, 1996). In that study it was further suggested that external Mg²⁺ was responsible for the observed voltage-dependent inhibition of inward Na⁺ currents as had been reported for histamine-activated Ca²⁺-permeant non-selective cation channels in endothelial cells (Yamamoto et al. 1992). This suggestion was confirmed in the present study. Omission of external Mg²⁺ linearized the I-V relationship for inward Na⁺ current, increasing slope conductance from 17.8 pS in the presence of 2 mM external Mg²⁺ (Lotshaw & Li, 1996) to 37.9 pS in its absence without affecting V_rev (Fig. 1B).

The effects of Mg²⁺ on unitary Na⁺ currents were further examined by comparing the I-V relationships obtained in the presence of external or internal 2 mM Mg²⁺ to that obtained in the absence of both external and internal Mg²⁺ (Fig. 2). In the absence of external and internal Mg²⁺, the I-V relationship for inward and outward Na⁺ current was nearly linear, exhibiting a mean slope conductance of 42.5 pS and a V_rev of 0 mV (Fig. 2B). Addition of 2 mM Mg²⁺ to the internal (bath) saline caused strong voltage-dependent inhibition of outward Na⁺ current with little effect on inward current. Addition of 2 mM Mg²⁺ to the external (pipette) solution, in the absence of cytosolic Mg²⁺, caused voltage-dependent inhibition of inward current that was much weaker than internal Mg²⁺ inhibition of outward current. External Mg²⁺ also inhibited outward Na⁺ current to some extent (Fig. 2A and B). V_rev was not significantly affected by either cytosolic or extracellular 2 mM Mg²⁺. The voltage dependence of Mg²⁺ inhibition and relief of inhibition by oppositely directed Na⁺ current suggested that Mg²⁺ inhibited open channel Na²⁺ current by reversibly blocking the pore at a site(s) within the transmembrane electric field.

Figure 2. Voltage-dependent inhibition of unitary Na⁺ currents by external and internal 2 mM Mg²⁺.

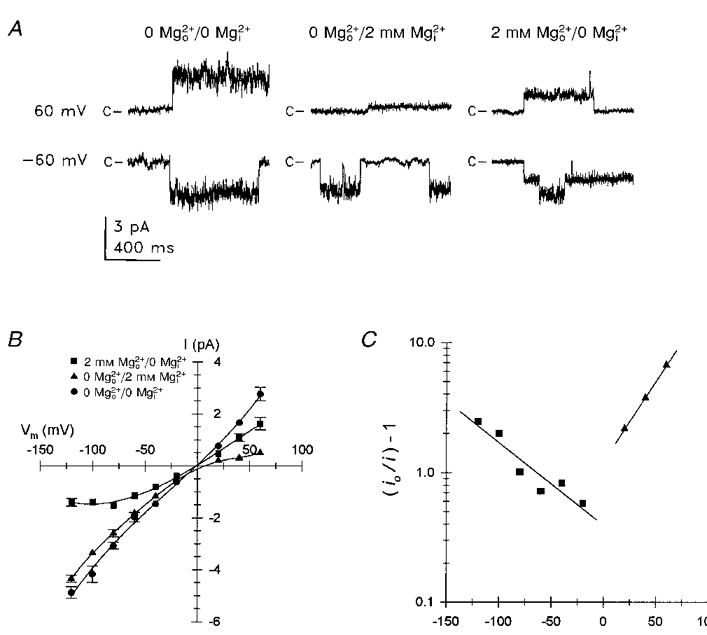
A, current traces illustrating representative single channel events obtained from inside-out patches at membrane potentials of 60 and -60 mV in the absence of both external and internal Mg²⁺ (left traces), with 2 mM internal Mg²⁺ (middle traces), and with 2 mM external Mg²⁺ (right traces). The patch recording for 2 mM external Mg²⁺ exhibited two open channel current levels. The closed channel current level is indicated by c at the left of each trace. Subscripts o and i designate external and internal Mg²⁺, respectively. Pipettes contained either solution 5 (0 Mg²⁺) or solution 14 (2 mM Mg²⁺) and the bath contained either solution 13 (0 Mg²⁺) or solution 15 (2 mM Mg²⁺) (Table 1). Current traces were low-pass filtered at 500 Hz for display. B, I-V relationship for single channel currents measured for each Mg²⁺ condition described in A. Symbols represent the mean (±s.e.m.) of unitary current amplitude from 3 or 4 separate patches in each configuration; error bars were omitted when error was less than symbol size. Lines represent polynomial least-squares regression fits to each data set. C, linearized logarithmic plot (eqn (2)) of voltage-dependent inhibition of unitary Na⁺ curent amplitude by extracellular and cytoplasmic 2 mM Mg²⁺. Symbols represent the reduction in current (i_o/i) - 1, where i_o represents the mean maximal current in the absence of Mg²⁺ and i represents the mean current recorded with 2 mM Mg²⁺_o/0 mM Mg²⁺_i (▪) or 0 mM Mg²⁺_o/2 mM Mg²⁺_i (▴); data from B. Curves represent the linear regression fit to the data.

Mg²⁺ inhibition of unitary Na⁺ current was modelled as a fast open channel block mechanism. Graphical analysis of a linearized logarithmic plot of the Mg²⁺ inhibition data (eqn (2)) was used to calculate the apparent affinity and location of Mg²⁺ binding sites (Fig. 2C). The slope and intercept from regression fits over the linear range of the data were used to calculate the fractional transmembrane electrical distance to the binding sites and the K_d(0) for Mg²⁺ binding. This analysis indicated that external Mg²⁺ blocked inward Na⁺ current by binding to a site exhibiting a K_d(0) of 5.1 mM for Mg²⁺ and located 19 % (δ= -0.19) of the distance through the transmembrane electrical field from the external surface. The slope of the curve for internal Mg²⁺ blockade was steeper than for external Mg²⁺ blockade and indicated that internal Mg²⁺ blocked the channel by binding to a site exhibiting a K_d(0) of 1.7 mM for Mg²⁺ and located 36 % (δ= 0.36) of the distance through the transmembrane electrical field from the internal surface. The data could not be approximated by assuming that extracellular and cytosolic Mg²⁺ acted by binding to the same site. The linearity of the inhibition curves with increasing membrane polarization indicated that Mg²⁺ was not measurably permeant. If Mg²⁺ was permeant, increasing membrane polarization would have been expected to facilitate permeation, reducing inhibition. This is consistent with the presence of distinct binding sites for external and internal Mg²⁺.

Ni²⁺ blockade

Further evidence supporting the hypothesis that external Ca²⁺ and Mg²⁺ inhibited unitary Na⁺ currents by blocking the open channel pore was provided by the observation that external Ni²⁺ caused discrete fluctuations in open channel Na⁺ currents. The effect of external Ni²⁺ on single channel currents is illustrated in cell-attached patch recordings (Fig. 3). Cell-attached patches were utilized for these experiments due to channel run-down in the inside-out configuration. However, no differences were observed between the effects of Ni²⁺ on cell-attached patches and the limited data obtained from inside-out patches. In the absence of Ni²⁺, single channel events exhibited long open and closed times which lasted up to several seconds but occasionally exhibited short open and closed times (Lotshaw & Li, 1996). Addition of Ni²⁺ induced rapid fluctuations between the open and closed channel current levels attributable to short-lived blockade of the open channel current. The frequency of blocking events increased with Ni²⁺ concentration and membrane hyperpolarization. At a Ni²⁺ concentration of 0.5 mM and membrane potential of -120 mV, open channel current amplitude was suppressed due to the high frequency of blocking events (Fig. 3). Ni²⁺ did not appear to affect channel gating; however, it was not possible quantitatively to assess Ni²⁺ effects on burst and interburst durations due to the high variability of these parameters and the small number of burst and interburst intervals actually recorded.

Figure 3. External Ni²⁺-induced fluctuations in unitary Na⁺ currents.

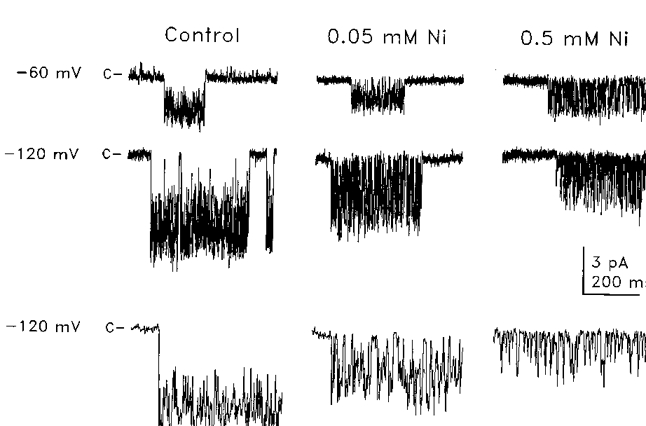
Current traces illustrating representative single channel events recorded from cell-attached patches at -60 mV (upper traces) and -120 mV (lower traces) in the absence of Ni²⁺ (control traces, left), in 0.05 mM Ni²⁺ (middle traces), and in 0.5 mM Ni²⁺ (right traces). The pipettes contained solution 5 (Table 1) with Ni²⁺ added hyperosmotically. Resting membrane potential was set to 0 mV with a high K⁺ saline (solution 3). Expanded time scale segments of current traces recorded at -120 mV are shown to illustrate Ni²⁺-induced blocking events. The closed and blocked channel current levels are indicated by c at the left of each trace. Current traces were low-pass filtered at 2 kHz.

Ni²⁺ blockade was modelled as a slow open channel block mechanism. Characterization of Ni²⁺ blockade required distinguishing the closed state from the blocked state, both of which are non-conducting states. In the absence of Ni²⁺ the channel was previously reported to exhibit multiple exponential components in the open and closed dwell time histograms during periods of active gating (Lotshaw & Li, 1996). Mean open times ranged from 33 to 491 ms and mean closed times ranged between 3.3 and 788 ms at the resting membrane potential (near -80 mV). Channel gating was weakly voltage dependent, which was manifested as a decrease in the long open state duration with membrane hyperpolarization. The short-lived closed state (mean closed time of 3.3 ms) could potentially bias measurement of the blocked state; however, channels did not typically exhibit this state. Furthermore, the frequency of Ni²⁺-induced blocking events greatly exceeded the frequency of normal channel closures and the mean duration of the closed/blocked state in the presence of Ni²⁺ was nearly 7-fold less than the short-lived closed state. Thus Ni²⁺ blocking events could be readily separated from closed states and quantitatively analysed from the intraburst open and closed state dwell time distributions.

Representative dwell time histograms for intraburst open and closed (blocked) states obtained from a single patch with 0.1 mM Ni²⁺ in the pipette solution are shown in Fig. 4. The dwell time distributions for both blocked and open states were best described by single exponential relaxations at all membrane potentials and Ni²⁺ concentrations examined. The voltage and concentration dependence of the mean blocked times (τ_b) are shown in Fig. 5. The relatively large variability in the time constants primarily reflects variability in the number of blocking events recorded from a given patch at each membrane potential. Each time constant measurement was based on at least 100, and as many as 900, blocking events. Mean blocked time was independent of Ni²⁺ concentration as required by the open channel blockade model and was not significantly voltage dependent at any Ni²⁺ concentration examined. In this regard the blocked state dwell times approached the temporal resolution of the recording when filtered at a cut-off frequency of 2 kHz. In favourable patches, the cut-off filter frequency was increased to 5 kHz; this did not alter the estimate of τ_b nor reveal a voltage dependence for τ_b. Mean blocked times could not usually be determined at membrane potentials below -60 mV due to interference from K⁺ channel currents. At high Ni²⁺ concentrations (0.5 mM) τ_b may have been artificially lengthened due to missed channel openings as mean open time (τ_o) progressively decreased with increasing Ni²⁺ concentration and hyperpolarization (Fig. 3).

Figure 4. Open and blocked state dwell time histograms for 0.1 mM Ni²⁺ blockade of unitary Na⁺ currents.

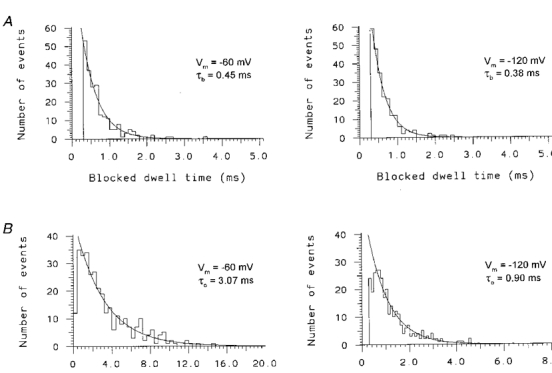
A, blocked state dwell time histograms measured at -60 mV (left graph) and -120 mV (right graph) from a single cell-attached patch with 0.1 mM Ni²⁺ in the pipette solution (solution 5, Table 1). B, open state dwell time histograms measured at -60 mV (left graph) and -120 mV (right graph) from the same patch as in A. The resting membrane potential was set to 0 mV with a high extracellular K⁺ saline (solution 3). The smooth curves in each graph represent the maximum likelihood fit of the data to a single exponential relaxation. The time constants of the fitted exponential relaxations for τ_b (A) and τ_o (B), and membrane potentials (V_m) are indicated in the inset of each histogram.

Figure 5. Effects of membrane potential and Ni²⁺ concentration on τ_b.

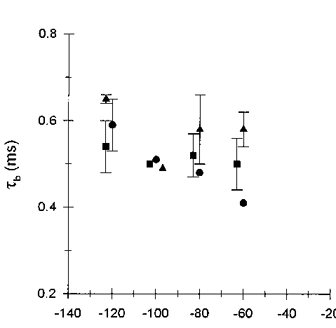
Mean blocked times measured in the presence of 0.05 mM (•), 0.2 mM (▪) and 0.5 mM (▴) Ni²⁺ at -60, -80, -100 and -120 mV; symbols are offset to illustrate clearly standard deviations of the data. Symbols represent the mean (±s.d.) of 3-4 separate patches at each voltage and Ni²⁺ concentration; symbols lacking error bars represent the mean value from two separate patches.

As shown in Fig. 4, the open state dwell time histograms were well described by single exponential functions. At all Ni²⁺ concentrations examined, τ_o determined from the exponential fit was severalfold less than the minimum τ_o measured in the absence of Ni²⁺ (33 ms; Lotshaw & Li, 1996). Thus the rate constant for channel closing, α, did not significantly affect the open state dwell time distributions obtained from analysis of intraburst open times in the presence of Ni²⁺. Patch-to-patch variation in τ_o, measured at each voltage and Ni²⁺ concentration, was similar to that shown for τ_b (data not shown). Again, the variability primarily reflected the number of events recorded from each patch at any given membrane potential.

In contrast to τ_b, τ_o was highly voltage and concentration dependent in the presence of Ni²⁺ (Fig. 6, see below). These data indicated that Ni²⁺ blocked the channel by binding to a single site located within the transmembrane electric field. Further experiments indicated that the Ni²⁺ binding site was located in the channel pore. As observed for Mg²⁺ blockade, if external Ni²⁺ blocked the channel by occluding the pore then blockade may be opposed by outwardly directed currents due to electrostatic repulsion between Ni²⁺ and permeating Na⁺. This effect was observed in inside-out patches bathed in Mg²⁺-free NaCl solutions on both sides of the patch (data not shown). High concentrations of external Ni²⁺ (2 mM) reduced inward open channel current to spike-like, small amplitude events as expected for high concentrations of a slow blocker, but had little effect on outward currents even at small positive membrane potentials (20-40 mV). Whereas the concentration of external Ni²⁺ at a site located within the transmembrane electric field is expected to decrease at positive potentials due to the effects of the electric field, this effect could not account for the observed decrease in channel block.

Figure 6. Determination of K_d(0) and location (δ) of the Ni²⁺ binding site in the absence and presence of external Mg²⁺.

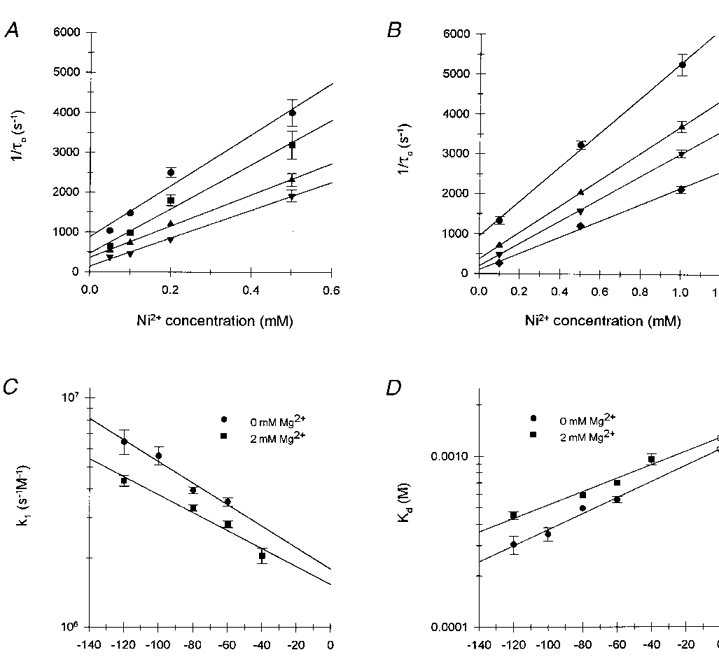
A, the reciprocal of τ_o for Ni²⁺ blockade in the absence of external Mg²⁺ (pipette solution 5) is plotted as a function of external Ni²⁺ concentration. Data are shown for membrane potentials of -120 mV (•), -100 mV (▪), -80 mV (▴) and -60 mV (▾). Values of τ_o represent single exponential maximum likelihood fits to pooled data from 2-4 patches at each voltage and Ni²⁺ concentration; the number of pooled blocking events for each τ_o ranged between 300 and 1400. Values of τ_o were corrected for missed blocking events. Error bars indicate the standard deviation and are not shown for values less than symbol size. B, reciprocal τ_o values for Ni²⁺ blockade, measured in the presence of 2 mM Mg²⁺ (solution 14), are plotted as a function of Ni²⁺ concentration. Data are shown for membrane potentials of -120 mV (•), -80 mV (▴), -60 mV (▾) and -40 mV (♦). Values of τ_o and error bars are as described in A; each value represents fits to pooled data from 2-4 patches containing 500-700 blocking events. C, voltage-dependent association rate constants, k₁(V), determined from the slope of the regression lines in A and B for Ni²⁺ blockade in the absence (•) and presence (▪) of 2 mM external Mg²⁺, respectively. Error bars represent the standard error of the regression coefficients. D, the voltage dependence of the dissociation constant, K_d, for Ni²⁺ binding in the absence and presence of 2 mM Mg²⁺. Open symbols represent K_d(0) determined from extrapolation of the linear regression fits to each data set (continuous curves). Error bars represent the error extrapolated from the standard errors for k₁(V). For all figures, smooth curves represent the linear regression fits to the data.

The dissociation constant (K_d) for Ni²⁺ binding and the location (δ) of the binding site in the transmembrane electric field were calculated from eqn (3). For these calculations τ_o was determined from single exponential fits of the pooled data from all patches at each Ni²⁺ concentration and membrane potential; τ_o was then corrected for missed blocking events using the voltage-independent τ_b obtained from all experiments (0.51 ± 0.02 ms, mean ±s.e.m.). Voltage-dependent Ni²⁺ association rate constants, k₁(V), shown in Fig. 6C, were determined from the slope of linear regression fits to 1/τ_o (Fig. 6A). Voltage-dependent dissociation constants, K_d(V), were calculated from k₁(V) and the voltage-independent dissociation rate constant (k_-1) determined from the reciprocal of the voltage-independent τ_b (0.51 ms). Linear regression analysis of the semilogarithmic plot of K_d(V) as a function of membrane potential (Fig. 6D) yielded a site exhibiting a zero voltage dissociation constant, K_d(0), of 1.09 mM for Ni²⁺ binding and located 13.7 % (δ= -0.137) of the distance through the transmembrane electric field from the extracellular surface.

Effect of Mg²⁺ on Ni²⁺ block

The similarity in δ values for channel blockade by external Ni²⁺ and Mg²⁺ suggested that the two ions blocked the channel by binding at the same site. If the two ions compete for binding then the apparent K_d for Ni²⁺ binding is expected to increase in the presence of Mg²⁺. This hypothesis was tested by repeating the measurement of K_d(0) and δ for external Ni²⁺ binding in the presence of 2 mM Mg²⁺. At this Mg²⁺ concentration unitary Na⁺ current amplitude remained large enough to allow measurement of Ni²⁺ blocking events. In the presence of Mg²⁺, Ni²⁺ again caused voltage- and concentration-dependent slow blockade of inward Na⁺ currents with open and blocked dwell time distributions best described by single exponential relaxations (data not shown). External 2 mM Mg²⁺ increased τ_o for Ni²⁺ blockade relative to values for the same Ni²⁺ concentration and voltage obtained in the absence of Mg²⁺. The voltage-dependent Ni²⁺ association rate constants, k₁(V), calculated as the regression coefficients of the data in Fig. 6A and B were significantly decreased by Mg²⁺ when measured at the same voltage (P < 0.05, analysis of covariance; Fig. 6C). External Mg²⁺ did not affect τ_b for Ni²⁺ blockade, which was again found to be independent of Ni²⁺ concentration and voltage (data not shown); τ_b was 0.51 ± 0.02 ms (mean ±s.e.m.) in the presence of Mg²⁺.

K_d(0) and δ for Ni²⁺ binding in the presence of 2 mM Mg²⁺ were again calculated using eqn (3) as described above (Fig. 6D). The Mg²⁺-induced decrease in k₁(V) increased the corresponding K_d(V) and K_d(0) determined by extrapolation of the regression fit to K_d(V). In the presence of 2 mM external Mg²⁺, K_d(0) for Ni²⁺ binding increased from 1.09 mM in the absence of Mg²⁺ to 1.27 mM. Although this increase was not statistically significant due to uncertainty in the slope of the regression lines, it was consistent with the hypothesis that external Mg²⁺ and Ni²⁺ compete for binding at a single site in the pore. If Mg²⁺ affected Ni²⁺ binding purely through competition for a single binding site then, from eqn (4), 2 mM Mg²⁺ would have been predicted to increase the K_d(0) for Ni²⁺ binding to 1.5 mM, slightly greater than the measured increase.

External Mg²⁺ also appeared slightly to decrease the voltage dependence of the K_d for Ni²⁺, shifting the calculated location of the Ni²⁺ binding site outwards to 11.5 % (δ= -0.115) of the transmembrane electric field. If Mg²⁺ was acting purely through competition for binding then the voltage dependence of the K_d for Ni²⁺ binding should not have been affected. This effect was small and not statistically significant but suggested that external Mg²⁺ may affect Ni²⁺ binding by surface charge screening as well as by competition for binding.

Surface charge effects

The presence of a negative surface potential affecting cation concentrations at the mouth of the pore was investigated in two ways: measuring Na⁺ conductance at fixed and varied ionic strengths (Green & Andersen, 1991), and measuring the effect of ionic strength on Ni²⁺ blockade (Kuo & Hess, 1992). The effect of decreasing external Na⁺ concentration on the single channel I-V relationship is shown in Fig. 7. When NaCl was decreased by replacement with glucose, allowing ionic strength to decrease, inward slope conductance decreased non-linearly with the external NaCl concentration (Fig. 7A and C) and V_rev shifted in accordance with changes in the Na⁺ equilibrium potential, E_Na (Fig. 7A). When ionic strength was maintained by substitution of NMDG⁺ for Na⁺ (Fig. 7B), V_rev again shifted with Na⁺ concentration but inward slope conductance decreased more strongly for a given change in external NaCl concentration (Fig. 7B and C). Single channel conductance is also shown for 225 mM NaCl concentration in the pipette and bath solutions (Fig. 7C); higher NaCl concentrations could not be examined due to instability of the patch seal under such conditions. Single channel conductance data for both glucose and NMDG substitutions could be approximated using the Michaelis-Menton equation although the fits were not very good and this equation is strictly applicable to a one-site single occupancy channel exhibiting a constant surface potential (Coronado & Affolter, 1986). The curve approximating the glucose substitution data assumed a maximum conductance of 55.2 pS and a K_m of 58 mM (continuous curve in Fig. 7C). When ionic strength was maintained by substitution of NMDG for NaCl, the data could be approximated by assuming a maximum conductance of 140 pS and a K_m of 370 mM (dashed curve in Fig. 7C). The greater conductance in lowered ionic strength saline suggested the presence of negative surface charge acting to increase the Na⁺ concentration at the mouth of the pore and, consequently, channel conductance. However, the decrease in channel conductance in the presence of NMDG may have been caused by NMDG blockade and/or permeability of the channel. In a separate experiment, channel permeability to NMDG was estimated from V_rev measurements from inside-out patches under biionic conditions (data not shown). In this experiment the pipette saline contained 150 mM NaCl (solution 5) and the bath saline contained 150 mM NMDG (solution 19). The mean V_rev was 72.5 ± 10.6 mV (mean ±s.d., n= 2), indicating a permeability ratio (P_Na:P_NMDG) of 17.7. Thus NMDG was weakly permeant and the reduction in channel conductance may be attributable to inhibition of Na⁺ current by NMDG binding and permeation.

Figure 7. Effects of ionic strength on Na⁺ conductance and Ni²⁺ blockade.

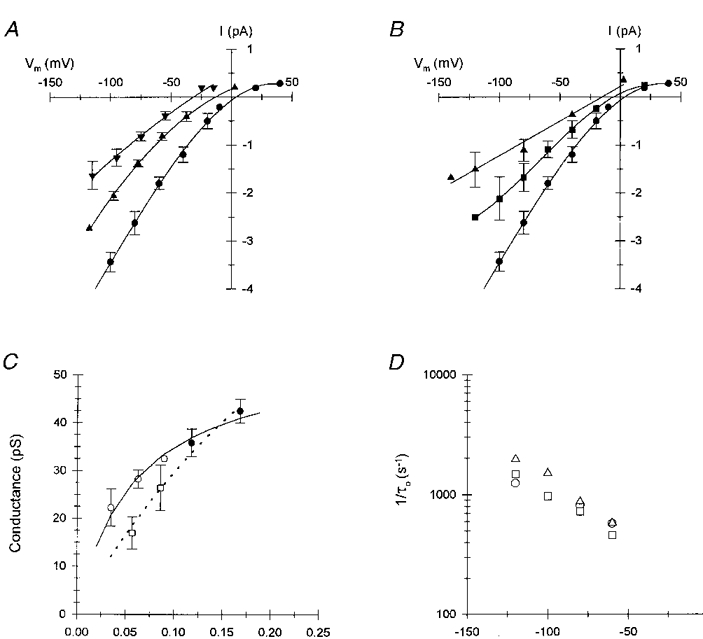
A, effect of decreasing external NaCl concentration and ionic strength on the I-V relationships of unitary currents obtained from inside-out patches; pipette contained 150 mM NaCl (•), 75 mM NaCl (▴) and 37.5 mM NaCl (▾). Ionic strength was decreased by substitution of glucose for NaCl (mixing solutions 5 and 18, Table 1); the bath contained solution 15. Symbols represent the mean (±s.d.) current amplitude from 3-5 patches at each NaCl concentration; errors less than symbol size are not shown. Smooth curves represent 3rd order or 2nd order (75 and 37.5 mM NaCl) regression fits to the data. B, effect of decreasing external NaCl concentration at constant ionic strength on the I-V relationship; pipette contained 150 mM NaCl (•), 112.5 mM NaCl (▪) and 75 mM NaCl (▴). Ionic strength was maintained by substitution of NMDG for NaCl (mixing of solutions 5 and 19); the bath contained solution 15. Symbols represent the mean (±s.d.) from 3-6 patches at each NaCl concentration. Smooth curves represent 3rd order or linear (75 mM NaCl) regression fits to the data. C, Na⁺ concentration dependence of inward slope conductance for variable ionic strength (glucose substitution, ○) and constant ionic strength (NMDG substitution, □) data from A and B. Filled circles represent channel conductance in 150 and 225 mM NaCl (pipette solution 16/bath solution 17). Symbols represent the mean (±s.d.) from 3-6 patches for each ionic condition. Continuous and dashed curves represent fits to the Michaelis-Menton equation for the glucose-substituted and NMDG-substituted data, respectively. D, effect of ionic strength on the voltage dependence of reciprocal τ_o for 0.1 mM Ni²⁺ blockade of unitary Na⁺ currents in cell-attached patches: 225 mM NaCl (pipette solution 16, ○), 150 mM NaCl (solution 5, □), or 112.5 mM NaCl (mixing solutions 5 and 18, ▵). Symbols represent reciprocal of corrected τ_o values determined from data pooled from 3 separate patches containing between 400 and 1500 blocking events at each ionic strength and membrane potential. Standard deviations were less than symbol size.

As described by Kuo & Hess (1992), Ni²⁺ blockade of Na⁺ current should provide a more sensitive assay for a surface potential affecting divalent cation concentrations near the mouth of the pore. The τ_o for Ni²⁺ blockade is steeply dependent on Ni²⁺ concentration (Fig. 6A) and should be sensitive to ionic strength if a significant surface potential exists near the mouth of the pore. The effect of ionic strength on the voltage dependence of reciprocal τ_o values measured in the presence of 0.1 mM Ni²⁺ is shown in Fig. 7D; the substitution of glucose for NaCl was used to maintain osmolarity of the external solution. As described previously, τ_o was determined from single exponential fits to data pooled from two to four patches at each potential and ionic strength and corrected for missed blocking events using the mean value for τ_b. Mean blocked time was not affected by increasing or decreasing ionic strength (data not shown). The Ni²⁺ association rate was not substantially affected by either increasing external ionic strength to 225 mM NaCl or decreasing ionic strength to 112.5 mM NaCl, although the association rate appeared to increase slightly at the reduced NaCl concentration. These results provided evidence against the presence of a significant negative surface potential affecting cation concentrations at the mouth of the pore under physiological ionic conditions.

DISCUSSION

As with many cation channels, external Ca²⁺ was found to inhibit monovalent cation conductance of the angiotensin II-regulated non-selective cation channel in rat adrenal glomerulosa cells. Ca²⁺ inhibition exhibited an IC₅₀ of 1.4 mM, demonstrating that this effect may occur under physiological conditions. Inhibition was attributable to slow Ca²⁺ permeation, binding of divalent cation-selective sites in the pore and blocking of the single-file flux of Na⁺ while bound. This type of mechanism has been widely invoked to explain Ca²⁺ inhibition of monovalent cation conductance in other Ca²⁺-permeant non-selective channels as well as in the highly Ca²⁺-selective voltage-dependent channels (for reviews see Tsien et al. 1987; Hollman & Heineman, 1994; Zagotta & Siegelbaum, 1996). If external Ca²⁺ inhibited inward Na⁺ current by binding within the pore then inhibition may be expected to exhibit a voltage dependence proportional to the location of the binding site within the transmembrane electric field. However, Ca²⁺ inhibition was voltage independent in these channels. Voltage-independent blockade by Ca²⁺ has been described previously in high threshold Ca²⁺ channels (Lansman et al. 1986; Kuo & Hess, 1993a). In these channels voltage-independent inhibition was attributed to the rapid, approximately diffusion-limited, association rate between Ca²⁺ and a readily accessible pore site located near the external mouth of the pore. This initial Ca²⁺ binding is postulated to occur much faster than overall ion translocation, resulting in voltage-independent inhibition. The present study also indicated the presence of a divalent cation binding site near the external mouth of the non-selective cation channel pore. This site may contribute to the rapid, voltage-independent association of Ca²⁺ with the channel pore. In this regard Ca²⁺ inhibition of Na⁺ current resembled fast open channel blockade characteristic of a low affinity pore binding site. The measured IC₅₀ for Ca²⁺ inhibition of Na⁺ current (1.4 mM) may then approximate the Ca²⁺ binding affinity of this site. In other Ca²⁺-permeant non-selective cation channels exhibiting approximately similar P_Ca:P_Na ratios the Ca²⁺ affinity of pore binding sites has been estimated to be much higher: 1 μm in CNG channels (Root & MacKinnon, 1993) and 77 μm in NMDA receptor channels (Iino et al. 1997). Thus the structure of Ca²⁺ binding sites in the glomerulosa cell channel may be expected to differ from those mediating Ca²⁺ binding in CNG channels and NMDA receptors.

This glomerulosa cell non-selective cation channel was previously reported to be Ca²⁺ permeant based on V_rev measurements from inside-out patches under biionic conditions (Lotshaw & Li, 1996). The shift in V_rev with increasing external Ca²⁺ concentration observed in the present study was consistent with that predicted by the GHK equation for a channel exhibiting a constant P_Ca:P_Na ratio of approximately 4. Estimates of the fractional Ca²⁺ current through other non-selective cation channels based on the GHK equation have not been well substantiated by cytosolic Ca²⁺ imaging methods (Schneggenburger et al. 1993; Frings et al. 1995). Nevertheless, such studies have demonstrated that channels exhibiting even low P_Ca:P_Na ratios may be expected to provide significant Ca²⁺ influx under physiological conditions. The IC₅₀ for Ca²⁺ inhibition of Na⁺ current demonstrated that this channel interacts with Ca²⁺ at physiologically relevant Ca²⁺ concentrations. Surface charge screening by external Ca²⁺ did not appear to contribute to inhibition of Na⁺ current. Two lines of evidence indicated that the mouth of the channel pore did not exhibit a significant negative surface potential under physiological ionic conditions: Ni²⁺ association rates were relatively insensitive to changes in ionic strength (Kuo & Hess, 1992), and low concentrations of Ca²⁺ or Mg²⁺ in the external saline did not affect V_rev (Lewis, 1979).

Divalent cation binding sites

The presence of two divalent cation binding sites within the channel pore was demonstrated by voltage-dependent blockade of Na⁺ current by Mg²⁺ and Ni²⁺. The voltage dependence of channel blockade suggested that blockers bound channel sites located within the transmembrane electric field (Woodhull, 1973). The location of these binding sites within the channel pore was indicated by the ability of oppositely directed Na⁺ current to oppose both Mg²⁺ and Ni²⁺ blockade, presumably by electrostatic repulsion between the permeating ion and the blocker. Thus Mg²⁺ and Ni²⁺, like Ca²⁺, are postulated to enter the open channel pore and block single-file ion flux by binding specific sites in the pore. Unlike Ca²⁺, these blockers appeared unable to permeate the selectivity filter and must exit from the same side as they entered, occluding ion flux as long as they remained bound. The impermeability of the channel to Mg²⁺ was indicated by the linear relationship between current inhibition and membrane potential (Fig. 2C). If Mg²⁺ was measurably permeant then increasingly negative (or positive) membrane potentials would have been expected to facilitate permeation, decreasing inhibition of Na⁺ current with increasingly large positive or negative membrane potential. Mg²⁺ was also reported to be impermeant to the endothelial histamine-activated non-selective cation channels based on the absence of measurable unitary currents using Mg²⁺-filled pipettes (Yamamoto et al. 1992). The impermeability of the glomerulosa cell channel to Ni²⁺ was indicated by the voltage independence of τ_b for Ni²⁺ blockade. If Ni²⁺ was measurably permeant then membrane hyperpolarization would have been expected to facilitate permeation, decreasing τ_b. Additionally, increasing the permeant ion concentration would have been expected to facilitate Ni²⁺ permeation and decrease τ_b as described for weakly permeant divalent blockers of L-type Ca²⁺ channels (Kuo & Hess, 1993b). However, τ_b for Ni²⁺ was insensitive to Na⁺ concentration.

The apparent impermeability of Mg²⁺ and Ni²⁺ is consistent with the asymmetric blockade of Na⁺ current by external and internal Mg²⁺. Analysis of these data indicated that external and internal Mg²⁺ blocked the channel by binding to different sites in the pore. We may further postulate that these binding sites are separated by the selectivity filter, which represents the major free energy barrier to ion permeation. Thus, Mg²⁺ blockade of the glomerulosa cell non-selective cation channel was similar to that of the histamine-activated Ca²⁺-permeant non-selective cation channel in endothelial cells (Yamamoto et al. 1992). In the endothelial channel Mg²⁺ was reported to be impermeant and blockade by external and internal Mg²⁺ asymmetric; blockade by internal Mg²⁺ was more effective than external Mg²⁺.

The hypothesis that external Mg²⁺ and Ni²⁺ blocked the channel by binding to the same site located near the external mouth of the pore was supported by data indicating that each blocker acted by binding a single site and by the apparent competition between these ions for binding. External Mg²⁺ inhibition of inward current yielded a straight line when plotted logarithmically as a function of voltage (Fig. 2C), as expected for a single binding site (Moczydlowski, 1992). Similarly, τ_b and τ_o for external Ni²⁺ blockade were well described by single exponential relaxations, and τ_o was linearly dependent on Ni²⁺ concentration, as expected for a single binding site. Competition between Mg²⁺ and Ni²⁺ was indicated by the increase in the apparent K_d(0) for Ni²⁺ in the presence of Mg²⁺ as expected for a competitive inhibitor. The increase in the apparent Ni²⁺K_d(0) from 1.09 to 1.27 mM was slightly less than predicted (1.5 mM) from eqn (4), which assumed a dissociation constant for Mg²⁺ at 0 mV (K_i(0)) of 5.1 mM. This discrepancy may be attributed to the determination of the apparent Mg²⁺K_d(0) based on data for a single Mg²⁺ concentration. The absence of a surface charge effect on Ni²⁺ binding (Fig. 7D) indicated that Mg²⁺ effects were not caused by surface charge screening.

The present study did not directly address the issue of whether the channel may be simultaneously occupied by two or more ions. The data collected are ambiguous on this point. The monotonic decrease in channel conductance with increasing external Ca²⁺ concentration would suggest the channel behaves as expected for single-ion occupancy. Similarly, the association rate for Ni²⁺ blockade exhibited a small increase with decreasing permeant ion concentration as expected for a single-ion pore (Zarei & Dani, 1994). On the other hand, oppositely directed Na⁺ current very effectively opposed blockade by Mg²⁺ or Ni²⁺. It remains to be determined whether this effect was due to simple competition for the external-most binding site or ion-ion interactions within a multi-ion pore.

The distinct differences between channel blockade by external Mg²⁺ and Ni²⁺ are postulated to reflect differences in their rates of entry into the pore and binding affinities as opposed to different binding sites for each ion. The observed inhibition of average Na⁺ current amplitude by Mg²⁺ is consistent with a fast block mechanism in which the Mg²⁺ association and dissociation rates are sufficiently fast that average open channel current amplitude is decreased without a measurable change in open channel current fluctuations. Fast blockade is generally considered to be characteristic of low affinity blockers. However, Ni²⁺ exhibited a K_d(0) of only 1 mM, not much less than that for external Mg²⁺ (approximately 5 mM), and a comparatively slow voltage-dependent association rate coefficient of 6.4 × 10⁶ M⁻¹ s⁻¹ at -120 mV, measured as the slope of the Ni²⁺ concentration dependence of 1/τ_o (Fig. 6A). The slow association rate for Ni²⁺ suggests that association with the binding site involved partial dehydration of the ion as postulated for Ni²⁺ blockade of Ca²⁺ channels (Winegar et al. 1991). The dehydration rate for Ni²⁺ is approximately 10-fold slower than for Mg²⁺, which is nearly 1000-fold slower than Ca²⁺ (Hille, 1992). Ni²⁺ also exhibited a slow voltage-independent first order dissociation rate of approximately 2000 s⁻¹ indicating a greater stabilization energy for Ni²⁺ binding than for Mg²⁺ binding. Similar binding energy differences among divalent cations have been described for other channels and indicate that non-coulombic properties such as co-ordination number and geometry are important determinants of divalent cation binding stability at the external-most binding site (Winegar et al. 1992).

Functional roles of divalent binding sites

The results of the present study indicate that at least two divalent cation binding sites are present within the pore structure of these non-selective cation channels. These sites mediate channel blockade by external and internal Mg²⁺ and external Ni²⁺, and may be involved in facilitating Ca²⁺ selectivity and permeation. The low P_Ca:P_Na ratio and fast block characteristic of Ca²⁺ suggest that divalent binding sites within the pore exhibit a low affinity for Ca²⁺, possibly near the IC₅₀ for Ca²⁺ inhibition of Na⁺ conductance. The external-most divalent binding site will mediate fast channel block by external Mg²⁺ under physiological conditions and this effect may have consequences for membrane potential responses and Ca²⁺ influx during channel activation by angiotensin II. Internal Mg²⁺ and possibly other cytosolic cations will block outward current through this channel by binding the internal-most binding site. However the physiological relevance of this inward rectification is uncertain in the adrenal glomerulosa cell since the membrane potential has not been reported to attain such depolarized values in this cell type.