Skip to main content
PMC home page
The Journal of Physiology logoLink to The Journal of Physiology
. 1999 Mar 1;515(Pt 2):367–376. doi: 10.1111/j.1469-7793.1999.367ac.x

Dual allosteric modulation of pacemaker (f) channels by cAMP and voltage in rabbit SA node

Dario DiFrancesco 1
PMCID: PMC2269155  PMID: 10050004

Abstract

  1. A Monod-Whyman-Changeux (MWC) allosteric reaction model was used in the attempt to describe the dual activation of ‘pacemaker’ f-channel gating subunits by voltage hyperpolarization and cyclic nucleotides. Whole-channel kinetics were described by assuming that channels are composed of two identical subunits gated independently according to the Hodgkin-Huxley (HH) equations.

  2. The simple assumption that cAMP binding favours open channels was found to readily explain induction of depolarizing voltage shifts of open probability with a sigmoidal dependence on agonist concentration.

  3. Voltage shifts of open probability were measured against cAMP concentration in macropatches of sino-atrial (SA) node cells; model fitting of dose-response relations yielded dissociation constants of 0.0732 and 0.4192 μM for cAMP binding to open and closed channels, respectively. The allosteric model correctly predicted the modification of the pacemaker current (If) time constant curve induced by 10 μM cAMP (13.7 mV depolarizing shift).

  4. cAMP shifted deactivation more than activation rate constant curves, according to sigmoidal dose-response relations (maximal shifts of +22.3 and +13.4 mV at 10 μM cAMP, respectively); this feature was fully accounted for by allosteric interactions, and indicated that cAMP acts primarily by ‘locking’ f-channels in the open configuration.

  5. These results provide an interpretation of the dual voltage- and cyclic nucleotide- dependence of f-channel activation.

Cardiac ‘pacemaker’ (f) and the equivalent neuronal (h) hyperpolarization-activated channels open upon membrane hyperpolarization and are activated at the same time by intracellular cAMP, which serves fundamental physiological functions such as the autonomic regulation of heart rate (Brown et al. 1979; DiFrancesco et al. 1989) and the control of rhythmic activity in various brain areas (Pape & McCormick, 1989).

In cardiac cells, cAMP binding to f-channels causes a concentration-dependent shift of their activation curve to more depolarized voltages, through a phosphorylation-independent process (DiFrancesco & Tortora, 1991). Shifting of activation and/or inactivation curves is, in fact, a widespread mode of regulation of channel activity by different agents, including phosphorylation, interaction with G-proteins and intracellular second messengers (Barret et al. 1982; Shubert et al. 1989; Bean, 1989; Ono et al. 1993; Brüggerman et al. 1993; Esguerra et al. 1994; Hille, 1994). However, the molecular mechanism underlying the shift is unknown.

Here it is shown that a depolarizing shift of the f-channel open probability curve and its cAMP concentration dependence are predicted by a cyclic allosteric activation mechanism, in the assumption that binding to f-channels of cyclic nucleotide agonists is facilitated in the open configuration. Thus, voltage and cyclic nucleotides can be viewed as channel modulators that co-operate to modify similarly the channel configuration.

METHODS

New Zealand white rabbits (0.8-1.2 kg) were anaesthetized by injection of 4.6 mg kg−1 xylazine and 60 mg kg−1 ketamine i.m., killed by cervical dislocation and exsanguinated before the hearts were extracted. The procedures conformed with the guidelines of the care and use of laboratory animals established by State (D.L. 116/1992) and European directives (86/609/CEE). Experiments were performed on the SA node (pacemaker) cells isolated as previously reported (DiFrancesco et al. 1986). The cells were stored at 4°C until they were dispersed into plastic Petri dishes and perfused with a high potassium solution containing (mM): KCl, 130; NaCl, 10; MgCl2, 1; Hepes-KOH, 10; D-glucose, 5 (pH 7.4). Inside-out macropatches were formed as described previously (DiFrancesco & Mangoni, 1994). The intracellular side of the patch was superfused by a solution containing (mM): potassium aspartate, 130; NaCl, 10; CaCl2, 2; EGTA, 5 and Hepes-KOH, 10 (pH 7.2, pCa 7). The patch pipette solution contained (mM): NaCl, 70; KCl, 70; CaCl2 1.8; MgCl2, 1; BaCl2, 1; MnCl2, 2; Hepes-KOH, 5 (pH 7.4). Temperature was 24-26°C. Open probability (Po) curves were measured by a ramp method previousy developed (DiFrancesco & Mangoni, 1994), using 60 s ramps from -35 to -145 mV. Shifts of the voltage dependence of pacemaker current (If) activation induced by perfusing cAMP on the intracellular side of macropatches (Fig. 2B) were evaluated by: (1) fitting of open probability curves by a square Boltzmann equation and measurement of the displacement of half-activation voltage (Fig. 2A) or (2) measurement of the change in holding potential producing superimposition of current traces in control and in the presence of cAMP, according to a previously developed protocol (Accili & DiFrancesco, 1996).

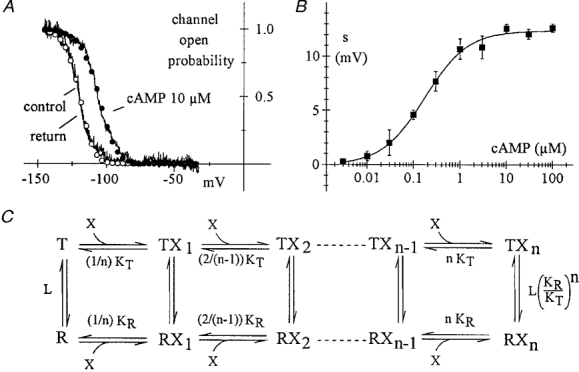
Figure 2. Allosteric model describing cAMP-induced activation of f-channels.

Figure 2

Open in a new tab
A, f-channel open probability (Po) curve measured by a ramp method (DiFrancesco & Mangoni, 1994) in an inside-out macropatch from a SA node myocyte, in a control solution, during and after perfusion of the intracellular side of the patch with 10 μM cAMP, as indicated. The patch contained approximately 103 f-channels, as calculated by the maximal current (at -145 mV) and the single-channel conductance of 0.98 pS (DiFrancesco, 1986). Curve fitting by the second power (Po = PR2) of the Boltzmann equation PR = 1/(1 + exp((V- V½)/v)), yielded V½ = -113.9 mV, v = 6.30 mV for the control curve (○) and V½ = -98.7 mV, v = 7.85 mV for the 10 μM cAMP curve (•). B, dose-response relation of shifts of Po curves against cAMP concentration. Plotted are mean ±s.e.m. values from 73 exposures in 47 macromatches. After setting the inverse slope factor (v) to 7.103 ± 0.231 mV (mean ±s.e.m. from 28 activation curves measured in control conditions), best fitting of experimental data to eqn (A3) (see Appendix):
graphic file with name tjp0515-0367-mu13.jpg
yielded the parameter values n = 0.782, KR = 0.0578 μM, KT = 0.5416 μM. The maximal shift at saturating cAMP concentrations (smax) was 12.4 mV. Since, due to physical constraint, the parameter n can only be an integer, a new fitting was performed with n = 1 which yielded KR = 0.0732 μM, KT = 0.4192 μM (smax = 12.4 mV, continuous curve). C, MWC allosteric activation scheme generating the s (X) curve plotted in B. An individual channel gating subunit is assumed to have tense (T) and relaxed (R) configurations, and n ligand binding sites (X denotes the ligand). All n binding sites are simultaneously in either the tense or relaxed state, such that transitions occur ‘concertedly’ (Monod et al. 1965). See text for further explanation.

Activation/deactivation of the f-channel was analysed assuming second-order Hodgkin-Huxley kinetics (see Fig. 4A and B), with voltage dependency for opening and closing rate constants of type:

graphic file with name tjp0515-0367-m1.jpg (1)

where a single value for the parameter Vr was selected based on evidence that fitting of experimental data yields nearly identical Vr values for α and β rate constants (Noble et al. 1989). This choice simplified to some extent the mathematical treatment (see Appendix), without affecting the conclusions of this paper (not shown).

Figure 4. Voltage dependence of time constant of f-channel gating in control conditions and in the presence of 10 μM cAMP.

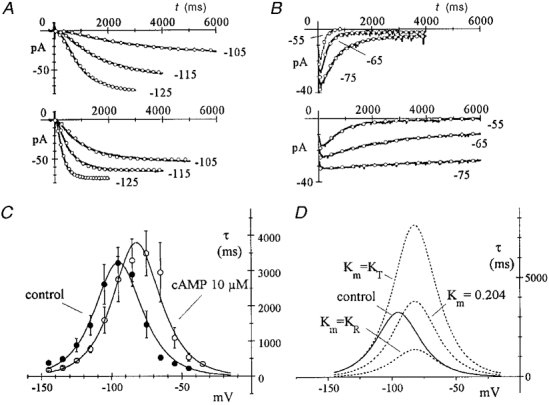
Figure 4

Open in a new tab

A and B, time constants were evaluated in the range -145 to -35 mV by square-exponential fitting of macropatch current traces during activation (A, holding potential = -35 mV) and deactivation (B, steps applied following 2 s hyperpolarizations to -135 mV). Continuous lines are experimental traces recorded in a macropatch at the voltages indicated in control conditions (upper) and during perfusion with 10 μM cAMP (lower), and ○ represent fitting curves. C, time constant mean ±s.e.m. values calculated from N = 7 inside-out macropatches, each sequentially exposed to control (•) and cAMP-containing solution (○, 10 μM). The control curve was fitted to eqn (A7) using the voltage dependence of rate constants expressed in eqns (1) and the setting X = 0, which yielded the parameters αo = 0.000283 s−1, βo = 83.1 s−1, Vr = 15.08 mV (corresponding to v = 7.54 mV, see eqn (2)). The cAMP curve was subsequently fitted to eqn (A7) by setting αo, βo and Vr to the control values, KR = 0.0732 μM, KT = 0.4192 μM (values obtained from fitting of dose-response relation in Fig. 2B) and X = 10μM. This yielded the parameter value Km = 0.204 μM. Peak-to-peak shift was 13.7 mV. D, sample model simulations illustrating the effect of changing the free parameter Km in the cAMP curve. The control (continuous line) and cAMP (dotted line) curve from C are replotted; the latter corresponds to Km = 0.204 μM, as indicated. Also plotted as dotted lines are two theoretical curves corresponding to Km =KR = 0.0732 μM and to Km =KT = 0.4192 μM. Changes in Km lead to changes in the peak level without modifying the peak voltage. Further explanation in text.

Although more complex kinetics have been proposed (DiFrancesco, 1984; Maruoka et al. 1994), the above description accounts for the major kinetic properties of the f-current (Noble et al. 1989). The recent cloning of hyperpolarization-activated channels and the suggestion that they are tetramers like K+ channels (Clapham, 1998), raises the question of whether kinetics with a power of four would not be more appropriate. However, use of a power of four resulted in a poorer fitting of activation current traces as compared with the power of two. Sample macropatch activation records fitted by either second (left) or fourth power exponentials (right) are shown in Fig. 1 for the voltage range -95 to -125 mV. The comparison shows that fitting with a power of two approximates the current activation time course better than a power of four, particularly in the mid-activation voltage range (Fig. 1A and B); also, best-fit activation and deactivation time constants greatly diverge at mid-potentials with the fourth power (Fig. 1C and D). Divergence is explained by the observation that choosing the fourth power results in doubling the deactivation time constant obtained with the second power (open symbols), while activation time constants are lowered (filled symbols). Note that deactivation best-fitting curves with second and fourth power overlap, and are not shown here (see Fig. 4A and B).

Figure 1. Comparison of pacemaker current (If) activation kinetics.

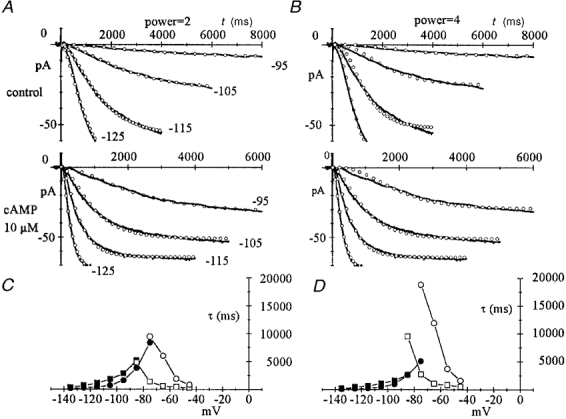
Figure 1

Open in a new tab

Comparison between second (left) and fourth power exponential description (right) of If activation kinetics. A and B, macropatch current (continuous lines) recorded in a macropatch in control conditions (upper panel) and in the presence of 10 μM cAMP (lower panel), at the voltages indicated (mV). Steps were applied from a holding potential of -35 mV. Also plotted (○) are best-fitting exponentials to the second (A) or fourth power (B). C and D, time constants of the best fits to activation (•, ▪) and deactivation traces (○, □) according to second (C) or fourth power (D). Control values are plotted as squares and cAMP values as circles.

The term ‘subunit’ used in this model thus refers to an individual gating element, rather than to a molecular entity. Current changes were therefore described by the relation:

graphic file with name tjp0515-0367-mu1.jpg

where Vf is reversal potential and gmax fully activated conductance. At steady state, the subunit ‘active’ (or ‘relaxed’) probability PR =α/(α+β) satisfies the Boltzmann relation:

graphic file with name tjp0515-0367-m2.jpg (2)

where V½ = -(Vr/2) ln(βo/αo) is the half-activation voltage and v =Vr/2 the inverse slope factor. A channel will be open when its subunits are in the ‘relaxed’ state, such that the channel open probability is Po =PR2.

The present work is based on data collected from 118 cAMP exposures on 99 macropatches.

RESULTS

Open probability curves Po(V) of f-channels in SA node cell macropatches were measured by application of voltage ramps as previously reported (DiFrancesco & Mangoni, 1994) and fitted by the second power of Boltzmann distribution functions (Noble et al. 1989) (Fig. 2A, eqn (2)). Intracellular cAMP and other cyclic nucleotides are known to activate f-channels by a depolarizing shift of the Po(V) curve, without altering channel conductance, or the slope of the Po(V) curve (DiFrancesco & Tortora, 1991; DiFrancesco & Mangoni, 1994) (Fig. 2A). When plotted against cAMP concentration, the shift of the Po(V) curve had a sigmoidal shape (Fig. 2B), previously described by a Hill function (DiFrancesco & Tortora, 1991).

f-Channel activation due to cyclic nucleotide binding and that due to voltage hyperpolarization have been considered until now as distinct processes. Since f-channels open upon hyperpolarization independently of cAMP (DiFrancesco & Tortora, 1991), a linear activation model, whereby closed channels need to bind the ligand before opening occurs, cannot operate. Furthermore, the action of cAMP is equivalent to a hyperpolarizing shift of the voltage dependence of gating (DiFrancesco & Tortora, 1991; DiFrancesco & Mangoni, 1994), suggesting that both mechanisms may involve similar modifications of the channel conformation. A reaction scheme able to accommodate equivalent effects of voltage and cyclic nucleotide binding is the cyclic allosteric MWC model (Monod et al. 1965) shown in Fig. 2C. Models of this type have been proposed to hold for cyclic nucleotide-induced activation of CNG (cyclic nucleotide-gated) channels, based on evidence that channel opening occurs even in the absence of agonist (Zagotta & Siegelbaum, 1996; Tibbs et al. 1997) and for intracellular Ca2+-induced gating of large-conductance Ca2+-dependent (BKCa) K+ channels (Cox et al. 1997). In the case examined here, the scheme of Fig. 2C represents one channel subunit in two possible configurations (active or relaxed, and inactive or tense), to which cAMP molecules (of concentration X (μM)) bind. The probability of the relaxed state is given by the relation:

graphic file with name tjp0515-0367-mu2.jpg

where n is the number of cAMP binding sites per subunit, L is the equilibrium constant of the relaxed-tense (R-T) transition in the absence of agonist and KR and KT are dissociation constants (μM) of agonist binding to relaxed and tense states, respectively (Monod et al. 1965) (eqn (A1) of Appendix). The ‘subunit’ represented in Fig. 2C refers to the Hodgkin-Huxley gating scheme, and does not necessarily coincide with a molecular subunit.

Allosteric models predict an increase of PR with increasing agonist concentrations when agonist binding affinity is higher for open than for closed configurations (KR < KT) (Tibbs et al. 1997). Since in voltage-gated channels PR also depends on voltage, an extra feature introduced here is the assumption that the equilibrium constant L is voltage dependent. Insertion of the appropriate Boltzmann L(V) relation in the relaxed probability function and rearrangement shows that the dual voltage and cyclic nucleotide dependence of relaxed probability predicted by the scheme shown in Fig. 2C can be described by the relation:

graphic file with name tjp0515-0367-mu3.jpg

see eqn (A2). This is a modified Boltzmann relation, in which the additional term:

graphic file with name tjp0515-0367-mu4.jpg

eqn (A3), results from the assumption of allosteric activation by cAMP, and represents an agonist concentration-dependent shift (in mV) of the PR(V) curve along the voltage axis.

It may be noted that according to the relaxed probability equation above, PR(V, X) =PR(V - s(X), 0) at any concentration X of agonist, implying that voltage shifts and agonist concentrations obeying this relation have indistinguishable effects on probability. Another feature of the proposed scheme is that the shift of the channel open probability curve (Po) is independent of the number of channel subunits (each of which is gated independently by voltage according to Hodgkin-Huxley kinetics), provided all subunits bind cAMP similarly. In the case examined here, for example, square exponential voltage dependent kinetics were used such that Po =PR2. Thus:

graphic file with name tjp0515-0367-mu5.jpg

i.e. the channel open probability function (Po) will undergo the same shift as PR for a channel subunit. The same applies for any number of subunits; that is the shift generated by agonist binding on the channel open probability is the same for any number of (identical) channel subunits.

The allosteric activation hypothesis therefore predicts that in voltage-dependent channels composed of identical subunits, each obeying the Boltzmann distribution, changes in agonist concentration lead to voltage shifts in the Po curve, whenever a differential affinity exists for open versus closed channel configurations.

Further, the predicted shift varies sigmoidally with agonist concentration as experimentally verified (Fig. 2B). Fitting experimental data to the s(X) function in Fig. 2B yielded the parameter values: n = 0.782, KR = 0.0578 μM, KT = 0.5416 μM (maximal shift, 12.4 mV). The value n = 0.782 suggests that agonist binding to a single cyclic nucleotide binding site is sufficient to induce a conformational change in each putative f-channel gating subunit. Since n can only be an integer due to physical constraints, fitting of the s(X)data in Fig. 2B was repeated after fixing n = 1, which resulted in a curve with the same maximal shift (12.4 mV, continuous line) and the parameter values KR = 0.0732 μM and KT = 0.4192 μM. This indicates an approximately 6-fold higher affinity of cAMP for open rather than closed f-channels.

The shift is directly correlated to the free energy change (ΔGX) of closed-to-open transitions contributed to by the binding of cAMP to channels. As shown in the Appendix, the free energy change of tense-relaxed transitions (for one subunit) is given by ΔG=RT ((V-V½ - s(X))/v), which at zero voltage and zero cAMP concentration gives a value of 7.63 kcal mol−1 (at 27°C) for V½ = -91.2 mV (as measured in cell-attached conditions, DiFrancesco & Mangoni, 1994) and v = 7.103 mV (Fig. 2). The contribution of a concentration X of cAMP to ΔG is calculated as ΔGX = -RTs (X)/v (eqn (A4)). In Fig. 3, the dependence predicted by the relation (see eqn (A4)) of -ΔGX with cAMP concentration (left) and that of ΔG with voltage in control conditions and in the presence of a saturating cAMP dose (right) are shown.

Figure 3. Free energy change of tense-relaxed transitions and contribution of agonist binding as predicted by the model of Fig. 2C for one gating subunit.

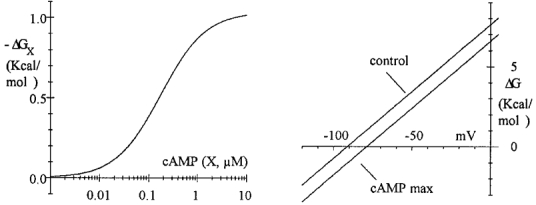
Figure 3

Open in a new tab

Left, ligand concentration dependence of the contribution of cAMP binding to free energy change (ΔGX); the equation is -ΔGX =RTs(X)/v =RT ln(((1 +X/KR)/(1 +X/KT))n), where X is cAMP concentration, R is the gas constant and T is absolute temperature (eqn (A4)). Calculations were performed with T= 300 K. The parameters n, KR and KT were set at the same values as obtained from Fig. 2B fitting (n = 1, KR = 0.0732 μM, KT = 0.4192 μM). The maximal free energy change contribution is 1.02 kcal mol−1. Right, voltage dependence of the free energy change predicted for zero ligand concentration (control) and saturating ligand concentration (cAMP max). The relation is ΔG=RT((V - V½ - s)/v) (see Appendix). Parameters were V½ = -91.2 mV (DiFrancesco & Mangoni, 1994), v = 7.103 mV (see legend of Fig. 2) and s= 0 (control) or s= 12.4 mV (cAMP max, Fig. 2B fitting). The model predicts that binding of cAMP lowers the ΔG curve by a constant amount, equivalent to a shift to the right on the voltage axis.

The plots were drawn using V½ = -91.2 mV and v = 7.103 mV. The function -ΔGX has a sigmoidal dependence on cAMP concentration, reflecting its proportionality to the shift function s(X), and saturates at 1.02 kcal mol−1, correlated to the maximal shift of 12.4 mV (see Fig. 2B). The action of cAMP on the free energy difference between tense and relaxed states is to displace the ΔG function to lower energy values, by the same amount at all voltages (Fig. 3, right). This plot illustrates the fact that cAMP binding is equivalent to a voltage shift. An interpretation of the shift in terms of free energy can be given as follows: according to the Boltzmann energy distribution function, the equilibrium constant of tense-relaxed transitions can be expressed as:

graphic file with name tjp0515-0367-mu6.jpg

where ω is the energy difference between the two states, e is the electronic charge, z is the equivalent valence of gating charge moved across the membrane field during transitions and R, T and F have their usual meaning (Hille, 1992); the comparison with equation L= exp((V - V½)/v) (see Appendix) then shows that V½ =ω/(ze) and v =RT/(zF). Insertion of the latter expression into eqn (A4) yields the relation:

graphic file with name tjp0515-0367-mu7.jpg

Thus, the cAMP-induced shift is the change, due to cAMP binding, of the free energy difference between tense and relaxed states, per unit electrical gating charge.

As well as open probability curves, experimental activation/deactivation time constant curves also undergo a positive voltage shift under circumstances which increase intracellular cAMP (Tsien, 1974). To see if the allosteric scheme proposed can predict this effect, activation (Fig. 4A)/deactivation (Fig. 4B) time constant data from macropatch experiments in control solution (A and B, upper panels) and in the presence of 10 μM cAMP (A and B, lower panels) were fitted to eqn (A7), which is based on the model of Fig. 2C under the assumption that n = 1 and that the distribution between free and bound states is sufficiently rapid, relative to voltage-dependent kinetics, to be considered always at equilibrium. Fitting of control and cAMP curves with identical rate constant functions (as described by eqn (1)) and the values KR, KT obtained previously (Fig. 2B fitting), showed that the allosteric description can indeed account for a depolarizing shift of the time constant curve. The fitting was obtained by setting X= 10μM and yielded the parameter value Km = 0.204 μM (Fig. 4C).

cAMP appeared not only to shift the τ curve, but also to slightly increase its peak height, and to shift the right-hand side of the bell-shaped curve somewhat more than the left-hand one. This aspect of cAMP action is investigated in more detail below (see Fig. 5). Here it is interesting to note that the MWC model is able to mimic these changes, through the parameter Km. To show this, the best-fitting control and cAMP curves were re-plotted in Fig. 4D together with two curves calculated with the same parameters as the cAMP curve, but with Km set to either KT (0.4192 μM) or KR (0.0732 μM). Clearly, changing Km modifies the peak value, without altering its position on the voltage axis, and modifies the degree by which left and right branches of the curve are differentially shifted by the agonist. When Km =KT, control and cAMP curves coincide at hyperpolarized voltages and are maximally separated at depolarized voltages, while the opposite occurs when Km =KR. As is discussed below in the analysis of Fig. 5 and in the Appendix, these two limit predictions correspond to situations where cAMP either acts solely by decreasing the rate of channel closing (without changing the rate of opening, Km =KT) or vice versa, acts solely by increasing the rate of opening (without changing the rate of closing, Km =KR).

Figure 5. Differential action of cAMP on f-channel activation and deactivation time constants.

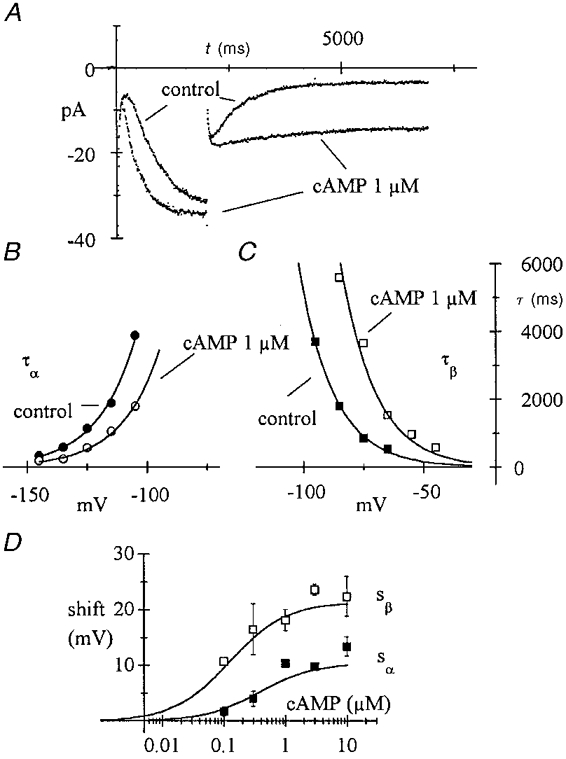
Figure 5

Open in a new tab

A, in one macropatch, activation steps were applied from -35 to -135 mV for 2 s and then to -85 mV for 5 s in control conditions and during exposure to 1 μM cAMP, as indicated. Time constants were evaluated according to square-exponential kinetics during activation and deactivation as in Fig. 4. These were 570 and 233 ms at -135 mV and 1792 and 5586 ms at -85 mV in control and cAMP, respectively. B and C, voltage dependency of time constants of activation (B, V < = -105 mV) and deactivation (C, V > = -95 mV) for the same patch as in A. cAMP-induced shifts were measured fitting time constant curves with the following eqns (reciprocals of rate constant eqns of type (1) of Methods): τα(V) =τ0α exp((V - sα) /Vr); τβ(V) =τ0β exp(- (V - sβ)/Vr) (curves). Control data (•, ▪) were first fitted setting sα = 0 (sβ = 0) and the resulting parameters τ0α and Vr (τ0β and Vr) were used to fit the corresponding cAMP data (○, □) by optimization of the shift parameter sα (sβ). D, plots of mean ±s.e.m. shifts for activation (□) and deactivation time constant curves (▪) against cAMP concentration. Data from 31 exposures on 17 patches. Differences between activation and deactivation values were significant at all cAMP concentrations (P < 0.05). Curves represent eqn (A8) with the fixed parameters: Vr = 2 v = 14.206 mV, KR = 0.0732 μM and KT = 0.4192 μM (from Fig. 2B fitting) and the free parameter Km = 0.26 μM, found by a least-squares fitting procedure.

The presence of a voltage displacement of the pacemaker current kinetics originally led to the proposal of a change in the voltage field sensed by the channel sensor (Tsien, 1974). Shifts of gating, for example due to changes in divalent ion concentrations, are commonly described by surface-potential theories such as the Gouy-Chapman-Stern theory (Hille, 1992). However, a major difficulty of this theory is that it predicts identical shifts of all gating parameters, whereas different effects are often found on activation and deactivation time constants (Hille, 1992).

cAMP had unequal effects on activation and deactivation rates, as suggested by the example of Fig. 5A, showing currents measured during activation at -135 mV and deactivation at -85 mV before and during perfusion with 1 μM cAMP in one macropatch. The activation time constant changed from 570 to 233 ms (2.45-fold acceleration) whereas the deactivation time constant changed from 1792 to 5586 ms (3.12-fold slowing). Extending the investigation to a fuller voltage range showed that cAMP-induced shifts of activation and deactivation time constants are not identical (see also Fig. 1), ruling out a surface charge screening action of cAMP. Activation time constant curves (measured at voltages ≤ -105 mV) shifted less than deactivation time constant curves (voltages ≥ -95 mV, Fig. 5B and C) at all cAMP concentrations used (Fig. 5D). For example at 1 μM cAMP, activation and deactivation time constant curves shifted by 10.34 ± 1.36 (N = 3) and 18.12 ± 3.74 mV (N = 4), respectively, where N is the number of patches.

The allosteric scheme of Fig. 2C can be shown to predict generally unequal shifts for activation and deactivation time constants (see Appendix) and to account for the experimental data. The continuous curves in Fig. 5D represent theoretical shifts of activation (sα) and deactivation time constants (sβ), as indicated, predicted by the allosteric model (eqn (A8)) for Km = 0.26 μM (all remaining parameters set to the values obtained in Fig. 2B fitting). According to theory (see Appendix), values of Km yielding higher shifts for deactivation than for activation curves indicate that most of the change in open probability is due to a decreased rate of closing, rather than to an increased rate of opening. The data of Fig. 5 thus indicate that a major contribution to the depolarizing shift of open probability of f-channels results from a ‘locking’ action of cAMP upon open channels.

DISCUSSION

Voltage shifts of gating represent a common mode by which several agents modify channel activity (Barret et al. 1982; Shubert et al. 1989; Bean, 1989; Ono et al. 1993; Brüggerman et al. 1993; Esguerra et al. 1994; Hille, 1994). For example, neuronal L-type Ca2+ channels are inhibited by neurotransmitters via G-proteins in a way which has been interpreted as due to two different channel populations, ‘willing’ and ‘reluctant’, which only differ by a voltage shift in the activation curve (Bean, 1989). Voltage shifts of activation/inactivation are also found in Ca2+-dependent K+ channels (due to changes in intracellular Ca2+, Barret et al. 1982; Cox et al. 1997), Na+ channels (due to phosphorylation, Ono et al. 1993), eag K+ channels (due to changes in internal cAMP, Brüggerman, et al. 1993). This latter example may be interesting since it is now known that eag, CNG and hyperpolarization-activated channels belong to the same family (Guy et al. 1991; Gauß et al. 1998; Ludwig et al. 1998; Santoro et al. 1998).

It is shown here that the assumption of an allosteric, voltage-dependent activation reaction scheme readily accounts for the shifting action of cAMP on the open probability curve of f-channels, explains its S-shaped dependence upon cAMP concentration and accommodates differential shifts of activation and deactivation time constant curves, as experimentally found. According to this interpretation, voltage hyperpolarization and ligand binding both act, within a single gating subunit, as allosteric activators; ligand concentration and voltage hyperpolarization have on-channel open probability indistinguishable effects according to the equivalence relation Po(V, X) =Po(V- s (X), 0) and the shift relation eqn (A3). The shift of the open probability curve is a function of the affinities of cAMP for the relaxed and tense channel subunit configurations, and is proportional to the relative increase in free energy change associated with cAMP binding in the transition from tense to relaxed configurations.

Although several models have been proposed to represent the voltage dependence and the ion concentration depencence of the kinetics of hyperpolarization-activated channels (Yanagihara et al. 1980; DiFrancesco & Noble, 1985; Noble et al. 1989; Maruoka et al. 1994; Demir et al. 1994; van Ginneken & Giles, 1991; Dokos et al. 1996), an integrated description of their voltage and cAMP dependence was lacking. On the other hand, cyclic allosteric models have been proposed for various channels, including CNG channels, (Zagotta & Siegelbaum, 1996) and Ca2+-activated K+ channels (Cox et al. 1997). In one of the models discussed to explain the Ca2+-induced modulation of large-conductance (BK) Ca2+-activated K+ channels, Cox et al. (1997) propose that the channels (α subunits) are homotetramers dually regulated by voltage and intracellular Ca2+ ions, such that each molecular subunit binds one Ca2+ ion and is independently gated by voltage. In the simplest case, by setting selective constraints on channel molecular and functional symmetry and on voltage-dependent gating, the initially large set of possible distinct channel configurations is reduced to ten (five open and five closed states), according to a MWC scheme (Cox et al. 1997, Fig. 4A). The Cox et al. (1997) model predicts Ca2+ concentration-dependent shifts of conductance-voltage relations along the voltage axis (to the hyperpolarizing direction upon increase of Ca2+ concentration), as well as many aspects of experimentally observed channel kinetics.

MWC models have been used to explain the activation of CNG channels by intracellular cyclic nucleotides (Goulding et al. 1994; Zagotta & Siegelbaum, 1996; Tibbs et al. 1997), based on evidence that opening of these channels can be recorded even in the absence of agonists, and cyclic allosteric models, rather than linear models, are therefore required to interpret channel behaviour. However, in more recent work (Liu et al. 1998), it has been proposed that gating of CNG channels is more compatible with an independent (Hodgkin-Huxley)-MWC hybrid model (see below).

One specific aspect of the model proposed in the present work is that the allosteric scheme refers to a ‘gating’ subunit, rather than to a full channel. This is necessary since a strict requirement for systems obeying MWC formulation is that all subunits undergo ‘concerted’ transitions, and are therefore all simultaneously either in the ‘relaxed’ (R) or ‘tense’ (T) state; in other words, mixed R/T configurations are not allowed (Monod et al. 1965). In ion channel proteins, a concerted transition occurs if all the channel components undergo simultaneous conformational changes, so as to be all in the R or T state at any one time. As a consequence, channels, or channel sub-components, should obey single-exponential kinetics in order to satisfy MWC models (see Cox et al. 1997). Gating of hyperpolarization-activated channels does not obey single-exponential kinetics and multistate models have been proposed to account for its detailed kinetics (DiFrancesco, 1984; Maruoka et al. 1994); the major gating properties can however be satisfactorily approximated by square-exponential kinetics over a range of voltages comprising the channel activation range (Noble et al. 1989; van Ginneken & Giles, 1991; Demir et al. 1994). In this case, only individual gating subunits are able to comply with the requirements of a cyclic allosteric MWC model.

The model presented here assumes a dual voltage- and agonist-dependent MWC modulation of a single channel subunit, whose gating contributes independently to channel open/close kinetics according to the Hodgkin-Huxley (HH) description. It is therefore a hybrid MWC-HH model. The results suggest that agonist binding to one cyclic nucleotide binding site is sufficient to affect the conformation of a gating subunit.

The recent cloning of hyperpolarization-activated channels (HCN clones) shows that they have a functional voltage sensor and a cyclic nucleotide binding site, and suggests that they belong to a specific class within the superfamily of CNG and voltage-gated channels (Gaußet al. 1998; Ludwig et al. 1998; Santoro et al. 1998). The indication that HCN channels may be tetramers like K+ channels of the same superfamily (Clapham, 1998) suggests that their voltage dependent kinetics may require a power higher than the power of two used in this paper. However, fitting of voltage-dependent kinetics by a power of four was not satisfactory, as shown in Fig. 1. Further, as discussed in Results, the dependence of the channel open probability function (Po) upon cAMP in the allosteric scheme proposed here is such that the same voltage shift is obtained regardless of the number of (Hodgkin-Huxley) gating subunits, as long as each subunit has a similar dependence upon cAMP binding.

If hyperpolarization-activated channels are tetramers, square-exponential kinetics would suggest the possibility that pairs of molecular subunits act concertedly in voltage-dependent gating, behaving as two individual gating subunits according to the Hodgkin-Huxley scheme. Although more complex, multistate gating may be required to reproduce finer kinetic details (DiFrancesco, 1984; Maruoka et al. 1994), it is interesting to note that a hybrid MWC and HH model in which four channel subunits are gated as two independent, coupled dimers has recently been proposed for CNG channels based on measurements of subunit stoichiometry (Liu et al. 1998). This observation may be relevant to the model used here especially in view of the structural similarities between CNG and hyperpolarization-activated channels (Clapham, 1998). In their work, Liu et al. (1998) measure maximal open probabilty as a function of the number of functional binding sites, and show that this dependence is not accounted for by either an independent (Hodgkin-Huxley) gating model where subunits open independently from each other, or a MWC model where all four subunits undergo concerted transitions. On the other hand, a mixed model where four-subunit channels are composed of two dimers, each of which obeys allosteric MWC kinetics and which are gated independently, such that channel opening occurs when both dimers are in the relaxed state, provides a satisfactory fit to experimental data. Dimeric structures have also been proposed for other types of K+ (Ketchum et al. 1995) and Cl− channels (Middleton et al. 1996; Ludewig et al. 1996).

The evidence presented here provides an interpretation for the functional co-existence of cyclic nucleotide- and voltage-dependent gating of hyperpolarization-activated channels, and suggests the existance of a gating mechanism that is locked in the open configuration upon cAMP binding.

Acknowledgments

This work was supported by the Ministero dell’ Università e della Ricerca Scientifica e Tecnologica (MURST) and by Telethon. I would like to thank E. Accili, C. Altomare, M. Baruscotti, M. Bianchi, A. Ferroni, A. Malgaroli and A. Moroni for assistance and discussion.

APPENDIX

The reaction scheme used to analyse kinetics of hyperpolarization-activated channels (Fig. 2C) represents a MWC (Monod et al. 1965) cyclic allosteric model in which binding of cyclic nucleotides (X) to channels modifies the relaxed (R)/tense (T) equilibrium ratio. n is the number of cyclic nucleotide binding sites per subunit, KR and KT (μm) are dissociation constants for agonist binding to relaxed and tense subunit configurations, respectively, and L=[T]/[R] is the equilibrium constant of relaxed/tense transitions in the absence of agonist. Partially bound states TX1, TX2, …, RX1, RX2, … and the corresponding transitions are indicated. The equilibrium constant of the transition TXn-RXn can be derived to be L (KR/KT)n.

The probability of the relaxed state in the presence of a given concentration X (μm) of agonist is (Monod et al. 1965):

graphic file with name tjp0515-0367-ma1.jpg (A1)

In the absence of agonist (X= 0), the relaxed probability in the reaction scheme of Fig. 2C is:

graphic file with name tjp0515-0367-mu8.jpg

comparison with eqn (2) (Methods) shows therefore that L(V) = exp((V - V½)/v). Inserting the latter expression into eqn (A1) and rearranging yields the modified Boltzmann equation:

graphic file with name tjp0515-0367-ma2.jpg (A2)

where

graphic file with name tjp0515-0367-ma3.jpg (A3)

represents a shift of the PR curve along the voltage axis. The shift is positive when KR < KT. The logarithmic function eqn (A3) is sigmoidal, and saturates at:

graphic file with name tjp0515-0367-mu9.jpg

The allosteric model allows an interpretation of the voltage shift in terms of free energy change associated with agonist binding to the channel. The free energy change for tense-relaxed transitions is ΔG= -RT ln(1/L), where R is the gas constant and T is the absolute temperature. Since L= (1/PR) - 1, inserting eqn (A2) and rearranging yields ΔG=RT ((V - V½ - s (X))/v). Using eqn (A3), the contribution due to addition of the agonist is therefore:

graphic file with name tjp0515-0367-ma4.jpg (A4)

indicating a direct relation between shift and ΔGX.

In the case n = 1, the cyclic allosteric model of Fig. 2C predicts four subunit states. Defining the gating rate constants α, β, α1, β1 such that L=β/α, and L1 =LKR/KT =β1/α1, rearrangement of the rate equations governing the system yields:

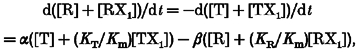graphic file with name tjp0515-0367-ma5.jpg (A5)

where Km =βKR/β1 =αKT/α1. An analytical solution of eqn (A5) can be obtained by the assumption that the distribution of relaxed (tense) subunits between states R and RX1 (T and TX1) is rapid compared with voltage-dependent kinetics, so that the ratio between free and X-bound configurations is always at equilibrium. Rearrangement of eqn (A5) leads to:

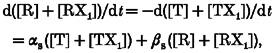graphic file with name tjp0515-0367-mu10.jpg

where

graphic file with name tjp0515-0367-mu11.jpg

and

graphic file with name tjp0515-0367-ma6.jpg (A6)

Under the assumptions made, the scheme of Fig. 2C thus predicts, for any individual channel subunit, single exponential relaxed/tense kinetics with time constant:

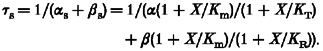graphic file with name tjp0515-0367-ma7.jpg (A7)

When rate constants have voltage dependencies as in eqn (1) of Methods, according to eqn (A6) they will shift by:

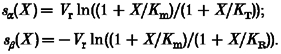graphic file with name tjp0515-0367-ma8.jpg (A8)

Although their sum is 2s(X) (see eqn (A3)), thus always twice as large as the shift of the PR curve, the shifts sα and sβ are in general unequal, depending on the value Km relative to KR and KT. Both shifts are positive for KR < Km < KT, and coincide when:

graphic file with name tjp0515-0367-mu12.jpg

Under this condition rate constants, time constant and relaxed probability (see eqn (A3) with n = 1, (A7) and (A8)) all undergo identical shifts.

Equations (A8) can be used to predict changes of rate constants. The condition for increased PR of bound channels is KT/KR > 1, and since according to definition (α1/α)/(β1/β) =KT/KR, we have either α1 > α, or β1 < β, or both. Two limiting conditions can thus be considered: (a) the ‘closing’ (relaxed-tense) rate does not change (β1/β= 1), leading to Km =KR and sα = 2s, sβ = 0; (b) the opening (tense-relaxed) rate does not change (α1/α= 1), leading to Km =KT and sα = 0, sβ = 2s. Cases (a) and (b) correspond to situations where PR of bound subunits increases exclusively because of an increased rate of opening and a decreased rate of closing, respectively. The value of Km giving best fit of experimental data to eqn (A8) can therefore be used to evaluate relative changes of opening and closing rate constants due to agonist binding (see treatment of data in Figs 4 and 5).

References

  1. Accili EA, DiFrancesco D. Inhibition of the hyperpolarization-activated current (if) of rabbit SA node myocytes by niflumic acid. Pflügers Archiv. 1996;431:757–762. doi: 10.1007/BF02253840. [DOI] [PubMed] [Google Scholar]
  2. Barret JN, Magleby KL, Pallotta BS. Properties of single calcium-activated potassium channels in cultured rat muscle. The Journal of Physiology. 1982;331:211–230. doi: 10.1113/jphysiol.1982.sp014370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bean BP. Neurotransmitter inhibition of neuronal calcium currents by changes in channel voltage dependence. Nature. 1989;340:153–156. doi: 10.1038/340153a0. [DOI] [PubMed] [Google Scholar]
  4. Brown HF, DiFrancesco D, Noble SJ. How does adrenaline accelerate the heart? Nature. 1979;280:235–236. doi: 10.1038/280235a0. [DOI] [PubMed] [Google Scholar]
  5. Brüggerman A, Pardo LA, Stühmer W, Pongs O. Ether-à-go-go encodes a voltage-gated channel permeable to K+ and Ca2+ and modulated by cAMP. Nature. 1993;365:445–448. doi: 10.1038/365445a0. [DOI] [PubMed] [Google Scholar]
  6. Clapham DE. Not so funny anymore: pacing channels are cloned. Neuron. 1998;21:5–7. doi: 10.1016/s0896-6273(00)80508-5. [DOI] [PubMed] [Google Scholar]
  7. Cox DH, Cui J, Aldrich RW. Allosteric gating of a large conductance Ca-activated K+ channel. Journal of General Physiology. 1997;110:257–281. doi: 10.1085/jgp.110.3.257. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Demir SS, Clark JW, Murphey CR, Giles WR. A mathematical model of a rabbit sinoatrial node cell. American Journal of Physiology. 1994;266:C832–852. doi: 10.1152/ajpcell.1994.266.3.C832. [DOI] [PubMed] [Google Scholar]
  9. DiFrancesco D. Characterization of the pacemaker (if) current kinetics in calf Purkinje fibres. The Journal of Physiology. 1984;348:341–367. doi: 10.1113/jphysiol.1984.sp015114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. DiFrancesco D. Characterization of single pacemaker channels in cardiac sino-atrial node cells. Nature. 1986;324:470–473. doi: 10.1038/324470a0. [DOI] [PubMed] [Google Scholar]
  11. DiFrancesco D, Ducouret P, Robinson RB. Muscarinic modulation of cardiac rate at low acetylcholine concentrations. Science. 1989;243:669–671. doi: 10.1126/science.2916119. [DOI] [PubMed] [Google Scholar]
  12. DiFrancesco D, Ferroni A, Mazzanti M, Tromba C. Properties of the hyperpolarizing-activated current (if) in cells isolated from the rabbit sino-atrial node. The Journal of Physiology. 1986;377:61–88. doi: 10.1113/jphysiol.1986.sp016177. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. DiFrancesco D, Mangoni M. The modulation of single hyperpolarization-activated (if) channels by cyclic AMP in the rabbit SA node. The Journal of Physiology. 1994;474:473–482. doi: 10.1113/jphysiol.1994.sp020038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. DiFrancesco D, Noble D. A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philosophical Transactions of the Royal Society B. 1985;307:353–398. doi: 10.1098/rstb.1985.0001. [DOI] [PubMed] [Google Scholar]
  15. DiFrancesco D, Tortora P. Direct activation of cardiac pacemaker channels by intracellular cyclic AMP. Nature. 1991;351:145–147. doi: 10.1038/351145a0. [DOI] [PubMed] [Google Scholar]
  16. Dokos S, Celler B, Lovell N. Ion currents underlying sinoatrial node pacemaker activity: a new single-cell mathematical model. Journal of Theoretical Biology. 1996;181:245–272. doi: 10.1006/jtbi.1996.0129. [DOI] [PubMed] [Google Scholar]
  17. Esguerra M, Wang J, Foster CD, Adelman JP, North RA, Levitan IB. Cloned Ca2+-dependent K+ channel modulated by a functionally associated protein kinase. Nature. 1994;369:563–565. doi: 10.1038/369563a0. [DOI] [PubMed] [Google Scholar]
  18. Gauß R, Seifert R, Kaupp BU. Molecular identification of a hyperpolarization-activated channel in sea urchin sperm. Nature. 1998;393:583–587. doi: 10.1038/31248. [DOI] [PubMed] [Google Scholar]
  19. Goulding EH, Tibbs GR, Siegelbaum SA. Molecular mechanism of cyclic-nucleotide-gated channel activation. Nature. 1994;372:369–374. doi: 10.1038/372369a0. [DOI] [PubMed] [Google Scholar]
  20. Guy HR, Durell SR, Warmke J, Drysdale R, Ganetzky B. Similarities in amino acid sequences of Drosophila eag and cyclic-nucleotide-gated channels. Science. 1991;254:730. doi: 10.1126/science.1658932. [DOI] [PubMed] [Google Scholar]
  21. Hille B. Ionic Channels of Excitable Membranes. Sunderland: Sinauer; 1992. [Google Scholar]
  22. Hille B. Modulation of ion-channel function by G-protein-coupled receptors. Trends in Neurosciences. 1994;17:531–536. doi: 10.1016/0166-2236(94)90157-0. [DOI] [PubMed] [Google Scholar]
  23. Ketchum KA, Joiner WJ, Seller AJ, Kaczmarek LK, Goldstein SA. A new family of outwardly rectifying potassium channel protein with two pore domains in tandem. Nature. 1995;376:690–695. doi: 10.1038/376690a0. [DOI] [PubMed] [Google Scholar]
  24. Liu DT, Tibbs GR, Paoletti P, Siegelbaum SA. Constraining ligand-binding site stoichiometry suggests that a cyclic nucleotide-gated channel is composed of two functional dimers. Neuron. 1998;21:235–248. doi: 10.1016/s0896-6273(00)80530-9. [DOI] [PubMed] [Google Scholar]
  25. Ludewig U, Pusch M, Jentsch TJ. Two physically distinct pores in the dimeric ClC-0 chloride channel. Nature. 1996;383:340–343. doi: 10.1038/383340a0. [DOI] [PubMed] [Google Scholar]
  26. Ludwig A, Zong X, Jeglitsch M, Hofmann F, Biel M. A family of hyperpolarization-activated mammalian cation channels. Nature. 1998;393:587–591. doi: 10.1038/31255. [DOI] [PubMed] [Google Scholar]
  27. Maruoka F, Nakashima Y, Takano M, Ono K, Noma A. Cation-dependent gating of the hyperpolarization-activated cation current in the rabbit sino-atrial node cells. The Journal of Physiology. 1994;477:423–435. doi: 10.1113/jphysiol.1994.sp020204. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Middleton RE, Pheasant DJ, Miller C. Homodimeric architecture of ClC-type chloride ion channel. Nature. 1996;383:337–340. doi: 10.1038/383337a0. [DOI] [PubMed] [Google Scholar]
  29. Monod J, Wyman J, Changeux J-P. On the nature of allosteric transitions: a plausible model. Journal of Molecular Biology. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
  30. Noble D, DiFrancesco D, Denyer J. Ionic mechanisms in normal and abnormal cardiac pacemaker activity. In: Jacklet JW, editor. Neuronal and Cellular Oscillators. New York: Dekker; 1989. pp. 59–85. [Google Scholar]
  31. Ono K, Fozzard HA, Hanck DA. Mechanism of cAMP-dependent modulation of cardiac sodium channel current kinetics. Circulation Reearch. 1993;72:807–815. doi: 10.1161/01.res.72.4.807. [DOI] [PubMed] [Google Scholar]
  32. Pape HC, McCormick DA. Noradrenaline and serotonin selectively modulate thalamic burst firing by enhancing a hyperpolarization-activated cation current. Nature. 1989;340:715–718. doi: 10.1038/340715a0. [DOI] [PubMed] [Google Scholar]
  33. Santoro B, Liu DT, Yao H, Bartsch D, Kandel ER, Siegelbaum SA, Tibbs GR. Identification of a gene encoding a hyperpolarization-activated pacemaker channel of brain. Cell. 1998;93:717–729. doi: 10.1016/s0092-8674(00)81434-8. [DOI] [PubMed] [Google Scholar]
  34. Shubert B, van Dongen AMJ, Kirsch GE, Brown AM. β-adrenergic inhibition of cardiac sodium channels by dual G-protein pathways. Science. 1989;245:516–519. doi: 10.1126/science.2547248. [DOI] [PubMed] [Google Scholar]
  35. Tibbs GR, Goulding EH, Siegelbaum SA. Allosteric activation and tuning of ligand efficacy in cyclic-nucleotide-gated channels. Nature. 1997;386:612–615. doi: 10.1038/386612a0. [DOI] [PubMed] [Google Scholar]
  36. Tsien RW. Mode of action of chronotropic agents in cardiac Purkinje fibres. Journal of General Physiology. 1974;64:320–342. doi: 10.1085/jgp.64.3.320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. van Ginneken ACG, Giles W. Voltage clamp measurements of the hyperpolarization-activated inward current if in single cells from rabbit sino-atrial node. The Journal of Physiology. 1991;434:57–83. doi: 10.1113/jphysiol.1991.sp018459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Yanagihara K, Noma A, Irisawa H. Reconstruction of sinoatrial node pacemaker potential based on voltage clamp experiments. Japanese Journal of Physiology. 1980;30:841–57. doi: 10.2170/jjphysiol.30.841. [DOI] [PubMed] [Google Scholar]
  39. Zagotta WN, Siegelbaum SA. Structure and function of cyclic-nucleotide-gated channels. Annual Review of Neuroscience. 1996;19:235–263. doi: 10.1146/annurev.ne.19.030196.001315. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES