Abstract
The linear membrane responses of CA3 interneurones were determined with the use of whole-cell patch recording methods. The mean input resistance (RN) for all cells in this study was 526 ± 16 MΩ and the slowest membrane time constant (τ0) was 73 ± 3 ms.
The three-dimensional morphology of 63 biocytin-labelled neurones was used to construct compartmental models. Specific membrane resistivity (Rm) and specific membrane capacitance (Cm) were estimated by fitting the linear membrane response. Acceptable fits were obtained for 24 CA3 interneurones. The mean Rmwas 61.9 ± 34.2 Ω cm2 and the mean Cm was 0.9 ± 0.3 μF cm−2. Intracellular resistance (Ri) could not be resolved in this study.
Examination of voltage attenuation revealed a significantly low synaptic efficiency from most dendritic synaptic input locations to the soma.
Simulations of excitatory postsynaptic potentials (EPSPs) were analysed at both the site of synaptic input and at the soma. There was little variability in the depolarization at the soma from synaptic inputs placed at different locations along the dendritic tree. The EPSP amplitude at the site of synaptic input was progressively larger with distance from the soma, consistent with a progressive increase in input impedance.
The ‘iso-efficiency’ of spatially different synaptic inputs arose from two opposing factors: an increase in EPSP amplitude at the synapse with distance from the soma was opposed by a nearly equivalent increase in voltage attenuation. These simulations suggest that, in these particular neurones, the amplitude of EPSPs measured at the soma will not be significantly affected by the location of synaptic inputs.
The firing of inhibitory interneurones, like all excitable neurones, is contingent upon how synaptic potentials are integrated and how action potentials are triggered. The electrotonic structure of a neurone, determined by its morphology and passive membrane properties, underlies the integration of synaptic signals, as well as voltage-dependent interactions between synapses (Rall, 1962). In turn, the analysis of electrotonic structure forms the framework for studying the active properties of neurones as it shapes the temporal and spatial distribution of potentials that activate non-linear conductances. The detailed examination of neuronal electrotonic structure has been performed for many types of neurones including CA1 pyramidal neurones, CA3 pyramidal neurones, neocortical pyramidal neurones, cerebellar Purkinje cells, motor neurones and CA1 interneurones (Stratford et al. 1989; Major et al. 1994; Rapp et al. 1994; Mainen et al. 1996; Carnevale et al. 1997). The general principles of cable theory, first developed by Rall (1962), are supported in all of these models (e.g. synaptic signals attenuate from the dendrite to the soma).
Miles (1990) demonstrated in a dual-cell recording study that CA3 interneurones fire with a high probability and short latency in response to a presumed unitary synaptic input from CA3 pyramidal neurones. More recent studies also report a short latency between principal neurone and interneurone firing (Ali et al. 1998; Csicsvari et al. 1998). To account for this result, Traub & Miles (1995) proposed that the dendrites of interneurones have active conductances that increase the likelihood of action potential firing. We do not know whether the dendrites of CA3 interneurones are capable of generating spikes or whether action potentials are typically generated at the initial segment or axon (see Traub & Miles, 1995). Will excitatory postsynaptic potentials (EPSPs) be of a sufficient magnitude at the soma or the dendrites to even trigger spikes? In either case, it is important to understand the underlying biophysical consequences of EPSP stimulation and integration in these neurones.
Here we describe the passive electrotonic properties of hippocampal CA3 interneurones, which are all presumed to be inhibitory (Johansen et al. 1989). For this analysis, the passive membrane parameters of individual neurones were estimated by fitting linear membrane responses with those of corresponding interneurone models. The electrotonic properties of interneurones from all five laminar substrata (stratum (s.) lacunosum-moleculare to s. oriens) of the CA3 region were analysed. We show how, in these neurones, despite differences in synaptic location onto the dendrites, the variation of postsynaptic potential (PSP) amplitudes at the soma may be surprisingly small.
METHODS
Hippocampal slices
Experiments were performed in accordance with the guidelines approved by the University of Texas at San Antonio Institutional Animal Care and Use Committee. Sprague-Dawley rats (17–30 days old) were anaesthetized with halothane (Sigma) and killed by decapitation. Coronal sections (300 μm) containing transverse sections of hippocampus were vibratome sliced in artificial cerebrospinal fluid (ACSF) at 4°C. The ACSF contained (mM): 124 choline chloride, 2.5 KCl, 26 NaHCO2, 4 MgCl2, 0 CaCl2, 1.25 NaHPO4 and 10 dextrose. Slices were maintained in a holding chamber at room temperature (∼25–27°C) in oxygenated ACSF (95 % O2-5 % CO2) in which choline chloride was replaced with NaCl, and both MgCl2 and CaCl2 were adjusted to 2 mM. Slices were transferred as needed to a submersion-type recording chamber perfused with oxygenated ACSF (∼1 ml min−1), also at room temperature.
Electrophysiology
Whole-cell patch clamp recordings were made from visually identified CA3 non-pyramidal cells using IR/DIC (infrared/differential interference contrast) video microscopy (Stuart et al. 1993). Initial micropipette resistance was 3–5 MΩ. Cell bodies were patched 50–100 μm from the surface of the slice. Series resistance was typically less than 10 MΩ. The pipette saline contained (mM): 120 potassium gluconate or potassium methyl sulphate, 20 KCl, 0.1 EGTA, 2 MgCl2, 2 Na2ATP and 10 Hepes (pH = 7.3). Pipettes were backfilled with saline containing 0.5–0.2 % biocytin (Sigma) or Neurobiotin (Vector Laboratories, Burlingame, CA, USA). Electrical recordings were made using an Axoclamp-2B (Axon Instruments, Foster City, CA, USA) in bridge mode and digitized at 1–3 kHz using an ITC-16 interface (Instrutech, Great Neck, NY, USA) connected to a Power Macintosh computer running AxoData (Axon Instruments) acquisition software. Analysis of electrical data was performed using custom software written with Igor Pro (Wavemetrics, Lake Oswego, OR, USA).
Voltage-current (V−I) relationships were constructed from a series of 350–500 ms hyperpolarizing and depolarizing current injections within the linear range of the membrane potential (≤± 10 mV of resting potential). Linear regression analysis of V−I relationships was used to determine the input resistance (RN) of each cell. The slowest membrane time constant (τ0) was determined by fitting either single or double exponential functions to the average of 50–100 membrane responses to identical current injections by either least-squares minimization or a Fourier method using DISCRETE (Provincher, 1976).
Histology
Cells were filled with biocytin or Neurobiotin by passive diffusion during whole-cell recordings (30–60 min). After each experiment, slices were immediately fixed in 3 % glutaraldehyde at 4°C for at least 24 h. They were then washed in 0.1 M phosphate buffer (PB) six times (5 min per wash) and incubated in 1 % Triton X-100 (30 min). Endogenous peroxidase activity was quenched by incubation in 0.5 % H2O2 for 30 min. Slices were again washed in 0.1 M PB six times (5 min per wash) and left overnight at 4°C with avidin-HRP conjugate (Vector Laboratories ABC Kit), diluted 1 : 200 with 0.1 % bovine serum albumin. The following day they were washed in 0.1 M PB for at least 1 h and then incubated in diaminobenzadine dihydrochloride (DAB; Cappel, West Chester, PA, USA) and 120 μM nickel ammonium sulphate for 1 h. Finally, slices were exposed to 1 % H2O2 for 30–60 min. The reaction was stopped by washing in 0.1 M PB. Slices were cleared in ascending concentrations of glycerol and stored at room temperature. Shrinkage of tissue was less than 5 % following histological processing.
Three-dimensional reconstruction, quantitative analysis and computer modelling
Non-resectioned slices were mounted and three-dimensional reconstructions were performed using a computer-controlled indexing system (Claiborne, 1992). Briefly, dendrites were visualized on a Nikon Optiphot microscope under a × 63 oil-immersion objective (1.3 NA). Co-ordinates and diameters were determined for the soma, dendritic branch points and dendritic continuations at approximately 5 μm intervals. Co-ordinates and diameters were converted to cylindrical compartments using custom software. The mean number of compartments was 1323 ± 450 for 63 non-pyramidal neurone reconstructions. Each neurone was compared, under low magnification (× 20–40), to a two-dimensional rendering of its geometry to confirm complete reconstruction of all dendrites. Low-magnification visualization was also used to assess the number of dendrites leaving the plane of the slice. Finally, the resolution of the reconstruction system was checked by comparing a sample of dendritic diameters to those determined from a × 100 oil-immersion objective (1.4 NA) on a Zeiss Axioskop. Measurements were performed by digitally capturing a micrograph of an identified segment and measuring the diameter with NIH Image (Research Services Branch, National Institute of Mental Health, Washington, DC, USA). Diameters taken from the reconstruction system were within 5 % of values determined under the × 100 objective. Dendritic co-ordinates and diameters were used to construct compartmental neurone models using NEURON (Hines & Carnevale, 1997). All simulations and calculations were computed on R4400 Silicon Graphic workstations. Least-squares minimization was performed using the principal axis method (PRAXIS), part of the standard distribution of NEURON (Hines & Carnevale, 1997).
To simulate the effects of a fast and slow conductance-change synapse, a model non-NMDA or NMDA receptor-mediated synaptic conductance (Holmes & Levy, 1990) was applied to each dendritic compartment of the model neurones.
Classical analyses of voltage attenuation assumes the imposition of a potential (at a given frequency) at one location while the transmitted voltage at some distal location is determined (Carnevale et al. 1997). Since unitary PSPs onto hippocampal interneurones are a very small percentage of the total driving force (Miles, 1990), they can be considered as a current source. Therefore, both transfer impedance (Zc) and input impedance (ZN) were analysed (1) to confirm the results using the non-NMDA receptor-mediated conductance model and (2) to provide a means of examining the membrane response at both the synapse and the soma over a wide range of frequencies. Specifically, the potential at location j (Vj) can be determined from the synaptic current applied at another location i (source; Ii) if one knows Zc between the two points, such that Vj=IiZc. In some cases, we found it convenient to express Zc normalized to the soma (c), where c approaches 1 for the most proximal input locations. Additionally, the local potential at a current source i (Vi) is determined from ZN, where Vi=IiZN. Both Zc and ZN at all dendritic locations were determined analytically with the methods developed by Tsai et al. (1994), part of the standard distribution of NEURON (Hines & Carnevale, 1997).
Statistics
All results are presented as means ±s.d. Comparisons between two groups were performed using Student's t test for unpaired data. Comparisons among more than two groups were analysed using a one-way analysis of variance (ANOVA) and Scheffé‘s multiple comparison.
RESULTS
Experimental
Linear membrane response
The V−I relationship was determined for all CA3 non-pyramidal neurones studied. The membrane responses to depolarizing and hyperpolarizing current steps (350–500 ms duration) were obtained from the resting potential (mean Vm=−64.9 ± 4.1 mV). As illustrated in Fig. 1B and D, the steady-state membrane response within ± 10 mV of the resting potential was linear, exhibiting no ‘sag’ due to the activation of a hyperpolarization-activated current (Ih). The lack of sag at these potentials does not rule out the activation of Ih with stronger hyperpolarization (Maccaferri & McBain, 1996; Spruston et al. 1997). Spontaneous PSPs were frequently observed in the steady-state portion of the response (> 200 ms from the onset of the current pulse), adding to the noise seen in some of the V−I relationships. RN was determined by taking the regression slope of the V−I relationship (Fig. 1B). The mean RN for all non-pyramidal cells studied was 526 ± 16 MΩ (n = 224). There were no significant differences in RN when we compared neurones across the five laminar substrata (Table 1).
Figure 1. Linear membrane response of a CA3 interneurone from s. lacunosum-moleculare.
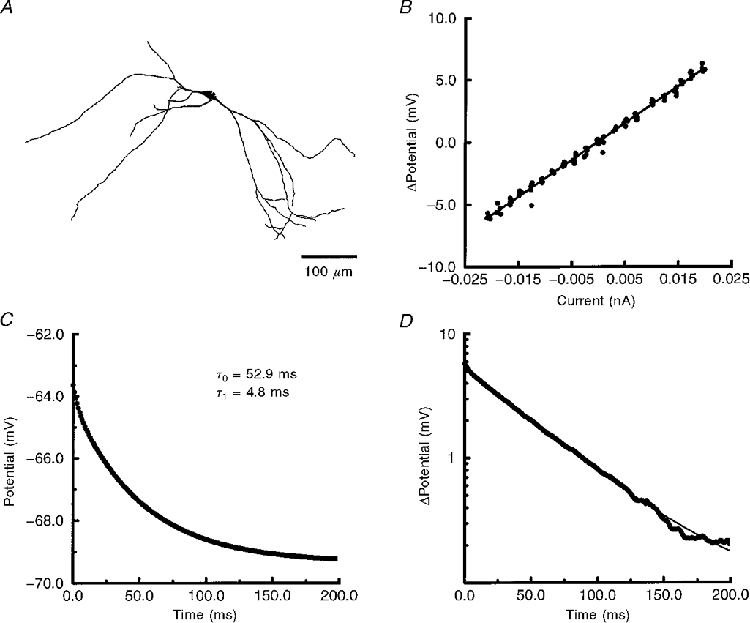
A, morphology of cell 970120A. B, voltage-current (V−I) relationship of the steady-state membrane response. The RN of this cell, determined from the slope of linear regression analysis (continuous line), was 296 MΩ. C, the average of 100 hyperpolarizing transients (continuous line) was best fitted by two exponentials (filled circles). The membrane response and fitted exponentials are superimposed. D, semilogarithmic analysis of the membrane transient. The membrane response (thick trace) was fitted by the two exponentials (thin trace). No significant ‘sag’ in the hyperpolarizing response was observed here or in the V−I relationship (B).
Table 1.
Measurements of τ0 and RN in CA3 interneurones
| Substratum | τ0(ms) | RN(MΩ) |
|---|---|---|
| s. oriens(5) | 48.8 ± 4.7 | 374.4 ± 110.8 |
| s. pyramidale(2) | 27, 54 | 219, 344 |
| s. lucidum(5) | 46.9 ± 16.7 | 388.8 ± 282.7 |
| s. radiatum(5) | 65.7 ± 21.3 | 527.4 ± 194.9 |
| s. lacunosum-moleculare(7) | 68.7 ± 35.6 | 505.4 ± 211.7 |
| Total(24) | 57.0 ± 24.4 | 439.8 ± 203.3 |
Numbers in parentheses are the total number of neurones.
Membrane charging responses, within the linear range of the cell (determined above), were acquired from the resting potential by taking the average of 50–100 hyperpolarizing current steps. Membrane charging was best fitted in 176 of 224 cells by two time constants (Fig. 1C). The mean slowest time constant (τ0) was 73 ± 3 ms (n = 224). Stationarity was checked by determining τ0 for five sub-averages taken sequentially across the total number of charging responses. We found no significant change in τ0 during the acquisition of the grand mean. When we compared τ0 across the five laminar substrata, there were no significant differences (see Table 1).
We were concerned that cut dendrites might be responsible for high values of RN. RN for each cell was plotted against the number of cut dendrites, identified as those dendrites leaving the surface of the slice and with typical ‘blebbing’ at the tips. There was no significant correlation (r2= 0.003, n = 63) between the number of cut dendrites and RN. Therefore the surface area lost by cut dendrites was not a significant proportion of the total surface area of these neurones.
Neurone models
Passive membrane properties
Measurements of τ0, RN and the averaged membrane response, determined above, were used to estimate the passive membrane parameters specific membrane resistivity (Rm), specific membrane capacitance (Cm) and intracellular resistance (Ri) for individual CA3 interneurones. A total of 63 neurone reconstructions were accepted for the modelling portion of this study. Reconstructions were not included if labelling was incomplete, the background was too high to resolve all dendrites, or if the soma was significantly distorted due to removal of the patch pipette.
We started by the common assumption that Cm might be close to 1 μF cm−2 (Spruston & Johnston, 1992; Carnevale et al. 1997). Rm was therefore determined from τ0 for each neurone. Ri was set to 200 Ω cm. Variation of Ri between 50–400 Ω cm had no significant effect on RN (described below). These parameters were used to construct 63 passive compartmental interneurone models. When we compared the RN of our model non-pyramidal neurones to their measured values of RN, we found that the mean difference was 12 ± 6 % (Fig. 2). This slight tendency for the models to have a higher RN was due to 11 cells whose difference in RN was greater than 50 %. However, the variance in the difference between measured and modelled RN could suggest cell-to-cell variability in passive membrane properties.
Figure 2. Distribution of the percentage difference between RN measured experimentally and RN of the 63 modelled interneurones.
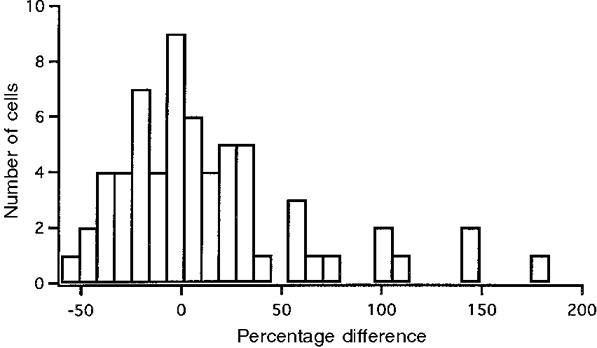
The mean of this sample was not significantly different from that predicted by the hypothesis that there was zero difference between modelled and measured RN.
We next estimated Rm, Ri and Cm for each CA3 interneurone. The methods used here were very similar to those used in a number of previous studies (Stratford et al. 1989; Rall et al. 1992; Major et al. 1994; Rapp et al. 1994; Thurbon et al. 1994; Thurbon et al. 1998). The general procedure is to fit (with the least-squares minimization routine PRAXIS) the membrane response of a model neurone to the membrane response determined experimentally by adjusting Rm, Ri and Cm (Rall et al. 1992). Optimal fits were accepted when they were within the 95 % confidence bands of the experimental average (Major et al. 1994; Thurbon et al. 1998).
Before determining the three passive membrane parameters, we performed a number of tests to evaluate: (1) how patch pipettes affected the experimentally measured membrane responses, (2) the effect on the membrane response of varying the three passive membrane parameters, (3) the fitting procedure, (4) the calibration of our measurements, and (5) how noise affected the accuracy of the fitting procedure.
As described in detail by both Major et al. (1994) and Thurbon et al. (1998), the pipette can contribute significant artifacts when measuring potential and passing current simultaneously. Our initial pipette resistances were 3–5 MΩ, while series resistance during whole-cell recordings was in worst cases still less than 25 MΩ. Unused 3–5 MΩ pipettes placed into the recording chamber at a depth equivalent to the hippocampal slices charged within 1 ms. Even if under worst-case conditions charging of the pipette was ∼5 ms, contamination would be less than 3 % of the total response. In addition, because of the high RN of CA3 interneurones the current needed to hyperpolarize the membrane by 5–10 mV was less than 30 pA. The steady-state error due to a lack of bridge balance would be less than 0.15 mV - less than 2 % of the steady-state response. Therefore, any contamination by the pipette should not significantly affect the measured membrane response.
The effects of varying Rm, Cm and Ri on the voltage response were examined. As shown in Fig. 3, the simulated response for a typical interneurone was most sensitive to Rm. Varying Rm affected both the transient and steady-state portions of the waveform, while varying Cm affected the transient, but not the steady-state, response, as expected (Johnston & Wu, 1995). In contrast, a 10-fold difference in Ri had very little effect on the waveform (Fig. 3C). Even though the 95 % confidence limits of our measured responses were typically less than ± 0.2 mV from the mean (see Fig. 5), there was an inherent difficulty in deriving Ri from these data.
Figure 3. Effects of varying passive membrane parameters on a simulated membrane response.
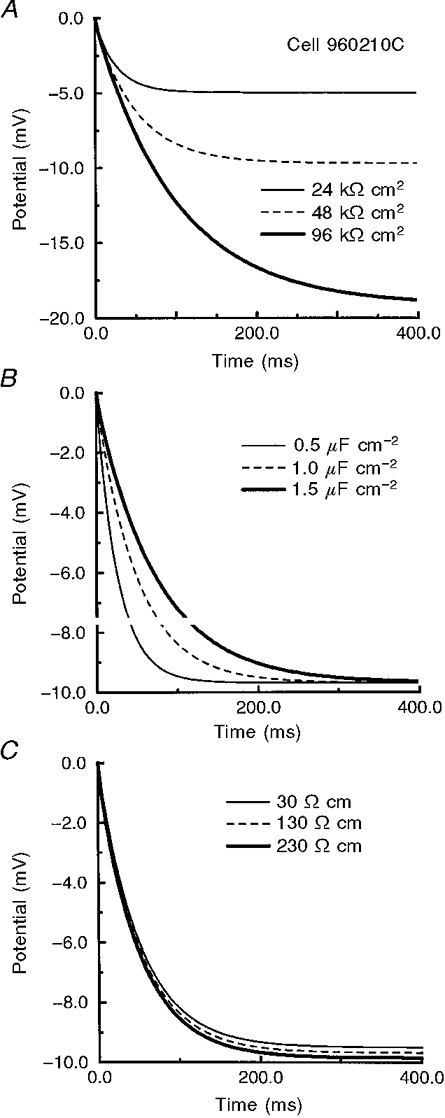
The membrane response of cell 960210C for various combinations of passive membrane parameters. Varying Rm (A) affected both the transient and steady-state portion of the response while differences in Cm (B) affected only the transient part of the response. When Ri was varied (C) there was less than a 0.5 mV difference in both the steady-state and transient portions of the response.
Figure 5. Examples of rejected and accepted fits.
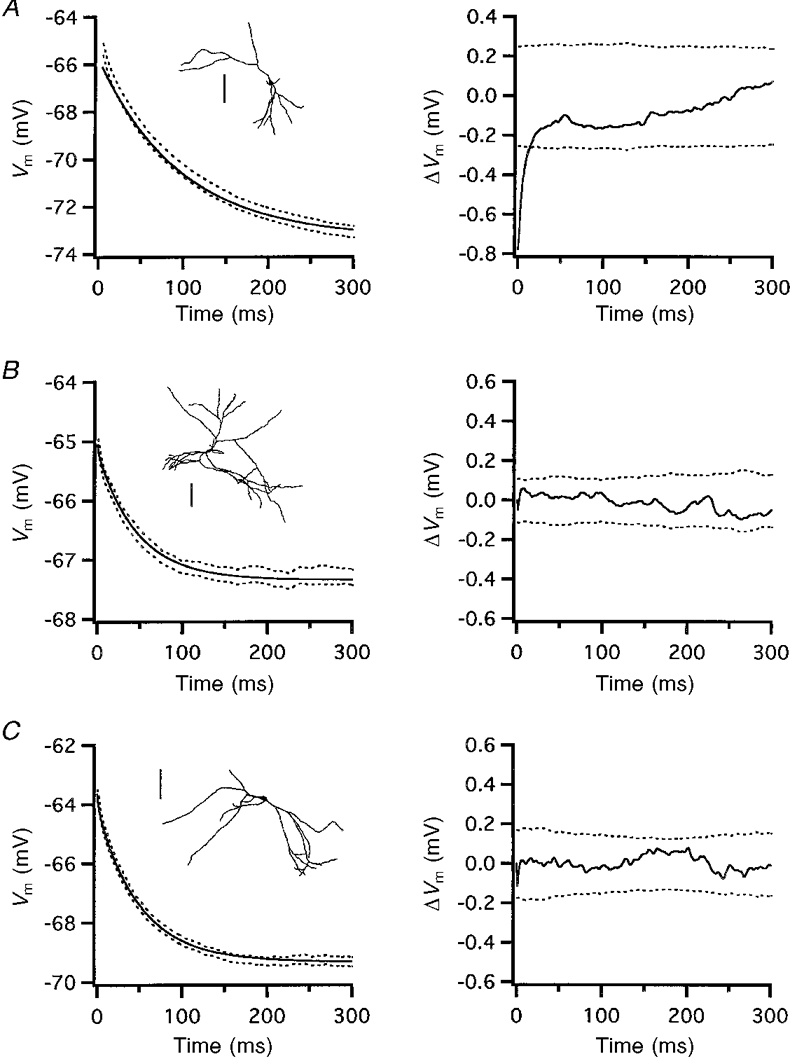
Insets in A−C, reconstructions of cells 970217B, 970212A and 970120A, respectively. Scale bars, 100 μm. A, rejected fit of 970217B. B and C, accepted fits of 970212A and 970120A. Fits were accepted if they were within the 95 % confidence bands. The graphs on the left show the best-fit simulated membrane transient (continuous lines) and the 95 % confidence bands from the grand mean of the membrane responses (dashed lines). The graphs on the right show mean residuals (continuous lines) with the residual 95 % confidence bands (dashed lines). Vm, membrane potential.
We evaluated the accuracy of the fitting procedure by a number of controls. First, we tested the fitting procedure on a parallel resistor/capacitor model cell. The exact values for the resistor and capacitor were recovered (data not shown). In addition to testing the fitting procedure, the model cell provided a confirmation of the calibration of the amplifier and the data acquisition system. Second, we checked the effect of noise on the fitting procedure. Worst-case root mean square (r.m.s.) noise, determined from a 1 s trace acquired in the absence of somatic current injection, was 0.58 mV. The noise-free response of a model cell was generated with known values of Rm, Ri and Cm (the ‘true’ values of these three parameters). A uniform distribution (uniform power density at all frequencies) of r.m.s. noise (range, 0.25–10 mV) was added to the noise-free response and averaged for 100 traces (Fig. 4). When the fitting procedure was applied to these waveforms, the true values of Rm and Cm, but not Ri, were recovered for r.m.s. noise ≤ 1 mV (Table 2). Ri was only recovered in the noise-free case. In the extreme case of 10 mV noise, the difference in Cm was less than 10 % of the true value. Finally, all results were independent of initial parameters (data not shown). Therefore the fitting procedure could resolve Rm and Cm, even with our worst-case experimental noise, but the estimates of Ri inherently would not be unique.
Figure 4. Experimental noise does not affect resolution of passive membrane parameters.
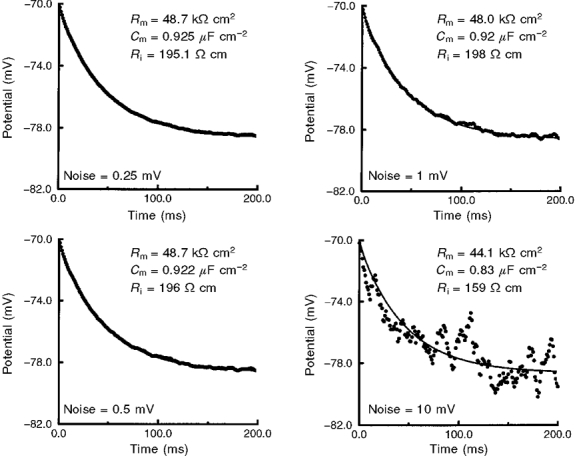
Experimental worst-case r.m.s. noise was 0.58 mV. White r.m.s. noise was added to the noise-free membrane response (generated with Rm= 49 kΩ cm2, Cm= 0.92 μF cm−2 and Ri= 184 Ω cm) of cell 960210B and averaged (n = 100). Resolved values of Rm, Cm and Ri are shown for each noise level. Rm and Cm, but not Ri, were resolved by the fitting procedure for r.m.s. noise between 0.25 and 1 mV. An acceptable fit was not achieved for 10 mV r.m.s. noise (lower right panel); the ‘true’ values of Rm and Cm were resolved.
Table 2.
Effect of noise on optimal fit parameters
| Rm(kΩ cm2) | Cm(μF cm−2) | Ri(Ω cm) | |
|---|---|---|---|
| ‘True’ values | 49 | 0.92 | 184 |
| r.m.s. noise | |||
| 0 mV | 49.0 | 0.92 | 184 |
| 0.25 mV | 48.7 | 0.925 | 195 |
| 0.5 mV | 48.7 | 0.922 | 196 |
| 1 mV | 48.0 | 0.92 | 198 |
| 10 mV | 44.1 | 0.83 | 159 |
Starting values: Rm= 10 kΩ cm2, Cm= 1 μF cm−2 and Ri= 100 Ω cm. r.m.s., root mean square.
When the fitting procedure was applied to each neurone model, acceptable fits were obtained for 24 cells (Table 3). Examples of the fits and residuals from two accepted and one rejected cell are shown in Fig. 5. Rejected cells typically failed in the initial 20–25 ms of the fit (Fig. 5A). None of the cells with a greater than 50 % difference in modelled versus measured RN (see Fig. 2) passed the 95 % confidence limit test.
Table 3.
Parameters estimated from optimal fits
| Substratum | Ri(Ω cm) | Rm(kΩ cm2) | Cm(μF cm−2) | τ0/RmCm |
|---|---|---|---|---|
| s. oriens(5) | 144 ± 58 | 56 ± 19 | 1.10 ± 0.58 | 1.15 ± 0.40 |
| s. pyramidale(2) | 55, 314 | 22, 78 | 1.38, 0.43 | 1, 0.53 |
| s. lucidum(5) | 140 ± 44 | 47 ± 19 | 0.91 ± 0.12 | 0.85 ± 0.90 |
| s. radiatum(5) | 222 ± 176 | 62 ± 12 | 0.98 ± 0.14 | 0.93 ± 0.14 |
| s. lacunosum-moleculare(7) | 235 ± 166 | 80 ± 55 | 0.92 ± 0.35 | 0.82 ± 0.15 |
| Total(24) | 189 ± 130 | 62 ± 34 | 0.92 ± 0.34 | 0.91 ± 0.25 |
Numbers in parentheses are the total number of neurones.
Mean estimated Rm was not significantly different from Rm determined from τ0 (Table 3). Correspondingly, there was no significant difference between the mean Cm and a hypothesized mean of 1 μF cm−2. Although the estimated values for Ri were within the range determined in previous studies (Stratford et al. 1989; Major et al. 1994; Thurbon et al. 1994, 1998; but see Stuart & Spruston, 1998), our initial tests of the fitting procedures suggested that we could not make an accurate determination of Ri (described above). Furthermore, we tested whether adjusting values of Ri affected the accuracy of the fit. As expected, fixing Ri to ± 50 % of its estimated value resulted in no significant difference between the values of Rm and Cm determined by the fitting procedure (data not shown).
The passive membrane properties of most neurones are not likely to be uniform throughout the dendritic tree. Stuart & Spruston (1998) recently demonstrated that Ih in neocortical pyramidal neurone dendrites increases with distance from the soma. Acceptable fits were obtained when Rm was allowed to linearly decrease or increase with distance from the soma (simulations not shown). In either case, acceptable fits were obtained when the mean Rm was equal to the uniformly distributed estimate of Rm (see Table 6).
Table 6.
Frequency and parameter dependence of synaptic ‘iso-efficiency’
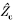 c c
|
||||
|---|---|---|---|---|
| DC | 20 Hz | 40 Hz | Normalized EPSP at soma | |
| Rm= 60.5 kΩ cm2 | 0.95 ± 0.04 | 0.89 ± 0.08 | 0.77 ± 0.16 | 0.87 ± 0.08 |
| Rm= 15 kΩ cm2 | 0.86 ± 0.10 | 0.81 ± 0.13 | 0.73 ± 0.19 | 0.76 ± 0.15 |
| Rm= 81 ± 35 kΩ cm2† | 0.95 ± 0.04 | 0.88 ± 0.09 | 0.77 ± 0.17 | 0.87 ± 0.08 |
| Ri= 80 Ω cm | 0.98 ± 0.02 | 0.95 ± 0.03 | 0.91 ± 0.07 | 0.95 ± 0.04 |
 c, transfer impedance normalized to the soma. Calculations from cell 951220A. Optimal fit parameters: Rm= 60.5 kΩ cm2, Ri= 169 Ω cm, Cm= 1.13 μF cm−2. All values are means ± S.D.
c, transfer impedance normalized to the soma. Calculations from cell 951220A. Optimal fit parameters: Rm= 60.5 kΩ cm2, Ri= 169 Ω cm, Cm= 1.13 μF cm−2. All values are means ± S.D.
Rm was decreased linearly with distance from the soma.
These 24 model neurones and their corresponding estimated passive membrane parameters were used in the following calculations and simulations.
Voltage attenuation
We started our examination by performing an analysis of voltage attenuation profiles (Stratford et al. 1989; Thurbon et al. 1994; Major et al. 1994; Rapp et al. 1994; Spruston et al. 1994; Mainen et al. 1996; Carnevale et al. 1997; Thurbon et al. 1998). Voltage attenuation was calculated as the ratio of potential at a given location (Vi) and the potential at some other distal location (Vj) as Vi/Vj. For the sake of comparison, we chose to present voltage attenuation as the logarithm of this ratio from either the soma to any dendritic location (Lout) or from any dendritic location to the soma (Lin) (Carnevale et al. 1997). Therefore, if there is no loss of signal between two points (Vi/Vj= 1), Lin or Lout between these two points would have a value of zero.
As demonstrated in other studies (Carnevale & Johnnston, 1982; Carnevale et al. 1997), two general ‘rules’ of voltage attenuation hold true for non-pyramidal neurones. First, Lin was greater than Lout (Table 4). For all 24 cells, mean Lin for 40 Hz signals was 1.7 ± 0.3 log units of attenuation. This translates to a mean 78 % loss of signal from any given synaptic location to the soma. In contrast, mean Lout for 40 Hz signals was 0.5 ± 0.3 log units of attenuation, corresponding to a mean 33 % decrease in signal amplitude. Second, AC signals (e.g. a synapse with fast kinetics) attenuated significantly more than DC signals. Both Lin and Lout increased with signal frequency (Table 4). A synaptic response with fast kinetics will attenuate more than a slow synaptic response or the temporal summation of synaptic potentials. When Lin and Lout were examined between interneurones in the five laminar substrata, again we found no significant differences.
Table 4.
Analysis of voltage attenuation in CA3 interneurones at different signal frequencies
| Lin | Lout | |||
|---|---|---|---|---|
| Substratum | DC | 40 Hz | DC | 40 Hz |
| s. oriens(5) | 0.39 ± 0.08 | 1.54 ± 0.37 | 0.08 ± 0.04 | 0.44 ± 0.24 |
| s. pyramidale(2) | 0.73, 0.36 | 1.63, 1.87 | 0.17, 0.04 | 0.49, 0.28 |
| s. lucidum(5) | 0.49 ± 0.19 | 1.56 ± 0.21 | 0.07 ± 0.03 | 0.30 ± 0.09 |
| s. radiatum(5) | 0.36 ± 0.13 | 1.62 ± 0.24 | 0.05 ± 0.02 | 0.37 ± 0.15 |
| s. lacunosum-moleculare(7) | 0.44 ± 0.13 | 1.82 ± 0.52 | 0.07 ± 0.03 | 0.53 ± 0.31 |
Lin, mean logarithm of voltage attenuation from any dendritic location to the soma (log(Vdendrite/Vsoma)); Lout, mean logarithm of voltage attenuation from the soma to any dendritic location (log(Vsoma/Vdendrite)). Numbers in parentheses are the total number of neurones.
The difference in voltage attenuation with the spatial location of a synapse onto a dendrite has been referred to as location-dependent variability of synaptic input (Cook & Johnston, 1997). As synapses are placed further from the soma, the strength of the synapse at the soma decreases. Therefore, given the large magnitude of voltage attenuation from most dendritic locations to the soma of these interneurones, one would predict that synapses placed at varying distances from the soma will produce a wide range of depolarization at the soma; proximal synapses should be more effective at reaching threshold than more distal synapses.
Conductance-change/current-source synapses
Measurements of voltage attenuation, such as presented above, tell us how much signal loss will occur between two points on a neurone. What is sometimes overlooked is that the local PSP amplitude at the synapse, assuming a given synaptic conductance, will vary depending on its dendritic location. In the next series of simulations, a 500 pS conductance-change synapse (reversal potential = 0 mV) was sequentially placed at all dendritic locations of model CA3 non-pyramidal neurones. The EPSP amplitude was determined simultaneously at two locations: in the dendrites at the site of synaptic input and at the soma.
The amplitude of EPSPs measured at the site of a synaptic input increased with distance from the soma (Fig. 6B), consistent with a progressive increase in dendritic input impedance (Rapp et al. 1994; Segev et al. 1995). There was, as expected, a significant loss of EPSP amplitude from the site of a dendritic synaptic input to the soma. On average, the EPSP amplitude at sites of synaptic input was approximately 2- to 3-fold larger than that at the soma (Table 5). As the position of a synapse was placed further from the soma, the EPSP reaching the soma decreased in amplitude (Fig. 6C). At the same time, the rise time increased as synaptic position was placed further from the soma (Fig. 6D), consistent with cable filtering. All of these findings are in accord with classical cable theory (Johnston & Wu, 1995).
Figure 6. Responses of simulated EPSPs at sites of synpatic input and at the soma.
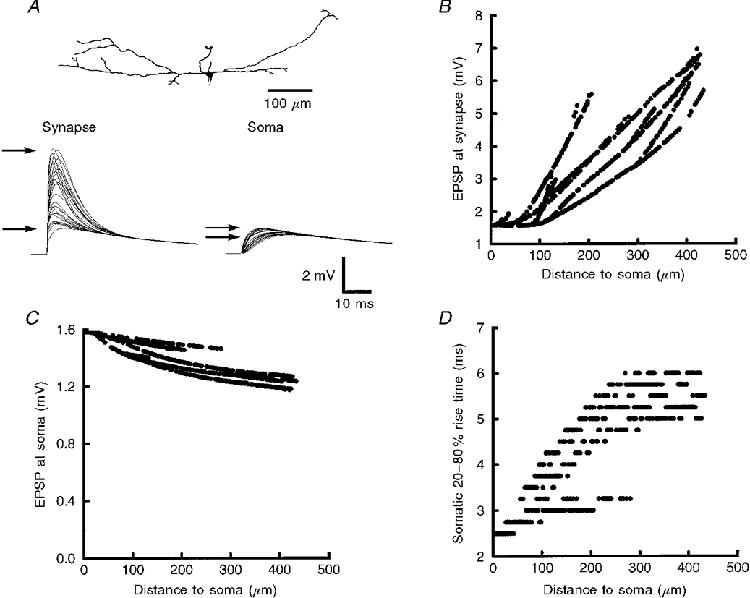
A, conductance-change synapses were individually activated at all dendritic locations of cell 960210B (top). A sample of 25 EPSPs at each site of synaptic input and the corresponding EPSPs at the soma are plotted (bottom). Arrows point to the difference in the range of EPSP amplitude at the synapses compared with EPSP amplitudes at the soma. B, EPSP amplitude measured at the site of synaptic input increased by more than 4-fold with distance from the soma. C, depolarization at the soma decreased as the location of synaptic input was progressively further from the soma by only 0.4 mV (≈25 %). D, EPSP rise time at the soma increased as inputs were further from the soma. The increase in rise time with distance from the soma was more than 2-fold.
Table 5.
Differences in location-dependent variability between the sites of synaptic input versus depolarization at the soma
| EPSPs at synaptic input(mV) | EPSPs at soma(mV) | |||
|---|---|---|---|---|
| Substratum | Mean | c.v. | Mean | c.v. |
| s. oriens(5) | 2.26 ± 0.10 | 0.42 ± 0.06 | 0.77 ± 0.24 | 0.10 ± 0.06 |
| s. pyramidale(2) | 2.84, 2.08 | 0.43, 0.45 | 0.75, 0.45 | 0.15, 0.06 |
| s. lucidum(5) | 2.39 ± 0.54 | 0.50 ± 0.13 | 0.79 ± 0.53 | 0.08 ± 0.05 |
| s. radiatum(5) | 2.82 ± 0.66 | 0.36 ± 0.03 | 1.26 ± 0.46 | 0.10 ± 0.06 |
| s. lacunosum-moleculare(7) | 2.39 ± 0.66 | 0.51 ± 0.22 | 0.88 ± 0.34 | 0.09 ± 0.06 |
c.v., coefficient of variation. Numbers in parentheses are the total number of neurones.
In spite of the fact that the magnitude of voltage attenuation from a synapse to the soma is highly dependent upon the location of the synapse on the dendrite, we noticed that the range and variance of depolarization at the soma were quite small (Fig. 6A and C). The difference in somatic EPSP amplitude produced by the most proximal and distal synaptic inputs was typically less than 25 %. In contrast, depolarization at sites of synaptic input was highly variable. The most distal synaptic inputs produced a local EPSP that was approximately 4 times larger than that from an equivalent synapse onto the soma (Fig. 6B). This is illustrated in Table 5 where the coefficient of variation of EPSP amplitude at the synaptic input was approximately 4-fold higher than that of the depolarization produced at the soma. In other words, there was very little effect of synaptic location on the amplitude of depolarization at the soma. All synaptic locations onto the dendrites of these neurones were relatively ‘iso-efficient’ (Segev et al. 1995). Analysis of all 24 cells from the five laminar substrata revealed similar results (Table 5). Finally, to test the effects of changes in driving force, we varied the strength of the synaptic input. Adjusting the peak amplitude of the conductance change from 0.5 to 2 nS had no significant effect on the coefficient of variation (simulations not shown).
To examine the effects of differing PSP kinetics, we performed identical simulations with a model NMDA receptor-mediated conductance. For this slower model synapse the voltage-dependent Mg2+ block was removed ([Mg2+]o= 0 mM). The iso-efficiency of these model synapses placed throughout the dendritic tree of CA3 interneurones was even greater than that for the non-NMDA receptor-mediated synapse. The difference in somatic depolarization produced by the most distal and proximal inputs was less than 10 % (simulations not shown).
We next compared the range of depolarization at the soma produced by synaptic inputs at varying dendritic locations against the distribution of transfer impedance (Zc) from these same sites to the soma. Analysis of Zc tells us what the relative amplitude of a PSP at the soma will be in response to a dendritic current at any chosen frequency (see Methods). This metric was utilized for two reasons. First, it represents an analytical comparison with our numerical simulations. Second, it is possible that these neurones are innervated by PSPs with differing kinetics. Because Zc can be analysed at any frequency, the frequency dependence of synaptic efficiency can be examined.
We first found that the range of depolarization at the soma produced by non-NMDA receptor model synapses placed sequentially at all dendritic compartments closely matched the profile of Zc for 20 Hz signals for the same dendritic locations (Fig. 7A and B). As shown in Table 6, the mean normalized EPSP amplitude at the soma closely matched the transfer impedance normalized to the soma (c) for this frequency.
Figure 7. Relationship between the location dependence of EPSP amplitudes, transfer impedance and input impedance.
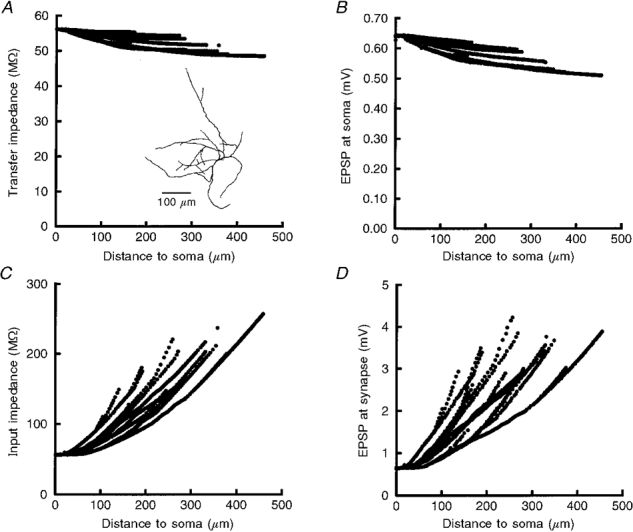
A, spatial profile of transfer impedance (Zc) for 20 Hz signals from all dendritic locations to the soma. The range differed across distance from the soma by less than 15 %, indicating that a 20 Hz current signal from the most distal sites will be only 15 % smaller at the soma than at the most proximal locations. Inset, reconstruction of cell 960427A. B, depolarization at the soma in response to synaptic inputs at all locations of the cell. Here the range of EPSP amplitudes was 0.13 mV (≈20 %). C, input impedance (ZN) calculated for 20 Hz signals increased with distance from the soma. D, consistent with the increase in input impedance with distance from the soma, EPSP amplitudes measured at all sites of synaptic input also progressively increased with distance from the soma. The multiple frequency components of the synaptic conductance change produce the subtle differences between panels A and B and C and D.
From the results in Fig. 7A and B, it can be seen that the maximum depolarization at the soma will be produced by those synapses closest to the soma. More interestingly, as described above, the range of EPSPs at the soma produced by the most proximal and distal synaptic inputs will vary by less than 25 %. When we analysed c between DC, 20 Hz and 40 Hz signals, we found that the mean c decreased and the variance of c increased with signal frequency (Table 6). In other words, as the kinetics of a synaptic response becomes faster, location-dependent variability of EPSPs arriving at the soma will increase. This is consistent with the difference in iso-efficiency of the non-NMDA receptor-mediated and the NMDA receptor-mediated synapse simulations, mentioned above. However, even with 40 Hz signals, depolarization at the soma still varied by less than 25 % between the most proximal and distal synaptic inputs for the non-NMDA receptor-mediated inputs.
What accounts for the relative lack of location-dependent variability in these neurones? The explanation is illustrated in Fig. 7C and D. Input impedance (ZN) increased progressively at dendritic locations progressively further from the soma (Fig. 7C). Correspondingly, the EPSP amplitude at the site of synaptic input increased (Fig. 7D) with distance from the soma; the spatial profile of ZN approximated the spatial profile of EPSP amplitudes at sites of synaptic input. At the same time, the filtering properties of the dendrite reduce the amplitude of the EPSPs propagating to the soma. As a synapse is placed further from the soma, cable filtering results in more voltage attenuation. These two competing properties, ZN and cable filtering, to a large extent cancel each other out leading to a relatively location-independent or iso-efficient response at the soma.
The parameter dependence of c and depolarization at the soma produced by synaptic inputs anywhere in the dendrites is shown in Table 6. Reducing Rm by 75 % (from 60.5 to 15 kΩ cm2), making Rm non-uniform (linearly decreasing Rm with distance from the soma from 81 to 35 kΩ cm2 so that the mean Rm= 60.5 kΩ cm2), or reducing Ri by ∼50 % had no significant effect on the range of somatic EPSP amplitude or c. Reducing Rm and Ri tended to decrease and increase the somatic response, respectively. Similar results were observed across frequencies from DC to 40 Hz.
All of the calculations and simulations described above were from the 24 neurones where acceptable fits of the linear membrane response were obtained. To expand the pool of data, in a second round of analyses the entire set of 63 interneurones was studied. Here Cm was set to 1 μF cm−2, Rm was calculated from τ0, and Ri was set to 200 Ω cm. A third round of simulations was also performed where Cm was 1 μF cm−2 and Ri was set to 200 Ω cm, while Rm was non-uniform and decreased linearly with distance from the soma (described above). We found no significant differences between the three sets of analyses.
DISCUSSION
Passive properties of hippocampal CA3 interneurones
We have shown in this study that both the membrane time constant and RN of CA3 interneurones are larger than those for interneurones located in other regions of the hippocampal formation (Spruston et al. 1997; Parra et al. 1998). Thurbon et al. (1994) and Morin et al. (1996) found that τ0 of CA1 non-pyramidal cells was 25–30 ms, while in dentate gyrus basket cells τ0 was less than 20 ms (Mott et al. 1997). A similar relationship exists for CA3 pyramidal neurones and other principal cells of the hippocampal formation (Spruston & Johnston, 1992). The relative differences in τ0 and RN between CA3 neurones and neurones in other regions of the hippocampal formation may compensate for differences in synaptic activity. Synaptic bombardment of neurones in the CA3 region may be significantly higher because of the strong recurrent excitatory circuitry in CA3, resulting in a reduction in τ0 and RN (Paréet al. 1998). A longer τ0 and higher RN could compensate for differences in synaptic connectivity and, in turn, enhance the relative responsiveness of CA3 neurones.
In neocortical pyramidal neurones and hippocampal CA1 pyramidal neurones, Stuart & Spruston (1998) and Magee (1998) recently reported that Ih increases with distance from the soma, resulting in a decrement in apparent Rm. We cannot eliminate the possibility that Rm in CA3 interneurones is also non-uniform. Holmes & Rall (1992) demonstrated that when the passive membrane properties are non-uniform, there can be more than one solution of Rm, Cm and Ri that fit the membrane response. Indeed, we found that acceptable fits could be obtained when Rm decremented from the soma to the dendrites (and vice versa), as long as the mean Rm was equal to τ0/Cm (see also Rapp et al. 1994; Thurbon et al. 1998). This suggests that estimated values of Rm may actually represent the average Rm of a cell.
Although we found that Cm was not significantly different from a mean of 1 μF cm−2, evidence is mounting that Cm is not a ‘biological constant’. The detailed study of Major et al. (1994) from CA3 pyramidal neurones found that Cm was 0.7–0.8 μF cm−2, while Thurbon et al. (1998) found that Cm was 2 μF cm−2 in motor neurones. Other studies have estimated Cm between these values (Rapp et al. 1994; Thurbon et al. 1994; Stuart & Spruston, 1998). One can no longer simply assume that Cm is 1 μF cm−2; this parameter needs to be determined for each class of neurone before their electrical properties can be modelled.
We found no significant differences in RN, τ0, Rm and Cm across the five laminar substrata. This is in spite of the qualitative differences in dendritic and axonal morphology between interneurones of the different laminae (Parra et al. 1998). Furthermore, there were no significant differences in voltage attenuation, Zc or depolarization in the dendrites or at the soma produced by the model synapse between these groups of neurones. The lack of significant differences between these cells suggests the possibility that, in spite of their morphological and biochemical diversity, they may have similar electrotonic properties.
Electrotonus
Most studies of the passive electrical properties of neurones have focused on the filtering of potentials with distance from their source (Stratford et al. 1989; Major et al. 1994; Rapp et al. 1994; Spruston et al. 1994; Thurbon et al. 1994; Turner et al. 1995; Mott et al. 1997; Stuart & Spruston, 1998; Thurbon et al. 1998). Such discussions of cable properties and electrotonus suggest that EPSPs arriving at the soma will have a large variability due to their differing electrotonic distances (Spruston et al. 1994; Mainen et al. 1996; Carnevale et al. 1997; Stuart & Spruston, 1998) and this clearly appears to be true for many neurone morphologies (Bernander et al. 1994; Major et al. 1994; Rapp et al. 1994; Mainen et al. 1996).
We found that depolarization at the soma was not strongly affected by the location of synapses in CA3 interneurones. A similar observation was made by Segev et al. (1995) for cortical spiny stellate neurones. In our study, we demonstrate that the spatial profiles of input impedance and voltage attenuation compete. As charge propagates down the dendrite, some of it is lost via leakage through the membrane and some is stored by the membrane capacitance. However, ZN increases with distance from the soma resulting in a larger EPSP at the site of synaptic input (Fig. 7C and D). It is this passive dendritic ‘boosting’ of EPSP amplitude that counteracts the effects of voltage attenuation so that depolarization at the soma varies little with synaptic location. In this way the geometry of hippocampal CA3 non-pyramidal neurones may normalize the variability produced by differences in synaptic location. Because of this effect, only minimal contributions by active conductances would be necessary for complete normalization (e.g. all synapses produce the same PSP amplitude at the soma) of synaptic inputs (Bernander et al. 1994; Cook & Johnston, 1997). Given the numerous types of dendritic morphologies in the mammalian CNS, it would not be surprising if different types of neurones (e.g. neocortical pyramidal neurones, cerebellar Purkinje cells) have significant variations in their dendrosomatic transfer impedance profiles.
The iso-efficiency of synaptic depolarization of the soma was relatively independent of variations in Rm. The limited range of simulated EPSP amplitudes at the soma for any dendritic location should be maintained when Rm is non-uniform and/or when Rm is effectively decreased in vivo (Paréet al. 1998). In contrast, this range was highly affected by the choice of Ri. In most of our simulations and calculations, values of Ri were close to or exactly 200 Ω cm. The recent study by Stuart & Spruston (1998) suggests that Ri may be closer to 70–100 Ω cm. Lower values of Ri will further decrease the range of EPSP amplitudes measured at the soma. It is therefore even more likely that synaptic location is not a significant factor in determining the magnitude of depolarization produced at the soma in these neurones.
Active membrane
The physiological significance of voltage attenuation, c and the effects of non-uniform dendritic ZN are critical factors when discussing the location of the spike generation. It is now clear that most, if not all, cortical pyramidal neurone dendrites contain active conductances (e.g. Na+, K+ and Ca2+ channels) (Johnston et al. 1996) that can influence synaptic potentials (Stuart & Sakmann, 1995; Lipowsky et al. 1996; Gillessen & Alzheimer, 1997; Schwindt & Crill, 1998), while action potentials can be triggered in either the dendrites or the axon depending on the strength of synaptic stimulation (Stuart & Sakmann, 1994; Mainen et al. 1995; Colbert & Johnston, 1996; Schwindt & Crill, 1998).
It seems quite reasonable to assume that non-pyramidal neurone dendrites also contain active membrane conductances (Traub & Miles, 1995). Miles (1990) demonstrated that excitatory synapses onto CA3 interneurones trigger action potentials with a relatively high probability and a very fast spike latency. If the threshold for these cells is above 20 mV from rest (R. A. Chitwood & D. B. Jaffe, unpublished observations), how could unitary EPSPs of 1–4 mV trigger spikes? Simulations by Traub & Miles (1995) suggest that active conductances in the dendrites of inhibitory interneurones can trigger dendritic action potentials, or amplify EPSPs, to produce the high probability of firing and a fast latency. Our results demonstrate that EPSPs in the dendrites may be as large as 10 mV, depending on the conductance of a single release site (Arancio et al. 1994). Large dendritic EPSPs, resulting from their high dendritic ZN, would be more likely to activate voltage-gated conductances in the dendrites and trigger dendritic action potentials than the filtered potentials arriving at the soma. This, of course, assumes that spikes can be generated in the dendrites of these cells and that unitary EPSPs can reach threshold. Our further understanding of interneurone function, relative to pyramidal neurones, is clearly dependent upon determining the distribution of active conductances in these cells and how they interact with their passive electrotonic structure.
Acknowledgments
We wish to thank Drs Ted Carnevale and Brenda Claiborne for critical reading of this manuscript and Dr Claiborne for use of her neurone reconstruction system. This work was supported by a grant from the NSF (IBN 9511309).
References
- Ali AB, Deuchars J, Pawelzik H, Thomson AM. CA1 pyramidal to basket and bistratified EPSPs: dual intracellular recordings in rat hippocampal slices. The Journal of Physiology. 1998;507:201–217. doi: 10.1111/j.1469-7793.1998.201bu.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arancio O, Korn H, Gulyas A, Freund T, Miles R. Excitatory synaptic connections onto rat hippocampal inhibitory cells may involve a single transmitter release site. The Journal of Physiology. 1994;481:395–405. doi: 10.1113/jphysiol.1994.sp020448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernander O, Koch C, Douglas RJ. Amplification and linearization of distal synaptic inputs to pyramidal cells. Journal of Neurophysiology. 1994;72:2743–2753. doi: 10.1152/jn.1994.72.6.2743. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Johnston D. Electrophysiological characterization of remote chemical synapses. Journal of Neurophysiology. 1982;407:606–621. doi: 10.1152/jn.1982.47.4.606. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Tsai KY, Claiborne BJ, Brown TH. Comparative electrotonic analysis of three classes of rat hippocampal neurons. Journal of Neurophysiology. 1997;78:703–720. doi: 10.1152/jn.1997.78.2.703. [DOI] [PubMed] [Google Scholar]
- Claiborne BJ. Use of computers for quantitative, three-dimensional analysis of dendritic trees. In: Conn PM, editor. Methods in Neuroscience. Vol. 10. San Diego, CA, USA: Academic Press; 1992. pp. 315–330. [Google Scholar]
- Colbert CM, Johnston D. Axonal action-potential initiation and Na+ channel densities in the soma and axon initial segment of subicular pyramidal neurons. Journal of Neuroscience. 1996;16:6676–6686. doi: 10.1523/JNEUROSCI.16-21-06676.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook EP, Johnston D. Active dendrites reduce location-dependent variability of synaptic input trains. Journal of Neurophysiology. 1997;78:2116–2128. doi: 10.1152/jn.1997.78.4.2116. [DOI] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurko A, Buzsáki G. Reliability and state dependence of pyramidal cell-interneuron synapses in the hippocampus: an ensemble approach in the behaving rat. Neuron. 1998;21:179–189. doi: 10.1016/s0896-6273(00)80525-5. [DOI] [PubMed] [Google Scholar]
- Gillessen T, Alzheimer C. Amplification of EPSPs by low Ni2+- and amiloride-sensitive Ca2+ channels in apical dendrites of rat CA1 pyramidal neurons. Journal of Neurophysiology. 1997;77:1639–1643. doi: 10.1152/jn.1997.77.3.1639. [DOI] [PubMed] [Google Scholar]
- Gray CM. Synchronous oscillations in neuronal systems: Mechanisms and functions. Journal of Computational Neuroscience. 1994;1:11–38. doi: 10.1007/BF00962716. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Computation. 1997;9:1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Holmes WR, Levy WB. Insights into associative long-term potentiation from computational models of NMDA receptor-mediated calcium influx and intracellular calcium concentration changes. Journal of Neurophysiology. 1990;63:1148–1168. doi: 10.1152/jn.1990.63.5.1148. [DOI] [PubMed] [Google Scholar]
- Holmes WR, Rall W. Estimating the electrotonic structure of neurons with compartmental models. Journal of Neurophysiology. 1992;68:1438–1452. doi: 10.1152/jn.1992.68.4.1438. [DOI] [PubMed] [Google Scholar]
- Johansen FF, Lin CT, Schousboe A, Wu JY. Immunocytochemical investigation of L-glutamic acid decarboxylase in the rat hippocampal formation: the influence of transient cerebral ischemia. Journal of Comparative Neurology. 1989;281:40–53. doi: 10.1002/cne.902810105. [DOI] [PubMed] [Google Scholar]
- Johnston D, Magee JC, Colbert CM, Christie BR. Active properties of neuronal dendrites. Annual Review of Neuroscience. 1996;19:165–186. doi: 10.1146/annurev.ne.19.030196.001121. 10.1146/annurev.ne.19.030196.001121. [DOI] [PubMed] [Google Scholar]
- Johnston D, Wu SM. Foundations of Cellular Neurophysiology. Cambridge, MA, USA: MIT Press; 1995. pp. 55–106. [Google Scholar]
- Lipowsky R, Gillessen T, Alzheimer C. Dendritic Na+ channels amplify EPSPs in hippocampal CA1 pyramidal cells. Journal of Neurophysiology. 1996;76:2181–2191. doi: 10.1152/jn.1996.76.4.2181. [DOI] [PubMed] [Google Scholar]
- Maccaferri G, McBain CJ. The hyperpolarization-activated current (Ih) and its contribution to pacemaker activity in rat CA1 hippocampal stratum oriens-alveus interneurones. The Journal of Physiology. 1996;497:119–130. doi: 10.1113/jphysiol.1996.sp021754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magee JC. Dendritic hyperpolarization-activated currents modify the integrative properties of hippocampal CA1 pyramidal neurons. Journal of Neuroscience. 1998;18:7613–7629. doi: 10.1523/JNEUROSCI.18-19-07613.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF, Carnevale NT, Zador AM, Claiborne BJ, Brown TH. Electrotonic architecture of hippocampal CA1 pyramidal neurons based on three-dimensional reconstructions. Journal of Neurophysiology. 1996;76:1904–1923. doi: 10.1152/jn.1996.76.3.1904. [DOI] [PubMed] [Google Scholar]
- Mainen ZF, Joerges J, Huguenard JR, Sejnowski TJ. A model of spike initiation in neocortical pyramidal neurons. Neuron. 1995;15:1427–1439. doi: 10.1016/0896-6273(95)90020-9. 10.1016/0896-6273(95)90020-9. [DOI] [PubMed] [Google Scholar]
- Major G, Larkman AU, Jonas P, Sakmann B, Jack JJB. Detailed passive cable models of whole-cell recorded CA3 pyramidal neurons in rat hippocampal slices. Journal of Neuroscience. 1994;14:4613–4638. doi: 10.1523/JNEUROSCI.14-08-04613.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miles R. Synaptic excitation of inhibitory cells by single CA3 hippocampal pyramidal cells of the guinea-pig in vitro. The Journal of Physiology. 1990;431:659–676. doi: 10.1113/jphysiol.1990.sp018200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morin F, Beaulieu C, Lacaille JC. Membrane properties and synaptic currents evoked in CA1 interneuron subtypes in rat hippocampal slices. Journal of Neurophysiology. 1996;76:1–16. doi: 10.1152/jn.1996.76.1.1. [DOI] [PubMed] [Google Scholar]
- Mott DD, Turner DA, Okazaki MM, Lewis DV. Interneurons of the dentate-hilus border of the rat dentate gyrus: morphological and electrophysiological heterogeneity. Journal of Neuroscience. 1997;17:3990–4005. doi: 10.1523/JNEUROSCI.17-11-03990.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paré D, Shink E, Gaudreau H, Destexhe A, Lang E. Impact of spontaneous synaptic activity on the resting properties of cat neocortical neurons in vivo. Journal of Neurophysiology. 1998;79:1450–1460. doi: 10.1152/jn.1998.79.3.1450. [DOI] [PubMed] [Google Scholar]
- Parra P, Gulyas AI, Miles R. How many subtypes of inhibitory cells in the hippocampus? Neuron. 1998;20:983–993. doi: 10.1016/s0896-6273(00)80479-1. 10.1016/S0896-6273(00)80479-1. [DOI] [PubMed] [Google Scholar]
- Provincher SW. A Fourier method for the analysis of exponential decay curves. Biophysical Journal. 1976;16:27–41. doi: 10.1016/S0006-3495(76)85660-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rall W. Theory of physiological properties of dendrites. Annals of the New York Academy of Sciences. 1962;96:1071–1092. doi: 10.1111/j.1749-6632.1962.tb54120.x. [DOI] [PubMed] [Google Scholar]
- Rall W, Burke RE, Holmes WR, Jack JJ, Redman SJ, Segev I. Matching dendritic neuron models to experimental data. Physiological Reviews. 1992;72:S159–186. doi: 10.1152/physrev.1992.72.suppl_4.S159. [DOI] [PubMed] [Google Scholar]
- Rapp M, Segev I, Yarom Y. Physiology, morphology and detailed passive models of guinea-pig cerebellar Purkinje cells. The Journal of Physiology. 1994;474:101–118. doi: 10.1113/jphysiol.1994.sp020006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwindt PC, Crill WE. Synaptically evoked dendritic action potentials in rat neocortical pyramidal neurons. Journal of Neurophysiology. 1998;79:2432–2446. doi: 10.1152/jn.1998.79.5.2432. [DOI] [PubMed] [Google Scholar]
- Segev I, Friedman A, White EL, Gutnick MJ. Electrical consequences of spine dimensions in a model of a cortical spiny stellate cell completely reconstructed from serial thin sections. Journal of Computational Neuroscience. 1995;2:117–130. doi: 10.1007/BF00961883. [DOI] [PubMed] [Google Scholar]
- Spruston N, Jaffe DB, Johnston D. Dendritic attenuation of synaptic potentials and currents: the role of passive membrane properties. Trends in Neurosciences. 1994;17:161–166. doi: 10.1016/0166-2236(94)90094-9. 10.1016/0166-2236(94)90094-9. [DOI] [PubMed] [Google Scholar]
- Spruston N, Johnston D. Perforated patch-clamp analysis of the passive membrane properties of three classes of hippocampal neurons. Journal of Neurophysiology. 1992;67:508–529. doi: 10.1152/jn.1992.67.3.508. [DOI] [PubMed] [Google Scholar]
- Spruston N, Lubke J, Frotscher M. Interneurons in the stratum lucidum of the rat hippocampus: an anatomical and electrophysiological characterization. Journal of Comparative Neurology. 1997;385:427–440. 10.1002/(SICI)1096-9861(19970901)385:3<427::AID-CNE7>3.3.CO;2-M. [PubMed] [Google Scholar]
- Stratford KJ, Mason AJR, Larkman AU, Major G, Jack JJB. The modelling of pyramidal neurones in the visual cortex. In: Drubin R, Miall C, Mitchison G, editors. The Computing Neuron. Reading, UK: Addison-Wesley; 1989. pp. 296–321. [Google Scholar]
- Stuart GJ, Dodt HU, Sakmann B. Patch-clamp recordings from the soma and dendrites of neurons in brain slices using infrared video microscopy. Pflügers Archiv. 1993;423:511–518. doi: 10.1007/BF00374949. [DOI] [PubMed] [Google Scholar]
- Stuart GJ, Sakmann B. Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature. 1994;367:69–72. doi: 10.1038/367069a0. [DOI] [PubMed] [Google Scholar]
- Stuart G, Sakmann B. Amplification of EPSPs by axosomatic sodium channels in neocortical pyramidal neurons. Neuron. 1995;15:1065–1076. doi: 10.1016/0896-6273(95)90095-0. [DOI] [PubMed] [Google Scholar]
- Stuart G, Spruston N. Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. Journal of Neuroscience. 1998;18:3501–3510. doi: 10.1523/JNEUROSCI.18-10-03501.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thurbon D, Field A, Redman SJ. Electrotonic profiles of interneurons in stratum pyramidale of the CA1 region of rat hippocampus. Journal of Neurophysiology. 1994;71:1948–1958. doi: 10.1152/jn.1994.71.5.1948. [DOI] [PubMed] [Google Scholar]
- Thurbon D, Luscher H, Hofstetter T, Redman SJ. Passive electrical properties of ventral horn neurons in rat spinal cord slices. Journal of Neurophysiology. 1998;79:2485–2502. doi: 10.1152/jn.1998.79.5.2485. [DOI] [PubMed] [Google Scholar]
- Traub RD, Miles R. Pyramidal cell-to-inhibitory cell spike transduction explicable by active dendritic conductances in inhibitory cell. Journal of Computational Neuroscience. 1995;2:291–298. doi: 10.1007/BF00961441. [DOI] [PubMed] [Google Scholar]
- Tsai KY, Carnevale NT, Claiborne BJ, Brown TH. Efficient mapping from neuroanatomical to electronic space. Network. 1994;5:21–46. [Google Scholar]
- Turner DA, Li XG, Pyapali GK, Ylinen A, Buzsáki G. Morphometric and electrical properties of reconstructed hippocampal CA3 neurons recorded in vivo. Journal of Comparative Neurology. 1995;356:580–594. doi: 10.1002/cne.903560408. [DOI] [PubMed] [Google Scholar]


