A re-examination of adult mouse nicotinic acetylcholine receptor channel activation kinetics

Abstract

1. During routine sequencing of our mouse muscle α subunit acetylcholine receptor channel (AChR) cDNA clones, we detected a discrepancy with the GenBank database entry (accession X03986). At nucleotides 1305-7 (residue 433, in the M4 domain) the database lists GTC which encodes a valine, while our putative ‘wild-type’ cDNA had the nucleotides GCC, which encodes an alanine. No other sequence differences were found.

2. PCR amplification of genomic DNA confirmed that the BALB/C mouse α subunit gene has a T nucleotide at position 1306, and, therefore, that the protein has a V at position 433 in the M4 segment.

3. In order to determine the functional consequences of this difference, either wild-type (V433) or mutant (A433) α subunits were co-expressed in HEK cells with mouse β, ε and δ subunits. Single-channel currents were recorded in cell-attached patches, and rate and equilibrium constants were estimated from open and closed durations obtained from a range of ACh concentrations. No significant differences were found between the activation rate constants or equilibrium constants of the V433 and A433 variants.

4. Kinetic modelling of αV433 AChR suggests that the two transmitter binding sites have similar dissociation equilibrium constants for acetylcholine (∼160 μM, in 142 mM extracellular KCl).

5. Diliganded AChRs occupy a closed state that has a lifetime of ∼1 ms. The rate constants for entering and leaving this state do not vary with the ACh concentration.

6. The kinetics of a mutant AChR that causes a slow channel congenital myaesthenic syndrome, αG153S, was re-examined. The properties of this mutant were similar with a V or an A at position α433.

The nicotinic acetylcholine receptor (AChR) is a ligand-activated ion channel that mediates neuromuscular transmission in vertebrates. It is composed of five subunits, α₂βδε (in adult muscle), and has two transmitter binding sites located, in part, in the two α subunits (Unwin, 1996; for a review, see Devillers-Thiéry et al. 1993; Karlin & Akabas, 1995). The activation kinetics of mouse muscle-type AChR have been the object of extensive investigation at the single-channel level (Sine & Steinbach, 1986; Jackson, 1988; Zhang et al. 1995; Sine et al. 1995; Akk & Auerbach, 1996; Auerbach et al. 1996; Wang et al. 1997). Here, we present new information regarding the functional equivalence of the two transmitter binding sites on the adult receptor, a diliganded closed state with a lifetime of ∼1 ms, and a mutation that causes a slow channel congenital myaesthenic syndrome (SCCMS).

These studies were motivated by a discrepancy detected in the course of routine sequencing. We discovered a difference between the GenBank database entry for the mouse α subunit (accession X03986) at nucleotide 1306, and our ‘wild-type’α sequence. The database lists a valine (V) at position 433 coded by nucleotides GTC, while our putative ‘wild-type’ cDNA had the nucleotides GCC, which encodes an alanine (A). No other differences between the two sequences were found. The original publication of the mouse α subunit sequences from the mouse myogenic cell line BC3H-1 reported a V at position 433 (Boulter et al. 1985; Isenberg et al. 1986). After we reported the discrepancy in abstract form (Zhou et al. 1998), the original clones were re-sequenced and found either to have the nucleotides GCC which code for an A (C. Labarca, H. Lester & N. Davidson, personal communication), or the nucleotides GTC which code for a V (J. Boulter, personal communication). Valine is highly conserved at position 433 in α subunits of other species (except for chicken where it is an isoleucine), and it was not known whether the V and A variants reflected a polymorphism specific to BC3H-1 cells or an accidental background mutation. We therefore sought to determine the mouse genomic DNA sequence coding for α433.

Residue 433 is in the fourth hydrophobic (M4) segment, and mutations in this region have been found to influence AChR gating significantly. A C-to-W mutation at α418 in Torpedo increases the open channel lifetime > 20-fold (Ortiz-Miranda et al. 1997), and residues L440 and M442 of the γ subunit have been implicated as determinants of the long open times of fetal AChR (Bouzat et al. 1994). It was therefore important to ascertain whether agonist binding, channel gating and/or desensitization are influenced by V vs. A residues at position α433.

Although the kinetics of adult mouse AChR activation have been described in detail, some elements have not been completely resolved. In adult-type mouse and frog muscle AChR the agonist binding properties of the two transmitter sites appear to be essentially equivalent (Akk & Auerbach, 1996; Wang et al. 1997; Prince & Sine, 1998). However, distinct agonist dissociation equilibrium constants for the two sites have been reported in fetal-type mouse (Jackson, 1988; Zhang et al. 1995) and Torpedo AChR (Sine et al. 1990). Also, Torpedo AChRs show clear structural differences between the two sites (Unwin, 1996). Moreover, certain antagonists bind with quite distinct affinities to the two transmitter binding sites (Sine & Taylor, 1979; Blount & Merlie, 1989; Pedersen & Cohen 1990; Sine & Claudio, 1991). Thus, we used the discovery of the V and A variants as an opportunity to compare the ACh association and dissociation rate constants at the two transmitter binding sites. Other incompletely resolved issues with regard to AChR activation kinetics that we address in this paper include the properties of a short-lived diliganded closed state (Colquhoun & Sakmann, 1985; Sine & Steinbach, 1986), and the effects of the SCCMS mutation αG153S at the two transmitter binding sites (Sine et al. 1995).

The results indicate that the BALB/C mouse genome codes for a V at position 433 of the α subunit, and that the rate constants for adult muscle AChR activation are the same with either an A or a V at this position. In addition, we find that in both adult wild-type and αG153S AChR the two transmitter binding sites have the same dissociation equilibrium constant for ACh.

METHODS

PCR amplification of genomic DNA

Genomic DNA was amplified using the method of Malumbres et al. (1997). Briefly, samples of mouse toes or liver (∼8 mm³ of tissue) were placed in 200 μl of GNT-K buffer (mM: 50 KCl, 1·5 MgCl₂, 10 Tris-HCl, pH 8·5, 0·01 % gelatin, 0·45 % Tween 20, 0·45 % Nonident P-40 and 100 μg ml⁻¹ proteinase K) and heated to 55°C for 2 h. Following this incubation, the samples were heated at 95°C for 15 min to inactivate the proteinase. The resulting mixture was spun down in a microcentrifuge for ∼2 min at 14 000 r.p.m., and 2·5 μl of the supernatant was used for PCR.

Standard PCR was performed in a total volume of 50 μl with 20 mM Tris-HCl, 50 mM KCl, 1·5 mM MgCl₂, 0·25 mM of each dNTP, ∼1 μM of each primer and 5 U of Taq polymerase. Typically, after an initial 5 min denaturation step at 94°C, 35 cycles consisting of 30 s at 94°C, 30 s at 58°C and 60 s at 78°C were performed. A final 7 min, 78°C extension step was used at the end of the cycling.

Primers were selected so as to straddle where the last intron was believed to be in the mouse α1 gene. The primers were: 5′-CTC CAC AAT GAA AAG ACC ATC CAG AGA TAA ACA AG-3′ and 5′-GAT GTA ACT CAA TGA GCC GAC CTG CAA ACA CAG-3′.

BALB/C mouse tissue (Harlan Laboratories, Indianapolis IN, USA) was kindly provided by Drs Arvind N. Thakur and Phillip Loverde (State University of New York at Buffalo Department of Microbiology, Buffalo, NY, USA). The animals were killed by ether anaesthesia overdose. Handling of live mice and the method of killing were in accordance with the policies of the State University of New York at Buffalo Institutional Animal Care and Use Committee.

Clones, mutagenesis and expression

The source of the mouse muscle AChR subunit cDNAs was the laboratory of Dr S. Sine (Mayo Foundation, Rochester, MN, USA), who had obtained the clones from the laboratories of the late Dr J. Merlie and Dr N. Davidson (Caltech, Pasadena, CA, USA). The cDNAs had been subcloned into the CMV-based expression vector pRBG4 (Sine, 1993). The reverse mutant αA433V was kindly provided by Dr C. Bouzat and Dr F. Barrantes (Instituto de Investigaciones Bioquímicas de Bahía Blanca, Universidad Nacional del Sur-Consejo Nacional de Investigaciones Científicas y Técnicas, Bahía Blanca, Argentina), and the mutant αG153S was kindly provided by Dr S. Sine. The αG153S + V433 mutation was constructed using the QuickChange (Promega, Madison, WI, USA) method; the point mutation was verified by restriction mapping and dideoxy sequencing.

Human embryonic kidney (HEK 293) cells were transiently transfected by calcium phosphate precipitation (Ausubel et al. 1992). Cells were plated 24 h before transfection so as to reach a confluency of about 50 %. cDNA (1-2 μg μl⁻¹) was added to 8·75 μl of ice-cold 2·5 mM CaCl₂ solution and diluted with distilled water to a total volume of 87·5 μl. A total of 3·6 μg of cDNA per culture dish in the ratio 2 : 1 : 1 : 1 (α : β : δ : ε) was used. This mixture was carefully layered onto 87·5 μl of cold buffer (mM: 280 NaCl, 50 Hepes, 1·5 Na₂HPO₄, pH 7·05) and allowed to stand at room temperature (22-24°C) for 10 min. After this incubation period, a hazy suspension was visible between the two layers. The solution was mixed and allowed to stand for an additional 15 min after which it was added to a 35 mm culture dish. This procedure produced small calcium phosphate crystals required for high transfection efficiency. The medium was changed after 24 h, and electrophysiological recordings were performed 24 h later.

Electrophysiology

Single-channel recordings were made using the patch-clamp technique in the cell-attached configuration (Hamill et al. 1981). Pipettes were pulled from capillary glass with a Narishige (Tokyo, Japan) upright puller (PP-83) to a resistance of about 5 MΩ. Pipettes were coated with Sylgard (Dow Corning, Midland, MI, USA). The bath and pipette solution consisted of (mM): 142 KCl, 5·4 NaCl, 1·8 CaCl₂, 1·7 MgCl₂, 10 Hepes, pH 7·4. The membrane potential was -70 mV, and the temperature was 22-24°C.

Currents were amplified with a Warner Instruments PC-505 (Hamden, CT, USA) and saved directly to hard disk in digital format using a National Instruments (Austin, TX, USA) PCI-MIO-16E-4 acquisition board. The incoming data was low-pass filtered at 20 kHz (-6 dB; 4-pole Bessel) and digitized at a rate of 100 kHz.

Cluster definition and selection

Segments of the current record containing channel activity were detected using a half-amplitude crossing algorithm after digitally low-pass filtering (Gaussian; -3 dB cut-off frequency, f_c= 4 kHz). A histogram of all closed interval durations was compiled and fitted by sums of exponentials. At low ACh concentrations (5-20 μM), this histogram had a small, very slow component (with a time constant > 200 ms) that varied greatly from patch to patch. We assume that this component reflects periods when all of the channels in the patch were desensitized. This histogram also had a component (with a time constant in the 0·1-10 ms range) that became shorter with increasing concentrations of agonist (see Fig. 7). We assume that this component reflects the set of transitions between unliganded closed and diliganded open states.

Figure 7. Interval duration histograms for αA433 and αV433 patches.

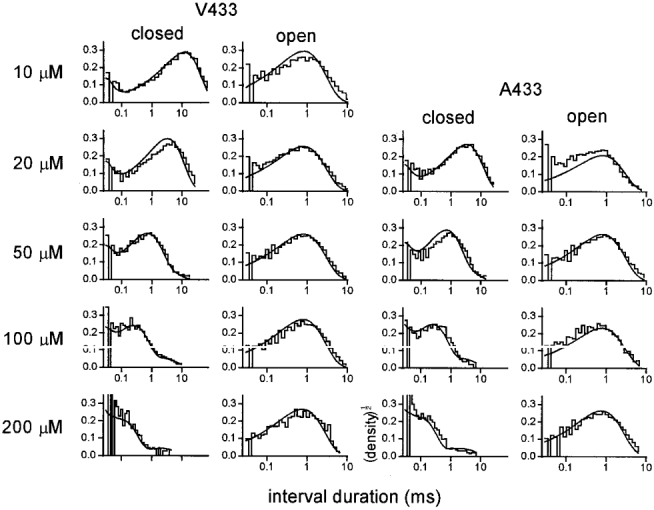
Smooth curves are computed using the rate constants of Model 1 (equal binding with channel block; β= 50 000 s⁻¹) obtained from a global fit to these 9 patches (Table 3). y-axes are in units of (normalized counts per bin)^½. Open and closed interval durations elicited by between 10 and 200 μM ACh are well described by the 7 rate constants.

Clusters of channel openings from single receptors elicited by high concentrations of agonist (Sakmann et al. 1980) were defined as a series of openings separated by closed intervals longer than a critical duration τ_c. Based on the fit to the closed interval histogram, τ_c was set to include the 0·1-10 ms component, and exclude the > 200 ms component, from clusters. The τ_c values were 70, 30 and 20 ms at 10, 20 and 50 μM ACh, respectively. At higher agonist concentrations, τ_c was set to 10 ms in order to include a 1 ms gap component (associated with state C₆ in Model 1, below).

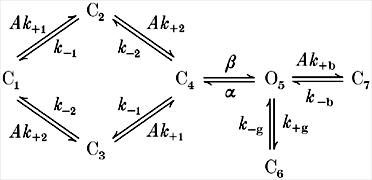
Model 1.

For the quantitative kinetic modelling studies it was necessary to ensure that a kinetically homogeneous population of clusters was selected. Four selection criteria were used: cluster duration, open interval amplitude, open interval duration, and the probability of being open in a cluster (P_o) (Neil et al. 1991; program LPROC). Regarding the first criterion, only clusters longer than 100 ms were retained. For the next three criteria, histograms were constructed and fitted by a Gaussian distribution to determine a mean and a standard deviation (s.d.), and only those clusters having values within 1 s.d. of the mean were retained. In one patch that had only 22 clusters, a window of ± 2 s.d. was used. Finally, all of the clusters that survived the selection procedure were examined by eye to eliminate any that had obvious artifacts. The final population of selected clusters was extracted at full bandwidth (20 kHz) for further analysis.

For example, in one patch (20 μM ACh, αV433 AChR) the closed interval distribution for the entire record was fitted by the sum of three exponentials: τ₁= 3·18 ms (23 394 events), τ₂= 7·49 ms (6671 events), and τ₃= 254 ms (409 events). The amplitude of open intervals in this patch was 5·08 ± 0·24 pA (mean ± s.d). Clusters were defined with τ_c= 30 ms, a value which is ∼10 times greater than the predominant component, and ∼10 times smaller than the slowest component of the closed interval duration histogram. After applying the first two selection criteria, 155 clusters were selected (clusters longer than 100 ms in duration and with a mean amplitude in the range 4·84-5·32 pA). After applying the open duration criterion 58 remained (0·73-0·93 ms), and only 35 survived the selection based on P_o (0·133-0·163). In this example the selection process was particularly severe, as only 22 % of the initial population of clusters was selected for extraction and kinetic analysis.

Considering all of the patches, about half (52 ± 10 %; mean ±s.d.) of the initial population of clusters was retained. Again, this highly selective process was implemented in order to maximize the probability that a homogeneous set of intervals was used for kinetic modelling. However, the final population of selected clusters is representative of the predominant population of AChR in the patch. For example, in the patch described above, the original cluster population (n= 155) contained 19 386 closed intervals, or 64 % of all closed intervals and 83 % of the predominant component of all closed intervals. The closed intervals from this original cluster population were described by an exponential with a time constant of 4·31 ± 0·16 ms. The final population of clusters (n= 35) contained only 5583 closed intervals, which were described by an exponential with a time constant of 4·77 ± 0·19 ms. The similarity of these time constants indicates that the events that were selected for kinetic analysis were representative of the entire population of AChR in the patch.

The selection process was not sensitive to the precise value of τ_c. As a test of the sensitivity of the rate constants to τ_c, in the 20 μM ACh (αV433 AChR) patch, clusters were defined using τ_c values in the range 10-100 ms. After applying the full selection procedure, the time constant of the closed intervals contained within the final population of clusters was 5·28, 4·75, 4·77, 4·69 and 4·67 ms using τ_c values of 10, 20, 30, 50 and 100 ms, respectively. We conclude that in this patch, values of τ_c between 20 and 100 ms resulted in final cluster populations having similar kinetic parameters.

Kinetic analysis

The intervals within the selected clusters were compiled into log bin width duration histograms (Sigworth & Sine, 1987) that were fitted by sums of exponentials. The effective opening rate (β‘) was defined as the inverse of the slowest component with a time constant that scaled with the agonist concentration (and therefore excluded the component associated with sojourns in state C₆). At high concentrations of agonist, the binding sites are almost always occupied and, according to Model 1 (below), the effective opening rate β’ approaches the opening rate constant β. Thus, a plot of β’versus agonist concentration asymptotically approaches β. β’ curves were fitted using an empirical equation to estimate β, n and EC₅₀:

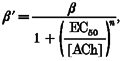(1)

where n is the Hill coefficient and EC₅₀ is the concentration yielding β/2. For kinetic analysis, the selected clusters were low-pass filtered (f_c= 15 kHz) and idealized using the segmented-k-means algorithm (Rabiner et al. 1986; Chung et al. 1990; program SKM). Rate constants were estimated from the interval dwell times using a maximum likelihood method that corrects for missed events (Qin et al. 1996, 1997; program MIL). The dead time was 25 μs. The standard deviations of the rate constants were estimated from the curvature of the likelihood surface at its maximum, using the approximate inverse Hessian matrix of second derivatives generated by the Davidon-Fletcher-Powell optimization algorithm.

The following scheme was used for model-based single-channel kinetic analysis (modified from Magleby & Stevens, 1972; Colquhoun & Hawkes, 1977):

where A represents the agonist concentration, C represents a closed (non-conducting) receptor and O represents an activated receptor with a conducting channel. In state C₁ the transmitter binding sites are unliganded, in states C₂ and C₃ they are monoliganded, and in states C₄, O₅, C₆ and C₇ they are diliganded. In our experiments, the state C₆ has a lifetime of ∼1 ms and is therefore distinct from the long-lived desensitized state(s) that give rise to the closed intervals between clusters. In state C₇ the channel is blocked by an ACh molecule. k_{+ 1} and k_{+ 2} are the agonist association rate constants, k_-1 and k_-2 are the agonist dissociation rate constants, α and β are the diliganded AChR closing and opening rate constants, k_{+ g} and k_-g are the rate constants for entry into and exit from state C₆, and k_{+ b} and k_-b are the channel blocking and unblocking rate constants.

Monoliganded openings were omitted from the kinetic model. The fraction of openings arising from monoliganded AChRs is equal to 2β₁K_d/(β₂A), where β₁ and β₂ (≡β) are the opening rate constants for mono- and diliganded receptors. For the analysis, the binding sites are assumed to be equivalent, and k_-1= 0·5k_-2=k_- and k₊₂= 0·5k₊₁=k₊. With β₂ fixed, the main consequences of omitting a monoliganded open state from the kinetic scheme are to increase the apparent values of k₊ and α. If K_d= 160 μM, β₂= 50 000 s⁻¹ and β₁= 216 s⁻¹ (Wang et al. 1997), then above 20 μM ACh < 7 % of channel openings arise from monoliganded AChR. The consequences of omitting monoliganded openings from Model 1 were determined by simulation. Single-channel currents were simulated (program SIMU; 35 000 intervals; equivalent binding sites) with the following rate constants: k₊= 3200 s⁻¹, k_-= 24 000 s⁻¹, β₂= 50 000 s⁻¹, α₂= 2200 s⁻¹, β₁= 216 s⁻¹ and α₁= 3320 s⁻¹. The simulated data were idealized and modelled (dead time = 25 μs, equivalent binding sites, β₂ fixed at 50 000 s⁻¹) using Model 1 with and without a monoliganded open state. Without these states the k₊ estimate was 5·5 % larger, while the k_- and α₂ estimates were not significantly different. We conclude that the presence of monoliganded openings does not have a substantial impact on the estimates of the activation rate constants.

Probability of being open

When the binding sites are equivalent, and ignoring channel block, the probability of being open (P_o) within a cluster is:

(2)

where K_d=k_-/k₊, θ=β/α, K_g=k_+g/k_-g and A is the agonist concentration. When the sites are not equivalent:

(3)

where K_a=k_-1/k_{+ 1} and K_b=k_-2/k_{+ 2}. In both equations, the maximum P_o is (Θ⁻¹+K_g+ 1)⁻¹. The relevant equilibrium constants were determined by fitting the parameters of these equations to a curve of P_oversus concentration, with K_g fixed to be 0·05 (see Fig. 4).

Figure 4. Estimating standard deviations of the rate constants.

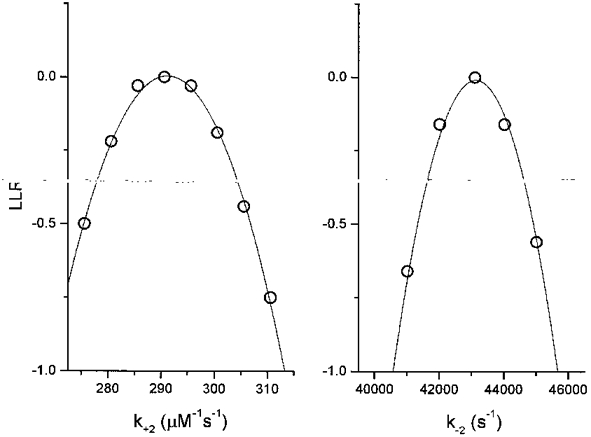
The log likelihood profiles near the optima for rate constants k_{+ 2} and k_-2 were calculated by fixing each of the rates while allowing all others (except β, which was 50 000 s⁻¹) to vary. The y-axis shows the log likelihood ratio (LLR), i.e. the difference between the global optimum and the calculated LL. The -0·5 log unit intervals define ± 1 standard deviation. The standard deviations computed in this way are in close agreement with those estimated using an approximation (Table 1). The single-channel currents were from αV433 AChR (10, 20 and 50 μM ACh), and the kinetic model was Model 1 without channel block and without constraints for equal association and dissociation rate constants.

RESULTS

Sequencing of mouse genomic DNA

In order to determine the amino acid present at position 433 in the mouse, we used the polymerase chain reaction to amplify a portion of the BALB/C mouse nicotinic acetylcholine receptor α subunit genomic DNA. We were unable to find a published map of this region of the mouse genome. Primers were selected on either side of the presumed location of the final intron based on its location in the human muscle α gene (Noda et al. 1983), which included the region of M4 in question. Sequencing of the amplification product revealed an intron at the same point as in the human gene, as well as the codon GTC at position 433 encoding a valine (Fig. 1). The intron was identified by the GT/AG rule (Breathnach et al. 1978) and the sequence 5′ to the intron near the codon for 433 was identical to that of the database (GenBank accession number X03986). This experiment was repeated three times with similar results. This result, plus the fact that the V is highly conserved at this position, leads us to conclude that the mouse genome encodes a V at position 433 of the muscle α subunit.

Figure 1. Wild-type mouse muscle α subunit sequences.

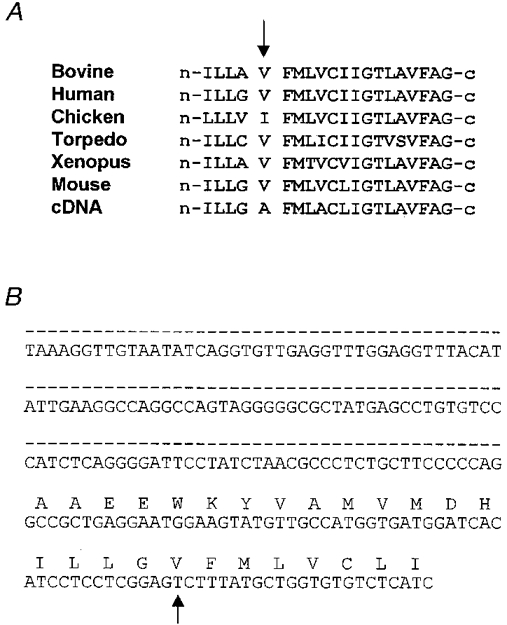
A, amino acid sequence alignment of the α subunit M4 segment from several species. The V at position 433 (arrow) is highly conserved, but is an I in the chicken. B, sequence of mouse genomic DNA. The intron is indicated by the dashed line. The valine at position 433 is encoded by a GTC (arrow).

Kinetic analysis of A and V variants

The kinetic properties of A and V variant adult mouse muscle-type channels were studied at desensitizing concentrations of agonist. The currents were analysed according to Model 1 without the channel blocked state (C₇). The results are shown in Fig. 2 for αV433, and in Fig. 3 for αA433.

Figure 2. Single-channel currents and the activation properties of αV433 AChR.

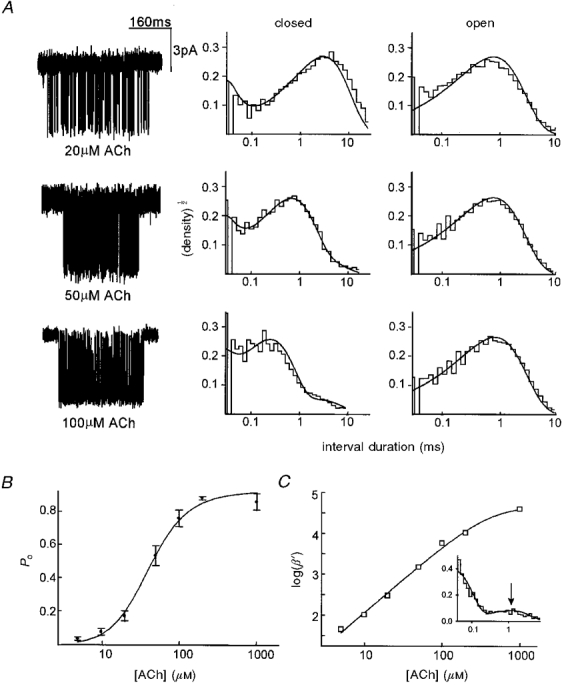
A, single-channel currents activated by various concentrations of ACh (filtered at 3 kHz for display). The membrane potential was -70 mV; inward current is down. To the right of the current traces are the corresponding intracluster closed and open duration histograms. Smooth curves are global fits (rate constants shown in Table 1). Intracluster closed intervals decrease in duration as the agonist concentration increases because dwells in un- and monoliganded states become shorter. B, single-channel dose-response curve. The probability of the channel being open within a cluster (P_o) is plotted as a function of agonist concentration. Error bars are ± 1 s.d. The continuous curve is fitted to data by eqn (2) (K_d= 221 ± 84 μM, θ= 36 ± 22, K_g was fixed at 0·05). C, effective opening rate (β‘) curve. The continuous curve is fitted to the data by eqn (1). From the high concentration limit, we estimate that β= 48 950 ± 13 490 s⁻¹ (n= 1·62 ± 0·08, EC₅₀= 410 ± 113 μM). The data are from 7 patches (one patch at each concentration), 233 clusters, 85 490 intervals. The inset shows a closed interval duration histogram ((normalized counts per bin)^½vs. time (ms)) from a patch at 1 mM ACh; the arrow indicates the ∼1 ms shut state component that corresponds to state C₆ in Model 1.

Figure 3. Single-channel currents and the activation properties of αA433 AChR.

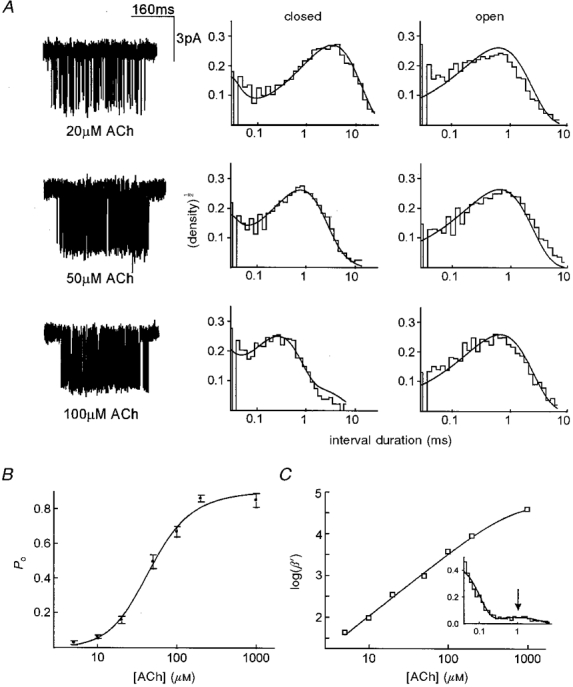
A, single-channel currents activated by various concentrations of ACh (filtered at 3 kHz for display). The membrane potential was -70 mV; inward current is down. To the right of the current traces are the corresponding intracluster closed and open duration histograms. Continuous curves are global fits (rate constants shown in Table 1). B, single-channel dose-response curve. The probability of the channel being open within a cluster (P_o) is plotted as a function of agonist concentration. The continuous curve is fitted to data by eqn (2) (K_d= 161 ± 44 μM, θ= 17·5 ± 7, K_g fixed at 0·05). C, effective opening rate (β‘) curve. The continuous curve is fitted to the data by eqn (1). From the high concentration limit, we estimate that β= 58 700 ± 17 420 s⁻¹ (n= 1·51 ± 0·06, EC₅₀= 650 ± 194 μM). The data are from 7 patches (one patch at each concentration), 138 clusters, 46 774 intervals. The inset shows a closed interval duration histogram ((normalized counts per bin)^½vs. time (ms)) from a patch at 1 mM ACh; the arrow indicates the ∼1 ms shut state component that corresponds to state C₆ in Model 1.

Currents elicited by 20, 50 and 100 μM ACh and the corresponding histograms of intracluster open and closed interval durations are shown in Figs 2A and 3A. The probability of being open within a cluster increased with agonist concentration, as shown in Figs 2B and 3B. The inverse time constant of the predominant intracluster closed interval component for each concentration (β‘) is plotted vs. concentration in Figs 2C and 3C. From the high concentration limits of these curves we estimate that the channel opening rate constant, β, equals 48 950 ± 13 490 s⁻¹ for V433, and 58 700 ± 17 420 s⁻¹ for A433 AChRs. These values are not significantly different, and are similar to published values for β in αA433 AChR obtained from single-channel analysis of mouse adult (55 000 s⁻¹, Sine et al. 1995; 49 000 s⁻¹, Wang et al. 1997) and fetal-type AChR (56 000 s⁻¹; Parzefall et al. 1998), and from ensemble averages of outside-out patches (Maconochie & Steinbach, 1998; 30 000-100 000 s⁻¹).

High resolution analyses indicate that gaps arising from channel block by ACh have an inverse duration of 40 000-74 000 s⁻¹ (Maconochie & Steinbach, 1995; Wang et al. 1997; Parzefall et al. 1998). It was therefore likely that the β’ values at high ACh concentrations were a weighted average of gating and channel block events. With regard to the A vs. V comparison, both variants open rapidly after becoming diliganded, and there is no indication that the channel opening rate constant depends on the side chain at position α433. Below, we show that in αG153S AChR, the V and A variants have the same channel opening rate constant (∼40 000 s⁻¹; Table 1). In these experiments, much lower ACh concentrations were used, and gaps from channel block did not represent a significant fraction of the events within clusters. The similarity of the opening rate constants in the V and A variants of αG153S AChR is strong supportive evidence that the side chain at position α433 does not alter the channel opening rate constant.

Table 1.

Activation rate and equilibrium constants for V433 and A433 AChR

		αV433	αV433 (equal binding)	αA433 (equal binding)	αV433/G153S	αA433/G153S
Rate constant	k+(k+1)	97 ± 3	158 ± 2	179 ± 3	138 ± 15	193 ± 14
	k−(k−1)	18 026 ± 585	25 267 ± 372	28 698 ± 684	770 ± 147	1620 ± 207
	k+2	291 ± 16	—	—	770 ± 121	860 ± 127
	k−2	43 010 ± 1835	—	—	9100 ± 647	5840 ± 271
	β	48 950 ± 13 490*	48 950 ± 13 490*	58 700 ± 17 420*	43 800 ± 3632	36 500 ± 1081
	α	2612 ± 24	2735 ± 20	2850 ± 43	775 ± 71	998 ± 28
	k+g	32 ± 3	36 ± 3	98 ± 17	—	—
	k−g	362 ± 26	377 ± 27	564 ± 48	—	—
	k+b	—	—	—	—	—
	k−b	—	—	—	—	—
	LL	364 719	364 667	—	—	—
Equilibrium constant	Ka (Kd) (μM)	186 ± 12	160 ± 4	160 ± 7	5.6 ± 1.8	8.4 ± 1.8
	Kb (μm)	148 ± 37	—	—	11.8 ± 3.2	6.8 ± 1.5
	Θ	19 ± 5	18 ± 5	18 ± 9	57	37
	Kg	0.09 ± 0.01	0.10 ± 0.01	0.17 ± 0.01	—	—
	Intervals	59 402	59 402	22 801	1392	7900

Rate constants (± standard deviation) were determined by kinetic modelling of single-channel interval dwell times, as described in Methods. The rate constants are defined in Model 1. The equilibrium constants were calculated from ratios of the rate constants. K_a is the dissociation equilibrium constant of the slow transmitter binding site, K_b is the dissociation equilibrium constant of the fast transmitter binding site, Θ is the gating equilibrium constant, and K_g is equilibrium constant for occupying a ∼1 ms closed state (state C₆ of Model 1). LL is the log likelihood. All rate constants are in units of s⁻¹, except for k₊₁, and k₊₂,which are μm⁻¹ s⁻¹. The αA433 and αV433 values were obtained by fitting Model 1 simultaneously to currents elicited at 20, 50 and 100 μm ACh. For modelling, the opening rate constant was fixed at 50 000 s⁻¹.

^*Values derived from fit of β' curve (Figs 2C and 3C) to eqn (1). For αG153S, the ACh concentration was 1 μm, and the inclusion of state C₆ did not improve the LL and was not part of the model. The number of clusters used in the fit was 118 (αV433), 54 (αA433), 14 (αV433/G153S) and 45 (αA433/G153S).

A preliminary estimate of the ACh dissociation equilibrium constant was obtained from fitting eqn (1) to the P_o curves (Figs 2B and 3B). This value was 221 ± 84 μM for αV433, and 161 ± 44 μM for αA433 AChR. These values are not significantly different and are similar to previously published values for αA433 mouse adult-type AChR in 142 mM extracellular KCl (Akk & Auerbach, 1996; Wang et al. 1997). This result suggests that the V-to-A substitution at position α433 does not significantly affect the K_d for activation by ACh.

Molecular rate constants were estimated for the V and A variants using a maximum interval likelihood method with a correction for missed events. Model 1 (without the channel block state C₇) was fitted simultaneously to intervals within clusters measured at 20, 50 and 100 μM ACh. These agonist concentrations were selected because they are on the rising part of the dose-response curve (Figs 2B and 3B), and thus provide information about transitions between un-, mono- and diliganded states. During the fit, the opening rate constant was constrained to be 50 000 s⁻¹ and the binding sites were assumed to be equivalent, so that there were only five free parameters in the fit: k₊, k_-, α, k_{+ g} and k_-g.

The results of the kinetic modelling are shown in Table 1. The rate constants were similar for the αV433 and αA433 variants. In 142 mM KCl and assuming equivalent binding sites, ACh associates with each site of the adult muscle AChR at ∼1·7 × 10⁸ M⁻¹ s⁻¹, and dissociates at ∼27 000 s⁻¹. From these values the K_d for ACh is ∼160 μM. Diliganded AChRs open at ∼50 000 s⁻¹ and close at 2800 s⁻¹. Thus at -70 mV and 22°C, the equilibrium gating constant, Θ, is ∼18.

Because the opening rate constant is not known precisely and may vary between patches, we fitted the intervals (αV433 patches) using a range of β values, from 30 000 s⁻¹ to 100 000 s⁻¹ (Maconochie & Steinbach, 1998). As β increased, so did α, but only by 2-fold (range: 2290-4449 s⁻¹). k_- values fell within a narrow range (24 500-27 830 s⁻¹) and did not vary with β in a consistent manner. k₊ values decreased by less than 30 % (range: 194-133 μM⁻¹ s⁻¹) as β increased. We conclude that only the estimate of the channel closing rate constant, and not those of the association or dissociation rate constants, is sensitive to the precise value of the channel opening rate constant that was used in the fit.

The inverse of the product of the mean cluster duration and open probability is an estimate of the microscopic desensitization rate constant (Auerbach & Akk, 1998). These values are shown in Table 2, and are similar for both the A and V variants.

Table 2.

Desensitization rate constants

	V			A
[ACh]	τcluster (ms)	Po (s−1)	kdesen	τcluster (ms)	Po	kdesen (s−1)
20	805	0.16	7.8	447	0.16	14
50	532	0.54	3.5	480	0.50	4.2
100	279	0.75	4.8	224	0.67	6.7

The cluster duration and the cluster P_o were measured for both the A433 and V433 variants. τ_cluster is the observed cluster duration minus 0.1 s, because of the requirement for clusters to be longer than 100 ms. The product of τ_cluster and P_o is independent of agonist concentration, and the inverse of this product reflects the desensitization rate constant k_desen (Auerbach & Akk, 1998). The mean values of k_desen were similar for the V and A variants. Each entry represents data from one patch.

From these results we conclude that a V-to-A mutation at α433 does not have a significant effect on agonist binding, channel gating, or desensitization rate constants.

Are the transmitter binding sites functionally different?

We used the discovery of A and V variants at position α433 as an opportunity to re-examine some unresolved issues in the kinetics of AChR activation. We were particularly interested in determining whether any differences could be detected in the association and dissociation rate constants at the adult muscle receptor's two ACh binding sites. Although in principle the P_o dose-response curve contains information about site-specific dissociation equilibrium constants, we found that such curves obtained from simulated currents were equally well described by equivalent (eqn (2)) and non-equivalent (eqn (3)) binding sites if K_a and K_b differed less than 25-fold. Thus, the dose-response curve is not a sensitive assay for detecting differences between binding site affinities.

In order to determine if the two transmitter binding sites are functionally different, intervals within clusters from αV433 were fitted by Model 1 without channel block and without the constraint of equal association and dissociation rate constants. The data fitted simultaneously to Model 1 consisted of 27 173 intervals from 67 clusters at 20 μM, 13 150 intervals from 17 clusters at 50 μM and 19 079 intervals from 34 clusters at 100 μM. The rate constant estimates and standard deviations are given in Table 1.

When the binding sites were assumed to be equivalent, the model had five free parameters and the maximum log likelihood (LL) was 364 667. When the constraint of equivalent binding was relaxed, the model had seven free parameters and the LL increased to 364 719. A log likelihood ratio (LLR) of 52 indicates that the probability of the unconstrained model is e⁵² times more than that of the constrained model. This probability is too large to be accounted for solely by the extra free parameters (Bozdogan, 1987).

We tested whether our assumption that β= 50 000 s⁻¹ influenced the LLR of the unequal vs. equal binding site model comparison. In these studies (αV433 intervals), β was fixed at values 30, 50, 75 and 100 ms⁻¹, which resulted in LLR values of 42, 52, 63 and 67, respectively. We conclude that the superior fit of the unequal binding site model was not sensitive to the precise value of β that was used.

We also considered the accuracy of the standard deviations of the rate constants shown in Table 1, because these were generated using an approximation that assumed that the errors are symmetric (see Methods). Figure 4 shows LL profiles for two rate constants. For k_{+ 2}, where the best-fitting value was 291 μM⁻¹ s⁻¹, the approximate standard deviation was 16 μM⁻¹ s⁻¹, and the standard deviations calculated by likelihood interval method were -16 μM⁻¹ s⁻¹ and +27 μM⁻¹ s⁻¹. For k_-2, where the best-fitting value was 43 010 s⁻¹, the approximate standard deviation was 1835 s⁻¹, and the standard deviations calculated using the likelihood interval were -1699 s⁻¹ and +2710 s⁻¹. We conclude that the approximate standard deviations that are shown in Table 1 are an accurate reflection of the true standard deviations of the rate constant estimates.

From the optimal rate constants using non-equivalent sites, the dissociation equilibrium constant values of the two sites were 186 ± 12 and 148 ± 37 μM and are not statistically different. Both sites have approximately the same dissociation equilibrium constant for ACh and in this sense can be considered to be equivalent.

Properties of a short-lived, diliganded closed state

At high ACh concentrations, a population of ∼1 ms duration gaps could be clearly observed within clusters (Fig. 5A). This component was also apparent in the closed interval duration histograms at 100 μM ACh and above (Fig. 5B). The fraction occupancies (f) and (τ) lifetimes of these gaps were obtained by fitting histograms of intracluster closed intervals and were (mean ±s.d.; n= 15 patches) f= 0·056 ± 0·028 and τ= 1·10 ± 0·38 ms. Neither f nor τ vary with the ACh concentration, which indicates that these gaps arise from diliganded AChRs. At high concentrations, AChRs open within ∼20 μs, and therefore the state that gives rise to the 1 ms gaps cannot lie in the main activation pathway.

Figure 5. Properties of a 1 ms diliganded closed state.

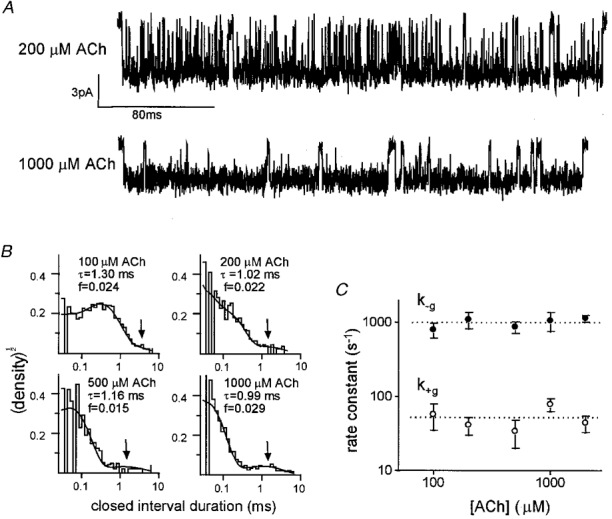
A, example clusters elicited by desensitizing concentrations of agonist (filtered at 3 kHz for display). The membrane potential was -70 mV; inward current is down. Both brief gaps arising mainly from channel gating, and ∼1 ms gaps are apparent in these high P_o clusters. The 1 ms gaps can be described by a diliganded closed state connected only to the diliganded open state (state C₆ in Model 1). B, closed interval duration histograms. The ∼1 ms lifetime component is indicated by an arrow. The fraction of all closures associated with this component (f) and its lifetime (τ) are shown for each histogram. The time constant of the faster component was 0·28 ms (100 μM; V433A), 0·096 ms (200 μM; V433A), 0·045 ms (500 μM; V433), and 0·03 ms (1000 μM; V433A). C, rate constants for entering and leaving state C₆vs. ACh concentration. The entry (k_{+ g}= 51 s⁻¹) and exit (k_-g= 982 s⁻¹) rate constants do not vary with the agonist concentration. Each symbol is the mean ± standard deviation of three patches (13 of 15 patches are V433). The dotted lines are the global means and are (± standard deviation) k_{+ g}= 51 ± 4 s⁻¹ and k_-g= 982 ± 38 s⁻¹.

We assume that sojourns in the short-lived shut state are present at all agonist concentrations, but are not obvious at lower ACh concentrations because they have a lifetime that is similar to other closed components. The rate constants for entering (k_{+ g}) and leaving (k_-g) this state were estimated from 15 patches (100-2000 μM ACh; Fig. 5C), assuming that this state is connected only to the open state of Model 1. The mean rate constants for entering and leaving this shut state were (mean ±s.d.) k_{+ g}= 51 ± 17 s⁻¹ and k_-g= 982 ± 149 s⁻¹, respectively. From these values we calculate an equilibrium constant K_g= 0·052 ± 0·022. These rate constant estimates obtained from high concentration experiments are more accurate than those obtained from kinetic modelling of lower concentration experiments.

Channel block

ACh blocks the AChR channel (Sine & Steinbach, 1984; Colquhoun & Ogden, 1988; Maconochie & Steinbach, 1995), and, depending on the blocking and unblocking rate constants, the omission of the blocked state (C₇) from Model 1 might have influenced the estimates of the association, dissociation and channel closing rate constants. If a significant number of blocking events are present in the record, ignoring block will cause both the α and the β/k_-1 and β/k_-2 ratios to be overestimated. Because β is fixed, the omission will cause k_-1 and k_-2 to be underestimated.

If the lifetimes of the blocked (C₇) and diliganded closed (C₄) state are equivalent, then the fraction of brief gaps that arise from channel block is Ak_+b/α. Wang et al. (1997) reported that in our preparation (adult-type mouse muscle AChR expressed in HEK cells, 22°C, -70 mV, 142 mM extracellular K⁺) k_{+ b} is 10 μM⁻¹ s⁻¹ and k_-b is 74 100 s⁻¹. According to these values, in the ACh concentration range that was used for kinetic modelling (20-100 μM; Table 1), approximately 25 % of the fast gaps were channel block events, raising the possibility that some of the rate constant estimates were indeed biased by omission of the blocked state from Model 1.

The magnitudes of the errors caused by the omission of channel block increase with the ACh concentration. Figure 6 shows the concentration dependence of the rate constant estimates. In these experiments, interval durations from single patches were individually fitted by Model 1 without the blocked state and without scaling by the agonist concentration. The left panel shows that the association rate increases linearly with the ACh concentration, with a slope of 158 ± 5 μM⁻¹ s⁻¹. This value is similar to the average value for k₊ for A and V variants that was determined by the global fit (20-100 μM ACh; Table 1). There is no indication of a deviation from linearity between 5 and 100 μM ACh, indicating that the omission of channel block from Model 1 did not bias the ACh association rate constant estimate. The middle panel shows that the estimate of k_- decreases with increasing concentration. The low concentration limit of this parameter was 30 540 ± 1433 s⁻¹, which is 13 % higher than the average values from the global fit. The decrease in the k_- estimate with concentration may arise from the omission of channel block, but is more likely to be caused by a loss of information about this rate constant at high agonist concentrations because of the paucity of sojourns in un- and monoliganded states. The right panel shows that the estimate of α increases with increasing concentration. The low concentration limit of this parameter was 2378 ± 346 s⁻¹, which is 15 % smaller than the average values from the global fit. The increase in the α estimate with concentration is probably caused by the omission of channel block from the model. The slope of this relationship, which is equal to k_+b, is 6 μM⁻¹ s⁻¹.

Figure 6. Concentration dependence of the rate constant estimates.

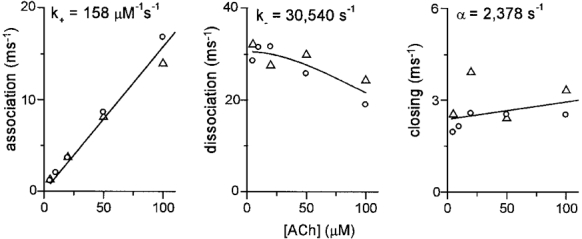
Intervals from individual patches were modelled (Model 1; k₊ not scaled by [ACh]; no state C₇) to test for the bias caused by the omission of channel block. ^, αV433; ▵, αA433. Left: the association rate increases linearly between 5 and 100 μM ACh; k₊ is the slope (fit constrained to go through the origin). Middle: the dissociation rate constant decreases with increasing [ACh]; k_- is the zero concentration asymptote. Right: the closing rate constant increases with increasing [ACh]; α is the zero concentration asymptote.

From the concentration dependence of the rate constant estimates we conclude that the omission of channel block from the kinetic scheme resulted in a modest underestimation of k_- and overestimation of α. A433 and V433 AChR were similar with regard to these errors, suggesting that channel block by ACh is not different in these two variants.

Finally, the rate constants were estimated by globally fitting Model 1 - with and without the channel block state - to interval durations obtained from a wide range of ACh concentrations (global fit, 9 patches, 10-200 μM ACh, A and V variants combined, 205 clusters, 83 932 intervals). The results are shown in Table 3 and Fig. 7. When all eight parameters of Model 1 were allowed to vary, the fit would not converge (β increased without limit). The other rate constants could only be estimated when β was fixed to be 50 000 s⁻¹. Without a channel block state, the intervals were better described by a model where ACh association and dissociation are both ∼3 times faster at one site (7 vs. 5 free parameters; LLR = 131). The effect of including a channel block event could only be investigated under the assumption of equivalent binding sites, however, because k_-2 increased without limit when this constraint was relaxed (9 free parameters). The incorporation of channel block to the model with equivalent binding sites significantly improved the fit (7 vs. 5 parameters, LLR = 366). With channel block, k₊ and k_- were faster, and α was slower, than without block. There was no significant difference in the k_+g and k_-g values, nor in the equilibrium constants for binding or gating.

Table 3.

Rate and equilibrium constants for V433 + A433 combined data set

		Unequal binding	Equal binding	Equal binding with block
Rate constant	k+ (k+1)	97.6 ± 1.88	167 ± 2.4	227 ± 6
	k− (k−1)	17 111 ± 481	24 745 ± 257	38 541 ± 1250
	k+2	347 ± 14	—	—
	k−2	47 807 ± 1833	—	—
	α	2426 ± 21	2570 ± 17	2024 ± 29
	k+g	35.1 ± 2.2	41.7 ± 2.4	49 ± 3
	k−g	441 ± 25	469 ± 19	512 ± 21
	k+b	—	—	6.9 ± 0.4
	k−b	—	—	57 186 ± 2067
	LL	544 882	544 751	545 117
Equilibrium constant	Ka (μm)	175 ± 9	148 ± 4	169 ± 10
	Kb (μm)	138 ± 11	—	—
	Θ*	21	19	25
	Kblock	—	—	0.10 ± 0.01

Rate constants (± standard deviation) were determined by kinetic modelling of single-channel interval dwell times, as described in Methods. The rate constants are defined in Model 1. k_+b and k_-b are the rate constants of channel block and unblock by ACh, respectively, and K_block is the dissociation equilibrium constant for block. All rate constants are in units of s⁻¹, except for k₊₁, k_{+ 2} and k_+b which are μm⁻¹ s⁻¹. There were 85 916 intervals from 232 clusters (9 patches; 10, 20, 50, 100 and 200 μm ACh; αA433 and αV433 AChR) globally fitted by Model 1.

^*The opening rate constant was fixed at 50 000 s⁻¹. The corresponding interval duration histograms are shown in Fig. 7.

Kinetics of αG153S + V433 AChR

Although the V-to-A mutation in M4 had no discernible effect on agonist binding or channel gating, it is possible that this mutation could interact with other mutations that themselves influence AChR affinity and gating. To test this possibility, we studied the mutation αG153S in the αV433 variant co-expressed with mouse muscle β, ε and δ subunits. It has been shown that (with the αA433 variant) the main effect of the αG153S mutation, which in humans causes SCCMS, is to slow the ACh dissociation rate constant (Sine et al. 1995).

Figure 8 shows examples of clusters and histograms of αV433/G153S as well as αA433/G153S activated by 1 μM ACh. Modelling results for both the A433 and V433 variants are shown in Table 1. The activation rate constants for αV433/G153S and αA433/G153S were similar, indicating that the M4 mutation does not significantly influence the consequences of this binding site mutation.

Figure 8. Activation of αG153S AChR.

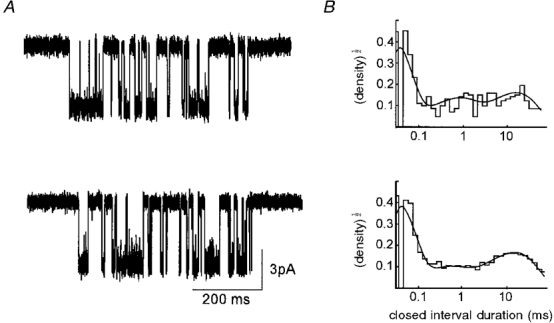
A, αG153S/V433 (top) and αG153S/A433 (bottom) receptor current clusters elicited by 1 μM ACh (filtered at 3 kHz for display). B, corresponding closed duration histograms. Continuous curves are fitted to the data using the rate constants in Table 1. The closed interval distribution comprises three distinct components having the time constants of 15·9, 0·68 and 0·019 ms for αV433/G153S, and 14·5, 0·40 and 0·023 ms for αA433/G153S.

As was the case with wild-type adult mouse muscle AChR, the dissociation equilibrium constants of the two transmitter binding sites are similar in αV433/G153S AChR (K_d≈ 8 μM). In addition, like wild-type AChR, one site was kinetically ‘fast’ and the other, ‘slow’. Although there was some asymmetry in the effect of the αG153S in the αV433 currents, the mutation had asymmetric effects at the two binding sites in αA433/αG153S AChR. At the fast site, the association rate constant increased, and the dissociation rate constant decreased by ∼3-fold. At the slow site, the association rate constant was unchanged, but the dissociation rate constant was decreased by more than 15-fold.

With regard to channel gating, the αG153S mutation has little or no effect on the opening rate constant for diliganded AChR. However, the channel closing rate constant of the mutant was reduced substantially. The net effect of the mutation was to increase the diliganded AChR gating equilibrium constant by 2- to 3-fold.

DISCUSSION

A previously unrecognized mutation in the mouse muscle α subunit clone - a V-to-A substitution in the fourth membrane spanning region - prompted us to revisit several aspects of AChR activation. After establishing that the mouse genome indeed codes for a V at position α433, we determined that the two adult mouse muscle transmitter binding sites have the same dissociation equilibrium constant for ACh. We also describe the properties of a diliganded closed state that has a lifetime of ∼1 ms that is independent of the ACh concentration.

Wild-type α433 is valine

Sequencing of genomic DNA confirms that the mouse muscle α subunit has nucleotides GTC, at positions 1305-1307, which code for a valine at position 433 of the polypeptide. We conclude that the database is correct, i.e. that mouse genome probably encodes a V at position 433 of the muscle α subunits. This conclusion is supported by the fact that the V is conserved in many other species (Fig. 1A). In addition, two original sequences of this gene (Boulter et al. 1985; Isenberg et al. 1986) show a V at position 433. Thus, the mouse αA433 variant probably reflects an accidental background mutation that has been present in some α subunit cDNA since at least 1986. As an aside we note that the sequence shown in Fig. 1B is, to our knowledge, the first published sequence for genomic mouse α subunit DNA, and shows that the final intron of the mouse is similarly positioned to the final intron of the human gene (Noda et al. 1983).

The V-to-A mutation has no measurable effect on ACh binding, channel gating, or receptor desensitization. Moreover, this mutation does not modify the effect of a binding site mutation that causes SCCMS (αG153S). Therefore, the results of previous studies that utilized the αV433A mutant clone are in all likelihood pertinent to the true wild-type AChR, at least with regard to the above-mentioned parameters.

That the αV433A mutation had no effect on AChR function was surprising given that another M4 mutation alters AChR activation (Lasalde et al. 1996). The lack of an effect suggests that the side chain of the amino acid at position 433 resides in energetically similar environments (perhaps the lipid bilayer) in closed, open and desensitized conformations of the protein.

The binding sites have equal affinity for ACh. The rate constants shown in Table 1 are quite similar to those presented previously for the same preparation (adult mouse AChR expressed in HEK 293 cells) under the same experimental conditions (-70 mV; 142 mM extracellular KCl, 22-24°C) (Akk & Auerbach, 1996; Wang et al. 1997). The results indicate that the two transmitter binding sites have the same dissociation equilibrium constant for ACh, ∼160 μM. This result is consistent with the observation that carbachol binds with a similar K_d to intracellular adult mouse αε and αδ complexes (Prince & Sine, 1998). Because K⁺ and Na⁺ compete with agonists (Akk & Auerbach, 1996), we estimate that the dissociation equilibrium constant for ACh in adult mouse AChR is ∼60 μM in pure water, and ∼120 μM in physiological saline.

A number of studies have shown that large antagonists such as curare (Sine & Claudio, 1991) and α-conotoxin (Groebe et al. 1995; Sine et al. 1995) have distinct affinities for the two transmitter binding sites. These differences in affinity may arise from ligand-protein interactions that are some distance from the quaternary amine group and may not be relevant to the interactions of ACh with residues that form the primary docking site.

Although the modelling results suggest that the binding sites of wild-type adult AChR have different kinetics, we cannot be certain of this distinction because the LLR may depend on the presence of only a few brief closed intervals. Studies using αG153S AChR, where slow agonist dissociation makes the distinction between the sites more readily apparent as multiple closed interval components in the closed interval duration histograms (Fig. 8), also suggest that the binding sites are not equivalent with regard to kinetics. The kinetic difference between the two transmitter binding sites is most simply explained by a small increase (∼1 k_BT, where k_B is the Boltzmann constant and T is the absolute temperaturein the barrier separating the bulk solution and the transmitter docking site at one of the sites. Nonetheless, the kinetics of binding at the two sites are not greatly different, and only small errors will accrue in analyses that assume the sites are identical.

If the sites are indeed kinetically different, our analyses do not provide evidence as to which is the ‘fast’ site and which is the ‘slow’ site. Akk et al. (1999) report that an ε subunit mutation (εE184Q) specifically increases the dissociation rate constant of only one site, which is presumably the αε site. The unaltered site, which is presumably the αδ site, has association and dissociation rate constants that are characteristic of the slower site (Table 1). We therefore speculate that ACh binding to the αδ site may be slower than to the αε site.

A 1 ms diliganded closed state

Another aspect of AChR kinetics that we explored was a population of ∼1 ms gaps that is apparent at high ACh concentrations. Between 100 and 2000 μM ACh the rate constants for entry and exit from this state were independent of the agonist concentration (Fig. 5C), which indicates that these gaps reflect closures of a fully occupied, diliganded state. The slope of the P_ovs.[ACh] curve indicates that two agonist binding events (K_d= 160 μM) occur < 200 μM, and there is no evidence for additional, low-affinity agonist binding events (aside from channel block) beyond this concentration. The 1 ms gap state has similar properties to an intermediate closed state identified by Colquhoun & Sakmann (1985) at the adult frog endplate and by Sine & Steinbach (1986) in BC3H-1 cells.

We cannot determine from our experiments whether this state (C₆) is connected to the O₅ state and/or to the C₄ state of Model 1. If the former is true, C₆ can be considered to be a short-lived desensitized state, but we do not know if this state is directly connected to the long-lived desensitized state(s) that separates clusters, or whether it arises from a completely different mechanism of channel inactivation. If C₆ and the long-lived desensitized states are not connected, then the apparent desensitization rate constant (Table 2) is the rate constant for the transition between the open and long-lived desensitized states. If the C₆ and long-lived desensitized states are connected in series, then the apparent desensitization rate constant is an aggregate of several molecular rate constants. For example, if k_+g= 40 s⁻¹ and k_-g= 800 s⁻¹, then with such a coupled reaction scheme an observed desensitization rate constant of 4 s⁻¹ (Auerbach & Akk, 1998) would reflect a molecular desensitization rate constant of ∼80 s⁻¹ (for the C₆-to-long lived desensitized state transition).

Sojourns into C₆ occur at all agonist concentrations, and, depending on the data selection, the exclusion of this state from the kinetic model could influence the estimates of the other activation rate constants. In modelling studies that do not incorporate this state at high agonist concentrations in order to account for the ∼1 ms gaps the dissociation rate constant estimate of one of the transmitter binding sites will become artificially slow. This generates an erroneously low estimate of the dissociation equilibrium constant at one binding site, which in turn leads to the erroneous conclusion that the binding sites have different affinities for the agonist (e.g. Sine et al. 1995). It is likely that some of the conflicting results in the literature regarding AChR activation rate constants obtained by single-channel kinetic modelling can be traced to the exclusion of this state from the kinetic scheme.

Kinetics of αG153S AChR

A previous study of the SCCMS mutant αG153S was done with αA433 AChR (Sine et al. 1995). The main conclusions of this previous study were that the αG153S mutation slows ACh dissociation, and that the effects of the mutation are different at the two transmitter binding sites. Here, we have shown that the αV433 and αA433 variants behave similarly with respect to the αG153S mutation and that the effects of the αG153S mutation on the association rate constant are similar at the two transmitter binding sites.

The αG153S mutation lowers the dissociation equilibrium constant for ACh of the closed AChR from ∼160 μM to ∼8 μM, or by a factor of 20. Using the relationship ΔG₀= -RT× ln(K_d), where R is the universal gas constant and T is the absolute temperature and ΔG₀ is the change in free energy at equilibrium, this corresponds to a net stabilization of each bound ACh molecule by -3·0 k_BT (-7·5 kJ mol⁻¹). Thus, the αG153S mutation makes it a little easier for ACh to reach its docking site, and much more difficult for ACh to escape back to the bulk solution.

Dose-response profile and the decay of the endplate current

We can calculate some consequences of the αG153S mutation from the activation rate constants shown in Table 1. From Model 1, and under conditions in which √Θ≥ 1,

and

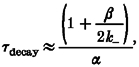where τ_decay is the decay time constant of the endplate current. The αG153S mutation will cause a pronounced shift the dose-response profile to the left and a substantial prolongation of the endplate current. Using the rate constants in Sine et al. (1995), at -70 mV and in 142 mM KCl, the αG153S mutation will lower the EC₅₀ for ACh from 30 to 1·3 μM, and will prolong the decay of the endplate current from 1 to 24 ms. The ionic composition of the extracellular solution influences the EC₅₀ because monovalent cations compete with ACh for the binding sites (Akk & Auerbach, 1996). The membrane potential influences both the EC₅₀ and τ_decay because the closing rate constant slows upon hyperpolarization (e-fold/66 mV; Auerbach et al. 1996). We estimate that the αG153S mutation will shift the EC₅₀ for the transmitter from 18 to 1 μM, and will prolong the decay time constant from 1 to 22 ms (-90 mV, 150 mM NaCl).

Jackson (1989) has discussed the design criteria for the ‘perfect’ receptor at the neuromuscular synapse. The activation rate constants for wild-type AChR shown in Table 1 are consistent with the essential criteria: there are two binding events, the opening and association rate constants are fast enough to generate a rapid response onset, and the dissociation rate constant is fast enough to rapidly terminate the response. Having one high affinity binding site modestly lowers the EC₅₀ and speeds the rise of the endplate current (Jackson, 1989). However, the synaptic ACh concentration is > 0·5 mM and the muscle membrane time constant is > 1 ms, and the presence of one higher affinity site would have little consequence with regard to the amplitude or shape of the endplate potential. Thus, there should be little, if any, selective advantage to having one high affinity binding site. Similarly, it is difficult to rationalize a significant functional consequence for having distinct kinetics at the two transmitter binding sites. The differences in the association and dissociation rate constants that we have detected are rather small and may not have a significant impact on neuromuscular transmission.