Effects of calcium buffering on glucose-induced insulin release in mouse pancreatic islets: an approximation to the calcium sensor

Abstract

• The properties of the calcium sensor for glucose-induced insulin secretion have been studied using cell-permeant Ca²⁺ buffers with distinct kinetics and affinities. In addition, submembrane cytosolic Ca²⁺ distribution has been modelled after trains of glucose-induced action potential-like depolarizations.

• Slow Ca²⁺ buffers (around 1 mmol l⁻¹ intracellular concentration) with different affinities (EGTA and Calcium Orange-5N) did not significantly affect glucose-induced insulin release. Modelling showed no effect on cytosolic Ca²⁺ concentrations at the outermost shell (0.05 μm), their effects being observed in the innermost shells dependent on Ca²⁺ affinity.

• In contrast, fast Ca²⁺ buffers (around 1 mmol l⁻¹ intracellular concentration) with different affinities (BAPTA and Calcium Green-5N) caused a 50% inhibition of early insulin response and completely blocked the late phase of glucose-induced insulin response, their simulations showing a decrease of [Ca²⁺]_i at both the inner and outermost shells.

• These data are consistent with the existence in pancreatic β-cells of a higher affinity Ca²⁺ sensor than that proposed for neurons. Moreover, these data are consistent with the proposed existence of two distinct pools of granules: (i) ‘primed’ vesicles, colocalized with Ca²⁺ channels and responsible of the first phase of insulin release; and (ii) ‘reserved pool’ vesicles, not colocalized and responsible for the second phase.

It is well established that changes in the cytoplasmic Ca²⁺ concentration ([Ca²⁺]_i) in pancreatic β-cells are essential for the regulation of insulin secretion (Ashcroft & Rorsman, 1989). This Ca²⁺ rise, most probably restricted to the submembrane region (Martin et al. 1997), promotes the fusion of the secretory granules with the plasma membrane. Aside from other effects, Ca²⁺ should interact with one or more sites located at the exocytotic machinery whose components and role have been recently identified (Kiraly-Borri et al. 1996; Martin et al. 1996; Lang et al. 1997).

In this regard, several components may affect the intensity and kinetics of glucose-induced insulin release. In addition to the affinity and kinetics of the Ca²⁺ sensor, the existence of a primed granule pool (Eliasson et al. 1997) in conjunction with steep concentration gradients (Martin et al. 1997) and the colocalization of the insulin secretory granule with the voltage-dependent Ca²⁺ channel (Bokvist et al. 1995) may condition the effect of cell-permeant exogenous Ca²⁺ buffers. The use of a new generation of Ca²⁺ buffers with known kinetic and affinity properties allows us to have indirect access to the properties of the secretory machinery.

Recent observations in other endocrine cells have demonstrated: (i) the existence of a latency between [Ca²⁺]_i and exocytosis (Chow et al. 1996; Eliasson et al. 1997); (ii) that secretion is relatively slow and continues for tens of milliseconds after Ca²⁺ entry through the voltage-dependent Ca²⁺ channels has ceased (Chow et al. 1996; Klingauf & Neher, 1997); and (iii) that endocrine cells have a higher Ca²⁺ sensitivity than neurones (Heinemann et al. 1994) and a lower maximum rate of secretion (Chow et al. 1994). All of these properties indicate a faint coupling of Ca²⁺ channels to the secretory machinery, with exocytosis being triggered by peaks of [Ca²⁺]_i of <10 μmol l⁻¹ at the release sites (Chow et al. 1994). These results contrast with those obtained from neurones (Zucker, 1996). If Ca²⁺ channels and vesicles are not strictly colocalized, then the amount of Ca²⁺ that enters during a single action potential may not be sufficient to trigger significant secretion, whereas trains of action potentials would be more effective (Zhou & Misler, 1995).

Pancreatic β-cells are unique in the sense that although they are endowed with the exocytotic and electrical machinery present in other excitable cells, the physiological trigger promoting insulin release is a nutrient that needs to be metabolized to initiate the sequence of events that links ATP-regulated K⁺ channel closure with insulin release (Ashcroft et al. 1984; Dunne & Petersen, 1991). It is known that in response to nutrient secretagogues, pancreatic β-cells display a series of trains of Ca²⁺ action potentials with a frequency of 2-6 Hz and a duration of 50-100 ms (Atwater et al. 1978). It is also accepted that: (i) these trains induce [Ca²⁺] changes beneath the plasma membrane (Martin et al. 1997); (ii) pancreatic β-cells are polarized (Martin et al. 1997); and (iii) Ca²⁺ channels seem to be strictly colocalized with secretory vesicles (Wiser et al. 1999). Taking into account all these aspects, we have studied the effects of several exogenous Ca²⁺ chelators on insulin release, in order to determine how cytosolic Ca²⁺ distribution affects the dynamics of insulin exocytosis in pancreatic β-cells. In addition, we have modelled buffered Ca²⁺ diffusion in the vicinity of channels and release sites by using trains of depolarizations that resemble the ones induced by stimulatory glucose concentrations.

METHODS

Islet isolation, cell isolation and culture

Islets from adult (8- to 10-week-old) Swiss albino male mice (OF1) killed by cervical dislocation in accordance with national guidelines were isolated as previously described (Lernmark, 1974). Briefly, after pancreas digestion with collagenase (Collagenase A, Boehringer Mannheim) in a stationary bath at 37°C, islets were separated by centrifugation and hand picked under a stereomicroscope. Once isolated, islets were dissociated into single cells in a low-calcium medium as previously described (Martin et al. 1997). Cells were then centrifuged, resuspended in culture medium RPMI 1640 (Sigma) supplemented with 10 % fetal calf serum, penicillin (Sigma; 100 i.u. ml⁻¹), streptomycin (Sigma; 0.1 mg ml⁻¹), and 5.6 mmol l⁻¹ glucose and plated on glass coverslips. Cells were kept at 37°C in a humidified atmosphere of 95 % O₂-5 % CO₂ and used within 10 h of culture. Cell viability was tested by Trypan Blue exclusion (96 % of the cells excluded Trypan Blue). For intracellular recording experiments, islets were isolated by microdissection as previously described (Sanchez-Andres & Soria, 1991).

Loading of islets and islet cells

Collagenase-isolated islets, microdissected islets and islet cells were incubated for 2 h at 37°C in modified Krebs buffer supplemented with 5.6 mmol l⁻¹ glucose and 3 % bovine serum albumin. The medium was continuously bubbled with 95 % O₂-5 % CO₂ for a final pH of 7.4. Then, pancreatic islets and islet cells were loaded as previously described (Martin et al. 1997) with EGTA AM, BAPTA AM, Calcium Orange-5N AM, Calcium Green-5N AM, Calcium Green-1 AM, Calcium Green-2 AM, dimethylBAPTA AM, dibromoBAPTA AM and dinitroBAPTA AM (Molecular Probes) by incubation for 1 h at 37°C in the described Krebs buffer with 100 μmol l⁻¹ of these acetoxymethyl (AM) derivatives. Exogenous Ca²⁺ chelators AM were added as a concentrated stock solution in dimethyl sulphoxide (DMSO) (Sigma; final DMSO concentration 0.3 % v/v). In order to facilitate the solubilization of the Ca²⁺ chelators in physiological media, the mixture also contained 10 % (w/w) of the non-ionic surfactant polyol pluronic F127 (Molecular Probes). After loading, islets and cells were incubated for 1 h with the modified Krebs buffer mentioned above. The Krebs buffer was kept at 37°C and was constantly gassed with 95 % O₂-5 % CO₂ for a final pH of 7.4. Finally, Trypan Blue exclusion after cell loading was 95 %.

Determination of intracellular exogenous Ca²⁺ chelator concentration

For fluorescent exogenous Ca²⁺ chelators (Calcium Green-1 AM, Calcium Green-2 AM, Calcium Orange-5N AM and Calcium Green-5N AM), 5 × 10⁵ cells were loaded with 100 μmol l⁻¹ of these AM derivatives by incubation for 1 h at 37°C in the described Krebs buffer. Next, cells were centrifuged for 5 min at 800 g, washed three times and sonicated twice in 1 ml of a CaEGTA Krebs buffer (final Ca²⁺ concentration 100 nm) for 5 s using a sonic dismembrator (Artek System Corp., Farmingdale, NY, USA) at 30 % maximum power. Finally, the suspension was centrifuged for 15 min at 16700 g and the fluorescence emitted by the supernatant was compared to that emitted for calibration curves built with exogenous Ca²⁺ chelator (sodium salt) solutions, in the same CaEGTA Krebs buffer, at different concentrations (0, 0.1, 1, 10 and 50 μmol l⁻¹). The emitted fluorescence (531 nm for Calcium Green-1, 536 nm for Calcium Green-2, 575 nm for Calcium Orange-5N and 532 nm for Calcium Green-5N) was measured with a spectrofluorometer (model U-2000, Hitachi Ltd, Tokyo) at different excitation wavelengths depending on the exogenous Ca²⁺ chelator (488 nm for Calcium Green-5N, Calcium Green-1 and Calcium Green-2; 545 nm for Calcium Orange-5N). For non-fluorescent exogenous Ca²⁺ chelators (BAPTA AM and EGTA AM), a calibration curve of quenching of indo-1 (sodium salt)-emitted fluorescence (excitation wavelength of 360 nm and emission wavelength of 410 nm) was performed at different EGTA and BAPTA concentrations (0, 1, 10, 100 and 1000 μmol l⁻¹) in the same EGTA buffer. Then, 5 × 10⁵ cells were loaded, centrifuged, washed and sonicated in the same manner as that used for fluorescent exogenous Ca²⁺ chelators. Finally, the quenching values of indo-1-emitted fluorescence elicited by the supernatant were extrapolated to the quenching of the indo-1 calibration curve. Cytosolic chelator concentrations were calculated from the total cell volume (10.45 × 10⁻⁷ l).

Electrophysiology

Membrane potential of the β-cell was recorded as previously described (Sanchez-Andres & Soria, 1991). Microdissected islets were fixed with micropins to the bottom of a 50 μl chamber and perifused at a rate of 0.8 ml min⁻¹ with fresh modified Krebs buffer and constantly gassed with 95 % O₂-5 % CO₂ for a final pH of 7.4. Different glucose concentrations (3 and 11.1 mmol l⁻¹) were added to the superfusion medium. The test agents reached the chamber with a delay of 3 s. These delays have been corrected for in the figures. Bath temperature was maintained at 36 ± 1°C by heating a stainless steel ring controlled by a thermostat. The temperature of the chamber was continuously monitored with a micro-thermistor. Recordings were made with an Axoclamp 2B amplifier (Axon Instruments). Data acquisition was performed with Axotape version 2.0 (Axon Instruments) and data analysis with MicroCal Origin version 3.7 (MicroCal Software, Northampton, MA, USA).

Insulin measurements

Insulin measurements were performed as previously described (Bolea et al. 1997). For static incubations, islets were incubated in groups of three in 1 ml of fresh modified Krebs buffer with 1 % bovine serum albumin plus the different glucose concentrations (3 and 22.2 mmol l⁻¹) for 30 min at 37°C. For islet perifusion experiments, batches of 10 islets were placed in a 50 μl chamber and perifused at a flow rate of 1 ml min⁻¹ at 37°C with fresh modified Krebs buffer with 1 % bovine serum albumin plus the different glucose concentrations (3 and 22.2 mmol l⁻¹). For islet cell perifusion experiments, 1 × 10⁵ cells were packed into a 1 cm diameter column and sandwiched between two layers of swollen Sephadex G-200 microcarrier beads (Sigma). The column was perifused at a flow rate of 1 ml min⁻¹ at 37°C with fresh modified Krebs buffer with 1 % bovine serum albumin plus the different glucose concentrations (3 and 22.2 mmol l⁻¹). The pancreatic islets and islet cells were first perifused in 3 mmol l⁻¹ glucose for 30 min to reach a state of stable insulin release. The solutions were prewarmed at 37°C and continuously gassed. Throughout the perifusion, effluent was continuously collected at 2 min intervals. The dead time was 2 min and has been corrected for in the figures. Both static incubation and perifused samples were kept at -20°C until insulin determination. Insulin was assayed by radioimmunoassay (RIA) using a kit from Diagnostic Products Corporation (Los Angeles, CA, USA). The RIA included the following steps: addition of anti-porcine insulin guinea-pig serum, incubation for 36 h at 4°C, addition of freshly labelled ¹²⁵I-labelled-(Tyr A19)-human insulin, incubation for 18 h at 4°C and precipitation of bound insulin by ethanol. Rat insulin provided by the above-mentioned kit was used to prepare the standard curves. Standard curves and samples were run in triplicate.

Statistical analysis

The results were expressed as means ± standard error of the mean (s.e.m.). For comparisons between two groups, Student's unpaired, two-tailed t test was used. *P < 0.001 was considered significant.

RESULTS

Intracellular concentration of exogenous mobile Ca²⁺ buffers

As demonstrated in Table 1 the estimated concentration of all permeant buffers was between 0.85 and 1.61 mmol l⁻¹. Theoretically, there may exist a limitation upon the maximum concentration of permeant chelator that can be introduced into cells (around 1 mmol l⁻¹, as indicated in Table 1), which may be set by finite intracellular esterase activity, by active extrusion of the compound, and/or by their metabolism into inactive forms.

Table 1.

Intracellular concentrations of exogenous mobile Ca²⁺ buffers

Exogenous Ca2+ buffer	Cytosolic concentration (μmol l−1)
EGTA	853 ± 14
BAPTA	927 ± 36
Calcium Green-1	1361 ± 57
Calcium Green-2	1612 ± 63
Calcium Green-5N	1416 ± 73
Calcium Orange-5N	1280 ± 41

Data are means ±s.e.m. All determinations were run in quadruplicate. For fluorescent exogenous Ca²⁺ chelators 5 × 10⁵ cells were loaded with 100 μmol l⁻¹ of their AM derivative by incubation for 1 h at 37 °C. Then, cells were centrifuged for 5 min at 800 g, washed and sonicated in a CaEGTA buffer. The suspension was then centrifuged for 15 min at 16 700 g and the fluorescence emitted by the supernatant was compared to that emitted for calibration curves built with exogenous Ca²⁺ chelator solutions, in the same CaEGTA buffer, at different concentrations. For nonfluorescent exogenous Ca²⁺ chelators a calibration curve was performed at different EGTA and BAPTA concentrations of quenching of indo-1-emitted fluorescence in the same CaEGTA buffer. Then, 5 × 10⁵ cells were loaded, centrifuged, washed and sonicated in the same manner as that used for fluorescent exogenous Ca²⁺ chelators. Finally, values of quenching indo-1-emitted fluorescence elicited by the supernatant were extrapolated to the quenching of the indo-1 calibration curve. Cytosolic chelator concentrations were calculated from the total cell volume.

Effects of mobile Ca²⁺ buffers on pancreatic β-cell electrical activity

To test the possible toxicity of these permeant Ca²⁺ buffers, we studied the effects of prolonged exposure to 100 μmol l⁻¹ BAPTA AM or EGTA AM on glucose-induced electrical activity. Figure 1A shows the typical pattern of electrical activity of a pancreatic β-cell stimulated with 11.1 mmol l⁻¹ glucose. This shows the onset of an oscillatory activity with membrane potential oscillating between silent (hyperpolarized) and active (depolarized) phases with fast spikes (Ca²⁺ action potential) superimposed upon them. Neither EGTA (Fig. 1B) nor BAPTA (Fig. 1C) significantly modified the 11.1 mmol l⁻¹ glucose-induced oscillatory pattern of electrical activity. In addition, we did not observe any inhibitory effect of EGTA or BAPTA on the fast spikes of Ca²⁺ action potential. Only a small increase, which was within the normal range for this glucose concentration, in the height of the action potentials was observed when BAPTA was used. This could be attributed to less inactivation of Ca²⁺ channels due to the presence of BAPTA. In addition, these results also indicate that electrical activity was measured in permeant Ca²⁺ buffer-loaded β-cells.

Figure 1. Effects of different exogenous Ca²⁺ chelators on glucose-induced electrical activity.

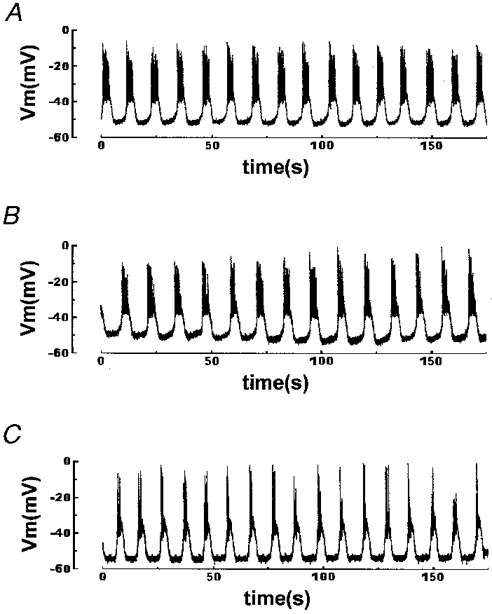
Islets were loaded for 1 h at 37 °C in modified Krebs buffer with 100 μmol l⁻¹ of the different exogenous chelators in AM form. The records show representative examples of the effects of 11.1 mmol l⁻¹ glucose on intracellularly recorded membrane potential of a pancreatic β-cell in an intact islet perifused with Krebs buffer. A, unloaded control islet. B, 100 μmol l⁻¹ EGTA-loaded islet. C, 100 μmol l⁻¹ BAPTA-loaded islet. Results are representative of 4 out of 4 cells.

Nutrient-induced insulin release depends on mobile Ca²⁺ buffers

We have studied the effects of the forward binding constant of the Ca²⁺ buffers on 22.2 mmol l⁻¹ glucose-induced insulin release, by loading the islets with diffusible exogenous buffers with different kinetic properties. Figure 2A shows that perifused mouse islets respond to a stepwise increase in glucose concentration with a rapid and transient burst of insulin secretion (first phase) followed by a plateau (second phase) which lasted as long as glucose was present. When 100 μmol l⁻¹ EGTA-loaded islets (a slow buffer with a forward binding rate (K_on) of 1.5 × 10⁶ l mol⁻¹ s⁻¹; Smith & Miller, 1985) were perifused with 22.2 mmol l⁻¹ glucose no significant change in insulin release was observed (Fig. 2B). In addition, loading the islets with Calcium Orange-5N (a relatively slow buffer with a K_on of 1 × 10⁷ l mol⁻¹ s⁻¹; Escobar et al. 1997) did not affect glucose-induced insulin release either, although a small delay in the onset of the first phase was observed (Fig. 2D). Both EGTA and Calcium Orange-5N have a very different Ca²⁺ affinity. In fact, EGTA K_d is 200-fold less than that of Calcium Orange-5N (0.1 vs. 20 μmol l⁻¹; Smith & Miller, 1985; Escobar et al. 1997). On the other hand, when islets were loaded with 100 μmol l⁻¹ of the very fast mobile exogenous Ca²⁺ buffers BAPTA (K_on of 4 × 10⁸ l mol⁻¹ s⁻¹; Grynkiewicz et al. 1985) and Calcium Green-5N (K_on of 1.3 × 10⁸ l mol⁻¹ s⁻¹; Escobar et al. 1997) a markedly impaired insulin release was observed (Fig. 2C and E, respectively). As shown in Fig. 2C and E, early insulin response was 50 % inhibited and late phase insulin response was completely abolished. Note that EGTA and BAPTA have a very similar Ca²⁺ affinity (K_d= 0.1 and 0.4 μmol l⁻¹, respectively; Smith & Miller, 1985; Grynkiewicz et al. 1985). When comparing buffers with the same Ca²⁺ affinity (Calcium Orange-5N and Calcium Green-5N; K_d= 20 μmol l⁻¹; Smith & Miller, 1985) we observed that only the faster one markedly inhibited both phases of glucose-induced insulin release (Fig. 2D and E). Other fast exogenous Ca²⁺ buffers such as Calcium Green-1 and Calcium Green-2 (K_on of 1 × 10⁸ l mol⁻¹ s⁻¹; Escobar et al. 1997) elicited the same pattern of inhibition (data not shown). The inhibitory effects of high concentrations of Ca²⁺ chelators on peripherally located α-cell [Ca²⁺]_i, which could be inhibiting glucagon secretion, which is very important for the insulin response of the islets, can be excluded for two reasons: (i) islet cell perifusion experiments with 100 μmol l⁻¹ EGTA (Fig. 3B) or BAPTA (Fig. 3C) showed the same results as whole-islet studies; and (ii) glucagon-containing α-cell [Ca²⁺]_i oscillations disappeared when islets were exposed to high glucose concentrations (Nadal et al. 1999).

Figure 2. Effects of different exogenous Ca²⁺ chelators on islet glucose-induced insulin release.

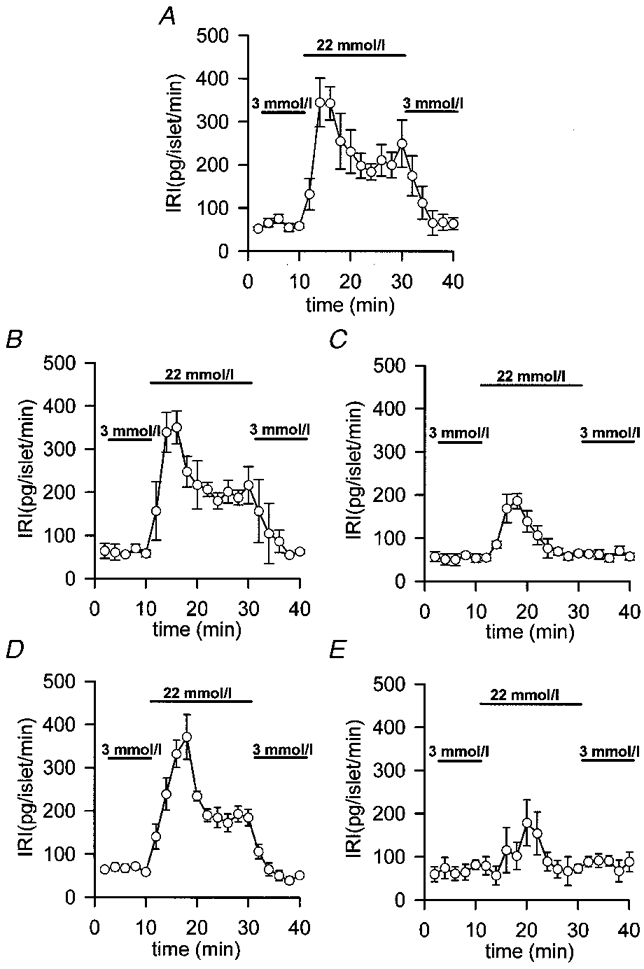
Islets were loaded for 1 h at 37 °C in modified Krebs buffer with 100 μmol l⁻¹ of the different exogenous chelators in AM form. Then, batches of 10 islets were perifused at a flow rate of 1 ml min⁻¹ at 37 °C with fresh modified Krebs buffer supplemented with 1 % bovine serum albumin. After a 30 min stabilization period with 3 mmol l⁻¹ glucose, the islets were perifused for 10 min with 3 mmol l⁻¹ glucose, then for 20 min with 22.2 mmol l⁻¹ glucose and finally for 10 min with 3 mmol l⁻¹ glucose. A, unloaded control islets. B, 100 μmol l⁻¹ EGTA-loaded islets. C, 100 μmol l⁻¹ BAPTA-loaded islets. D, 100 μmol l⁻¹ Calcium Orange-5N-loaded islets. E, 100 μmol l⁻¹ Calcium Green-5N-loaded islets. Insulin was assayed by radioimmunoassay and determinations were run in triplicate (IRI, immunoreactive insulin). Values are expressed as means ±s.e.m. of 7 experiments. Bars represent the addition of the different glucose concentrations.

Figure 3. Effects of different exogenous Ca²⁺ chelators on isolated islet cell glucose-induced insulin release.

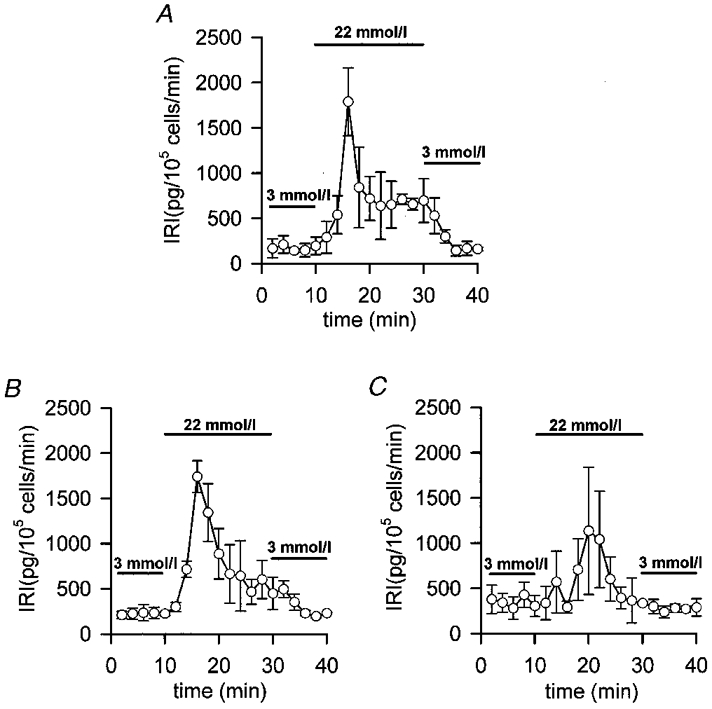
Islet cells were loaded for 1 h at 37 °C in modified Krebs buffer with 100 μmol l⁻¹ of the different exogenous chelators in AM form. Then, 1 × 10⁵ islet cells were perifused at a flow rate of 1 ml min⁻¹ at 37 °C with fresh modified Krebs buffer supplemented with 1 % bovine serum albumin. After a 30 min stabilization period with 3 mmol l⁻¹ glucose, the islet cells were perifused for 10 min with 3 mmol l⁻¹ glucose, then for 20 min with 22.2 mmol l⁻¹ glucose and finally for 10 min with 3 mmol l⁻¹ glucose. A, unloaded control islet cells. B, 100 μmol l⁻¹ EGTA-loaded islet cells. C, 100 μmol l⁻¹ BAPTA-loaded islet cells. Insulin was assayed by radioimmunoassay and determinations were run in triplicate. Values are expressed as means ±s.e.m. of 4 experiments. Bars represent the addition of the different glucose concentrations.

To further investigate the effects of mobile Ca²⁺ buffers with different calcium affinities on glucose-induced insulin release, the effects of several BAPTA derivatives with different K_d were determined. Table 2 shows that in islet batch incubations basal insulin release (3 mmol l⁻¹ glucose) was not affected by the different BAPTA derivatives after 30 min incubation. On the other hand, three of the four compounds were capable of significantly reducing 22.2 mmol l⁻¹ glucose-induced insulin release (Table 2). DibromoBAPTA (K_d= 3.6 μmol l⁻¹; Tsien, 1980) elicited a higher reduction in insulin release (54 %). The reduced insulin release produced by dimethylBAPTA (K_d= 0.04 μmol l⁻¹; Tsien, 1980) was 43 %, while the reduction produced by BAPTA (K_d= 0.1 μmol l⁻¹) was 47 %. Finally, dinitroBAPTA (K_d= 3 × 10⁴μmol l⁻¹; Pethig et al. 1989) did not reduce glucose-induced insulin release.

Table 2.

Effects of mobile Ca²⁺ buffers with different calcium affinities on glucose-induced insulin release

	IRI (pg islet−1 (30 min)−1)
	3 mmol l−1 glucose	22.2 mmol l−1 glucose
Control	376 ± 38	2587 ± 256
BAPTA	428 ± 47	1388 ± 199*
DibromoBAPTA	436 ± 35	1209 ± 240*
DimethylBAPTA	331 ± 41	1491 ± 118*
DinitroBAPTA	381 ± 53	2371 ± 343

Islets were loaded for 1 h at 37 °C in modified Krebs buffer with 100 μmol l⁻¹ of the different BAPTA derivatives in AM form. Then, islets were incubated in groups of 3 in 1 ml of modified Krebs buffer with 1% bovine serum albumin plus the different glucose concentrations (3 and 22.2 mmol l⁻¹) for 30 min at 37 °C. Insulin was assayed by radioimmunoassay and determinations were run in triplicate. Values are expressed as means ±s.e.m.

^*P < 0.001.

Modelling [Ca²⁺]_i signals in pancreatic β-cells loaded with mobile Ca²⁺ buffers

The simulations presented here show the complicated submembrane [Ca²⁺]_i dynamics after a rapid train of short depolarizations. Time courses were plotted of [Ca²⁺]_i for a train of 60 depolarizations (50 ms each separated by 150 ms) at different depths (0.05, 2 and 2.5 μm). Note that after 10 s the cytosolic calcium concentrations reached a steady state in all cases, thus validating the data obtained in the insulin release experiments which were carried out on a different time scale from the model. Figure 4A-E shows that in the absence of exogenous buffers and with different exogenous Ca²⁺ chelators the [Ca²⁺]_i progressively increases. More and more residual Ca²⁺ is accumulated in the innermost shells with subsequent potential-like depolarizations until a state of equilibrium is reached. The maximal cytosolic Ca²⁺ concentrations reached in the outermost shell are different in each case (with endogenous fixed buffer only, 14 μmol l⁻¹, Figs 4A and 5A; with EGTA, 13.7 μmol l⁻¹, Figs 4B and 5B; with BAPTA, 5.2 μmol l⁻¹, Figs 4C and 5C; with Calcium Orange-5N, 5.9 μmol l⁻¹, Figs 4D and 5D; and with Calcium Green-5N, 4.4 μmol l⁻¹, Figs 4E and 5E). After finishing the potential-like depolarizations [Ca²⁺]_i drops to basal levels within a few seconds (data not shown). Running the model we observed that the concentration of fixed endogenous buffer available to bind Ca²⁺ was always higher than 130 μmol l⁻¹. For Calcium Orange-5N and Calcium Green-5N these concentrations were always higher than 1033 and 1166 μmol l⁻¹, respectively. Finally, EGTA and BAPTA are close to their saturation levels (10 and 70 μmol l⁻¹, respectively). Figure 5B and Figure 6 show that the slow exogenous Ca²⁺ buffer EGTA did not significantly modify the [Ca²⁺]_i pattern in the different shells and the cytosolic Ca²⁺ gradient. On the other hand, the fast Ca²⁺ buffer BAPTA (Fig. 5C) lowered [Ca²⁺]_i more effectively. When we compared the effects of two low-affinity Ca²⁺ buffers (K_d= 20 μmol l⁻¹) with different K_on, such as Calcium Orange-5N (Fig. 5D) (K_on= 10⁷ l mol⁻¹ s⁻¹) and Calcium Green-5N (Fig. 5E) (K_on= 10⁸ l mol⁻¹ s⁻¹), we observed that whereas Calcium Green-5N (Fig. 5E) (fast buffer) almost completely removed the cytosolic Ca²⁺ gradient near the cell membrane (see 0.05-0.5 μm shells) (Figure 5E and Figure 6), Calcium Orange-5N (slow buffer) still permitted a significant Ca²⁺ gradient (Figure 5D and Figure 6).

Figure 4. Effects of exogenous Ca²⁺ chelators with similar affinity and different forward binding constant on [Ca²⁺]_i.

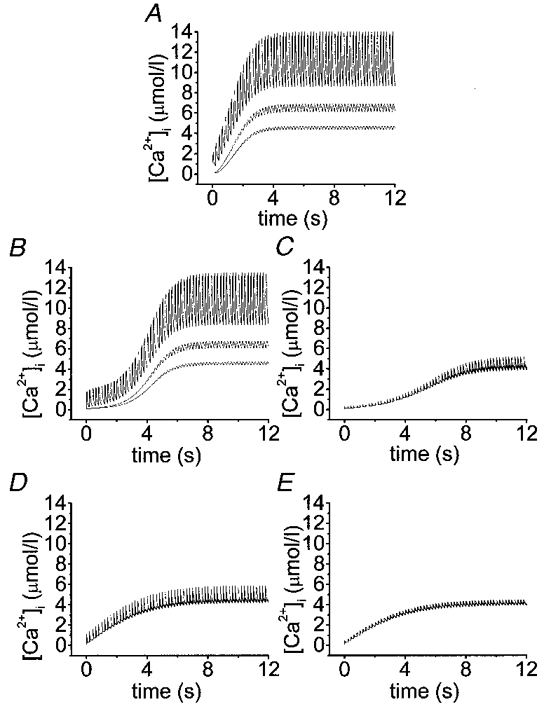
Simulation of time courses of cytosolic Ca²⁺ transients for a train of 60 potential-like depolarizations (50 ms each separated by 150 ms). Different profiles in each panel correspond to Ca²⁺ transients at shells positioned 0.05 (outermost), 2.0 and 2.5 μm underneath the membrane. Other parameters are as in Table 1. In addition to the endogenous fixed buffers (A), the effects of 853 μmol l⁻¹ EGTA (B), 927 μmol l⁻¹ BAPTA (C), 1280 μmol l⁻¹ Calcium Orange-5N (D) and 1416 μmol l⁻¹ Calcium Green-5N (E) have been simulated as indicated.

Figure 5. Detailed effects of exogenous Ca²⁺ chelators with similar affinity and different forward binding constant on [Ca²⁺]_i.

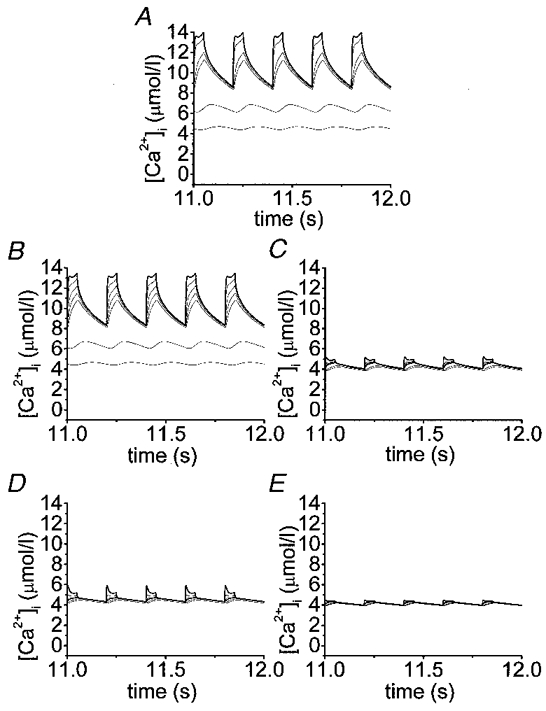
Simulation of time courses of cytosolic Ca²⁺ transients after reaching the steady state (last 5 pulses of a train of 60 potential-like depolarizations; 50 ms each separated by 150 ms). Different profiles in each panel correspond to Ca²⁺ transients at shells positioned 0.05 (outermost, represented as bold trace), 0.2, 0.4, 0.6, 0.8, 2.0 and 2.5 μm beneath the membrane. Other parameters are as in Table 1. In addition to the endogenous fixed buffers (A), the effects of 853 μmol l⁻¹ EGTA (B), 927 μmol l⁻¹ BAPTA (C), 1280 μmol l⁻¹ Calcium Orange-5N (D) and 1416 μmol l⁻¹ Calcium Green-5N (E) have been simulated as indicated.

Figure 6. Computer simulation of the effects of exogenous Ca²⁺ chelators on [Ca²⁺]_i gradients within a β-cell at various distances from the plasma membrane.

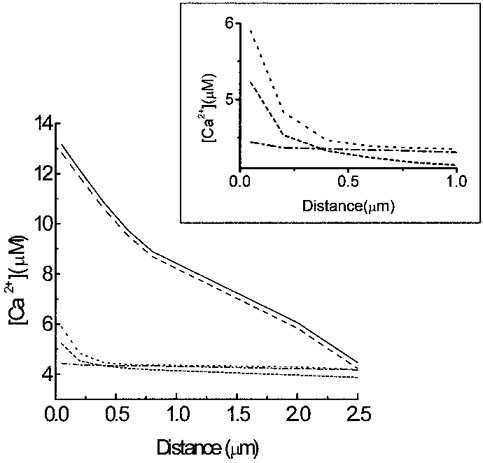
Simulation of cytosolic Ca²⁺ gradients built during the last Ca²⁺ transient after a train of 60 potential-like depolarizations. In addition to the endogenous fixed buffer (continuous line), the effects of 853 μmol l⁻¹ EGTA (dashed line), 927 μmol l⁻¹ BAPTA (short-dashed line), 1280 μmol l⁻¹ Calcium Orange-5N (dotted line) and 1416 μmol l⁻¹ Calcium Green-5N (dashed-dotted line) on submembrane [Ca²⁺]_i gradient have been simulated as indicated. Inset, detailed [Ca²⁺]_i gradients in the first micrometre from the plasma membrane.

DISCUSSION

Experiments involving capacitance measurements of exocytosis and photorelease of Ca²⁺ enabled Eliasson et al. (1997) to estimate the delay between elevation of [Ca²⁺]_i and fusion of the granular membrane with the plasma membrane between <17 and 45 ms in pancreatic β-cells. Such behaviour can be described in other ways if one assumes that before any stimulation a small number of secretory vesicles are already docked very close to the membrane and the rest of them are located at approximately a 300 nm distance. Due to the fact that neuroendocrine cells have significant amounts of endogenous fixed Ca²⁺ buffers which tend to prolong [Ca²⁺]_i transients, the time course of the Ca²⁺ and the resulting delay is expected to be highly dependent upon the relative amount of endogenous fixed Ca²⁺ buffer (Sala & Hernandez-Cruz, 1990). We have therefore tested the effects of increasing mobile Ca²⁺ buffers on glucose-induced insulin release and modelled their effects on the Ca²⁺ signal near the plasma membrane.

An estimate of intracellular buffer concentration is required to compare the action of different buffers and predict their probable effects on calcium concentrations and insulin release. Our observations show that pancreatic β-cells have a cytoplasmic chelator accumulation of around 1 mmol l⁻¹, close to the maximum limit of permeant chelator that can be introduced into cells (Tsien, 1981). These data suggest that the approximations used to determine buffer concentrations are reasonable. Another problem is that the insulin release and the [Ca²⁺]_i effects of permeant Ca²⁺ buffers can be attributable to the hydrolysed AM ester moiety. In addition, other mechanisms of chelator action cannot be excluded. These could include the direct pharmacological effects of the chelators or their by-products and reduction of the resting [Ca²⁺]_i to levels in the order of 10⁻⁹ mol l⁻¹. The fact that after Ca²⁺ buffer loading, glucose-induced electrical activity and insulin release are conserved, even in dinitroBAPTA-loaded islets (a very low Ca²⁺-affinity buffer), indicates that pancreatic β-cell metabolism, ATP-regulated K⁺ channels, Ca²⁺-dependent action potentials and exocytotic machinery are operative in the physiological range. In addition, it suggests that cellular homeostatic mechanisms can maintain resting [Ca²⁺]_i at a ‘set point’ near normal levels despite the presence of high amounts of exogenous calcium buffer.

It has been demonstrated that a step increase in [Ca²⁺]_i elicits a fast ATP-independent component of capacitance increase and a slowly developing ATP-dependent component (Eliasson et al. 1997). It was suggested that these components are the single cell counterparts of the first and second phase of insulin secretion (Grodsky, 1994). This reflects the existence of at least two functionally distinct pools of granules: first, the ‘readily releaseable’ or ‘primed’ pool; second, the ‘reserve’ pool. As observed, whereas fast mobile exogenous Ca²⁺ buffers completely blocked the second phase and partially affected the first phase, slow mobile exogenous Ca²⁺ buffers did not modify any phase of glucose-induced insulin release. That is to say, whereas fast Ca²⁺ buffers completely block the mobilization of granules from the reserve pool into the readily releasable pool, slow buffers did not affect this mobilization. According to the results, fast Ca²⁺ buffers (BAPTA and Calcium Green-5N) should partially block the exocytosis of granules which have reached the ultimate station before the final Ca²⁺-dependent step, the primed vesicles (first phase), which should be located in close proximity to Ca²⁺ channels; and should block the mobilization of the reserve pool of vesicles, not colocalized with Ca²⁺ channels and placed at approximately a 300 nm distance, as predicted by the model. In the simulations we observed the slow Ca²⁺ buffer Calcium Orange-5N decreasing [Ca²⁺]_i at innermost shells (farther away than 400 nm), whereas fast buffers (BAPTA and Calcium Green-5N) decreased [Ca²⁺]_i mostly at outer (beyond 50 nm) shells and to the same extent as slow buffers in the innermost shells. Thus, we suggest that the first phase of glucose-induced insulin release is due to exocytosis of a primed pool of secretory granules located in close proximity to Ca²⁺ channels (around 50 nm), whereas the second phase is due to mobilization of a reserve pool of granules placed at approximately 300 nm from the plasma membrane.

In pancreatic β-cells, it appears that [Ca²⁺]_i at secretory sites reaches 7 μmol l⁻¹ during depolarization (Bokvist et al. 1995) and around 2 μmol l⁻¹ during glucose stimulation (Martin et al. 1997). The model also predicts a [Ca²⁺]_i in the outermost shells not higher than 14 μmol l⁻¹. This apparent difference could be due to an underestimation of [Ca²⁺]_i caused by Ca²⁺ imaging techniques which do not allow measurements in close proximity to the plasma membrane.

Finally, fast Ca²⁺ buffers with low affinity, like the BAPTA derivative dinitroBAPTA (K_d= 3 × 10⁴μmol l⁻¹), did not inhibit glucose-induced insulin release. Note that dinitroBAPTA itself reduced transmitter release in the presynaptic terminal of the giant squid synapse by 27 % (Adler et al. 1991). On the other hand, the fast Ca²⁺ buffer dibromoBAPTA (K_d= 3.6 μmol l⁻¹) was the most efficient at inhibiting glucose-induced insulin release. All these data suggest that the Ca²⁺ receptor that initiates release does not need to have such a low affinity for Ca²⁺ as is the case in neurons.

In conclusion, these results provide additional evidence in favour of the existence of two different vesicle types responsible for glucose-induced insulin release: (i) primed vesicles, located very close to the Ca²⁺ channels and (ii) reserve vesicles, not strictly colocalized with the Ca²⁺ channels. Due to the fact that the second phase of glucose-induced insulin release may last for longer periods (from minutes to hours), it can be assumed that the speed of secretion is usually not so critical for pancreatic β-cell function. Moreover a low affinity Ca²⁺ sensor would require very high [Ca²⁺]_i for hours, a condition which is not compatible with cell survival.

APPENDIX

Computational model

The model takes into account several different species, namely Ca²⁺ and either of two buffer systems (B₁, B₂) in both their free and Ca²⁺-bound forms. The characteristics of B₁ were chosen to mimic endogenous fixed buffers (Thomas et al. 1990; Neher & Augustine, 1992). B₂ represents an exogenous Ca²⁺ buffer and its characteristic change depending on buffer characteristics modelled. The partial differential equation describing diffusion for all species can be written as (Crank, 1975):

(A1)

where [S] is the concentration of diffusible species, r is the radial distance and D_sis the diffusion coefficient of the diffusible species.

The model is composed of 50 concentric shells of uniform thickness, δ= 50 nm. The diffusional properties of each shell are considered to exist only at the shell interfaces and are represented as a set of rate constants between shell surface limits. Diffusional distance (shell thickness), and diffusion coefficients are taken into account. The result of this assumption is that for the ith of n shells eqn (A1) becomes:

(A2)

where [S]_i is the concentration of the diffusible species (Ca²⁺ or a diffusible buffer), di is the effect of the diffusion of the diffusible species, D_s is the diffusion coefficient of the diffusible species, δ is the shell thickness, and V_i is the shell volume. A_i-1 and A_i are, respectively, the surface areas of the outer and inner spherical boundaries of the ith shell. To solve this equation, initial and boundary conditions must be defined. All species are initially assumed to be homogeneously distributed throughout the cell with known total concentrations of each buffer and initial calcium. Given the equilibrium constants (K_d) for the three buffers, the initial concentrations of bound and unbound Ca²⁺ buffers can be easily calculated according to the mass-action law for each individual case. The boundary conditions specify that diffusion does not occur across the outermost spherical boundary or out of the innermost sphere. Thus, A_i-1 is set to zero for the first (outermost) shell, while A_i is set to zero for the nth (innermost) shell.

The effect of buffering on concentration of the different species (B₁, B₂ and Ca ²⁺) is represented by:

(A3)

where [C]_i is the concentration of free Ca²⁺, Bi is the effect of the Ca²⁺ binding, [B]_i is the concentration of the unbound buffer, [CB]_i is the concentration of bound buffer and finally, k_off and k_on are, respectively, the reverse and forward rate constant of the binding reaction.

Active extrusion of Ca²⁺ out of the spherical model from the first shell is defined according to Michaelis-Menten kinetics (Sala & Hernandez-Cruz, 1990). This system is described by the following equation:

(A4)

where Ex is the effect of the Ca²⁺ extrusion, V_max is the maximal speed of transport, A is the area of the cell, V is the volume of the outermost shell, [C]is the concentration of Ca²⁺ in the outermost shell and K_m is the half-maximal activating concentration. As noted by Sala & Hernandez-Cruz (1990), a steady leakage of calcium into the outermost shell is needed to maintain a fixed [Ca²⁺]_i at rest. This leak is thus constant and defined by eqn (A4) with the exception that the concentration of Ca²⁺ used equals the initial ‘intracellular’ Ca²⁺ concentration (0.1 μmol l⁻¹, see Table 1).

The rate of change of free Ca²⁺ due to influx in the first (outermost) shell is defined by:

(A5)

where In is the effect of the inward Ca²⁺ curent on the first shell, I_Ca is the inward Ca²⁺ current, F is Faraday's constant, and V is the volume of the first shell. I_Ca was fitted to an exponential decay whose values decreased from 250 pA to 41 pA; a similar Ca²⁺ current was evoked by Bokvist et al. (1995) by a 50 ms depolarization in pancreatic islet cells. In all cases, we used a series of 60 consecutive depolarizations, lasting 50 ms, separated by 150 ms silent phases.

The effect of calcium-transporting ATPase flux into the ER lumen in the last shell (innermost shell) was described by Saleet et al. (1992):

(A6)

where ER is the effect of Ca²⁺ uptake by endoplasmic reticulum, K_pump is the rate constant of ATPase and [C] is the concentration of Ca²⁺ in the innermost shell.

Finally, the following equations (by combining eqns (2)–(6)) describe the change in the concentration for each diffusible species involved in each shell:

(A7)

(A8)

(A9)

(A10)

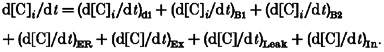(A11)

The ER term in eqn (A11) take values different from zero only at the innermost shell and the last three terms take a zero value in all shells except in the outermost shell.

Equations (A7)-(A11) were integrated using the first-order Euler algorithm. The simulations were run on a PC-compatible computer with a program written in Labview. The parameters used in the model are indicated in Table 3.

Table 3.

Parameters used for simulations

Symbol	Definition	Standard value	Comment
Geometry
R	Cell radius	5 μm	Cell size of a pancreatic β-cell
δ	Shell thickness	0.05 μm
Calcium
ICa	Whole-cell current	250-41 pA	Fitted to an exponential decay whose values decreased from 250 pA to 41 pA, Bokvist et al. (1995)
[C]i	Basal calcium concentration	0.1 μmol l−1
Ds	Diffusion constant for free Ca2+ in cytoplasm	2 × 10−6 cm2 s−1	Values used by Nowycky & Pinter (1993)
Calcium extrusion
Vmax	Maximum velocity of transport	2 pmol cm−2 s−1	Sala & Hernandez-Cruz (1990)
Km	Michaelis-Menten constant	0.83 μmol l−1	Sala & Hernandez-Cruz (1990)
Endoplasmic reticulum
Kpump	Pump rate into the endoplasmic reticulum	300 s−1	Estimated from values used for sarcoplasmic reticulum by Ogawa et al. (1981)
Endogenous buffers
Fixed buffer
[B2]	Total concentration	500 μmol l−1	Nowycky & Pinter (1993)
Kd	Dissociation constant	5 μmol l−1	Nowycky & Pinter (1993)
Kon	Forward binding rate	1 × 108 l mol−1 s−1	Nowycky & Pinter (1993)
Exogenous buffers
Ds	Diffusion constant for free and Ca2+-bound buffers in cytoplasm	2 × 10−6 cm2 s−1	Nowycky & Pinter (1993)
EGTA
[B3]	Total concentration	853 μmol l−1	Our estimated value
Kd	Dissociation constant	0.1 μmol l−1	Measured at Molecular Probes
Kon	Forward binding rate	1.5 × 106 l mol−1 s−1	Smith & Miller (1985)
BAPTA
[B3]	Total concentration	927 μmol l−1	Our estimated value
Kd	Dissociation constant	0.4 μmol l−1	Measured at Molecular Probes
Kon	Forward binding rate	4 × 108 l mol−1 s−1	Grynkiewicz et al. (1985)
Calcium Orange-5N
[B3]	Total concentration	1280 μmol l−1	Our estimated value
Kd	Dissociation constant	20 μmol l−1	Measured at Molecular Probes
Kon	Forward binding rate	1 × 107 l mol−1 s−1	Escobar et al. (1997)
Calcium Green-5N
[B3]	Total concentration	1416 μmol l−1	Our estimated value
Kd	Dissociation constant	20 μmol l−1	Measured at Molecular Probes
Kon	Forward binding rate	1.3 × 108 l mol−1 s−1	Escobar et al. (1997)
Time increment
Δt		2 μs