Mode of Ca²⁺ action on ciliary beat frequency in single ovine airway epithelial cells

Abstract

1. We analysed the kinetics of coupling between cytoplasmic calcium ([Ca²⁺]_i) and ciliary beat frequency (CBF) using simultaneous single cilium recording and single cell [Ca²⁺]_i measurements from cultured ovine tracheal epithelial cells.

2. CBF and [Ca²⁺]_i (indicated by fura-2) were measured at rest and in response to activation of the G-protein coupled M3 muscarinic receptor by 10 μM acetylcholine (ACh).

3. Fourier transform analysis of 3 s data segments of light intensity from phase-contrast microscopy showed no significant delay between changes in [Ca²⁺]_i and CBF during a 2 min exposure to ACh and subsequent washout.

4. CBF time resolution was improved by computing instantaneous beat frequency. This revealed that CBF lagged the rapid increase in [Ca²⁺]_i in response to ACh with a delay of less than 1 beat cycle (143 ms at 7 Hz). When CBF was estimated by an improved Fourier method, this delay was observed to be 70 ± 30 ms (mean ± s.e.m.; n = 20 cilia). During the slower return to baseline, a lag of 8 ± 3.2 s was observed, indicative of hysteresis.

5. While calmodulin inhibitors (calmidazolium and W-7; each n = 5) decreased baseline CBF by an average of 1.1 ± 0.1 Hz, they did not alter the kinetic relationship between [Ca²⁺]_i and CBF. Similarly, phosphatase inhibitors (okadaic acid and cyclosporin A; each n = 5), changed neither baseline CBF nor the kinetic coupling between [Ca²⁺]_i and CBF.

6. These data suggest that the timing of Ca²⁺ action on CBF in ovine airway epithelial cells, is unlikely to be determined by phosphorylation reactions involving calmodulin or kinase/phosphatase reactions.

7. A simple model for Ca²⁺ stimulation of CBF is presented. Fits of the model to the data suggest four or more Ca²⁺ ions bind cooperatively to speed up CBF.

Although ciliary beating plays a critical role in airway mucociliary clearance, the mechanisms responsible for the regulation of ciliary beat frequency (CBF) are poorly understood. In unicellular organisms, widely used for the study of ciliary motility, [Ca²⁺]_i regulates the speed and the direction of ciliary beating. In Paramecium, for instance, rising [Ca²⁺]_islows CBF to the point where the beat direction is reversed (Naitoh & Kaneko, 1972). Mammalian cilia, on the other hand, always beat in the same direction with respect to their effective stroke. In fact, it has been shown by us and others, using a variety of methods, that CBF follows the direction of [Ca²⁺]_i changes (Verdugo, 1980; Girard & Kennedy, 1986; Villalon et al. 1989; Di Benedetto et al. 1991a; Lansley et al. 1992; Korngreen & Priel, 1994, 1996; Salathe & Bookman, 1995a). It is important to note here, however, that in most of these studies, the [Ca²⁺]_i and CBF measurements were not done simultaneously and usually not on the same cell or cells. A significant advance is the work by Korngreen & Priel (1994, 1996) who were the first to report simultaneous measurements. Our own earlier analyses of [Ca²⁺]_i and CBF signals measured in the same cell, but carried out some 15 min apart, suggested that CBF and [Ca²⁺]_i change with comparable kinetics in response to a muscarinic agonist. This was evident from statistically indistinguishable times from agonist addition to the peak response and similar time constants for the relaxation of Ca²⁺ and CBF from this peak back towards baseline (Salathe & Bookman, 1995a). Despite such kinetic information, the molecular mechanisms coupling [Ca²⁺]_i and CBF cannot be discerned from data using different cells for Ca²⁺ and CBF measurements or using the same cell at different time points for at least three reasons. First, there is sufficient variation in the cell to cell responses that correlation of one cell's Ca²⁺ response with another cell's CBF response is of uncertain value. Second, these studies were carried out with limited CBF time resolution (new CBF value every 3.2 s). Finally, rundown and desensitization of the muscarinic response are a concern, so comparing one cell's Ca²⁺ response to the first addition of agonist to the same cell's CBF response to a second addition might not be reliable. In short, high resolution, simultaneous measurements of CBF and [Ca²⁺]_i, where accurate kinetic relationships between these two signals could be assessed (Lansley & Sanderson, 1996; Salathe & Bookman, 1996), are needed to advance our understanding of how Ca²⁺ regulates CBF.

Broadly speaking, there are at least two types of mechanisms by which Ca²⁺ could influence CBF: activation/inhibition of an enzyme or direct Ca²⁺ binding to a protein that is part of the axonemal motile machinery. If enzymes are involved in CBF regulation, they may control the phosphorylation of specific axonemal proteins, as shown for cAMP-dependent protein kinase (Hamasaki et al. 1989, 1991). Alternatively, a Ca²⁺ binding axonemal protein might undergo a conformational change when Ca²⁺ binds (analogous to troponin C in muscle) and could directly influence CBF, for instance by decreasing dynein cycle times (Hamasaki et al. 1991, 1995).

In this paper, we analyse the kinetics of coupling between [Ca²⁺]_i and CBF during simultaneous recordings of both signals from single cells with improved resolution. This analysis provides constraints on the number and type of reactions that link changes in [Ca²⁺]_i to changes in CBF. We hypothesized that a direct influence of [Ca²⁺]_i on CBF, e.g. by rapid Ca²⁺ binding to a ciliary protein, should produce only small lags between rapid changes in [Ca²⁺]_i (at least near the cilium) and changes in CBF. Such a lag would be due solely to Ca²⁺ diffusion and are likely to be less than 100 ms (estimated from simple Ca²⁺ diffusion kinetics as the time needed for Ca²⁺ to diffuse from the endoplasmic reticulum to the cilium). However, such delays can only be measured if rapid changes in CBF, i.e. in the 10–100 ms range, are resolved and compared to the [Ca²⁺]_i signal. Here we describe such a method to measure simultaneously cytoplasmic [Ca²⁺] and single cilium beat frequency from a single ciliated cell. Manipulation of phosphorylation events via phosphatase inhibitors in these cells failed to alter the measured kinetic relationships, thereby supporting a direct mechanism of Ca²⁺ action on the frequency of ciliary beating. A simple ciliary motility model with cooperative binding of four or more calcium ions can account for our results.

METHODS

Chemicals

Dulbecco's modified Eagle's medium (DMEM), Ham's F-12 nutrient mixture and Hanks' balanced salt solution were purchased from Gibco Laboratories (Grand Island, NY, USA). Fura-2 AM (F-1225) was from Molecular Probes (Eugene, OR, USA) and all other chemicals were obtained from Sigma Chemicals (St Louis, MO, USA).

Preparation of tracheal epithelial cultures

Primary cultures of ovine tracheal epithelial cells were prepared as previously described (Salathe & Bookman, 1995a). Briefly, trachea was obtained from freshly killed sheep (30 mg kg⁻¹ pentobarbital intravenously, according to NIH and local animal care use committee approved protocols) and the mucosa was dissected from the underlying submucosal layers and cartilage. Pieces of dissected mucosa were rinsed with DMEM, incubated in 0.05 % protease (Sigma, type 14) for 18 h at 4°C and the epithelial cells released by vigorous shaking. Cells were plated on collagen-coated glass coverslips (human placental collagen, type VI, Sigma) and the cultures maintained in an incubator at 37°C in 5 % CO₂-95 % air. The culture medium consisted of 50 % DMEM, 50 % Ham's F-12 nutrient mixture supplemented with insulin (10 μg ml⁻¹), transferrin (5 μg ml⁻¹), hydrocortisone (0.36 μg ml⁻¹), triiodothyronine (20 ng ml⁻¹), endothelial cell growth supplement (7.5 μg ml⁻¹), penicillin (100 U ml⁻¹) and streptomycin (100 μg ml⁻¹). The medium was exchanged every other day. Cultures were used 2–14 days after plating.

Simultaneous measurement of CBF and estimation of [Ca²⁺]_i

Incubation protocol for fura-2 dye loading

Coverslips were rinsed several times with Hanks' balanced salt solution-10 mM Hepes, pH 7.4 (referred to as HBSS) and then loaded at room temperature on a rocking table with 4 μM fura-2 AM, 2.5 % fetal calf serum (Hyclone Laboratories, Logan, UT, USA), in HBSS for 45–60 min. The dishes were washed several times with HBSS and left at least 30 min before estimating [Ca²⁺]_i.

General imaging set-up

Coverslips were put on the stage of a Nikon Diaphot inverted microscope in a perfusion chamber (Warner Instrument Corp., RC-25F) at room temperature (20–22°C), bathed in HBSS. The extracellular solution could be rapidly exchanged from a group of syringe reservoirs connected to a manifold at the chamber inlet. Continuous suction at the other end of the chamber removed all excess fluid to maintain a chamber volume of ∼150 μl. Cells were imaged using a ×100 Fluor DL oil objective (NA 1.3), providing a final optical gain of ×1000. This level of magnification included ∼10 cells per field and allowed us to visualize individual cilia and basal bodies. A multi-image module (Nikon, Inc.), attached to the side port of the microscope, held a PaulTek CCD Camera System (PaulTek Imaging, Grass Valley, CA, USA) and a photomultiplier tube (PMT; Hamamatsu Photonic Systems, Bridgewater, NJ, USA).

Single cilium recording of CBF

For on-line CBF measurements, transillumination was provided by an IR- and red-filtered 100 W tungsten source, thus providing only long wavelengths for phase contrast imaging (> 600 nm). The light path was directed through the multi-image module to the CCD camera. Video signals were digitized and processed with an IC300 Image Processing Workstation (Inovision Corp., Durham, NC, USA). Using software we developed, single pixels (180 nm × 180 nm) from the live, digitized, contrast-enhanced video image were selected and the light intensity of the selected pixels recorded on a frame by frame basis at 30 Hz (RS-170 video timing; Inoue, 1997). In addition, the magnitude spectrum from a fast Fourier transform (FFT) of the pixel intensity signal was computed on-line and displayed on the workstation monitor to provide direct feedback on the quality of the recorded intensity signal. We found it best to focus the microscope objective just at or above the level of the basal body of the cilium and to monitor nine pixels in a 3 × 3 box (∼0.5 μm²) centred on the selected pixel. This allowed us to record nine individual intensity signals and to select from each set of nine the one with the best signal to noise ratio for CBF analysis.

Three different approaches were used to estimate CBF from such intensity recordings (for evaluation of these, see Results). Our first method sequentially digitized the video signal for 3 s, stopped acquisition, and then computed the FFT, acquired the next 3 s data segment and computed, etc. This ‘staggered’ FFT analysis resulted in a CBF time resolution of ∼3.2 s. Secondly, two different beat-to-beat analyses of the light intensity signal were evaluated. In the first beat-to-beat method, the mean value of a 120 s data segment was subtracted and the positive-going zero crossing points were determined. Then the time interval between crossings was used to estimate CBF (method referred to as ‘zero crossings’). In the second beat-to-beat approach, peaks of the intensity signal were determined and the time from peak to peak was used to estimate CBF on a beat-to-beat basis. Both of these ‘instantaneous’ beat analyses provide CBF time resolutions that depend on the ciliary beat frequency, giving values of approximately 150 ms (at CBF of 7 Hz). Thirdly, we continuously digitized the video signal and used a sliding Hanning window containing 32, 64, or 128 data points to compute a new FFT every video frame time, taking the highest peak in the magnitude spectrum to indicate CBF. This analysis provided a CBF frequency resolution of 0.11 Hz (using resolution enhancement) and a new estimate of CBF for every video sample (33 ms, with RS-170 video timing). The software we developed for an SGI workstation is available upon request (rbookman@miami.edu).

The fast Fourier transform (FFT) is equivalent to a bank of N/2 bandpass filters each with the same bandwidth. There is a fundamental inverse relationship between the number of samples (N) in the data window and the bandwidth in the bandpass filters. Larger windows provide finer frequency resolution (more filters with narrower bandwidth). The responsiveness of each bandpass filter to changes in frequency is proportional to the bandwidth of the filters, so that narrow band filters have poor temporal resolution (i.e. poor responsiveness to rapid parameter changes). If the data window includes too many data samples, the ability to track frequency changes accurately is decreased. For that reason, different data window sizes were evaluated using simulated intensity data to optimize this method for accuracy (see Results).

Estimating [Ca²⁺]_i

Changes in [Ca²⁺]_i were followed semi-quantitatively by recording the fluorescence intensity of fura-2, excited with 380 nm light with a photomultiplier tube (PMT). Control measurements with excitation at the isobestic wavelength (357 nm) showed no significant photobleaching during the exposure times required for these experiments. The single excitation wavelength was obtained by directing the output of a 100 W mercury lamp through a 10 nm wide interference filter centred at 380 nm (Chroma Technology Corp., Brattleboro, VT, USA). The emission intensity was monitored by a Hamamatsu PMT, restricting the acquisition field by an iris mounted in front of the PMT to the one cell from which CBF was measured. The data were acquired using an Instrutech ITC-16 A/D converter and PulseControlsoftware (Herrington et al. 1996) on a Macintosh computer. Epifluorescence was recorded at a sampling interval of 1000 μs channel⁻¹. For analysis, the fluorescence emission signal was digitally filtered with a Gaussian filter (Marchand & Marmet, 1983) using IgorPro software (WaveMetrics, Inc., Lake Oswego, OR, USA). A TTL line under the control of the imaging computer triggered the start of acquisition to the Macintosh computer thereby making the correct temporal alignment of the two measurements (CBF and Ca²⁺) possible.

Since the F₃₈₀ epifluorescence signal and [Ca²⁺]_i are not linearly related (Grynkiewicz et al. 1985), the kinetics of an F₃₈₀ change can differ significantly from the kinetics of a [Ca²⁺]_i change. To improve kinetic accuracy, we had to transform the recorded epifluorescence signal (F₃₈₀) into a [Ca²⁺]_i signal. Two different methods were used for this conversion: (1) Neher's single wavelength conversion to [Ca²⁺]_i (Neher & Augustine, 1992) and (2) the formula of Grynkiewicz et al. (1985) using dual wavelength excitation. Both methods rely on some additional fluorescence measurements that we could not do during these simultaneous recordings. Thus, we had to make some estimates in both approaches. For Neher's approach, an initial and maximal [Ca²⁺]_i had to be chosen; for Grynkiewicz's approach, we estimated the isobestic wavelength fluorescence based on initial and final values. Both approaches yielded identical [Ca²⁺]_i estimates as far as the kinetic changes in the signal were concerned. We want to stress, however, that the given [Ca²⁺]_i values are estimates and will therefore be referred to as estimated [Ca²⁺]_i values.

Statistical analysis

The statistical analysis used a one-way analysis of variance (ANOVA) to compare the means of more than two groups (e.g. delays during upstroke or relaxation of CBF compared to [Ca²⁺]_i under different conditions) using JMP software from SAS Institute Inc. (Cary, NC, USA).

RESULTS

Coupling of [Ca²⁺]_i and CBF

As suggested by our earlier analysis of non-simultaneous measurements from the same cell (Salathe & Bookman, 1995a), simultaneous recordings of [Ca²⁺]_i and CBF transients in response to 10 μM ACh from single cells (n = 15) showed that tight kinetic coupling existed between [Ca²⁺]_i and CBF in these ovine preparations (Fig. 1). These records used ‘staggered’ FFT CBF estimates (see Methods), where the light intensity signal was digitized for 3 s and then an FFT was computed for each segment. CBF was taken to be the frequency of the peak value of the FFT magnitude spectrum. Since the computation required 0.1–0.2 s, this method provided a new estimate of CBF every 3.2 s. Any lags or phase shifts less than this would be difficult to discern. This tight coupling could be observed not only during the increase but, in these recordings, also during the relaxation phase of both signals, i.e. throughout the responses to a 2 min application of 10 μM ACh. In other words, the delay between the half-maximal CBF response and the [Ca²⁺]_i response was always within the CBF measurement time resolution, during both the increase and decrease of the signals. These findings are illustrated in Fig. 1 where the two signals are superimposed.

Figure 1. Simultaneous measurement of [Ca²⁺]_i and CBF in response to 10 μM ACh.

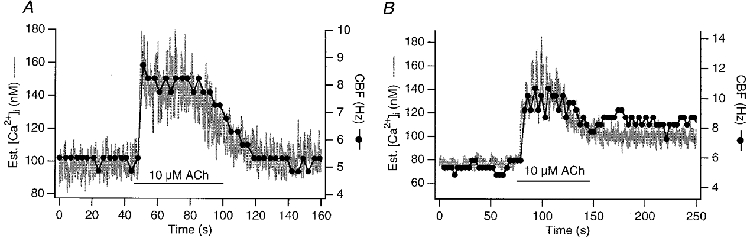
Two examples of simultaneous [Ca²⁺]_i and CBF transients in response to 10 μM ACh are shown. CBF was estimated using the ‘staggered’ FFT approach (see Methods) and [Ca²⁺]_i was estimated from a single wavelength recording with excitation at 380 nm as outlined in Methods. A high degree of correlation between [Ca²⁺]_i and CBF can be appreciated in the examples: both signals return to the original baseline after the ACh transient in A, whereas they stay above the original baseline in B.

To provide constraints on the number and type of reactions that link changes in [Ca²⁺]_i to changes in CBF, however, a more detailed kinetic analysis with better time resolution was necessary. This was initially achieved by analysing the intensity data on a beat-to-beat basis (see Methods). The first beat-to-beat method used the reciprocal of time between positive-going crossings of the mean value of light intensity (computed as a running average over 120 s) to estimate CBF (referred to as ‘zero crossings’). This method proved to be unacceptably noisy, probably due to the fact that, in many intensity traces, the mean value did not provide a sufficiently stable baseline and therefore many zero crossings were missed. Some of these fluctuations might be attributable to instabilities of the light source.

Alternatively, we determined the peaks of the intensity signal and used the time from peak to peak to estimate CBF on a beat-to-beat basis. As illustrated in Fig. 2, changes in CBF could then be estimated with a time resolution of ∼150 ms (for cilia beating at 6–7 Hz at 20–22°C). The average frequency of data analysed with this method matched the frequency obtained with the FFT analysis of the whole data set (given the frequency resolution of the FFT, 0.24 Hz, in this example). However, Fig. 2 also makes clear that such CBF estimates were prone to large frequency fluctuations (here ∼2 Hz). Thus, this instantaneous frequency estimation method often suffered from unacceptable noise, mostly due to poor peak definition of the intensity signal. This problem results in part from the relatively slow data acquisition rate of RS-170 video (30 Hz).

Figure 2. Analysing the intensity signal on a beat-to-beat basis.

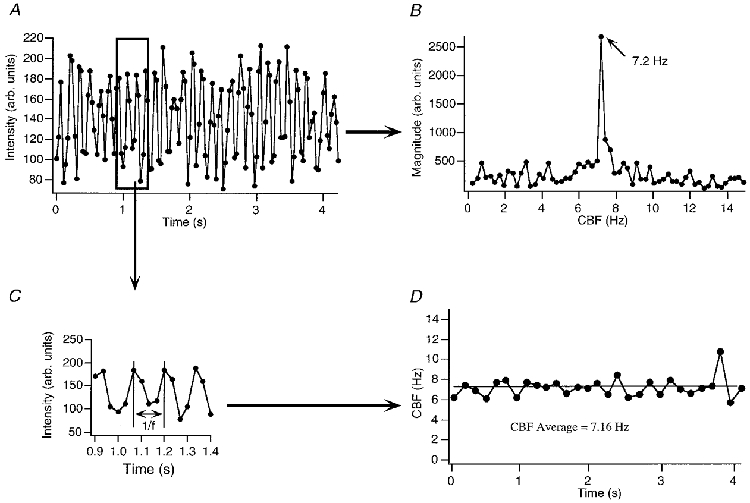
To increase the time resolution of the CBF measurement, intensity data (A) were analysed, instead of computing an FFT from the whole data set (B), on a peak-to-peak (or beat-to-beat) basis (C and D). As illustrated in this example, CBF is estimated beat to beat with a time resolution of ≈150 ms (for cilia beating at ≈6–7 Hz at 20–22 °C), albeit at the cost of CBF ‘noise’ of up to 2 Hz during a continuous and stable recording (see Methods and Results for a discussion of this point). The average frequency of the beat-to-beat analysis matches the frequency obtained with the FFT analysis over the same time range (given the frequency resolution of the FFT).

Analysis of these traces suggested, despite the noise, that CBF did not clearly lag behind the increase in [Ca²⁺]_i during the fastest changes in both signals (i.e. during the initial exposure to ACh). In fact, CBF followed the increase in [Ca²⁺]_i within ≤1 beat cycles. This was true for the initial increase in [Ca²⁺]_i and CBF in response to 10 μM ACh as well as for increases in the two signals during oscillatory responses of [Ca²⁺]_i and CBF. The lack of significant delay was corroborated by measuring the time between the points of each half-maximal response: there, the CBF traces always lagged, but within the time resolution of the CBF estimate, namely 90 ± 30 ms behind the [Ca²⁺]_i signals (mean ±s.e.m.; n = 20 cells). The relaxation phase of these records was not analysed because of noise in the analysed signal that made the slower changes hard to interpret.

In order to improve the signal to noise ratio and the time resolution of the CBF estimates, we digitized the video signal continuously and then applied a ‘sliding’ Hanning window before computing the Fourier transform. The use of Hanning windows should provide a more accurate estimate of the frequency at the time point of the CBF estimate (chosen to be at the midpoint of the FFT data window). To ensure that such an approach would yield correct CBF estimates, we first used this method on simulated intensity data (Fig. 3). We simulated data using a sine function with a baseline frequency of 7.2 Hz, displaying measurement points every 33 ms thereby mimicking the sampling rate of an RS-170 video-camera (i.e. 30 Hz). The accuracy of CBF estimation was evaluated using 32, 64 and 128 sample windows for FFT analysis (Fig. 3). These windows were advanced through the simulated intensity data sets by one frame or sample at a time. By using frequency resolution enhancement (sinx/x interpolation), sliding window FFT analyses provided a frequency resolution of 0.11 Hz and a new CBF estimate for every video sample, i.e. every 33 ms. Two different scenarios were then simulated: one with an ‘instantaneous’ CBF increase (i.e. within 33 ms) from 7.2 to 8.5 Hz and one with a gradual CBF increase over 1.033 s to the same frequency. As seen in Fig. 3, windows of 64 video frames per FFT were able to detect accurately both rapid and slow CBF changes. Windows with 128 samples underestimated the true duration of a gradual CBF change by delaying the apparent time of CBF increase by as much as 700 ms. A 32-sample FFT window overestimated the true duration of an instantaneous change by ∼66 ms, but was able to track slower changes in CBF accurately. Additional simulations with changes in CBF starting at different phases of the underlying oscillation (90, 180 and 270 deg) suggested that the true CBF time resolution, i.e. the time it takes to accurately detect a CBF change after it occurred, was two to three video frames or 66–99 ms. Thus, a 64-frame Hanning window, advanced through the data one frame at a time, provided the best overall accuracy for tracking CBF changes and provided a CBF time resolution of <100 ms.

Figure 3. Analysing the intensity signal with FFT of ‘sliding’ Hanning windows.

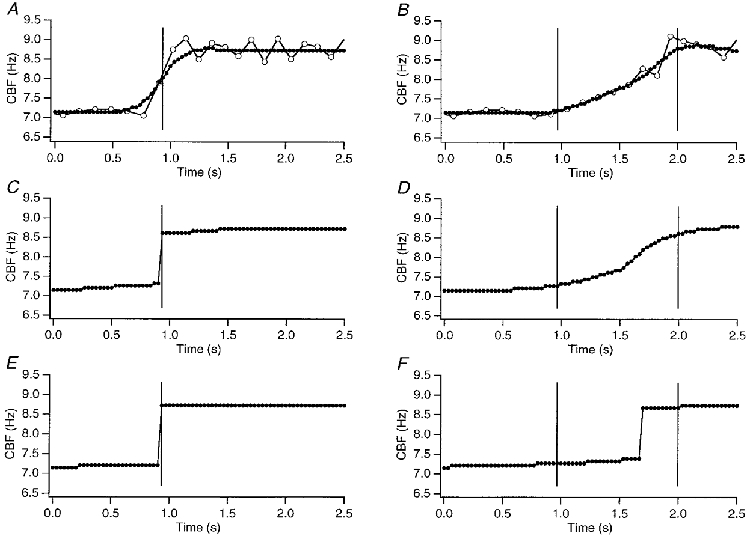
To assure accuracy of CBF estimates with respect to frequency and the time course of frequency changes using the ‘sliding’ Hanning window FFT approach (see Methods), we simulated intensity data using a sine function. Two scenarios were tested: an instantaneous change from 7.2 to 8.5 Hz (A, C and E) and a gradual change from 7.2 to 8.5 Hz over 1.033 s (B, D and F). All Hanning windows were advanced through the data set by one video frame. The Hanning window size was selected to contain 32 video frames (A and B), 64 video frames (C and D), or 128 video frames (E and F). The open circles in A and B represent the peak-to-peak CBF estimates of the simulated intensity data. Hanning windows with 64 video frames provided the most accurate CBF estimates (C for instantaneous change, D for gradual change). A data window with 32 video samples distorted the immediate change to look gradual, whereas windows with 128 video samples underestimated the duration of the gradual change and indicated a delay of 0.7 s from the start of the increase.

Using this method, we analysed simultaneous recordings of CBF and [Ca²⁺]_i responses to 10 μM ACh from 20 additional cells (examples are shown in Fig. 4). To estimate the delay of the CBF increase in relation to the [Ca²⁺]_i increase in these experiments, we measured the time the sliding Hanning window FFT signal lagged behind the [Ca²⁺]_i signal at the point of each half-maximal response. This delay was 70 ± 30 ms (n = 20 cells). Using the same approach, CBF lagged the [Ca²⁺]_i decrease during the relaxation phase back to baseline by an average of 8 ± 3 s at half-maximal response (the median, however, was only 3 s).

Figure 4. Coupling of [Ca²⁺]_i and CBF: high resolution measurement using Hanning windows.

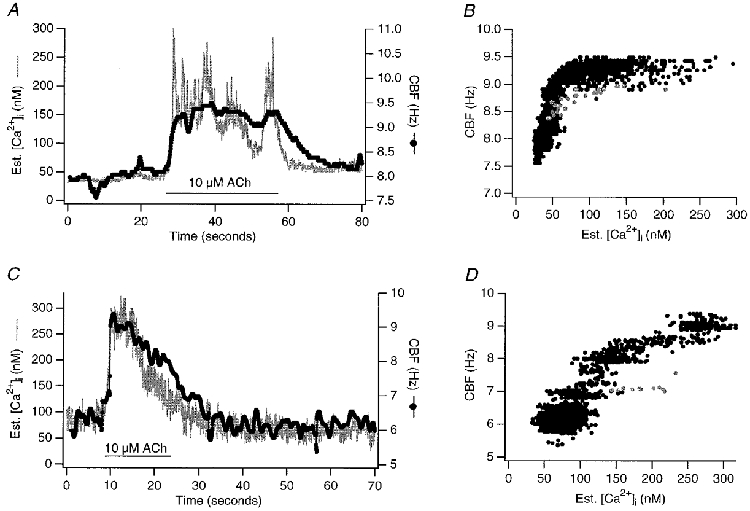
Two examples of high resolution ‘sliding’ Hanning window FFT estimates are shown, correctly aligned with the estimated [Ca²⁺]_i signal to visualize the coupling between the two signals. A and C display the data on the time axis, whereas B and D represent the corresponding pair of [Ca²⁺]_i and CBF data points plotted against each other. The trajectory in grey represents data points during the fastest change in both signals in response to 10 μM ACh. A depicts an oscillatory response of Ca²⁺ and CBF to ACh as often seen in early culture (Salathe & Bookman, 1995a). These measurements revealed that during the rise of both signals, no significant delay of the CBF signal, relative to the change in the [Ca²⁺]_i signal, could be measured: the point of half-maximal increase in the CBF signal occurred 70 ± 30 ms (mean ±s.e.m., n = 20 cells) after the [Ca²⁺]_i increase, an amount that was within the CBF time resolution. However, the relaxation of CBF towards baseline trailed [Ca²⁺]_i by 8 ± 3 s (mean ±s.e.m., n = 20 cells, median 3 s). These differences are represented by the hysteresis of the CBF vs. [Ca²⁺]_i data (grey vs. black points).

To eliminate some of the complexities in the time course figures (e.g. oscillatory responses to ACh), we have also plotted the correlation between CBF and [Ca²⁺]_i as parametric plots (Fig. 4B and D). From such plots, it was clear that there was no linear relation between Ca²⁺ and CBF and that some hysteresis existed between the initial, fast increase in both signals and the relaxation phase back to baseline as already indicated in the lag times of CBF compared to [Ca²⁺]_i. Such parametric plots were later also used for the modelling efforts.

Since the CBF measurements were done on a single cilium, we tried to identify differences in response to ACh between different, spatially distinct cilia on the same cell. Measurements of up to three cilia at different locations on the same cell revealed that all cilia responded within the CBF time resolution, i.e. in less than 100 ms (n = 3 cells). In addition, the analysis of the fluorescence signal at these subcellular regions showed that [Ca²⁺]_i also changed within the same time range at all locations. Therefore, we did not find any evidence for spatial differences in the data obtained from individual cilia on a single cell.

The measured delay between CBF and [Ca²⁺]_i during the fastest changes in both signals could be accounted for by simple Ca²⁺ diffusion from internal Ca²⁺ stores to the cilium. This result doesn't leave much time for numerous enzymatic reactions to mediate Ca²⁺ action, but it does not rule them out. We wanted to examine, therefore, whether a Ca²⁺-triggered enzymatic cascade could be responsible for an increase in CBF. Since phosphorylation reactions have been shown to be important in the regulation of CBF (e.g. Hamasaki et al. 1991), we evaluated whether changes in phosphorylation were important for the Ca²⁺ regulation of CBF. Figure 5 summarizes the types of kinase/ phosphatase reactions that might be involved and the expected results for specific inhibitors if phosphorylation was involved in coupling Ca²⁺ changes to changes in CBF.

Figure 5. How does Ca²⁺ change CBF?

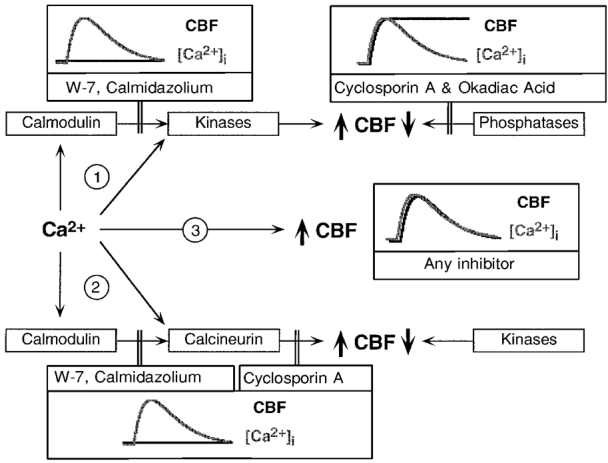
Shown are possible mechanisms by which Ca²⁺ could influence CBF, the different pharmacological tools used to probe for these possibilities experimentally, and the expected outcomes if the putative mechanism was inhibited by the drug. 1, Ca²⁺ acts either through calmodulin or directly to stimulate a Ca²⁺-dependent kinase; blocking calmodulin or phosphatases should then alter the coupling between [Ca²⁺]_i and CBF as depicted. 2, Ca²⁺ acts either through calmodulin or directly to stimulate a Ca²⁺-dependent phosphatase; blocking calmodulin or phosphatases should again alter the coupling between [Ca²⁺]_i and CBF as depicted. 3, Ca²⁺ acts directly on a ciliary response element; no inhibitor should influence the coupling between [Ca²⁺]_i and CBF.

Initial experiments were performed with the calmodulin antagonists W-7 (160 μM) and calmidazolium (1 μM). Both inhibitors were used at concentrations shown to inhibit calmodulin in other cell systems (Della Bruna et al. 1992; Khan et al. 1993; Tohda et al. 1994; Virginio et al. 1997; Chessell et al. 1998). Trifluoperazine (10 μM) in conjunction with UV irradiation invariably caused ciliostasis and cell death and was therefore not used. It needs to be noted here, that calmidazolium was also toxic to ciliated cells at a concentration of 10 μM and was thus used at a lower concentration (1 μM), but one still shown to be effective in systems investigating G-protein coupled receptor responses (Virginio et al. 1997; Chessell et al. 1998).

Both W-7 and calmidazolium decreased baseline CBF by 1.1 ± 0.1 Hz (n = 5 cells with each inhibitor), suggesting a possible role for calmodulin in regulation of baseline CBF. However, neither inhibitor (after a preincubation of the cells for 15 min prior to exposure to 10 μM ACh) affected the coupling of [Ca²⁺]_i and CBF in response to ACh (Fig. 6). Compared to the same cells which served as their own controls (first exposure to ACh in the absence of the calmodulin inhibitors), the increase in CBF during the fastest changes in [Ca²⁺]_i still lagged behind by <100 ms (i.e. within the time resolution of the CBF measurement) and the lag in the recovery of both responses did not change significantly (ANOVA not significant; see Table 1). Thus, it seemed that calmodulin inhibitors influenced baseline CBF, but had little influence on the coupling of Ca²⁺ and CBF during stimulation of muscarinic receptors.

Figure 6. Calmodulin inhibitors: no influence on kinetic relationship between [Ca²⁺]_i and CBF.

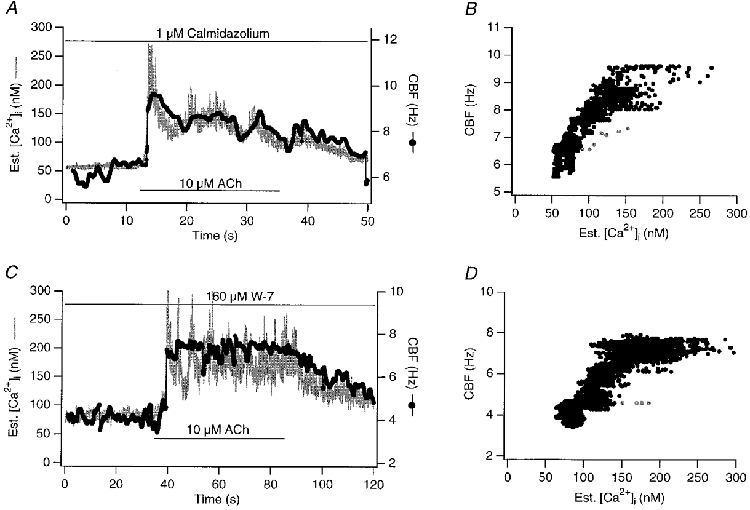
Shown are simultaneous recordings of [Ca²⁺]_i and CBF in response to 10 μM ACh in the presence of calmodulin inhibitors (cells pretreated with inhibitors for 15 min). A and B, 160 μM W-7 (IC₅₀ for calmodulin-dependent protein kinase: 31 μM) lowered baseline CBF by an average of 1 ± 0.3 Hz (n = 5) but did not change the kinetic coupling between [Ca²⁺]_i and CBF in response to ACh. C and D, similarly, 1 μM calmidazolium (IC₅₀ for calmodulin-dependent phosphodiesterase: 0.04 μM) lowered baseline CBF, but did not change the kinetic coupling between [Ca²⁺]_i and CBF in response to ACh. Grey data points in B and D represent points during the fastest change in both signals in response to 10 μM ACh.

Table 1.

Delay (s) of CBF compared to Ca²⁺ at half-maximal response

	Upstroke	Relaxation
No inhibitor (n = 20)	0.07 ± 0.03	8.00 ± 3.00
W-7 (n = 5)	0.04 ± 0.02	5.75 ± 1.00
Calmidazolium (n = 5)	0.05 ± 0.02	4.33 ± 0.72
Okadaic acid (n = 5)	0.05 ± 0.04	6.00 ± 2.83
Cyclosporin A (n = 5)	0.04 ± 0.02	4.92 ± 0.97

Data are means ±S.E.M. There was no significant difference from control (no inhibitor) for any of the values, which were compared by ANOVA.

Since additional kinases/phosphatases, not directly dependent on calmodulin activation, might participate in the Ca²⁺ control of CBF, we examined whether phosphatase inhibitors influenced the coupling of Ca²⁺ and CBF during exposure to ACh. To block all phosphatases shown to be present at least in flagella (phosphatase 1, 2a and 2b) we used 150 nM okadaic acid (Klumpp et al. 1994; Venant et al. 1994; Habermacher & Sale, 1996; Kroner et al. 1996) and 2.5–10 μM cyclosporin A, a specific phosphatase 2a inhibitor (Zweifach & Lewis, 1995; Raufman et al. 1997). Neither inhibitor influenced baseline CBF or the kinetic coupling of Ca²⁺ and CBF during exposure of the cells to ACh (ANOVA not significant; see Fig. 7 and Table 1). These data suggest that phosphorylation is not a necessary component of Ca²⁺ modulation of CBF and support a direct action of Ca²⁺ on ciliary proteins.

Figure 7. Phosphatase inhibitors: no influence on kinetic relationship between [Ca²⁺]_i and CBF.

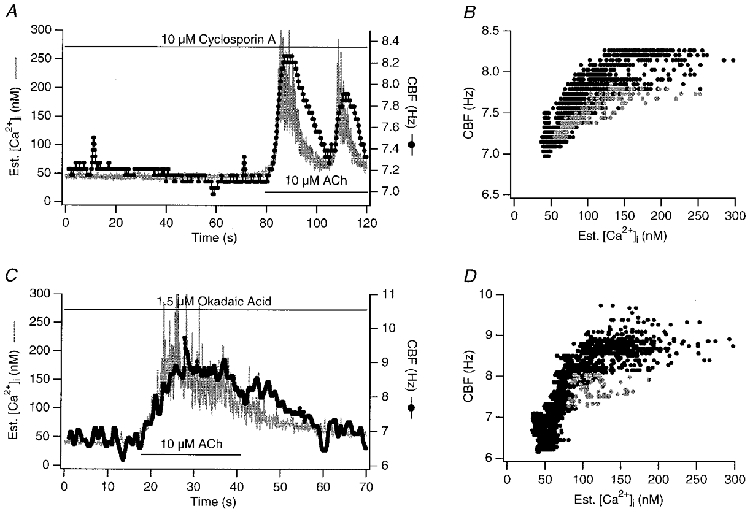
Shown are simultaneous recordings of [Ca²⁺]_i and CBF in response to 10 μM ACh in the presence of phosphatase inhibitors (cells pretreated with inhibitors for 15 min). A and B, 2.5 μM cyclosporin A (IC₅₀ for the inhibition of phosphatase 2b or calcineurin in Jurkat cell lysates: 5 nM). C and D, 1.5 μM okadaic acid (IC₅₀ for phosphatase 1 is 10 nM and for phosphatase 2a 0.5 μM). Phosphatase inhibitors did not change the kinetic coupling of [Ca²⁺]_i and CBF in response to ACh. Grey data points in B and D represent points during the fastest change in both signals in response to 10 μM ACh. Again, A depicts an oscillatory response of Ca²⁺ and CBF to ACh, and the same cell showed also an oscillatory response in the absence of cyclosporin A.

Modelling the coupling of [Ca²⁺]_i and CBF

To model the effect of Ca²⁺ on CBF, we made three assumptions, based in part on published literature: (1) ciliary dynein arms move microtubules with either a ‘slow’ or ‘fast’ duty cycle; (2) dynein ATPase activity is shifted between ‘fast’ and ‘slow’ modes by a change in [Ca²⁺]; and (3) N_total complete and sequential dynein ATPase cycles are necessary to complete one ciliary stroke (in accordance with the ciliary motility model by (Holwill & Satir, 1994; Holwill et al. 1995)).

Thus,

(1)

where T_dyneincycle is the time (s) required for binding and hydrolysis of ATP and unbinding of P_i and ADP. Using published data on dynein conformational changes, we estimated the minimum number of sequential dynein arm actions necessary for one single ciliary stroke as follows (Holwill & Satir, 1994; Holwill et al. 1995). Two outer doublets separate by ∼0.1 μm at the end of a full ciliary bend, and a single stroke of a dynein arm can move a microtubule 4–16 nm. Thus, anywhere between 12 and 50 sequential dynein arm movements are necessary to complete a single ciliary stroke (Fig. 8). Picking an intermediate value, we assumed that a total of 25 sequential dynein arm movements are necessary to complete a single ciliary cycle of effective and recovery strokes. Therefore eqn (1) can be rewritten as:

(2)

or

(3)

where f_fast is the fraction of the dynein arms that are operating in ‘fast’ mode, f_slow is the fraction of the dynein arms that are operating in ‘slow’ mode ( = 1 −f_fast), T_fast is the time (s) required for a dynein ATPase cycle in ‘fast’ mode, and T_slow is the time (s) required for a dynein ATPase cycle in ‘slow’ mode.

Figure 8. Modelling the action of Ca²⁺ on CBF.

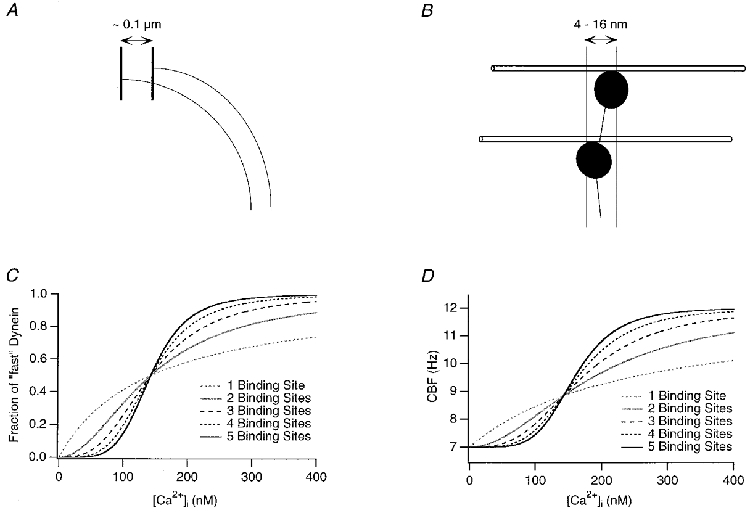
Using published data on dynein conformational changes, we estimated the minimum number of sequential dynein arm actions necessary for one single ciliary stroke. Two outer doublets are separated ≈0.1 μm at the end of ciliary bending as indicated in A, and a single stroke of one dynein arm can move a microtubule 4–16 nm (B). Thus, between 12 and 50 sequential dynein arm movements are necessary to complete a single ciliary stroke (for all calculations, 25 were used). C, the fraction of fast vs. slow dynein arms was computed using the Hill equation and is simulated here with a total K_d of 0.007 μM. The traces shown in the graph simulate the relationship between [Ca²⁺]_i and the fractional occupancy of 1 to 5 cooperative Ca²⁺ binding sites. D, using the Hill equation to calculate the fast and slow dynein arm fraction's dependence on [Ca²⁺]_i, we simulated CBF traces, arbitrarily choosing a baseline frequency of 7 Hz and a maximal frequency of 12 Hz (however, this is not the limit of the model in general).

To fit the parameters of the model for Ca²⁺-CBF coupling to our data, we first simulated the model by computing the fraction of fast vs. slow dynein arms using the Hill equation assuming a total K_d of 0.007 μM (Fig. 8C). The traces shown in the graph simulate the relationship between [Ca²⁺]_i and the fraction of fast dynein arms assuming one to five cooperative Ca²⁺ binding sites. With this use of the Hill equation to calculate the fast and slow dynein arm fraction's dependence on [Ca²⁺], CBF can be estimated.

Figure 8D shows a simulation for which the slow dynein arm duration was chosen to result in a ‘resting’ CBF of 7 Hz (based on our data from recordings at 20°C), whereas the switch to all fast dynein arms results in a maximal CBF of 12 Hz. We should stress that this frequency range was only used for the purpose of simulation and these specific values are not a general feature (or limit) of the model. The fraction of fast vs. slow was taken from the simulated Hill equation as mentioned above (Fig. 8C). Such graphs now start to resemble recorded data, especially with three or more cooperative binding sites.

Finally, we fitted this model to recorded data as shown in Fig. 9. The slow and fast dynein cycle duration, and the K_d were free parameters of the fit, thereby allowing basal and maximal frequencies to assume any value. These fits suggested that models with four or more cooperative Ca²⁺ binding sites best fit the recorded data (in a least-squares sense). Using the fit parameters for four cooperative Ca²⁺ binding sites, the average K_d was 0.02 μM, the slow dynein cycle duration 9 ms, and the fast dynein cycle duration 4.5 ms (n = 9 cells). These nine experiments were also combined into a single data set and again fitted with the model (Fig. 9B). Again, using four or more cooperative Ca²⁺ binding sites resulted in the best fit. Note that the model does not require that Ca²⁺ binds directly to dynein. It does require that the ciliary Ca²⁺ binding protein can communicate its Ca²⁺ binding state to the dynein ATPase so rapidly that it is not rate limiting in this situation.

Figure 9. Fitting the model to the experimental data.

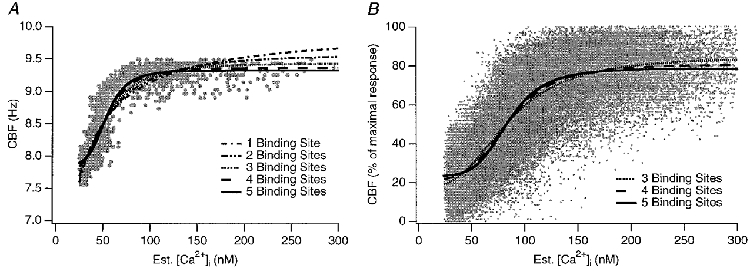
The CBF model was fitted to actual data using the slow and fast dynein motion duration and the total K_d as parameters of the fit (thereby not limiting CBF of the model to any specific range). A, a model with ≥ 4 cooperative Ca²⁺ binding sites results in a reasonable fit. B, data points from 9 experiments are plotted and the model parameters are fitted to the combined data set. Again, using ≥ 4 cooperative Ca²⁺ binding sites resulted in the best fit. The mean K_d was 0.02 μM, the slow dynein arm duration 9 ms, and the fast dynein arm duration 4.5 ms.

DISCUSSION

It has been known for some time that intracellular calcium plays an important role in the regulation of mammalian CBF. However, it remains unclear how changes in [Ca²⁺]_i influence CBF at the molecular level. One approach to unravel the mechanisms requires the acquisition of high resolution records of ciliary motility and cytoplasmic calcium, first described by Priel and his group (Korngreen & Priel, 1994). We therefore carried out simultaneous measurements of intracellular calcium and single cilium recording of beating frequency from cultured ovine tracheal epithelial cells. Using three different methods to analyse the CBF data, we found that the only discernible lag between rapid increases in Ca²⁺ and increases in CBF is within the time resolution of our measurements (<100 ms). By contrast, we found a lag of several seconds in the recovery of CBF compared to the return of [Ca²⁺]_i to its resting level.

Several features of the data presented here support the hypothesis that Ca²⁺ binds directly to a ciliary calcium binding element to change CBF. Such a calcium binding element could be a dynein light chain, analogous to the cAMP-dependent phosphorylation of a dynein light chain to increase CBF (Hamasaki et al. 1991; Barkalow et al. 1994). The measurements of CBF and [Ca²⁺]_i showed that during the fastest changes in both signals, the CBF increase did not lag measurably behind the [Ca²⁺]_i increase (i.e. within 100 ms). This average measured delay could therefore be accounted for by simple diffusion kinetics of Ca²⁺ from the intracellular stores, from which it is released upon muscarinic stimulation (Salathe et al. 1997), to the base of a cilium.

A Ca²⁺-stimulated enzymatic cascade to change CBF, on the other hand, cannot be excluded solely by the argument that the delay between the CBF and [Ca²⁺]_i rise was <100 ms. It is clear that phosphorylation reactions play an important role in the regulation of CBF (Di Benedetto et al. 1991b; Hamasaki et al. 1991, 1995; Wyatt et al. 1998; Wong et al. 1998; Uzlaner & Priel, 1999) and it is possible that a few phosphorylation events could have taken place during that short period of time. It is also plausible that only a small number of phosphorylation events are sufficient to change CBF. Data from Paramecium suggest that only about 5 % of the outer dynein arm light chain p29 needs to be phosphorylated to increase CBF maximally (Hamasaki et al. 1991).

Thus, it was important to test specifically for a role for phosphorylation. As depicted in Figs 6 and 7, we examined the role of calmodulin as well as different phosphatase inhibitors in regulating Ca²⁺-dependent changes in CBF. But neither calmodulin inhibitors nor phosphatase inhibitors changed the kinetic relationship between [Ca²⁺]_i and CBF. Okadaic acid has previously failed to inhibit a CBF increase upon Ca²⁺ entry into rabbit airway epithelial cells (Venant et al. 1995). Despite their utilization in unicellular organisms (e.g. Klumpp et al. 1994; Habermacher & Sale, 1996), the use of such pharmacological agents brings with it the necessity to carry out positive controls in order to prove that the particular enzymes were really inhibited in our cells. In these coverslip cultures, however, where the ciliated cell population makes up only ∼5 % of the cells, biochemical controls are impossible since we cannot resolve changes in phosphorylation in a single cell. Nevertheless, the phosphatase inhibitors we used (okadaic acid plus cyclosporin A) did prolong the increase in CBF elicited by the β-agonist adrenaline (data not shown). This supports the view that phosphorylation does play a modulatory role in ovine cells and suggests that these inhibitors are active in our cultures. Nevertheless, their use did not change the coupling between CBF and Ca²⁺ during transient increases in response to ACh. Thus, we do not find evidence in support of a mechanism that Ca²⁺ acts via phosphorylation.

We did not evaluate any kinase inhibitors in these simultaneous measurements. The rationale for this decision was outlined in Fig. 5, in which we argue that the use of broad phosphatase inhibitors should be able to reveal any important Ca²⁺-dependent (inhibitory or stimulatory) phosphorylation events mediated by kinases or phosphatases. However, we have previously used KN-62, a calcium/ calmodulin kinase II inhibitor, in an effort to assess the role of this kinase on the CBF transient in response to ACh (M. Salathe and R. J. Bookman, unpublished observations). KN-62 did not change the CBF transient compared to a response to ACh in the absence of the inhibitor, further suggesting that this calcium-dependent kinase is not involved in the calcium regulation of CBF, at least in response to a muscarinic agonist. Taken all together, it seems unlikely that phosphorylation reactions are involved in the Ca²⁺ regulation of CBF in response to ACh in ovine tracheal cells. We cannot, of course, rule out the possibility that ovine cilia contain unique phosphatases or kinases that are not blocked by okadaic acid, cyclosporin A and KN-62.

The limited sampling rate (30 Hz) of our measurements raises another concern, namely that our CBF estimates do not provide sufficient time resolution. However, we have carefully simulated CBF increases to test our approach for accuracy. For both instantaneous and slower changes in CBF, our method can reliably detect the true CBF change within two to three video frames (or <100 ms) independent of the phase of the beat cycle at which the frequency started to change. Therefore, this approach yields an accurate CBF estimate with good time resolution and provides an acceptable noise filter. Obviously, an increase in the video frame acquisition rate will further improve the quality of the intensity signal. We are currently revising our software to take advantage of higher frame rate cameras (i.e. 60–120 Hz with a Sony XC7500/CMA-87).

An interesting biological feature of our measurement was the lag of CBF compared to [Ca²⁺]_i during the recovery phase from the peak back to baseline. Something similar was previously described by Korngreen & Priel (1994, 1996) who were the first to report simultaneous measurements of CBF and [Ca²⁺]_i in response to ATP and ionomycin. In contrast to their reports, however, we observed only a modest divergence of the two signals on the time axis (mean 8 s, median 3 s) with either cholinergic or purinergic stimulation and we also observed tight coupling between CBF and [Ca²⁺]_i during spontaneous Ca²⁺ oscillations of cells (with no exposure to agonist). As explained below, one possible explanation for this difference could be a species difference in the amount of Ca²⁺ influx across the plasma membrane and the duration of agonist application. For instance, rabbit cells might exhibit a more pronounced Ca²⁺ influx through the plasma membrane after ATP exposure and local Ca²⁺ concentrations at the membrane and/or ciliary base might differ from the ones we are measuring in the whole cell. Therefore, the local [Ca²⁺] might stay elevated for a longer period than the cytoplasmic concentration during continued agonist exposure and this phenomenon could explain at least some of the hysteresis seen and also some of the differences between the work from Priel's group and ours.

What else could account for the hysteresis? There are at least two additional possibilities with little published data to favour either one. First, the off-rate of Ca²⁺ from the calcium binding target could be much slower than the on-rate. Second, the dynein arm might have a built-in memory function, in which a particular conformation would persist long after the Ca²⁺ had unbound. There is some precedent for this in the recently described results for myosin (Ishijima et al. 1998): faster dynein ATPase activity might thereby be maintained for a period of time even after Ca²⁺ has been released from the Ca²⁺ binding sites.

The muscarinic stimulation of ciliated cells increased CBF by 2.1–4.3 Hz from baseline. This absolute CBF increase is smaller than the CBF changes reported by others in experiments carried out at 37°C or in vivo (for instance, Wong et al. 1990; Korngreen & Priel, 1996). But comparisons should only be done with work in vitro, and the absolute changes should be corrected for the difference in the baseline values at room temperature and 37°C, respectively. Thus, when our data are expressed as a percentage change above baseline (here on average 33 % above baseline), it lies somewhere in the middle of the reported relative changes in CBF upon stimulation with a variety of different compounds in cell culture, whether measured at 20°C or at 37°C (e.g. Lansley et al. 1992; Geary et al. 1995; Smith et al. 1996b).

Analysing the data, it became clear that there was no simple, linear relationship between CBF and [Ca²⁺]_i as already pointed out by Korngreen & Priel (1996). In addition, initial attempts at building a model with cooperative Ca²⁺ binding to a target that directly influences CBF failed to account for our results. Since it is clear that dynein arm movements provide the mechanism for ciliary bending, we started to explore a model that takes dynein arm action into account. Making three simple assumptions, the model we developed can account for the relationship between CBF and Ca²⁺. However, this model cannot account fully for the hysteresis of the response and we decided not to complicate the model until we have further experimental data to inform modelling choices. Both explanations given above suggest enhancements of the model that would be likely to provide better fits. Nevertheless, the model presented here does fit the data as depicted in Fig. 9. The fit of the model to measured data revealed several interesting findings. First, the average value of the total K_d (a variable in the fit) was 0.02 μM. Second, the fast dynein cycle is about twice as fast as the slow dynein cycle (duration of slow dynein action 9 ms, duration of fast dynein action 4.5 ms). This is in the range of the reported ATPase activity of dynein in the presence of microtubules, reported to be 150 s⁻¹ (Shimizu et al. 1989). Third, fast dynein moved microtubules 100 nm within 56 ms, a duration within the measured time (50–100 ms) it takes isolated single dynein molecules to move a microtubule the same distance in vitro (Shingyoji et al. 1998). However, this is slightly slower than the measured activity of isolated outer dynein arms on glass slides in vitro where the velocity was assessed as 4–9 μm s⁻¹ (Sale & Fox, 1988).

The technical approach of high resolution measurements that we (as well as others, i.e. M. Sanderson, personal communication) are following can provide the resolution needed to explore and elucidate the mechanistic basis for Ca²⁺-CBF coupling. While our results provide no support for a role of phosphorylation in mediating Ca²⁺ action in ovine ciliated airway epithelial cells, they lend support to the idea that Ca²⁺ binds directly to a ciliary protein that is capable of modulating the rate of dynein-microtubule interaction.

Just recently, Uzlaner & Priel (1999) measured Ca²⁺ and CBF simultaneously from rabbit airway epithelial cells at 37°C. These experiments indicated that phosphorylation by protein kinase G (PKG), stimulated by the NO-guanylyl cyclase-cGMP pathway, can mediate some of the effects of Ca²⁺ on CBF. Their main conclusion is therefore quite different from the one presented here. The CBF responses to increasing [Ca²⁺]_i in their work, however, clearly have two phases: an initial rapid CBF response to increasing [Ca²⁺]_i followed by a much slower increase in CBF which reaches its maximum about 2 min after the initial [Ca²⁺]_i increase. In fact, the second, slower CBF increase seems to be the one mediated by the kinase reaction (Uzlaner & Priel, 1999). In ovine cells, however, we see only a single phase rapid increase of CBF in response to rising [Ca²⁺]_i. The simplest explanation of these differences is that the modulation by PKG seen in Uzlaner & Priel's experiments on rabbit cells is simply lacking in the ovine cells. This might also explain the differences in lag time of CBF during the return to baseline as discussed above: Uzlaner & Priel reported this to be very long (i.e. minutes) whereas we see only seconds of delay (see Fig. 4). If this lag is mediated by phosphorylation reactions and the PKG activation is absent in our system, it is not surprising that we didn't see such long delays.

The next question then would be: why is the NO-PKG pathway not active in our ovine cells? There are at least three possible explanations. First, Uzlaner & Priel's measurements were done at 37°C, ours at room temperature. It could therefore be that NOS cannot be activated by Ca²⁺ at room temperature. This is unlikely, however, because previous reports investigating the NO system as it relates to CBF indicate that NOS can be stimulated at room temperature (Jain et al. 1993, 1995). A second possibility is that NOS is not expressed in ovine ciliated cells; however, NADPH-diaphorase staining (indicative of NOS presence) of ovine airway epithelial cells showed positive staining in ciliated cells (Salathe & Bookman, 1995b). But despite its presence, we could not block the CBF response to rising [Ca²⁺]_i by up to 10 mM L-NAME (Salathe & Bookman, 1995b).

A third possibility is that PKG is either not present or is not activated in ovine airway epithelial cells, possibly because the measurements were done at room temperature. Therefore, the question remains whether experiments investigating the role of kinases in biological functions can be done at room temperature. Substantial evidence suggests that the answer is yes. There have been several papers published implicating kinases in ciliary frequency regulation where CBF was measured at room temperature (Di Benedetto et al. 1991a,b; Lansley et al. 1992; Smith et al. 1996a; Wong et al. 1998; Wyatt et al. 1998). In addition, there is direct evidence that PKA and PKG can be stimulated at room temperature by cyclic nucleotides in bovine ciliated cells and that the time course of this stimulation coincides with the time course of ciliary stimulation (personal communication, T. Wyatt, University of Nebraska Medical Center).

In summary, it is becoming more and more evident that mammalian ciliated cells show species differences in their mechanisms of CBF regulation (e.g. the differences found between CBF responses of different species to exposure to membrane-permeable cGMP: in bovine and human ciliated cells, CBF increases (Geary et al. 1995; Wyatt et al. 1998) whereas in rabbit and sheep, CBF remains stable (Salathe & Bookman, 1995b; Uzlaner & Priel, 1999) and, in one paper, cGMP production has even been associated with a decrease in CBF (Tamaoki et al. 1991)).

So is Uzlaner & Priel's and our work contradictory? We believe that the answer is no. Uzlaner & Priel also showed that CBF increases in response to Ca²⁺ without NO/PKG activation and the increase was about 1.3-fold compared to baseline. This response was much faster than the further increase due to NO/PKG activation. Therefore, we believe that the sheep is an appropriate model to study the kinase-independent pathways of CBF regulation by Ca²⁺. In fact, regulation of mammalian CBF is likely to be species dependent and more complex than previously thought. Thus, there now seem to be at least three partially independent mechanisms to regulate CBF: (1) cAMP-dependent phosphorylation; (2) NO/cGMP-dependent phosphorylation; and (3) direct Ca²⁺ action.