Structural responses to the photolytic release of ATP in frog muscle fibres, observed by time-resolved X-ray diffraction

Abstract

1. Structural changes following the photolytic release of ATP were observed in single, permeabilised fibres of frog skeletal muscle at 5–6 °C, using time-resolved, low-angle X-ray diffraction. The structural order in the fibres and their isometric function were preserved by cross-linking 10–20 % of the myosin cross-bridges to the thin filaments.

2. The time courses of the change in force, stiffness and in intensity of the main equatorial reflections (1,0) and (1,1), of the third myosin layer line (M3) at a reciprocal spacing of (14.5 nm)⁻¹ on the meridian and of the first myosin-actin layer line (LL1) were measured with 1 ms time resolution.

3. In the absence of Ca²⁺, photolytic release of ATP in muscle fibres initially in the rigor state caused the force and stiffness to decrease monotonically towards their values in relaxed muscle fibres.

4. In the presence of Ca²⁺, photolytic release of ATP resulted in an initial rapid decrease in force, followed by a slower increase to the isometric plateau. Muscle fibre stiffness decreased rapidly to ≈65 % of its value in rigor.

5. In the absence of Ca²⁺, changes on the equator, in LL1 and in M3 occurred with a time scale comparable to that of the changes in tension and stiffness.

6. In the presence of Ca²⁺, the changes on the equator and LL1 occurred simultaneously with the early phase of tension decrease. The changes in the intensity of M3 (I_M3) occurred on the time scale of the subsequent increase in force. The time courses of the changes in tension and I_M3 were similar following the photolytic release of 0.33 or 1.1 mM ATP. However the gradual return towards the rigor state began earlier when only 0.33 mM ATP was released.

7. In the presence of Ca²⁺, the time course of changes in I_M3 closely mimicked that of force development following photolytic release of ATP. This is consistent with models that propose that force development results from a change in the average orientation of cross-bridges, although other factors, such as their redistribution, may also be involved.

Photolytic release of ATP from an inactive precursor has provided an approach to studying some of the elementary steps of energy transduction in muscle (Goldman et al. 1982). Photolytic release of nucleotides is an effective way to initiate contraction in cellular systems in which the internal structural organisation plays an essential role in defining function. In muscle cells, the three-dimensional packing of arrays of protein filaments is integral to in vivo muscular function. The order also enables time-resolved information about protein movements to be obtained by means of low-angle X-ray diffraction (Huxley et al. 1983).

Here we show, with a time resolution of 1 ms, the structural changes in permeabilised fibres isolated from frog skeletal muscle in response to rapid addition of ATP resulting from DMB-caged ATP photolysis (Thirlwell et al. 1994), in the absence and presence of Ca²⁺, at 5–6°C. The purpose of the study is to determine the changes in structure, at high time resolution, which accompany force generation when a muscle fibre in the rigor state is activated by photogeneration of ATP. These changes characterise the nature of molecular changes which are responsible for the generation of force and for shortening.

In previous studies using flash-photolysis experiments, X-ray diffraction data were collected on a variety of permeabilised fibres from insect muscle (Goody et al. 1985), rabbit muscle (Poole et al. 1987, 1991), Limulus and slow skeletal muscle of the rabbit (Poole et al. 1988), but most of the results related to the equatorial reflections only, and also to experiments carried out in the absence of Ca²⁺ where the relaxation from rigor, rather than activation, is observed. Recently, experiments with and without Ca²⁺ were carried out in slow and fast muscles of the rat (Horiuti et al. 1997; Yagi et al. 1998) with a time resolution of 16 ms. Observations of the X-ray changes in frog muscle following the photolytic release of ATP have been carried out previously (Brenner et al. 1989; Yagi et al. 1992), but these studies were limited to the equatorial region of the diffraction pattern. The studies mentioned above used NPE-caged ATP (the P³-1-(2-nitrophenyl)ethyl ester of ATP), which releases ATP relatively more slowly (∼10² s⁻¹ at 20°C upon photolysis with a Q₁₀ of about 2; Barabás & Keszthelyi, 1984) than the P³-[1-(3,5-dimethoxyphenyl)-2-phenyl-2-oxo]ethyl ester of ATP as caged nucleotide (DMB-caged ATP, ≥ 10⁵ s⁻¹; Thirlwell et al. 1994; Brown et al. 1995). The by-product of the cage moiety (5,7-dimethoxy-2-phenyl benzofuran; Thirlwell et al. 1994) is not reactive towards muscle proteins.

Time courses of the changes seen when muscle fibres in the rigor state are provided with photolytically produced ATP are shown, both in the presence and absence of Ca²⁺. In each case, the intensities of the main equatorial, meridional and off-meridional reflections change with a complex time course, revealing the movements of the proteins responsible for force transduction.

METHODS

Muscle fibres

Male Rana temporaria were killed by decapitation and destruction of the spinal cord. Fibres were isolated from the semitendinosus muscle and prepared as described previously (Bershitsky et al. 1996).

Apparatus

The experimental chamber, force transducer, length change motor and sarcomere length monitor were those used previously (Bershitsky et al. 1996). Photolysis was achieved by means of a Q-switched frequency-doubled ruby laser (Type QSR 2; Lumonics Ltd., Rugby, UK), which produced 30 ns light pulses at 347 nm with an energy of 80–150 mJ at the fibre (He et al. 1997) and was suspended from the ceiling above the X-ray beam-pipe. The laser light was directed to the muscle fibre through two fused silica right-angle prisms and focused on the fibre by means of a fused silica spherical lens with a 0.3 m focal length.

Length steps were applied to the muscle fibres before and after each photolytic light flash to assess the stiffness of the muscle fibre from the tension response, and in the case of active fibres, to record the time course of force recovery. In some experiments, a 1 kHz sinusoidal length change (amplitude, 0.1 %) was applied continuously to measure the change in stiffness. The oscillating component of tension was extracted by subtraction of a sliding average of tension over 1 ms. The resulting oscillating signal was rectified (by taking the square root of the squared signal) and smoothed using a 0.5 ms sliding average. For each fibre, sarcomere length was monitored from the same section of the fibre as that exposed to the X-ray beam by means of the electronic recording of the position of the first order diffraction line produced by a He-Ne laser (Bershitsky et al. 1996). The sarcomere signal was often difficult to observe from muscle fibres suspended in air because of beads of solution moving on the fibre surface during force or length change.

X-ray recording and analysis

Photolysis and recording of the muscle fibre response was carried out while the muscle fibres were suspended in air, in a moist chamber (Bershitsky et al. 1996). X-ray diffraction patterns were collected on station 16.1 on two-dimensional electronic X-ray detectors, at the Daresbury Synchrotron Radiation Source, Daresbury Laboratory, Warrington, Cheshire, UK (2 GeV multibunch, gapped beam mode), as described previously (Bershitsky et al. 1996), with a fibre to detector distance of 3.7 m. A 14 mm square lead beam-stop was placed in front of the detector in the evacuated beam-pipe to absorb un-diffracted photons. The air gap between the end of the X-ray beam-line and the nose cone of the camera beam-pipe was approximately 120 mm, 50 mm of which was taken up by the fast X-ray shutter and 25 mm by the ion chamber used for monitoring the X-ray beam intensity. The shutter, X-ray detector and triggering of the near-UV laser were controlled by the station computer running the NCD program. Control of the length motor was achieved from a personal computer (PC; INTEL 486) equipped with a digital-to-analog converter on a timer card (L-154; L-Card, Moscow, Russia). The PC recorded signals from the tension transducer, length transducer and sarcomere monitor via an analog-to-digital converter card (DAS-50; Keithley Metrabyte, Taunton, MA, USA). The X-ray data were collected on the station computer in time bins. Their duration was set to 1 ms when signals changed rapidly, and increased to up to 0.5 s for the periods when structural changes were slow. The detector was operated in a 256 pixel × 256 pixel mode. The detector characteristics were determined by the recording of the detector response to exposure to a radioactive ⁵⁵Fe source placed 1 m from the detector, for 2 h each day. This detector response was used to obtain pixel to pixel normalisation of the detector sensitivity. At the end of the experiment on each fibre, the X-ray pattern was recorded in the absence of a fibre in the set-up, for a collection time of at least 60 s. This ‘camera background’ response was subtracted, after scaling for exposure time, from each time frame to remove the X-ray beam scatter from the experimental data. The intensities of the X-ray reflections were calculated from each time frame for the main diffraction peaks, after subtraction of the background under the peak and averaging the data in the four quadrants (Fig. 1).

Figure 1. Two-dimensional X-ray diffraction patterns recorded before and after photolytic release of 1.1 mM ATP in the absence (A, C and E) and presence (B, D and F) of Ca²⁺.

White corresponds to higher intensity. The equator is vertical and attenuated 30 times to make stronger and weaker reflections visible on the same pattern. The X-ray data in the absence and presence of Ca²⁺ were summed from 32 and 75 runs of the experimental protocol obtained from 8 and 18 fibres, respectively. The rigor patterns in A and B were collected during 100 ms long frames before the laser flash; the post-flash patterns in C and D were collected for 50 and 30 ms, respectively, beginning 10 ms after the flash; the steady-state patterns in E and F were collected for 1 s each beginning 0.5 s after the flash. The X-ray intensities were scaled for exposure in each state to allow quantitative comparison. The main equatorial ((1,0) and (1,1)) and meridional (M3) X-ray reflections as well as the first actin layer line (A1) are indicated in A. Rectangles in A show the areas of integration for the meridional reflections and for the layer lines, resulting in one-dimensional X-ray plots which were used to determine the intensities of the reflections.

The X-ray data were analysed using the software programs BSL, OTOKO and FIT provided by Daresbury Laboratory and CCP13 (Collaborative Computational Project for fibre diffraction, supported by the BBSRC). The time course of the intensity of the strongest reflections ((1,0), (1,1) equatorials and M3 (third myosin layer line) meridional at (14.5 nm)⁻¹) was determined for each muscle fibre after summing the diffraction patterns obtained for each laser flash. For the weaker or diffuse reflections such as layer lines, the diffraction patterns from muscle fibres submitted to identical protocols were summed, and the time course determined from these summed patterns, with the consequent loss of statistical evaluation of fibre-to-fibre variation. To check for the effect of fibre deterioration, the diffraction patterns obtained from the first flash to which each fibre was subjected were added, and the time courses of intensity changes were also determined from this summed pattern (Fig. 1). Figure 1A shows an example of the summed patterns obtained for muscle fibres in rigor, in the presence of 10 mM DMB-caged ATP. The main intensities of interest are indicated, together with the areas of integration.

Measurement of the intensity of the (1,0) and (1,1) equatorial reflections was carried out by integration of the two-dimensional pattern over an area extending (104 nm)⁻¹ from the centre in the meridional direction (Fig. 1A). The (1,0) and (1,1) peak intensities were measured from the resulting one-dimensional pattern by integration, after interpolating a linear background for each reflection. The intensity of the third myosin layer line (M3), a bright spot at (14.5 nm)⁻¹ along the meridian, was measured after integration of the two-dimensional pattern over an area extending (91 nm)⁻¹ from the centre in the equatorial direction. The M3 peak intensity was calculated by integration of the one-dimensional pattern after interpolation of a linear background.

The intensities of the first myosin and actin layer lines (M1 and A1) were measured by integration of the summed two-dimensional patterns along the layer line from the centre to (23.2 nm)⁻¹ in the meridional direction and from (35 nm)⁻¹ to (9 nm)⁻¹ in the equatorial direction (Fig. 1A). For the brightest set of data (flash photolysis of 10 mM DMB-caged ATP in the presence of Ca²⁺), the one-dimensional pattern was also fitted with two Gaussians centred on M1 and A1 in the meridional direction. The position of M1 was determined by fitting a single Gaussian to the diffraction pattern obtained from fibres in the relaxed state. The position of A1 was determined by fitting a single Gaussian to the pattern of fibres in rigor. The two Gaussians had centres at (45.5 nm)⁻¹ and (35.5 nm)⁻¹ for M1 and A1, respectively. The background under the reflections (in the meridional direction) was best fitted with a Pearson VII curve (Young et al. 1980; a Gaussian with a wider tail) centred on the diffraction centre. Before and following photolysis in the presence of Ca²⁺, the intensity of M1 never rose to more than 7 % of the intensity of A1, so that no further account was taken of the intensity of M1.

Experimental solutions

The solutions used for preparing the muscle fibres and for their rigorisation were as described previously (Bershitsky et al. 1996). The experimental solutions had an ionic strength of 150 mM and a pH of 7.1 at 20°C, buffered with 60 mM Tes, with their composition calculated by a computer program as described previously (Thirlwell et al. 1994). Ionic strength was adjusted by addition of potassium propionate. In all solutions, the free Mg²⁺ concentration was 2 mM. All experiments were carried out at 5–6°C, the temperature of the fibres suspended in air, unless specified. Activating solution contained 25 mM Ca-EGTA (calcium complexed with ethylene glycol bis-[β-aminoethyl ether]-N,N,N′,N′-tetraacetic acid, pCa 4.5). Relaxing solution contained 5 mM MgATP and 5 mM EGTA (pCa > 8). Rigor solution contained 5 mM EGTA and no added calcium. ‘Pre-rigor’ solution contained 0.4 mM MgATP and 5 mM 2,3-butanedione monoxime (BDM) which reduced force development during rigorisation and thus minimised the disordering of sarcomere structure (Bershitsky et al. 1996). ‘Super-relaxing’ solution, containing 5 mM MgATP, 50 mM BDM and 20 mM inorganic phosphate (P_i), was used to relax muscle fibres partially cross-linked with 1-ethyl-3-[3-dimethylaminopropyl]carbodiimide (EDC) (Bershitsky et al. 1996). ‘Loading-activating’ solution contained 10 or 2 mM DMB-caged ATP in addition to Tes, Ca-EGTA and propionate, while ‘loading-relaxing’ solution contained no added Ca²⁺, as described by Thirlwell et al. (1994). Loading-relaxing solution also contained 50 mM BDM and 20 mM P_i to prevent reattachment of the cross-bridges to the thin filaments in the fibres partially cross-linked with EDC. The solutions with DMB-caged ATP maintained the rigor state until the caged compound was photolysed. This either caused relaxation or activation of the muscle fibre, depending on the absence or presence of Ca²⁺, respectively. The DMB-caged ATP solutions contained 0.3 mg ml⁻¹ apyrase (A-6535, Grade VII; Sigma Chemical Co., St Louis, MO, USA) to remove contaminating ADP in the DMB-caged ATP solution (Thirlwell et al. 1994). Although photolysis of DMB-caged ATP does not result in damaging by-products, the light pulse itself caused damage which was somewhat alleviated by inclusion of 10 mM glutathione in the DMB-caged ATP solutions.

Extent of ATP release by photolysis of DMB-caged ATP

The extent of photolysis was measured in a parallel series of experiments by the method of He et al. (1997), as illustrated in their Fig. 5. The main differences in experimental conditions were that the temperature was 8.5°C instead of 5–6°C and the fibres were immersed in silicone oil at the time of photolysis instead of being suspended in air. With 10 and 2 mM DMB-caged ATP, the extent of photolysis was 10.8 ± 0.7 % (mean ±s.e.m., n = 3) and 16.4 ± 1.1 % (n = 2), respectively. These values correspond to the photolytic release of 1.08 ± 0.07 and 0.33 ± 0.02 mM ATP from 10 and 2 mM DMB-caged ATP, respectively. The extent of photolysis measured by this method is identical to that measured by HPLC of the nucleotide and caged nucleotide by Thirlwell et al. 1994, who obtained a value of 1.1 mM ATP released by photolysis of a solution containing 10 mM DMB-caged ATP.

Figure 5. Structural responses following photo-liberation of 1.1 mM ATP from 10 mM DMB-caged ATP in the presence of Ca²⁺ in single partially EDC cross-linked frog muscle fibres at 5–6 °C.

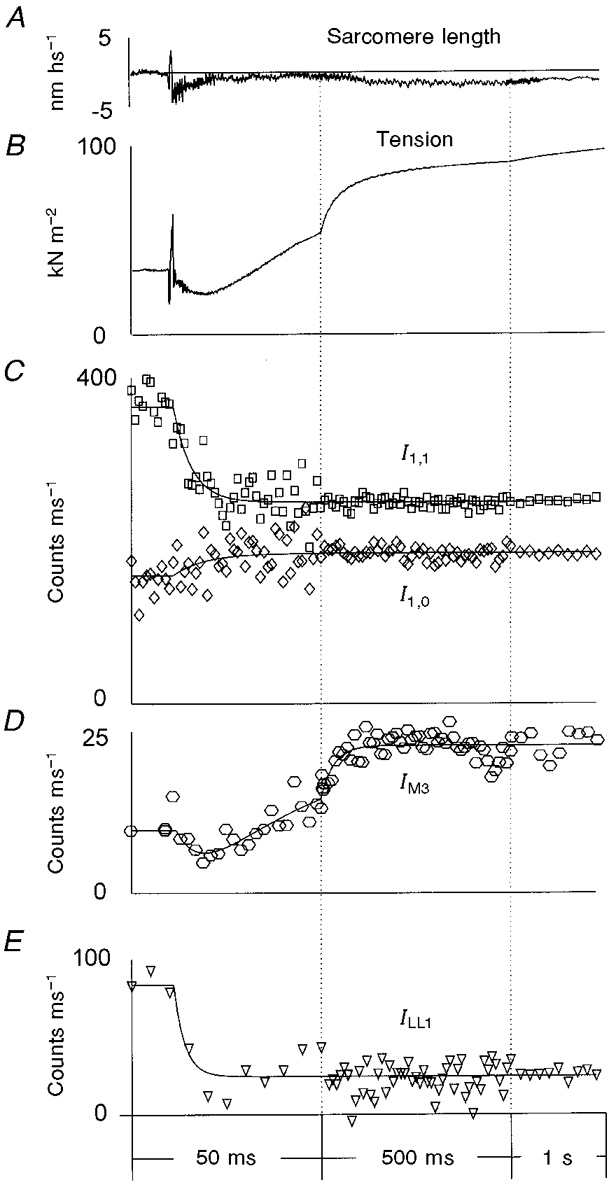
A, typical sarcomere length record; B, averaged tension transients; C, the intensity of the equatorial X-ray reflections, I_1,0 (⋄) and I_1,1 (□); D, the intensity of the meridional reflection at (14.5 nm)⁻¹, I_M3; E, the intensity of the myosin-actin layer line, I_LL1. The tension trace shown in B was averaged from 69 experiments in 18 muscle fibres; the X-ray data were collected from 75 experiments in the same fibres. The curves in C-E are exponential fits to the data (see legend to Fig. 4 and text). The vertical dotted lines show where the time scale was changed. In D and E, the 1 ms time frames were averaged into 5 ms time bins during the first 50 ms, for clarity. The averaged values were assigned a time corresponding to the centre of the time interval. In E, the intensity I_LL1 was determined by radial off-meridional integration from (35 nm)⁻¹ to (8 nm)⁻¹ and with subsequent meridional integration and linear background subtraction, so both the first actin layer line at ≈(37 nm)⁻¹ and the first myosin layer line at ≈(43 nm)⁻¹ contributed to I_LL1, although the first myosin layer line remained constant at 7 % of the total intensity.

Protocol

Isolated fibres were permeabilised by incubation in relaxing solution containing 0.5 % (v/v) Triton X-100 followed by immersion in a 50 % mixture of the relaxing solution with glycerol (Bershitsky et al. 1996) for 15–30 min each at 5–10°C. Muscle fibres were transferred to the experimental bath in a drop of the relaxing solution on a glass coverslip, and glued to the transducers by means of a shellac-ethanol paste (Bershitsky & Tsaturyan, 1992). After adjustment of the sarcomere length and alignment of the fibre in the X-ray beam, the fibre was exposed to X-rays for 1 s in air to obtain a diffraction pattern of the relaxed state. The bathing medium was replaced with pre-rigor and rigor solutions. The onset of rigor was monitored by periodic application of a rapid stretch, 0.1 % of the fibre length. Stiffness and lack of force recovery indicated rigor. The onset of rigor could be accelerated by increasing the bath temperature from ∼2 to 5–10°C or by using a rigor solution devoid of Mg²⁺. The rigor X-ray diffraction pattern was recorded during a 1 s exposure in air. Protective cross-linking of 10–20 % of the myosin cross-bridges with EDC was performed by incubation in 10 mM EDC in the presence of 2 mM MgCl₂ and 60 mM P_i at 15°C for 10–15 min depending on fibre diameter (Bershitsky et al. 1996). Cross-linking was not necessary for Ca²⁺-free experiments. Then fibres were returned to rigor solution and another 1 s X-ray diffraction pattern was recorded.

Next, fibres were transferred to DMB-caged ATP solution at ∼2°C. After 5 min incubation, the fibre was suspended in air in a moist chamber under subdued lighting using a remote-controlled mechanism (Bershitsky et al. 1996). Within 1–2 s, the X-ray shutter was opened and the data collection protocol begun. A 100 ms long pre-flash pattern was recorded, followed by a light pulse to induce relaxation (absence of Ca²⁺) or activation (presence of Ca²⁺) and fibres were returned to super-relaxing solution. DMB-caged ATP solution in the trough was shielded from the near-UV laser light so it could be used for several runs of the protocol. Fibres were again taken through the cycle of rigorisation and loading with DMB-caged ATP solution, up to 11 times for each fibre or until active isometric force decreased to 60 % of its level during the first contraction. Fibre damage caused by the light pulse seemed to be more severe than that caused by X-ray radiation.

In some fibres, +Ca²⁺ and -Ca²⁺ protocols were alternated, as well as protocols with different concentrations of DMB-caged ATP. Data are presented ± one standard error of the mean for the number of experiments, n, or ± one standard deviation to illustrate fibre-to-fibre variation. In the case of regression analysis, the parameters are presented ± one standard error of the estimate as determined from the Marquardt-Levenberg algorithm. Exponential rate constants were obtained by analysis of the data using the program DISCRETE (Provencher, 1976), and are expressed ± one standard error of the mean.

RESULTS

Changes in tension and stiffness following the photolytic release of ATP

The time courses of tension change following the photolytic release of ATP from 2 and 10 mM DMB-caged ATP in a muscle fibre are shown in Fig. 2, in the presence and absence of Ca²⁺. Note the monotonic decrease in force observed in the absence of Ca²⁺, as described by Thirlwell et al. (1994) for rabbit muscle fibres, which results from the use of DMB-caged ATP, the removal of contaminating ADP with apyrase and addition of BDM and P_i to the loading solution to prevent reattachment of the cross-bridges to the thin filaments. The initial phase of force decrease in the absence of Ca²⁺ (trace 1), and in the presence of Ca²⁺ (traces 2 and 3), results from initial cross-bridge detachment. In Fig. 2, the initial force decrease was slower in the absence than in the presence of Ca²⁺, but this was not always the case (compare Figs 4B and 5B). Force generation in the presence of Ca²⁺ (Fig. 2, traces 2 and 3) was complex. A fast component of the tension rise was followed by a slow component and, when the amount of liberated ATP was low (0.33 mM), tension then decayed towards the pre-flash rigor level on a time scale of several seconds (trace 3). The fast components of the tension rise were similar irrespective of whether 0.33 or 1.1 mM ATP was liberated. However, at the lower concentration, the amplitude of the slower component and maximal isometric tension were higher because tension was generated at a low concentration of MgATP which is known to induce high force (Ferenczi et al. 1984). Also, less P_i was released through hydrolysis, so the inhibitory effect of P_i on force was less (Pate et al. 1998). With 1.1 mM ATP the isometric plateau remained steady for 2–3 s.

Figure 2. Tension responses to the photolytic release of 1.1 mM ATP from 10 mM DMB-caged ATP (1 and 2) or 0.33 mM ATP from 2 mM DMB-caged ATP (3) in a single frog muscle fibre slightly cross-linked with EDC in the absence (1) and presence (2 and 3) of Ca²⁺.

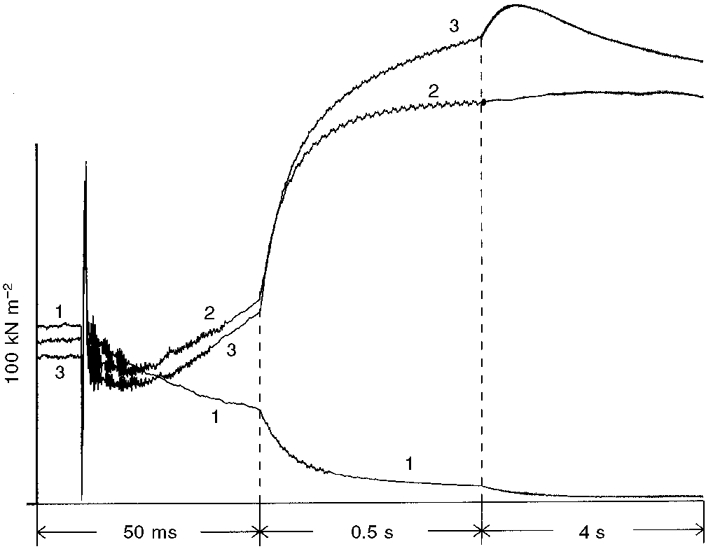
The time of the laser flash is visible as an artefact on the tension records. The dashed vertical lines indicate the points at which the time scale was changed, so that the fast initial changes and the slow later changes could be clearly seen on a single graph. Fibre dimensions: 3.43 mm × 19 600 μm²; sarcomere length measured in relaxing solution, 2.1 μm.

Figure 4. Structural responses following photo-liberation of 1.1 mM ATP from 10 mM DMB-caged ATP in the absence of Ca²⁺ and in the presence of 50 mM BDM and 20 mM P_i at 5–6 °C.

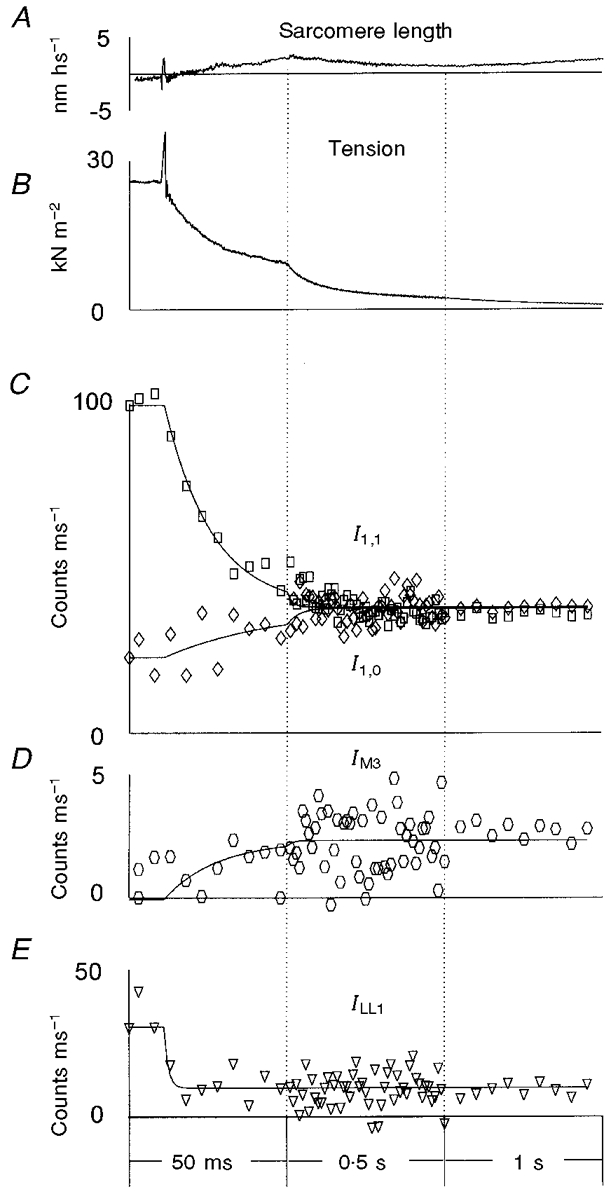
The time of the laser flash is marked by the movement artefact on the tension trace (B) 10 ms after the beginning of the record. A shows a typical sarcomere length record. As in Figs 5 and 6, the sarcomere length change is expressed in terms of nanometres per half sarcomere (hs), as the half sarcomeres are the functional elements arranged in series. B shows the averaged tension change for 28 runs of the protocol in 8 frog muscle fibres. Four of these 8 fibres were slightly cross-linked with EDC; 4 were not cross-linked. A further 4 experiments included the application of oscillations to the fibre for the determination of stiffness. These are not included in the data shown in B. The X-ray intensities (I) from the 32 experiments in the same fibres were added together and expressed as counts on the detector per millisecond. Data are shown in C-E: the intensity of the equatorial X-ray reflections, I_1,0 (⋄) and I_1,1 (□) (C); the intensity of the meridional reflection at (14.5 nm)⁻¹, I_M3 (D); and the intensity of the myosin-actin layer line, I_LL1 (E). The time frames of the X-ray data collection varied from 1 ms before and just after the laser flash, to 10 ms near the plateau of relaxation. In C-E, the 1 ms time frames were averaged into 5 ms time bins during the first 50 ms, for clarity. The averaged values were assigned a time corresponding to the centre of the time interval. The vertical dotted lines show changes in the time scale. In C, the curves are double exponential fits to the time courses of I_1,1 and single exponential fit to I_1,0. In D, I_M3 was fitted with a double exponential function to determine the lag phase and the rate of increase in the intensity. In E, the intensity I_LL1 was determined by radial off-meridional integration from (35 nm)⁻¹ to (8 nm)⁻¹ and with subsequent meridional integration and linear background subtraction, so both the first actin layer line at ≈(37 nm)⁻¹ and the first myosin layer line at ≈(43 nm)⁻¹ contributed to I_LL1.

Figure 3 shows examples of the stiffness changes following the photolytic release of 1.1 mM ATP in the absence and presence of Ca²⁺ together with the smoothed tension traces (dashed lines). In the absence of Ca²⁺, stiffness decreased with about the same time course as tension (Fig. 3A), showing that reattachment of the cross-bridges in the slightly cross-linked fibres was effectively abolished by the use of apyrase, BDM and P_i. In the presence of Ca²⁺ (and absence of BDM and added P_i), the apparent stiffness quickly decreased following the laser flash to about 65 % of its rigor value and then increased slowly to about 80 % of the rigor value when isometric tension developed (Fig. 3B). Sarcomere length measurements showed that little length change took place in our preparation (Figs 4, 5 and 6), as expected from partially cross-linked fibres (Bershitsky et al. 1996), indicating that the time courses observed here relate to isometric conditions.

Figure 3. Stiffness changes initiated by the photolytic release of 1.1 mM ATP from 10 mM DMB-caged ATP in the absence (A) and presence (B) of Ca²⁺ in single frog muscle fibres slightly EDC cross-linked.

Continuous lines represent fibre stiffness extracted from the tension responses to 1 kHz sinusoidal length changes (0.2 % of the fibre length peak-to-peak), as described in the text and normalised for rigor stiffness before the laser flash. The dashed lines show tension smoothed using 1 ms sliding averaging in the same experiments normalised for maximal tension (pre-flash rigor tension in A and maximal isometric tension in B). The traces were interrupted for ≈2 ms when the laser flash perturbed the tension records (vertical dotted lines) making calculation of stiffness impossible. Force decay was described by a double exponential with rate constants of 169 ± 98 and 9.5 ± 17 s⁻¹ (mean ± one standard error of the estimate obtained from the Marquardt-Levenberg algorithm). Stiffness decay was described by a single exponential process of 30 ± 0.8 s⁻¹. Fibre dimensions: A, 3.47 mm × 17 200 μm²; B, 3.55 mm × 13 800 μm²; sarcomere length 2.1 μm for both fibres.

Figure 6. Structural responses following photo-liberation of 0.33 mM ATP from 2 mM DMB-caged ATP in the presence of Ca²⁺ in single partially EDC cross-linked frog muscle fibres at 5–6 °C.

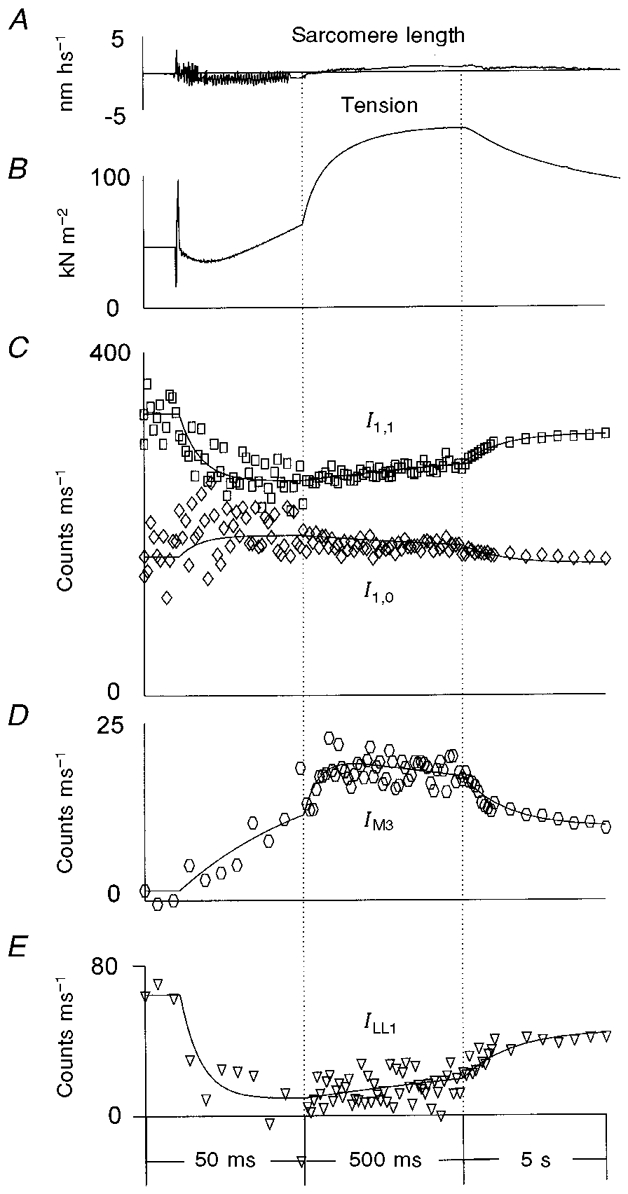
A, typical sarcomere length record; B, averaged tension transients; C, the intensity of the equatorial X-ray reflections, I_1,0 (⋄) and I_1,1 (□); D, the intensity of the meridional reflection at (14.5 nm)⁻¹, I_M3; E, the intensity of the myosin-actin layer line, I_LL1. The tension trace in B was averaged from 48 experiments in 11 muscle fibres; the X-ray data were collected from 54 experiments in the same fibres. The vertical dotted lines show where the time scale was changed. Other details as for Fig. 5.

The time course of changes in tension and stiffness in the absence of Ca²⁺

The data shown in Fig. 4A and B were obtained from 28 flash-photolysis experiments in eight muscle fibres in the presence of 10 mM DMB-caged ATP, 20 mM P_i and 50 mM BDM, and in the absence of Ca²⁺. The sarcomere length recording (Fig. 4A) shows that no rapid shortening of the fibre took place: experimental conditions remained close to isometric throughout. Four of eight fibres were slightly cross-linked with EDC, as described above. Four were not cross-linked. There was little difference in the mechanical responses or the X-ray diffraction intensities between these two sets of fibres: some residual tension (< 5 % of its pre-flash level in rigor) and stiffness (< 20 % of its rigor value) were seen in EDC-treated fibres due to cross-linked myosin heads preventing full relaxation. Pre-flash rigor tension was 31.2 ± 1.7 kN m⁻² and did not change significantly with the flash number in each experiment. The sarcomere length signal changed little following release of ATP, indicative of the low compliance of the preparation. Tension relaxation (Fig. 4B and trace 1 in Fig. 2) was well fitted with two exponential components. The rate constants k₁ and k₂ were 87 ± 3 and 7.4 ± 0.4 s⁻¹, respectively (n = 28), and did not depend significantly on the flash number in each experiment. However, the amplitude of the slow component increased with the flash number from about 30 % of the pre-flash tension after the first flash to ∼70 % after four to seven flashes.

The time course of changes in tension in the presence of Ca²⁺

In these experiments (Fig. 5 and Table 1) 1.1 mM ATP was released by photolysis of 10 mM DMB-caged-ATP in the presence of Ca²⁺. The pre-flash rigor tension was 38 ± 2 kN m⁻² (n = 75). Rigor tension did not change significantly with the flash number in each experiment. In most cases, the time course of tension following photolysis was well fitted with the sum of three exponential components, as follows:

(1)

where a₁, a₂ and a₃ are the amplitudes and k₁, k₂ and k₃ the rate constants of the initial tension relaxation, and of the fast and slow components of the tension rise, respectively, and where T_r is the pre-flash rigor tension level. In 21 of a total of 69 traces, only two exponential components could be extracted from the data. These data were not included in Table 1 to avoid ambiguity in attributing the kinetic parameters to one of the three exponential components described above.

Table 1.

Kinetic parameters of the tension responses to the flash photolysis of 10 mm DMB-caged ATP in the presence of Ca²⁺

Exponential component	Rate constant (s−1)a		Normalised amplitudeb
Tension relaxation, k1 and a1	117 ± 52 (69),	121 ± 5	0.21 ± 0.08
	r = 0.21		r = −0.34
Fast tension rise, k2 and a2	20.2 ± 5.3 (48),	19.7 ± 3.3	0.56 ± 0.18
	r = −0.21		r = −0.62
Slow tension rise, k3 and a3	2.2 ± 1.0 (48),	2.1 ± 0.1	0.33 ± 0.09
	r = 0.16		r = −0.005

Values are means ±s.d.

^aNumbers in parentheses are the number of the tension responses used for the analysis; the second (right-hand) set of values is the value calculated from the averaged time course.

^bThe amplitudes were normalised to the maximal active tension achieved after the flash. r is the correlation coefficient with the flash number.

The amplitude of the isometric tension, T₀, achieved after the photolytic liberation of ATP, decreased with the flash number, indicating the damage caused to the contractile proteins by the light pulse. For this reason, the data from repeated flashes on a single fibre were used only while T₀ was ≥ 0.6T₀₁, where T₀₁ is T₀ after the first flash in the experiment. T₀₁ was 117 ± 8.5 kN m⁻² (n = 16).

Experiments in which 0.33 mM ATP was photolytically released were carried out (54 experiments in 11 fibres). The pre-flash rigor tension was 49 ± 6 kN m⁻² (n = 11) and did not correlate significantly with the flash number, whereas as before, the amplitude of the maximal isometric tension, T₀, achieved after the photolytic liberation of ATP, significantly decreased with the flash number. T₀₁ was 167 ± 11 kN m⁻² (n = 11). The time course of the tension rise was more complex than that following photolytic release of 1.1 mM ATP (Fig. 6). Four exponential components were needed to fit the data instead of the three used in eqn (1). The fourth component described the decrease in tension after the isometric tension plateau was reached (Fig. 6B, trace 3 in Fig. 2), which was attributed to exhaustion of the photolytically released ATP and the slow return towards the rigor state (Table 2).

Table 2.

Kinetic parameters of the tension responses to the flash photolysis of ATP from 2 mm DMB-caged ATP in the presence of Ca²⁺

Kinetic component	Rate constant (s−1)a		Normalised amplitudeb
Fast tension relaxation, k1 and a1	119 ± 25 (48),	95 ± 5	0.35 ± 0.88
	r = 0.36		r = −0.45
Fast tension rise, k2 and a2	28.3 ± 8.7 (43),	28.8 ± 2.2	0.53 ± 0.24
	r = −0.005		r = −0.56
Slow tension rise, k3 and a3	5.8 ± 1.6 (43),	5.7 ± 0.3	0.54 ± 0.07
	r = −0.44		r = −0.25
Slow tension decrease, k4 and a4	0.33 ± 0.2 (48)		0.46 ± 0.17
	r = 0.16		r = −0.45

Values are means ±s.d.

^aNumbers in parentheses are the number of the tension responses used for the analysis; the second (right-hand) set of values is the value calculated from the averaged time course.

^bThe amplitudes were normalised to the maximal active tension reached after the flash. r is the correlation coefficient with the flash number.

Changes in the X-ray diffraction pattern following the photolytic release of ATP

The time course of structural changes in the absence of Ca²⁺

As the rate constants did not depend on the flash number and did not differ in cross-linked and non-cross-linked fibres, the intensities of the X-ray reflections for 32 experiments with eight muscle fibres were added together to optimise the signal. These include 28 experiments whose average is shown in Fig. 4A and B and four experiments in which length oscillations were applied to the fibre for the determination of stiffness. Time-resolved X-ray intensities are shown in Fig. 4. The intensity of the (1,1) equatorial reflection, I_1,1, decreased monotonically (Fig 4C and Fig 7). Its time course was described by two exponential components with rate constants of 94 ± 19 and 6.2 ± 4.6 s⁻¹, and the amplitude of the fast component accounted for ∼80 % of the process (Table 3). Overall, I_1,1 decreased to 36 % of its value in rigor. The intensity of the (1,0) reflection, I_1,0, was described by a single exponential component with a rate constant of 28.5 ± 10.2 s⁻¹, increasing to 165 % of its value in rigor (Fig. 4C).

Figure 7. Comparison of the first 0.2 s of the time course of the change in I_1,1 obtained in the presence and absence of Ca²⁺.

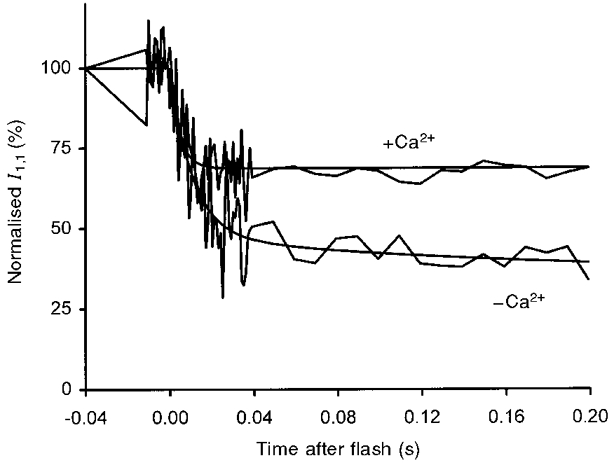
The data and exponential traces obtained by regression to the data, shown in Figs 4 and 5, are superimposed. The data were normalised so that the rigor intensities in the presence and absence of Ca²⁺ were identical. It can be seen that the amplitude of the initial changes in the absence of Ca²⁺ is greater than that in the presence of Ca²⁺, pointing to truncation of the underlying process in the latter case, but the changes in the initial 10 ms overlap.

Table 3.

Main changes in the X-ray diffraction pattern following the photolytic release of ATP from 10 mm DMB-caged ATP

	k1(s−1)	a1	k2(s−1)	a2	Final amplitude relative to that in rigor
−Ca2+
Tension	72.1 ± 30.5	0.5	7.9 ± 3.4	0.5	0
I1,1	94.1 ± 19.0	0.81	6.2 ± 4.6	0.19	0.36
I1,0	28.5 ± 10.2	1.0	—	—	1.65
IM3	59.1 ± 18.2	1.0	—	—	1.86
ILL1	637 ± 480	1.0	—	—	0.23
+Ca2+
I1,1	208 ± 21	1.0	—	—	0.68
I1,0	122 ± 49	1.0	—	—	1.17
IM3	20.1 ± 2.3	1.0	—	—	2.38b
	118 ± 63a	−0.82	29 ± 7	1.82	—
ILL1	79 ± 21	1.0	—	—	0.32

The variables k₁ and k₂ refer to the rate constants describing the two exponential components of amplitudes a₁ and a₂. When the data were fitted to a single process, no values are given for k₂ and a₂. The data are shown ± 1 s.e.m., obtained by the algorithm of Provencher (1976).

^aThe second set of parameters is for the double exponential fit of the IM3 data

^bThe increase in I_M3 in experiments in the presence of Ca²⁺ was measured from summed data, rather than from the average of experimental traces.

The increase in intensity of the third meridional myosin layer line M3 at a reciprocal spacing of (14.5 nm)⁻¹, I_M3, was described by a single exponential process with a rate constant of 59 ± 18 s⁻¹. Analysis of the time course obtained after summing all experiments (Fig. 1A, C and E) showed that the intensity of M3 increased 1.86-fold following photolytic release of ATP, but that most of the change occurred relatively slowly, as averaging the intensity of the M3 reflection from 10 to 60 ms after photolytic release of ATP resulted in a value that was only 1.3-fold higher than that prior to the laser flash (Fig. 8A). Figure 8A also shows that there was no detectable change in width or spacing of the M3 reflection in these experiments.

Figure 8. Meridional profile in rigor, immediately following photolysis and in the steady state, in the absence and presence of Ca²⁺.

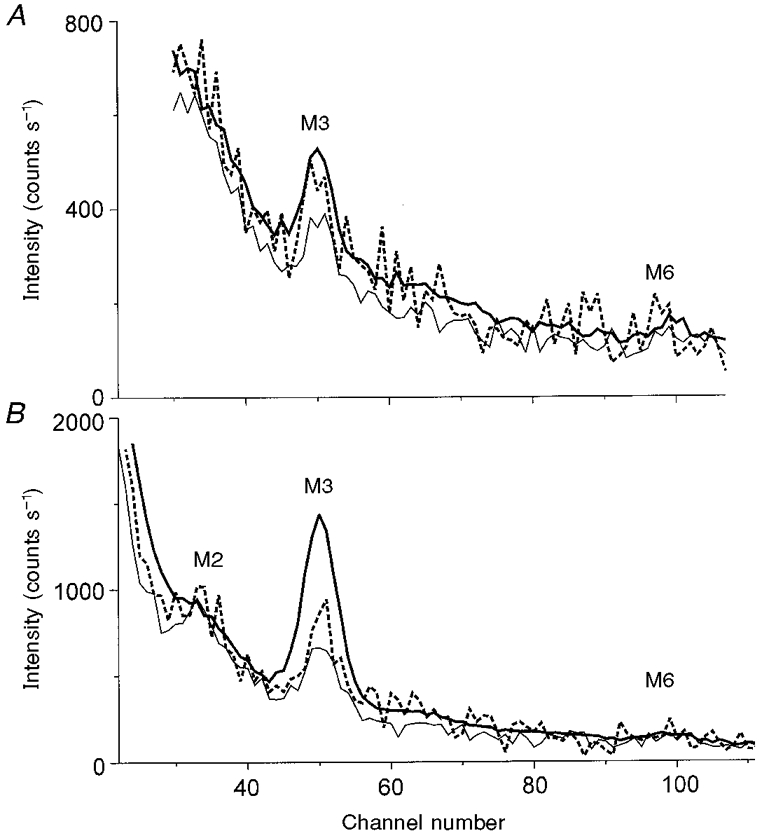
A, absence of Ca²⁺. The data were integrated vertically from -(104 nm)⁻¹ to (104 nm)⁻¹. The pre-flash (Fig. 1A), post-flash (Fig. 1C) and steady state (Fig. 1E) profiles are shown by the thin, dashed and thick lines, respectively. The post-flash data were obtained by summing and scaling for exposure time the data collected 10–60 ms following photolytic release of ATP. The positions of the M3 and M6 reflections are shown; one channel corresponds to (725 nm)⁻¹. B, presence of Ca²⁺. The meridional profiles of the X-ray intensity before and after flash photolysis of 1 mM ATP in the presence of Ca²⁺. The data shown in Fig. 1 were integrated vertically from -(104 nm)⁻¹ to (104 nm)⁻¹. The pre-flash (Fig. 1B), post-flash (Fig. 1D) and steady-state (Fig. 1F) profiles are shown by the thin, dashed and thick lines, respectively. The positions of the meridional reflections M2, M3 and M6 are indicated. One channel corresponds to (725 nm)⁻¹. The post-flash data were obtained by summing and scaling for exposure time the data collected in the interval 10–40 ms following photolytic release of ATP.

The intensity of the first actin-myosin layer line, I_LL1, decreased almost instantaneously to ∼23 % of its rigor value (Fig. 4E). The rate constant describing the process could not be determined accurately (637 ± 480 s⁻¹), but indicates that the change was at least as rapid as the main change in I_1,1.

Despite the noise in the data, the changes in four regions of the diffraction pattern following photolytic liberation of ATP in the absence of Ca²⁺ and in the presence of P_i and BDM were seen to move from their rigor levels towards relaxation either simultaneously with the tension and stiffness decay or faster.

The time course of structural changes following photolytic release of 1.1 mM ATP in the presence of Ca²⁺

The constancy in the rate constants of the exponential components of the tension transients allowed us to add together the intensities of the X-ray reflections for 75 experiments in 18 muscle fibres to improve the signal (Fig. 5 and Table 3). However, to ensure that fibre deterioration did not affect the kinetics of the X-ray reflections, we also analysed separately the X-ray diffraction patterns obtained in the first responses in 18 fibres.

The intensities of the (1,1) and (1,0) equatorial reflections (I_1,1 and I_1,0) changed monotonically, with exponential time courses characterised by rate constants of 208 ± 21 and 122 ± 49 s⁻¹, respectively. I_1,1 decreased to 67.7 % of its value in rigor (Fig. 7) and I_1,0 increased to 117 % of its value in rigor (Fig. 5C). The ratio of equatorial intensities (I_1,1/I_1,0) decreased from a value of 2.32 in rigor to 1.36 at the plateau of isometric contraction (data not shown), in a process described by a single exponential component with a rate constant of 137 s⁻¹. The changes in the equatorial intensities were complete within 20 ms of the laser flash and liberation of ATP. The strongest X-ray reflections which provide information about cross-bridge disposition appear to be insensitive to the development of active isometric force.

The difference in the rate constants describing the changes in the time course of the equatorial reflections in experiments in the presence and absence of Ca²⁺ is a consequence of the higher amplitude of the change in intensity observed in the latter case where the process appears to go to completion. This is shown in Fig. 7 where the intensities in the rigor state were normalised, and where the time courses of the changes in I_1,1 were superimposed for experiments in the presence and absence of Ca²⁺. It is clear that in the first 10 ms the time courses were indistinguishable in spite of the large difference in the rate constants for the fast initial process of 94.1 and 208 s⁻¹ in the absence and presence of Ca²⁺, respectively (Table 3). The difference in the time courses of I_1,0 is also explained by the different amplitude of the changes.

I_M3, shown in Figs 5D and 8B, decreased initially, and then increased with rate constants of 118 ± 63 and 29 ± 7 s⁻¹, respectively. Averaging the data for the first 30 ms following photolytic release of ATP showed that I_M3 was 92 % of its value in rigor, increasing by a factor of 2.38 in the steady state during contraction (Fig. 8). Overall, changes in I_M3 had a time course very similar to that of force (compare Fig. 5B and D). For comparison with the changes observed in the absence of Ca²⁺, the increase in I_M3 was adequately described by a single rate constant of 20.1 ± 2.3 s⁻¹.

The intensity of the M6 meridional reflection (I_M6) at ∼(7.2 nm)⁻¹ was too weak to measure during force development. It was possible, however, to compare I_M6 in rigor before the laser flash and at the plateau of contraction after adding the X-ray diffraction patterns obtained from all fibres subjected to the same protocol (Figs 1 and 8). For the measurement of M6, an integration area 3 times wider than that used for M3 was used, as M6 was broader than M3 in the direction parallel to the equator. When active tension had developed, I_M6 slightly decreased compared with rigor, so that the ratio of the intensities of the M6 and M3 reflection, I_M6/I_M3, also decreased.

The intensity of the layer line in the region of the first myosin and actin layer lines, I_LL1 (see Fig. 1A), decreased rapidly following the photolysis of DMB-caged ATP to 32 % of its pre-flash value, with a rate constant of 79 ± 21 s⁻¹ (Fig. 5E).

Exhaustion of nucleotide was observed in some experiments where recording of the diffraction pattern continued for 6 s after release of ATP (data not shown). Two seconds after photolysis, the intensities of all observed reflections were seen to begin to return towards their rigor values. At 6 s, the values for I_1,1, I_1,0 and I_M1 were 0.85, 1.1 and 2.84 of the values prior to photolysis, still far from the values for the rigor end-point.

Response to the first laser flash only

The X-ray diffraction patterns obtained from 18 fibres subjected to a first near-UV laser flash were added, and the time courses of the main reflections were calculated. The rate constant for the decrease in I_1,1 was 234 s⁻¹ with I_1,1 decreasing to 74.5 % of its rigor value. The rate constant for I_1,0 was 120 s⁻¹ with I_1,0 increasing to 126 % of the rigor value. I_M3 increased to 450 % of its rigor value in a monotonic process described by two exponential rate constants of 23.2 and 1.73 s⁻¹ of approximately equal amplitude, or a single exponential rate constant of 20.3 s⁻¹ which was close to the value found when the data from all flashes were fitted by a single process. The initial drop in I_M3 (Fig. 5D) was not seen here, probably because of the lower photon count. All processes began to return slowly towards their rigor values 2 s after the light flash.

The changes in I_1,1 and I_1,0 following the first flashes occurred with the same rate constants as those calculated from the average of several flashes, suggesting that the amplitude and time course of the equatorial structural changes may not be as affected by flash damage as that of tension. The width and position of the (1,1), (1,0) and M3 reflections were determined by fitting a Gaussian to the summed data. No change in the width of these reflections was detectable (Fig. 8 for M3). The position of M3 did not change following photolysis (Fig. 8), but the position of (1,0), and more noticeably that of (1,1), was seen to change from a reciprocal spacing of (21.64 nm)⁻¹ with a time course similar to that of tension in the direction of lattice shrinkage, to (21.32 nm)⁻¹, 0.51 s after the photolytic release of ATP.

Changes in I_LL1 were not analysed for first flashes as the total number of photons collected in single flash experiments did not allow discrimination of the time course of intensity change above the photon noise.

The time course of structural changes following photolytic release of 0.33 mM ATP in the presence of Ca²⁺

The time courses of the intensities of the X-ray reflections collected from 54 experiments are shown in Fig. 6. The initial time courses (the first 200 ms) were indistinguishable from those observed following photolysis of 10 mM DMB-caged ATP, but a return towards the values in rigor was seen in all processes. Force reached a peak 0.54 s after photolysis, but the return towards rigor was already noticeable after 0.2 s in most diffraction signals, whilst tension was still rising. The data were fitted with two exponential processes, one describing the rapid immediate changes following photolysis of DMB-caged ATP, which occurred in the same direction as the processes observed following photolysis of 10 mM DMB-caged ATP, and a second process, in the opposite direction, indicating exhaustion of ATP and return towards the rigor state (Table 4). The largest changes in intensity, before the beginning of the return to rigor, had approximately the same amplitudes and rate constants (k₁) as those seen following photolysis of 10 mM DMB-caged ATP. The second rate constants (k_rigor) for each process were approximately equal (mean of 0.76 s⁻¹) and appeared to accompany the decline in force, even though the rate constant describing the decrease in force towards rigor had a value of 0.33 s⁻¹ (Table 2).

Table 4.

Main changes in the X-ray diffraction pattern following the photolytic release of ATP from 2 mm DMB-caged ATP

	k1(s−1)	krigor(s−1)	Maximum change in amplitude relative to that in rigor
+Ca2+
I1,1	152 ± 22	0.86 ± 0.22	0.76
I1,0	732 ± 320	0.78 ± 0.28	1.15
IM3	24.0 ± 2.1	0.73 ± 0.23	13
ILL1	197 ± 56	0.67 ± 0.26	0.31

The variables k₁ and k_rigor refer to the rate constants describing two exponential components fitted to the time courses. k₁ describes the initial changes, whereas k_rigor describes the subsequent and slower return towards the rigor state which accompanies exhaustion of ATP. The data are shown ± 1 s.e.m., obtained by the algorithm of Provencher (1976).

DISCUSSION

Two vs. 10 mM DMB-caged ATP and binding of caged compounds

The structural processes observed here are not controlled by the rate of ATP appearance from DMB-caged ATP, as this is much faster than the fastest process reliably measured here (208 s⁻¹ for the decrease in I_1,1 following photolysis in the presence of Ca²⁺; Table 3). The rate of I_1,1 decrease corresponds to a second order binding constant for ATP of 2 × 10⁵ M⁻¹ s⁻¹ at 5–6°C, considering that photolysis of 10 mM DMB-caged ATP results in the appearance of 1.1 mM ATP. In experiments with 2 mM DMB-caged ATP, photolysis results in the appearance of ∼0.33 mM ATP and the rate of I_1,1 decrease corresponds to a second order binding constant for ATP of 4.6 × 10⁵ M⁻¹ s⁻¹, close to the values reported by Ma & Taylor (1994). The rate of ATP binding should be reduced by a factor of three compared with that when 1.1 mM ATP is released. However, the rate of decrease of I_1,1 was hardly affected, suggesting that processes other than ATP binding may limit the rate of structural change; this is discussed below.

At 20°C, the apparent K_m for ATP binding to rabbit muscle fibres was found to increase from 170 to 470 μM by the addition of 2 mM NPE-caged ATP, corresponding to competitive inhibition of ATP binding by caged ATP with an apparent K_i of 1–2 mM (Thirlwell et al. 1995). A similar inhibition was found with DMB-caged ATP. Assuming that such binding is similar in frog muscle fibres at 6°C as it is in rabbit muscle fibres at 20°C, in the presence of 10 mM DMB-caged ATP, the myosin sites will be largely occupied by DMB-caged ATP prior to photolysis. Even in the presence of 2 mM DMB-caged ATP, half of the ATP binding sites on myosin may be occupied by DMB-caged ATP. The lack of a difference in the rate constants observed in experiments carried out with 2 or 10 mM DMB-caged ATP may therefore be because dissociation of DMB-caged ATP limits ATP binding. Alternatively, ATP binding to the cross-bridges is faster than a slower process which gives rise to the structural changes. A combination of these effects should also be considered.

Isometric force following photolysis of DMB-caged ATP in the presence of Ca²⁺

Photolysis of 2 mM DMB-caged ATP in the presence of Ca²⁺ caused tension to rise higher than by photolysis of 10 mM DMB-caged ATP (167 vs. 117 kN m⁻²). Such an effect of ATP concentration on isometric force was reported previously in permeabilised muscle fibres of the frog at 0–5°C (Ferenczi et al. 1984), although the force enhancement observed here is somewhat more marked. Force enhancement is probably caused by the longer life-time of attached, force-generating states obtained at low ATP concentrations. The larger difference observed here may stem from the absence of an ATP-regenerating enzyme system, and hence from ADP accumulation. The amplitude of the initial changes in I_1,1 from the rigor value is smaller following photolysis of 2 mM DMB-caged ATP than that following photolysis of 10 mM (24 vs. 32 %), suggesting that the higher force observed at the low ATP concentration is caused by a higher fraction of attached cross-bridges, as may be caused by an enhancement of strongly bound (rigor-like) cross-bridges at the expense of detached or weakly bound ones, as would be the case if the life-time of A.M.ADP states was prolonged in the presence of a relatively low concentration of ATP and high concentration of ADP. The appearance of rigor-like features (namely an increase in I_1,1 and I_LL1 and a decrease in I_1,0) during the slow tension rise following photolysis of 2 mM DMB-caged ATP can be seen in the diffraction pattern (Fig. 6C and E). The time courses of the initial decrease in force and that of the subsequent fast component of tension rise are similar, whether resulting from the photolytic release of 0.33 or 1.1 mM ATP (Tables 1 and 2). The slow component of tension rise appears to be faster following photolytic release of 0.33 mM ATP compared with 1.1 mM ATP, but this may result from truncation of the final tension rise by the subsequent decrease in force brought about by exhaustion of ATP.

Comparison with other results

Absence of Ca²⁺

In the absence of Ca²⁺, the decrease in I_1,1 following the photolytic release of ATP was described by a predominant rate constant of 94 s⁻¹ (t_½ = 7.4 ms) and a slower minor process of 6.2 s⁻¹, in line with previous measurements (Brenner et al. 1989). Overall, I_1,1 in the relaxed fibres was 36 % of its value in rigor, whereas in similar fibres in the steady state, I_1,1 in relaxed fibres was found to be 20 % of the intensity in rigor at the same temperature (Bershitsky et al. 1996). The changes observed here are not as pronounced as those seen in steady-state conditions, and may be a consequence of the presence of caged ATP in the solution, which may bind to the rigor cross-bridges (Thirlwell et al. 1995) and attenuate the rigor features in the diffraction pattern. The decay in I_1,1 is similar to that described for rabbit psoas muscle (Poole et al. 1988, 1991, at 11°C) and rat psoas muscle (Yagi et al. 1998, at 15°C; Horiuti et al. 1994, at 24°C), where a fast component with t_½ < 5 ms was observed. The change in I_1,0 is more difficult to measure than that in I_1,1. I_1,0 increases 1.65-fold in a process somewhat slower than that for I_1,1, as observed previously for rat psoas muscle (Horiuti et al. 1994; Yagi et al. 1998). The overall increase in I_1,0 is smaller than that observed in the steady state in a similar preparation (Bershitsky et al. 1996), where I_1,0 in the relaxed pattern was 2.85 times brighter than in the rigor state. This difference may be caused by some enhancement of I_1,0 in rigor by the presence of caged ATP. The rate constant describing the change in I_1,0 is similar to that of the change in muscle fibre stiffness (Fig. 3), so that it may provide a measure of cross-bridge detachment from actin.

The change in I_M3 appears to accompany the time course of force relaxation, increasing from a near-zero value with an approximate rate constant of 60 s⁻¹. Yagi et al. (1998) found a small increase in intensity in rat psoas and soleus muscle, but found that, in soleus muscle, the intensity of the reflection decreased marginally. This may be because the M3 reflection is particularly fragile, and force generation during rigorisation causes irreversible loss of intensity. As shown in Fig. 8, the change in intensity of this reflection is much less during relaxation than during activation.

I_LL1 decreases rapidly to 23 % of its value in rigor, in a process at least as fast as that for the change in I_1,1, as reported for rat soleus and psoas muscle (Yagi et al. 1998) at the higher temperature of 15°C.

The stiffness and structural changes observed following photolytic release of ATP indicate a rapid phase of cross-bridge detachment upon nucleotide binding, which is responsible for the rapid changes in intensity of the equatorial and layer-line reflections. This rapid phase is followed by a slower phase of net cross-bridge detachment, which is shown by the decrease in force and by the increase in I_M3. This slower phase may be characterised by the presence of a population of cross-bridges which transiently reattach to the thin filaments, although the presence of BDM and P_i probably prevents reattachment.

Presence of Ca²⁺

In the presence of Ca²⁺, photolytic release of 1.1 mM ATP causes I_1,1 to decrease exponentially by 32 % of its rigor value with a rate constant of 208 s⁻¹. As pointed out by Yagi et al. (1998), the slow component in the time course they observed may result from the use of fibre bundles, thus suffering from the disordering effect sometimes seen with bundles, but which is avoided by using single fibres. The half-time for the change in I_1,1 for frog muscle fibres (∼3 ms) is similar to that in mammalian muscle at higher temperature (Poole et al. 1991; Horiuti et al. 1994). The change in I_1,1 is complete during the initial drop in force, and no further change is seen during active force generation (Fig. 5). I_1,0 increases by 17 % from its rigor value with a rate constant of 122 s⁻¹. Again the changes in I_1,0 are complete by the time tension begins to rise, and, as in the case of experiments in the absence of Ca²⁺, may indicate cross-bridge detachment from actin. Similar processes are observed following photolysis of 2 mM DMB-caged ATP (Table 4).

The rate constants describing the changes in I_1,1 and I_1,0 appear considerably faster for experiments in the presence of Ca²⁺ than the rate constants measured during the relaxation phase following photolytic release of ATP in the absence of Ca²⁺. This discrepancy is a consequence of the differences in amplitude of the changes in equatorial intensities measured in the presence and absence of Ca²⁺. After normalisation (Fig. 7), the changes in I_1,1 coincide for the first 10 ms. At this time, the decreases in intensity have reached 68 and 72 % of their initial value in the absence and presence of Ca²⁺, respectively. After 10 ms, the time courses diverge. In the absence of Ca²⁺ the intensity continues to decrease to 36 % of the initial value, whereas by that time, in the presence of Ca²⁺, the intensity is close to its final value, 68 % of the initial intensity. The coincidence of the time course of the changes in the equatorial intensities suggests that the initial process corresponds to cross-bridge detachment, which, in the case of experiments in the presence of Ca²⁺, is interrupted by reattachment. The change in I_1,1 measured in the absence of Ca²⁺ goes to completion, so that the rate constant of 94 s⁻¹ (Table 3) provides a reasonable estimate for cross-bridge detachment.

I_M3 was found to increase 2.38-fold with tension (Fig. 8B), as was observed previously in the steady state in an identical preparation (Bershitsky et al. 1996), where I_M3 was found to be 2.65 times brighter during contraction than in rigor. The attenuation of rigor I_M3 with time in the current experiments, where flash photolysis caused progressive deterioration of the meridional pattern, explains why the increase in I_M3 calculated from the response to the first laser flashes only is higher, showing a 4.5-fold increase in intensity. In mammalian muscle, the amplitude of the change was smaller (Yagi et al. 1998), reflecting a poorer meridional order during contraction in mammalian muscle preparations. The time course of I_M3 was described adequately by a single rate constant of 20 s⁻¹ (t_½ = 34 ms), similar to the time course observed in rabbit psoas muscle at 15°C (Yagi et al. 1998; see also Poole et al. 1991) and similar to the fast component of tension rise (20 s⁻¹; t_½ = 35 ms; Table 1). However, an initial decrease in I_M3 upon photolytic release of ATP is detected, which matches the initial drop in force (Fig. 5). This feature was not reported previously because of the lack of time resolution in the measurements. Describing the time course of I_M3 changes by a double exponential process to account for the initial fall in I_M3 gives a rate constant for the subsequent rise in intensity of 29 s⁻¹ (Table 3).

The change in I_LL1 is also fast; the data are too noisy to assign a rate constant to this process, but are comparable with those obtained with rat muscle at 15°C (Yagi et al. 1998).

Interpretation of the results

The most noteworthy observations resulting from this work are that the rigor structure disappears quickly upon photolytic release of ATP, with no further discernible changes on the equator or on the layer line intensities 30 ms after photolysis. In the presence of Ca²⁺, these changes are complete before tension begins to rise, and the only structural changes still to be seen beyond 30 ms are the changes in I_M3. The changes on the equator and layer line suggest that the number of attached cross-bridges changes rapidly following photoliberation of ATP, but that the change during force development is rather small. The increase in stiffness from ∼65 to ∼80 % of the rigor value seen in Fig. 3B is probably an overestimation because of the difficulty in maintaining reliable sarcomere signals throughout the protocol. Force development per se is not reflected in changes on the equator, although force development is accompanied by structural changes as shown by the large increase in I_M3. It has been suggested (Harford & Squire, 1992; Brenner & Yu, 1993; Bershitsky et al. 1997; Tregear et al. 1998; Tsaturyan et al. 1999) that force generation is caused by a redistribution of weakly, non-stereospecifically attached cross-bridges to strongly, stereospecifically bound cross-bridges. This interpretation is consistent with the hypothesis that the weakly bound cross-bridges contribute to stiffness as much as the strongly bound cross-bridges (Bershitsky et al. 1997).

In the experiments shown here, the photolytic appearance of ATP is instantaneous when compared with the time course of tension and X-ray diffraction changes. The limiting factors controlling the time course of equatorial changes are likely to be the rate constants for ATP binding to the cross-bridges and for their subsequent detachment. The experiments show that the changes in I_1,1 are faster and larger than those in I_1,0.

The value for I_LL1 was found to be higher at the end of the protocol in the presence of Ca²⁺, compared with the value in the absence of Ca²⁺ (0.32 vs. 0.23 of the rigor value; Table 3). At 5°C, I_LL1 was 12 % of the rigor value during maximal activation of frog muscle fibres (Tsaturyan et al. 1999). In temperature jump experiments, the first actin layer line (A1) was found to increase with temperature (Bershitsky et al. 1997; Tsaturyan et al. 1999). This was interpreted as providing a measure of the fraction of strongly bound cross-bridges. The difference in I_LL1 observed here in the absence and presence of Ca²⁺ indicates that more cross-bridges are attached in the presence of Ca²⁺ and is compatible with the view that I_LL1 is dependent on the fraction of strongly attached cross-bridges.

In the presence of Ca²⁺, the time course of the changes in I_M3 is much slower than that of the equatorial changes, and is described by a rate constant similar to that of the fast component of tension rise. In the absence of Ca²⁺, the time course of the change in I_M3 was comparable to the fast component of tension drop, suggesting a close correlation between force and I_M3.

The M3 intensity depends on several factors such as the number of myosin heads that are ordered with the 14.5 nm axial repeat and the deviation of their axial positions from this repeat. When the deviation increases, I_M3 decreases. The effect of the deviation can be estimated by looking at the higher orders of the myosin reflections, as their intensities are more sensitive to the deviation than I_M3. Although in our experiments the intensity of the M6 meridional reflection was too low to measure during force development, we were able to estimate I_M6 in rigor before the laser flash and at the plateau of contraction and found that I_M6 does not scale with I_M3, but decreases when the fibre is activated from rigor by photolytic release of ATP. Assuming that the M6 meridional reflection arises from the same population of myosin heads as the M3 reflection, the observed change in I_M6/I_M3 suggests that no increase in axial order occurs during force development. Therefore the increase in I_M3 during activation cannot be accounted for by a reattachment of myosin heads resulting in better preservation of the 14.5 nm repeat.

The orientation of myosin heads with respect to the filament axis also affects I_M3. When the heads or their light chain domains become more perpendicular to the filament axis, I_M3 increases. It was suggested that in contracting muscle the light chain domains are more perpendicular to the filament axis than in rigor and that this difference in tilt is responsible for the increase in I_M3 when muscle fibres contract (Dobbie et al. 1998). Our data showing an increase in I_M3 when fibres are activated from rigor are consistent with this interpretation.

One more factor which affects I_M3 is the axial disorder of neighbouring myosin filaments, as this determines the volumes of coherent diffraction within a sarcomere (Huxley et al. 1982). When the disorder increases, the width of the M3 reflection along the equator increases and I_M3 decreases (Huxley et al. 1982). In rigor the M3 reflection is sharp suggesting high axial order of the filament lattice while during contraction its equatorial width increases (Fig. 1). The increase in axial disorder results from force generation and is not avoided by the cross-linking procedure used here. However, we show that I_M3 increases during contraction in spite of this disordering, suggesting that the myosin heads are most probably more perpendicular to the filament axis during contraction than in rigor.