Identification of fast and slow ventilatory responses to carbon dioxide under hypoxic and hyperoxic conditions in humans

Abstract

1. Under conditions of both euoxia and hypoxia, it is generally accepted that the ventilatory response to CO₂ has both rapid (peripheral chemoreflex) and slow (central chemoreflex) components. However, under conditions of hyperoxia, it is unclear in humans whether the fast component is completely abolished or merely attenuated in magnitude.

2. The present study develops a technique to determine whether or not a two-compartment model fits the ventilatory response to CO₂ significantly better than a one-compartment model. Data were collected under both hypoxic (end-tidal P_O2= 50 Torr) conditions, when two components would be expected, and under hyperoxic (end-tidal P_O2= 200 Torr) conditions, when the presence of the fast compartment is under question.

3. Ten subjects were recruited, of whom nine completed the study. The end-tidal P_CO2 of each subject was varied according to a multi-frequency binary sequence that involved 13 steps into and 13 steps out of hypercapnia lasting altogether 1408 s.

4. In four out of nine subjects in hypoxia, and six out of nine subjects in hyperoxia, the two-compartment model fitted the data significantly better than the one-compartment model (F ratio test on residuals). This improvement in fit was significant for the pooled data in both hypoxia (P < 0·05) and hyperoxia (P < 0·005). Mean ventilatory sensitivities for the central chemoreflex were (mean ± s.e.m.) 1·69 ± 0·39 l min⁻¹ Torr⁻¹ in hypoxia and 2·00 ± 0·32 l min⁻¹ Torr⁻¹ in hyperoxia. Mean ventilatory sensitivities for the peripheral chemoreflex were 2·42 ± 0·36 l min⁻¹ Torr⁻¹ in hypoxia and 0·75 ± 0·16 l min⁻¹ Torr⁻¹ in hyperoxia.

5. It is concluded that the rapid and slow components of the ventilatory response to CO₂ can be separately identified, and that a rapid component persists under conditions of hyperoxia.

It is generally recognised that carbon dioxide stimulates ventilation (V̇_E) through both rapidly responding peripheral and more slowly responding central chemoreceptors. It is also well recognised that the background level of oxygen affects the magnitude of the peripheral component such that there is a greater peripheral sensitivity to CO₂ under conditions of hypoxia. Under conditions of hyperoxia in anaesthetised cats, there is direct evidence both that the carotid body exhibits a residual sensitivity to hypercapnia (Fitzgerald & Parks, 1971; Lahiri & DeLaney, 1975) and that there is a residual reflex ventilatory response to CO₂ at the carotid body (van Beek et al. 1983). In humans, however, experimental approaches are necessarily more indirect, and there remains uncertainty as to whether the peripheral response to carbon dioxide is completely abolished by hyperoxia or merely attenuated in magnitude.

One approach to the problem in humans has been based around the idea that the peripheral chemoreflex has a shorter latency of response to change in alveolar gas composition than the central chemoreflex. In a study of rapid withdrawal of CO₂ in hyperoxia, Miller et al. (1974) failed to detect any effect on V̇_E with a latency appropriate to the peripheral chemoreceptors, although such an effect was clearly present during rapid withdrawal of CO₂ under hypoxic conditions. However, Dahan et al. (1990) have argued that this result might be expected on statistical grounds, even if there were residual peripheral chemoreflex sensitivity to CO₂ under hyperoxic conditions.

Another approach in humans has been based around the notion that the peripheral and central chemoreflex contributions may be separable on the basis of the differing speeds of response of the two reflexes. The idea is that, following a step change in end-tidal P_CO2 (P_ET,CO2), there is a rapid component of the response that is associated with the peripheral chemoreflex and a slow component that is associated with the central chemoreflex. The validity of this dynamic approach is supported by the following two observations. First, in the anaesthetised cat, DeGoede et al. (1985) have shown that the magnitudes of the fast and slow components of the ventilatory response to step changes in P_ET,CO2 correspond with more direct measurements of peripheral and central chemoreflex sensitivity obtained using an artificial brainstem perfusion technique. Second, in humans who had undergone carotid body resection, Bellville et al. (1979) found very low values for the sensitivity to CO₂ of the rapid component that were not significantly different from zero.

Under conditions of both euoxia and hypoxia in intact subjects, the dynamic approach has led to reported values for both rapid (peripheral) and slow (central) chemoreflex sensitivities (Swanson & Bellville, 1975; Bellville et al. 1979; Gardner, 1980; Dahan et al. 1990). Under conditions of hyperoxia, Gardner (1980) considered that the ventilatory response to a step change in P_ET,CO2 was adequately described by a single component. On the other hand, Dahan et al. (1990) observed a rapid component in the ventilatory response in some, but not all, of their subjects.

There are, however, a number of technical limitations in all the above studies of the dynamics of the ventilatory response to CO₂ in humans. First, none of the studies has actually shown that a two-compartment model fits the data significantly better than a single compartment model. Thus, although there are good physiological reasons for believing that the response has two components (at least in euoxia/hypoxia), it has not been shown that the components are separately identifiable in practice. Secondly, for use in system identification, a stimulus should be persistently exciting (Godfrey, 1993). In the above studies, V̇_E was typically examined following a single step increase and decrease in P_ET,CO2 in an overall experimental period of 15–20 min. Assuming a peripheral time constant of 15 s (Cunningham et al. 1986), the peripheral response would be 95% complete within 45 s of the step. Thus the peripheral response effectively would be varying for at most 1·5 min of the 15–20 min period of study. This is a very limited amount of data from which to identify the peripheral chemoreflex component.

The present study seeks to examine the ventilatory responses to CO₂ under conditions of both hypoxia and hyperoxia in a manner that addresses the technical concerns raised above. Firstly, rather than using a single step increase and then decrease in P_ET,CO2 as the input function, the study uses a multi-frequency binary sequence in P_ET,CO2 that was devised specifically to spread its power over the frequency range of interest for identification of both peripheral and central chemoreflex responses. Secondly, the study specifically examines whether a two-compartment model can be shown statistically to provide a better fit to the data than a single compartment model. As it is already well accepted that there are two components to the ventilatory response to CO₂ in hypoxia, the data collected under hypoxic conditions really provide a test of the method when two components are known to be present. The data gathered under hyperoxic conditions are used to examine whether the rapid (peripheral) component of the CO₂ response is completely abolished or merely reduced in magnitude.

METHODS

Subjects

Ten healthy young adults were studied (4 females and 6 males aged 20–27 years). One of the subjects did not complete the study because he felt uncomfortable with the high levels of ventilation during hypoxic hypercapnia. All subjects received written and verbal descriptions of the experiment before they gave their consent. The study had been approved by the Central Oxford Research Ethics Committee.

Protocols

Each subject rested for half an hour after arriving in the laboratory. Their natural P_ET,CO2 was then determined using a nasal catheter connected to a mass spectrometer whilst the subjects were distracted by watching television. This P_ET,CO2 was used to decide the actual level of the P_ET,CO2 stimuli to be used on that day.

Before the main experiments were undertaken, each subject came into the laboratory for a preliminary test. This involved three step increases in P_ET,CO2 (+1·5, +5·0 and +8·5 Torr) with 8 min spent at each level, the first 6 min at an end-tidal P_O2 (P_ET,O2) of 100 Torr and the following 2 min at P_ET,O2 of 50 Torr. The data from this test enabled us to calculate values for the constants of the Lloyd-Cunningham equation (Lloyd et al. 1958) for each subject. These constants were used in the prediction of the inspired P_CO2 and P_O2 required to generate the desired P_ET,CO2 and P_ET,O2 forcing functions (see below).

There were two main protocols. Each subject undertook both on the same day in random order with a break of at least 1 h between them. The two protocols differed only in respect of the P_ET,O2. One protocol (hypoxic protocol) was carried out at a P_ET,O2 of 50 Torr apart from the first 5 min which was undertaken at a P_ET,O2 of 100 Torr, and the other protocol (hyperoxic protocol) was carried out at a P_ET,O2 of 200 Torr. Both protocols were 44 min long. In each protocol, P_ET,CO2 was held constant at 1·5-2·0 Torr above its normal value for the first 20 min. The purpose of this period was, in the hypoxic protocol, to allow time for hypoxic ventilatory decline to develop prior to investigating the responses to CO₂. This 20 min period was followed by a 1408 s (23 min and 28 s) period during which P_ET,CO2 followed a multi-frequency binary sequence (MFBS). The particular MFBS used (Fig. 1) covered six harmonics and was the Van den Bos Octave (Godfrey, 1993). The pulse duration was chosen at 11 s, and had been optimised along with the choice of MFBS for estimation of peripheral and central chemoreflex sensitivities (see Appendix). The two levels between which P_ET,CO2 alternated in the MFBS were 1·5-2·0 Torr and 10·0 Torr above the subjects’ normal level.

Figure 1.

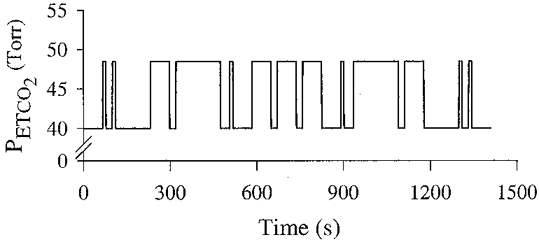
End-tidal P_CO2 in the design of a multi-frequency binary sequence.

Experimental technique

During the experimental protocols, subjects sat in a chair and breathed through a mouthpiece with their nose occluded. Respiratory volumes were sensed using a bi-directional turbine-measuring device (Howson et al. 1986) and respiratory phase transitions were detected using a pneumotachograph. Respired gas was sampled continuously at the mouth and analysed by mass spectrometry.

The MFBS in P_ET,CO2 was generated using an end-tidal forcing system that also regulated P_ET,O2. This system has been described in greater detail elsewhere (Robbins et al. 1982; Howson et al. 1987). In brief, the time profiles for inspiratory P_CO2 and P_O2 that were likely to produce the desired sequence in P_ET,CO2 and P_ET,O2 were predicted before the experiment started using a physiological model. In the present study, subject-specific constants for the Lloyd-Cunningham equation (Lloyd et al. 1958) were used to improve the quality of this prediction. Then, once the experiment began, a computer-controlled gas-mixing system started to generate this time profile for P_CO2 and P_O2. During the course of the experiment, the actual values for P_ET,CO2 and P_ET,O2 were fed back to this computer breath by breath. These were compared with the desired P_ET,CO2 and P_ET,O2, and the actual inspiratory gas profile was then adjusted breath by breath in order to force the P_ET,CO2 and P_ET,O2 towards the desired values.

Modelling and data analysis

Deterministic models

In order to determine whether both fast and slow components could be identified in the ventilatory response to P_ET,CO2, both a single and a two-compartment model were fitted to the data. Both models were based on that of Bellville et al. (1979). The simple model, describing only central chemoreflex parameters (Model 1) is given by:

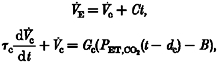where V̇_c is the output of the central chemoreflex, G_c is the central chemoreflex sensitivity and τ_c is the central chemoreflex time constant. P_ET,CO2(t - d_c) is the stimulus to the central chemoreflex loop at time t delayed by the central transport delay time, d_c, and B is a bias term equivalent to the P_ET,CO2 for which V̇_c= 0. C is a trend term.

Assuming that P_ET,CO2 remains constant throughout a single breath, this differential equation can be solved to provide a set of difference equations:

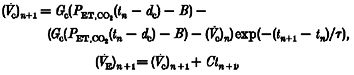where t_n is the time of the nth breath.

The two-compartment model, which describes both central and peripheral chemoreflexes (Model 2) is given by:

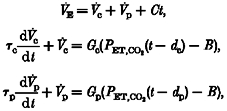where V̇_p is the output of the peripheral chemoreflex, G_p is the peripheral chemoreflex sensitivity, τ_p is the peripheral chemoreflex time constant and d_p is the peripheral transport delay time.

Again, assuming P_ET,CO2 remains constant over a single breath, these differential equations can be solved to provide the following difference equations:

Noise models

The two deterministic models were fitted both without and with a parallel noise model that was used to describe the correlation that exists between successive breaths. The particular noise model employed was the state-space model of Liang et al. (1996):

where x(n) is the system state for breath n, y(n) is the observation at breath n and f is the system gain. v(n) and w(n) are mutually independent, white noise sequences, representing the process and the measurement noise, respectively, with means of zero and a constant variance ratio of R_v/R_w. In this model of the noise process, provided f, R_v and R_w are known, the system state (and variance) for breath n+ 1 can be predicted from the measurement y(n) through a Kalman filter (Anderson & Moore, 1979), and updated once y(n+ 1) becomes known. In our study the parameters of the Kalman filter were to be estimated, but in the case of scalar observations, R_v and R_w cannot be separately identified. Consequently, for this case the standard Kalman filter equations needed to be modified to work with the parameters f and R_v/R_w (Liang et al. 1996).

Minimisation process

The data used to fit the model were the breaths associated with the MFBS. However, solutions to the difference equations using the actual experimental input functions were started 2 min prior to the start of the MFBS in order to allow time for any start-up transients in the predictions to die away. The process of fitting the models to the data was undertaken using a standard subroutine for minimising a sum of squared residuals (subroutine E04FDF, Numerical Algorithms Group, Oxford, UK). In the case of the models that did not contain the noise model, the objective function was given by:

where V̇_E,meas denotes the measured value and V̇_E,det the predicted value from the deterministic model.

In the case of models that did contain the noise model, the objective function to be minimised contained both predicted output from the deterministic model and the prediction of the system state from the noise model. This objective function is given by:

where x∧(n|n - 1)is the predicted system state at n, given values to breath n - 1. In all fits, all parameters were constrained to be positive.

Statistical analysis

The purpose of the noise model was to describe the autocorrelation that remains between the residuals after the response to the input function has been described by the deterministic model. Thus, for fits that included the noise model, the residuals should be white. In order to test the whiteness of residuals (i.e. whether the models describe the correlation within the data sequences satisfactorily) we employed the ‘Portmanteau’ test introduced by Box & Jenkins (1976) for autoregressive moving average models, where the test statistic (Q) is defined as:

where n is the number of observations,_k is the estimated autocorrelation value for the sequence of residuals with lag k, K is an integer, the exact choice of which is arbitrary (we used 12), and p and q are the numbers of autoregressive and moving average coefficients, respectively. Our model of the noise processes is given in state-space form, rather than as an autoregressive moving average process, but it can be shown that this state-space form will reduce to an autoregressive moving average process in which p=q= 1 (Liang et al. 1996). This test statistic was computed for both fits to individual data sets, and for overall combinations of data where the values of _k were calculated as the mean of the values of _k for the individual data sets weighted by the number of breaths.

The variance ratio test (F ratio test) was used to compare the goodness of fit between the two models. This test indicates whether, after allowing for the difference in the number of parameters between the models, the larger model still provides a statistically significant improvement in the fit to a common data sequence, compared with the smaller model. The F statistic was calculated as follows (Armitage & Berry, 1987):

where RSS₁ and df₁ refer to the residual sum of squares and degrees of freedom of the smaller model, and RSS₂ and df₂ refer to the residual sum of squares and degrees of freedom of the larger model. An important assumption in the F ratio test is that the residuals are uncorrelated. Thus, this test statistic can only be applied to the residuals from the fits that include the model of the noise processes, where the residuals should be either white or close to white.

RESULTS

An example of the results for one subject is shown for hyperoxic data in Fig. 2 and for hypoxic data in Fig. 3. Individual parameter estimates for Model 1 are shown in Table 1 (hyperoxic data) and Table 2 (hypoxic data). Individual parameter estimates for Model 2 are shown in Table 3 (hyperoxic data) and in Table 4 (hypoxic data).

Figure 2.

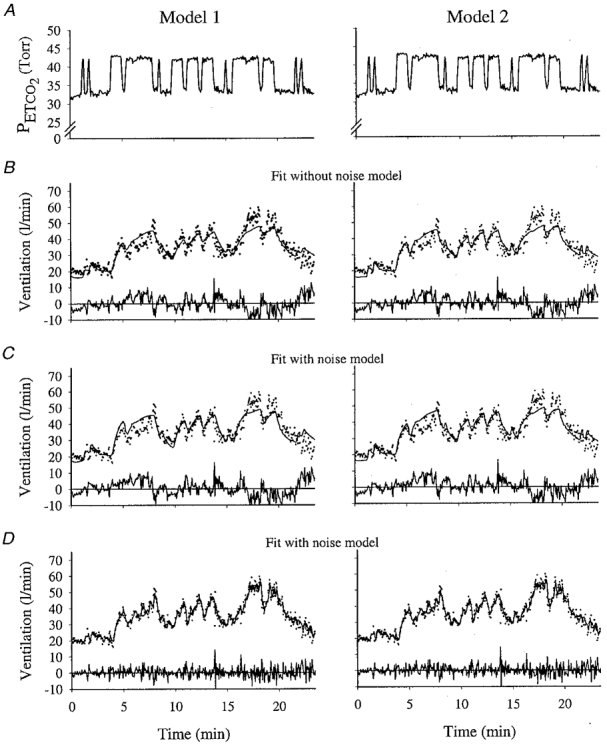
Example of model fits to hyperoxic data for Model 1 and Model 2 for one subject

A, end-tidal P_CO2. B, the fitted output from the model that does not contain a noise model. C, fitted output from the model containing a noise model; line shows deterministic component only of the output. D, the fitted output from the model containing a noise model; line shows total output (deterministic + noise). For ventilation, dots indicate data, and lines indicate fitted model output. The residuals are shown below each fit.

Figure 3.

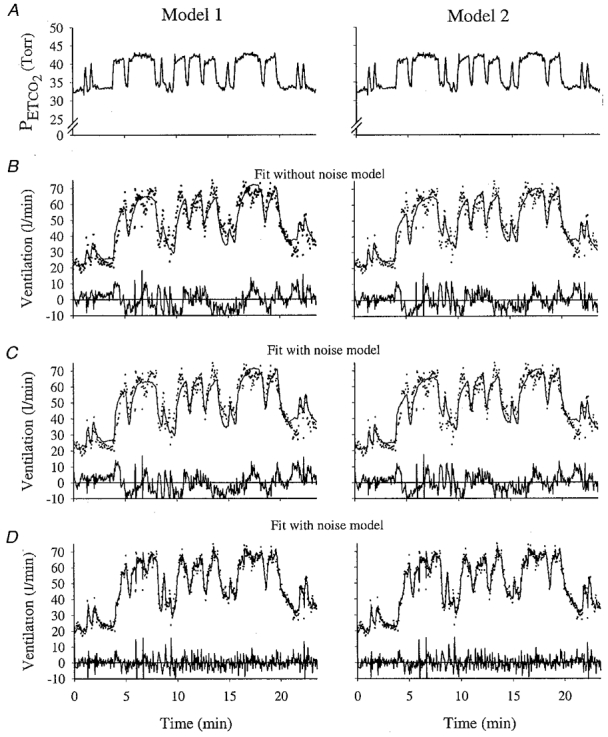
Example of model fits to hypoxic data for Model 1 and Model 2 for one subject

A, end-tidal P_CO2. B, the fitted output from the model that does not contain a noise model. C, fitted output from the model containing a noise model; line shows deterministic component only of the output. D, the fitted output from the model containing a noise model; line shows total output (deterministic + noise). For ventilation, dots indicate data, and lines indicate fitted model output. The residuals are shown below each fit. Same subject as in Fig. 1

Table 1.

Parameter values for the hyperoxic data for Model 1 estimated without and with a noise model

Subject no.	Gc(l min−1 Torr−1)	τc(s)	dc(s)	B(Torr)	C(l min−1 min−1)	f	Rv/Rw	Whiteness
	No noise model
973	3.67	85.0	0.1	32.2	0.228	—	—	NW
974	2.74	59.6	3.5	26.4	0.360	—	—	NW
1003	1.75	89.0	2.9	27.6	0.078	—	—	NW
1004	1.86	31.0	7.9	34.0	0.276	—	—	NW
1023	4.69	38.0	5.6	40.7	0.504	—	—	NW
1069	1.08	40.6	4.1	24.8	0.300	—	—	NW
1091	1.65	31.3	7.7	32.4	0.756	—	—	NW
1093	1.49	54.9	5.0	34.3	0.198	—	—	NW
1103	2.31	42.4	18.9	37.6	0.792	—	—	NW
Mean	2.36	52.4	6.2	32.2	0.390	—	—	NW
s.e.m.	0.39	7.3	1.8	1.7	0.084	—	—	—
	With noise model
973	3.27	55.1	5.4	31.9	0.414	0.93	0.40	W
974	2.49	35.2	5.2	25.2	0.378	0.92	0.66	W
1003	1.74	86.0	2.6	27.3	0.078	0.81	0.21	W
1004	1.86	28.9	8.2	33.8	0.270	0.80	0.41	W
1023	4.44	34.1	7.0	40.1	0.438	0.92	0.84	W
1069	1.06	38.2	3.1	24.1	0.282	0.75	1.34	NW
1091	1.64	30.7	8.5	31.6	0.678	0.91	0.33	W
1093	1.48	43.8	5.8	34.1	0.216	0.77	0.71	W
1103	1.30	27.1	18.9	32.7	0.738	0.97	0.09	W
Mean	2.14	42.1	7.2	31.2	0.390	0.86	0.55	W
s.e.m.	0.36	6.2	1.6	1.7	0.072	0.03	0.13	—

Abbreviations: G_c, central chemoreflex sensitivity; τ_c, central chemoreflex time constant; d_c, central chemoreflex delay; B, bias term equivalent to P_ET,CO2 for which V̇_c= 0; C, trend term; f, system gain for noise component; R_v/R_w, variance ratio for process and measurement noise; Whiteness, result of Portmanteau test on residuals (NW, non-white; W, white).

Table 2.

Parameter values for the hypoxic data for Model 1 estimated without and with a noise model

Subject no.	Gc(l min−1 Torr−1)	τc(s)	dc(s)	B(Torr)	C(l min−1 min−1)	f	Rv/Rw	Whiteness
	No noise model
973	2.85	21.3	3.8	27.3	0.000	—	—	NW
974	4.15	17.7	2.2	27.8	0.612	—	—	NW
1003	1.90	29.2	1.6	28.1	0.324	—	—	NW
1004	3.11	19.9	3.8	40.2	0.288	—	—	NW
1023	7.60	30.2	1.5	41.8	0.000	—	—	NW
1069	2.73	19.3	0.7	32.6	0.024	—	—	NW
1091	3.70	10.9	2.6	32.5	0.000	—	—	NW
1093	1.39	25.9	3.5	29.2	0.000	—	—	NW
1103	6.45	36.2	0.9	37.2	0.000	—	—	NW
Mean	3.76	23.4	2.3	33.0	0.138	—	—	NW
s.e.m.	0.68	2.6	0.4	1.8	0.072	—	—	—
	With noise model
973	3.16	23.5	2.9	28.9	0.000	0.94	0.26	W
974	3.81	11.3	4.5	27.1	0.702	0.87	1.37	W
1003	1.89	22.3	2.8	28.1	0.342	0.90	0.06	W
1004	2.96	15.2	4.1	39.3	0.204	0.95	0.27	W
1023	6.75	24.4	3.2	41.0	0.000	0.95	0.22	NW
1069	2.65	17.3	1.9	32.2	0.036	0.83	0.52	W
1091	3.80	14.6	1.8	26.0	0.000	1.00	0.27	NW
1093	1.47	24.5	4.3	29.8	0.000	0.49	7.59	NW
1103	5.61	24.9	3.5	36.5	0.096	0.95	0.07	NW
Mean	3.57	19.8	3.2	32.1	0.156	0.88	1.80	W
s.e.m.	0.57	1.7	0.3	1.8	0.078	0.05	0.81	—

Abbreviations as in Table 1.

Table 3.

Parameter values for the hyperoxic data for Model 2 estimated without and with a noise model

Subject no.	Gp(l min−1 Torr−1)	τp(s)	dp(s)	Gc(l min−1 Torr−1)	τc(s)	dc(s)	B(Torr)	C(l min−1 Torr−1)	f	Rv/Rw	Whiteness	F ratio
	No noise model
973	1.57	18.4	5.8	2.95	206.2	19.9	33.2	0.000	—	—	NW	—
974	0.83	5.9	7.2	2.17	87.9	15.8	27.1	0.300	—	—	NW	—
1003	0.68	29.6	2.5	1.32	163.3	18.3	28.8	0.000	—	—	NW	—
1004	1.37	16.5	10.3	1.25	276.4	19.4	36.2	0.042	—	—	NW	—
1023	0.08	13.7	2.3	4.60	39.3	5.44	40.7	0.498	—	—	NW	—
1069	0.67	17.5	6.1	1.20	287.5	19.8	30.1	0.066	—	—	NW	—
1091	0.25	30.0	8.4	1.39	30.8	8.4	32.3	0.756	—	—	NW	—
1093	0.28	1.2	8.6	1.27	64.5	13.5	34.6	0.186	—	—	NW	—
1103	0.53	5.5	5.3	2.45	60.6	19.1	38.3	0.648	—	—	NW	—
Mean	0.70	15.4	6.3	2.07	135.2	15.5	33.5	0.276	—	—	NW	—
s.e.m.	0.34	3.4	0.9	0.38	33.7	1.8	1.5	0.096	—	—	—	—
	With noise model
973	1.65	22.6	6.2	2.98	218.2	19.9	33.4	0.000	0.90	0.44	W	P < 0.05
974	0.87	6.4	6.7	2.19	80.1	15.3	27.0	0.264	0.91	0.65	W	P < 0.05
1003	0.64	20.5	3.5	1.41	164.0	20.0	29.1	0.000	0.78	0.26	W	n.s.
1004	1.40	17.7	9.2	1.16	229.3	19.8	36.1	0.072	0.71	0.52	W	P < 0.01
1023	0.45	13.6	6.3	4.00	36.2	8.4	40.2	0.420	0.93	0.73	W	n.s.
1069	0.59	19.2	4.7	1.33	298.4	5.2	30.3	0.060	0.60	2.35	NW	P < 0.005
1091	0.20	4.6	3.7	1.49	31.3	11.1	31.9	0.672	0.91	0.34	W	n.s.
1093	0.40	1.4	7.9	1.25	69.2	13.9	35.0	0.174	0.77	0.67	W	P < 0.01
1103	0.51	1.7	9.5	2.15	68.6	19.1	37.6	0.252	0.93	0.05	W	P < 0.005
Mean	0.75	12.0	6.4	2.00	132.8	14.7	33.4	0.246	0.83	0.70	W	P < 0.005
s.e.m.	0.16	2.8	0.7	0.32	32.4	1.8	1.4	0.102	0.04	0.22	—	—

Abbreviations: G_p, peripheral chemoreflex sensitivity; τ_p, peripheral chemoreflex time constant; d_p, peripheral chemoreflex delay; F ratio, result of goodness-of-fit comparison between Model 1 and Model 2 (n.s., no significant improvement with Model 2; otherwise P value indicates significance of improvement). Remaining abbreviations as in Table 1.

Table 4.

Parameter values for the hypoxic data for Model 2 estimated without and with a noise model

Subject no.	Gp(l min−1 Torr−1)	τp(s)	dp(s)	Gc(l min−1 Torr−1)	τc(s)	dc(s)	B(Torr)	C(l min−1 Torr−1)	f	Rv/Rw	Whiteness	F ratio
	No noise model
973	2.24	12.1	4.7	0.73	48.7	16.7	27.9	0.000	—	—	NW	—
974	3.36	8.9	4.3	2.42	210.9	20.0	29.5	0.156	—	—	NW	—
1003	1.45	14.7	3.4	1.28	263.2	20.0	31.1	0.084	—	—	NW	—
1004	2.63	13.4	4.8	1.72	295.4	18.7	40.8	0.000	—	—	NW	—
1023	3.85	8.7	3.5	3.86	39.7	16.9	41.9	0.000	—	—	NW	—
1069	2.07	10.3	2.3	0.81	54.6	15.3	32.9	0.000	—	—	NW	—
1091	3.01	12.5	1.0	0.71	0.1	11.6	32.6	0.000	—	—	NW	—
1093	0.59	5.8	5.2	0.91	40.5	9.4	30.4	0.000	—	—	NW	—
1103	3.38	8.6	4.1	3.55	64.1	18.2	37.6	0.000	—	—	NW	—
Mean	2.51	10.6	3.7	1.78	113.0	16.3	33.9	0.024	—	—	NW	—
s.e.m.	0.35	0.9	0.4	0.41	37.0	1.2	1.7	0.018	—	—	—	—
	With noise model
973	2.81	19.5	3.0	0.48	81.7	20.0	29.3	0.006	0.94	0.26	W	n.s.
974	3.20	7.9	4.9	1.99	136.7	19.3	29.0	0.354	0.83	1.52	W	P < 0.01
1003	1.45	11.2	3.9	1.11	161.2	20.0	30.8	0.162	0.84	0.04	W	P < 0.005
1004	2.70	13.0	4.3	1.49	243.3	19.0	40.6	0.000	0.93	0.29	W	n.s.
1023	4.40	12.9	3.6	2.80	54.8	16.2	41.3	0.000	0.96	0.19	NW	n.s.
1069	1.52	5.2	3.0	1.18	15.7	16.6	32.4	0.024	0.81	0.60	W	P < 0.05
1091	2.76	7.1	3.0	1.17	20.8	20.0	27.3	0.186	1.00	0.33	NW	n.s.
1093	0.73	5.5	5.9	0.80	37.8	15.0	30.4	0.000	0.50	5.29	NW	n.s.
1103	2.23	2.0	5.2	4.21	37.3	14.4	37.2	0.000	0.94	0.08	NW	P < 0.005
Mean	2.42	9.4	4.1	1.69	87.7	17.8	33.1	0.084	0.86	0.96	W	P < 0.05
s.e.m.	0.36	1.8	0.4	0.39	25.8	0.76	1.7	0.042	0.1	0.56	—	—

Abbreviations as in Tables 1 and 3.

Input function

The upper panels in Figs 2 and 3 illustrate, breath by breath, the values obtained for P_ET,CO2 using the end-tidal forcing technique. This subject demonstrated a P_ET,CO2 sequence that was close to the design of the MFBS (see Fig. 1). In general, all subjects demonstrated P_ET,CO2 profiles that were close to the design of the MFBS.

Comparisons of results with and without the noise model

Figures 2 and 3 show example fits of Models 1 and 2 (left and right, respectively) for one subject with and without the noise model. The fitted output from the model that does not contain a noise model (B in Figs 2 and 3) and the deterministic component of the output from the model that does contain a noise model (C in Figs 2 and 3) appear close to identical. This was generally true for all subjects.

The residuals associated with the deterministic outputs in the figures are clearly non-white. This was true for all data sets (Portmanteau test). The effect of incorporating the noise model is shown in the lower panels. The residuals here appear much closer to white. In the Portmanteau test, 26 out of the overall total of 36 sets of residuals from the fits that contained a noise model were white. The remaining 10 were much closer to white than were the original sequences. Averaged autocorrelation functions are shown in Fig. 4, where the effect of the noise model in removing autocorrelation is clear. None of the four sets of averaged autocorrelation functions for the residuals from the models containing a noise model tested as non-white. The results from all Portmanteau tests are included in Tables 1–4.

Figure 4.

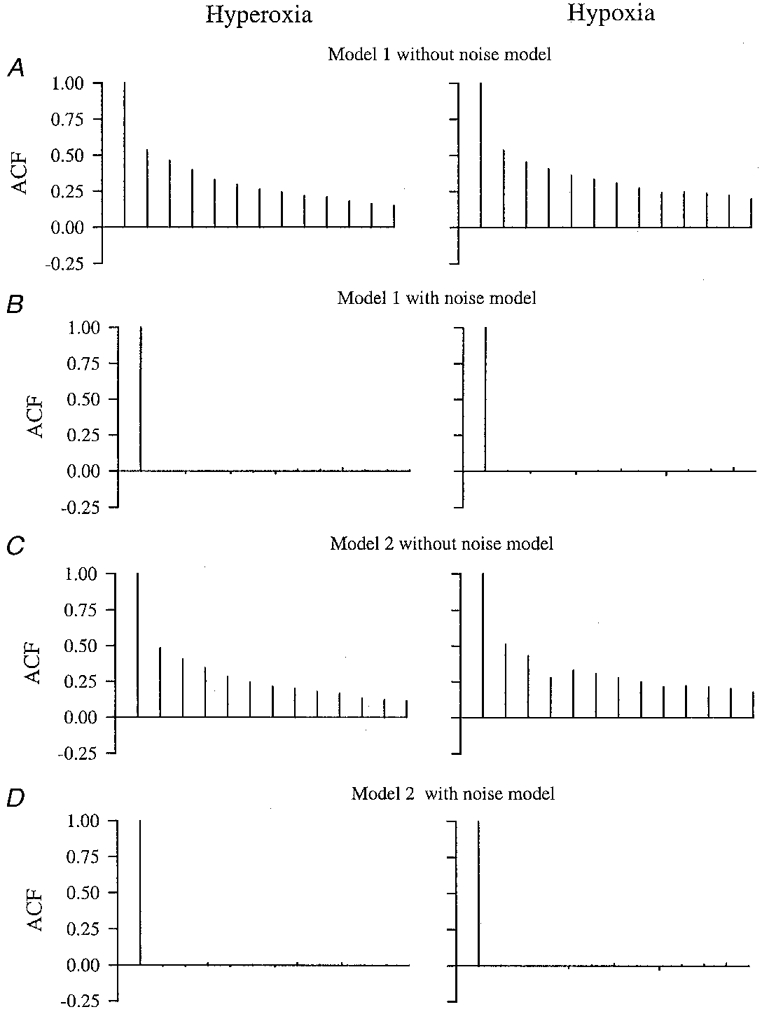
Averaged autocorrelation function outputs for the different model fits for hyperoxia and hypoxia

A, Model 1. B, Model 1 with the noise model incorporated. C, Model 2. D, Model 2 with the noise model incorporated.

Individual and mean parameter values for Models 1 and 2 both with and without the noise model are listed in Tables 1–4. In general, the parameter estimates appear quite similar from the two techniques. For Model 1, the central time constant (τ_c) was significantly smaller and the central delay significantly larger when the fitting process included the noise model (P < 0·05, ANOVA). There were no significant differences in parameter estimates for Model 2 when fitted without or with a noise model.

Comparison of Model 1 and Model 2

Differences in output between Model 1 (left-hand column of Figs 2 and 3) and Model 2 (right-hand column of Figs 2 and 3) appear fairly subtle, although in the deterministic component it is possible in places to observe the difference between one- and two-compartment behaviour. Since the residuals from fits that contained the noise model were either white or close to white, and the averaged autocorrelation functions could be accepted as white overall, it was possible to compare the two models model used in this study was essentially the same as the two-compartment model introduced by Swanson & Bellville (1975). The only embellishment associated with the present study was the introduction of a trend term, as used previously by Dahan et al. (1990). The purpose of this trend term was to fit a very slow component of the ventilatory response to CO₂ that has been observed on previous occasions (Khamnei & Robbins, 1990; Tansley et al. 1998), and is not described by the dynamics of the model. This component has a time constant of ∼1 h (Tansley et al. 1998), and therefore a linear rise in ventilation over the 24 min of the MFBS in response to the mean elevation in P_ET,CO2 would seem a reasonable representation of this dynamic.

Apart from the inclusion of the trend term, a number of other modifications have been proposed to the original model of Swanson & Bellville (1975) - none of these has been adopted in the present study. The first of these proposed modifications was to include an element of asymmetry in the slower of the time constants. Both Swanson & Bellville (1975) and Bellville et al. (1979) found that this time constant was shorter for the ventilatory response to the step increase in P_ET,CO2 than for the step decrease in P_ET,CO2. This observation has not been supported by subsequent work (Gardner, 1980; Dahan et al. 1990). In view of this, coupled with the fact that neither the study by Swanson & Bellville (1975) nor the study by Bellville et al. (1979) included a trend term in the model, it was decided that the evidence was insufficient to warrant such an addition to the models employed in the present study.

The second of the proposed modifications was to incorporate a degree of interaction between the peripheral and central chemoreflexes in determining ventilation. Such a modification is not supported by data from anaesthetised cats, where stimulation of the peripheral and central chemoreflexes can be varied independently of each other using an artificial brainstem perfusion technique. In these experiments, the reflex effects on ventilation have been found to be independent and additive (van Beek et al. 1983).

In humans, the stimuli to the peripheral and central chemoreceptors cannot be separated so clearly. Robbins (1988) applied a hypoxic stimulus shortly after a decrease in P_ET,CO2 when the P_CO2 at the peripheral chemoreceptors should have fallen, but when the P_CO2 at the central chemoreceptors should still have been elevated. In two out of three subjects he found that the response to the hypoxic stimulus was greater than it was against a background of low P_CO2 at both central and peripheral chemoreceptors, indicating the presence of some central-peripheral interaction. However, this finding could not be confirmed by St Croix et al. (1996), who suggested that the findings of Robbins (1988) had arisen as an artefact associated with the particular protocols that he had employed.

The issue of central-peripheral interaction has also been pursued by varying central chemoreflex stimulation by varying P_ET,CO2 and at the same time holding arterial (peripheral) pH constant by varying degrees of metabolic acidosis or alkalosis. No variation in the ventilatory sensitivity to hypoxia at constant arterial pH has been detected, either in the case where metabolic acidosis was induced by a brief bout of prior exercise (Clement et al. 1992) or where metabolic acidosis/alkalosis was induced by infusion of acid/bicarbonate (Clement et al. 1995). Taken together, these findings do not lend much support for including central-peripheral chemoreflex interaction in the model of the chemoreflexes. Furthermore, in one attempt to fit such a model to data obtained with step changes in P_ET,CO2, the model was found to be overparameterised (Dahan et al. 1990).

Relationship between central and peripheral chemoreflexes and dynamics of the ventilatory response

A fundamental assumption required to give this study physiological meaning is that the rapid component of the two-compartment model may be associated with the peripheral chemoreflex and the slow component may be associated with the central chemoreflex. Experiments in anaesthetised cats have provided some support for this notion. Daubenspeck (1973) found that the rapid component of the ventilatory response to sinusoidal variations in P_CO2 could be abolished by carotid body denervation. DeGoede et al. (1985) have reported that the magnitudes of the rapid and slow components identified in the ventilatory response to step changes in P_ET,CO2 agree well with subsequent measurements of central and peripheral chemoreflex sensitivities obtained using an artificial brainstem perfusion technique. Berkenbosch et al. (1989) have found that step changes in the arterial P_CO2 of blood perfusing just the brainstem result in ventilatory responses that can be described by a single slow component.

In humans, there is less evidence available to link the fast and slow components of ventilatory response to CO₂ directly to the peripheral and central chemoreflexes, respectively. Bellville et al. (1979) fitted a two-compartment model to the ventilatory responses to step changes in P_ET,CO2 in four subjects who had previously undergone carotid body resection. They reported very low sensitivities for the rapid component of the ventilatory response to hypercapnia of (mean ±s.d.) 0·16 ± 0·09 l min⁻¹ Torr⁻¹ under euoxic conditions and 0·20 ± 0·14 l min⁻¹ Torr⁻¹ under hypoxic conditions. It seems unlikely that with such low values for these sensitivities a two-compartment model would have produced a significantly better fit than a model with just a single compartment.

Peripheral chemoreflex sensitivity to CO₂ in hyperoxia

In the anaesthetised cat, there is strong evidence to support the notion that an element of peripheral chemoreflex sensitivity to CO₂ remains under conditions of acute hyperoxia. The response to CO₂ of afferent fibres from the carotid body is not abolished by hyperoxia (Fitzgerald & Parks, 1971; Lahiri & Delaney, 1975). Under conditions of artificial brainstem perfusion, a ventilatory sensitivity remains to variations in peripheral P_CO2 under conditions of hyperoxia (van Beek et al. 1983).

In humans, Miller et al. (1974) observed latencies for the first significant fall in ventilation that were substantially longer for withdrawal of CO₂ against a background of hyperoxia compared with those for withdrawal of CO₂ against a background of hypoxia. On the basis of this, they proposed that the (short latency) peripheral chemoreflex to CO₂ was abolished under conditions of hyperoxia. However, Dahan et al. (1990) have argued that the observations of Miller et al. (1974) are consistent with a simple reduction, rather than abolition of the peripheral chemoreflex.

Evidence in support of a residual peripheral chemoreflex sensitivity to CO₂ in hyperoxia has arisen from the identification of a rapid component of the ventilatory response to step changes in P_ET,CO2 when fitting two-compartment models of the response to the data (Dahan et al. 1990). However, this study did not show that a two-compartment model provided a statistical improvement in the fit compared with a one-compartment model. As such, the two-compartment model employed in the study may simply have been overparameterised. The present study demonstrates that this is not the case overall with an input stimulus in the form of a MFBS.

In the study by Dahan et al. (1990), the overall peripheral chemoreflex sensitivity to CO₂ in hyperoxia was 0·17 l min⁻¹ Torr⁻¹, or 13% of the total CO₂ sensitivity. This compares with a value of 0·75 l min⁻¹ Torr⁻¹ in the present study, or 27% of the total CO₂ sensitivity. Assuming that Dahan et al. (1990) were able to obtain an accurate estimate of this sensitivity from their step data, the most likely reason for the difference between their study and ours would seem to be that their level of hyperoxia was considerably greater (P_ET,O2 > 500 Torr) than that employed in the present study (P_ET,O2= 200 Torr). A second difference between the present study and that of Dahan et al. (1990) is that Dahan et al. found a decrease in the value of B with hyperoxia whereas in the present study the value of B was unchanged. Again, the most likely reason for this difference resides with the level of hyperoxia, as Becker et al. (1996) have reported that the increase in V̇_E with hyperoxia (which probably arises through central mechanisms) is dose dependent.

APPENDIX

This appendix describes the process that was followed to choose the particular MFBS employed in these experiments. The procedure was based on a calculation of the optimal frequencies of a sinusoidal forcing for determining the gain and time constant for each compartment of the respiratory model. The optimal frequency was defined as the frequency that would minimise the variance of the parameter estimates. Expressions for the variances were obtained from the Cramér-Rao lower bound or inverse information matrix. From a knowledge of the optimal frequencies, it was then possible to select the range of frequencies desired in the input, and from this to choose an appropriate MFBS.

Frequency response of peripheral and central chemoreflex to CO₂

Each compartment of the respiratory model (central and peripheral) can be written in the form:

(A1)

where, for the central compartment, y = V_c, T =τ_c, g = G_c and x(t) = (P_ET,CO2(t - d_c) - B) and, for the peripheral compartment, y = V_p, T =τ_p, g = G_p and x(t) = (P_ET,CO2(t - d_p) - B).

Taking Laplace's transform gives:

(A2)

Using the initial condition Y(0) = 0:

(A3)

The transfer function H is defined as Y(s)/X(s) and substituting for s (= -i ω):

(A4)

Thus

(A5)

where H_R(ω) and H_I(ω) are the real and imaginary components of the response, respectively.

Obtaining the Cramér-Rao lower bound

The Cramér-Rao lower bound(Cp) is given by the inverse of the information matrix. The information matrix (Fi) can be given as a function of second order derivatives of the likelihood function L (Schoukens & Pintelon, 1991):

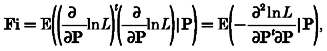(A6)

where P = (α₁, α₂, …) is the set of parameters.

The likelihood function for a single observation z of a normally distributed random variable with mean μ and standard deviation σ is:

(A7)

In our case, although we need only consider a single observation, both the system output and observation are complex. Assuming that the real and imaginary components are uncorrelated and have a common variance σ², we may write the likelihood function:

(A8)

where z_R and z_I are the real and imaginary components of the complex observation z, and y_R and y_I are the real and imaginary components of the complex system output y. In order to determine the information matrix we require the expected values of the second order derivatives of the log-likelihood function with respect to the parameters of the model. The log-likelihood function is given by:

(A9)

Hence the diagonal elements of the information matrix are given by:

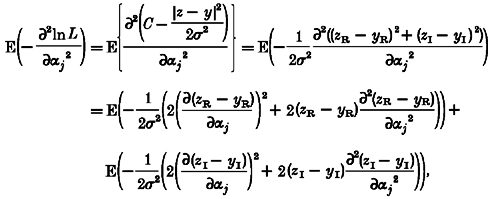(A10)

and using E(z_R - y_R) = E(z_I - y_I) = 0:

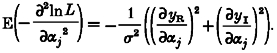(A11)

The off-diagonal elements of the information matrix are given by:

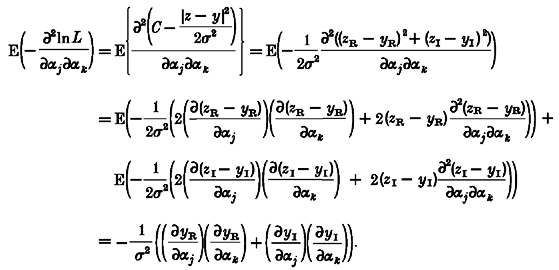(A12)

In our case, y_R=H_R(ω) and y_I=H_I(ω). There are two parameters, α₁=g and α₂=T, and the information matrix may be written:

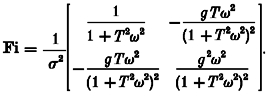(A13)

The Cramér-Rao lower bound is given by the inverse of this matrix:

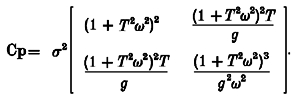(A14)

where σ²(1 +T²ω²)² is the lower bound for the variance for g and σ²(1 +T²ω²)³/g²ω² is the lower bound for the variance for T.

Selection of MFBS

Typical values for g and T were used to calculate the angular velocities (ω) corresponding to the minimum variance for each variable and also for the determinant of Cp (Fig. 5). Since the peripheral and central components were to be separated on the basis of their relative speeds of response, we focused particularly on the minima for the variances for the time constants. For the central component g was chosen as 2·0 l min⁻¹ Torr⁻¹ and T as 80 s; for the peripheral component g was chosen as 0·2 l min⁻¹ Torr⁻¹ and T as 10 s (Cunningham et al. 1986). The values for ω at which the variances for the time constants were at a minimum were 0·009 rad s⁻¹ for the central component and 0·07 rad s⁻¹ for the peripheral component (Fig. 5). These correspond to periods (2π/ω) of 700 and 90 s, respectively. We chose to include frequencies in the input function extending from about one octave below that calculated for the central component to one octave above that calculated for the peripheral component. Starting at 45 s and ascending in octaves gives us six harmonics: 45, 90, 180, 360, 720 and 1440 s. A MFBS covering six octaves in this manner is the Van den Bos Octave (Table 7.1, Godfrey, 1993). This MFBS has a length of 128 bits, and therefore the duration of each bit is 1440/128 s. This approximates to 11 s, giving an actual length for the MFBS of 1408 s.

Figure 5.

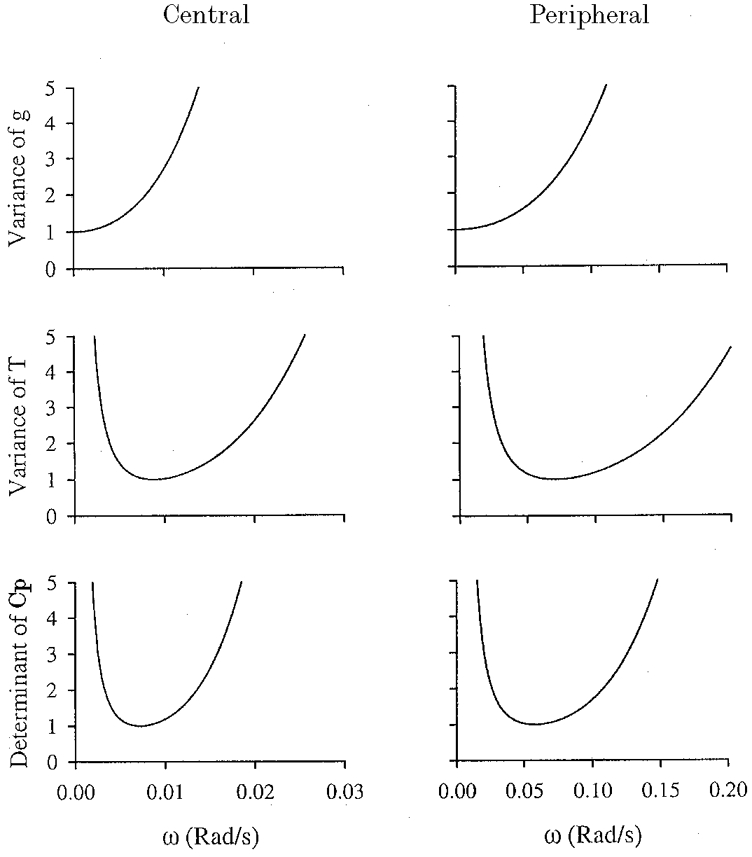
Variance of gain (g) and time constant (T) together with the determinant of the Cramér-Rao lower bound (Cp), all as a function of angular velocity (ω) of sinusoidal stimulation

Left, central chemoreflex. Right, peripheral chemoreflex. Units for the variance and determinant have been chosen so that the value at the minimum is unity.