Solvent effects on squid sodium channels are attributable to movements of a flexible protein structure in gating currents and to hydration in a pore

Abstract

1. Solvent effects on the time course of gating and sodium currents were analysed in squid sodium channels using four non-electrolytes of different size, glycerol, erythritol, glucose and sucrose, to separate effects of viscosity from those of osmolarity and to obtain viscosity and osmolarity parameters that were independent of molecular size.

2. The gating and sodium currents were reversibly slowed in a voltage-independent manner as the non-electrolyte concentration increased.

3. Solvent effects were analysed using a model in which the percentage change in time constant was expressed by an equation involving the viscosity parameter α and the osmolarity parameter δ: t/t₀ =α((η/η₀) – 1 + 100α⁻¹)exp(δΔΠ), where η/η₀ is solution viscosity and ΔΠ is increase in osmolarity. Since the solution viscosity was found experimentally to be a function of the solution osmolarity, solvent effects are described by an equation with one independent variable η/η₀ or ΔΠ.

4. Voltage sensor movement, reflected in gating currents, was primarily sensitive to viscosity, as its decay time constant was a function of η/η₀, with only a minor sensitivity to osmolarity (δ was 2–3 water molecules).

5. For sodium currents, α was equal to that of gating currents but δ was 2–3 times greater, suggesting that the final channel opening was primarily sensitive to osmolarity (Δδ was 5 water molecules). The relative ineffectiveness of the largest non-electrolyte, sucrose, suggested that this osmolarity-sensitive step in channel opening occurred in the narrow pore region.

6. Sodium channel inactivation was primarily sensitive to osmolarity (Δδ was 8–12 water molecules).

7. The observed viscosity dependence of the sodium current activation and inactivation processes was attributable to the viscosity-dependent process accompanying the gating current.

8. This model explains why non-electrolytes slow sodium currents while electrolytes do not.

9. Viscosity effects on gating currents can be explained by a process in which non-electrolytes interact with the flexible hydrophilic parts of sodium channel proteins, but osmolarity effects on the final step need to be explained by a local interaction of several water molecules with fluctuating protein segments in the pore.

Sodium channels are typical voltage-gated ion channel proteins, with a larger hydrophilic region than required for a simple pore (Noda et al. 1986). Sodium channel kinetics are affected by interactions of their hydrophilic parts with non-electrolytes and water molecules in the solution (Kukita & Yamagishi, 1976, 1979; Kukita, 1997). Recently the role of hydrophilic parts of ion channels has been widely discussed, especially for a voltage-gated sodium channel (Yang et al. 1996) and the Shaker B voltage-gated potassium channel (Kreusch et al. 1998). It has been proposed that an interaction of solvent molecules with the hydrophilic flexible region of proteins may determine the overall kinetics of sodium channel gating (Kukita, 1997).

Classical ideas explaining solvent effects on ion channel function include a viscosity model (Kukita & Yamagishi, 1976, 1979) and an osmotic stress model for the pore region (Zimmerberg & Parsegian, 1986). In the classical viscosity model, the friction that viscosity imparts onto ions and rigid parts of the sodium channel is supposed to be able to slow the overall kinetics of sodium channel gating (Kukita & Yamagishi, 1979) but this cannot explain the slowing of the gating kinetics on the millisecond time scale (Kukita, 1997). The classical osmotic stress model cannot explain how small molecules which easily enter the pore are able to exert solvent effects (Kukita, 1997).

The present paper is focused on separating the effects of viscosity from those of osmolarity using non-electrolytes of different sizes to obtain viscosity and osmolarity parameters that were independent of non-electrolyte size. In a previous paper, solvent effects were explained using the combination of a viscosity model and an osmolarity model independently described (Kukita, 1997). In the present paper, the data are analysed using an expanded model which includes both viscosity and osmolarity effects. Only in an extreme case could this expanded model be reduced to the models described in the previous paper. Analysing the data using the revised model, the relation between bulk viscosity and osmolarity obtained experimentally enabled the data to be fitted with an equation with only one independent variable, i.e. viscosity or osmolarity. Finally, parameters describing viscosity and osmolarity effects were obtained at the same time and were found to be independent of non-electrolyte size. Applying these procedures to the gating current and sodium current data, viscosity and osmolarity parameters were obtained for different steps during the activation and inactivation processes.

The viscosity and osmolarity parameters obtained showed the following. (1) Voltage sensor movement, reflected in gating currents, was primarily sensitive to viscosity, and only slightly sensitive to osmolarity (the osmolarity parameter δ was 2–3 water molecules). (2) Channel opening was primarily sensitive to osmolarity (Δδ was 5 water molecules). The relative ineffectiveness of the largest non-electrolyte, sucrose, suggested that this osmolarity-sensitive step occurred in the pore. Effects of viscosity on sodium ionic currents were attributable to the effects on the voltage sensor movement. (3) Channel inactivation was primarily sensitive to osmolarity (Δδ was 8–12 water molecules).

The present paper describes the first quantitative analysis of solvent effects on the gating currents using different sizes of non-electrolyte. It is concluded that solvent effects on gating current have common characteristics with those on flexible hydrophilic proteins (Gutfreund, 1995). The additional effects of non-electrolytes on sodium current can be assigned to osmolarity effects on the final opening step and was attributable to hydration of a flexible structure of the pore, such as the P loop. The present data will help us understand the molecular mechanism of ion channel gating in relation to the 3D-structure which is expected to be revealed in the near future (Doyle et al. 1998; Armstrong & Hille, 1998).

METHODS

Squid (Doryteuthis bleekeri) were obtained at Ine (Kyoto, Japan) and kept in a circulating tank for a few weeks before the experiments. On removal from the tank, the squid were immediately killed by decapitation with sharp scissors following the guidelines for animal care of the National Institute for Physiological Sciences (Japan). The hindmost stellar giant axons (400–800 μm in diameter) were prepared and intracellularly perfused by a modified axoplasm-squeezing method (Kukita, 1982). A further improvement was achieved by changing the length of the squeezed region depending on the condition of the axons.

The membrane potential was measured using an asbestos-tipped glass capillary electrode containing a floating platinum wire (Conti et al. 1984). Voltage clamping was performed as previously described (Kukita & Mitaku, 1993). The holding potential was kept constant at −60 or −70 mV. Series of test pulses were applied from a preconditioning pulse of 0.5 s at −100 mV. The series resistance was made as small as possible by the proper alignment of electrodes and was carefully compensated to minimize its effects, particularly when the concentration of non-electrolytes was increased. All membrane current data were digitized with a 12-bit A/D converter (Autonics 204C, Japan; Kukita, 1998) using a sampling time of 5 μs after passing through a low-pass Bessel filter of 20–50 kHz. Data were analysed using a microcomputer (NEC PC9801FA & PC9821V200, Japan). Most of the capacitive transient current was subtracted on-line using a variable transient current produced in a dummy membrane circuit. The remaining linear response was subtracted off-line (Conti et al. 1984).

The control external solution was tetramethylammonium-containing artificial sea water (TMA-ASW) containing (mM): 460 TMA-Cl, 20 CaCl₂, 30 MgCl₂ and 15 Tris-Hepes (pH 8.0). TTX (200–600 nM) was added to the external solution for gating current measurement. The control internal solution was Cs⁺-containing internal solution (Cs-IS) which contained (mM): 200 CsF, 50 caesium phosphate, 20–50 tetraethylammonium (TEA) phosphate and glucose to adjust osmolarity. For measurement of sodium current, the control external solution was 1/5 Na-ASW which contained 100 mM NaCl (replacing an equimolar amount of TMA-Cl) and the control internal solution was Na-containing Cs-IS (Na-Cs-IS) which contained 10 mM NaF (replacing an equimolar amount of CsF).

Non-electrolyte solutions were prepared by adding non-electrolytes to the external and the internal control solutions, keeping the molar concentration of electrolytes equal as described in the previous paper (Kukita, 1997). The four species of non-electrolytes used were glycerol, erythritol, glucose and sucrose. The osmolarity of solutions was measured with a freezing-point osmometer (Fiske Mark 3, USA) as described in the previous paper (Kukita, 1997). Osmolarities above 4000 mosmol l⁻¹ were obtained by extrapolating the data as a function of the molar concentration of non-electrolytes. The viscosity of solutions was measured with a rotating cone disc viscosimeter (ELD, Tokyo Keiki, Japan).

External and internal solutions were pairs of solutions with the same molar concentration of non-electrolytes and roughly the same osmolarity. The osmolarity of the external and internal solutions was balanced within 5%. These symmetrical non-electrolyte concentrations helped to minimize errors in the membrane potential due to changes in the junction potential of the internal and external electrodes and errors due to the increase of ionic activity in non-electrolyte solutions (Kukita & Yamagishi, 1979). The relative solution viscosity was defined as the ratio of the solution viscosity of the non-electrolyte solution to that of the control solution. The relative solution viscosity for internal and external solutions was obtained separately, then they were averaged at each concentration of non-electrolyte to obtain the relative viscosity (η/η₀) which was used for the data analysis. The mean value of the osmolarity of a pair of internal and external solutions was used as the solution osmolarity.

Gating currents were measured in the four non-electrolyte solutions. Data were averaged 50 times. Sodium currents in glycerol solutions were measured as previously described (Kukita, 1997). Data of sodium currents in erythritol, glucose and sucrose solutions from the previous paper (Kukita, 1997) were used for the analysis. The calculated values of parameters are not exactly the same as those shown in the previous paper (Kukita, 1997), because the weighting for the curve fitting was slightly different and the definition of the relative viscosity (η/η₀) was different. The temperature was maintained by circulating external solution through a heat exchange unit. All experiments were performed at ∼10°C.

RESULTS

Gating currents are slowed at all membrane potentials as non-electrolyte concentration is increased

Typical traces of sodium channel gating currents (I_g) in glucose solutions of different concentration are shown at different membrane potentials in Fig. 1. The amplitude of gating currents decreased as the glucose concentration increased (from Fig. 1A to E). At the same time, gating current decay was slowed reversibly without a change in the area under the curve, but there was no significant change in the rate of the initial rising phase. The slowing was observed at all membrane potentials. At a glucose concentration of 2 M, the time constant increased 2.5-fold (Fig. 1E). The same amount of slowing was observed at −40 mV (Fig. 1Ba, Ca, Da and Ea), where practically no activation of sodium conductance was observed (see Fig. 2E), as at +50 mV (Fig. 1Bd, Cd, Dd and Ed) where both sodium and gating currents reached saturation levels. The data at different membrane potentials were averaged and are listed in Table 1.

Figure 1. Slowing of sodium channel gating currents in glucose solutions of increasing concentration.

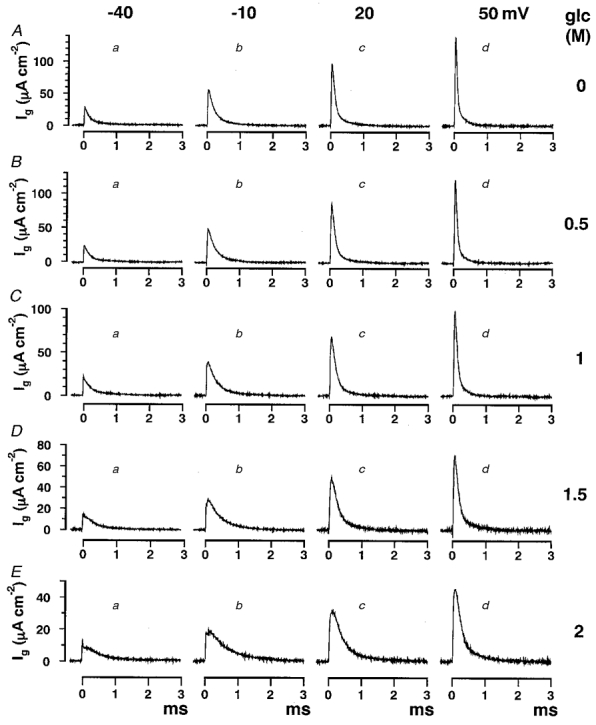
The time course of gating currents (I_g) slowed as the glucose concentration increased. External solution was TMA-ASW containing 500 nM TTX. Internal solution was Cs-IS. Current traces were obtained at membrane potentials from −40 mV to +50 mV in 30 mV steps (a to d) as indicated at the top of the figure. Glucose (glc) concentrations were 0 (A), 0.5 (B), 1 (C), 1.5 (D) and 2 M (E) as indicated to the right. Data were acquired through a low-pass Bessel filter of 50 kHz and were averaged 50 times.

Figure 2. The voltage dependence of gating current time constants and Q_g in glucose solutions.

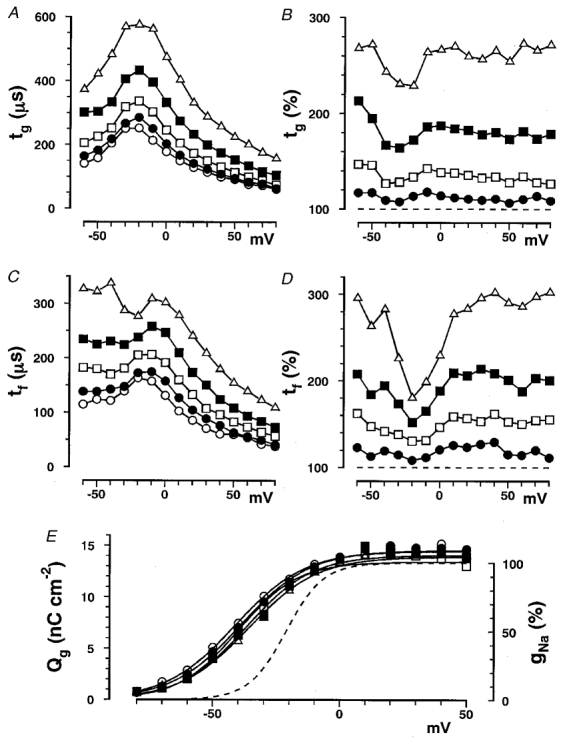
A, t_g plotted as a function of membrane potential in glucose solutions at concentrations of 0 (○), 0.5 (•), 1 (□), 1.5 (▪) and 2 M (▵). Averaged values obtained from 12 experiments are plotted. The standard deviations (s.d.s) are not indicated for clarity. Percentage errors are defined by the ratio (in %) of s.d. to the mean. The averaged percentage errors at membrane potentials between −30 and +30 mV at glucose concentrations of 0, 0.5, 1, 1.5 and 2 M were 9, 8, 8, 11 and 11%, respectively, and those between −60 and +80 mV were 14, 12, 11, 14 and 15%, respectively. B, the percentage change in t_g plotted as a function of membrane potential in glucose solutions at concentrations of 0.5 (•), 1 (□), 1.5 (▪) and 2 M (▵). The dashed horizontal line indicates 100%. The percentage changes were obtained for each experiment and then averaged in 12 experiments. Percentage errors averaged between −30 and +30 mV at glucose concentrations of 0.5, 1, 1.5 and 2 M were 7, 8, 11 and 11%, respectively, and those between −60 and +80 mV were 13, 14, 17 and 19%, respectively. C, t_f plotted as a function of membrane potential in glucose solutions at concentrations of 0 (○), 0.5 (•), 1 (□), 1.5 (▪) and 2 M (▵). Averaged values obtained from 12 experiments are plotted. The averaged percentage errors at membrane potentials between −30 and +30 mV are at glucose concentrations of 0, 0.5, 1, 1.5 and 2 M were 16, 15, 14, 18 and 23%, respectively, and those between −60 and +80 mV were 20, 13, 15, 18 and 22%, respectively. D, the percentage change in t_f plotted as a function of membrane potential in glucose solutions at concentrations of 0.5 (•), 1 (□), 1.5 (▪) and 2 M (▵). The dashed horizontal line indicates 100%. The percentage changes were obtained for each experiment and then averaged in 12 experiments. Percentage errors averaged between −30 and +30 mV at the glucose concentrations of 0.5, 1, 1.5 and 2 M were 19, 17, 22, and 27%, respectively, and those between −60 and +80 mV were 20, 19, 22 and 27%, respectively. E, total charges (Q_g) obtained by integrating gating current traces are shown on the left-hand ordinate and are plotted as a function of membrane potential in glucose solutions at concentrations of 0 (○), 0.5 (•), 1 (□), 1.5 (▪) and 2 M (▵). Data were averaged and fitted with eqn (1) with Q_g,0 = 0. Values of V_½ at concentrations of 0, 0.5, 1, 1.5 and 2 M were −40, −38, −38, −34 and −34 mV, respectively. Original data in each experiment were fitted with eqn (1) and values of V_½, z and Q_g,∞ from 12 experiments were averaged; averaged values are listed in Table 1. The dashed line shows a typical g_Na-V curve, in which g_Na (in %) on the right-hand ordinate is plotted against the membrane potential.

Table 1.

Percentage changes in time constants for gating currents and V_1/2, z and Q_g,∞ at different concentrations of glycerol, erythritol, glucose and sucrose

	tg(%)	tf(%)	ts(%)	V1/2(mV)	z	Qg,∞(nC cm−2)
[Glycerol] (m)
0	100	100	100	−33.9 ± 5.0	1.8 ± 0.3	11.8 ± 3.6
1	119 ± 3	126 ± 8	133 ± 2	−36.3 ± 3.8	2.1 ± 0.2	12.8 ± 3.5
2	144 ± 5	150 ± 14	143 ± 16	−33.2 ± 3.0	2.0 ± 0.2	13.2 ± 4.0
3	191 ± 13	201 ± 21	163 ± 12	−32.6 ± 2.9	2.0 ± 0.3	14.0 ± 4.3
4	270 ± 23	283 ± 38	208 ± 21	−29.4 ± 2.9	1.9 ± 0.2	14.7 ± 4.0
[Erythritol] (m)
0	100	100	100	−41.0 ± 3.3	1.8 ± 0.1	15.8 ± 4.1
0.5	106 ± 4	112 ± 7	136 ± 41	−36.7 ± 5.6	1.9 ± 0.3	15.0 ± 3.0
1	120 ± 4	124 ± 8	138 ± 25	−36.9 ± 4.8	1.7 ± 0.2	14.8 ± 2.9
1.5	142 ± 4	144 ± 9	172 ± 17	−36.0 ± 4.9	1.7 ± 0.3	14.9 ± 3.5
2	167 ± 10	167 ± 7	189 ± 66	−33.9 ± 4.3	1.7 ± 0.2	15.1 ± 3.0
[Glucose] (m)
0	100	100	100	−40.1 ± 7.1	1.7 ± 0.2	14.8 ± 3.8
0.5	111 ± 3	119 ± 8	141 ± 11	−36.1 ± 12.3	1.8 ± 0.3	15.9 ± 6.1
1	134 ± 7	147 ± 8	145 ± 13	−37.9 ± 4.9	1.8 ± 0.2	14.4 ± 1.8
1.5	177 ± 10	190 ± 11	197 ± 50	−35.4 ± 5.2	1.8 ± 0.3	14.7 ± 2.7
2	254 ± 14	257 ± 17	191 ± 31	−33.9 ± 4.0	1.6 ± 0.2	14.4 ± 2.6
[Sucrose] (m)
0	100	100	100	−38.2 ± 5.1	1.6 ± 0.2	14.2 ± 2.6
0.25	114 ± 4	119 ± 17	128 ± 5	−38.2 ± 3.9	1.9 ± 0.2	13.5 ± 2.4
0.5	132 ± 4	133 ± 8	139 ± 27	−36.2 ± 3.6	1.9 ± 0.1	13.0 ± 1.0
0.75	168 ± 7	166 ± 11	313 ± 37	−36.2 ± 3.6	1.8 ± 0.2	14.0 ± 1.3
1	215 ± 13	201 ± 10	165 ± 31	−32.5 ± 2.9	1.8 ± 0.1	12.8 ± 1.1

Values are given as means ± s.d. Data were averaged between −50 and +50 mV for t_g and t_f and between +10 and +40 mV for t_s. Q_g–V curves in each experiment were fitted with eqn (1) with Q_g,0 = 0. The number of experiments was 5 for glycerol, erythritol and sucrose and 12 for glucose.

The decay of the gating current could be fitted reasonably well with a single exponential over a wide range of membrane potentials, although there were noticeable slow components in some traces, especially at membrane potentials above +30 mV (Armstrong & Gilly, 1979). At +50 mV, a slow component of the decay was observed in control solution (Fig. 1Ad), but the fit with a single exponential became better, as the glucose concentration was increased.

The data were also fitted with a double exponential (fast time constant, t_f, and slow time constant, t_s), giving a better fit than with a single exponential (time constant, t_g). The value of t_g is larger than that of t_f and is a weighted average of two time constants t_f and t_s, to characterize approximately the decay time course. The percentage change in t_g was closely correlated with that in t_f (Table 1, second and third columns). The percentage change in t_s was more variable and so was not suitable for further qualitative analysis (Table 1, fourth column), although t_s was slowed to the same extent as t_f and t_g as the glucose concentration was increased. The percentage change in t_g was the most suitable measure of the slowing of the gating current time course, and was used for all further analysis.

Similar results were obtained in glycerol, erythritol and sucrose solutions by curve fitting with either a single or a double exponential. The percentage changes in these time constants are listed in Table 1.

The slowing of gating current appeared without any change in the t_g-V and total charge carried (Q_g)-V curves

In Fig. 2A, t_g is plotted as a function of membrane potential (t_g-V curve). As the glucose concentration was increased, the t_g values at different membrane potentials increased to the same extent leaving the bell-shaped characteristic of the t_g-V curve unchanged with a peak voltage of around −20 mV. The percentage change in t_g is plotted as a function of membrane potential in Fig. 2B. The percentage change did not significantly depend on membrane potential, although there was a noticeable but not significant bend in the t_g-V curve between −40 and −20 mV, mainly because of a slight shift in the t_g-V curve to a more negative potential in control solutions (Fig. 2A, open circles). No attempt was made to correct for the effect of this shift to obtain a flatter relation between percentage change in t_g and membrane potential, and data were averaged over the full range of membrane potentials.

In Fig. 2C, t_f is plotted as a function of membrane potential (t_f-V curve). The percentage change in t_f (Fig. 2D) was almost the same as that in t_g and was also voltage independent, although there was a marked bend at −20 mV because of the shift of the peak in the t_f-V curve. Curve fitting with a double exponential was not suitable at membrane potentials below 0 mV where there was no observable slow component.

The total charge carried (Q_g) was obtained by integrating the gating current trace for about 3 ms, or for a longer period at higher glucose concentrations. Q_g was plotted as a function of membrane potential (Q_g-V curve) in Fig. 2E. Relative to the unitary sodium conductance (g_Na)-V curve (dashed curve), the Q_g-V curve shifted in a hyperpolarizing direction by about 20 mV. The Q–V curves were fitted with the following equation:

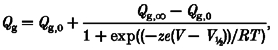(1)

where Q_g,0, Q_g,∞, z, V_½, R and T are the gating charge at the most negative membrane potential, the gating charge at the most positive membrane potential, the valency of gating charge, the membrane potential of half-activation, the gas constant and the absolute temperature, respectively.

The Q_g-V curves did not change significantly in glucose solutions of different concentration. The values of V_½, Q_g,∞ and z at different glucose concentrations are listed in Table 1. There was a slight shift in V_½ in a depolarizing direction as the glucose concentration was increased, which was slightly smaller than that observed in the g_Na-V curve (Kukita, 1997). This shift was at most 7 mV at the highest concentration and was hence too small to affect the calculated time constants.

Similar data were obtained in glycerol, erythritol and sucrose solutions and values of V_½, z and Q_g,∞ in these solutions are listed in Table 1.

The slowing of the gating current is viscosity dependent

The percentage change in t_g in the four different non-electrolyte solutions is plotted as a function of relative viscosity (t_g-η/η₀ curve) in Fig. 3A. The t_g-η/η₀ curve in Fig. 3A is fitted roughly with eqn (2), as was the case for time constants of the sodium current shown in the previous paper (Kukita, 1997).

(2)

where α and η/η₀ are the proportionality constant (in %) and the relative solution viscosity, respectively.

Figure 3. Gating current time constants as a function of viscosity.

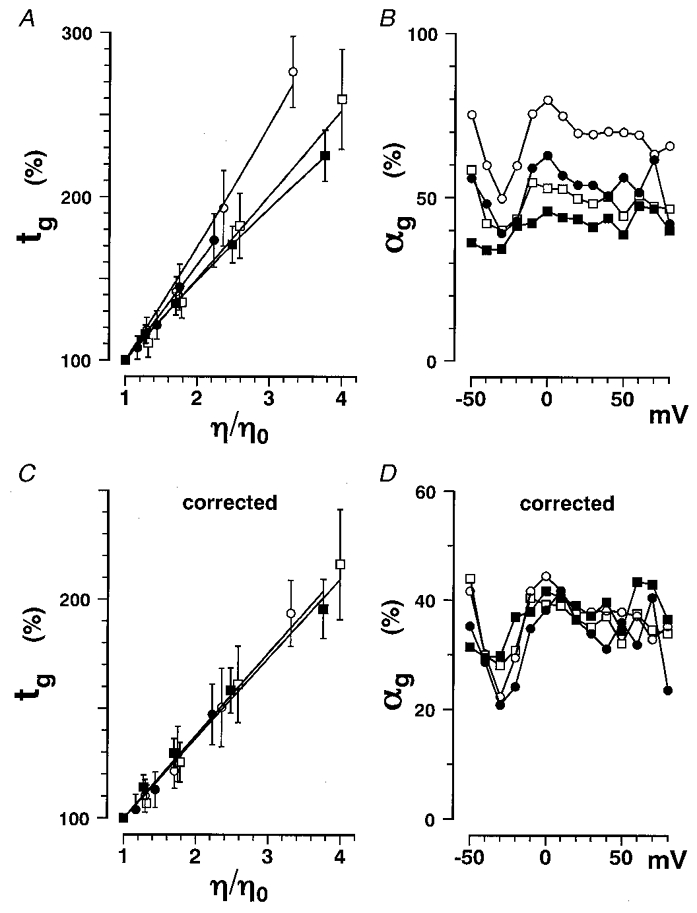
Data obtained in glycerol (○), erythritol (•), glucose (□) and sucrose (▪) solutions are plotted. A, the percentage change in t_g at +20 mV is plotted as a function of η/η₀. The averaged values from 12 experiments are plotted with s.d. values (vertical bars). Data were fitted with eqn (18) in place of eqn (2) to show a detectable non-linearity. B, α_g values obtained by fitting the t_g-η/η₀ curve in Fig. 3A with eqn (2) are plotted as a function of membrane potential. C, the t_g data in A were corrected using eqn (8) with δ_g fixed at 0.05 l osmol⁻¹ and are plotted as a function of η/η₀ (corrected t_g-η/η₀ curve). The corrected data could be fitted with eqn (2) better than the original data in A.D, α_g values obtained by fitting the corrected t_g-η/η₀ curve in C with eqn (2) are plotted as a function of membrane potential.

The α values obtained for the gating current by curve fitting with eqn (2) are here designated α_g. The α_g values for different non-electrolytes (the second column of Table 2) were around 50% and slightly decreased as the molecular weight of non-electrolytes increased (Fig. 3B). The t_g-η/η₀ curves are not strictly straight, they are slightly curved especially at lower concentrations of non-electrolyte (see the legend of Fig. 3A). To clarify this non-linearity, a more general analysis is necessary which takes into account additional effects of solution osmolarity, as in the following procedure.

Table 2.

Viscosity and osmolarity parameters for gating currents α_g, β_g, δ_g and p in solutions containing nonelectrolytes of different size

	αg(%)	Corrected αg (%)	βg (l osmol−1)	p (l osmol−1)	αg (%)	δg(l osmol−1)
Glycerol	73.2 ± 4.2	40.2 ± 2.8	0.142 ± 0.006	0.170	36.6 ± 0.9	0.053 ± 0.007
	(68.0 ± 8.5)	(36.2 ± 6.4)	(0.134 ± 0.012)		(33.4 ± 6.9)	(0.049 ± 0.011)
Erythritol	56.2 ± 4.4	36.0 ± 3.7	0.157 ± 0.010	0.246	41.9 ± 0.9	0.034 ± 0.012
	(52.3 ± 7.0)	(32.5 ± 6.1)	(0.147 ± 0.016)		(41.7 ± 1.0)	(0.025 ± 0.017)
Glucose	51.4 ± 2.4	37.9 ± 2.0	0.244 ± 0.008	0.379	36.1 ± 0.5	0.057 ± 0.007
	(48.2 ± 4.8)	(35.0 ± 4.2)	(0.231 ± 0.019)		(36.6 ± 2.3)	(0.044 ± 0.021)
Sucrose	43.4 ± 1.6	3903 ± 1.7	0.374 ± 0.011	0.638	42.0 ± 3.6	0.030 ± 0.018
	(41.5 ± 4.3)	(37.2 ± 4.5)	(0.365 ± 0.026)		(39.2 ± 5.6)	(0.036 ± 0.039)

α_g and β_g were respectively obtained using eqns (2) and (15), which are derived from the independent model described in the previous paper (Kukita, 1997). They were dependent on the nonelectrolyte size. Parameter p (from eqn (16)) indicates the relationship between bulk viscosity and osmolarity (Fig. 4A). Corrected α_g was obtained by fitting data with eqn (2) after the data had been divided by a factor exp(δ_gΔπ) using eqn (8) with δ_g = 0.05 l osmol⁻¹ (the corrected t_g−η⊂η₀ curve in Fig. 3C). α_g and δ_g were obtained by fitting the t_g−π curve in Fig. 4B with eqn (17). These parameters are independent of the non-electrolyte size. Values are given as means ± s.d. The data were averaged between −10 and +40 mV (upper line) or between −40 and +60 mV (in parentheses, lower line) for each non-electrolyte.

A general description of time constants is given in eqn (3) where the rate of the conformational change depends on the solution viscosity (Kramers, 1940; Gavish, 1986):

(3)

where A, η, c and ΔG‡ are the proportionality constant (in mPa⁻¹), the solution viscosity (in mPa s), the constant indicating the contribution of the viscosity-independent process (in mPa s) and the activation free energy, respectively.

The relative change in time constants is expressed as:

(4)

where t₀, η₀ and ΔG‡_ne are the time constant in control solution, the viscosity of the control solution and the change in activation free energy of the gating process in non-electrolyte solutions, respectively.

ΔG‡_ne can be expressed in terms of solution osmolarity as:

(5)

where δ, Π, Π₀ and ΔΠ are the parameters (in l osmol⁻¹) characterizing the osmolarity effects, the osmolarity of the non-electrolyte solution, the osmolarity of the control solution and their difference, respectively.

As the osmolarity is traditionally given in osmol l⁻¹, the osmotic pressure in N m⁻² is obtained by multiplying the value in osmol l⁻¹ by RT (Kukita, 1997, eqn (19)). The osmolarity was measured by freezing-point depression, and is therefore the osmolarity at 0°C. Strictly, a small correction should be applied for the difference of temperature in physiological experiments (10°C) and osmolarity measurements (0°C) to estimate the ‘solute inaccessible volume’ at the temperature of experiment (10°C).

Combining eqn (4) and eqn (5) gives:

(6)

The parameter α (in %) is defined as:

(7)

As c is positive, α would be expected to be less than 100%. In the case of sodium currents, α is sometimes found to be greater than 100%, which is one of the reasons that a simple viscosity model could not be applied to sodium currents (Kukita, 1997).

Using α, the percentage change in the time constant is given by:

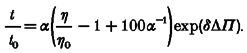(8)

Equation (8) is a general description of solvent effects, since this equation can be reduced to eqn (2) if δ = 0 l mol⁻¹ and to eqn (15) if α = 0%. Although δ is variable in a later analysis as shown in eqns (17) and (18), the last term exp(δΔΠ) can be used as a correction factor for the additional effect due to ΔΠ whenever δ is small enough.

The percentage change in t_g for each non-electrolyte was corrected using eqn (8) with δ_g = 0.05 l osmol⁻¹. Corrected values are plotted as a function of η/η₀ in Fig. 3C. They were linearly related to the relative viscosity and data points in the different non-electrolytes lie on a straight line and were completely described by eqn (2). The α_g values obtained from the corrected curves in Fig. 3C are plotted as a function of membrane potential in Fig. 3D. The derived α_g values were voltage independent and almost the same for different non-electrolytes. This result strongly supports the idea that the process accompanying the gating current is mainly viscosity dependent rather than osmolarity dependent. In addition, considering that δ was as small as 0.05 l osmol⁻¹, it is concluded that osmolarity effects were not dominant in the gating process and can be attributed to the solute inaccessible volume being smaller than the volume of three water molecules, assuming the volume of water to be 18 ml mol⁻¹ (see also Fig. 7B).

Figure 7. Molecular weight dependence of α and δ.

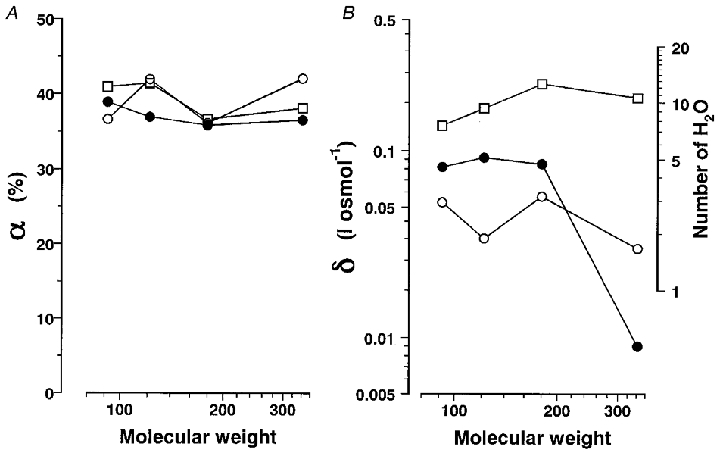
A, α_g (○), α_p (•) and α_h (□) (in %) plotted as a function of molecular weight on a logarithmic scale. B, δ_g (○), Δδ_p (•) and Δδ_h (□) (in l osmol⁻¹) on a logarithmic scale (left-hand ordinate) are plotted as a function of molecular weight on a logarithmic scale. The number of water molecules contributing the transient hydration during each process was obtained assuming the volume of water to be 18 ml mol⁻¹ (0.03 nm³ per molecule) and is shown on the right-hand ordinate.

The mean values of α_g before and after correction for osmolarity are listed in Table 2. After correction, α_g decreased by half in glycerol solutions but decreased by only 10% in sucrose solutions. The α_g values were almost equal regardless of the non-electrolyte molecular weight and did not depend on membrane potentials (Fig. 3D). All these results confirm that a simple viscosity model (Kukita, 1997) can be applied to the conformational change accompanying gating currents.

The fact that α_g is 40% and c is 1.5η₀ (1.5 times the viscosity of the control solution) shows that, even in physiological conditions, 40% of the time constant is determined by the viscosity of the solution (mainly water and cytoplasm), because its value is not zero.

The viscosity-dependent process is related to the fluctuation of sodium channel proteins

Estimating the extent to which viscosity will affect the movements of proteins and their segments might be useful for the interpretation of viscosity effects at a molecular level.

The energy dissipated in a process by which a rigid sphere of radius r moves over a distance of Δx is estimated by the following procedure.

The force due to the viscosity friction (F) is given by:

(9)

where f and v are the friction coefficient and the velocity, respectively.

The friction coefficient is described by Stoke's equation as in:

(10)

where η is the viscosity of the solution.

The work done during the displacement over a distance of Δx is given by equations

(11)

and

(12)

where ΔW is the energy dissipation in this process and τ is the time taken for a single movement.

When the displacement takes 1 ms, the value of ΔW can be calculated for different values of r and Δx using the viscosity of water (1.31 mPa s) and 2 M glucose solution (7.12 mPa s), as listed in Table 3.

Table 3.

Estimation of ΔW and τ calculated for variable r and Δx relating to a dimension of sodium channel protein

		η = 1.31 mPa s		η = 7.12 mPa s
r(nm)	Δx(nm)	ΔW(10−6kBT)	τ(ns)	ΔW(10−6kBT)	τ(ns)
0.56	4.2	62.3	62.3	339	339
0.35	0.5	0.551	0.551	3.00	3.00
0.35	1	2.21	2.21	12.0	12.0
0.2	0.5	0.315	0.315	1.72	1.72
0.2	1	1.26	1.26	6.87	6.87

Values of r and Δx are the radius and the length, respectively, of the sodium channel S4 segment, which is assumed to be a cylinder. Values of r are close to the radius of amino acid residues. ΔW is the value of the energy dissipation when the displacement occurs in 1 ms. τ is the time required for a single step of movement to dissipate the energy of 1k_BT. ΔW and τ were calculated at a solution viscosity (η) of 1.31 (control TMAASW) and 7.12 mPa s (2 M glucose solution).

The time in which a single stroke of movement dissipates energy of 1k_BT (∼24 meV) (τ) is given by:

(13)

where k_B is the Boltzmann constant and T is the absolute temperature. Alternatively, eqn (13) can be derived assuming a diffusion process over time τ, with the diffusion coefficient D defined by the following equation:

(14)

where f is the friction coefficient as in eqn (10).

Values of τ are useful parameters to show viscosity-dependent processes and are listed in Table 3. Values of r and Δx are chosen to characterize possible movements in the sodium channel gating assuming that an S4 segment is 0.56 nm in radius and 4.2 nm in length.

If an S4 segment movement took a few hundred microseconds, the energy dissipation would be much less than 1k_BT, and would have no effect on the gating time constant. A rapid movement of parts of the protein in a single stroke over a few nanoseconds is necessary to dissipate energy close to 1k_BT which could affect the time constants. Thus 1000 steps of elementary movement each 1 μs in duration could dissipate a total of 1k_BT energy during the overall movement of 1 ms. According to the viscosity model, the hydrophilic components of the sodium channel must make small but extremely rapid movements during the overall conformational change.

The viscosity dependence of sodium channel gating is apparently osmolarity dependent

The previous paper (Kukita, 1997) compared solvent effects using the classical osmotic stress model, in which plotting of the data as a function of osmolarity was the first step of the analysis. The data were well described as a function of osmolarity by the following equation:

(15)

where ΔΠ and β are the increase in solution osmolarity (in osmol l⁻¹) and a constant (in l osmol⁻¹) which is equivalent to the solute inaccessible volume in l mol⁻¹, respectively.

The percentage change in t_g is well fitted by eqn (15). The β_g values are listed in Table 2 and show a clear molecular weight dependence. Considering only this result, it looks as if there is an osmolarity-dependent, but not a viscosity-dependent, rate-limiting step in the gating process. However, this is incompatible with the fact that electrolytes did not alter the time course of sodium currents, even the osmolarity was higher than that of effective non-electrolyte solutions (Fig. 9 of Kukita, 1997). To explain electrolyte effects, it is reasonable to consider that the osmolarity effects might be additional to the viscosity effects as in the previous section.

In the present study, as in other similar experiments, non-electrolyte was added to increase the solution viscosity, so the osmolarity of the solution inevitably increased at the same time. There is a simple relation between the relative viscosity η/η₀ and the osmolarity difference ΔΠ(Fig. 4A) as described in the following equation:

(16)

where p is the constant (in l osmol⁻¹).

Figure 4. The gating current time constants as a function of solution osmolarity.

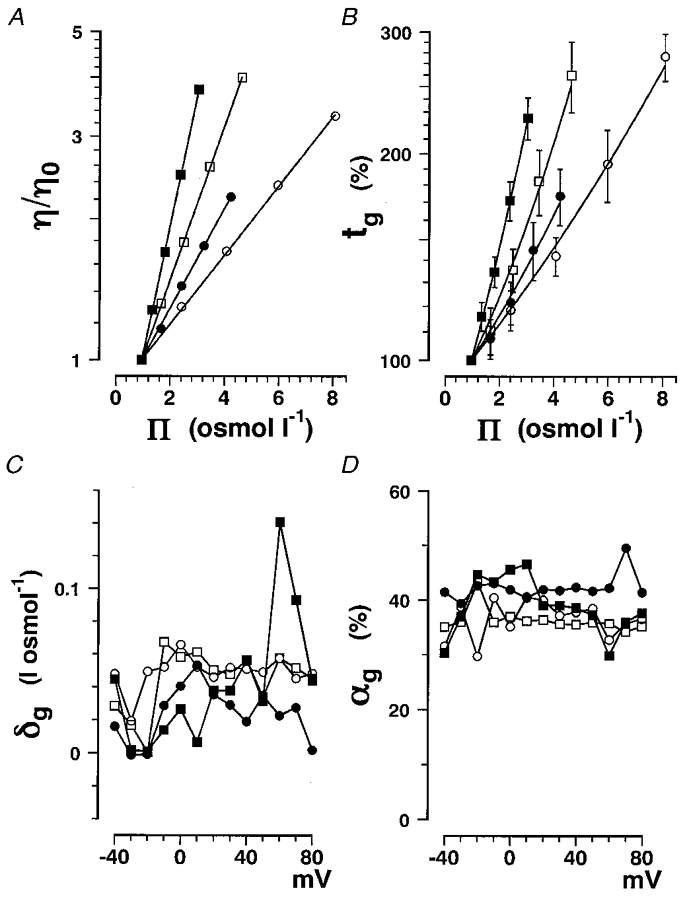
Data obtained in glycerol (○), erythritol (•), glucose (□) and sucrose (▪) solutions are plotted. A, η/η₀ is plotted on a logarithmic scale as a function of solution osmolarity for the different non-electrolytes. The data are fitted with eqn (16). The p values obtained are listed in Table 2. B, the percentage change in t_g at +20 mV plotted as a function of Π. The same data as in Fig. 3A are plotted with s.d. values (vertical bars). The data were fitted with eqn (17) and then α_g and δ_g for the four different non-electrolytes were derived. C, δ_g plotted as a function of membrane potential. D, α_g plotted as a function of membrane potential.

The values of p for the four non-electrolytes are listed in Table 2.

The osmolarity dependence of time constants and the non-electrolyte molecular weight dependence of β were apparent and were attributable to the close correlation between the solution viscosity and solution osmolarity.

Using eqns (8) and (16), the percentage change in the time constant can be expressed by:

(17)

The percentage change in gating current time constant was plotted as a function of solution osmolarity (t_g-Πcurve) and then fitted with eqn (17) in Fig. 4B, in place of eqn (15) as previously.

By this procedure, α_g and δ_g were derived at the same time. The α_g values were almost the same as those obtained in t_g-η/η₀ curves with a fixed δ_g value of 0.05 l osmol⁻¹. The derived δ_g values were roughly equal to 0.05 l osmol⁻¹. Therefore, the analysis using the corrected t_g-η/η₀ curves and that using t_g-Πcurves proved to be equivalent and the α_g and δ_g values obtained were similar as listed in Table 2.

δ_g and α_g are plotted as a function of membrane potential in Fig. 4C and D, respectively, and show no dependence on membrane potential. Since δ_g values are much smaller than β_g values and do not depend on the non-electrolyte molecular weight (Table 2), it can be concluded that the observed solvent effects on the gating currents do not significantly depend on molecular weight (Table 2).

Combining eqns (8) and (16), the equation equivalent to eqn (17) for the t_g-η/η₀ curve is given by eqn (18), which is a more general description of eqn (13) in the previous paper (Kukita, 1997):

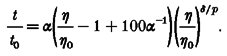(18)

The α_g and δ_g values obtained by fitting the t_g-η/η₀ curve with eqn (18) were much more scattered than those obtained using eqn (17) in the t_g-Πcurve. So, for further analysis, eqn (17) was used for the t-Πcurve.

Osmolarity effects on time course are larger for sodium current than for gating current

The same analysis was performed on the sodium current data. The percentage change in time-to-peak sodium current (t_p) is plotted as a function of osmolarity in Fig. 5A. The data were fitted well with eqn (17). The α_p values obtained are plotted as a function of membrane potential in Fig. 5B and show considerable scatter because the number of data points was not large enough compared with the number of free parameters (two), but the averaged values were almost equal to or slightly smaller than those for the viscosity parameter of the gating current (α_g). On the other hand, δ values for the activation of sodium current (δ_p) were greater than those of the gating current (δ_g). If α_p was fixed equal to the mean α_g, δ_p showed less scatter (Fig. 5D) than when using variable α_p values (Fig. 5C). The δ_p values were slightly larger at more negative membrane potentials showing a tendency similar to β_p values as shown in the previous paper (Kukita, 1997), although the β_p values are twice as large as the δ_p values as shown in Table 4. It is notable that δ_p values are much less dependent on non-electrolyte molecular weight than are β_p values.

Figure 5. The time-to-peak sodium current in non-electrolyte solutions as a function of solution osmolarity.

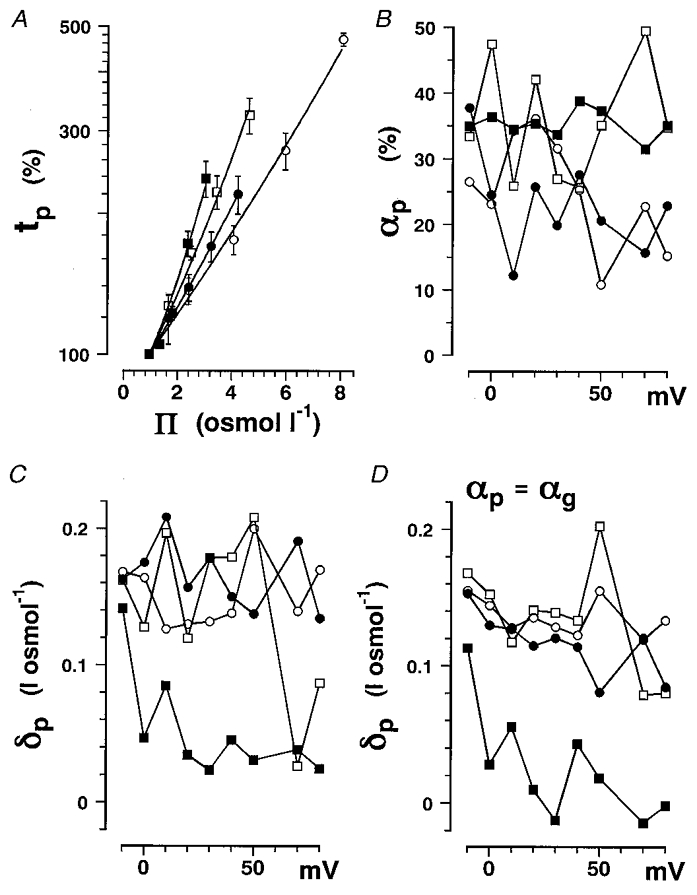
Data obtained in glycerol (○), erythritol (•), glucose (□) and sucrose (▪) solutions are plotted. A, the percentage change in t_p at +20 mV plotted as a function of Π. The data are plotted with s.d. values (vertical bars). Data were fitted with eqn (17), and then parameters α_p and δ_p for four different non-electrolytes were obtained. B, α_p plotted as a function of membrane potential. C, δ_p plotted as a function of membrane potential. D, δ_p obtained by fitting the data with eqn (17) with α_p fixed equal to the averaged α_g for the gating current (Table 2) are plotted as a function of membrane potential.

Table 4.

Viscosity and osmolarity parameters for sodium currents α_p, β_p, δ_p, α_h, β;_h and δ_h in solutions containing nonelectrolytes of different size

A. tp parameters
				if αp =αg
Non-electrolyte	βp(l osmol−1)	αp(%)	δp(l osmol−1)	δp(l osmol−1)	Δδp(l osmol−1)
Glycerol	0.214 ± 0.012	38.9 ± 12.3	0.127 ± 0.024	0.135 ± 0.012	0.082
Erythritol	0.252 ± 0.015	36.9 ± 10.5	0.139 ± 0.030	0.126 ± 0.014	0.092
Glucose	0.346 ± 0.024	35.8 ± 10.3	0.146 ± 0.043	0.142 ± 0.017	0.085
Sucrose	0.375 ± 0.044	36.5 ± 1.6	0.057 ± 0.040	0.039 ± 0.043	0.009

B. th parameters
				if αh =αg
Non-electrolyte	βh(l osmol−1)	αh(%)	δh(l osmol−1)	δh(l osmol−1)	Δδh(l osmol−1)
Glycerol	0.256 ± 0.022	40.9 ± 13.4	0.167 ± 0.016	0.189 ± 0.021	0.136
Erythritol	0.318 ± 0.019	41.4 ± 1.2	0.193 ± 0.018	0.202 ± 0.018	0.168
Glucose	0.458 ± 0.026	36.6 ± 2.9	0.269 ± 0.021	0.283 ± 0.032	0.226
Sucrose	0.548 ± 0.032	38.1 ± 2.3	0.220 ± 0.019	0.221 ± 0.016	0.191

A, β_p, α_p and δ_p were obtained for the time-to-peak (t_p) sodium current. β_p values were obtained by fitting the t_p–π curve (Fig. 5A) with eqn (15) and were dependent on the nonelectrolyte size. α_p and δ_p (fourth column) values were obtained by fitting the t_p–π curve with eqn (17). δ_p values in the fifth column were obtained by fitting the t_p–π curve (Fig. 5A) with eqn (15) but this time fixing α_p equal to averaged values of α_g (from the sixth column in Table 2). The δ_p difference (Δδ_p) was calculated by subtracting δ_g (seventh column, Table 2) from δ_p (fifth column, this table). Data were averaged between −10 and +40 mV. B, β_h, α_h and δ_h were obtained for the inactivation time constant (t_h). Parameters were obtained by fitting the t_h–π curve (Fig. 6A) with eqn (15). α_h and δ_h (fourth column) values were obtained by fitting the t_h–π curve with eqn (17). δ_h values in the fifth column were obtained by fitting the t_h–π curve (Fig. 6A) with eqn (15) but this time fixing α_h equal to averaged values of α_g (from the sixth column in Table 2). The δ_h difference (Δδ_h) was calculated by subtracting δ_g (seventh column, Table 2) from δ_h (fifth column, this table). Data were averaged between −10 and +40 mV.

The δ_p values are around three times greater than δ_g values in the gating current analysis and probably reflect osmolarity effects on the final step of sodium channel activation.

The δ_p–δ_g difference (Δδ_p) shows the osmolarity dependence of the final opening step and was almost equal for glycerol, erythritol and glucose but was much smaller (∼10%) for sucrose. The osmolarity effects on the final opening step may occur in the pore region, since these results suggest that this region can exclude sucrose molecules.

The data for the sodium channel inactivation time constant (t_h) were analysed in the same way as data for t_p. The percentage change in t_h is plotted as a function of osmolarity in Fig. 6A, and fitted with eqn (17). The α_h and δ_h values obtained are plotted as a function of membrane potential in Fig. 6B and C, respectively. The δ_h values obtained with a fixed value of α_h (=α_g) as in Fig. 5D are plotted as a function of membrane potential in Fig. 6D and showed a similar trend to the plot of δ_h values obtained with variable α_h (Fig. 6C). The δ_h values show a clear voltage dependence like β_h as shown in the previous paper (Kukita, 1997) and are almost equal among the four non-electrolytes. Unlike Δδ_p, Δδ_h for sucrose is larger than that for glycerol and erythritol. Thus osmolarity dependence in the inactivation process may be attributable to the whole flexible surface of the sodium channel protein.

Figure 6. The inactivation time constant in non-electrolyte solutions as a function of solution osmolarity.

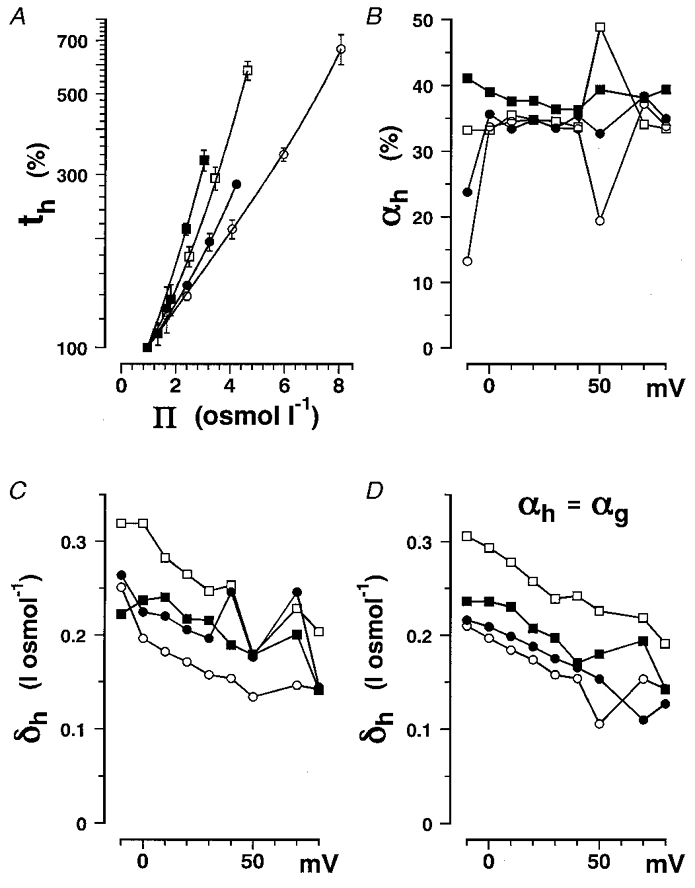
Data obtained in glycerol (○), erythritol (•), glucose (□) and sucrose (▪) solutions are plotted. A, percentage change in t_h at +20 mV plotted as a function of Π. The data are plotted with s.d. values (vertical bars). Data were fitted with eqn (17), and then α_h and δ_h for the four different non-electrolytes were obtained. B, α_h plotted as a function of membrane potential. C, δ_h plotted as a function of membrane potential. D, δ_h obtained by fitting the data with eqn (17) with α_h fixed equal to the averaged value of α_g (Table 2), as in Fig. 5D, plotted as a function of membrane potential.

The t_p value is a suitable measure of activation kinetics with negligible errors under conditions where the kinetics of both the activation and inactivation processes are slowed as in the solvent effects. The t_p value in squid sodium channels, which have a fast activation rate and a relatively slow inactivation rate, was changed by only 4% when the inactivation time constant increased by 40%. This is quite different from the situation in mammalian sodium channels, which have a slow activation rate and a fast inactivation rate, where t_p and the peak sodium current at t_p are drastically affected by the inactivation process (Aldrich & Stevens, 1987; Armstrong & Hille, 1998). Since the ratio of t_h to t_p was larger in glucose solutions than in other non-electrolyte solutions, t_p, and hence α_p and δ_p, could be slightly overestimated in glucose solutions. However, this does not affect the final conclusion that the ineffectiveness of sucrose could be attributed to the exclusion of sucrose from the pore.

The molecular weight dependence of α and δ is summarized in Fig. 7. The viscosity-dependent process (described by α) in sodium channel activation and inactivation was the same as that for the gating current and did not depend on non-electrolyte molecular weight (Fig. 7A). Therefore, the observed viscosity dependence of the sodium current is mainly attributable to the viscosity-dependent process accompanying the gating current.

The osmolarity dependence (described by δ) may be attributed to the transient hydration of 2–3, 5 and 8–12 water molecules during the gating current, the final opening step and the inactivation process, respectively. The δ and Δδ values have a different molecular weight dependence from β values (Kukita, 1997, Fig. 14). Particularly, the osmolarity dependence of activation (Δδ_p) was much smaller for sucrose, suggesting that the hydration occurred in the pore region, from which sucrose molecules are excluded. Furthermore, a small number for δ and Δδ suggests that the interaction with water molecules in the pore is local and specific to a flexible interior such as the P loop.

DISCUSSION

The solvent effects on gating currents can be simply explained by a viscosity model similar to that used for viscosity-dependent conformational change of hydrophilic proteins (Gutfreund, 1995), because they did not depend on the membrane potential over a wide range or on the molecular weight of non-electrolytes. Flexible hydrophilic parts including the S4 segment and its guide, play important roles in determining the time constant of the channel gating process. Considering that voltage sensing is effective in a hydrophobic insulating medium (Armstrong & Hille, 1998), it is surprising that the conformational change accompanying gating current is affected by hydrophilic non-electrolytes in a viscosity-dependent manner. Voltage sensors such as the S4 segment may be separated only by narrow hydrophobic boundaries from other channel parts facing the extracellular and intracellular solutions allowing ready interaction with hydrophilic non-electrolytes on both sides, directly and/or indirectly through linker loops. Since one-third of the time constant is determined by a viscosity-dependent process in the control solutions, the whole surface of the S4 segment need not be exposed to the aqueous environment. The S4 segment and its surrounding channel could well be a flexible structure capable of rapid movements, in which elementary movements take a few microseconds and dissipate a total energy of 1k_BT during the succeeding thousand processes, so that friction effects on the aqueous surface could readily affect the channel interior. The present results are compatible with the finding that upon depolarization for a few milliseconds part of the inward-facing S4 segment moves and becomes exposed to the aqueous phase outside, where it can interact with large hydrophilic molecules (Yang et al. 1996).

Using a model-independent analysis, the remaining solvent effect on the final opening step is concluded to be osmolarity dependent and to be attributable to hydration in the pore. The model-independent analysis procedure is summarized as follows. The percentage change in t_g and that in t_p are plotted as a function of the osmolarity difference (ΔΠ) or relative viscosity (η/η₀) and then fitted with eqn (17) or (18). The analysis using eqn (17) is equivalent to that using eqn (18), since η/η₀ is not independent of ΔΠ and is a function of ΔΠ given by eqn (16). The α values obtained are independent of molecular weight and so confirm the validity of viscosity model, although a correction for the osmolarity effect needs to be made and is expressed as δ, which is much less dependent on non-electrolyte molecular weight than the β value derived from the former osmolarity model (Kukita, 1997). This important finding regarding the solvent effects could only be obtained from experiments using several species of homologous non-electrolytes with different molecular weights. Solvent effects on sodium channel activation are expressed by the following sequential model, in which the final transition to open state is added to the original model (Armstrong & Matteson, 1982): where α and β are the forward and backward rate constants, respectively, in Hodgkin & Huxley equations (Hodgkin & Huxley, 1952) and α₀ and β₀ are the forward and backward rate constants, respectively, for the voltage-independent final transition to the open state.

The results in the present paper show that the process accompanying the gating current was viscosity dependent and the final transition was osmolarity dependent to give the following more simplified model: where k(V,η) and k′(V,η) are the voltage- and viscosity-dependent forward and backward rate constants during the gating current, respectively, and k(Π) is the osmolarity-dependent (voltage-independent) forward rate constant during the final transition.

In this model, the reverse process for the final transition, which is solvent and voltage dependent, as shown in the previous paper (Kukita, 1997), is omitted for simplicity. Further analysis using several non-electrolytes of different size is required to complete the model. As it stands, however, this model is adequate enough to explain the fact that there is no observable slowing of ionic current in hyperosmolar electrolyte solutions (Kukita, 1997) or in heavy water (Alicata et al. 1990; Rayner et al. 1992). Since the overall kinetics cannot be described by a simple function except in a Hodgkin-Huxley model, it is difficult to fit the data with the necessary functions to obtain those parameters which are sensitive to solvent. Furthermore, it is not fruitful to perform the simulation according to existing models such as Schemes 1 and 2, because the obtained conclusion will strongly depend on the model used and be less reliable than that obtained by the model-independent analysis in the present paper.

Scheme 1.

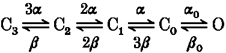
Scheme 2.

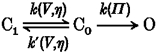
The osmolarity effects during the final opening steps probably occur in the pore since only the largest molecule, sucrose, has little effect on this process. This osmolarity-dependent process might be related to the hydration process in the pore but is incompatible with the osmotic stress model (Zimmerberg & Parsegian, 1986), in which the opposite effects would be expected. The hydration effects may be related to a hydrophilic interaction of ions and solvent, i.e. water and non-electrolytes, with flexible parts in the pore region, probably P loops (Bénitah et al. 1997; Tsushima et al. 1997).

A hydration model of the pore has been proposed by other investigators (Rayner et al. 1992; Starkus et al. 1995) to explain solvent effects on the sodium and potassium channel activation, but this model ignores the effects of solution viscosity. Furthermore, the model was developed on the basis that Rayner et al. (1992) did not observe slowing of the crayfish sodium channel gating current in the hyperosmolar media but observed the slowing of the sodium current, a situation similar to that seen with heavy water effects (Alicata et al. 1990). In the present paper, the viscosity-dependent slowing of the gating current was clearly demonstrated. The reason why the gating current results were different is not altogether clear at this moment, but one particular difference between procedures, besides animal species, is apparent. Rayner et al. (1992) examined the solvent effects by unilateral exposure to the hyperosmolar solution. Another difference is that their estimated solute inaccessible volume was about 1 nm³, which equates to more than 33 water molecules, but in the present study it was 0.15 nm³, which equates to the volume of five water molecules. A large solute inaccessible volume indicates rather bulky effects in the pore as in the classical osmotic stress model (Zimmerberg & Parsegian, 1986), but a small solute inaccessible volume indicates a local interaction with flexible segments. The model proposed by Rayner et al. (1992) is more complicated than the model outlined in Scheme 2, because they introduced two parallel transition pathways, i.e. one solvent dependent and the other voltage dependent, which interact to compensate the voltage-dependent transitions in these pathways to reveal the voltage-independent solvent effects.

Using the same analysis for the inactivation process, it was clear that this process is remarkably osmolarity dependent but it does not show any clear molecular weight dependence, because in this process the inactivation ball interacting with its receptors may be essential for the rate-limiting step and there may not be a limited size comparable with sucrose molecules (Armstrong & Hille, 1998; Kreusch et al. 1998). The osmolarity effects on the inactivation process may be derived from the flexible structures (e.g. tetramerization domains in Shaker BK channel) surrounding the inactivation ball and its receptors (Kreusch et al. 1998) and/or the flexibility of the inactivation ball and its receptors themselves.

The slowing of gating currents cannot be explained by the extreme case in which only the final transition to open state was slowed in a solvent-dependent manner, resulting in the preceding overall kinetics of gating current being slowed down. This is not plausible in the present experiment, because the amount of slowing of the gating current remained unchanged at membrane potentials more negative than −30 mV, where only a few sodium channels make the final transition to the open state. However, a slight osmolarity effect on gating currents described by δ_g might be a trait of this effect influenced by an osmolarity-dependent final step to the open state.

Solvent dependence has been demonstrated in more complex systems like membrane enzymes, in which the activity was determined by the solution viscosity of glycerol solutions but not by membrane viscosity (Zakim et al. 1992). Zakim et al. also argued against the popular idea that the membrane viscosity, which is inversely related to membrane fluidity, can regulate enzyme activity, and showed that regulation by membrane viscosity was not involved in major aspects of the enzyme activity examined. In most experiments in which membrane fluidity is changed by temperature, it is difficult to determine whether the enzyme activity is regulated by membrane fluidity or directly by temperature. For example, early studies showed functional squid sodium channels in glycerol solutions at −20°C, where the lipid membrane would be expected to be in a gel phase (Kukita, 1982); moreover, there was no discontinuity or break in the activity-temperature curve above this temperature. It is therefore extremely unlikely that the non-electrolyte-mediated slowing of sodium channel gating in the present paper was an indirect action via decreased membrane fluidity. Furthermore, several alcohols have been found to have no effect on the kinetics of sodium currents (Kukita & Mitaku, 1993; F. Kukita, unpublished data) at anaesthetic concentrations which increase membrane fluidity (Zavoico & Kutchai, 1980).

Solvent effects might be a useful means of assessing the flexibility of a protein. Generally, fluctuation in structure is an important physical property of proteins (Karplus & Petsko, 1990) in relation to solvent effects (Gutfreund, 1995), especially in sodium channel proteins (Kukita, 1997). Non-electrolytes and/or water molecules can interact with a protein on its surface and decrease the fluctuation of macromolecules with the effect of slowing macroscopic transitions involved in biological activity. The image of flexible channel protein structures is not incompatible with the 3D structure obtained by X-ray crystallography (Doyle et al. 1998). The X-ray crystallographical image is a time and space average of rapidly fluctuating structures (Karplus & Petsco, 1990), i.e. in a nanosecond time scale. There is evidence that the P loop of the sodium channel may be able to move in the pore and this flexibility might have functional importance (Bénitah et al. 1997; Tsushima et al. 1997). The 3D structure of the tetramerization domain which can separate inactivation balls and their receptor sites in H4 loops are suggested to be looser and more flexible than the impression gained from X-ray crystallography (Kreusch et al. 1998).

The physical properties of solutions, i.e. viscosity and/or osmolarity, are just as important in determining the kinetics of sodium channel gating as temperature (Hodgkin & Huxley, 1952) and pressure (Conti et al. 1984). All these parameters can be regarded as classical physicochemical parameters governing channel kinetics and should be reconciled by recent molecular biological studies, since they are compatible with the Hodgkin-Huxley model and other more recent kinetic models. In the context of the large body of information concerning the structure of ionic channels (Armstrong & Hille, 1998), solvent effects on the hydrophilic surface of these proteins can give additional information essential to understanding the molecular machinery of these proteins.