Weak common parallel fibre synapses explain the loose synchrony observed between rat cerebellar Golgi cells

Abstract

1. In anaesthetized rats, pairs of cerebellar Golgi cells fired synchronously at rest, provided they were aligned along the parallel fibre axis. The observed synchrony was much less precise, however, than that which would be expected to result from common, monosynaptic parallel fibre excitation.

2. To explain this discrepancy, the precision and frequency of spike synchronization (i.e. the width and area of the central peak on the spike train cross-correlogram) were computed in a generic model for varying input, synaptic and neuronal parameters.

3. Correlation peaks between model neurons became broader, and peak area smaller, when the number of afferents increased and each single synapse decreased proportionally in strength. Peak width was inversely proportional to firing rate, but independent of the percentage of shared afferents. Peak area, in contrast, scaled with the percentage of shared afferents but was almost firing rate independent.

4. Broad correlation peaks between pairs of model neurons resulted from the loose spike timing between single model neurons and their afferents. This loose timing reflected a need for long-term synaptic integration to fire the neurons. Model neurons could accomplish this through firing rate adaptation mediated by a Ca²⁺-activated K⁺ channel.

5. We conclude that loose synchrony may be entirely explained by shared input from monosynaptic, non-synchronized afferents. The inverse relationship between peak width and firing rate allowed us to distinguish common parallel fibre input from firing rate covariance as a primary cause of loose synchrony between cerebellar Golgi cells in anaesthetized rats.

Neurons that show repeated very precisely synchronized firing must be coupled by a fast electrical process, such as the joint activation of synapses from a shared afferent. The proposition that loose synchrony cannot be induced by shared input is often implicitly accepted. Whereas this latter statement may be valid when synapses are strong, it is certainly unsubstantiated, as we will demonstrate, for neurons that receive hundreds or thousands of weak-efficacy synapses.

Synchronous firing, with no neuron leading the other, is recognized as a peak at 0 ms offset on the spike train cross-correlation histogram (CCH) (Moore et al. 1970). The sharpness of the central peak is a measure of the precision of synchrony and reflects, indirectly, the precision with which each neuron fires in response to a shared afferent spike. In general it is assumed that this precision is determined by the time course of the unitary excitatory postsynaptic potential (EPSP), followed by a linear or static non-linear transformation caused by spike generation. Peaks narrower than predicted from the EPSP time course, for example, have been attributed to an increased firing probability during the upstroke of an EPSP (Kirkwood, 1979).

In experimental recordings, however, many central peaks have widths of several tens of milliseconds, which is broader than that which can theoretically result from the time course of unitary EPSPs. Such broad central peaks have therefore been considered inconclusive for shared monosynaptic input. Instead, they have been ascribed to burst firing in the postsynaptic neurons (Eggermont & Smith, 1996), to loose synchronization between the afferents (Kirkwood et al. 1982; Datta et al. 1991) or to temporal dispersion caused by conduction delays and polysynaptic transmission (Nelson et al. 1992). Broad central peaks are commonly regarded as designating covariances in firing rate between the neurons over time (Eggermont & Smith, 1996).

A key assumption in all the inferences referred to above is that the central peak on a CCH is static and that its width is independent of the firing rate of the component neurons. Because of the broad dynamic ranges over which neurons can fire, it is conceivable, however, that neurons are capable of scaling the intervals between ‘synchronous spikes’ proportional to the intervals between non-synchronous spikes. If this were the case, peak width would be dynamic and inversely proportional to firing rate.

We report here that both phenomena (static and dynamic synchronization) were found in pairs of model neurons that shared input from randomly firing, monosynaptic afferents. Whether the central peak was static or dynamic depended on the organization of the input (the strength of the synapses) and on the intrinsic dynamics of the model neurons (their excitability and need for synaptic integration). With a dynamic synchronization, peak width was defined by the size and frequency of the EPSPs rather than by their time course, and the peaks could be much broader than would be considered possible if the EPSP time course were the only criterion.

The relevance of this theoretical finding was demonstrated by means of an analysis of the synchronicity observed between pairs of cerebellar Golgi cells, recorded extracellularly in anaesthetized rats (Vos et al. 1999a). Golgi cells, the major inhibitory interneurons in the granular layer of the cerebellar cortex, are presumed to receive excitation from hundreds to thousands of parallel fibres through weak synapses (Pellionisz & Szentagothai, 1973; Dieudonné, 1998). Owing to this, they fulfil a major requirement for dynamic synchronization in the model. The parallel fibres (granule cell axons) are unique with regard to their length (up to 5 mm in rats; Pichitpornchai et al. 1994) and their alignment parallel to the transverse axis of the cerebellum, both of which enhance the probability that transversely aligned Golgi cells receive input from the same parallel fibres. In the above study (Vos et al. 1999a), 25 of 26 pairs of Golgi cells aligned along the parallel fibre axis, and hence presumed to share monosynaptic parallel fibre excitation, spontaneously discharged synchronous spikes, whereas 12 of 16 orthogonally oriented pairs did not. However, the central CCH peaks were generally broad (29.8 ± 12.5 ms; mean ± s.d.), particularly when the mean Golgi cell firing rate was low. We therefore analysed the relationship between the precision of synchrony and the instantaneous Golgi cell firing rate. From this relationship, two mechanisms of loose synchronization could be distinguished: common parallel fibre excitation, causing broad central CCH peaks when the Golgi cells fired at low rates, and covariances in firing rate, causing broad peaks when the instantaneous firing rate was high.

METHODS

Aim and outline of the model

In order to explain the broad central peaks on CCHs between spike trains from cerebellar Golgi cells presumed to receive common monosynaptic parallel fibre excitation (Vos et al. 1999a), a model was simulated containing only Golgi cells and their afferent parallel fibres (without the source granule cells). The generic configuration of this pure feed-forward model (Fig. 1A) makes it applicable to almost any neuronal population. For convenience we indicate the neurons as Golgi cells, their afferents as parallel fibres (PFs) and the synapses as PF synapses. In essence, a pair of Golgi cells received excitation from a set of PFs of which a restricted, variable number made synapses on both Golgi cells. The PFs discharged randomly, at a constant mean rate, and evoked steady levels of ‘spontaneous’ activity in Golgi cells. Figure 1A is a schematic representation of this configuration with each Golgi cell receiving 108 PF synapses, 90 of which were synapses made by PFs shared with the other Golgi cell of the pair.

Figure 1. Cross-correlation analysis of model Golgi cell responses.

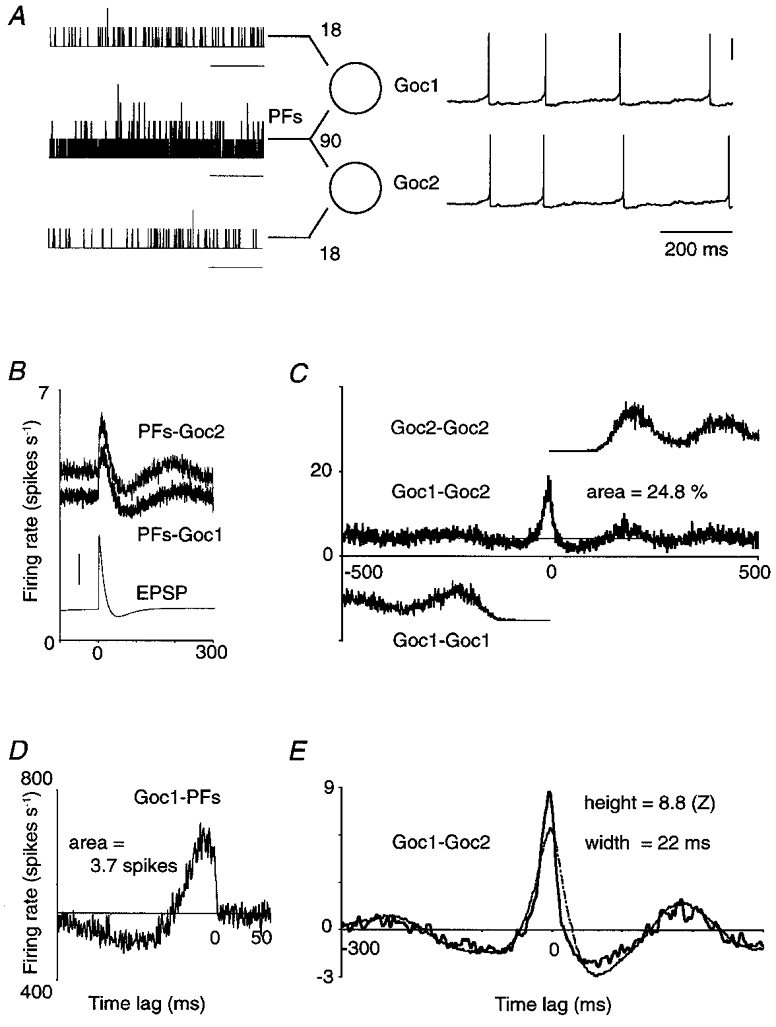
A, two Golgi cells (Goc1 and Goc2) which each receive input from 108 parallel fibres (PFs). Of the set of afferents, 90 PFs make synapses on both Golgi cells. The spike train histograms on the left, compiled for illustration only, show in 1 ms bins the number of spikes selectively conveyed by 18 PFs to Goc1 (upper trace), by 18 other PFs to Goc2 (lower trace) and by the joint set of 90 PFs to both Golgi cells (middle trace). Three of the four spikes which Goc1 and Goc2 fired during this input pattern were almost synchronous (membrane potential traces on right; vertical scale bar, 0.2 V). To calculate the cross-correlation histograms (CCHs) in B-E, a mean firing rate of 5 spikes s⁻¹ was maintained in each PF for 1200 s, yielding a record of 4847 ‘spontaneous’ spikes in Goc1 (mean firing rate, 4.04 spikes s⁻¹; resting potential, −63.3 mV) and 5679 spikes in Goc2 (4.73 spikes s⁻¹; resting potential, −62.8 mV). Horizontal scale bars in A, 200 ms. Horizontal axes in B-E, time lag (ms). B, PFs-Goc1: non-smoothed CCH between the entire set of 108 PFs afferent to Goc1, and Goc1; PFs-Goc2: same for Goc2. Vertical axis, Golgi cell firing rate. The thin trace is a unitary EPSP (holding potential, −68 mV; vertical scale bar, 0.2 mV). C, Goc1-Goc2: non-smoothed CCH between Goc1 and Goc2, expressed as Goc2 firing rate. The central peak is a few milliseconds offset to the left because Goc2 fired faster than Goc1, due to its less negative resting membrane potential. The peak area, integrated above the mean (thin horizontal line), measured 0.248 spikes indicating that a quarter of the spikes were synchronous. Goc1-Goc1 and Goc2-Goc2: vertically offset, one-sided autocorrelograms. D, Goc1-PFs: non-smoothed CCH between Goc1 and its population of 108 afferent PFs. Vertical axis, firing rate of the PF population; area above the mean in absolute spike count, 3.7 spikes. E, thick curve is the CCH of C after smoothing and normalization. Thin curve is the predicted CCH obtained, after smoothing and normalization, by cross-correlating the CCHs labelled PFs-Goc1 and PFs-Goc2 from B.

In practice, 30 Golgi cells and a variable number of PFs were evenly positioned along a one-dimensional array. Each PF connected to all Golgi cells within a fixed distance (half the PF length; Maex & De Schutter, 1998b). Consequently, the total number of PF synapses onto each Golgi cell was defined by the total number of PFs in the array, whereas the number of PF synapses shared with other Golgi cells in the array varied when pairs with different intervals were selected. Within this arrangement, a single simulation yielded responses from more than 20 Golgi cell pairs for a range of overlap between the spike trains to a pair. Variability between pairs was introduced by randomizing the Golgi cell resting potentials and the strengths of the PF synapses (see Maex & De Schutter, 1998b). This variability also accounted for differences in firing rate between the neurons of a pair (Fig. 1A).

Neuron models

A Golgi cell was modelled as a single isopotential compartment with six voltage-gated channels (see Maex & De Schutter, 1998b, for the complete equations). This model reproduced the responses to current injection of in vitro rat Golgi cells (Dieudonné, 1998). In summary, spike current was carried through an inactivating Na⁺ channel, a high-threshold Ca²⁺ channel, and both an inward rectifying and a fast inactivating K⁺ channel, whereas spike afterhyperpolarization was effectuated predominantly by a voltage- and Ca²⁺-dependent K⁺ channel (K_Ca; Moczydlowski & Latorre, 1983). During an action potential the [Ca²⁺]_i sharply rose and then slowly decayed to its resting level with a time constant of 200 ms. This decay time determined, through the effect of [Ca²⁺]_i on K_Ca channel activation, the time course of firing rate adaptation. In addition, the model Golgi cell had a hyperpolarization-activated H channel, causing a rebound depolarization following prolonged hyperpolarization. Compared to our previous study (Maex & De Schutter, 1998b), model Golgi cells were here assigned more negative resting membrane potentials, resulting in lower discharge rates at rest (range, 0–7 spikes s⁻¹), which enhanced the detectability of correlations in their discharges during PF stimulation (Melssen & Epping, 1987).

In order to assess whether intrinsic neuronal mechanisms of synaptic integration and spike generation affected the precision of interneuronal synchrony, control simulations were performed on model Golgi cells that showed, after substitution of their voltage-gated channels, the dynamics of model cerebellar granule cells (Gabbiani et al. 1994; Maex & De Schutter, 1998b) (see Fig. 5). Like model granule cells, these modified model Golgi cells had a high firing threshold and lacked firing rate adaptation. Simulations were also conducted on leaky integrate-and-fire neurons, which were derived from model Golgi cells by inactivating all voltage-gated channels. In these passive neurons, dummy spikes (with a 2 ms refractory period) were generated at a fixed threshold of −40 mV. The neurons were repolarized by an autapse on their GABA_A channel. Simulations were run with various values for the membrane time constant.

Figure 5. Regular firing favours, but is not necessary for, loose synchronization.

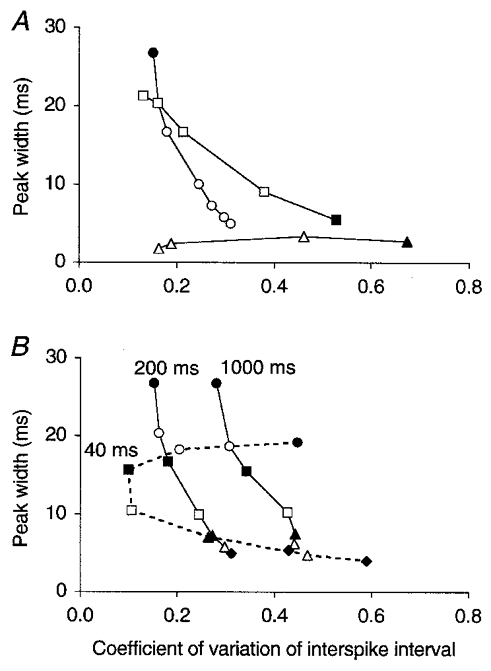
Relationship between the regularity of firing of model Golgi cells (coefficient of variation of the interspike interval, c.v.) and the precision of their synchronization (the width of the central peak on the CCH). The c.v. was calculated as standard deviation of interspike interval/mean interspike interval, averaged over > 20 Golgi cells (see Methods). A, data obtained by varying the strength of a PF synapse (and in inverse proportion the number of PF afferents) at a constant PF firing rate of 5 spikes s⁻¹ (squares; ▪ for lowest number, i.e. 6 synapses per Golgi cell; data from Fig. 3) or by varying the PF firing rate in the 108 AMPA configuration (circles; • for lowest firing rate; data from Fig. 2A). The triangles represent data points from Golgi cells with granule cell dynamics (see Methods) in the 108 AMPA configuration and at increasing PF firing rates (▴ for lowest firing rate; non-smoothed CCHs; synaptic strength needed to be taken 4 times larger to compensate for the increased firing threshold). B, reference curve of the 108 AMPA configuration copied from A (200 ms, middle curve), together with data obtained after the decay time constant of the [Ca²⁺]_i of Golgi cells had been increased 5 times (1000 ms, right curve) or decreased (40 ms, left dashed curve). Symbols represent different PF firing rates. Varying the time constant of [Ca²⁺]_i changed the excitability and hence the firing rate of Golgi cells compared to the reference curve, which was compensated for by adjusting the peak conductance of the Ca²⁺-dependent K⁺ channel for each particular condition. Owing to this, the same symbols on different curves also represent similar Golgi cell firing rates: about 5, •; 8, ○; 11, ▪; 17, □; 27, ▴; 34, ▵; and 41 spikes s⁻¹, ♦.

The PF synapses of model Golgi cells had AMPA receptor channels with rise and decay time constants of 0.03 and 0.5 ms, respectively (EPSP time to peak, 1.7 ms at 37°C; Maex & De Schutter, 1998b). In order to analyse the effect of synaptic kinetics, which has so far been considered as the major factor determining the precision of synchrony (Moore et al. 1970; Kirkwood, 1979), the time constants of the synaptic conductance were varied. In addition, simulations were run in which voltage-dependent NMDA receptor channels (Maex & De Schutter, 1998b) were substituted for the AMPA receptor channels (Fig. 2). Currents through NMDA receptor channels have been recorded in rat Golgi cells in vitro during PF stimulation, but their contribution to the EPSPs is probably negligible at physiological levels of the membrane potential (Dieudonné, 1998). NMDA receptor channels were simulated for theoretical considerations only, as instances of slow synapses (EPSP time to peak, 13.6 ms at 37°C).

Figure 2.

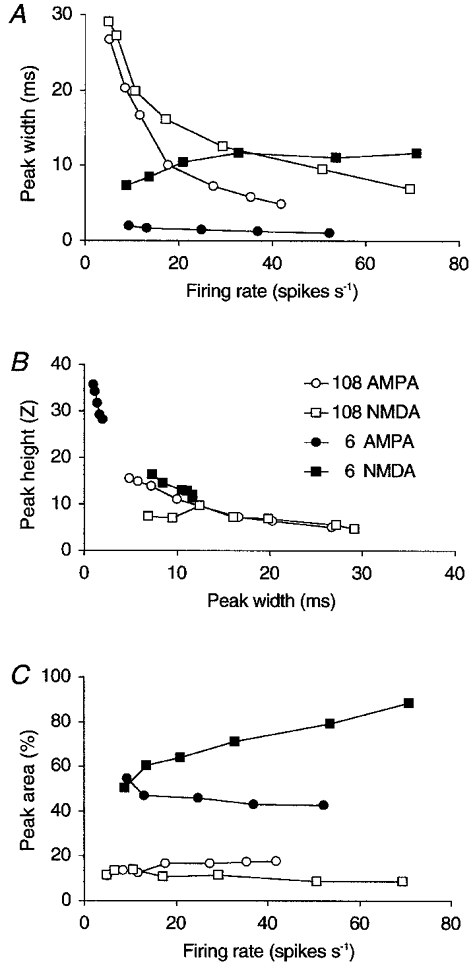
Different synaptic organizations can be distinguished by the effect of firing rate on synchronization

The effect of the strength and type of common afferent synapses and of the postsynaptic firing rate on the precision of synchronization (the width at half height of the central peak on the CCH; A and B) and on the percentage of synchronous spikes (the area of the central peak; C). Four synaptic configurations are compared. Both Golgi cells of a pair had either 6 or 108 PF afferents making either AMPA or NMDA receptor synapses (○, 108 AMPA synapses; □, 108 NMDA synapses; •, 6 AMPA synapses; ▪, 6 NMDA synapses). Each Golgi cell invariably shared five-sixths of its PF afferents with the other Golgi cell of the pair. The synaptic strength of a PF afferent was inversely proportional to the number of PF synapses. Golgi cell firing rate was varied by varying the PF firing rate. Peak height (B) and full width at half height (A and B) were measured on the smoothed, normalized CCH except for the 6 AMPA data points for which the CCH was non-smoothed. Peak area (C) was measured on the raw CCH (see Methods). Each data point represents the mean of 24 Golgi cell pairs with randomized resting membrane potentials and synaptic weights.

Finally, a PF was modelled as a time series of spike events (step size, 20 μs) with a Poisson interval distribution except for a 5 ms absolute refractory period. Each PF fired at a constant mean rate, drawn from a Gaussian distribution with a standard deviation of 20 % of the mean. Input was provided to a Golgi cell by convolving these time series with the conductance of its PF synaptic channel (see below).

The PF excitation of model Golgi cells

As will be shown in Results, the precision of synchrony between a pair of model Golgi cells was well explained by the precision with which each single Golgi cell fired in response to the PF stimulus (Fig. 1), and it was largely independent of the degree of input overlap (Fig. 4A). The PF stimulus to a Golgi cell was specified by three variables: the strength of a single PF synapse, the number of PF synapses (or PF afferents) and the mean PF firing rate.

Figure 4. Peak area, not peak width, depends on the degree of common input.

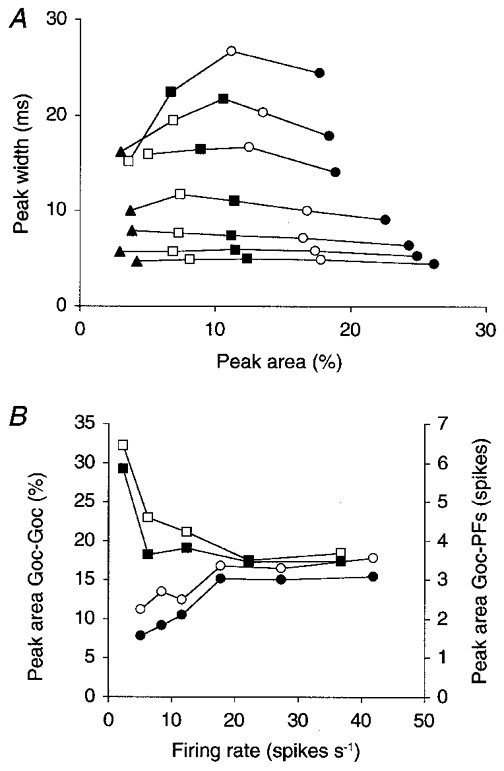
A, the data for the 108 AMPA configuration of Fig. 2A and C are completed with data for the same configuration but from Golgi cell pairs with lower and higher degrees of input overlap. Each curve was generated with a different PF firing rate (increasing from the upper to the lower curve); the resultant mean Golgi cell firing rates measured 5.1 (uppermost curve), 8.5, 11.7, 17.7, 27.4, 35.3 and 41.9 spikes s⁻¹ (lowermost curve). Different symbols represent pairs with different percentages of shared input. Of the 108 PF afferents to each Golgi cell, the number shared with the other Golgi cell of a pair was 108 (•), 90 (○, same data points as in Fig. 2A and C), 72 (▪), 54 (□), or 36 (▴). All data points are mean values of the central peak sizes measured on more than 20 CCHs (see Methods). When the percentage of shared afferents was small, not all CCHs showed a central peak. Data are therefore shown only for those parameter conditions in which at least half of the CCHs had a central Z-value > 3. B, the area of the central peak on the CCH is plotted versus the mean Golgi cell firing rate for the pairs with 90 shared afferents from A (○, same data). Hyperpolarizing the model Golgi cells by using more negative reversal potentials for their leak currents (E_leak between −80 and −75 mV instead of −70 and −60 mV) suppressed all spontaneous activity and increased peak area selectively at the lowest firing rates (□). The corresponding areas of the peaks on the CCHs between Golgi cells and their afferent PFs are plotted in filled symbols (right vertical axis; see Fig. 1D for measurement of this peak area).

In the computer implementation of the model, all PF synapses onto a Golgi cell were grouped onto a single synaptic channel, in which all synaptically induced conductances summed linearly. Repeated activation of this channel resulted in EPSCs of a given size and frequency (Wilson & Bower, 1989). The size of a unitary EPSC (more exactly, the unitary postsynaptic conductance) was defined by the strength of a single PF synapse. The resultant EPSC frequency was the product of the number of PF afferents and the mean PF firing rate. It is obvious that the same EPSC frequencies could be generated by an infinite number of combinations of values for these latter two variables. The number of PF synapses and the mean PF firing rate were therefore underconstrained, i.e. similar results were produced by varying either of them (at least when minor factors such as the PF refractory period or the randomization of synaptic strength are not taken into account). The sizes of the central peaks on the CCHs consequently did not depend on the actual values chosen for these two parameters, for which no experimental data are available. Instead, the combined effect of these variables, for a given synaptic strength, determined the Golgi cell firing rate.

In the Results section, the central peak sizes are therefore presented as functions of only two, instead of the above three, variables: the strength of a single PF synapse (Fig. 3) and the mean Golgi cell firing rate (Fig. 2). These variables can be directly compared with experimentally obtained data of EPSC sizes in vitro (Dieudonné, 1998) and of Golgi cell firing rates in anaesthetized rats (Vos et al. 1999b), respectively.

Figure 3. Peak width decreases, and area increases, with the strength of PF synapses.

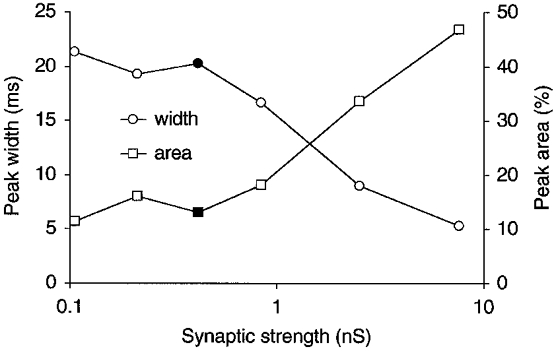
The width (○) and area (□) of the central peak on the CCH between a pair of model Golgi cells are compared for configurations with different strengths of PF synapses. The peak conductance of a single PF synapse was varied from 105.3 pS to 7.6 nS, but the firing rate of Golgi cells was held approximately constant by varying in inverse proportion the number of PF afferents (from 432 to 6). All PFs fired at 5 spikes s⁻¹ and made AMPA receptor synapses. Five-sixths of the synapses were shared with the other Golgi cell of the pair. Peak width was measured on smoothed CCHs. The data points at 421 pS (filled symbols) represent the 108 AMPA configuration of Fig. 2, in which the EPSC size measured 28.4 pA, which is similar to the size of EPSCs recorded in vitro in rat Golgi cells (Dieudonné, 1998).

For clarity of presentation, however, network configurations are described by the number of PF synapses on each Golgi cell, although these numbers should be interpreted in the light of the above. It is then always assumed that the strength of a single PF synapse scaled in inverse proportion to the number of PF synapses, a strategy also used by others (Segundo et al. 1968). The Golgi cell firing rate was then varied independently by varying the PF firing rate.

Model simulations

The models were constructed and numerically solved with GENESIS 2.1 (De Schutter & Beeman, 1998) on a dedicated Sun UltraSparc computer. Differential equations were integrated with a Crank-Nicholson method using a fixed step size of 20 μs.

Cross-correlation analysis of model spike trains

The spike trains of a pair of neurons, A and B, were cross-correlated to count the number of times neuron B fired within an interval [nΔt, (n+ 1)Δt] about neuron A (-1000 ≤n < 1000; bin width Δt = 1 ms). In each bin the constant count fr_Afr_BTΔt (fr_A and fr_B, mean firing rate of A and B; T recording period) was subtracted, which is the expected, constant correlation value according to the null hypothesis, i.e. uncorrelated firing between A and B. After division of the counts by the standard deviation of the counts in the CCH, the histogram values measured standard or Z-scores. This normalization guaranteed peak height to be independent of T (R. Maex, B. Vos & E. De Schutter, unpublished observations). Because the background counts vanish in such a normalized CCH, however, most illustrations show the mean firing rate of the second spike train around a spike of the first, reference spike train. This was obtained after division of the CCH counts by the number of reference spikes and the bin width.

The criterion for a significant central peak was a Z-score > 3 in the interval [-20 < n < 20]. Peak height was the highest Z-score in this interval (Fig. 1E). The full width at half height of the central peak was the interval between the n values, on either side, marking the first of three successive entries below half height. It is a measure of the precision of synchrony (Fig. 1E). The area of the central peak was calculated on the raw CCH, by summating the counts above the mean and dividing by the (geometric) mean number of spikes per neuron (Datta et al. 1991; Alonso et al. 1996). Peak area corresponds to the time integral of the central peak (expressed as firing rate) above the mean firing rate level. When multiplied by 100, peak area represents the mean percentage of synchronous spikes above the chance level (Fig. 1C).

Peak width and height were calculated on a smoothed CCH. Smoothing was necessary to obtain a reliable peak for every CCH, and was performed by four convolutions with a temporal filter {1/3, 1/3, 1/3} before normalization. The resulting decrease in standard deviation of the CCH compensated for the decline in peak height, so that the normalized peak height hardly changed after smoothing. Only CCHs with a very narrow peak were left unsmoothed, as mentioned in the figure legends.

In the graphs of Figs 2–6, all central peak variables represent mean values from more than 20 CCHs between pairs of Golgi cells with randomized resting membrane potentials and EPSC sizes (see above). Similarly, when we use the Golgi cell firing rate or the coefficient of variation of the interspike interval as an independent variable, these values represent mean values over all Golgi cells.

Figure 6. Irregular firing favours spike synchronization.

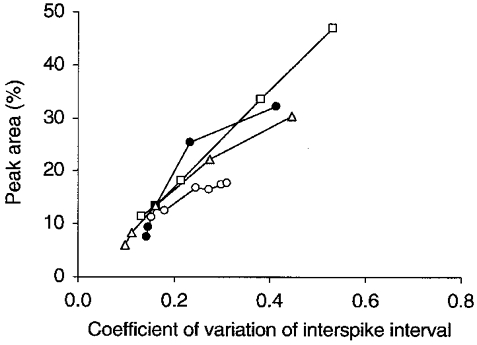
The area of the central peak on the CCH between a pair of model Golgi cells is plotted versus the mean coefficient of variation of the interspike interval of Golgi cells (see legend to Fig. 5). Starting from a standard configuration with 108 PF afferents to each Golgi cell and a PF firing rate of 5 spikes s⁻¹, the curves were generated by varying (1) the PF firing rate (○), (2) the strength of a single PF synapse and in inverse proportion the number of PF afferents (□), (3) the strength of a PF synapse for a fixed number of 108 PF afferents (▵) or (4) the Golgi cell resting membrane potential (•). Peak area increases when the PF firing rate increases (○), when the strength of a PF synapse increases (□ and ▵) and when the resting potential is more negative (•). The resultant Golgi cell firing rates varied between 5.1 and 41.9 spikes s⁻¹ (○), between 8.4 and 13.1 spikes s⁻¹ (□), between 5.6 and 20.2 spikes s⁻¹ (▵) and between 16.9 and 2.4 spikes s⁻¹ (•).

Experimental procedures

We re-analysed, in the way explained below, the spontaneous spike trains of 24 pairs of Golgi cells (Vos et al. 1999a), completed with six more recently recorded pairs, all pairs being aligned along the PF axis. The experimental procedures, described in detail elsewhere (Vos et al. 1999a,b), are summarized here. All testing procedures were approved by the Ethical Committee of the University of Antwerp, in accordance with Federal Laws.

Pairs of Golgi cells were recorded extracellularly in the cerebellar cortex (Crus I and II) of anaesthetized rats. Twenty-six pairs were recorded in 21 ketamine-xylazine-anaesthetized rats (ketamine HCl, 75 mg kg⁻¹, i.p.; xylazine HCl, 3.9 mg kg⁻¹, i.p.; supplements of one-third initial dose every 2 h, i.m.). Four pairs were recorded in two α-chloralose-anaesthetized rats (50 mg kg⁻¹, i.p.; supplements of 37.5 mg kg⁻¹ every 2 h, i.p.).

Spikes detected by different electrodes were discriminated on-line with a PC-controlled Multichannel Neuronal Acquisition Processor (Plexon, Inc., Dallas, TX, USA). Putative Golgi cells were identified based on electrode depth and tuning distance, spike waveform and the slow characteristic firing pattern (Miles et al. 1980; Edgley & Lidierth, 1987; Van Kan et al. 1993; Atkins et al. 1997). Multiple 400–600 s periods of spontaneous activity were recorded to yield at least 3000 spikes for each unit. An electrolytic lesion was made at the electrode tip for subsequent histological confirmation that the unit recorded from was positioned in the granular layer. At the end of the experiment, rats received a lethal dose of sodium pentobarbital (120 mg kg⁻¹, i.p.).

Cross-correlation analysis of experimentally recorded spike trains

The experimentally recorded spike trains were converted to the same file format as the spike trains generated by the simulation program. Thereafter, cross-correlation analysis was performed as described above. For some Golgi cell pairs, low-frequency oscillations (typically < 3 Hz) dominated the CCH and lifted the central peak, making the measured peak area too large. These slow waves were removed with a high-pass filter. To this end, the discrete Fourier transform of the CCH was calculated with a fast Fourier transform algorithm (Press et al. 1992) and the lowest non-zero harmonic frequencies were cut. For each CCH, the cut-off frequency was adjusted to maximize the normalized peak height, which amounted to minimizing the standard deviation of the CCH.

Decomposing spike trains and CCHs by windowing in the firing rate domain

As will be shown in Results, the model predicts that Golgi cells that are excited by a common PF input synchronize more precisely when their firing rates increase. For the model Golgi cells, which received a steady PF input throughout a simulation (see above), this relationship was established by plotting the width of the central peak on the CCH versus the mean Golgi cell firing rate (Fig. 2A). For experimentally recorded spike trains of Golgi cell pairs, however, two factors impaired this analysis: the restricted domain of observed mean firing rates (0.92–10.85 spikes s⁻¹) and the fast variations in instantaneous firing rate (coefficient of variation of the interspike interval: mean, 0.45; range, 0.13–0.7; Vos et al. 1999b). Calculating CCHs on sliding time windows of the paired spike trains, the technique of choice, yielded insufficient counts to calculate central peak sizes reliably.

In order to establish the relationship between the precision of synchrony and the firing rate of experimentally recorded Golgi cells, the instantaneous firing rate was calculated for every recorded spike. The instantaneous firing rate was subsequently used as a criterion to partition either each spike train of a pair, or the CCH itself. To this end, the broad domain of instantaneous firing rates (from < 2 spikes s⁻¹ to > 80 spikes s⁻¹) was divided into seven non-overlapping windows (see Figs 7–9).

Figure 7. Decomposition of the CCHs in the firing rate domain.

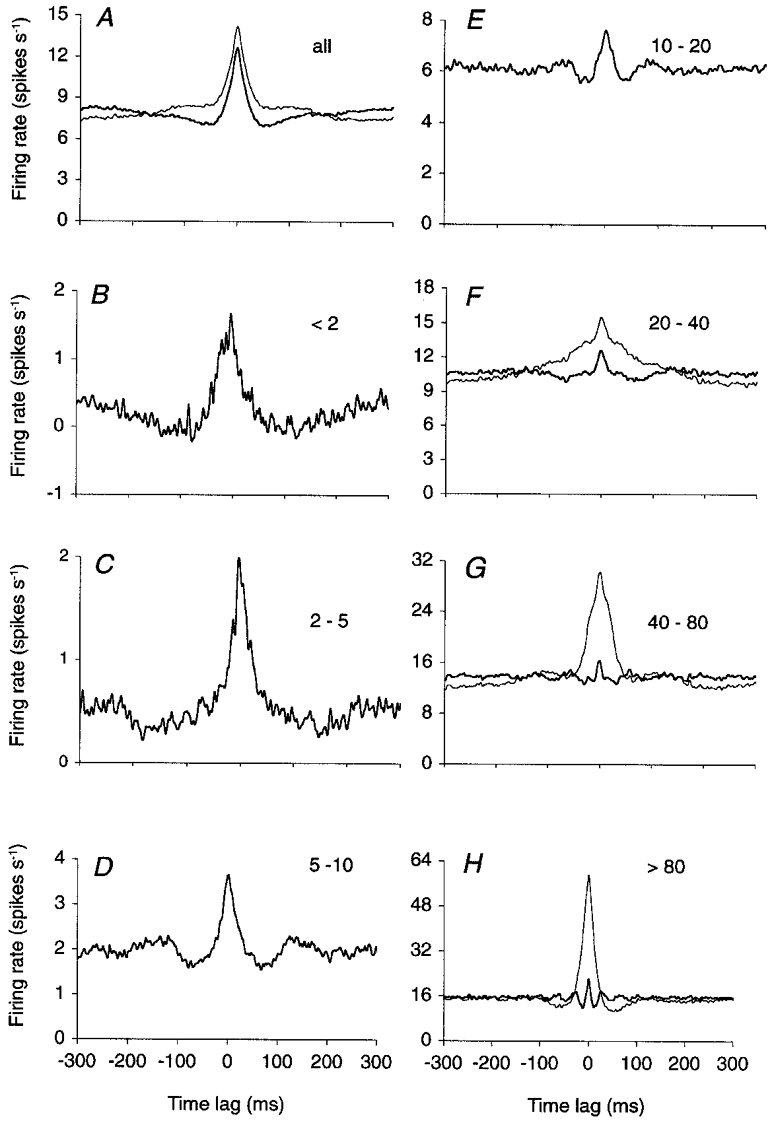
The CCH in A (thin curve) is the cumulative CCH of 30 cerebellar Golgi cell pairs recorded in anaesthetized rats (Vos et al. 1999a). This CCH was decomposed into seven firing rate-selective CCHs (see Methods), ranked by increasing instantaneous firing rate domains (B–H, labels show spikes s⁻¹). The number of reference spikes was 409 837 (A), 5112 (B), 19 596 (C), 65 402 (D), 148 519 (E), 111 340 (F), 42 435 (G) and 17 433 (H). The CCHs indicated by thick lines in A–H were obtained after cutting the lowest non-zero harmonic frequencies in a discrete Fourier transform of the CCH in the −1024 to 1024 ms time domain. In each CCH, the number of frequencies cut was adjusted to maximize the normalized central peak height (see Methods) and measured 5 (A), 4 (B), 0 (C), 0 (D), 4 (E), 9 (F), 29 (G) and 55 (H). The thin curves in F–H are non-filtered CCHs.

Figure 9. Cerebellar Golgi neurons with similar firing rates synchronize more easily.

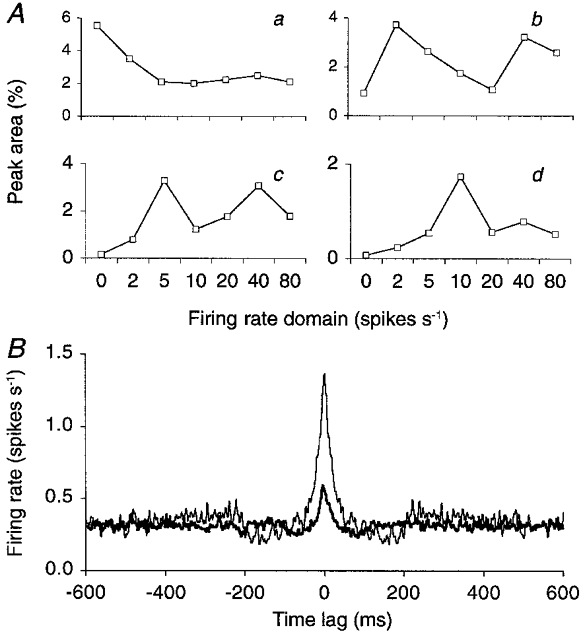
The experimentally recorded spike trains of a pair of Golgi cells were decomposed independently according to their instantaneous firing rates, to yield two sets of seven spike trains selective to disjunct firing rate domains (see Methods, data cumulated over all Golgi cell pairs). A, the resultant seven spike trains of the second Golgi cell are represented on the horizontal axes, and ranked by the firing rate domain to which their spikes belong. They were cross-correlated one by one with the firing rate-selective spike trains of the first Golgi cell. The four curves plot, for the lowest four firing rate domains of the first Golgi cell, the area of the central peak on the resultant CCH. The firing rate domains of the first Golgi cell are: < 2 spikes s⁻¹ (a), 2–5 spikes s⁻¹ (b), 5–10 spikes s⁻¹ (c) and 10–20 spikes s⁻¹ (d). At the highest three firing rate domains, rate covariance caused the central peak to increase in area again. B, the spike train containing the spikes of the 2–5 spikes s⁻¹ firing rate window of the second Golgi cell was cross-correlated with the spike train of the first Golgi cell representing the same firing rate domain (thin curve) or the 5–10 spikes s⁻¹ firing rate window (thick curve). In each curve the spikes from the first Golgi cell were used as reference spikes. Hence the two CCHs plot the rate of the same spikes of the second neuron (2–5 spikes s⁻¹) around the spikes belonging to two different firing rate windows of the first neuron. Peak area was 4.7 times larger when the two Golgi cells fired at the same rate (2–5 spikes s⁻¹; 3.71 %versus 0.79 %). Peak width measured 29 ms (thin curve) and 26 ms (thick curve). Smoothed CCHs without high-pass filtering.

In the first procedure, homogeneous, firing rate-selective subsets of spikes were generated for every Golgi cell by assigning each spike of the original spike train to one of seven subset spike trains, based on its instantaneous firing rate. The instantaneous firing rate associated with a spike was defined as the inverse of the smaller of the interspike intervals preceding and following that spike. This procedure yielded seven spike trains for each Golgi cell, and hence 49 CCHs for each pair.

In a variant of this technique, the CCH itself was decomposed into seven disjunct subsets, similarly ranked by firing rate. Each original pair of spikes from simultaneously recorded Golgi cells was assigned to one subset CCH, based on the instantaneous firing rate of the pair, and only in that CCH was the interval counter incremented. The instantaneous firing rate of a pair of Golgi cell spikes was defined as the higher of the instantaneous firing rates measured for each spike.

For example, suppose that the first Golgi cell produced a sequence of spike events (values in ms) {…, 20, 100, 140, …}, and that the other Golgi cell of the pair fired at times {…, 10, 110, 240, …}. In this case, the instantaneous firing rate of the first neuron at its second spike measured 25 spikes s⁻¹ ((40 ms)⁻¹), and that of the second neuron at its second spike 10 spikes s⁻¹ ((100 ms)⁻¹). For this pair of spikes, the instantaneous firing rate measured consequently 25 spikes s⁻¹ (the higher of the two firing rates), and the counter of the bin for the 10 ms interval was incremented in the CCH representing the firing rate domain window between 20 and 40 spikes s⁻¹.

Finally, before applying these procedures, all paired Golgi cell records were concatenated so that each CCH, in the present analysis, was cumulated over the entire population of Golgi cell pairs. The restrictions and advantages of this pooling are discussed later.

RESULTS

We first demonstrate that model Golgi cells synchronize loosely when they receive common monosynaptic PF excitation through realistic, weak-efficacy synapses. Because this finding could apply to other systems as well, we further analyse in detail which synaptic and neuronal parameters determined the precision and frequency of spike synchronization. Finally, this knowledge is used to derive the putative mechanisms underlying the loose synchrony that was experimentally observed between cerebellar Golgi cells in anaesthetized rats (Vos et al. 1999a).

The precision of synchrony between model Golgi cells is firing rate dependent

Pairs of model Golgi cells showed a broad central peak on their CCH, with a width of up to 30 ms, provided that both Golgi cells received PF input through weak synapses and that they had a low mean firing rate. This is illustrated in Fig. 1 for a configuration with 108 AMPA receptor-mediated PF synapses on each Golgi cell. Activation of a single PF synapse caused an EPSC of 28.4 pA, which is comparable in size to the EPSCs recorded from Golgi cells in rat cerebellar slices (Dieudonné, 1998) but which is too small to evoke a spike by itself (see EPSP in Fig. 1B). Ninety of the 108 PF afferents to each Golgi cell also innervated the other Golgi cell of the pair. It should be noted that the ratio of shared PF afferents, for which experimental data are lacking, was only made high to obtain the most reliable peak sizes possible. Lower degrees of input overlap yielded peaks with very similar widths, but smaller areas (see below, Fig. 4A). Most importantly, in this realistic configuration, peak width changed in inverse proportion to the mean firing rate of the Golgi cell pair (Fig. 2A, 108 AMPA curve, ○).

We assessed the relationship between peak width and Golgi cell firing rate for three other configurations with different types and strengths of PF synapses. Peaks were always narrow (width < 5 ms) and independent of firing rate when Golgi cells had only a small number of strong PF synapses. This is illustrated in Fig. 2 for a configuration with six PF synapses (6 AMPA curve, •). Each PF synapse was 18 times stronger than in the 108 AMPA configuration so that its single activation sufficed to evoke a Golgi cell spike. As expected (see Introduction), slow EPSPs yielded broader CCH peaks than fast EPSPs, but this effect became small when the strength of the PF synapses decreased. For example, the configuration with 108 NMDA receptor synapses (108 NMDA curve, □) showed a firing rate dependency which was quite similar to that of the 108 AMPA configuration. In contrast, when NMDA receptor channels were used in the configuration with six PF synapses, peak width even slightly increased with firing rate because the temporal summation of slow EPSPs, combined with the voltage amplification of the NMDA receptor channel, caused the Golgi cells to fire synchronous bursts (6 NMDA curve, ▪).

Peak height was inversely proportional to peak width in the AMPA synapse configurations (Fig. 2B). Again, peak width and peak height showed much less variation when there were only six, but strong, PF synapses on each Golgi cell.

Peak area, or the percentage of synchronous spikes, depended on the synaptic configuration rather than on the mean Golgi cell firing rate, as shown in Fig. 2C. Note that peak area was calculated from the raw CCH as it could not be inferred from the height and width values alone, which were measured after normalization. A constant finding in all configurations was that peak area decreased when the difference in firing rate between the neurons of a pair increased (not shown; see Fig. 9 for the same effect with experimentally recorded Golgi cells).

The firing rate of the Golgi cells was varied in Fig. 2 by decreasing or increasing the firing rate of the afferent PFs. To distinguish between effects related to the presynaptic (PF) versus postsynaptic (Golgi cell) firing rate, simulations were run in which the resting membrane potential of the Golgi cells was varied and the PF firing rate was held constant. The effect on peak width was very similar to the effect produced by varying the PF firing rate: peak width increased when the Golgi cell firing rate decreased.

Peak width increases, and area decreases, when the same excitatory load is distributed over growing numbers of synapses

The effect of the strength of a single PF synapse on the width and area of the central CCH peak is further elaborated in Fig. 3. The peak conductance following activation of a single PF synapse was varied from 0.1 to 7.6 nS on the horizontal axis. This range covers values 4 times smaller to 18 times larger than the 421 pS with which a 28.4 pA EPSC was elicited in the 108 AMPA configuration of Fig. 2 (these reference values are plotted as filled symbols). The number of PF afferents was varied in inverse proportion to the synaptic peak conductance (from 432 to 6) to ensure a similar mean excitatory load to model Golgi cells throughout (see Methods). Nevertheless, because activation of a single, strong synapse was more effective for firing Golgi cells than dispersed activation of many weak synapses (Segundo et al. 1968), Golgi cells fired at moderately higher rates when they had smaller numbers of afferents (from 8.4 spikes s⁻¹ with 432 afferents to 13.1 spikes s⁻¹ with 6 afferents). Most importantly, decreasing the strength of the individual PF synapses made synchronization less precise (broader central CCH peak; Fig. 3, ○) and the occurrence of synchronous spikes less frequent (smaller peak area; Fig. 3, □).

The degree of common input determines peak area, but not peak width

The degree of common PF input to a pair of Golgi cells (i.e. the relative number of shared PF afferents) was varied for a range of Golgi cell firing rates, and the width of the central peak on the CCH was plotted versus peak area (Fig. 4A). Each curve connects data points from Golgi cell pairs with the same mean pair firing rate but with different degrees of input overlap, increasing from left to right. These curves run almost horizontally, indicating that peak width is primarily determined by the mean Golgi cell firing rate, not by the degree of input overlap. Similar symbols on different curves, conversely, represent data points from Golgi cell pairs with the same degree of input overlap but with different mean pair firing rates, increasing from the upper to the lower curves. These symbols are scattered mostly along the vertical axis, indicating that peak area is determined much more by input overlap than by the mean Golgi cell firing rate.

The apparent reduction of peak area at the lowest Golgi cell firing rates (upper three curves in Fig. 4A) was due to a dilution of the PF-locked Golgi cell spikes with spontaneous spikes. This effect could be neutralized, and even inverted, by choosing more negative resting membrane potentials for the model Golgi cells (Fig. 4B).

Loose synchronization through temporal integration of synaptic input

The broad central peaks on the CCHs between pairs of model Golgi cells could not be explained by any of the mechanisms of loose synchronization listed in the Introduction, at least when the EPSPs had fast kinetics (AMPA-type). First, individual Golgi cells did not fire with intervals shorter than the width of the central peak on their CCH (compare the one-sided autocorrelograms and the CCH in Fig. 1C). Hence, the unprecisely timed ‘synchronous spikes’ on a CCH always appeared as isolated spikes, not as bursts, in the single spike trains (Fig. 1A). Second, the afferent PFs fired randomly and at a constant mean rate. The interspike interval of PFs had a Poisson interval distribution (beyond the refractory period) and the PF autocorrelograms and CCHs were flat (not shown). Hence, there was no burst firing in PFs, nor loose synchronization between PFs. Finally, conduction delays were indeed found to increase central peak width, but only if they were random between the neurons of a pair (not shown). This mechanism did not cause the broad central peaks, however, as in the results shown (Figs 1–6) each PF activated its synapses on both Golgi cells instantaneously. In conclusion, the broad peaks must have arisen from a variability in the timing of isolated spikes, which both Golgi cells of a pair fired in response to simultaneously received PF input.

This variability in timing appeared as a broad peak on the spike train CCH between a model Golgi cell and its entire set of afferent PFs. The two CCHs in Fig. 1B, which plot the mean firing rate of each Golgi cell after a PF spike, have peaks that are broader than the time course of an EPSP (thin trace in Fig. 1B). In order to assess whether these broad peaks explained the width of the central peak on the inter-Golgi cell CCH (Fig. 1C), the PF-Golgi cell CCHs of Fig. 1B were cross-correlated. The resulting CCH should be equal to the actual inter-Golgi CCH of Fig. 1C, if Golgi cell 1 (Goc1) and Golgi cell 2 (Goc2) fired independently within their windows of increased activity following a joint PF spike. In Fig. 1E, the predicted CCH and the actual Goc1-Goc2 CCH are superimposed, after normalization. The predicted CCH always closely matched the actual CCH but, like in Fig. 1E, the central peak on the actual CCH was slightly narrower. Hence the loose synchronization between a pair of model Golgi cells was completely explained by the loose spike timing between a single Golgi cell and its PF afferents.

The PF-Goc1 CCH of Fig. 1B is reversed in Fig. 1D and plots the mean firing rate of the entire set of 108 presynaptic PFs around a Goc1 spike (Eggermont et al. 1983). There was an interval of increased PF activity extending up to 40 ms before a Golgi cell spike. Integrating the peak over time gives the mean number of PF spikes, in excess of the background input, preceding an isolated Golgi cell spike. This number was small (3.7 spikes in Fig. 1D) and it was fairly independent of the PF firing rate (Fig. 4B). It reflected the degree to which the firing pattern of Golgi cells followed the PF firing pattern. Between simulations, the area of the peak on the Goc1-PFs CCH (Fig. 1D) covaried with the area of the central peak on the Goc1-Goc2 CCH (Fig. 1C), as can be seen by comparing the curves with open and filled symbols in Fig. 4B. The inverse relationship between peak width and firing rate along with the fair constancy of peak area (Fig. 2A and C) therefore suggests that model Golgi cells reached their firing threshold by integrating a small, constant number of EPSPs (3.7 in Fig. 1D), and that this was arrived at more rapidly when the PF firing rate was high (resulting in a sharper central peak).

Broad peaks, regular firing and the Ca²⁺-activated K⁺ current

The above explains why Golgi cells synchronized loosely when their firing rate was low (Fig. 2A) and the PF synapses were weak (Fig. 3). However, an additional mechanism is required as not all types of model neurons displayed loose synchronization (see below). An indication of the neuronal process underlying this behaviour was provided by the close relationship between the width of the central peak and the regularity of the individual Golgi cell spike trains. In fact, more regularly firing model Golgi neurons (lower coefficient of variation (c.v.) of the interspike interval) generated broader central CCH peaks (Fig. 5A). This relationship was apparent when the strength of PF synapses was varied and the Golgi cell firing rate was kept constant (Fig. 5A, □, data from Fig. 3), or when the Golgi cell firing rate was varied with a constant synaptic strength (Fig. 5A, ○, data from the 108 AMPA configuration in Fig. 2A). Decreasing the strength of afferent synapses (and increasing concomitantly their number) has previously been reported to regularize the firing pattern of computer-simulated neurons (Segundo et al. 1968; Maex & De Schutter, 1998a). The regularization of Golgi cell spikes when firing rate decreased, on the other hand, was less straightforward because the opposite relation was found in other active model neurons. For example, model neurons with granule cell dynamics, and passive integrate-and-fire neurons (see Methods), were found to fire more regularly when their firing rate increased (Fig. 5A, ▵). It should be noted that pairs of the latter two types of model neurons always produced narrow correlation peaks.

This regular firing at low rates was sustained in the model Golgi cells by a voltage- and Ca²⁺-activated K⁺ channel (K_Ca). The slow effective kinetics of the K_Ca channel was secondary to the slow decay of the [Ca²⁺]_i (De Schutter & Smolen, 1998), which had a time constant of 200 ms, and it produced a low resonant frequency. To dissociate the effects of channel kinetics and firing rate on peak width, model Golgi cells with slower (1000 ms) and faster (40 ms) [Ca²⁺]_i decay kinetics were simulated over the same range of firing rates as standard Golgi cells. Data points for similar Golgi cell firing rates (represented in Fig. 5B by the same symbols) were found to lie on approximately horizontal lines (except at the lowest firing rate, •). This indicated that peak width was determined by the Golgi cell firing rate, whereas the [Ca²⁺]_i decay time constant clearly determined the regularity of firing (rightward shift at higher values).

The curve for the fastest [Ca²⁺]_i decay (40 ms, dashed curve in Fig. 5B) appeared more complex than those for slower decays because in this case the regularity of firing was tuned around an optimal Golgi cell discharge rate of 11 spikes s⁻¹ (▪ on dashed curve). Moreover, the faster K_Ca channel kinetics made the firing threshold more sensitive to small changes in resting potential, resulting in larger differences in firing rate between the neurons of a pair. Decreasing the time constant even further made the firing threshold unrealistically brisk. A reliable output could then only be obtained by shifting the rate constants of all voltage-gated channels towards more positive voltages, so that the firing threshold moved away from the resting potential. After these manipulations, the model Golgi cells acquired the same dynamics as model granule cells, i.e. a high firing threshold, no firing rate adaptation, narrow correlation peaks and more regular firing at high rates (Fig. 5A, ▵).

It can thus be concluded that a slow K_Ca current was essential to generate broad CCH peaks. However, the exact width of the peak did not depend on its kinetics (i.e. the decay rate of [Ca²⁺]_i) but on the neuronal firing rate. As such, the regularity of firing and the precision of synchronization could be made to vary independently (Fig. 5B).

Dissociation between peak width and the regularity of firing of model Golgi cells

In anaesthetized rats, cerebellar Golgi cells did not fire very regularly as assessed from the coefficient of variation of their interspike interval (mean c.v., 0.45; range, 0.13–0.7; Vos et al. 1999b). The model provided several mechanisms that might explain loose synchronization in the absence of regular firing, i.e. that produced a shift in the width versus c.v. curve of Fig. 5A rightwards or upwards. Making the model resting membrane potential more negative or the K_Ca current stronger both reduced the Golgi cell firing rate, increased central peak width and area, and also increased the c.v. When random conduction delays were assigned to the PF-Golgi cell synapses, peak width increased at all firing rates and, at high PF firing rates, peak area decreased. Finally, adding a common, randomly firing, inhibitory afferent to the configuration of Fig. 1A (e.g. a basket or stellate axon; Palay & Chan-Palay, 1974) appeared very effective for increasing the c.v. The addition of a common inhibitory afferent also generated broad correlation peaks through a new mechanism. The activation of the H channel during inhibition (Dieudonné, 1998) caused a rebound Golgi cell depolarization of several tens of milliseconds, upon which small EPSPs were able to evoke an unprecisely timed spike. Again, this phenomenon was firing rate dependent and was never observed in model Golgi cells with granule cell dynamics, nor in leaky integrate-and-fire neurons.

The relation between the regularity of firing of model Golgi cells and central peak area was less complex: irregular firing almost always increased the percentage of synchronous spikes (Fig. 6), an observation that was also made for human motoneurons (Nordstrom et al. 1992). As PFs were (approximate) Poisson processes in the model, the c.v. of their interspike interval was close to one. Hence this relationship confirms our previous statement that Golgi cells synchronized to the extent that their firing pattern was determined by shared PF activity (Fig. 4B). Figure 6 also confirms the strong sensitivity of peak area to the strength of the PF synapses (Fig. 3) and its weak dependency on the Golgi cell firing rate (Fig. 2C). Of all variables tested, PF firing rate had the largest effect on Golgi cell firing rate and the smallest effect on peak area, which also validates our conclusion that peak area was fairly insensitive to naturally occurring variations in Golgi cell firing rate (Fig. 2C).

Loose synchrony between model Golgi cells caused by covariation of their firing rate over time

As noted in the Introduction, broad central CCH peaks are classically regarded as signalling covariation in firing rate between the component neurons. This mechanism was therefore also investigated in the model, as a reference for the analysis of the experimental data. Covarying Golgi cell firing rates were simulated by superimposing in all PFs synchronous, rectangular bursts of increased firing upon the background, random activity. As a result, the Golgi cells also fired synchronous bursts, which produced broad central peaks on their CCHs, irrespective of whether the bursts were induced by common PFs or not.

If a pair of model Golgi cells did not share PF afferents and if the interval between the synchronous bursts was randomized, then only the excess spikes during a burst were correlated and contributed to the central peak. The central peak was then completely explained by a convolution of the bursts. As a result, repeated rectangular bursts caused a triangular central peak on the CCH with a full width at half height equal to the burst duration. The area of the peak was proportional to the number of bursts and to the number of spikes within a burst. Note that Golgi cell spikes were no longer isolated in this condition, so that a spike of the reference neuron could be ‘synchronous’ with multiple spikes of the target neuron, raising peak area to potentially over 100 % (e.g. right vertical axis in Fig. 8B).

Figure 8. Two mechanisms of loose synchronization operate in separate firing rate domains.

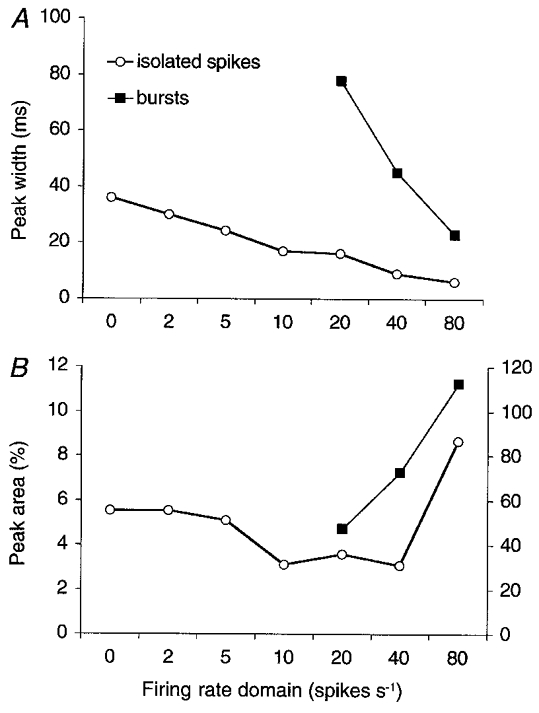
A, plots of the width of the central peak on the high-pass filtered CCHs of Fig. 7B–H (○) and on the non-filtered CCHs of Fig. 7F–H (▪). The two resulting curves are presumed to represent the effect of firing rate on two different mechanisms of loose synchronization: common monosynaptic PF excitation (○) and burst firing or rate covariance (▪). B, the corresponding peak areas. Square data points read on right vertical axis. Note that the horizontal axes in A and B are non-linear and that the labels indicate the lower boundaries of the disjunct firing rate windows.

When bursts were evoked in common PF afferents, a small, narrow peak was found on top of the broad central peak, indicating that some Golgi cell spikes now precisely synchronized during a burst (model data not shown; see e.g. Fig. 7F and G).

Loose synchronization of cerebellar Golgi cells in anaesthetized rats: common PF input versus covariances in Golgi cell firing rate

In a multielectrode study in anaesthetized rats (Vos et al. 1999a), Golgi cells aligned along the PF axis of the cerebellum fired synchronously at rest, but most orthogonally oriented pairs at similar interelectrode distances did not, indicating that the Golgi cells were synchronized by a common PF input. However, even when the slow PF conduction speed was taken into account, the central peaks on the CCHs were much broader than that which would be expected to result from shared monosynaptic input through fast AMPA receptor channels (see Introduction).

We therefore analysed the experimentally obtained spike trains and their CCHs using a new technique (see Methods). The aim was to attribute the observed broad central peaks either to common monosynaptic PF input or to firing rate covariance. In the first case we expected to find a relationship between the precision of synchrony and the instantaneous firing rate of a Golgi cell pair, similar to what was demonstrated in the present modelling study, whereas in the latter case synchronously fired bursts should be observed. It will be shown that both mechanisms contributed to the widths of the central peaks, although they operated in different firing rate domains.

The analysis is based on a partitioning of Golgi cell spike trains in the firing rate domain. Every recorded Golgi cell spike was assigned to one of seven firing rate windows, based on the instantaneous rate at which it fired (the inverse of the shorter of the interspike intervals of that spike; see Methods). Firing rate-selective spike trains from both Golgi cells of a pair were then cross-correlated. In a shorter method which we will consider first, the partitioning was performed directly on the CCH, by assigning each pair of spikes from simultaneously recorded Golgi cells to one of seven firing rate windows (more particularly to the domain of the fastest spike).

For the sake of robustness, the analyses were performed on the concatenated spike trains of all recorded Golgi cell pairs. Figure 7A (thin curve) shows the cumulative CCH of all pairs, irrespective of firing rate. Central peak height, width and area measured 8.8 (Z-score), 32 ms and 31 %, respectively. The central plateau was removed by cutting the lowest five non-zero harmonic frequencies of the CCH (thick curve; see Methods), raising peak height to its maximal value of 9.7. After this, peak width and area measured 24 ms and 13.3 %.

In a first analysis, the counts of the cumulative CCH (Fig. 7A) were distributed over seven subset CCHs, each one selective for a particular firing rate domain (Fig. 7B–H). Central peak width decreased from 36 ms at firing rates < 2 spikes s⁻¹ (Fig. 7B) to 17 ms at firing rates between 10 and 20 spikes s⁻¹ (Fig. 7E). Note that the central peaks of Fig. 7B–E counted exclusively intervals between isolated spikes, i.e. no burst firing contributed to their width. Indeed, the selection procedure (see Methods) excluded spikes that were preceded or followed by another spike (in the same spike train) within an interval that progressively decreased from 500 ms in Fig. 7B to 50 ms in Fig. 7E. The small side peaks in Fig. 7E were also apparent on the autocorrelograms and indicate that spikes in this firing rate domain tended to be fired not only synchronously but also in a regular fashion (see Discussion). At firing rates higher than 20 spikes s⁻¹ (Fig. 7F–H), a narrow central peak is seen on top of a much broader one. These narrow peaks were isolated by high-pass filtering of the CCH (thick curves in Fig. 7F–H) and showed, in comparison to the central peaks in Fig. 7B–E, an additional decrease in width from 16 ms (Fig. 7F) to 6 ms (Fig. 7H).

The broad peaks in Fig. 7F–H (thin curves) were caused by the synchronous discharge of bursts of spikes, instead of isolated spikes, because they merged with paracentral peaks on the autocorrelograms (not shown). Hence, the broad peaks in Fig. 7F–H represented concerted bursts of firing, increasing in spike rate but decreasing in duration from Fig. 7F to H (thin curves), whereas the small peaks on top of them represented the precise synchronization of individual spikes during the bursts (thick curves).

Based on these relationships between central peak width and instantaneous firing rate, two mechanisms of loose Golgi cell synchronization could be distinguished: common monosynaptic PF excitation (Fig. 8A, ○) and covariance of firing rate (Fig. 8A, ▪). They are represented by the two curves of Fig. 8 and produced broad central peaks in separate firing rate domains: common PF synapses produced loose synchrony when the instantaneous Golgi cell firing rate was low (○), firing rate covariance appeared as loose synchrony when the firing rate was high (▪). From the distribution of the central peak area over these two kinds of peaks (i.e. over the two curves in Fig. 8B), the contribution of each mechanism to synchronization was estimated. It appeared that common monosynaptic PF input accounted for 12 % of the area of the central peak of Fig. 7A. If the broad central peak of Fig. 7F, which formed the CCH plateau in Fig. 7A, were neglected, this contribution rose to 27 %. In both the calculations, this meant that Golgi cells aligned along the PF axis spontaneously fired 3.5–4 % of their spikes synchronously as a consequence of joint excitation by common PFs. Another 9–10 % of the spikes only appeared synchronous through covariations in firing rate.

In a second analysis, all spikes recorded from a given Golgi cell were distributed over seven firing rate-selective spike trains (see Methods). Cross-correlating each resultant spike train with the corresponding spike train derived from the other, simultaneously recorded Golgi cells yielded a set of seven CCHs, each one selective for a different firing rate domain. These seven CCHs revealed the same inverse relationship between central peak width and firing rate as that found in Figs 7 and 8 (not shown). When, on the other hand, spike trains of different firing rate windows of the respective neurons were cross-correlated (e.g. the ‘slowest’ spikes of Goc1 with the ‘second to slowest’ spikes of Goc2), a drastic fall in central peak area was observed (see Fig. 9B). This means that cerebellar Golgi cells had a much higher probability of firing synchronously when they were firing at similar rates. This is demonstrated in Fig. 9A for CCHs which again, for reasons of robustness, have been accumulated over all Golgi cell pairs. It should be noted that a similar reduction of synchronicity was found in the model when the two Golgi cells of a pair fired at different rates because they had been assigned, after randomization, different resting membrane potentials (not shown).

Figure 9B shows an example of this fall in peak area by an imbalance in Golgi cell firing rate. The CCH between spike trains of the same firing rate domain (thin curve) had a central peak area which was 4.7 times larger than the peak area of the CCH between spike trains of slightly different firing rate domains (thick curve). It is important that this effect was not a corollary of rate covariance. Indeed, if cerebellar Golgi cells had a tendency to fire at similar rates most of the time, and if the enlarged peak area simply were a consequence of that, then the two CCHs in Fig. 9B would scale over their entire length to the same degree, i.e. the ratio 4.7 of their peak areas. In contrast, only the values of the central peak were different. Hence, in the lowest four firing rate domains considered in Fig. 9A, there was no covariation in firing rate which could explain the observed loose synchronization and the associated broad central peak.

DISCUSSION

The classical analysis of coherent firing in multiunit recordings assumes that only very precisely synchronized spikes result from the joint excitation of neurons by shared monosynaptic afferents. Loosely synchronized spikes are considered to indicate only a concerted, temporary increase in firing rate. The present study demonstrates that loose synchronization of model neurons, firing at a constant rate, can entirely result from excitation through shared monosynaptic afferents. In this case, the precision of synchrony is firing rate dependent. We have also shown, by means of an analysis of multielectrode-recorded spike trains of rat cerebellar Golgi cells, that this firing rate dependency can be used to distinguish loose synchronization caused by common monosynaptic excitation from loose synchronization resulting from covariance in firing rate.

Firing rate-dependent synchronization of model neurons

In the present modelling study, broad central peaks on spike train CCHs were produced by common excitation through monosynaptic afferents, as for very narrow peaks. The same common synapses that generated a tight synchrony between the postsynaptic neurons (narrow peak on the CCH) produced a loose synchrony (broad peak) when their strength was reduced and when their rate of activation was enhanced in such a way as to keep the postsynaptic firing rates constant (Fig. 3). Broad peaks were limited to low firing rate regimes, and could therefore only be produced when both neurons possessed intrinsic dynamics enabling them to fire at these low rates (Fig. 5A).

Characteristically, an inverse relationship was found between peak width and the mean postsynaptic firing rate, whereas peak area was almost firing rate independent (Fig. 2A and C). These results are in agreement with a time scale-invariant mode of processing. If, in an imaginary experiment, the time scale of the spike trains were changed so that the same spikes were distributed over a 5 times longer epoch, then firing rate would become 5 times slower and synchrony 5 times less precise. However, because the relative positions of the spikes were left unchanged and the CCH peak was 5 times broader, the percentage of synchronous spikes would not alter and peak area would remain constant.

Loose synchronization and neuronal dynamics

A broad central peak was only found on the CCH between a pair of model Golgi cells if the PF synapses were weak (Fig. 3). Because the resulting unitary common-input EPSPs were ineffective in raising the membrane potential above the firing threshold, they had to be temporally integrated with other EPSPs, derived from common afferents or not. The second requirement for loose synchrony was a low Golgi cell firing rate (Fig. 2A). Hence, in order to generate loose synchrony, neurons needed to be able to fire at very low rates during weak stimulation. This required the presence of an outward current in addition to the spike-generating voltage-dependent currents (Connor & Stevens, 1971; Jack et al. 1975; Theunissen et al. 1993). This outward current was carried in the model Golgi cells through a Ca²⁺-activated K⁺ channel, and resulted in a more gradual firing threshold. The combined effect of a need for synaptic integration, a low firing rate and a gradual threshold made firing less predictable, and less precise between neurons.

Moreover, the two processes (i.e. excitation through high-frequency, small-size EPSPs on the one hand and activation of Ca²⁺-activated K⁺ channels on the other) had the same side effect: they promoted rhythmic or periodic firing (see Segundo et al. 1968 and Hille, 1992, respectively). This explains our initial observation of a close relationship between broad peaks and low coefficients of variation of the interspike interval (Fig. 5A). Central peaks can then be expected to acquire their width through small deviations in spike timing from the basic rhythm. These deviations, and hence the width of the peak, are proportional to the mean interspike interval, and hence inversely proportional to the mean firing rate. Because peak width was determined by synaptic and neuronal properties, it remained largely independent of the fraction of input shared by the neurons. Lowering this shared fraction reduced peak height and area, but not width (Fig. 4A).

Regular firing of model Golgi cells produced periodicities on their autocorrelograms (Fig. 1C) and, to the extent that the rhythm was reset by the common PF afferents, these periodicities were copied to one side of the CCH each (see Perkel, 1970). It should be clear, however, that the broad CCH peaks were not a secondary effect of the oscillatory pattern on the Golgi cell autocorrelograms. Indeed, the broad central peaks remained unaffected, whereas the oscillations on the CCH disappeared, after application of a deconvolution algorithm to correct the CCHs for the features of the autocorrelograms (Perkel, 1970; Eggermont & Smith, 1996). In addition, broad peaks could be dissociated from rhythmic firing by increasing either the strength or the time course of the Ca²⁺-activated K⁺ current (the latter by manipulating the decay constant of the Ca²⁺ pool; Fig. 5B). Other strategies, such as adding common inhibition or applying more irregular input patterns, were also effective at increasing the coefficient of variation of the interspike interval, while preserving broad peaks.

Moreover, the opposite combination, rhythmic firing with a narrow central peak, was found as well. Indeed, integrate-and-fire neurons fired rhythmically (c.v. < 0.35) without any tendency to form a broad central peak on the CCH, even when the pre- and postsynaptic firing rates were indistinguishable from those at which a very loose synchrony was observed between model Golgi cells. In such simulations, the central peak was always narrow (< 1 ms at half height), at most sitting on top of a slow, low-amplitude wave. The inability to produce broad peaks in simulations of passive neurons, and also of some active model neurons (the neurons with granule cell dynamics; Fig. 5A), explains why broad correlation peaks have not been reported in modelling studies previously.

Finally, because the Ca²⁺-activated K⁺ current, due to its slow time course, also causes firing adaptation (Hille, 1992; Sah, 1996), it is predicted that broad peaks will be found primarily, if not exclusively, on CCHs between adapting neurons.

Windowing in the firing rate domain

In the model, peak width was primarily determined by the EPSP size (Fig. 3) and the postsynaptic firing rate (Fig. 2A). Peak area, on the other hand, was rather independent of the postsynaptic firing rate (Figs 2C and 4B), but did depend on the EPSP size (Fig. 3), the degree of input overlap (Fig. 4A), the resting membrane potential (Fig. 4B) and the difference in firing rate between the two neurons of a pair (model data not shown).

For the analysis of experimentally recorded Golgi cells, however, relating peak width (and area) to firing rate faced contradictory requirements. On the one hand, peak width could only be calculated reliably on spike trains of sufficient length, preventing windowing in the time domain. Excessive smoothing of the CCH or the use of wider bins would have reduced the reliability of the measured peak sizes. On the other hand, the firing rate of the Golgi cells was highly variable over time, making the mean rate a bad predictor of the instantaneous rate. We therefore developed a windowing technique in the firing rate domain which could be applied either to the individual spike trains of a pair or to the CCH itself (see Methods). This windowing by firing rate was an appealing approach as opposite outcomes were expected for loose synchronization resulting from common monosynaptic input compared to loose synchronization resulting from covariation in firing rate. The model predicted that the first mechanism would produce broad peaks at the lowest firing rates. In contrast, the second mechanism, correlated burst firing, should produce broad peaks at high instantaneous firing rates. In fact both tendencies were found in the recorded Golgi cell spike trains, and at intermediate firing rates two central peaks could be detected on top of each other.

The two mechanisms of central peak formation (common monosynaptic excitation and rate covariance; Figs 7 and 8) could be separated by filtering the CCHs in the frequency domain. This high-pass filtering was comparable to the subtraction of a 50 ms predictor for rate covariance as used by Eggermont & Smith (1995). The degree of filtering, however, could be adjusted in an objective way (see Methods).

To obtain sufficient numbers of spikes in every window of the firing rate domain, all Golgi cell pairs were pooled, which was achieved by concatenating all the paired spike recordings. Concatenating the spike records amounts to summation of the counts of the respective CCHs. Conceptually, this pooling was justified because exactly the same relationship between peak width and firing rate was predicted when pairs of Golgi cells with different mean pair firing rates were compared as when synchrony was followed in a single pair at different instantaneous firing rates over time. From a mathematical point of view, pooling was allowed because only linear operations were applied before peak width and area were measured: counting interspike intervals, smoothing (convolution with a boxcar filter) and high-pass filtering (using the discrete Fourier transformation). Pooling had one disadvantage: because the peaks of the single CCHs were sometimes asymmetrical or even a few milliseconds offset from zero, the peaks measured on the pooled CCHs could appear too broad. Nevertheless, the central peaks of the experimentally obtained CCHs were only a few milliseconds broader than those predicted by the model (Fig. 8A versusFig. 2A). The small unexplained fraction of peak width can be completely accounted for by the PF conduction delays. Finally, the narrow central peaks isolated through high-pass filtering in Fig. 7F–H were so small, compared to the broad peaks on which they were sitting, that they would have been missed without pooling.

The constancy of peak area predicted by the model was less apparent for the experimentally recorded Golgi cells, which is possibly a consequence of the large number of parameters affecting this peak size (see above).

In retrospect, the need for pooling along with the presence of two mechanisms of peak generation explains why some clear relationships found in the model (e.g. peak area versus degree of common input, Fig. 4A; peak area versus firing rate, Fig. 4B) were much harder or not at all detectable on the CCHs from single pairs of experimentally recorded Golgi cells (data not shown).

Relevance to rat cerebellar Golgi cells

PFs span about 5 mm along a one-dimensional, transverse trajectory in the molecular layer of the cerebellar cortex in rats, making enpassant synapses on the dendritic trees of Golgi cells (Pichitpornchai et al. 1994). Because of this anisotropy, the percentage of PFs making a synapse on both Golgi cells of a pair will be very sensitive to the orientation of the pair with respect to the PF axis. In the case of a parallel alignment, an almost complete overlap of PF input is conceivable. Since in multielectrode-recorded sets of rat Golgi cells most orthogonally oriented pairs (12/16) did not synchronize at all, the broad central peaks observed for 25 of the 26 transverse pairs were most probably caused by common input from shared PF afferents (see Vos et al. 1999a). Common excitation of a pair of Golgi cells by mossy and climbing fibres or common inhibition by basket and stellate cells are unlikely to be substantial because of the absence of synchrony between most sagittally oriented pairs. Hence, the present minimal model, comprising only Golgi cells and PFs, should suffice to explain the observed looseness of synchronicity, at least insofar as common input is the cause (see below for rate covariance).

It can also be concluded that the synaptic organization and neuronal dynamics that were required to produce broad correlation peaks in the model are indeed present in rat cerebellum. Model Golgi cells with 108 AMPA synapses generated broad correlation peaks through EPSCs of the same size (28.4 pA) as those recorded in invitro Golgi cells (Dieudonné, 1998). The model EPSCs were even 2–3 times faster because their rate constants were adjusted to in vivo conditions (Maex & De Schutter, 1998b). Moreover, unlike many inhibitory neurons in other systems (McCormick et al. 1985), cerebellar Golgi cells typically fire at low rates (Edgley & Lidierth, 1987; Van Kan et al. 1993) and show firing rate adaptation (Dieudonné, 1998), which are both, according to the present study, favourable if not necessary for generating broad correlation peaks.

Common PF excitation was estimated to synchronize 4 % of all spikes recorded in pairs of cerebellar Golgi cells. This is a conservative estimate as any contribution of burst firing was prohibited. Indeed, by assigning pairs of spikes to the firing rate domain of the fastest spike (see Methods), loose spike coincidences in which only one of the spikes took part in a burst were entirely attributed to rate covariance. Nevertheless, this value is comparable to the percentage of synchronous spikes found in other systems, such as human motoneurons (e.g. 4.7 % in Schmied et al. 1993).

It still needs to be explained how covariance in firing rate, which caused the apparent synchronization of another 10 % of the recorded Golgi cell spikes, is selectively induced along the PF axis. Cerebellar Golgi cells do not have an intrinsic propensity to fire in bursts (Dieudonné, 1998). Hence, the experimentally observed bursts of Golgi cell spikes (Vos et al. 1999a) probably reflected burst activity in the afferent PFs. We suggest that these bursts may be a consequence of the PF-induced synchronicity of Golgi cells itself. Indeed, Golgi cells exert feedback inhibition on granule cells. Modelling and experimental studies have shown that inhibitory neurons loosely synchronize their targets (Lytton & Sejnowski, 1991; Cobb et al. 1995; Maex & De Schutter, 1998b). Hence, synchronously firing Golgi cells will loosely synchronize the afferent PFs. The side peaks observed on some CCHs (Fig. 7D and E) might be a sign of the rhythmicity caused by this inhibitory feedback (Maex & De Schutter, 1998b). Note that this feedback inhibition synchronizes both common and non-common PF afferents, which explains the superposition of a narrow and a broad central peak on the CCH.

Implications for cerebellar physiology

When the common input to a pair of model neurons was distributed over a growing number of low-efficacy synapses the percentage of synchronous spikes decreased, as evidenced from the decreased central peak area on the CCH (Fig. 3). In the end, the randomly firing afferents were unable to synchronize their targets, however large the chosen degree of input overlap. From this and from the huge number of PF synapses on Purkinje cells (Harvey & Napper, 1988) compared to Golgi cells, the important prediction follows that no synchronicity between Purkinje cell simple spikes will be found when the PFs fire randomly. This prediction assumes that Purkinje neurons, like Golgi cells, poorly phase-lock their spikes to PF spikes, as demonstrated recently in a modelling study (Jaeger et al. 1997).

The synchronicity observed between Golgi cells aligned along the PF axis might therefore serve to transiently synchronize the PFs, and in this way their postsynaptic Purkinje cells. Indeed, in a realistic granular layer model, synchronized Golgi cells always synchronized their efferent granule cells, and hence the respective PFs. This synchronization was enhanced by the Golgi cell-granule cell feedback loop, and its accuracy could be dynamically modulated by the rate of mossy fibre firing (Maex & De Schutter, 1998b).

Conclusions

The present study relates the precision of spike synchronization between two neurons to the strength of their common afferent synapses. Computer simulations explain the finding of both very precise (Alonso et al. 1996) and loose synchronization (Nelson et al. 1992; Eggermont & Smith, 1996), and explain in particular the loose synchrony that was observed between rat cerebellar Golgi cells (Vos et al. 1999a). When broad correlation peaks are caused by common input through weak synapses, peak width is predicted to be inversely related to firing rate. In contrast, loose synchrony caused by covariance in firing rate will be most apparent at high firing rates. A windowing technique in the firing rate domain distinguishes between these two mechanisms.