The β subunit dominates the relaxation kinetics of heteromeric neuronal nicotinic receptors

Abstract

1. The ACh-induced voltage-jump relaxation currents of the nicotinic receptors formed by pair-wise expression of the rat α2, α3, or α4 subunits with the β2 or β4 subunit in Xenopus oocytes were fitted best by the sum of two exponentials and a constant between -60 and -150 mV.

2. As the ACh concentration approached zero, the relaxation time constants approached limiting values that should equal the single-channel burst duration at low ACh concentrations and the synaptic current decay time constants. β4 co-expression prolonged the zero ACh concentration limits for the relaxation time constants. The fast β4 zero ACh concentration limits ranged from 40 to 121 ms between -60 and -150 mV, and the slow β4 zero ACh concentration limits ranged from 274 to 1039 ms. In contrast, the fast β2 limits were 4–6 ms over the same voltage range and the slow β2 limits were 30–53 ms.

3. Expression with the β4 subunit increased the voltage sensitivity of the α2, α3 and slow α4 relaxation time constants but not that of the fast α4 relaxation time constant.

4. Reducing the temperature from 22°C to 8–9°C increased the α4β2 and α3β4 relaxation time constants 2.3- to 6.6-fold and reduced the fractional amplitude of the fast relaxation component. It also increased the voltage dependence of the fast α3β4 relaxation time constant and decreased that of the slow time constant. The Q₁₀ for α4β2 and α3β4 relaxation time constants ranged from 1.9 to 3.9 between 10 and 20°C.

5. The β subunit appears to have a dominant influence on the voltage-jump relaxation kinetics of heteromeric neuronal nicotinic receptors.

The slow muscle nicotinic receptor burst duration determines the rate of decay of excitatory postsynaptic currents (EPSCs) at the neuromuscular junction (Colquhoun & Sakmann, 1985; reviewed in Edmonds et al. 1995). During normal neuromuscular synaptic transmission, motor neurons release a brief pulse of acetylcholine (ACh) that diffuses across the synaptic cleft and binds to the postsynaptic nicotinic receptors. Diffusion and hydrolysis by acetylcholinesterase remove the free ACh from the cleft so quickly that the mean time which two ACh molecules remain bound to the postsynaptic nicotinic receptors determines the EPSC decay time constant (Magleby & Stevens, 1972; Anderson & Stevens, 1973; Katz & Miledi, 1973). The slow muscle nicotinic burst duration matches the muscle miniature EPSC (MEPSC) decay time constant (Colquhoun & Sakmann, 1985; Mishina et al. 1986) and, therefore, represents the mean time that two ACh molecules remain bound to the receptor. The slow neuronal nicotinic receptor burst duration also determines the nicotinic EPSC decay time constant at ganglionic synapses (Skok et al. 1982; Derkach et al. 1987; Mathie et al. 1987, 1991).

The non-α subunits appear to dominate the bursting behaviour of muscle nicotinic receptors (Sakmann et al. 1985). Muscle nicotinic receptors contain α1, β1, δ, and γ or ε subunits. The presence of two adjacent cysteine residues in the amino-terminal domain distinguishes the α from the non-α subunits. The burst duration of wild-type (WT) calf muscle nicotinic channels is long and voltage dependent (Sakmann et al. 1985). In contrast, the burst duration of WT Torpedo nicotinic channels is short and voltage independent (Sakmann et al. 1985). Similar to the WT calf channels, the burst duration of hybrid channels containing Torpedoα1, β1 and γ, and calf δ subunits is long and voltage dependent. Similar to the WT Torpedo channels, the burst duration of hybrid channels containing calf α1 and Torpedoβ1, δ and γ subunits is short and voltage independent (Sakmann et al. 1985). Thus, the non-α subunits appear to dominate the muscle nicotinic receptor burst duration and its voltage dependence.

Similar to muscle nicotinic receptors, the neuronal non-α subunits (β2 and β4) affect the bursting behaviour of neuronal nicotinic receptors (Papke & Heinemann, 1991; Figl et al. 1996; Nelson & Lindstrom, 1999). Co-expression with β4, instead of β2, prolongs the burst duration of α3 neuronal nicotinic receptors (Papke & Heinemann, 1991; Figl et al. 1996; Nelson & Lindstrom, 1999). However, we do not know how β4 co-expression affects the burst duration of α2 and α4 nicotinic receptors.

Pair-wise expression of the α2, α3 or α4 neuronal nicotinic subunits with the β2 or β4 subunit in Xenopus oocytes yields six functional receptor subtypes (Boulter et al. 1987; Duvoisin et al. 1989). The single-channel bursting behaviour and the voltage-jump relaxation kinetics of all six subtypes have not been previously studied. As the ACh concentration approaches zero, the relaxation time constants should approach limiting values that equal the single-channel burst duration at low ACh concentrations and the synaptic current decay time constants. To determine whether the non-α subunits dominate the relaxation kinetics of these receptor subtypes, we measured their ACh-induced voltage-jump relaxation currents at the lowest possible ACh concentrations. We chose voltage-jump relaxations rather than single-channel recordings for this study because the analysis of voltage-jump relaxations is (1) less time consuming than single-channel kinetic analysis, (2) dispenses with the need for statistical definitions of the critical shut time between bursts, and (3) does not suffer from length-biased sampling. Furthermore, the rapid run-down of neuronal nicotinic channels in excised patches makes it difficult to construct reliable single-channel burst length distributions (Papke & Heinemann, 1991; Sivilotti et al. 1997; Nelson & Lindstrom, 1999). However, the size of the Xenopus oocyte limits the temporal resolution of the relaxation time constants to ∼2 ms. Our results show that the voltage-jump relaxations of all the nicotinic subtypes produced by pair-wise expression of the rat α2, α3 and α4 subunits with the β2 or β4 subunit contain two exponential components. The β subunits have a greater effect on the voltage-jump relaxation time constants than the α subunits. Thus, one major function of the β subunit may be to modulate the burst duration of neuronal nicotinic receptors.

Previous patch-clamp (Papke et al. 1989) and pharmacological studies (Zwart & Vijverberg, 1998) suggest that variations in the α:β neuronal nicotinic subunit stoichiometry may produce subpopulations with different pharmacological and biophysical properties. Consistent with this hypothesis, the single-channel open-time distributions, single-channel amplitude distributions, and voltage-jump relaxations for the α3β2, α3β4 and α4β2 receptors contain more than one component (Papke et al. 1989; Papke & Heinemann, 1991; Figl et al. 1996, 1998; Kuryatov et al. 1997; Sivilotti et al. 1997; Nelson & Lindstrom, 1999). However, we cannot say with certainty whether two channel populations with different burst durations or a single channel population with two rate-limiting steps governing channel bursting generates the two-component voltage-jump relaxations reported in this and previous studies (Figl et al.1996, 1998).

METHODS

Oocyte expression

We surgically isolated stage V-VI Xenopus oocytes following previously published procedures (Quick & Lester, 1994) approved by the University of California Committee on Laboratory Animal Care. Mature female Xenopus laevis were anaesthetized by a 45–60 min immersion in 0.2 % tricaine methanesulphonate (Sigma, St Louis, MO, USA). The ovarian lobes were extracted through a small abdominal incision. After the first surgery, the incision was ligated and the animals were allowed to recover in isolation for 24 h before being returned to their home tank. After the second surgery, the anaesthetized animals were killed by decapitation. The follicular layer of the oocytes was removed with a collagenase treatment (1–2 h in 2 mg ml⁻¹ collagenase Type A, Boehringer-Mannheim, Indianapolis, IN, USA). After 24 h, we injected the oocytes with 24 ng of the rat α cRNA and 36 ng of the β cRNA. Capped cRNA was synthesized in vitro using the mMessage mMachine RNA transcription kit (Ambion, Austin, TX, USA) from linearized pBluescript cDNA. The GenBank accession numbers of the rat α2, α3, α4, β2 and β4 cDNA clones were L10077, X03440, L31620, L31622 and U42976, respectively. The rat α2, α3, α4, β2 and β4 cDNA clones contained 35, 151, 11, 189 and 61 bp long 5′ untranslated regions and 101, 282, 195, 506 and 913 bp long 3′ untranslated regions. The injected oocytes were incubated for ≥48 h at 18°C in a modified Barth's solution (96 mM NaCl, 5 mM Hepes, 2.5 mM sodium pyruvate, 2 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, 2.5 μg ml⁻¹ gentamicin (Sigma) and 5 % horse serum, pH 7.4) before electrophysiological recordings were attempted.

Electrophysiological recordings

The oocytes were voltage clamped with two 3 M KCl-filled microelectrodes (1.5–4 MΩ resistance) using a GeneClamp voltage clamp (Axon Instruments, Foster City, CA, USA) equipped with a bath clamp. The oocytes were continually superfused with a nominally Ca²⁺-free physiological saline (98 mM NaCl, 1 mM MgCl₂, 5 mM Hepes, pH 7.4) at room temperature (19–22°C) during the experiments unless otherwise indicated. Nominally Ca²⁺-free saline was used to prevent activation of the endogenous Ca²⁺-activated Cl⁻ current (Vernino et al. 1992). Extracellular Ca²⁺ at concentrations of 0–5 mM appears to have little, if any, effect on the neuronal nicotinic burst duration (Mulle et al. 1992) or the ganglionic EPSC decay time constant (Sacchi et al. 1998). Reducing the extracellular [Ca²⁺] from 4 to 0 mM does not affect the burst duration distribution of nicotinic channels in habenular neurons (Mulle et al. 1992), and reducing the extracellular [Ca²⁺] from 5 to 2 mM reduces the rat sympathetic ganglionic EPSC decay time constant only 21 % (Sacchi et al. 1998). ACh was bath applied with a time constant of 30 s. We digitally recorded the voltage-clamp currents using a personal computer equipped with a DigiData 1200 A/D interface and pCLAMP v. 6 software (Axon Instruments). To avoid aliasing, the analog current was filtered at one-third the sampling frequency with an eight-pole, low-pass Bessel filter prior to digitization. The β2 voltage-jump relaxation currents were filtered at 800 Hz and sampled at 3000 Hz. The β4 voltage-jump relaxation currents were much slower than the β2 voltage-jump relaxation currents. We filtered the β4 voltage-jump relaxation currents at 100 Hz and sampled them at 300 Hz to allow us to resolve the entire β4 voltage-jump relaxations using a reasonable sample buffer size.

Analysis of the relaxation currents

We fitted the ACh-induced relaxation subtype relaxation currents to the sum of two negative exponential functions and a constant term using a Chebyshev polynomial transform (pCLAMP v. 6):

(1)

where I_f and I_s are the amplitudes of the fast and slow exponential components, τ_f and τ_s are the fast and slow relaxation time constants, I_ss is the steady-state ACh-induced current, and t is the time after the start of the voltage jump. We defined the fractional amplitude of the fast exponential component (I_f/I_tot) as:

(2)

Linear regression was used to determine whether the logarithm of the relaxation time constants was significantly dependent on the membrane potential. Multiple linear regression (MLR) was used to determine whether the I_f/I_tot was significantly voltage and/or ACh concentration dependent.

Calculation of the apparent activation energy and Q₁₀

The apparent activation energy (E_a) and the Q₁₀ for the relaxation time constants were calculated from the Arrhenius equation (Segel, 1976, pp. 278–279). ACh-induced voltage-jump relaxation currents were recorded at two different temperatures T₁ and T₂. The E_a for the relaxation time constants was calculated from the following equation:

(3)

where R is the universal gas constant, T₁ and T₂ are in kelvins and τ₁ and τ₂ are the relaxation time constants at T₁ and T₂, respectively. The Q₁₀ between 10 and 20°C was calculated from the E_a (in kJ mol⁻¹) using the following equation:

(4)

ACh concentration dependence of the relaxation time constants at low occupancies

The standard kinetic model for ACh activation of the nicotinic receptor is (Model 1):

Model 1.

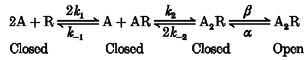
A is the agonist ACh; R is the nicotinic receptor; k₁-k_-2, α and β are rate constants; and A₂R* is the sole conducting state (Aidley & Stanfield, 1996). If channel closing (α) is the rate-limiting step in this reaction, then we can recast Model 1 in terms of the following empirical model:

[A] is the ACh concentration, n_H is the apparent Hill coefficient for ACh binding, k_f and k_b are rate constants and the other symbols have the same meaning as in Model 1 (above). Model 2 assumes that states R, AR and A₂R are in rapid equilibrium with each other. Thus, we can use the Hill equation to empirically describe the fractional occupancy of the doubly liganded closed state [A₂R] as a function of the ACh concentration (Segel, 1976, pp. 309–311). Thus [A₂R] is given by:

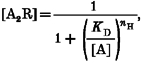(5)

where:

(6)

Model 2.

If one or more rate constants in Model 1 are voltage dependent, then the macroscopic ACh-induced voltage-clamp current will relax exponentially to a new steady state in response to a voltage-step perturbation. Model 2 predicts that the time constant τ of this relaxation is related to the ACh concentration as follows:

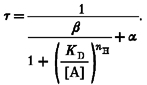(7)

At low A₂R fractional occupancies:

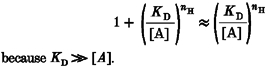(8)

because K_d≫[A].

Using this approximation, eqn (7) simplifies to:

(9)

where:

(10)

and

(11)

As the ACh concentration approaches zero in eqn (9), the τ in this equation approaches a limiting value τ(0). We fitted eqn (9) to the ACh concentration-time constant data at a particular membrane potential to estimate the limits τ(0)_f and τ(0)_s approached by the fast and slow relaxation time constants τ_f and τ_s as the ACh concentration approached zero at that membrane potential. A non-linear least-squares regression routine in SigmaPlot v. 5 (SPSS, Chicago, IL, USA) was used to fit eqn (9) to the data. To reduce parameter covariance during the fits, we fixed the value of the n_H before fitting eqn (9) to the data, leaving the τ(0) and K as free parameters. We determined the optimum fixed value for the n_H by varying this parameter until the best possible visual fit of eqn (9) was achieved with τ(0) and K as free parameters.

RESULTS

Bi-exponential voltage-jump relaxations

The voltage-jump relaxation currents of the six neuronal nicotinic subtypes produced by pairwise expression of the rat α2, α3 or α4 subunit with the β2 or β4 subunit were best fitted by the sum of two negative exponentials and a constant (Fig. 1A–D). To generate the subtype relaxation currents, a series of ten voltage jumps were made from the holding potential (-50 mV) to +50 mV and then back again to a voltage between -60 and -150 mV, in the presence (Fig. 1B) and in the absence of ACh (Fig. 1A). The initial jump was to -150 mV and the subsequent jumps were incremented by +10 mV. The interjump interval was 4 s. We defined the ACh-induced relaxation current as the difference between the relaxation current in the presence and absence of ACh (Fig. 1C). Because of the large signal-to-noise ratios, averaging the relaxation currents from several trials was unnecessary. We waited until the ACh response reached a steady state to initiate the voltage-jump protocol. Sag of the ACh response during the voltage jumps was negligible because receptor desensitization was slow at the foot of the ACh concentration-response relation. Double-exponential fits superimposed on the ACh-induced relaxation currents (Fig. 1D). Single-exponential fits (dashed line in Fig. 1D) increased too slowly during the initial part of the relaxation and then saturated too quickly (Fig. 1D). All the subtype relaxation currents displayed deviations from a single-exponential fit. In contrast, double-exponential fits superimposed on the relaxation currents, similar to previous results for the α3β2 and α3β4 subtypes (Figl et al. 1996). Examples of 1 μM ACh-induced relaxation currents from the six nicotinic receptor subtypes are shown in Fig. 2A–F

Figure 1. Bi-exponential neuronal nicotinic voltage-jump relaxation currents.

A–C, the upper traces are the command potential protocols and the lower traces are the voltage-clamped currents. We used a 75 ms prepulse from -50 mV (holding potential) to +50 mV to increase the relaxation amplitudes. Following the pre-pulse, 10 voltage jumps (2.4 s long) were made from +50 mV to a potential between -60 and -150 mV in 10 mV increments. After these jumps, the voltage returned to the holding potential. A, α3β4 voltage-jump currents in the absence of ACh. B,α3β4 relaxation currents in 1 μM ACh. C, difference of currents in A and B. D, fits of the α3β4 ACh-induced difference current at -150 mV to the sum of one (dashed line) or two (continuous line) negative exponentials and a constant. The fit to two exponential components and a constant superimposes on the data. For the two-exponential fit, the fast (τ_f) and slow (τ_s) time constants were 96 and 343 ms, respectively. The amplitudes of the fast (I_f), slow (I_s) and steady-state (I_ss) relaxation components were 6.8, 5.7 and -14.6 μA, respectively. The fractional amplitude of the fast component (I_f/I_tot) was 0.54. The time constant, relaxation amplitude and steady-state current for the single-exponential fit were 218 ms, 11.0 μA and -14.5 μA, respectively. (See Methods for acquisition filter frequencies and sampling rates.)

Figure 2. ACh-induced voltage-jump relaxation currents for the receptor subtypes.

A-F, the upper traces are the voltage-clamp command potential protocols and the lower traces are 1 μM ACh-induced voltage-jump relaxation currents. The short lines at the top left of the current traces denote zero current. The voltage command protocols were the same as in Fig. 1 (above) except that their duration was adjusted for the optimal temporal resolution of the relaxation currents.

Estimation of the zero ACh concentration limits for the relaxation time constants

Regardless of whether we assume that agonist unbinding or channel closing is the single rate-limiting step in the activation of neuronal nicotinic receptors by ACh (see Model 1 in Methods), the macroscopic relaxation time constant should approach a limit τ(0) as the ACh concentration approaches zero. This limit should approximate the slow single-channel burst duration at low ACh concentrations (Colquhoun & Hawkes, 1995) and the synaptic current decay time constant (Edmonds et al. 1995). The previous section shows that the ACh-induced voltage-jump relaxations for the nicotinic subtypes we studied actually contained two exponential components rather than the single exponential component predicted by a kinetic model with one rate-limiting step. These two components could originate from two kinetically distinct receptor subpopulations or a kinetic model with two rate-limiting steps (see Discussion). In either case, previous results (Figl et al. 1996) show that eqn (7) in Methods gives an accurate empirical description of the ACh concentration dependence of both α3β2 and α3β4 relaxation time constants over a wide ACh concentration range. Thus, to estimate the zero ACh concentration limits for the relaxation time constants, we measured the subtype relaxation time constants at five to eight ACh concentrations near the foot of the ACh concentration-response relationship (Fig. 3A–F) and fitted the data to an approximation to eqn (7) (eqn (9)) that is valid at low ACh concentrations (see Methods). Equation (9) fitted the subtype relaxation data at low ACh concentrations reasonably well (Fig. 3A–D). However, the signal-to-noise ratio of the relaxation currents and the temporal resolution of the whole-oocyte voltage clamp (∼2 ms) limited the low and high end of the usable ACh concentration range for the β2 subtypes. Fixing the n_H at 1.6 (α2β2), 1.7 (α3β2) and 1.8 (α4β2) gave the best fits to the β2 data. Fixing the n_H at 1.0 (α2β4, α4β4) and 0.8 (α3β4) gave the best fits to the β4 data. The most straightforward explanation for the low n_H (≤1) of the β4 ACh concentration-τ relations is that subpopulations within each β4 subtype have heterogeneous values of K in eqn (9) but, similar values of τ(0). The optimum n_H for the α3β2 and α3β4 subtypes was similar to that previously reported for the rat α3β2 (n_H= 1.6–2.0) and α3β4 (n_H= 0.9–1.0) relaxation time constants over a wider ACh concentration range (Figl et al. 1996). Adequate fits to eqn (9) do not imply that channel closing is the rate-limiting step in Model 1 (see Methods) because an equation derived from a model assuming that ACh dissociation from state A₂R was rate limiting (k_-2 in Model 1), rather than channel closing (α in Model 1), could also fit the low ACh concentration-τ data. Nevertheless, eqn (9) provided a good empirical approximation for the ACh concentration-τ data at low ACh concentrations.

Figure 3. Fits of eqn (9) to the relaxation time constants at low ACh concentrations and -150 mV.

A, fits of the α2β2, α3β2 and α4β2 τ_f at various ACh concentrations to eqn (9) (see Methods). The symbols are the means for 4–15 oocytes. The error bars are ±s.e.m. The lines are non-linear least-squares fits to eqn (9) using the regression routine in SigmaPlot v. 5. The fitted values for the α2β2, α3β2 and α4β2 τ(0)_f and K were 4.3 ± 0.2 ms (± s.e.) and 18 ± 5 μM, 6.1 ± 0.2 ms and 4.4 ± 0.7 μM, and 5.9 ± 0.3 ms and 1.5 ± 0.3 μM, respectively. The n_H values used to obtain these fits are given in the text. B, fits of the α2β2, α3β2 and α4β2 τ_s to eqn (9). The fitted values of the α2β2, α3β2 and α4β2 τ(0)_s and K were 32 ± 3 ms and 12 ± 4 μM, 53 ± 2 ms and 2.8 ± 0.3 μM, and 52 ± 5 ms and 0.8 ± 0.2 μM, respectively. C, fits of the α2β4, α3β4 and α4β4 τ_f to eqn (9). The symbols are the means for 3–8 oocytes. The fitted values for the α2β4, α3β4 and α4β4 τ(0)_f and K were 77 ± 9 ms and 2.0 ± 0.8 μM, 125 ± 4 ms and 12 ± 2 μM, and 42 ± 4 ms and 1.3 ± 0.5 μM, respectively. D, fits of the α2β4, α3β4 and α4β4 τ_s to eqn (9). The fitted values of the α2β4, α3β4 and α4β4 τ(0)_s and K were 800 ± 200 ms and 0.5 ± 0.3 μM, 550 ± 40 ms and 12 ± 6 μM, and 900 ± 140 ms and 0.3 ± 0.1 μM, respectively.

Expression with β4 prolonged the relaxation time constants

The β4 time constants were larger than the β2 relaxation time constants at all the ACh concentrations tested (Fig. 4A–F). The lowest ACh concentration that yielded measurable relaxation currents between -80 and -150 mV was 50 nM for α4β2, 100 nM for α4β4, 200 nM for α2β4 and α3β4, and 500 nM for α2β2 and α3β2. At these ACh concentrations and membrane potentials, the β2 τ_f ranged from 4 to 7 ms, and the β2 τ_s ranged from 31 to 73 ms (Table 1). In contrast, the β4 τ_f was 32–116 ms and the β4 τ_s was 220–1000 ms (Table 1). All the β2 subtype (Fig. 4A–F insets), the α3β4 (Fig. 4C–D) and the fast α2β4 (Fig. 4A) relaxation time constants reached a plateau as the ACh concentration approached zero. However, the slow α2β4 (Fig. 4B) and the α4β4 (Fig. 4E–F) relaxation time constants continued to rise even at the lowest ACh concentrations we used. Except for the α4β4 fast relaxation, the increased scatter of the β4 relaxation time constants at a fixed ACh concentration in Fig. 4A–F shows that the β4 relaxation time constants were more voltage dependent than the β2 relaxation time constants. Membrane hyperpolarization enhanced the difference between the β2 and β4 time constants for all the subtype relaxations except those for the α4 fast relaxations. At -80 mV and the ACh concentrations given above, the β4 τ_f was 7–19 times larger than the β2 τ_f (with the same α subunit) and the β4 τ_s was 5–12 times larger than the β2 τ_s. At -150 mV, the β4 τ_f was 5–23 times larger than the β2 τ_f and the β4 τ_s was 14–19 times larger than the β2 τ_s. Increasing the ACh concentration reduced the voltage sensitivity of the β4 relaxation time constants (except the α4β4 τ_f). This reduction suggests that the β4 channel opening rate constant is either not voltage dependent or has a voltage dependence opposite that of the channel closing rate constant. The α3β2 τ_s (32 ± 6 ms, n = 11) at -80 mV in 2 μM ACh was within error of the time constant previously reported (29 ms) for 5 μM ACh-induced noise at -80 mV in bovine chromaffin cells at 20–22°C (Fenwick et al. 1982).

Figure 4. ACh concentration dependence of the relaxation time constants at membrane potentials between -60 and -150 mV.

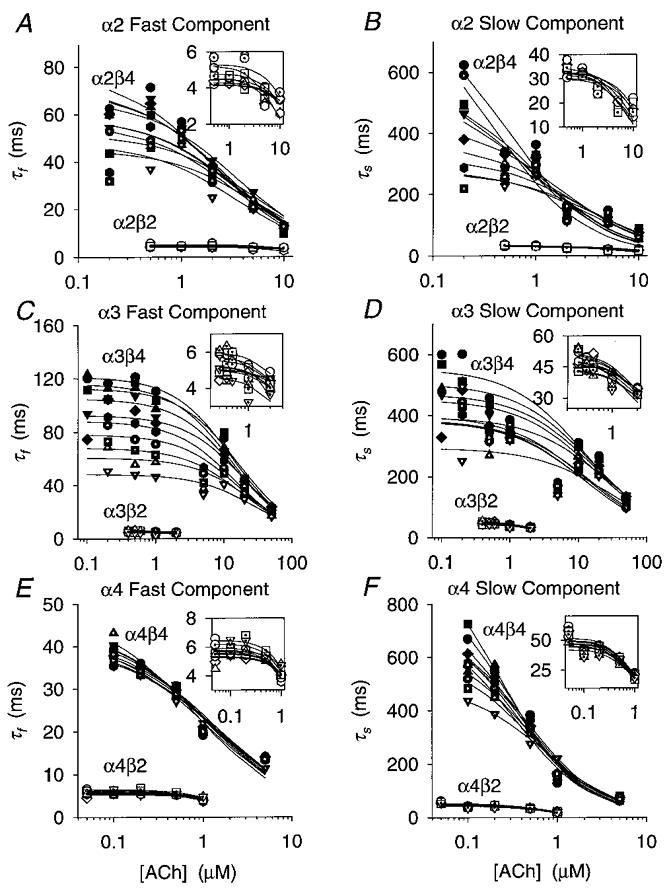
A-F, plots of the α2β2, α2β4, α3β2, α3β4, α4β2 and α4β4 fast (τ_f) and slow (τ_s) relaxation time constants versus the ACh concentration ([ACh]) for 10 (8 for α2β2) different membrane potentials (-60 to -150 mV in 10 mV increments). The symbols denote the means of 3–15 oocytes (error bars are omitted for clarity). The lines are non-linear least-squares fits of the relaxation time constants at a given membrane potential to eqn (9) (see Methods). SigmaPlot v. 5 was used to fit eqn (9) to these data. Insets are plots of the β2 data at a greater temporal resolution. Each symbol type denotes a different membrane potential. Filled circles, -150 mV; filled squares, -140 mV; filled upright triangles, -130 mV; filled inverted triangles,-120 mV; filled diamonds,-110 mV; filled hexagons,-100 mV; dotted circles, -90mV; dotted squares,-80 mV; dotted upright triangles,-70 mV; and dotted inverted triangles,-60 mV.

Table 1. Values of τ_f and τ_s at -150 and -80 mV at low ACh concentrations.

		−150 mV		−80 mV
Subtype	[ACh] (mm)	τf (ms)	τs (ms)	τf (ms)	τs (ms)
α2β2	500	5.1 ± 0.3 (5)	33 ± 1 (5)	4.4 ± 0.5 (6)	43 ± 2 (6)
α3β2	500	5.0 ± 0.5 (12)	50 ± 2 (12)	4.5 ± 0.2 (4)	35 ± 3(4)
α4β2	50	7 ± 1 (4)	73 ± 6 (4)	5.5 ± 0.4 (3)	57 ± 3 (3)
α2β4	200	97 ± 20 (3)	620 ± 50 (3)	32 ± 7 (3)	220 ± 20 (3)
α3β4	200	116 ± 8 (6)	600 ± 40 (6)	85 ± 6 (6)	430 ± 70 (6)
α4β4	100	39 ± 5 (4)	1000 ± 200 (4)	37 ± 2 (4)	480 ± 50 (4)

Values are means ±s.e.m. (number of oocytes).

Expression with β4 increased the τ(0)_f and τ(0)_s

Expression with β4 dramatically increased the zero ACh concentration limits estimated by fitting the ACh concentration-relaxation time constant data to eqn (9). We measured the τ(0)_f and τ(0)_s for eight to ten different membrane potentials between -60 and -150 mV for the six nicotinic receptor subtypes we studied. The β2 τ(0)_f ranged from 4 to 6 ms between -60 mV (-80 mV for α2β2) and -150 mV (Fig. 5A). The β2 τ(0)_s ranged from 30 to 53 ms (Fig. 5B). In contrast, the β4 τ(0)_f was 40–121 ms over the same voltage range (Fig. 5A). The β4 τ(0)_s was 274–1039 ms (Fig. 5B). At membrane potentials in the typical range of neuronal resting potentials (-80 to -60 mV), the β4 τ(0)_f was 7–14 times larger than the β2 τ(0)_f, and the β4 τ(0)_s was 7–18 times larger than the β2 τ(0)_s. The difference between the β2 and β4 zero ACh concentration limits became more pronounced as membrane hyperpolarization increased (except for the α4 τ(0)_s, Fig. 5A–B). The α4β4 τ(0)_f and τ(0)_s may be less reliable than the other estimates because the time constants did not reach a clear plateau at the lowest ACh concentrations used (Fig. 4E–F). However, the ranges of standard errors for the α4β4 τ(0)_f and τ(0)_s between -150 and -60 mV (2–4 ms and 16–140 ms) were similar to those (3–7 ms and 25–200 ms) for the corresponding α2β4 and α3β4 estimates. The α3β2 τ(0)_f (5–6 ms) and τ(0)_s (44–49 ms) between -60 and -100 mV were close to previously reported values for the fast (5–9 ms) and slow (35–45 ms) ganglionic EPSC decay time constants (Rang, 1981; Yawo, 1989) over the same voltage range and at similar temperatures (20 and 25°C). The α3β2 τ(0)_f at -80 mV (5.0 ± 0.6 ms, ±s.e.m.) was nearly identical to the slow burst duration (5.3 ± 0.7 ms) reported previously for human α3β2 channels at that voltage (Nelson & Lindstrom, 1999). The α3β2 τ(0)_s at -80 mV (45 ± 2 ms, ±s.e.m.) was also within error of the previously reported burst duration (37 ± 15 ms, ±s.d.) for nicotinic channels in rat PC12 cells at that voltage and 23–24°C (Ifune & Steinbach, 1992). The α3β4 τ(0)_f at -80 mV (68 ± 4 ms, ±s.e.m.) was somewhat longer than the slow burst duration (16 ± 1 ms) reported previously for human α3β4 channels at that voltage (Nelson & Lindstrom, 1999). However, the α3β4 τ(0)_s at -100 mV (380 ± 30 ms, ±s.e.m.) was similar to the slowest burst duration (480 ± 11 ms) previously reported for rat α3β4, α3β4β2 and α3α5β4 channels at that voltage (Sivilotti et al. 1997). Finally, the α4β2 τ(0)_f (6.4 ± 0.2 ms, ±s.e.m.) and τ(0)_s (45 ± 5 ms) at -60 mV closely matched the intermediate (7 ± 2 ms) and slow (37 ± 5 ms) burst durations previously reported for 41 pS nicotinic channels in rat medial habenular neurons at that voltage (Connolly et al. 1995).

Figure 5. Voltage dependence of the zero ACh concentration limits for the relaxation time constants.

A and B, plots of the zero ACh concentration limits for the fast and slow α2β2, α2β4, α3β2, α3β4, α4β2 and α4β4 relaxation time constants τ_f(0) and τ_s(0) versus membrane potential. Table 2 gives the slopes of the regression line (i.e. the voltage dependence of τ(0)). A, the extrapolated τ_f(0) at 0 mV was 6, 5, 7, 35, 31 and 42 ms for the α2β2, α3β2, α4β2, α2β4, α3β4 and α4β4 subtypes, respectively. B, the extrapolated τ_s(0) at 0 mV was 32, 41, 40, 138, 234 and 398 ms for the α2β2, α3β2, α4β2, α2β4, α3β4 and α4β4 subtypes, respectively. The error bars are ±s.e.m..

Effects of the β subunit on the voltage dependence of τ(0)_f and τ(0)_s

Co-expression with β4 increased the voltage dependence of the τ(0)_f and τ(0)_s over the voltage range we studied (Fig. 5A–B) in all but one case (α4β4 fast relaxation, Fig. 5A). The β2 τ(0)_f and τ(0)_s displayed little (less than an e-fold change per 500 mV, correlation coefficient r = 0.73–0.84, degrees of freedom (d.f.) = 6–8, P < 0.05) or no significant voltage dependence (r = 0.03–0.55, d.f. = 6–9, P > 0.10) between -60 mV (-80 mV for α2β2 and α2β4) and -150 mV (Table 2). Previous studies show that ganglionic EPSC decay time constants also display little voltage dependence over this voltage range (Rang, 1981; Yawo, 1989). In contrast, the τ(0)_f and τ(0)_s for all the β4 subtypes except the α4β4 τ(0)_f (r = 0.12, d.f. = 8, P > 0.70) displayed significant voltage dependence (e-fold increases per -102 to -209 mV, r = 0.83–0.97, d.f. = 8, P < 0.01) between -60 and -150 mV (Table 2). The α2β4 τ(0)_s and α3β4 τ(0)_f displayed the greatest voltage dependence over this voltage range (e-fold increases per -94 to -102 mV). Their voltage dependencies matched that (e-fold increase per -104 mV) previously reported for the rat muscle ACh-induced voltage-jump relaxation time constant (Horn & Brodwick, 1980) and corresponded to the movement of 0.25–0.27 elementary charges through the entire membrane electric field, or 1 elementary charge through 0.25–0.27 of the electric field.

Table 2. Voltage dependence of τ(0).

	Fast		Slow
Receptor subtype	Voltage dependence of τ(0) (mV/e-fold increase)	Equivalent gating charge	Voltage dependence of τ(0) (mV/e-fold increase)	Equivalent gating charge
α2β2	n.s.	0	n.s.	0
α3β2	n.s.	0	< −500	< 0.05
α4β2	n.s.	0	< −500	< 0.05
α2β4	−209	0.12	−94	0.27
α3β4	−102	0.25	−186	0.14
α4β4	n.s.	0	−174	0.15

n.s., value of τ for the logarithm of τ(0) versus voltage was not significant.

Voltage and ACh concentration dependence of the relaxation amplitudes

Figure 6A–F shows the fractional amplitude of the fast relaxation versus the ACh concentration for eight to ten different membrane potentials between -60 and -150 mV. Expression with β4 increased the voltage dependence of the α2 and α3 I_f/I_tot (Fig. 6A–F). The α2β2 (Fig. 6A), α4β2 (Fig. 6E) and α4β4 I_f/I_tot (Fig. 6F) were not significantly voltage dependent between -80 and -150 mV (MLR, t = 0.04–1.70, d.f. = 44–47, P > 0.05) at the ACh concentrations tested (0.2–20 μM for α2β2, 0.05–1 μM for α4β2, 0.1–10 μM for α4β4). The α3β2 (Fig. 6C), α2β4 (Fig. 6B) and α3β4 I_f/I_tot (Fig. 6D) were significantly voltage dependent (MLR, t = 6.1 (α3β2), 5.4 (α2β4) and 17.8 (α3β4); d.f. = 44, 45 and 51; P < 0.01) between -70 and -150 mV. However, the α2β4 and α3β4 I_f/I_tot decreased 5–7 times faster (0.3–0.4 % mV⁻¹) with membrane hyperpolarization than the α3β2 I_f/I_tot (0.06 % mV⁻¹). The ACh concentration ranges for the α3β2, α2β4 and α3β4 measurements were 0.4-2, 0.2–10 and 1–50 μM. Thus, co-expression with the β4 subunit had similar effects on the voltage dependence of the relaxation time constants and fast fractional amplitudes.

Figure 6. ACh concentration dependence of the fast fractional amplitude.

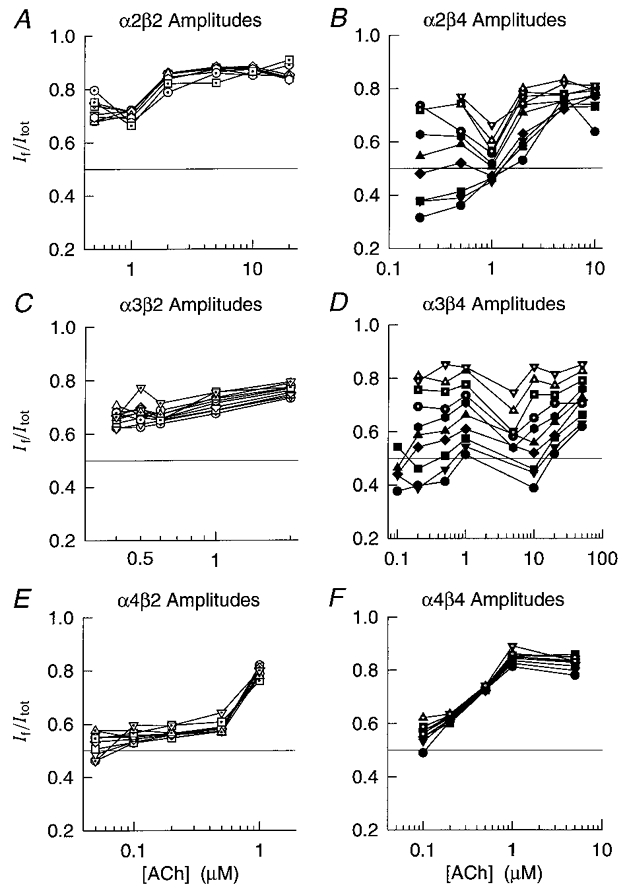
A-F, plots of the fractional amplitude of the α2β2, α2β4, α3β2, α3β4, α4β2 and α4β4 fast relaxation component (I_f/I_tot) versus ACh concentration for 10 (8 for α2β2) different membrane potentials (-60 to -150 mV in 10 mV increments). Each point is the mean of 3–15 oocytes. Straight lines connect the I_f/I_tot at the same membrane potential. For clarity, we omitted the s.e.m. of individual points. The symbol assignment is the same as that in Fig. 4.

Temperature dependence of the α4β2 and α3β4 relaxation parameters

The temperature dependence of neuronal nicotinic relaxation time constants has not been previously studied. To measure the temperature dependence of the relaxation time constants (E_a and Q₁₀), we recorded α4β2 and α3β4 voltage-jump relaxations at 8–9 and 22°C (Fig. 7A–D) using the lowest possible ACh concentrations (100 nM ACh for α4β2, 1 μM ACh for α3β4). We chose the α4β2 receptor as the representative β2 subtype because its robust expression permitted us to record relaxation currents at 9°C in low ACh concentrations. Reducing the temperature from 22 to 8–9°C prolonged the α4β2 (Fig. 8) and α3β4 (Fig. 9) relaxation time constants 2.3- to 6.6-fold. It also reduced the relative amplitude of the fast relaxation and changed the voltage dependence of the α3β4 relaxation time constants and relative relaxation amplitudes. At 22°C, the α4β2 τ_f ranged from 3.0 to 3.5 ms between -70 and -150 mV, the τ_s ranged from 27 to 29 ms, and the I_f/I_tot ranged from 0.65 to 0.70 (n = 5 oocytes). At 9°C, the α4β2 τ_f increased to 13–17 ms over the same voltage range, the τ_s increased to 76–91 ms, and the I_f/I_tot dropped to 0.4–0.5 (n = 5). At 22°C, the α3β4 τ_f was 47–110 ms between -60 and -150 mV, the τ_s was 319–385 ms, and the I_f/I_tot was 0.5–0.8 (n = 7). At 8°C, the α3β4 τ_f increased to 240–355 ms over this voltage range, the τ_s increased to 1300–2350 ms, and the I_f/I_tot dropped to 0.07–0.25 (n = 3). Thus, the α3β4 relaxations slowed considerably at 8°C and the fast relaxation component almost disappeared (Fig. 8C). Reducing the temperature from 22 to 8°C abolished the voltage dependence of the α3β4 τ_f but raised that of the α3β4 τ_s from less than an e-fold increase per -500 mV at 22°C to an e-fold increase per -109 mV at 8°C (Fig. 9A–B). In contrast, previous experiments on muscle nicotinic receptors show that reducing the temperature from 23 to 10°C increases the voltage dependence of the endplate current decay time constant by only 34 % (Magleby & Stevens, 1972). Thus, the voltage dependence of the α3β4 relaxation time constants was more temperature sensitive than that of the endplate current decay time constant. The α4β2 relaxation time constants displayed little voltage dependence (≤ an e-fold change per -330 mV) at 9 or 22°C (Fig. 7A–B). However, reducing the temperature increased the voltage dependence of the α4β2 I_f/I_tot (Fig. 8C). Thus, reducing the temperature from 23 to 10°C had opposite effects on the voltage dependence of the α4β2 and α3β4 I_f/I_tot.

Figure 7. Temperature dependence of the α4β2 and α3β4 relaxation currents.

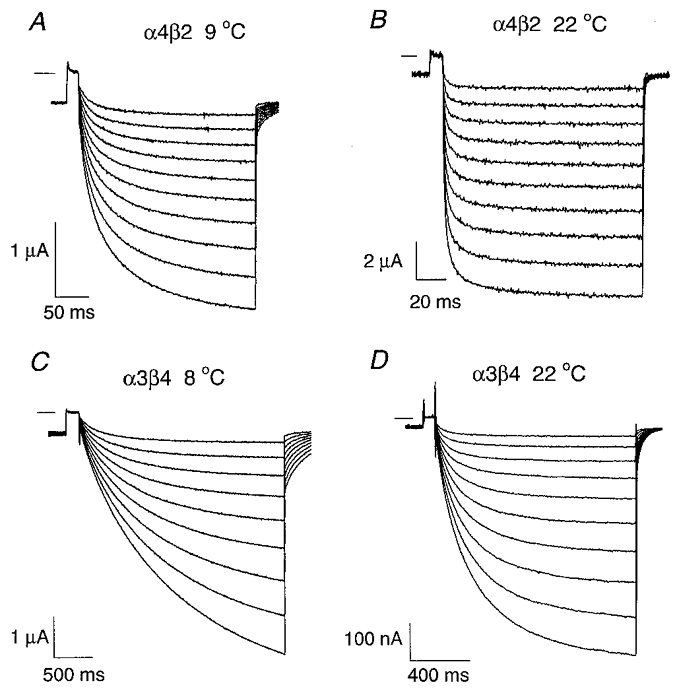
A-B, the traces are ACh-induced α4β2 relaxation currents at 9 °C (A) and at 22 °C (B). [ACh]= 100 nM. The relaxation currents were generated with a command voltage protocol (not shown) similar to that used in Fig. 1. Following a prepulse from -50 to +50 mV, the potential was jumped to a voltage between -60 and -150 mV (in 10 mV increments) and then jumped back again to -50 mV. The short horizontal line near the upper left corner of each set of traces denotes zero current. C-D,α3β4 relaxation currents at 8 °C (C) and 22 °C (D). [ACh]= 1 μM. The voltage protocol was the same as in C–D as in A–B but the jump duration was increased to compensate for the slower α3β4 relaxation time constants.

Figure 8. Reducing the temperature prolonged the α4β2 relaxation time constants and reduced the fast component fractional amplitude.

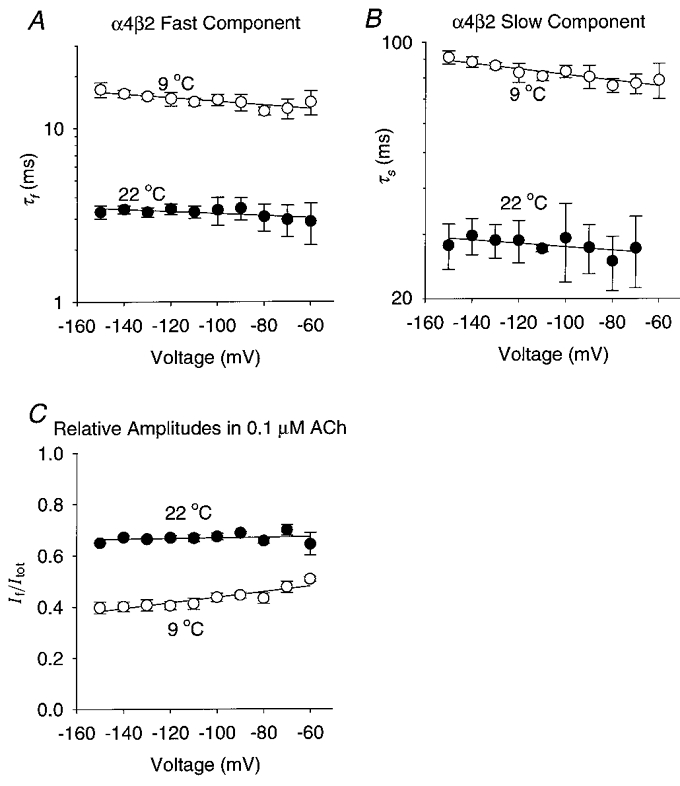
A-C, plots of the α4β2 τ_f, τ_s and I_f/I_totversus membrane potential at 9 and 22 °C. [ACh]= 100 nM. The symbols are the means of 5 oocytes. The error bars are ±s.e.m. The straight lines were fitted using least-squares regression. A, the α4β2 τ_f increased e-fold per -395 mV at 9 °C (r = 0.86, d.f. = 8, P < 0.01) and e-fold per -725 mV at 22 °C (r = 0.69, d.f. = 8, P < 0.05). The extrapolated α4β2 τ_f at 0 mV decreased from 11 ms at 9 °C to 3 ms at 22 °C. B, the α4β2 τ_s increased e-fold per -557 mV at 9 °C (r = 0.92, d.f. = 8, P < 0.01) but was not significantly correlated with voltage at 22 °C (r = 0.60>, d.f. = 7, P > 0.05). The extrapolated α4β2 τ_s at 0 mV was 68 ms at 9 °C. C, the slope of the α4β2 I_f/I_tot regression line at 9 °C was 0.0025 mV⁻¹ (r = 0.91, d.f. = 8, P < 0.01). The α4β2 I_f/I_tot at 22 °C was not significantly correlated with voltage (r = 0.2, d.f. = 8, P > 0.10). The extrapolated α4β2 I_f/I_tot at 0 mV was 0.6 at 9 °C.

Figure 9. Reducing the temperature also prolonged the α3β4 relaxation time constants and reduced the fast component fractional amplitude.

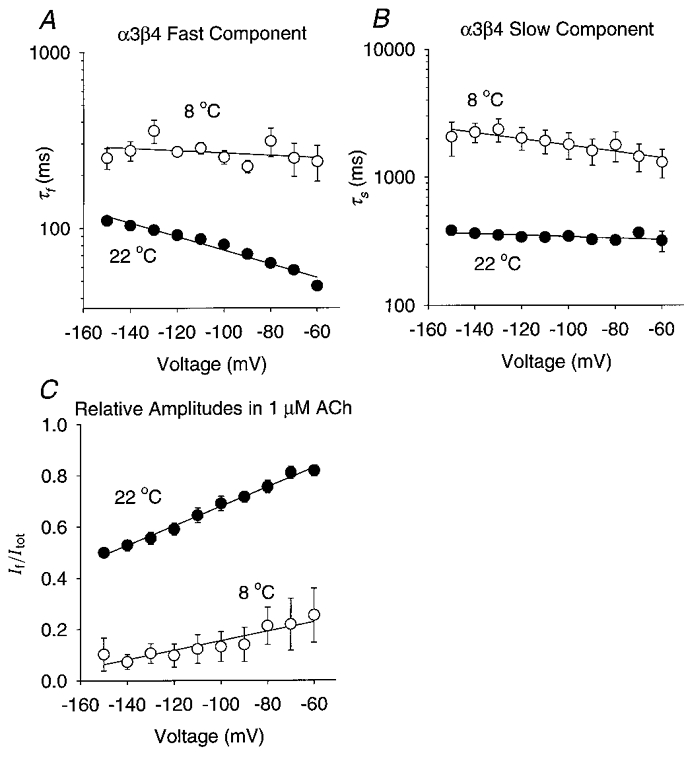
A-C, the α3β4 τ_f, τ_s and I_f/I_totversus membrane potential at 8 °C (n = 3 oocytes) and 22 °C (n = 7). [ACh]= 1 μM. The error bars are ±s.e.m.A, the α3β4 τ_f was not significantly correlated with voltage at 8 °C (r = 0.35, d.f. = 8, P > 0.10). It increased e-fold per -111 mV at 22 °C (r = 0.98, d.f. = 8, P < 0.01). B, the α3β4 τ_s increased e-fold per -174 mV at 8 °C (r = 0.91, d.f. = 8, P < 0.01) and e-fold per -612 mV at 22 °C (r = 0.77, d.f. = 8, P < 0.01). The extrapolated α3β4 τ_s at 0 mV was 68 ms at 9 °C and 25 ms at 22 °C. C, the slope of the α3β4 I_f/I_tot regression line increased from 0.002 mV⁻¹ at 9 °C (r = 0.92, d.f. = 8, P < 0.01) to 0.004 mV⁻¹ at 22 °C (r = 0.99, d.f. = 8, P < 0.01). The extrapolated α3β4 I_f/I_tot at 0 mV was 0.3 at 9 °C and 1.0 at 22 °C.

Activation energies and Q₁₀ of the relaxation time constants

The Q₁₀ for the neuronal nicotinic relaxation time constants was more variable than that previously reported (2.7–3.2) for muscle nicotinic voltage-jump relaxation time constants (Neher & Sakmann, 1975; Sheridan & Lester, 1975) and EPSC decay time constants (Magleby & Stevens, 1972). The E_a for the α4β2 and α3β4 relaxation time constants ranged from 42 to 88 kJ mol⁻¹ between -150 and -60 mV (-70 mV for α4β2). The Q₁₀ between 10 and 20°C for these time constants ranged from 1.9 to 3.9. The major difference between the α3β4 and α4β2 E_a and Q₁₀ was that the α3β4 values were more voltage dependent. The E_a and Q₁₀ for the α3β4 τ_f (r = 0.86, d.f. = 8, P < 0.05) and τ_s (r = 0.78, d.f. = 8, P < 0.01) were significantly voltage dependent between -60 and -150 mV. The E_a for the α3β4 τ_f went from 40 kJ mol⁻¹ at -150 mV to 80 kJ mol⁻¹ at -60 mV. The Q₁₀ went from 1.8 to 3.2. The E_a (67–84 kJ mol)⁻¹ and Q₁₀ (2.7–3.3) for the α3β4 τ_s changed less than that for the α3β4 τ_f. The E_a and Q₁₀ for the α4β2 τ_f (r = 0.80, d.f. = 7, P < 0.01), but not for the τ_s (r = 0.66, d.f. = 7, P > 0.05), were significantly voltage dependent between -70 and -150 mV. However, the change in the E_a (77–87 kJ mol⁻¹) and the Q₁₀ (2.9–3.5) for α4β2 τ_f over this voltage range was less than that for the α3β4 τ_f and τ_s. The E_a (55–62 kJ mol⁻¹) and Q₁₀ (2.2–2.5) for the α4β2 τ_s were also less than those for the α4β2 τ_f. At potentials near the neuronal resting potential (-80 to -60 mV), the major difference between the temperature dependence of the α4β2 and α3β4 relaxation time constants was the slightly lower Q₁₀ of the α4β2 τ_s. The Q₁₀ for the α4β2 τ_s ranged from 2.2 to 2.4 between -80 and -60 mV whereas the Q₁₀ for the iα3β4 τ_f, α3β4 τ_s and α4β2 τ_f ranged from 2.6 to 3.4.

DISCUSSION

Our results show that the β subunit plays a dominant role in determining the voltage-jump relaxation kinetics of neuronal nicotinic receptors formed by pair-wise expression of the rat α2, α3 or α4 subunits with the β2 or β4 subunit. These receptors provide an excellent system for studying the relative contributions of the α and β subunits to the receptor relaxation kinetics because each α forms a functional receptor with either β2 or β4. The voltage-jump relaxation currents of all the subtypes formed by pair-wise expression of the rat α2-α4 with the β2 or β4 subunit contain two exponential components. Co-expression with the β4 subunit prolongs the zero ACh concentration limits for the relaxation time constants by 7- to 18-fold (depending on the membrane potential) and, therefore, should also prolong the single-channel burst duration at low ACh concentrations and the synaptic current decay time constants. Except for the fast α4 relaxations, β4 co-expression also increases the voltage dependence of the zero ACh concentration limits for the relaxation time constants. Thus, similar to the muscle non-α nicotinic subunits (Sakmann et al. 1985), the neuronal non-α nicotinic subunits appear to exert a dominant influence over the bursting behaviour of the receptor and its voltage dependence.

Single-channel kinetic analysis provides a degree of temporal resolution and microscopic detail not available from voltage-jump relaxations analysis. However, there are several reasons for preferring voltage-jump relaxations for an initial comparison of the neuronal nicotinic subtype bursting kinetics. First, each subtype has multiple conductance states (Papke et al. 1989; Papke & Heinemann, 1991). The time required to measure the burst duration distribution for every conductance state of every receptor subtype we studied would be prohibitive. Second, single-channel burst analysis requires a statistical definition of the critical shut time between bursts. Determining the appropriate critical shut time can be a problem in any study of this kind (reviewed in Colquhoun & Sigworth, 1995) but it is particularly difficult for neuronal nicotinic receptors (Papke & Heinemann, 1991). Third, long bursts tend to be under-represented in single-channel recordings because of the limited record lengths (reviewed in Colquhoun & Sigworth, 1995). Fourth and finally, the rapid and irreversible run-down of neuronal nicotinic receptors in excised patches makes burst analysis difficult (Sivilotti et al. 1997).

The previously reported rat α3β2 and human α4β2 single-channel long open times (Papke & Heinemann, 1991; Kuryatov et al. 1997; Sivilotti et al. 1997) are similar to the zero ACh concentration limits for the fast α3β2 and α4β2 relaxation time constants. The rat α3β2 τ(0)_f at 19–22°C (5–6 ms) is slightly longer than the long open time (4.0 ± 0.2 ms) previously reported for the main rat α3β2 channel at 23–25°C (Papke & Heinemann, 1991). The rat α4β2 τ(0)_f at -80 mV (6.2 ± 0.4 ms, ±s.e.m.) is slightly shorter than the long open time (8.1 ± 0.6 ms) previously reported for 28 pS human α4β2 channels at that voltage and temperature (Kuryatov et al. 1997). More recent results (Nelson & Lindstrom, 1999) show that the long burst duration of human α3β2 channels at -80 mV (5.3 ± 0.7 ms, ±s.e.m.) closely matches the rat α3β2 τ(0)_f at this voltage (5.0 ± 0.6 ms, ±s.e.m.). Therefore, we cannot say with certainty whether the rat β2 τ(0)_f represents a single, long channel opening or a burst of several openings.

The α3β4 τ(0)_f is clearly longer than the previously reported α3β4 single-channel open times. The rat α3β4 τ(0)_f at -100 mV and 19–22°C (88 ± 4 ms, ±s.e.m.) is twice as long as the rat α3β4 open time (48 ± 9 ms) reported previously by Sivilotti et al. (1997) at that voltage and temperature and 10 times longer than the long open time (7 ± 2 ms) reported by Papke & Heinemann (1991) for the primary rat α3β4 channel. The rat α3β4 τ(0)_f at -80 mV (68 ± 4 ms, ±s.e.m.) is also ∼10 times longer than the long open time (6.5 ± 0.8 ms) for human α3β4 channels (Nelson & Lindstrom, 1999). Thus, the rat β4 τ(0)_f probably represents a multi-opening burst.

A parallel or sequential kinetic model could generate voltage-jump relaxation currents with two exponential components. Model 3 (below) is an example of a parallel scheme (Model 3):

Model 3.

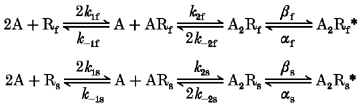
R_f and R_s are receptor subpopulations with different kinetic properties (R_f opens in short bursts, R_s opens in long bursts); k_1f-k_-2f, k_1s-k_-2s, α_f, α_s, β_f and β_s are rate constants; A₂R_f* and A₂R_s* are the sole conducting states; and the other symbols have the same meaning as in Model 1 (see Methods). If both relaxation components represent multi-opening bursts, then the rate constants in Model 3 for agonist dissociation from the doubly liganded states A₂R_f and A₂R_s (k_-2f, k_-2s) must be rate limiting for both receptor subpopulations. Previous results (Figl et al. 1996) show that the fast α3β2 and α3β4 relaxation time constants exhibit nearly the same ACh concentration dependence as the slow relaxation time constants do. Therefore, if Model 3 is correct, then we must also assume that k_1f, k_-1f and k_2f equal k_1s, k_-1s and k_2s, respectively. Otherwise, the relaxation time constants would exhibit different ACh concentration dependence. For any parallel model, this or a similar constraint would be necessary for the relaxation time constants to display similar ACh concentration dependence. A sequential model (Model 4) could also generate double-exponential voltage-jump relaxations:

Model 4.

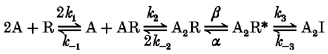
A₂I is an inactivated (or blocked) state, A₂R* is the sole conducting state, k₁-k_-3 are rate constants, and the other symbols have the same meaning as in Model 1. We refer to A₂I in Model 4 as an inactivated (or blocked) state rather than a desensitized state because a significant proportion of the channels entering A₂I must re-enter the open state to generate a slow relaxation component. In contrast, desensitized receptors usually return to the free receptor state (R) without re-entering the open state A₂R* (Katz & Thesleff, 1957). Model 4 could also generate voltage-jump relaxations with two exponential components when two steps in the reaction are rate limiting. For example, either the rate constant for ACh dissociation from the doubly liganded state (k_-2) or the channel closing rate constant (α) could be rate limiting in addition to the channel re-activation (unblocking) rate constant (k_-3). In either case, the time constants of the two relaxation components will display similar ACh concentration dependence, as previously demonstrated for the fast and slow α3β2 relaxation time constants (Figl et al. 1996), without any additional constraints on the agonist association and dissociation rate constants.

Several potential mechanisms could account for the domination of the receptor bursting kinetics by the non-α subunits. First, if the receptor subunits undergo independent, step-wise conformational changes during channel bursting (Auerbach, 1991), then the non-α subunit conformational changes could be rate limiting. Second, if the subunits undergo concerted conformational changes during channel opening (reviewed in Changeux & Edelstein, 1998), then the stability of an interface between a conserved α and a variable non-α region could determine the rate-limiting step in channel bursting. Third and finally, if agonist dissociation from the doubly liganded state is rate limiting, then an interface between a conserved α and a variable non-α region could determine the rate constant for agonist dissociation from the doubly liganded state.

Previous single-channel studies of nicotinic receptors expressed in oocytes (Papke & Heinemann, 1991; Kuryatov et al. 1997; Nelson & Lindstrom, 1999) have failed to detect channel open times or bursts long enough to match the β2 τ_s(0). There are at least three possible explanations for this discrepancy. First, if there are two channel subpopulations, then the subpopulation generating the long bursts may run down too quickly to be detected in excised patches. Second, if an intracellular blocker, rather than receptor inactivation, generates the slow bursts, then this blocker could be rapidly washed out of an excised patch. Third, if the slow β2 bursts contain only a few openings separated by long closures, then they might not be recognized as bursts in single-channel records. Burst durations similar to the β4 τ_s(0) have been reported in previous studies of rat α3β4, α3β4β2 and α3α5β4 channels expressed in Xenopus oocytes (Sivilotti et al. 1997).

Channel closing is generally considered to be the voltage-dependent step in the reaction between ACh and muscle nicotinic receptors (Magleby & Stevens, 1972). Most of the β4 relaxation time constants display greater voltage dependence than the corresponding β2 relaxation time constants between -150 and -60 mV. However, the rat β2 and β4 amino-acid sequences contain the same number and polarity of charged amino-acid residues around the proposed transmembrane segments (Duvoisin et al. 1989). Thus, it seems unlikely that sequence differences are responsible for the differences between the voltage dependence of the β2 and β4 relaxation time constants. Alternatively, non-voltage-dependent rate constants (or rate constants with opposite voltage dependence) could contribute to the β2 relaxation time constant in a way that masks the voltage dependence of the channel closing rate constant. For example, if the β2 channel closing rate constant in Model 4 (α) is voltage dependent but the inactivation rate constant (k₃) is not (or has the opposite) voltage dependence, then the β2 fast relaxation time constant might not appear voltage dependent. We also cannot exclude the possibility that the voltage dependence of the β2 relaxation time constants dramatically increases at membrane potentials more positive than -60 mV. The voltage dependence of some ganglionic EPSC decay time constants is clearly non-uniform over the entire voltage range in which they have been measured (Rang, 1981; Yawo, 1989). For example, the voltage dependence of the mouse and fast rat ganglionic EPSC decay time constants (in 2.5 mM Ca²⁺) increases dramatically at voltages more positive than -50 mV (Rang, 1981; Yawo, 1989).

The α4β2 subtype appears to be the major brain nicotinic receptor (Whiting & Lindstrom, 1988; Zoli et al. 1995). The zero ACh concentration limits for the fast and slow rat α4β2 relaxation time constants match the intermediate and long single-channel burst duration for the 41 pS rat habenular nicotinic channel (Connolly et al. 1995). Rat α4β2 receptors expressed in oocytes display two main conductance states at 34 ± 2 and 49 ± 1 pS (Figl et al. 1998). Thus, at least one native rat CNS nicotinic channel displays a burst duration and conductance similar to those of rat α4β2 receptors expressed in Xenopus oocytes.

Previous pharmacological (Covernton et al. 1994), in situ hybridization (Rust et al. 1994), and single-channel studies (Lewis et al. 1997; Nelson & Lindstrom, 1999) suggest that α3β4 is the major ganglionic nicotinic subtype. However, α7 receptors generate the rapidly decaying phase of the chick ganglionic EPSC and α3β2-containing receptors appear to generate the slowly decaying phase (Zhang et al. 1996; Ullian et al. 1997). Moreover, a significant fraction of ganglionic nicotinic receptors may contain the α5 subunit (in addition to α3 and β4) and some may contain both β4 and β2 (Conroy & Berg, 1995). Thus, the precise subunit composition of the ganglionic nicotinic subtypes has not been settled.

A wide range of channel burst durations and EPSC decay time constants have been reported for native ganglionic nicotinic receptors (reviewed in Papke, 1993). Ganglionic EPSC time constants have been measured at membrane potentials between -100 and 0 mV (Rang, 1981; Derkach et al. 1983; Yawo, 1989; Sacchi et al. 1998). Unfortunately, the signal-to noise-ratio at the low ACh concentrations we used limited us to measuring the relaxation time constants at membrane potentials more negative than -60 or -50 mV. Thus, the overlapping voltage range for the ganglionic EPSC decay time constants and our relaxation time constants is limited to membrane potentials between -50 and -100 mV. Within this voltage range, all we can say is that the magnitude and voltage dependence of the α3β2 τ(0)_f and τ(0)_s match those of the corresponding rat and mouse ganglionic EPSC decay time constants more closely than do those of the α3β4 τ(0)_f and τ(0)_s. For example, the fast time constant for the mouse ganglionic EPSC decay is ∼8 ms between -60 and -100 mV at 25–30°C (Yawo, 1989) and the slow time constant is 30–40 ms. The fast time constant for the rat ganglionic EPSC decay is 8.3–8.6 ms between -60 and -100 mV in 2.5 mM external Ca²⁺ at 20°C (Rang, 1981). The slow time constant is 37–45 ms between -60 and -80 mV (Rang, 1981). In the absence of external Ca²⁺, the α3β2 τ(0)_f ranges from 4.7 ± 0.5 ms (±s.e.m.) at -60 mV to 5.3 ± 0.3 ms at -100 mV (19-22°C). The α3β2 τ(0)_s ranges from 44 ± 3 to 49 ± 2 ms. In contrast, the α3β4 τ(0)_f ranges from 49 ± 3 ms at -60 mV to 88 ± 4 ms at -100 mV. The α3β4 τ(0)_f ranges from 290 ± 40 ms to 380 ± 30 ms. The rabbit ganglionic EPSC decay time constant at 21°C and -80 mV (∼46 ms, Derkach et al. 1983) also matches the α3β2 τ(0)_s (45 ± 2 ms, ±s.e.m.) at that temperature and voltage. The α3β2 τ(0)_s is similar to the rat PC12 nicotinic channel burst duration at -80 mV (Ifune & Steinbach, 1992) and the slow ACh noise time constant in bovine chromaffin cells (Fenwick et al. 1982). However, the predominant single-channel conductance of rat (15 pS, Papke & Heinemann, 1991) and human α3β2 channels (26 pS, Nelson & Lindstrom, 1999) expressed in oocytes is less than that of nicotinic channels in rat PC12 (45–50 pS, Ifune & Steinbach, 1992) and bovine chromaffin cells (44 pS, Fenwick et al. 1982). Thus, the zero ACh concentration limits for the α3β2 relaxation time constants resemble the burst durations of the native ganglionic nicotinic receptors and the EPSP decay time constants but there are significant differences between the single-channel conductance of α3β2 and native ganglionic receptors.

The host cell type could account for some of the kinetic differences between the native ganglionic and heterologously expressed α3β4 nicotinic receptors (Lewis et al. 1997; Sivilotti et al. 1997). However, changes in the α3β4 single-channel conductance and burst duration attributed previously to the host cell type are inconsistent. For example, mouse fibroblasts express two kinds of rat α3β4 channels (Lewis et al. 1997). The larger channel has a conductance (30–40 pS) and lifetime similar to those of the native rat ganglionic nicotinic channel (Lewis et al. 1997). The smaller channel has a conductance (20–26 pS) similar to that of rat α3β4 channels expressed in oocytes and, similar to those channels, opens in long bursts (Lewis et al. 1997). Oocytes, in contrast, only express small conductance rat α3β4 channels (Lewis et al. 1997). Thus, mammalian cell lines appear to be able to express a rat α3β4 channel similar to the native ganglionic nicotinic receptors that Xenopus oocytes cannot express. However, Xenopus oocyte expression appears to have little, or no, effect on the conductance of human α3β4 channels. Moreover, it appears to affect the long human α3β4 burst duration in a manner opposite to that of the rat α3β4 channels (Nelson & Lindstrom, 1999). The predominant conductance of human α3β4 channels expressed in oocytes (31 pS) is nearly identical to that (32 pS) of human α3-containing nicotinic channels in IMR-32 neuroblastoma cells (Nelson & Lindstrom, 1999). Likewise, the fast burst duration of human α3β4 channels expressed in oocytes (1.7 ± 0.2 ms, ±s.e.m.) is nearly identical to that (1.6 ± 0.4 ms) of human α3-containing nicotinic channels in IMR-32 neuroblastoma cells (Nelson & Lindstrom, 1999). However, the long burst duration of the channels expressed in oocytes (16 ± 1 ms) is shorter than that (25 ± 3 ms) of the channels expressed in neuroblastoma cells (Nelson & Lindstrom, 1999). Thus, if the host cell type is responsible for the kinetic differences between expressed and native α3β4 nicotinic channels, then these effects must be highly species dependent. For the rat α3β4 channels (Lewis et al. 1997), oocyte expression appears to reduce the single-channel conductance and prolong the burst duration. For the human channels (Nelson & Lindstrom, 1999), oocyte expression does not affect the single-channel conductance but it does appear to reduce the slow burst duration. Therefore, it seems premature to conclude from this evidence that the host cell type is responsible for the differences between the relaxation time constants of the rat α3β4 receptors expressed in oocytes and the ganglionic EPSC decay time constants.