Kinetics of Ca²⁺ binding to parvalbumin in bovine chromaffin cells: implications for [Ca²⁺] transients of neuronal dendrites

Abstract

1. The effect of parvalbumin (PV) on [Ca²⁺] transients was investigated by perfusing adrenal chromaffin cells with fura-2 and fluorescein isothiocyanate (FITC)-labelled PV. As PV diffused into cells, the decay of [Ca²⁺] transients was transformed from monophasic into biphasic. The proportion of the initial fast decay phase increased in parallel with the fluorescence intensity of FITC, indicating that PV is responsible for the initial fast decay phase.

2. The relationship between the fast decay phase and the [Ca²⁺] level was investigated using depolarizing trains of stimuli. Within a train the relative amplitude of the fast decay phase was inversely dependent on the [Ca²⁺] level preceding a given stimulus.

3. Based on these observations, we estimated the Ca²⁺ binding ratio of PV (κ_P), the apparent dissociation constant of PV for Ca²⁺ (K_dc,app), and the unbinding rate constant of Ca²⁺ from PV (k_c-) in the cytosol of chromaffin cells. Assuming free [Mg²⁺] to be 0.14 mm, we obtained values of 51.4 ± 2.0 nm (n = 3) and 0.95 ± 0.026 s⁻¹ (n = 3), for K_dc,app and k_c-, respectively.

4. With the parameters obtained in the perfusion study, we simulated [Ca²⁺] transients, using two different Ca²⁺ extrusion rates (γ) – 20 and 300 s⁻¹– which represent typical values for chromaffin cells and neuronal dendrites, respectively. The simulation indicated that Ca²⁺ is pumped out before it is equilibrated with PV, when γ is comparable to the equilibration rates between PV and Ca²⁺, resulting in the fast decay phase of a biexponential [Ca²⁺] transient.

5. From these results we conclude that Ca²⁺ buffers with slow kinetics, such as PV, may cause biexponential decays in [Ca²⁺] transients, thereby complicating the analysis of endogenous Ca²⁺ binding ratios (κ_S) based on time constants. Nevertheless, estimates of κ_S based on Ca²⁺ increments provide reasonable estimates for Ca²⁺ binding ratios before equilibration with PV.

In the preceding paper (Lee et al. 2000), we estimated endogenous Ca²⁺ binding ratios (κ_S) in cultured hippocampal neurons using the single compartment model (Neher & Augustine, 1992; Helmchen et al. 1996; Neher, 1998). This model makes two major assumptions: (1) chemical reactions between Ca²⁺ and buffers are instantaneous; (2) there is no saturable buffer in a given compartment, and thus calcium binding ratios within the dynamic range of the [Ca²⁺] signal can be approximated as constant incremental Ca²⁺ binding ratios (Neher & Augustine, 1992). The model predicts that impulse-like Ca²⁺ influx results in a monoexponential decay of the [Ca²⁺] transient. In the previous study, however, [Ca²⁺] transients in some of the inhibitory neurons required a double exponential time course for a satisfactory fit. We took this as evidence that some assumptions of the model are not satisfied in such anomalous cases and suggested that slow saturable Ca²⁺ buffers are involved. We presumed parvalbumin (PV) to be the most plausible candidate for the slow saturable buffer, since it is known that PV is present only in a subpopulation of inhibitory neurons (Celio, 1986).

Although much is known about the physicochemical properties of PV, the shaping of [Ca²⁺] transients by PV has rarely been studied in vivo. Chard et al. (1993) reported that PV reduces the peak calcium increment and increases a fast component in Ca²⁺ decay, using internal perfusion of cultured dorsal root ganglion neurons with fluorescently labelled PV. This observation is consistent with PV being capable of promoting the relaxation rate in fast-twitch skeletal muscle (Schwaller et al. 1999). Such acceleration of [Ca²⁺] transients or muscle relaxation does not fit the single compartment model, which predicts a slowing of the Ca²⁺ decay rate when the Ca²⁺ binding ratio is increased.

In order to test whether or not the slow kinetics of PV were responsible for such a discrepancy, we performed a perfusion study of chromaffin cells with FITC-labelled PV. This allowed us to estimate the kinetic parameters of Ca²⁺ binding to PV in vivo. Finally, a numerical simulation using the in vivo parameters reproduced the double exponential [Ca²⁺] decay when the Ca²⁺ extrusion rate was high enough to prevent the reaction between PV and Ca²⁺ from reaching chemical equilibrium.

METHODS

Chromaffin cell culture

Chromaffin cells from bovine adrenal glands were prepared and cultured as described previously (Smith, 1999). Briefly, adult bovine adrenal glands were acquired fresh from local slaughterhouses. After dissecting glands free of fat tissue, they were perfused with Locke's Ringer solution and incubated at 37°C in a shaking water bath for 5 min. Glands were then perfused twice with Dulbecco's minimal essential medium (DMEM, Life Technologies, Karlsruhe, Germany) containing collagenase (type I; 1.0 mg ml⁻¹; Worthington, Lakewood, NJ, USA) and GMS-X (Life Technologies). Each perfusion was followed by a 15 min incubation at 37°C in a shaking water bath. After manual separation of medulla from cortex, the medulla was dissociated with a scalpel and a blunt-ended Pasteur pipette. The dissociated cells were harvested using a Percoll (Pharmacia, Uppsala, Sweden) gradient, resuspended in DMEM growth medium, and cultured at 37°C in 10 % CO₂. Experiments were carried out 1–2 days after cell preparation.

Solutions

The standard internal dialysis solution for chromaffin cells contained (mM): 140 caesium glutamate, 20 Cs-Hepes, 7 CsCl, 5 NaCl, 3 MgATP, 5 Na₂ATP. The external solution contained (mM): 130 NaCl, 2.8 KCl, 10 Na-Hepes, 2 MgCl₂, 1.4 CaCl₂, 10 TEA-Cl, 2 mg ml⁻¹ glucose; and 1 μM tetrodotoxin (TTX, Alamone Labs, Jerusalem, Israel). The pH of both the internal and external solutions was adjusted to 7.2 and 7.3, respectively, with the bases of the main cation in a given solution. The final osmolarity of external solutions was 315 ± 5 mosmol l⁻¹. All experiments were performed at room temperature (22-25°C).

Conjugation of FITC to PV

Purified rat recombinant PV (kind gift of T. Pauls, Fribourg, Switzerland) or BSA (Sigma, UK) were dissolved in 150 mM NaCl- 200 mM NaHCO₃ (pH 8.8) at a protein concentration of 2 mg ml⁻¹. This pH was selected in order to preferentially label the α-amino groups of the proteins. Fluorescein-5-isothiocyanate (FITC, 10 % adsorbed on Cellite; Molecular Probes, Eugene, OR, USA) dissolved in ethanol (10 mg ml⁻¹) was added to the protein solutions (5 μl per tube) and incubated in the dark for 30 min at room temperature. A saturated solution of glycine (50 μl, in the same buffer as above) was added to react with excess FITC in the reaction tube for 15 min. FITC-labelled proteins (termed FITC-BSA and FITC-PV) were purified on PD-10 desalting columns (Pharmacia, Uppsala). The absorbances at 280 and 495 nm were determined and the molecular FITC/protein ratio calculated. FITC-BSA contained 1.5 mol FITC (mol protein)⁻¹ and two separate batches of FITC-PV contained 0.05 and 0.14 mol FITC (mol protein)⁻¹. The low labelling efficiency of PV was due to a blocked amino-terminus in a large proportion of recombinant PV molecules.

Spectral properties of fura-2 and FITC-PV

We studied the excitation spectra of fura-2 and FITC-BSA, in order to establish that the two types of fluorescence could be separated. Each dye was dissolved in standard internal solution for chromaffin cells to obtain final concentrations of 50 μM for fura-2 and 8 μM for FITC-BSA. Their excitation spectra were checked in vitro with a 1.0 ND filter in the optical pathway.

We found that the fura-2 fluorescence at an excitation wavelength of 488 nm (F_fura2,488) was negligible, whereas at 350 nm/380 nm (F_350/380) it was slightly contaminated by FITC.

FITC fluorescence at 350 nm (F_FITC,350) was 2.6 % of that at 488 nm (F_FITC,488), and F_FITC,380 was 5.0 % of F_FITC,488. Thus, in the presence of both dyes in the cell, F₃₅₀– 0.026F₄₈₈ and F₃₈₀– 0.05F₄₈₈ were regarded as F_fura2,350 and F_fura2,380, respectively, for conversion of F₃₅₀ and F₃₈₀ to [Ca²⁺].

Imaging of [Ca²⁺] transients in chromaffin cells

The same optical system and imaging software as used in the preceding paper (Lee et al. 2000) was employed, except for two optical filters. A dichroic mirror (DC500LP, Omega Optical, Brattleboro, VT, USA) was used for simultaneous fluorescence measurement of fura-2 and FITC. A long pass emission filter (Q515LP, Omega Optical) was used for separating emission light and residual scattered excitation light.

Calibration parameters were determined using an in vivo calibration (Neher, 1989). Briefly, the fura-2 fluorescence ratios at minimal and maximal Ca²⁺ concentrations, R_min and R_max, were determined by loading chromaffin cells with the standard internal solutions plus 10 mM K₅-BAPTA and 10 mM CaCl₂, respectively. The effective dissociation constant (K_eff) was determined by loading cells with an intracellular solution containing 3.33 mM K₅-BAPTA and 6.66 mM Ca-BAPTA. K_eff was calculated from the equation:

where [Ca²⁺] was entered as 444 nM (assuming a dissociation constant (K_d) for BAPTA of 222 nM at pH = 7.2). The K_d of fura-2 was calculated from K_d =K_eff(α+R_min)/(α+R_max), where α is the isocoefficient (Zhou & Neher, 1993). The estimated values (μM) for R_min, R_max and K_eff were typically 0.36, 5.0 and 1.47, respectively.

For high time resolution and minimization of the photobleaching effect we adopted the following protocol. Images taken with single wavelength excitation at 380 nm (F₃₈₀), at a frequency of 10–20 Hz, were preceded and followed by images taken with dual excitation at wavelengths of 350 and 380 nm at 2–3 Hz. In addition, a 0.3-0.6 ND filter was placed in the excitation light pathway. During off-line analysis, a region of interest (ROI) was set on the chromaffin cell for determining fura-2 fluorescence (F). Adjacent to the ROI, another ROI was set in an area with no cellular structures for background fluorescence (F_b). The fluorescence intensities from the two ROIs were averaged to get F and F_b. The value of F – F_b was regarded as the relevant fura-2 fluorescence of the ROI. Subsequently, isosbestic fluorescence (F_iso) was calculated from images of the double wavelength excitation period using the equation:

and the values thus obtained were linearly interpolated between points just before and after the period of single wavelength excitation. The ratios R =F₃₅₀/F₃₈₀ and R′ =F_iso/F₃₈₀ were converted to [Ca²⁺] using the equations:

and

respectively.

Estimation of calcium binding ratios in chromaffin cells

Within 20 s of establishing a whole cell configuration, we started to apply single pulses or trains of depolarizing pulses (to +10 mV, for 20 ms) every 20–60 s in order to evoke [Ca²⁺] transients while taking F₃₈₀ images at 10–20 Hz. These images were preceded and followed by double wavelength image pairs at 2–3 Hz such that Ca²⁺ concentration could be calculated as described in the previous section.

During off-line analysis, F_iso was calculated and the time course of F_iso was regarded as the loading curve of fura-2. The concentration of fura-2 in the cell was estimated assuming that the F_iso at the plateau of the loading curve represents full loading of fura-2.

Theory of the single compartment and linear approximation model

The calcium binding ratio κ_X of buffer X is defined as:

(1)

where [X]_T is the total concentration of calcium buffer X and K_d,X is its dissociation constant (Neher & Augustine, 1992). Practically, κ_X was replaced by the incremental calcium binding ratio (κ_X‘), since κ_X is not completely linear within the dynamic range of [Ca²⁺]_i in our study. κ_X‘, the incremental Ca²⁺ binding ratio of a buffer X, is defined by (Neher & Augustine, 1992):

(2)

where [Ca²⁺]_i,rest and [Ca²⁺]_i,peak represent [Ca²⁺]_i values before and at the peak of the perturbation.

According to the single compartment model (Neher & Augustine, 1992; Helmchen et al. 1996; Neher, 1998), the initial increment of [Ca²⁺] (d[Ca²⁺]_{t = 0}) induced by an impulse-like Ca²⁺ influx into a compartment which contains an endogenous Ca²⁺ buffer (S) and a Ca²⁺ indicator dye (B), can be calculated as:

(3)

where d[Ca²⁺]_T is the total Ca²⁺ increase evoked by the influx. The decay time constant τ of the subsequent [Ca²⁺] transient is:

(4)

Ca²⁺ binding kinetics of parvalbumin (PV)

Since Ca²⁺ and Mg²⁺ compete for the same binding site on PV, we consider the following model:

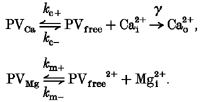Here, γ is the Ca²⁺ extrusion rate, k_{c +} and k_c- are on- and off-rates of Ca²⁺ binding to PV, and k_{m +} and k_m- are the corresponding rates of Mg²⁺ binding to PV.

If it is assumed that Mg²⁺ is so highly buffered (e.g. by ATP) that the binding reaction between Mg²⁺ and PV does not perturb [Mg²⁺] substantially (assumption 1), and the binding reaction between Mg²⁺ and PV is much faster than that between PV and Ca²⁺ (assumption 2), the above model can be simplified to:

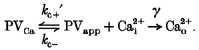(5)

Here k_{c +} and PV_free are replaced by k_{c +}′ and PV_app, which are the apparent on-rate and the apparent concentration of free PV, respectively, given as:

(6)

and

(7)

where K_dm is the dissociation constant of PV for Mg²⁺.

Moreover, in the simplified model the apparent dissociation constant of PV for Ca²⁺ is defined as:

(8)

where K_dc is the dissociation constant of PV for Ca²⁺.

Assuming that the perturbation of Ca²⁺ is so small that the system could be linearized around the equilibrium point (assumption 3), and Ca²⁺ buffers other than PV satisfy the condition of the linear approximation (assumption 4), the system of differential equations describing the simplified model is:

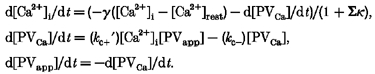Here, it is assumed that Ca²⁺ can bind to a number of additional fast buffers, which satisfy the linear approximation model and that Σκ is the sum of all Ca²⁺ binding ratios of such buffers. The system of linearized differential equations has the following eigenvalues λ_fast and λ_slow:

(9)

(10)

If the condition:

(11)

which is (assumption 2), does not hold, the ‘≌’ in eqn (9) has to be replaced by ‘<‘.

According to the above eigenvalues, the [Ca²⁺] transient in the presence of PV is composed of a phase of kinetic equilibration and a slower phase of exponential decay. If the Ca²⁺ extrusion rate (γ) is slow enough to ensure that kinetic equilibrium is reached at every sampling point, [PV_free] in the definition of β can be replaced by its steady state value:

(12)

This allows the term β/α to be reduced to:

which is the definition of Ca²⁺ binding ratio for PV, κ_P. If, in addition, 1/α is negligible compared to other terms in 1/λ_slow, eqn (10) reduces to eqn (4), i.e.

(13)

Data analysis and numerical simulation

Data were analysed on a PC with IgorPro (version 3.12, WaveMetrics, Lake Oswego, OR, USA). For numerical simulations, the 4th order Runge-Kutta method was used. Data were compared statistically using Student's t test. The statistical data are presented as means ±s.d., with n indicating the number of cells.

RESULTS

Simultaneous loading of chromaffin cells with fura-2 and FITC-labelled PV

In order to study the effect of parvalbumin on [Ca²⁺] transients, the transients need to be recorded at various concentrations of PV whilst the concentration of Ca²⁺ indicator dye, which can also act as Ca²⁺ buffer, is fixed. To examine whether or not this condition can be obtained when fura-2 and FITC-PV are co-perfused through a patch pipette, the loading time of each dye was measured. After whole cell configuration was established, isosbestic fluorescence from fura-2 (F_iso) and fluorescence from FITC (F_FITC) were recorded and plotted against time after break-in. The time constants for fura-2 and FITC loading were measured by fitting an exponential function to each loading curve. The time constant for FITC loading was longer than that of fura-2 by a factor of 4.3 ± 1.0 (n = 6). This difference, however, was not sufficient for the purpose of our measurement since FITC-PV was already more than 50 % loaded before fura-2 loading reached completion (> 95 %).

To make the difference in the loading time course between the two dyes larger, whole cell measurements were performed consecutively: first a whole cell recording was established with a pipette containing a high concentration of fura-2 (400 μM) for a short time (67 s); then another pipette containing fura-2 (150 μM) and FITC-PV (nominally 100 μM) was used. Two [Ca²⁺] transients obtained in the second patch experiment are compared in Fig. 1B. Both [Ca²⁺] transients were recorded after F_iso values had reached 95 % of steady state (marked with ‘2′, ‘3′ in Fig. 1A). At these two points, we presume that the difference between [Ca²⁺] transients is mainly due to additional PV, since [fura-2] stayed almost constant. The [Ca²⁺] transient in the presence of PV showed two phases of decay: an initial fast drop followed by a slower exponential decay phase. The decay time constant of the initial fast drop phase was clearly faster than that of the [Ca²⁺] transient recorded in the absence of PV taken during the first patch recording (marked with ‘1′ in Fig. 1A and shown in the inset of Fig. 1B). This shows that PV generated an additional fast drop phase in the [Ca²⁺] transient, while it delayed the decay time constant of its slower phase. Interestingly, the initial amplitude of d[Ca²⁺] was not decreased by raising PV. An accidental compensatory change in Ca²⁺ current (I_Ca) cannot be responsible for the similarity in d[Ca²⁺]_{t = 0} between the two [Ca²⁺] transients, since the I_Ca recorded at ‘2′ was indistinguishable from that recorded at ‘3′ (see inset of Fig. 1A). The relative independence of d[Ca²⁺]_{t = 0} to PV indicates that PV does not function as an instantaneous Ca²⁺ buffer.

Figure 1. Consecutive patch recording on a chromaffin cell.

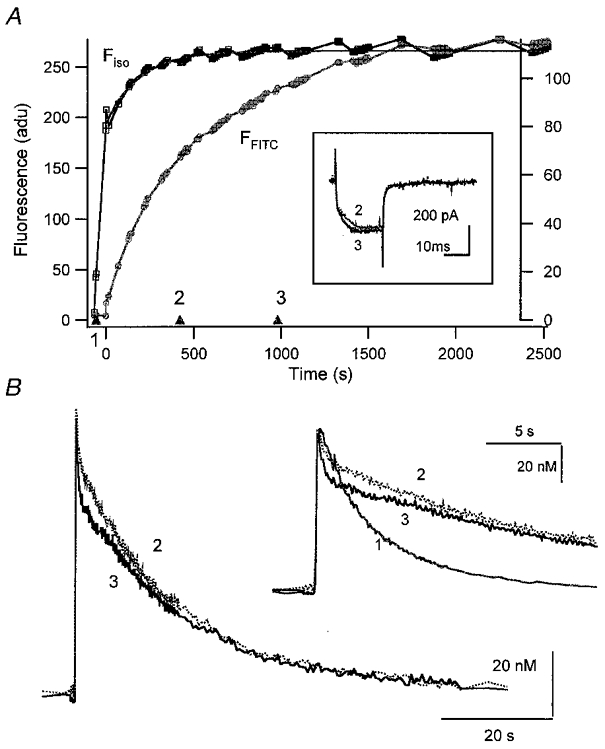
A first whole cell patch pipette contained 400 μM fura-2; a second one contained 150 μM fura-2 and nominally 100 μM PV. A, plot of fluorescence at the isosbestic wavelength (F_fura2, left ordinate) and that at 488 nm (F_FITC, right ordinate) against the whole cell patch recording time. The first whole cell patch was maintained for 67 s. After that, the second whole cell recording was obtained at 0 s. Fura-2 and FITC diffused into the cell via the second whole cell patch pipette with time constants of 190 and 595 s, respectively. Calcium currents recorded at times ‘2′ and ‘3′ are shown in the inset. B, two [Ca²⁺] transients obtained at times ‘2′ (313 s) and ‘3′ (965 s) marked in A. The intracellular fura-2 concentrations at ‘2′ and ‘3′ in A were calculated from the fura-2 loading curve to be 142 and 150 μM, respectively. In the same way, nominal PV concentrations at ‘2′ and ‘3′ were calculated as 46.8 and 80.2 μM, respectively. In the inset, the same [Ca²⁺] transients are shown on an expanded time scale. For comparison, the [Ca²⁺] transient obtained in the first patch experiment in the absence of PV (at −57 s; marked with ‘1′ in A) is also shown in the inset. The vertical scale bar in the inset represents 127.5 nM for the [Ca²⁺] transient ‘1′, and 20 nM for ‘2′ and ‘3′.

Estimation of the calcium binding ratio κ_P by intracellular perfusion of chromaffin cells with FITC-PV

For further quantitative analysis of the effect of PV on [Ca²⁺] transients, pulse trains with a variable number of successive depolarizations (to 0 mV, 20 ms duration, 2 s interval) were applied to the cells during wash-in of FITC-PV (nominally 150 μM), as shown in Fig. 2A and B (▴ in A indicate time points of stimulation; examples of early and late Ca²⁺ responses are given in Ba and b and Ca and b, respectively). This way the high dependence of the Ca²⁺ binding ratio of PV on [Ca²⁺] could be readily documented.

Figure 2. Parvalbumin loaded into adrenal chromaffin cells.

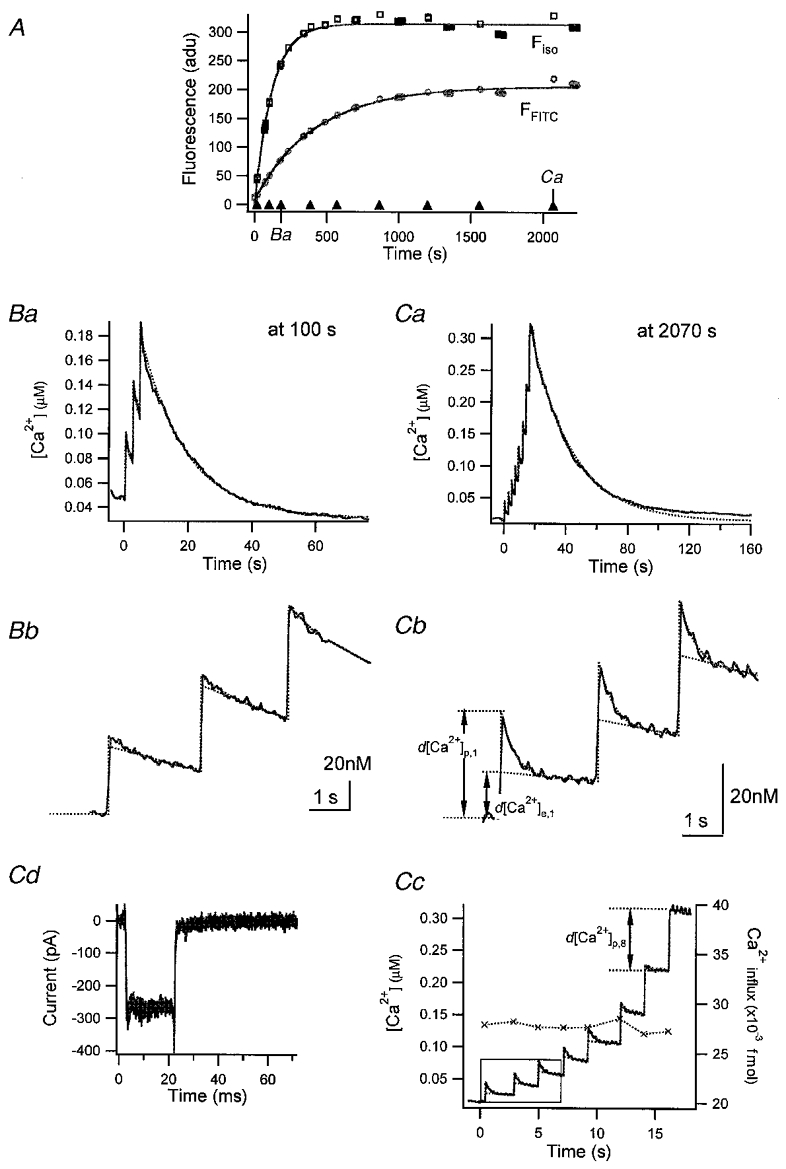
A, loading curve of fura-2 and FITC-PV. The quantities F_iso and F₄₈₈ (see Methods) were plotted against time (s) elapsed after break-in. The loading curves were fitted with monoexponential curves (continuous lines) with τ_fura = 106.4 s for F_iso and τ_FITC = 372.3 s for F₄₈₈. ▴, times when bursts of depolarizing pulses were given. In addition, the times when the Ca²⁺ traces displayed in Ba and Ca were recorded are marked. Ba, [Ca²⁺] transients evoked at 100 s after break-in. Bb, the [Ca²⁺] trace between 0 s (the time when the 1st pulse of this burst was given) and 7 s is depicted on an expanded time scale. Ca, [Ca²⁺] transients evoked by a train of 8 pulses given at 2070 s after break-in. Cb and c, [Ca²⁺] transients in the interval of 0 and 7 s (b) and those between −1 and 18 s (c) are re-displayed on an expanded time scale. Examples used for the estimation of various kinds of [Ca²⁺] increments (as defined in the text) are illustrated in Cb and c. The amount of calcium influx during pulses as calculated from Ca²⁺ current traces (Cd) is included in Cc (×, right axis).

As more parvalbumin entered the cell, an initial fast drop in [Ca²⁺] developed following individual pulses, resulting in a two-phase [Ca²⁺] decay: an initial fast drop followed by a later exponential decay in [Ca²⁺] (Fig. 2Bb and Cb). In addition, as [Ca²⁺]_i increased within a burst, the amplitudes of the fast drop phases became smaller, and eventually disappeared, as can be seen following the last pulse of a burst depolarization (Fig. 2Cc). The more PV was contained in the cell, the higher was the number of pulses required to abolish the fast drop phase.

After the end of burst depolarizations [Ca²⁺] gradually decayed. The slow decay phases, however, were not well described by single exponentials, since the slope of the decay was extremely low around the resting level of [Ca²⁺]_i (Fig. 2Ca). The deviation of the Ca²⁺ decay from a single exponential suggests that there should be a substantial change in the Ca²⁺ binding ratio of Ca²⁺ buffers within the dynamic range of the [Ca²⁺] transients shown in Fig. 2C.

The close correlation between F_FITC (or [PV]_i) and the amplitudes of fast decay phases indicates that PV is responsible for these kinetic components. Moreover, an inverse relationship between [Ca²⁺]_i and the amplitude of the fast phase suggests that its abolition represents saturation of PV with Ca²⁺. That initial acceleration of [Ca²⁺] transients by [PV], which is in contrast to the effect of most fast buffers on [Ca²⁺] relaxation, can be explained if we assume that the fast drop phase represents the phase of kinetic equilibration between PV and Ca²⁺.

For the analysis of [Ca²⁺] transients in the presence of PV we defined two kinds of [Ca²⁺] excursion amplitudes for the υth [Ca²⁺] transient in a burst, as indicated in Fig. 2Cb: a peak excursion d[Ca²⁺]_p,υ and an extrapolated value d[Ca²⁺]_e,υ. We describe them by the following equations:

(14)

(15)

where d[Ca²⁺]_t,υ represents the total intracellular [Ca²⁺] increment evoked by the υth calcium influx. Equation (14) represents the equilibrium between the newly added calcium and endogenous buffers as well as the Ca²⁺ indicator dye fura-2 (represented by κ_B,υ). All of these reactions are assumed to be rapid. The Ca²⁺ binding ratio of the endogenous buffer, κ_S, is assumed to be constant. The parameter κ_B,υ′ is the incremental Ca²⁺ binding ratio of fura-2 for the υth [Ca²⁺] increment, as given by eqn (2). Equation (15) represents the situation after equilibration of parvalbumin, but before appreciable Ca²⁺ extrusion sets in. The parameter κ_P,υ′ is the incremental κ of parvalbumin valid for the transition in [Ca²⁺] between the value before the stimulus, and that after equilibration of parvalbumin. The parameters κ_B,υ′ and κ_B,υ‘’ are not identical, but the difference, in practice, is very small and is neglected in some calculations. Furthermore the quantity d[Ca]_t,υ can be calculated from the integral of the Ca²⁺ current during the υth pulse, Q_υ, with the equation:

(16)

We determined the accessible cell volume, V_cell, by evaluating responses to a series of pulse trains while the cell was loaded with fura-2. The slope of a plot of Q_υ/(2F d[Ca²⁺]_p,υ) against κ_B,υ‘, according to eqns (14) and (16), should be given by V_cell. In the presence of a large rapidly decaying phase, however, the measurement of d[Ca²⁺]_p,υ might be erroneous due to limited time resolution. Hence, we restricted this analysis to values obtained from the last few pulses in a given train where the amplitudes of the fast drop phases are negligible (• in Fig. 3A). The slope and x-axis intercept of the fitted line (continuous line in Fig. 3A) gives values for V_cell and κ_S as 1.1 pl and 87, respectively. The estimated V_cell is 80 % of a sphere with a radius of 6.9 μm, where the latter is a size estimate for a chromaffin cell derived from the measured cell capacitance of 6.0 pF and a geometric specific capacitance of 10 fF μm⁻².

Figure 3. Analysis of data presented in Fig. 2.

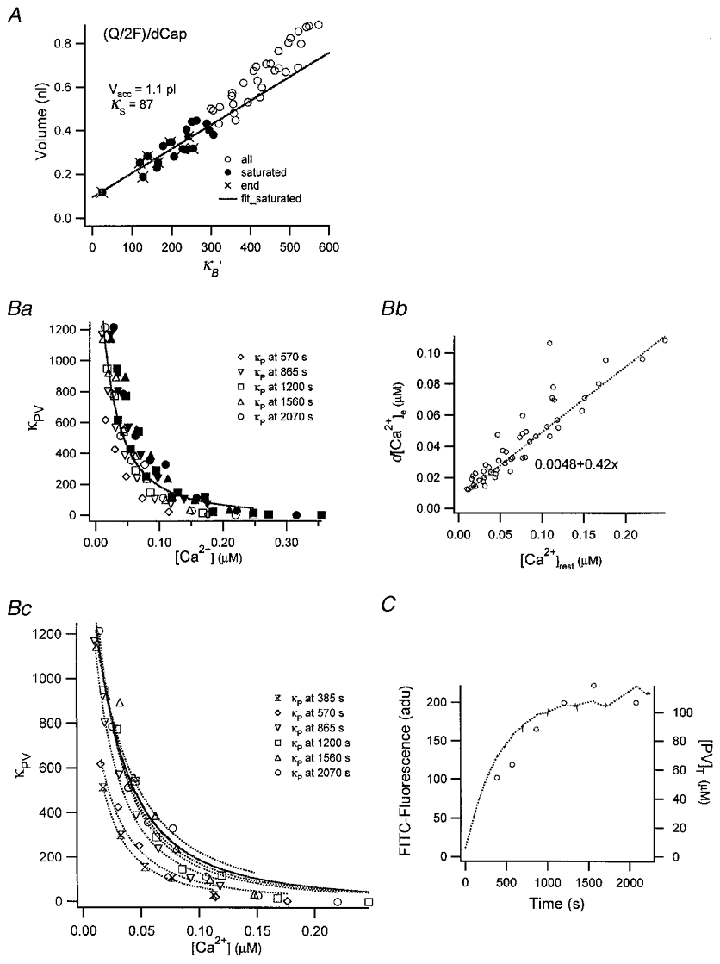
A, plot of the ratios between total amounts of Ca²⁺ influx (Q_υ/2F) and peak amplitudes of [Ca²⁺] transients (d[Ca²⁺]_p,υ) as a function of κ_B‘. Only the ratios measured from those [Ca²⁺] transients which lacked a fast drop phase (•) were used for the fit (continuous line). Accessible cell volume and κ_S were calculated from the slope ( = 1.1 pl) and the x-axis intercept ( = 87) of the regression line, respectively. Ba, plot of κ_P′ estimated from eqn (18) against [Ca²⁺]_rest (the [Ca²⁺] before a given pulse, open symbols) and [Ca²⁺]_peak (filled symbols). Values from fourth to eighth bursts are superimposed. Bb, plot of d[Ca²⁺]_e as a function of [Ca²⁺]_rest. d[Ca²⁺]_e was fitted by 0.42[Ca²⁺]_rest+ 0.0048 (μM). Bc, plot of κ_P′ estimated from eqn (18) as a function of [Ca²⁺]_rest. Values for κ_P′ from different bursts are represented by different symbols. Dotted curves represent fits to values from a given burst. Parameters for the fits, [PV]_T, are displayed in panel C. The continuous curve in Bc is the fit for κ_P′ obtained by pooling values from the last 3 bursts. C, plot of F_FITC (dotted line, left axis) and [PV]_T (○, right axis) estimated in panel Bc against loading time.

Now, if d[Ca²⁺]_p,υ and d[Ca²⁺]_e,υ are known, we can readily measure κ_P,υ for each pulse. As mentioned already, we can avoid possible erroneous estimation of d[Ca²⁺]_p,υ by measuring d[Ca²⁺]_p at the last pulse, where the d[Ca²⁺]_p is not contaminated by the fast drop phase. This is because the buffer capacity of PV is very small as PV is being saturated, when [Ca²⁺]_i increases during successive pulses in a burst. More explicitly, in the last pulse the fast component is missing in the majority of pulse trains, such that d[Ca²⁺]_p,last is about equal to d[Ca²⁺]_e,last and can be measured very accurately. Then the calcium binding capacity for the increment during the υth pulse, κ_P,υ‘, can be calculated from the difference between d[Ca²⁺]_e,υ and d[Ca²⁺]_p,last, by combining eqn (15) applied to the υth pulse with eqn (14), applied to the last one:

(17)

Here d[Ca²⁺]_e,υ has to be measured by extrapolating the slowly decaying phase to initiation time. The quantity Δκ_B,υ is the difference between the value of κ_B′ for the υth pulse and that for the last pulse. Together with eqn (16), eqn (17) yields:

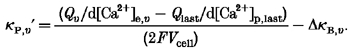(18)

Estimation of the apparent dissociation constant of PV for Ca²⁺

A plot of κ_P′ estimated by eqn (18) as a function of initial or peak Ca²⁺ level (referred to a given pulse) illustrates a high dependence of κ_P′ on [Ca²⁺]_i (Fig. 3Ba). From this dependence an apparent dissociation constant (K_dc,app) of PV for [Ca²⁺]_i can be calculated. However, κ_P‘, as defined in eqn (2) depends both on [Ca²⁺] before a given pulse (termed [Ca²⁺]_rest) as well as on the [Ca²⁺] following the stimulus. Due to this ambiguity no straightforward fit can be applied to the data in Fig. 3Ba. Fortunately, however, the data show that d[Ca²⁺]_e has quite a linear relationship with [Ca²⁺]_rest in the experiment of Fig. 2 (see Fig. 3Bb). This allows us to express κ_P′ as a function of [Ca²⁺]_rest alone:

where [Ca²⁺] values are in μM.

Assuming [PV]_T is constant within a burst, fitting the estimated κ_P′ obtained in a burst with this equation yields [PV]_T and K_dc,app (Fig. 3Bc). The [PV]_T estimated in this way compared favourably with the loading time course of F_FITC in Fig. 3C. Since values for [PV]_T in the last three bursts of this experiment were not so different from each other, we pooled the κ_P′ estimates from these bursts and fitted them with the above equation. This yielded [PV]_T = 110 μM and K_dc,app = 51 nM. A similar analysis performed on three cells resulted in K_dc,app = 51.4 ± 2.0 nM. A small downward deviation of the data from the fit for [Ca²⁺] above 100 nM indicates that κ_P might be underestimated in this range. Problems in distinguishing between λ_fast and λ_slow at higher [Ca²⁺] may be responsible for this underestimation.

The apparent K_d of PV for Ca²⁺ (K_dc,app) can also be estimated by comparing two κ_P′ values at any two different [Ca²⁺] levels in a burst. From the definition of κ‘, the ratio of κ_P′ normalized to [PV]_T at two [Ca²⁺] transients should be:

(19)

If the two [PV]_T values are assumed to be the same in a burst, we have only one unknown variable in this quadratic equation, since κ_P,υ′ could be calculated for the υth pulse by eqn (18). Solving this quadratic equation for 83 pairs of κ_P,υ′ (values from 7 bursts), K_dc,app was calculated as 52 ± 22 nM. The κ_P′ estimates from the last two pulses in a burst were excluded from this analysis since the estimation of d[Ca²⁺]_e is prone to be erroneous at high [Ca²⁺]_i.

The intracellular [Mg²⁺] in this study could be assumed to be constant since it was highly buffered by free ATP, included in the internal dialysis solution. Assuming that the K_d of ATP for Mg²⁺ is 0.1 mM (Martell & Smith, 1977), [Mg²⁺] in the pipette solution was calculated as 0.14 mM. Taking into account that [Mg²⁺]_i is 0.14 mM and that the dissociation constant of PV for Mg²⁺, K_dm, is 31 μM at 25°C (Eberhard & Erne, 1994), the dissociation constant of the parvalbumin-Ca²⁺ complex was calculated as 9.2 nM from eqn (8).

Ca²⁺ binding kinetics of PV in chromaffin cell

The time course of the fast decay phase of the Ca²⁺ signal and the value for κ_P′ estimated in the previous section allow us to estimate the kinetic properties of PV. Assuming that our experimental conditions satisfy the conditions of assumptions (1), (3) and (4) (see Methods), an upper limit for the time constant of the fast equilibration phase can be obtained from eqn (9), where the terms which are not yet known can be calculated as follows.

1. γ is estimated in a burst of calcium transients, if total calcium influx is known, according to Neher (1998):

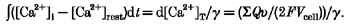
   (20)

2. κ′ and eqn (12), assuming K_dm as 31 μM (Eberhard & Erne, 1994). Parameters in eqn (12) such as the K_dc,app and [Mg²⁺] have been determined in the previous section.

3. κ_S is constant in the dynamic range of the [Ca²⁺] transient, Σκ can be readily calculated from κ_S measured above and from the definition of κ_B‘.

4. K_dc =k_c-/k_{c +} = 9.2 nM, we have only one unknown variable in eqn (9).

An example of such a calculation is illustrated in Fig. 4, where k_c- was estimated as 0.98 s⁻¹ according to the fit shown by the dotted line. In two other cells, we obtained similar values for k_c-. Altogether the mean value for k_c- was 0.95 ± 0.026 s⁻¹ (n = 3). This is quite close to the value of 1 s⁻¹ measured in vitro (Hou et al. 1992). If we assume the dissociation rate for Mg²⁺, k_m-, to be 25 s⁻¹ (Permiakov et al. 1987; Carroll et al. 1997), it can be confirmed that eqn (9) is quite a good approximation for λ_fast under the conditions of Fig. 4, where [Ca²⁺] = 25 nM, [Mg²⁺] = 0.14 mM, [PV]_free = 7.68 μM and Σκ = 608. For these values the terms in the left- and right-hand sides of the inequality (11) were calculated as 138.4 s⁻¹ and 5.03 s⁻¹, respectively, if the value of k_c- obtained in Fig. 4 was adopted.

Figure 4. Example for the measurement of kinetic parameters of Ca²⁺ binding to PV.

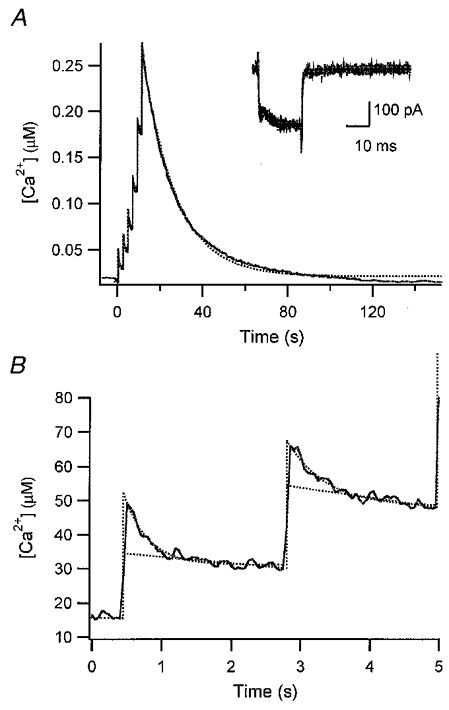
A, composite [Ca²⁺] transient evoked by 6 successive depolarizing pulses, the 1st one of which was given at 570 s after break-in in the experiment of Fig. 2. Ca²⁺ currents in response to all depolarizing pulses are superimposed in the inset. B, individual [Ca²⁺] transients in response to the first 2 pulses are depicted on an expanded time scale. Kinetic properties of PV were calculated from this trace using eqn (9), as follows. The fast drop phase in the 1st transient (B) was fitted with an exponential with a rate constant of 2.86 s⁻¹. The time integral of the whole [Ca²⁺] transient evoked by the train of 6 pulses was 5.35 μM s and the sum of Ca²⁺ influxes during the burst measured from 6 calcium current traces (as shown in the inset of A) was 0.15 fmol. Thus, the Ca²⁺ extrusion rate (γ) was calculated to be 25.25 s⁻¹ according to eqn (20), together with d[Ca]_T = 0.136 mM (= 0.15 fmol (1.1pl)⁻¹, when the cellular volume was taken from the estimate of Fig. 3A). The total concentration of parvalbumin ([PV]_T) had already been estimated in Fig. 3B and C as 63.5 μM. From this, [PV]_free was calculated as 7.68 μM using the definition of κ_P‘, eqn (12), and assuming that [Mg²⁺] = 0.14 mM, K_dm = 31 μM (Eberhard & Erne, 1994). Furthermore, the Σκ was calculated as 608 from κ_S = 87 and κ_B′ = 521 which, in turn, was based on the following values: [B]_T = 150 μM and K_d (fura2-Ca) = 210 nM. Finally, using eqn (9) and the relationship K_dc =k_off/k_on = 9.2 nM, k_on and k_off could be calculated to be 107.5 μM⁻¹ s⁻¹ and 0.98 s⁻¹.

Effect of the Ca²⁺ extrusion rate on [Ca²⁺] transients in the presence of PV

In the previous section, the [Ca²⁺] increment after equilibration of parvalbumin d[Ca²⁺]_e was estimated by back-extrapolation of a line fitted to the slower phase of a [Ca²⁺] transient. This procedure is valid only when the following two conditions are satisfied: (1) the equilibration time constant between PV and Ca²⁺ is faster than the Ca²⁺ extrusion rate, or

(21)

and (2) chemical equilibrium is reached at all sample points during the slower decay phase, or

The above two inequalities are exactly the same mathematically. If the inequality (21) is satisfied, the rate constants expressed by eqns (9) and (10) can be approximated as:

and

The former is the rate constant for equilibration of PV with Ca²⁺ when γ = 0 s⁻¹, and the latter is the same form as eqn (4). The two equations represent the relaxation time course of [Ca²⁺] upon a Ca²⁺ perturbation when a buffer satisfies the condition of fast buffer or inequality (21). The inequality (21) does not hold in neuronal dendrites, if the kinetic parameters of PV are assumed to be similar to those measured in chromaffin cells. The average value of γ estimated in dendrites of hippocampal cultured neurons was 323 ± 86 s⁻¹ (n = 21; see companion paper: Lee et al. 2000), which is at least 10 times higher than that in chromaffin cells. Moreover, β might be substantially lower than that in our perfusion study, since immunohistochemical estimates of [PV]_T in neurons were in the range 20–100 μM (in terms of Ca²⁺ binding sites; Plogmann & Celio, 1993).

In order to simulate the effect of γ on the shape of the [Ca²⁺] transients, when PV is present, we integrated numerically the following equations:

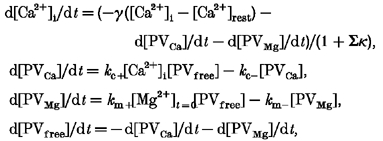(21)

according to the model:

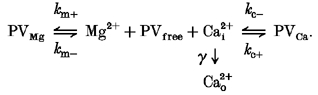Here we assumed that [Mg²⁺]_i was fixed at 150 μM. Figure 5 illustrates the simulation results, comparing the case of γ = 20 s⁻¹ with that of γ = 300 s⁻¹, two values representative for chromaffin cells and neuronal dendrites, respectively. All the other parameters were identical in the two cases. The total intracellular Ca²⁺ increase, d[Ca]_T, was obtained in neuronal dendrites from eqn (3), and the average value was 14.2 ± 5.4 μM (n = 37). The kinetic parameters for Ca²⁺ binding were chosen according to the results from the perfusion study of chromaffin cells, as described above. Parameters for Mg²⁺ binding were taken from the literature (Permiakov et al. 1987; Eberhard & Erne, 1994; Carroll et al. 1997).

Figure 5. Numerical simulation of [Ca²⁺] transients.

A, the results from numerical integration of eqn (22) with the following parameters: [Ca²⁺]_rest = 30 nM, [Mg²⁺] = 150 μM, d[Ca]_T = 14 μM, [PV]_T = 20 μM, k_c- = 1 s⁻¹, k_m- = 25 s⁻¹, K_dc = 10 nM, K_dm = 50 μM, and Σκ = 200. A time interval of d t = 5 ms was used for the integration. The two [Ca²⁺] transients whose γ values are 20 and 300 s⁻¹ are well described by double exponential curves:

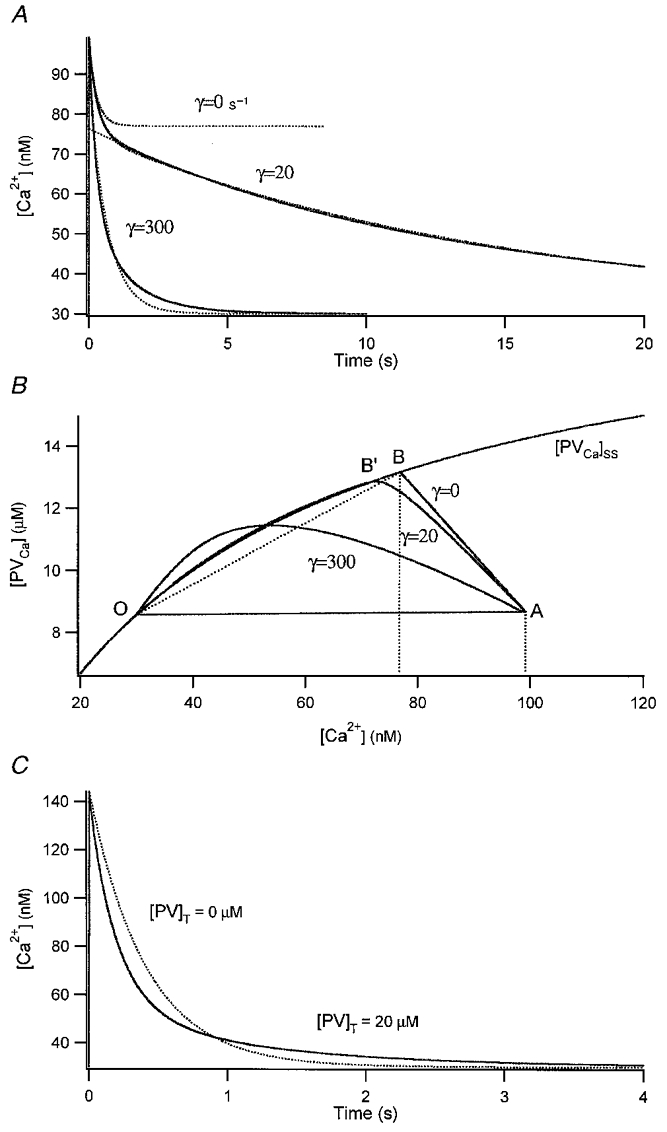
Least square fits of the simulation results gave the following parameters: w₁ = 43 nM, λ₁ = 3.64 s⁻¹, w₂ = 25 nM, λ₂ = 0.74 s⁻¹ for the high-γ curve; w₁ = 22.8 nM, λ₁ = 3.08 s⁻¹, w₂ = 44.9 nM, λ₂ = 0.067 s⁻¹ for the low-γ curve. The equilibrated amplitude d[Ca²⁺]_e was estimated by back-extrapolation of a straight line fitted to the section of the transient between 1.4 and 2 s. The theoretical expectation for the kinetic parameters for the low-γ curve was λ₁ < 3.28 s⁻¹, λ₂ = 0.067 s⁻¹ according to eqns (9) and (10), respectively. A simulation result with γ = 0 s⁻¹ is superimposed onto the traces for comparison (dotted curve). B, plot of the same simulation results in the [PV_Ca]-[Ca²⁺] plane. The x-value of point B is the [Ca²⁺] level reached when Ca²⁺ is equilibrated with PV for γ = 0 s⁻¹. This corresponds quite well to the value for d[Ca²⁺]_e obtained in A of this figure. C, simulated [Ca²⁺] transients with and without PV in a neuronal dendrite. PV accelerates the [Ca²⁺] decay at early times, whereas it slows down the final clearance of residual Ca²⁺. Parameters used for this simulation were the same as those of the high-γ curve in A except for Σκ which was 120.

In the case of γ = 20 s⁻¹, the faster kinetic phase overlaps with that corresponding to γ = 0 s⁻¹, which indicates that γ has no appreciable effect on the [Ca²⁺] drop during the kinetic equilibration phase. Hence, the faster kinetic phase could be readily discerned from the late slower phase in the time domain. In contrast, using γ = 300 s⁻¹ and comparing the fast kinetic phase of the transient with the case of γ = 0 s⁻¹, it is evident that a substantial amount of newly added calcium is already pumped out while PV and Ca²⁺ equilibrates. The situation is clearer when the same data are shown in a two-dimensional plot of [PV_Ca]versus[Ca²⁺] (Fig. 5B). The point ‘O’ represents the equilibrium state before the perturbation. Upon addition of 14 μM Ca²⁺, the system is perturbed and displaced to point A (at 5 ms). The trajectories from point A to point B (when γ = 0 s⁻¹) or point B’ (when γ = 20 s⁻¹) represent the kinetic equilibration phase between PV and Ca²⁺. With higher γ values, the curves deviate progressively from the curve of γ = 0 s⁻¹ in a counter-clockwise direction. With γ = 20 s⁻¹, the trajectory follows faithfully the steady state curve, which was calculated from:

As long as the trajectory follows the steady state curve, PV can be regarded as a fast buffer. In this case, it is possible to estimate d[Ca²⁺]_e by back-extrapolation of the slower phase in the time domain. In particular, eqn (13) is readily applicable to such a slow phase, if the perturbation is small enough to ensure that the incremental κ′ of PV is a good approximation to the instantaneous κ. When γ = 300 s⁻¹, however, such extrapolation is impossible because the high value of γ prevents chemical equilibration between PV and Ca²⁺ throughout the transient. Nevertheless, the presence of PV together with a high γ value shortens the major part of the [Ca²⁺] transient, mimicking an even higher value of γ. In addition, residual Ca²⁺ persists longer in the late period of the transient, due to the slow dissociation rate of Ca²⁺ from PV, resulting in a two component transient (Fig. 5C).

The simulation results show that the decay time τ of a [Ca²⁺] transient is profoundly affected when the inequality condition (21) is violated, whilst the initial increment d[Ca²⁺] is relatively robust, as long as it can be estimated by back-extrapolation of the [Ca²⁺] transient, regardless of the presence of slow buffers. Thus, analysis of the calcium binding ratio based on d[Ca²⁺] still provides a reliable estimate of the overall calcium binding ratio of fast buffers if the sampling rate is fast enough. This estimate, however, does not include the contribution of slow buffers.

Effects of the Ca²⁺ indicator dye on dendritic [Ca²⁺] transients in the presence of PV

To understand the change of τ as a function of the Ca²⁺ binding ratio of fura-2 (κ_B‘) in the anomalous case of our preceding paper (Fig. 7 in the companion paper: Lee et al. 2000), we simulated that experiment by numerical integration of the equation system (22) using the same parameters as those of the high-γ curve in Fig. 5A with the following exceptions: d[Ca²⁺]_T = 17 μM, κ_S = 150, [Ca²⁺]_rest = 20 nM, [Mg²⁺] = 300 μM. The value for [Mg²⁺] was adopted from Stout et al. (1996). We integrated the equations for seven cases in which all parameters were kept constant except for κ_B‘, which was varied in the range 20–350.

Figure 7. Simulated [Ca²⁺] transient responses.

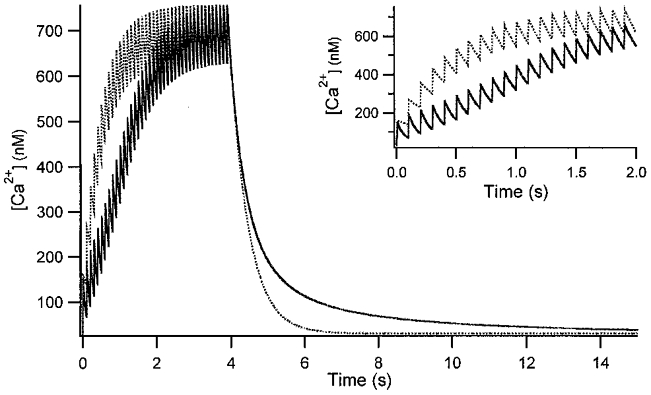
10 Hz stimulation with a Ca²⁺ influx (d[Ca]_T) per pulse of 20 μM in the absence (dotted line) and in the presence of 200 μM PV (continuous line) was assumed. Other parameters are the same as those in Fig. 6. The same traces are depicted on an expanded time scale in the inset.

The condition for fast buffering, inequality (21), indicates that the amount of fast buffer, lumped into Σκ, has an effect on the equilibration rate between PV and Ca²⁺ as well as on the Ca²⁺ extrusion rate. Under the conditions of Fig. 6, β is calculated to be 221, which is of the same order of magnitude as γ ( = 300 s⁻¹). Since in eqn (21) both β and γ are scaled by the term 1 +Σκ, an increase in the amount of fast buffer (κ_B‘) slows down the equilibration rate constant (right-hand side of inequality (21)) as well as the Ca²⁺ extrusion rate (left-hand side of inequality (21)) to the same degree. In addition, the value for α ( = 1.3) is not dominant over the value for β/(1 +κ_S) (= 1.46). Thus, a decrease in Ca²⁺ extrusion rate exerted by newly added indicator dye will have no substantial effect on the inequality (21). The simulation results (Fig. 6B) support the argument that the condition for fast buffering is not satisfied in the presence of PV when κ_B′ is in the range 20–350, which is similar to the κ_B′ range in the anomalous case described in the preceding paper (Lee et al. 2000). Examining the simulated transients (Fig. 6A), one can see that, nevertheless, they can be reasonably fitted by single exponentials. Similarly, some late [Ca²⁺] transients in Fig. 7D of the companion paper (Lee et al. 2000), with κ_B′ values between 200 and 350, are hardly distinguishable from single exponential curves.

Figure 6. Simulation of a fura-2 loading experiment.

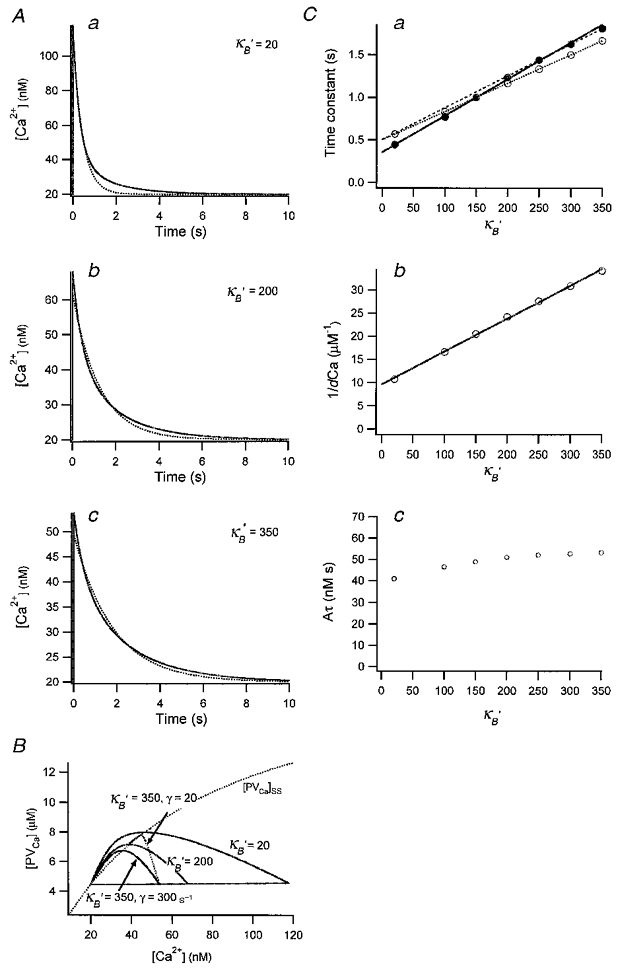
A, [Ca²⁺] transients obtained by numerical integration with κ_B′ = 20 (a), κ_B′ = 200 (b), κ_B′ = 350 (c). Other parameters are given in the main text. Each transient is fitted with a single exponential (dotted curve). The time constants obtained were 0.44, 1.23 and 1.81 s. B, plot of the three [Ca²⁺] transients shown in A on the plane of [PV_Ca]-[Ca²⁺]. The steady state relationship between [PV_Ca] and [Ca²⁺] is also superimposed (dotted curve). C, plot of single exponential fit results, τ (a) and 1/dCa (b) against κ_B‘. Time integrals of single exponential fits (or Aτ) are also depicted against κ_B‘. From the line fit of τ and 1/d[Ca²⁺]_{t = 0} against κ_B‘, estimates for κ_S(τ) and κ_S(dCa) were obtained. They were 82 and 135, respectively (continuous line in a and b). When only the latest 3 points of τ were fitted (dashed line), the x-axis intercept of the line is κ_S(τ) = 134. The τ values for simulations with [PV]_T = 0 were also plotted in C (○): fitting to these values resulted in the correct κ_S(τ) of 150.

Comparing the time constants of such fits for [PV]_T = 0 (○, Fig. 6Ca) with those for [PV]_T = 20 μM, it becomes evident that the contribution of PV to τ is increasing as κ_B′ increases (•, Fig. 6Ca). The differential effect of PV depending on κ_B′ causes the slope of τ in Fig. 6Ca to be steeper than that in the case when [PV] = 0. This steeper slope will result in an erroneously low estimate of κ_S(τ), if the data (in the presence of small amounts of PV) are interpreted within the framework of the single compartment model.

DISCUSSION

In the present study, we measured the kinetic parameters of Ca²⁺ binding to parvalbumin (PV) in vivo. The numerical simulations, using the in vivo parameters, indicate that a slow endogenous buffer, such as PV, which is found almost exclusively in GABAergic neurons (Celio, 1986, 1990), can accelerate the initial decay of action potential evoked [Ca²⁺] transients and slows down the complete clearance of residual Ca²⁺, thus producing two phases in the [Ca²⁺] decay. We found the signature of such a slow buffer in a fraction of inhibitory cells in the preceding paper (Lee et al. 2000). The effect of PV, which accelerates initial decays of dendritic [Ca²⁺] transients, is similar to that of EGTA which has slower binding kinetics than BAPTA and Ca²⁺ dyes. Markram et al. (1998) observed [Ca²⁺] transients in apical dendrites of pyramidal neurons evoked by single action potentials before and after the addition of 1 mM EGTA, and reported that the peak of ΔF/F of the transients was little affected but its decay was much faster in the presence of EGTA than under control conditions. Such an acceleration effect due to PV on [Ca²⁺] transients has also been observed in rat sensory neurons and skeletal muscles. When PV was perfused into dorsal root ganglion cells, it selectively increased a fast component in the decay of the [Ca²⁺] signals (Chard et al. 1993). In addition, [Ca²⁺] transients in fast-twitch muscles of PV-deficient mice showed significantly slower decay rates than those of wild-type mice, while their amplitudes were preserved (Schwaller et al. 1999).

Calbindin-D_28K might behave like a fast buffer in dendrites

Though it seems to be generally accepted that calbindin-D_28K (CB) has one very high affinity calcium binding site (K_d∼1 nM) and two or three lower affinity calcium binding sites (K_d∼10 μM) (Gross et al. 1993), the details of the calcium binding properties of CB are not yet known. Based on our findings, together with immunohistochemical observations, we can infer that CB should behave like a fast buffer in dendrites. Celio (1990) reported that most CB-immunoreactive cells in the neocortex belong to the class of GABAergic interneurons with the exception of faintly stained pyramidal cells in layer II/III and that all other neocortical pyramidal cells are negative for both PV and CB, while CA1 pyramidal cells are CB immunoreactive. This is consistent with a higher value for κ_S in CA1 pyramidal cells than that found in neocortical cells: the values were estimated to be about 170 and 110, respectively (Helmchen et al. 1996). In this study no deviations from the predictions of the single compartment model were described for either kind of cell. If the presence of CB is the major difference in the buffer systems of the two cell types, one may conclude that CB behaves like a fast buffer in pyramidal dendrites, probably acting through its low affinity binding sites.

Another clue supporting this argument can be obtained from the study by Airaksinen et al. (1997). Cerebellar Purkinje cells are known to express CB and PV abundantly, but not to have calretinin (Rogers, 1989; Airaksinen et al. 1997). Airaksinen et al. (1997) compared [Ca²⁺] transients of Purkinje cells from wild-type mice with those from mutant mice lacking CB. They found no upregulation of Ca²⁺ binding proteins in null mutant mice. Interestingly, they observed a double exponential decay in [Ca²⁺] upon synaptic stimulation, which was more exaggerated in the dendrites of Purkinje cells from null mutants than in those from wild-type mice. The [Ca²⁺] transients they observed in null mutants and wild-type mice are strikingly similar to our simulation results in Fig. 6, where a high Ca²⁺ extrusion rate, γ = 300 s⁻¹, was assumed. Wild-type results resemble simulations where κ_B′ > 20, and the mutant phenotype resembles simulations where κ_B′ = 20 (Fig. 6). If we assume that PV is the dominant Ca²⁺ binding protein in null mutant Purkinje cells, the alteration of [Ca²⁺] transients by knock-out of CB could well be mimicked by the removal of a fast buffer (fura-2) in the presence of a slow buffer.

Possible physiological role of PV in information processing in the cortical column

We can speculate about possible roles for PV in neuronal Ca²⁺ signalling based on the peculiar property that distinguishes it from fast buffers. The time constant required for Ca²⁺ to equilibrate with PV is determined by 1/(α+β/(1 +Σκ)) when the effects of other fast buffers are lumped into the term Σκ (see eqn (9)). The first and second terms in the denominator of the equation are quite comparable to each other under physiological conditions (α = 1.43, β/(1 +Σκ) = 1.32 when [PV]_T = 20 μM, Σκ = 150, [Mg²⁺] = 300 μM and [Ca²⁺]_rest = 30 nM). As we have shown already, the binding of Ca²⁺ to the non-Ca²⁺- bound fraction of PV (PV_free+ PV_Mg) and the Ca²⁺ extrusion mechanism (γ) contribute to the initial fast decay phase of a [Ca²⁺] transient. From this, we can expect that, as PV is saturated with Ca²⁺ during repetitive activity, the width of [Ca²⁺] transients will become broader.

This argument is relevant to Ca²⁺ build-up in dendrites during burst-like action potentials. We compared the responses of two buffer systems upon 10 Hz stimulation in Fig. 7, one of which has 200 μM PV, the other one has none (dotted line). The former will be referred to as slow buffer system and the latter as fast buffer system. The steady state [Ca²⁺] level during burst-like action potentials is dependent on Δt/τ, where Δt is time interval between action potentials and τ is the [Ca²⁺] relaxation time constant of individual [Ca²⁺] transients (Helmchen et al. 1996). Since the τ of a slow buffer system becomes the same as that of a fast one when PV is saturated with Ca²⁺, the steady state [Ca²⁺] level of the slow buffer systemwill eventually catch up with that of the fast buffer system. The time course towards the steady state of a slow buffer system, however, is quite different from that of a fast buffer system. The time for the [Ca²⁺] of the slow buffer system to reach its steady state level during the burst is delayed due to the faster τ of the slow buffer system during the early period of the burst, when PV is not yet saturated with Ca²⁺.

The discrepancy in the time required to reach a steady state [Ca²⁺] level between fast and slow buffer systems provokes an interesting speculation, together with the known histological connectivity of PV-immunoreactive neurons in cortical circuits: PV is known to be present only in a fraction of inhibitory neurons such as basket cells and axo-axonic (chandelier) cells, whose axons terminate at or close to the soma and the axon initial segment of pyramidal cells, while CR-immunoreactive cells innervate mostly other GABAergic cells (Nitsch et al. 1990; Sorvari et al. 1996; Gulyas et al. 1996). Thus, PV-immunoreactive neurons seem to be represented in a subgroup of GABAergic non-pyramidal cells which control very effectively the main excitatory pathway in the hippocampus. Considering that extrinsic excitatory afferent fibres terminate on both dendrites of pyramidal and GABAergic inhibitory neurons in cortical columns, PV-positive GABAergic cells would play a role in feed-forward inhibition of the main excitatory output from such cortical columns (Nitsch et al. 1990). Furthermore, PV would affect both pre- and postsynaptic Ca²⁺ signals, since axons and axon terminals are reported to have the same or higher immunoreactivity for PV than dendrites and somata (Kosaka et al. 1993).

If we associate pyramidal and PV-positive GABAergic cells with fast and slow buffer systems, respectively, [Ca²⁺]_i in the former would build up faster than in the latter upon burst-like repetitive depolarizations. This would cause a time delay in the activation time course of inhibitory action between non-pyramidal and pyramidal cells. If the axon terminals show a similar [Ca²⁺] transient during a burst, the delayed increase in [Ca²⁺] represents a very favourable condition for short term facilitation, since paired pulse facilitation is closely linked to the ‘residual Ca²⁺′ in the terminal (Kamiya & Zucker, 1994). Therefore, a discrepancy in the activation time courses during burst-like input may contribute to a recent finding that excitatory postsynaptic currents showed stronger depression in response to high frequency activation than inhibitory currents, a property which could explain the stability of cortical columns subjected to extrinsic excitatory inputs (Galarreta & Hestrin, 1998). Altogether, these observations suggest that the specific kinetic features of slow buffers are very important for understanding the role of PV-immunoreactive GABAergic neurons in stabilizing cortical neuronal activity.