Subthreshold oscillation of the membrane potential in magnocellular neurones of the rat supraoptic nucleus

Abstract

1. Electrophysiological properties and ionic basis of subthreshold oscillation of the membrane potential were examined in 104 magnocellular neurones of the rat supraoptic nucleus using intracellular recording techniques in a brain slice preparation.

2. Subthreshold oscillation of the membrane potential occurring in all neurones examined was voltage dependent. Oscillation was initiated 7-12 mV negative to the threshold of fast action potentials. Oscillation was the result of neither excitatory nor inhibitory synaptic activity nor of electric coupling.

3. Frequency analyses revealed a broad band frequency distribution of subthreshold oscillation waves (range 10-70 Hz). The frequency band of 15-33 Hz was observed in neurones depolarized close to the threshold of discharge.

4. Subthreshold oscillation was blocked by TTX (1.25-2.5 μM) as well as by TEA (15 mM). Subthreshold oscillation was not blocked by low Ca²⁺-high Mg²⁺ superfusate, CdCl₂, TEA (1-4.5 mM), 4-aminopyridine, apamin, charybdotoxin, iberiotoxin, BaCl₂, carbachol and CsCl.

5. During application of TTX, stronger depolarization induced high-threshold oscillation of the membrane potential at a threshold of about -32 mV. These oscillation waves occurred at a mean frequency of about 35 Hz and were blocked by CdCl₂.

6. Effects of ion channel antagonists suggest that subthreshold oscillation is generated by the interaction of a subthreshold sodium current and a subthreshold potassium current. The generation of high-threshold oscillation during TTX involves a high-threshold calcium current.

7. Subthreshold oscillation of the membrane potential may be important for the inter-neuronal synchronization of discharge and for the amplification of synaptic events.

The hypothalamic supraoptic nucleus (SON) contains two major populations of magnocellular neurosecretory neurones, producing and secreting vasopressin and oxytocin, respectively (for review see Poulain & Wakerley 1982). Neurones of a subpopulation of supraoptic neurosecretory cells share the capability of generating phasic bursts of action potentials. In these neurones, action potentials are succeeded by a depolarizing afterpotential (DAP; Andrew, 1987; Armstrong et al. 1994; Li et al. 1995). Depending on the discharge frequency, DAPs summate, eventually resulting in the generation of a plateau potential that gives rise to the discharge of a long-lasting train of action potentials. Thus, DAPs may provide a mechanism for the maintenance of the active state. The initiation of rhythmic bursting, i.e. the repetitive slow transition between active and inactive states, was assumed to depend on the occurrence of slow depolarizations (Andrew, 1987). The duration of phasic burst discharge in rat supraoptic neurones in vitro was reported to range from 1 s to 5 min (Inenaga et al. 1993). In SON neurones displaying both phasic discharge and DAPs, intrinsic oscillatory burst activity was reported to occur during perifusion of brain slices with low-calcium perifusion medium (Li & Hatton, 1996). These bursts were observed to repeat with a mean interval of 453 ms. Damped rhythmic oscillation of the membrane potential with an initial duration of 140 to 300 ms were reported to occur in magnocellular neurones of the guinea-pig SON (Erickson et al. 1993). On a shorter time scale, repetitively occurring non-synaptic depolarizing potentials (NSDPs) of 20 to 125 ms duration were observed to be generated 5-7 mV subthreshold to the initiation of spike discharge in rat supraoptic neurones (Bourque et al. 1986). NSDPs were suggested to be involved in spike and burst triggering. Similar functional roles for the regulation of neuronal activity in other brain regions were attributed to higher frequency subthreshold oscillatory activity (Alonso & Klink, 1993; Lampl & Yarom, 1993). The occurrence of endogenous subthreshold oscillatory activity was demonstrated in a variety of neuronal systems including the neocortex (Gray et al. 1989; Gutfreund et al. 1995), the entorhinal cortex (Alonso & Klink, 1993), the thalamus (McCormick & Pape, 1990), the nucleus basalis magnocellularis (Alonso et al. 1996), the amygdaloid complex (Paréet al. 1995; Pape et al. 1998; Pape & Driesang, 1998), the inferior olive (Llinás & Yarom, 1986; Bal & McCormick, 1997) and the dorsal root ganglia (Amir et al. 1999).

Ionic mechanisms involved in rhythmogenesis of repetitive fluctuations of the membrane potential seem to be as manifold as the characteristics of oscillatory phenomena. The generation of slow oscillatory activity in SON neurones seems to depend on the rhythmic increase and decrease of calcium influx (Andrew, 1987) or depends on calcium currents and TTX-sensitive sodium currents (Inenaga et al. 1993). Rapid mobilization of calcium from intracellular stores, influx of sodium through persistent sodium channels (I_Na,P) as well as gap junctions were reported to be important for the generation of slow oscillatory activity in supraoptic neurones of the rat observed during perifusion with low calcium medium (Li & Hatton, 1996). In SON neurones of the guinea-pig, a T-type calcium current (I_T) and mechanisms generating depolarizing afterpotentials were associated with damped membrane potential oscillations (Erickson et al. 1993). Concerning the generation of fast oscillatory activity, the interplay between I_T and a hyperpolarization-activated cation current (I_h) was shown to be important in the lateral geniculate nucleus (McCormick & Pape, 1990) as well as in the inferior olive (Bal & McCormick, 1997). In other neuronal systems TTX-sensitive conductances seem to be of high importance for the generation of subthreshold oscillation of the membrane potential. Oscillations in stellate cells of the entorhinal cortex are generated by the interplay of I_Na,P and an outward rectifying potassium conductance blocked by barium (Klink & Alonso, 1993). Fast oscillations in cortical pyramidal cells were blocked by TTX or a high concentration of tetraethylammonium (TEA; Gutfreund et al. 1995) and were simulated in a model to be generated by the interaction of I_Na,P and a slow non-inactivating potassium current. In the basolateral amygdala, subthreshold oscillations were blocked by TTX or carbachol (Pape & Driesang, 1998) suggesting the contribution of I_Na,P and the M-type potassium current (I_M) to the rhythmogenesis. Additionally, oscillatory activity in dorsal root ganglion neurones was demonstrated to be sensitive to the application of the local anaesthetic lidocaine (Amir et al. 1999).

In the present study, we report the occurrence, properties and ionic basis of rhythmic subthreshold oscillation of the membrane potential in magnocellular neurones of the rat SON in a brain slice preparation. The initiation of subthreshold oscillation is voltage dependent and is eliminated by TTX, procaine or 15 mM TEA, but is not blocked during superfusion with low Ca²⁺-high Mg²⁺ artificial cerebrospinal fluid (ACSF) or by Cd²⁺. The latter is also true for various potassium channel antagonists and the I_M channel agonist carbachol. Furthermore, subthreshold oscillation can still be induced during the application of the uncoupling agent heptanol. Part of this work has been presented in abstract form (Greffrath et al. 1999).

METHODS

Experiments were performed in vitro on coronal hypothalamic slices obtained from young adult male Sprague-Dawley rats (140-250 g; Charles River, Germany). The preparation procedures are described elsewhere (Greffrath et al. 1998). Briefly, animals were anaesthetized with diethyl ether and then decapitated. The whole brain was rapidly removed from the skull and chilled in ACSF at 4°C. A block of tissue containing the hypothalamus was dissected from the chilled brain. Coronal brain slices were cut on a vibratome (Vibroslice 752/M, Campden Instuments, UK). During the cutting procedure, the tissue was covered with chilled ACSF. Slices were allowed to equilibrate for at least 2 h in ACSF at room temperature. For recording, a single slice was transferred to the stage of a Haas-type recording chamber and was superfused with ACSF at 32 ± 1°C. The flow rate of ACSF was 2-3 ml min⁻¹. Throughout the experiment including the preparation procedures, ACSF was saturated with carbogen gas (95 % O₂, 5 % CO₂).

The membrane potential of supraoptic neurones was intracellularly recorded with microelectrodes filled with 2-3 M potassium acetate (resistance 140-190 MΩ). Microelectrodes were fabricated from borosilicate glass capillaries (o.d. 1.2 mm, i.d. 0.6 mm; Hilgenberg, Germany) using a horizontal puller (P-87, Sutter Instruments, USA). Membrane potentials were recorded with an Axoclamp 2A amplifier (Axon Instruments, USA) in bridge mode. A steppermotor-driven micromanipulator (developed by E. Martin) was used to facilitate membrane penetration. Pick up of noise was carefully controlled and maximally reduced by several measures: (i) the registration site was enclosed in a Faraday chamber (Siemens, Germany), (ii) the microelectrode was additionally shielded using a mu-metal tube, and (iii) digital equipment was connected to a separate power line using mains filters. Neurones included in this study, with the exception of 5 spontaneously bursting neurones, had a resting membrane potential of at least -50 mV. During injection of suprathreshold depolarizing direct current, all cells discharged trains of action potentials overshooting 0 mV. Neurones not displaying activity-dependent spike broadening (Bourque & Renaud, 1985) were excluded from further evaluation. After each experiment, changes in the electrode tip potential were controlled by measuring the DC offset of the electrode in the bathing medium. If necessary, the recorded neuronal membrane potential was corrected accordingly. Neuronal signals were stored on videotape. Off-line analysis of neuronal activity was performed on a PC-based system using a fast AD/DA board (TL-1-125 or Digidata 1200, Axon Instruments) and the appropriate software (Axotape2 and pCLAMP6, Axon Instruments). The acquisition rate was 1-4.2 kHz.

Mechanisms involved in the generation of rhythmic membrane potential fluctuations were pharmacologically characterized by addition of specific agents to the bath: 4-aminopyridine (4-AP, 0.5-5 mM; Sigma), apamin (50-500 nM; Alomone, Israel), bicuculline methochloride (1-50 μM; Sigma), carbamylcholine chloride (carbachol, 50-100 μM; Sigma), charybdotoxin (ChTX, 5-15 nM; Alomone), 1-heptanol (2-3 mM; Merck, Germany), iberiotoxin (IbTX, 50-200 nM; Alomone), kynurenic acid (2-3 mM; Sigma), procaine (100 μM; Sigma), TEA (1-15 mM; Sigma), TTX (1.25-2.5 μM; Sigma), BaCl₂ (1-2 mM; Sigma), CdCl₂ (0.3-1 mM; Merck) and CsCl (2-6 mM; Sigma). Heptanol was dissolved in dimethyl sulfoxide (DMSO); the final concentration of DMSO in the superfusate was less than 0.1 %, which had no detectable effect on the neuronal activity. All other agents were dissolved in standard ACSF. The standard ACSF contained (mM): NaCl 124; KCl 2; KH₂PO₄ 1.25; MgSO₄ 1.3; CaCl₂ 2.5; NaHCO₃ 26; glucose 10. The osmolality of the ACSF was 295 mosmol kg⁻¹, and pH was 7.4 ± 0.1. Low Ca²⁺-high Mg² superfusion medium contained: NaCl 124; KCl 6.25; MgCl₂ 4; CaCl₂ 0.2; glucose 10. For the application of CdCl₂, KH₂PO₄ and MgSO₄ were replaced by KCl and MgCl₂, respectively. For the application of ChTX and IbTX, the superfusate contained 0.01 % bovine serum albumin (BSA; Sigma). In the latter experiments, the standard ACSF used for superfusion during the control and washout periods also contained 0.01 % BSA. Quantitative properties of neurones are given as means ± standard deviation. Statistical evaluation was performed using Student's t test. Probability of error (P) smaller than 0.05 for differences between mean values was considered statistically significant.

The cycle duration of membrane potential oscillation was measured from peak to peak in a train of oscillation waves. The periodicity of the rhythmic membrane potential fluctuations in supraoptic neurones was analysed by calculating frequency spectra of the membrane voltage fluctuations using a discrete Fourier transform (DFT) algorithm (Embree & Kimble, 1991):

where N is the number of data samples and n is the discrete time index. The DFT coefficients used in the DFT kernel, W, are:

Before digitisation, analogue data were low-pass filtered at 100 Hz upper corner frequency (4-pole Butterworth filter; 24 dB octave⁻¹). Data were recorded with digitisation rates of 1-4.2 kHz. Under these conditions, the digitisation rates sufficiently oversample (Nyquist critical sampling frequency: 0.5-2.1 kHz). Short spike-free sequences of membrane potential oscillation (0.2-0.8 s) were selected for DFT analysis. Edges of the selected sequences of oscillatory activity were filtered using a 10 % Hanning window. Before analysis, the selected sequences were high-pass filtered using a software based finite impulse response (FIR) filter (Stearns & David, 1988) with square filter characteristic. The midpoint frequency of the FIR high-pass filter, i.e. the frequency of 50 % transmission, was 10 or 20 Hz; the filter length was 35 samples. Rejection in the stop band of the FIR filter was >40 dB.

RESULTS

Stable low-noise intracellular recordings in this study were obtained from 104 magnocellular supraoptic neurones. The resting membrane potential of these neurones was -56.9 ± 7.1 mV (mean ±s.d.). The apparent input resistance, as calculated from the hyperpolarization induced by low direct current injection, was 198.1 ± 118.0 MΩ. The time constant τ of the neuronal membrane, as determined from the initial potential trajectory of the current-induced hyperpolarization, was 13.1 ± 6.1 ms.

Properties of subthreshold membrane potential oscillation

In spontaneously active neurones showing tonic and clustered discharge patterns (n = 23), or burst discharge of short duration (100-400 ms; n = 2), rhythmic fluctuations of the membrane potential were observed during spike intervals (Fig. 1A), cluster intervals (Fig. 1B) or burst intervals (see Fig. 8B). In phasic neurones that discharged bursts of 14-47 s duration (n = 3), oscillation waves were observed during onset and termination of the burst as well as during longer spike intervals occasionally occurring during the course of the burst (Fig. 1C). In the latter neurones, oscillation of the membrane potential was not observed during interburst intervals. In spontaneously discharging neurones, rhythmic oscillation of the membrane potential could be suppressed by the injection of hyperpolarizing direct current. The remainder of the neurones examined in this study were not active during the control period. In these neurones, oscillation of the membrane potential was not present at the resting membrane potential, but could be induced by injection of depolarizing direct current pulses. During depolarization of the neuronal membrane by direct current injection, oscillation of the membrane potential was initiated 7-12 mV (8.6 ± 1.8 mV; n = 10) negative to the threshold for the discharge of action potentials. In the example shown (Fig. 2A), oscillation of the membrane potential was initiated at a membrane potential of -48 mV, i.e. 5 mV positive to the resting potential and 9 mV negative to the threshold for the initiation of action potentials (threshold not shown). Due to these characteristics, the rhythmic fluctuations of the membrane potential were interpreted in terms of ‘subthreshold oscillation’. The initiation of oscillation was voltage dependent. At the membrane potential for the initiation of subthreshold oscillation, the amplitude of oscillation waves was small, but increased with increasing depolarization level (Fig. 2A), thus becoming more prominent. However, during the course of a train of oscillation waves the oscillation amplitude varied in an apparently unsystematic manner.

Figure 1. Subthreshold oscillation of the membrane potential in spontaneously active magnocellular neurones.

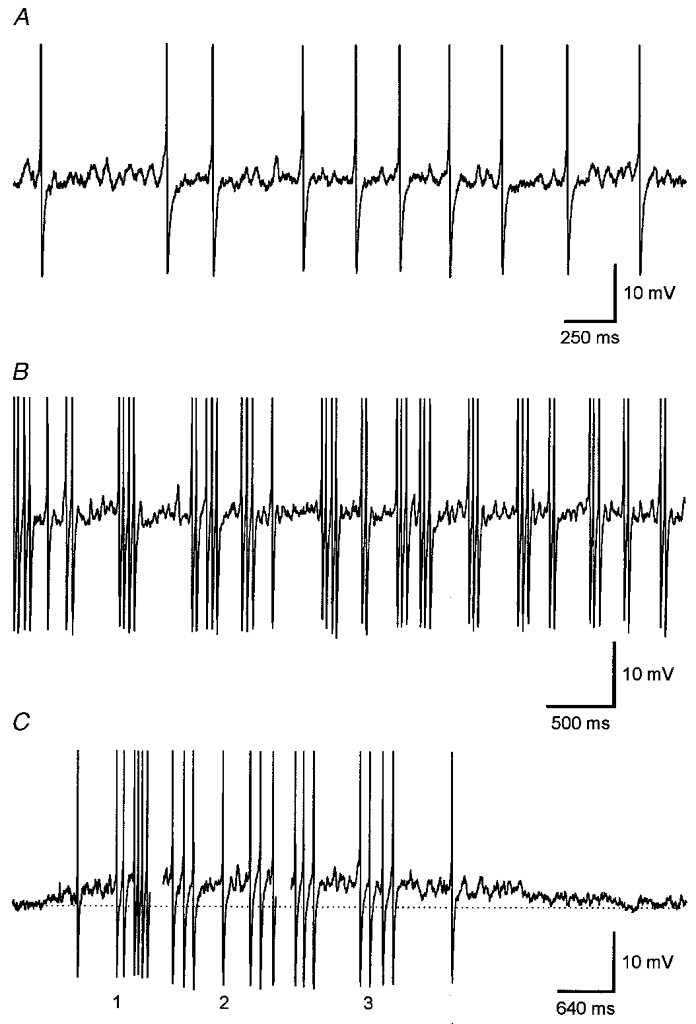
Continuous recordings of the membrane potential of supraoptic magnocellular neurones with different discharge pattern. A, in a randomly discharging neurone with low discharge rate, rhythmic fluctuations of the membrane potential were generated during spike intervals. B, in a magnocellular neurone discharging regenerative clusters of action potentials, oscillation waves of varying amplitude were generated during cluster intervals. C, in a neurone discharging phasic bursts of action potentials (burst duration about 15 s), oscillation waves were generated during the onset (1) and during the termination (3) of the burst. Throughout the burst, oscillation waves were generated during interspersed longer spike intervals (2). Records are truncated in all cases. Dotted line represents the resting membrane potential (-49 mV).

Figure 8. Subthreshold oscillation of the membrane potential in spontaneously active magnocellular neurones.

A, subthreshold oscillation of the membrane potential with waves of more ore less equal amplitude is generated during subthreshold depolarization by direct current injection. B, in a neurone spontaneously initiating short bursts of action potentials, subthreshold oscillation with an apparently random distribution of wave amplitudes is generated during burst intervals. Occasionally, short sequences of high-amplitude oscillation waves are generated that may give rise to spike discharge. C, during a long-lasting plateau potential succeeding an induced train of action potentials, subthreshold oscillation waves are generated during intervals of clustered discharge and disappear during the decay of the plateau. Traces represent voltage. The dotted lines represent the mean membrane potential during burst intervals and the resting membrane potential. Records are truncated. D, plot of the discharge frequency (F_AP) as a function of the frequency of subthreshold oscillation of the membrane potential (F_osci). The frequency of the 10th action potential in a spike train or the 4th action potential in a spike cluster is plotted against the preferred frequencies of subthreshold oscillation as deduced from the major power density peaks (n = 28) in DFT spectrograms calculated from the oscillatory activity of 16 magnocellular supraoptic neurones. The continuous line represents the calculated regression line. The dotted lines indicate the 95 % confidence interval. The dashed line represents the hypothetical regression of equity.

Figure 2. Subthreshold oscillation of the membrane potential and EPSPs in magnocellular neurones.

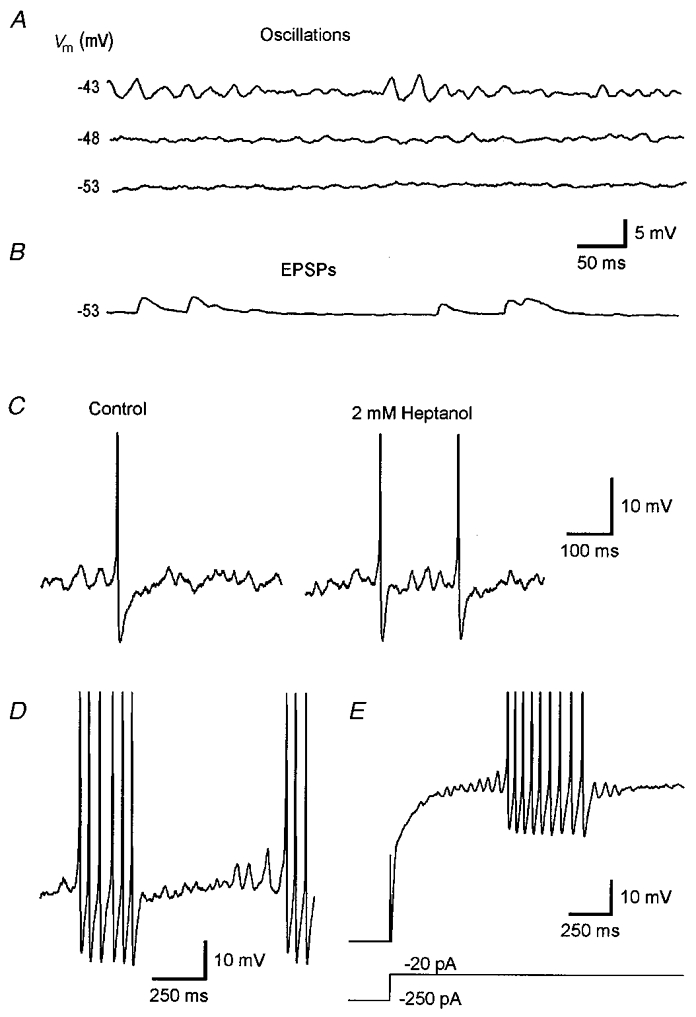
A, voltage dependence of the initiation of subthreshold oscillation of the membrane potential in a magnocellular neurone. Shallow oscillation waves are generated at -48 mV, a membrane potential 5 mV positive to resting membrane potential of -53 mV. Close to the threshold for the initiation of action potentials, prominent oscillation waves with varying amplitude are generated. B, in another neurone with identical resting membrane potential spontaneously occurring EPSPs are recorded at rest. The decay phase of EPSPs is markedly slower compared to that of oscillation waves. C, application of 2 mM 1-heptanol did not block the generation of membrane potential oscillation. D, close to the threshold for initiation of action potentials large amplitude oscillation waves are generated. E, relaxation from long-lasting hyperpolarization is followed by a rebound depolarization, resulting in the generation of subthreshold oscillation with waxing amplitude finally inducing a short burst of action potentials. The lower trace in E represents current recording. The initial hyperpolarized part of the voltage trace is out of range. Records are truncated in C-E.

In the brain slice preparation used in the present study, synaptic activity was only rarely recorded from supraoptic neurones. When present, the properties of the synaptic activity differed in several respects from those of subthreshold oscillation waves. (i) EPSPs were observed during the control recording period, i.e. at membrane potentials negative to the potential for induction of subthreshold oscillation (Fig. 2B). (ii) The rising phase of EPSPs was faster while the phase of decay was slower than the respective phases of subthreshold oscillation waves; rise time to peak was 9.5 ± 2.2 ms in EPSPs (n = 12) and 15.1 ± 2.2 ms in oscillation waves of about 32 Hz (n = 20; P = 0.001), while the half-width, i.e. the duration at 50 % amplitude of EPSPs and oscillation waves, was 25.5 ± 6.8 and 15.7 ± 3.0 ms (P = 0.001), respectively. (iii) Subthreshold oscillation of the membrane potential could still be induced during superfusion of the brain slice with low Ca²⁺-high Mg²⁺ ACSF (n = 4; see Fig. 6A). The slightly increased potassium concentration of the low Ca²⁺-high Mg²⁺ ACSF had no detectable effect on neuronal activity. (iv) Subthreshold oscillation of the membrane potential was blocked neither by the application of 2 mM kynurenic acid (n = 2) nor by the application of 1-50 μM bicuculline (n = 6; results not presented).

Figure 6. Calcium-dependent mechanisms are not involved in the generation of subthreshold oscillation.

A, subthreshold oscillation is not blocked during superfusion of the brain slice with low Ca²⁺-high Mg²⁺ ACSF, whereas the duration of spike trains is strongly enhanced. B, subthreshold oscillation of the membrane potential is not blocked by addition of 0.5 mM CdCl₂to the ACSF. C, subthreshold oscillation is not blocked by the application of 300 nM apamin together with 3 mM TEA (please note that spike repolarization is delayed). D, subthreshold oscillation is not blocked by 10 nM charybdotoxin. Upper traces represent voltage while lower traces in A-C represent current recordings. The initial hyperpolarized part of the voltage trace in A is out of range. Records are truncated in A, B and D.

Coupling of magnocellular neurones in the SON of the rat by gap junctions was suggested to be involved in the generation of rhythmic activity (Li & Hatton, 1996). To examine the possible involvement of gap junctions in the generation of subthreshold oscillation of the membrane potential in supraoptic magnocellular neurones, brain slices were superfused with ACSF containing the common uncoupling agent heptanol (2-3 mM; n = 5). Heptanol had no detectable effect on the initiation and expression of subthreshold membrane potential oscillation in these neurones (Fig. 2C). Effects of heptanol were not examined in phasically discharging neurones.

Examination of the peak to peak cycle duration and calculation of the respective frequency of single subthreshold oscillation waves as analysed in a subpopulation of neurones (n = 15) revealed a broad frequency distribution of oscillation waves in the range between 10 and 70 Hz (in most cases 15 to 60 Hz). Two preferred frequency bands of subthreshold membrane potential oscillation were established: a frequency band between 40 and 60 Hz and a lower frequency band between 15 and 33 Hz. Oscillation waves in the latter frequency band primarily were observed in spontaneously active neurones at membrane potentials close to the threshold for the discharge of fast action potentials. The amplitude of these oscillation waves was increased when compared to the amplitude of oscillation waves from the higher frequency band (Fig. 2D). The mean amplitude was 4.6 ± 0.82 mV for high-amplitude oscillation waves (n = 20) and 2.1 ± 0.71 mV (n = 20) for low-amplitude oscillation waves. The transition from low to high-amplitude oscillation waves is evident during the ramp-like potential trajectory induced by the rebound depolarization (RD) after the break of long-lasting hyperpolarization (Fig. 2E). In some neurones a continuous increase of the amplitude of oscillation waves with increasing depolarization was observed. Regression analysis revealed a statistically significant inverse relation of the amplitude and the frequency of oscillation waves (r = -0.6512; n = 38); oscillation waves of high amplitude were of low frequency, whereas high-frequency oscillation waves were generated with low amplitude (see Fig. 2D). However, in most neurones examined, oscillation waves of different amplitude and frequency were generated in an apparently unsystematic sequence (e.g. Fig. 5B).

Figure 5. Potassium dependence of subthreshold oscillation of the membrane potential.

A, subthreshold oscillation of the membrane potential is strongly attenuated by 15 mM TEA. Note that the duration of spikes is increased and that spike broadening is reversed by TEA. The generation of oscillation waves is blocked neither by the application of 50 μM carbachol (B) nor by the application of 2 mM BaCl₂ (C). The lower trace in A represents current recording. Records are truncated in all cases.

No systematic relation of the mean oscillation frequency and the time constant of the membrane was detected by regression analysis (r = 0.481; n = 15; n.s.). Essentially the same was true for the oscillation frequency and the membrane potential; during moderate depolarization, the mean oscillation frequency was not significantly altered compared to the mean frequency at threshold for the initiation of oscillation (47.4 ± 14.8 and 46.7 ± 14.1 Hz; n = 12). In contrast, depolarization close to the threshold for the initiation of action potentials resulted in a significant reduction of the oscillation frequency (38.4 ± 13.7 Hz; P = 0.05). The former result probably reflects the unsystematic generation of various frequency components of oscillatory activity, while the latter result most probably reflects the preference for generation of low-frequency/high-amplitude waves close to the threshold for the initiation of action potentials.

In a subpopulation of magnocellular neurones (n = 16), the analysis of short membrane potential sequences with the DFT method revealed two major types of spectral power density distribution. One type of power density spectrum was characterized by a prominent peak in the high-frequency range with no obvious peaks in the low-frequency range (Fig. 3A). A second type of power density spectrum was characterized by a prominent peak in the low- (Fig. 3B) or intermediate- (Fig. 3C) frequency range with lower power density in a broader frequency range. The former type of power density spectrum was found in data sets taken from neurones that were silent during control recordings and generated sinusoidal oscillation waves during depolarization by direct current injection. The latter type of power density spectrum was found in records taken from spontaneously discharging neurones or from active plateau potentials generated by silent neurones sufficiently depolarized by direct current pulses (see Fig. 8C). Power spectra calculated from oscillatory activity containing an unsystematic sequence of various oscillation frequencies were dominated by a prominent peak in the lower frequency range, while high-frequency peaks were comparatively low. This amplitude distribution may be due to the observed inverse relation of the oscillation frequency and oscillation amplitude, resulting in higher power density of low-frequency/high-amplitude waves compared to high-frequency/low-amplitude oscillation waves.

Figure 3. Spectral composition of subthreshold oscillation in magnocellular neurones.

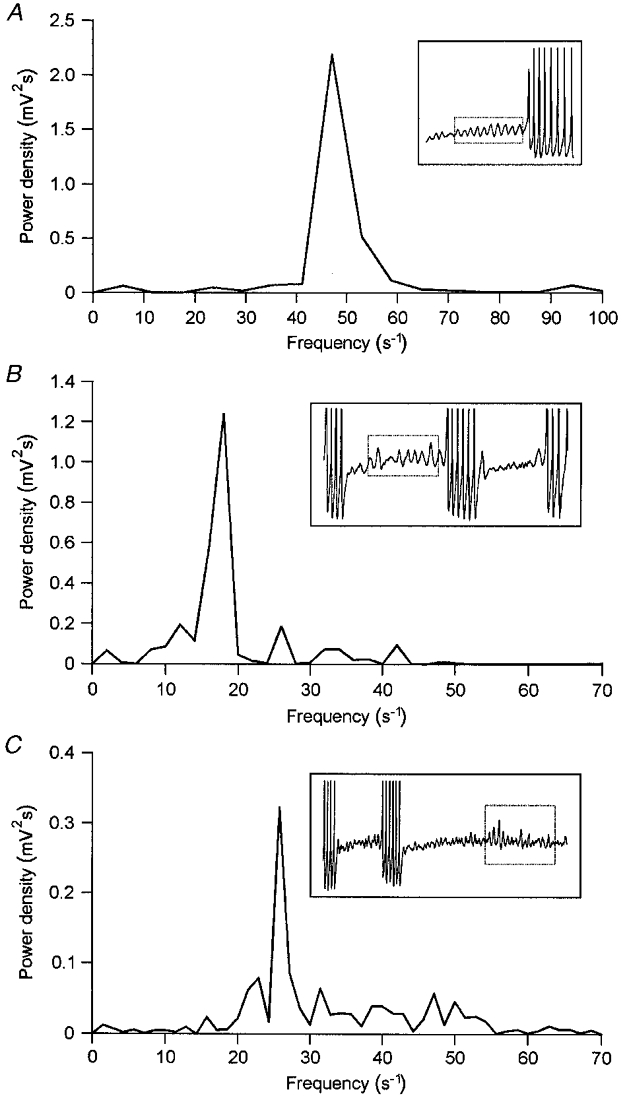
A, DFT power density spectrogram of the sinusoidal subthreshold oscillation induced by depolarization in a neurone not spontaneously discharging during control recording. A high-frequency peak at 47 Hz dominates the spectrogram. B, DFT power density spectrogram of the oscillatory activity generated during burst intervals by a neurone discharging short bursts of action potentials. The spectrogram is composed of a narrow low-frequency peak at 18 Hz and smaller peaks at 12, 26 and 42 Hz. C, DFT power density spectrogram of the oscillatory activity generated during a burst interval in a neurone discharging bursts of action potentials with highly variable burst intervals. The broad band spectrogram is dominated by a low-frequency peak at 26 Hz. Insets represent the original voltage recordings; the respective sequence of oscillation waves selected for DFT analysis is indicated by a dotted box. Records are truncated.

Ionic basis of subthreshold membrane potential oscillation

The initiation of subthreshold membrane potential oscillation in supraoptic neurones during current-induced depolarization or during the rebound depolarization following the break of current-induced hyperpolarization was blocked by bath application of 1.25-2.5 μM TTX (n = 15; Fig. 4A and B). The same was true for the generation of fast action potentials. The generation of both subthreshold oscillation of the membrane potential and fast action potentials were also blocked by the application of 100 μM procaine (n = 4). However, the generation of subthreshold oscillation was blocked early during the application period whereas the discharge of fast action potentials was blocked after prolonged application (up to 20 min) of procaine (Fig. 4C), indicating a higher sensitivity of membrane potential oscillation to procaine when compared to that of fast action potentials.

Figure 4. Sodium dependence of subthreshold oscillation of the membrane potential.

A, action potentials as well as subthreshold oscillation of the membrane potential are blocked by 1.5 μM TTX. B, subthreshold oscillation of the membrane potential induced by the rebound depolarization following the break of hyperpolarization is blocked by 1.25 μM TTX. C, subthreshold oscillation of the membrane potential is blocked by 100 μM procaine during the early phase of application while spike discharge is more resistant to the block by procaine. Upper traces represent voltage while lower traces represent current recordings. Records are truncated in all cases.

Subthreshold oscillation of the membrane potential was strongly attenuated or blocked during the superfusion of brain slices with ACSF containing 15 mM TEA (n = 6; Fig. 5A). In contrast, oscillation was not affected by the application of 1-4.5 mM TEA (n = 16; results not presented, but see Fig. 6C). These results suggest an important contribution of potassium channels with low TEA sensitivity to the generation of subthreshold membrane potential oscillation. The contribution of other potassium channels was examined by the application of various potassium channel blockers. The generation of oscillation waves was not blocked by the application of 4-AP (0.5-5 mM; n = 5) and CsCl (2-6 mM; n = 3). The same was true for the application of 50-100 μM carbachol (n = 4; Fig. 5B) and 1-2 mM BaCl₂ (n = 2; Fig. 5C).

The contribution of calcium channels to the generation of subthreshold membrane potential oscillation was examined by superfusion of brain slices with ACSF of low Ca²⁺-high Mg²⁺ concentration (n = 4) or by the application of 0.3-1 mM CdCl₂ (n = 7). However, the generation of oscillation waves was not affected by superfusion of brain slices with low Ca²⁺-high Mg²⁺ ACSF (Fig. 6A); a delay of the termination of spontaneous discharge was observed in these neurones, but subthreshold membrane potential oscillation was neither eliminated nor attenuated. In neurones examined during superfusion of brain slices with ACSF containing CdCl₂, the subthreshold membrane potential oscillation initiated by the injection of depolarizing direct current of lower intensity was not affected by CdCl₂ (Fig. 6B). In contrast, the activity-dependent spike broadening during the course of a current-induced train of action potentials was strongly reduced and the hyperpolarizing after-potentials following each spike were attenuated (results not presented) indicating an effective action of Cd²⁺ on calcium influx.

The contribution of different subtypes of calcium-dependent potassium channel to the generation of subthreshold membrane potential oscillation was examined by the application of selective toxin antagonists. However, the generation of subthreshold oscillation was not blocked by the application of the SK channel antagonist apamin (50-500 nM; n = 7; Fig. 6C). The same was true for the application of BK and IK channel antagonists. Neither IbTX (50-200 nM; n = 5) nor ChTX (5-15 nM; n = 5; Fig. 6D) attenuated or blocked the expression of oscillation waves.

When the generation of subthreshold oscillation of the membrane potential and the initiation of fast action potentials was blocked by TTX, stronger direct current-induced depolarization resulted in the initiation of a second type of voltage-dependent membrane potential oscillation (Fig. 7A). The amplitude of these oscillation waves increased with increasing current-induced depolarization. The membrane potential for initiation of these TTX-resistant oscillation waves was -32.2 ± 0.93 mV (n = 5). In these neurones the frequency of TTX-resistant oscillation waves was 34.8 ± 10.46 Hz. The TTX-resistant high-threshold oscillation was blocked when 0.3-1 mM CdCl₂ was added to the superfusion medium (Fig. 7B; n = 3). A closer examination of the properties of TTX-resistant high-threshold membrane potential oscillation is not included in the present study.

Figure 7. Sodium-independent high-threshold oscillation of the membrane potential.

A, high-threshold oscillation of the membrane potential is generated during sufficient depolarization when sodium channels are blocked by 2 μM TTX. B, high-threshold oscillation is blocked during sufficient depolarization when 0.5 mM CdCl₂ is added to the superfusate containing 2 μM TTX. Upper traces represent voltage recordings while lower traces represent current recordings.

Subthreshold membrane potential oscillation in spontaneously discharging neurones

In neurones depolarized by the injection of direct current, rhythmic subthreshold oscillation of the membrane potential was generated with oscillation waves of more or less constant amplitude (Fig. 8A, see also Fig. 3A). In neurones generating an RD after relaxation from hyperpolarization, the oscillation waves initiated during the course of the RD steadily increased in amplitude, gave rise to a short train of action potentials and decreased again (see Fig. 2E). In contrast to the latter systematic alteration of the oscillation amplitude, oscillation waves in spontaneously active neurones with tonic (see Fig. 1A) or clustered discharge patterns (see Fig. 1B), as well as in neurones discharging short repetitive bursts of action potentials (Fig. 8B) were generated with amplitudes varying in frequency and amplitude in an apparently unsystematic manner. In many cases, the initiation of action potentials in these neurones was preceded by a single high-amplitude oscillation wave or by a sequence of high-amplitude oscillation waves. In a subpopulation of magnocellular neurones examined in this study, a spike train induced by injection of a depolarizing direct current was succeeded by a sequence of an AHP and a DAP (n = 29). Depending on the discharge activity during the evoked spike train, the DAP increased in amplitude eventually initiating subthreshold oscillation of the membrane potential. With further increasing discharge frequency of the evoked spike train, a super-threshold DAP and finally a plateau potential developed (Fig. 8C). The plateau potential gave rise to either tonic or clustered discharge of action potentials. During the single spike intervals or during the spike cluster intervals, subthreshold oscillation of the membrane potential was generated in a mode closely resembling that observed in neurones with comparable spontaneous discharge activity (see Fig. 1B). Furthermore, oscillatory activity during the plateau potential and during its decay phase closely resembled that observed during bursts of action potentials discharged by phasic neurones (please see Fig. 1C).

To examine the functional relation of the oscillation frequency and the frequency of spike discharge, the frequency of the 10th action potential (in spontaneously generated or current-induced bursts) or of the 4th action potential (in spike clusters) was plotted against the frequency of all major peaks (n = 28) of the power density spectra as determined by the DFT analysis of oscillatory activity in 16 magnocellular neurones (Fig. 8D). The regression analysis revealed a significant correlation of the frequencies of subthreshold oscillation and the discharge frequency in these neurones (r = 0.807; P = 0.001). The intercept of the regression line with the ordinate was 11.5 ± 30.2 spikes s⁻¹, which was not statistically different from 0 spikes s⁻¹. Probability calculation revealed that the regression line was not statistically different from the hypothetical regression of equity.

DISCUSSION

Results of the present study demonstrate that all magnocellular neurones examined are capable of generating rhythmic oscillation of the membrane potential when depolarized close to the threshold for the initiation of fast action potentials. The subthreshold oscillation waves are independent from excitatory and inhibitory synaptic inputs to the respective neurone, since oscillation was not affected or blocked during superfusion of the brain slice with low Ca²⁺-high Mg²⁺ ACSF, kynurenic acid or bicuculline. This assumption is confirmed by the clear difference between oscillation waves and synaptic events in the time constants of the rising phase and decay as well as in the voltage dependence. Moreover, the subthreshold oscillation of the membrane potential in magnocellular neurones seems to be independent from neuronal coupling by gap junctions, since oscillation was not blocked by the common uncoupling agent heptanol. Together, these results suggest that subthreshold oscillation of the membrane potential is generated by a mechanism intrinsic to each single magnocellular neurone independent from the type of discharge pattern. Thus, it is very likely that oscillatory activity is not restricted to a specific type of magnocellular neurone, i.e. to oxytocin (OT) or vasopressin (VP) cells. However, this assumption must remain somewhat speculative, since an immunohistochemical identification was not performed in the present study and the patterns of spontaneous activity observed in the examined neurones including phasic discharge do not allow an unequivocal classification (for review see Armstrong, 1995).

The periodicity of subthreshold oscillation of the membrane potential is demonstrated by results of the DFT analysis. In neurones of the supraoptic nucleus the frequency of oscillation waves is relatively high compared to those of neurones of the inferior olive nucleus (Llinás & Yarom, 1986; Bal & McCormick, 1997), the basolateral amygdaloid complex (Paréet al. 1995; Pape et al. 1998) and the entorhinal cortex (Alonso & Klink, 1993), but closely resembled that of non-cholinergic nucleus basalis neurones (Alonso et al. 1996). In neurones oscillating with frequencies in the low-frequency band, i.e. in neurones depolarized close to the initiation threshold of fast spikes, in neurones producing a plateau potential and in spontaneously discharging neurones, the frequency of oscillation waves meets that of neocortical pyramidal cells (Gutfreund et al. 1995).

Involvement of sodium currents in the generation of subthreshold oscillation

Subthreshold oscillation of the membrane potential of magnocellular neurones was blocked by TTX, suggesting a major contribution of sustained TTX-sensitive sodium currents to the generation of the membrane potential oscillation. This assumption is supported by the finding that the application of procaine resulted in suppression of both spike discharge and the generation of subthreshold oscillation. TTX-sensitive persistent mechanisms have been discussed in relation to the generation of subthreshold oscillatory activity in a variety of other neuronal systems including pyramidal cells of the neocortex (Gutfreund et al. 1995) and stellate cells of the entorhinal cortex (Klink & Alonso, 1993). Two types of sustained sodium currents have to be considered: a non-inactivating (persistent) subthreshold sodium current, i.e. I_Na,P (for a review see Crill, 1996) or alternatively a sustained sodium current that is predicted by the Hodgkin-Huxley analysis for a narrow potential range and arises from the partial overlap of the steady-state inactivation and activation curves for sodium conductance (‘window current’; Attwell et al. 1979). As demonstrated in hippocampal pyramidal neurones, I_Na,P was much more resistant to inactivation by depolarization than the transient sodium current and could be recorded with >50 % of its maximal amplitude when the transient sodium current was completely inactivated (French et al. 1990). The presence of a persistent sodium current in magnocellular supraoptic neurones has been demonstrated with voltage-clamp technique (Li & Hatton, 1996). Like I_Na,P this current had a low activation threshold and displayed little inactivation during depolarization steps of hundreds of milliseconds. A persistent sodium current was suggested to be an important factor underlying the generation of bursting activity in magnocellular supraoptic neurones (Inenaga et al. 1993).

There is no pharmacological agent that selectively distinguishes the persistent sodium current from the fast transient sodium current (Crill, 1996). However, several results of the present and other studies support the assumption that the persistent sodium current may underlie subthreshold oscillation of the membrane potential in magnocellular neurones of the supraoptic nucleus. (i) Subthreshold oscillation was more sensitive to procaine than were fast sodium spikes. This result is compatible with the observation that in hippocampal CA1 neurones I_Na,P is more sensitive to lidocaine than is the transient sodium current (Hammarström & Gage, 1998). (ii) Subthreshold oscillation of the membrane potential was generated 7-12 mV negative to the threshold for initiation of fast action potentials. This observation is compatible with the result that the persistent sodium current I_Na,P is activated about 10 mV negative to the threshold of the transient sodium current in isolated neocortical neurones (Brown et al. 1994), and in supraoptic neurones (Li & Hatton, 1996). The possibility that oscillation waves represent aborted spikes can be excluded since in contrast to run-down phenomena, stable oscillatory activity was recorded during long periods of depolarized states. In contrast, a contribution of the ‘window current’ to the generation of subthreshold oscillatory activity cannot be excluded. The ‘window current’ is active in a narrow potential window close to the threshold of spike discharge (for review see Taylor, 1993) and may thus complement I_Na,P in generating high-amplitude oscillation waves that were observed when the membrane was depolarized close to the threshold for the initiation of action potentials. Furthermore, the contribution of the ‘window current’ cannot be excluded from being involved in the generation of membrane potential oscillation since results of the present study do not provide direct evidence for the importance of I_Na,P for the initiation of oscillatory activity.

Involvement of potassium currents in the generation of subthreshold oscillation

The strong attenuation of oscillatory activity in magnocellular neurones by 15 mM TEA suggests the involvement of potassium channels in the genesis of oscillation waves. However, based on results of the present study a variety of K⁺ currents may be considered unlikely to contribute to the generation of oscillation waves. (i) The delayed rectifier K⁺ current (I_K) most probably is not involved in the generation of subthreshold oscillation since I_K in magnocellular neurones has an activation threshold of -40 mV (Cobbett et al. 1989), whereas in most neurones of the present study membrane potential oscillation was fully expressed at this potential. Furthermore, oscillation waves were not affected by 1-4.5 mM TEA, while repolarization of action potentials was considerably delayed by these concentrations of TEA (see Fig. 6C). (ii) The transient outward potassium current (A-current) is probably not involved in the generation of subthreshold membrane potential oscillation, since the A-current in magnocellular neurones of the rat is blocked by 4-AP (Bourque, 1988), whereas the oscillatory activity was not affected by the application of 4-AP. Furthermore, in magnocellular neurones of the rat supraoptic nucleus, the A-current is completely inactivated at steady state membrane potentials positive to about -55 mV and a 50 % removal of inactivation is achieved by hyperpolarization to -80 mV (Bourque, 1988). The mean time constants of fast and slow inactivation of the A-current are 9 to 41 ms (Fisher et al. 1998). Thus, the result of the present study that sustained subthreshold oscillation was observed when neurones were steadily depolarized from the resting potential to membrane potentials positive to -45 mV is incompatible with the properties of the A-current. (iii) The hyperpolarization-activated cationic current (I_h) is probably not involved in the generation of subthreshold oscillation of the membrane potential, since the deactivation and activation characteristics of I_h as well as the sensitivity of I_h to Cs⁺ (for a review see Pape, 1996) are not compatible with results of the present study. I_h was demonstrated to be present in magnocellular neurones of the guinea-pig (Erickson et al. 1990), but oscillation waves were not blocked by Cs⁺. Furthermore, sustained oscillatory activity could be evoked when neurones were steadily depolarized from holding potentials 10-20 mV positive to the activation potential of I_h. (iv) Calcium-dependent potassium currents were demonstrated to be important for the generation of spike train after-hyperpolarization in magnocellular neurones of the supraoptic nucleus (Bourque & Brown, 1987; Armstrong et al. 1994; Greffrath et al. 1998). However, none of the three major subtypes of calcium-dependent potassium channel (for a review see McManus, 1991), i.e. SK channels (small conductance), BK channels (large conductance) and IK channels (intermediate conductance), seem to be involved in the initiation of subthreshold oscillation of the membrane potential, since none of the selective toxin blockers had any effect on oscillation waves; neither the scorpion venom peptides iberiotoxin (BK channels) and charybdotoxin (BK and IK channels), nor the bee venom toxin apamin (SK channels) blocked or attenuated subthreshold oscillation of the membrane potential.

In a variety of neuronal systems including pyramidal cells of the neocortex, stellate neurones of the entorhinal cortex and spiny neurones of the basolateral amygdaloid complex, a subthreshold sustained potassium current seems to be essential for the generation of subthreshold membrane potential oscillation (Klink & Alonso, 1993; Gutfreund et al. 1995; Pape & Driesang, 1998). The outward rectifying I_M has the unique characteristic of sustained activation and is the only potassium current active at voltages near the threshold for action potential initiation (Marrion, 1997). The sensitivity of subthreshold oscillation in neurones of the basolateral amygdaloid complex to Ba²⁺ and to carbachol was interpreted in terms of the contribution of I_M to the generation of oscillatory activity (Pape & Driesang, 1998). Subthreshold oscillation in neurones of the entorhinal cortex was also blocked by Ba²⁺ (Klink & Alonso, 1993). However, arguing against a significant contribution of I_M to the generation of subthreshold oscillation in these neurones, the underlying outward rectification was not affected by carbachol. In this context, Klink & Alonso (1993) hypothesize that specific cell types may express a specific subtype of potassium current that is optimal for the individual activity profile. In supraoptic OT neurones of the female rat the pharmacological properties of an outward rectifying potassium channel also were demonstrated to be aberrant from those of the classical I_M (Stern & Armstrong, 1997). In these neurones, the conductance underlying the SOR had properties resembling those of the classical M-current (Brown, 1988) but was insensitive to muscarine. Recently, it was demonstrated that in male rats, OT cells also are characterized by the presence of SOR and RD (Armstrong & Stern, 1998). In both sexes of rat, the majority of VP cells lack the SOR and if present it is weakly expressed (Stern & Armstrong, 1995; Armstrong & Stern, 1998). Thus, the conductance underlying the SOR and the RD is unlikely to be involved in the generation of subthreshold oscillation of the membrane potential in magnocellular neurones, since oscillatory activity was not blocked by Cd²⁺ or Ba²⁺, and it was observed in all neurones examined in the present study, probably including VP cells. For a closer characterization of membrane currents involved in the generation of subthreshold oscillation of the membrane potential, voltage-clamp experiments on isolated SON neurones will provide more information.

When the sodium/potassium-dependent subthreshold oscillatory activity and the discharge of action potentials was blocked by TTX, a second type of membrane potential oscillation could be elicited by stronger depolarization at a higher threshold when compared to that of sodium-dependent activity. The properties of this high-threshold oscillation in supraoptic neurones are in accordance with high-threshold oscillation of the membrane potential observed in neurones of the guinea-pig basolateral amygdaloid complex (Pape et al. 1998). These high-threshold oscillation waves were blocked by cadmium, suggesting the dependence of this type of membrane potential oscillation on an activation of high-threshold calcium currents. High-threshold calcium currents of the N-, L- and P-type were demonstrated to be expressed in magnocellular neurones of the supraoptic nucleus (Fisher & Bourque, 1995). In supraoptic neurones recorded from perfused explants of the rat hypothalamus, the threshold of NSDPs (see Introduction) was shifted to a more positive membrane potential when Na⁺-dependent action potentials were blocked by TTX, and they were reduced in size and frequency when Ca²⁺ was replaced with Co²⁺ or Mn²⁺ (Bourque et al. 1986). Thus, the properties of NSDPs in several respects resemble those of sodium/potassium-dependent oscillation waves and calcium-dependent oscillation waves, respectively.

Possible functional significance of subthreshold oscillation

The interaction between I_Na,P, a slowly activating and non-inactivating potassium current (I_K,s) and a leak current was demonstrated in a model to be sufficient to produce membrane potential oscillation (Gutfreund et al. 1995). In this model, the variation of the relative magnitude of I_K,s compared to that of I_Na,P resulted in either tonic repetitive discharge (small I_K,s) of depolarized neurones or in generation of subthreshold oscillation (larger I_K,s). Furthermore, this modelling study demonstrated that I_Na,P and a slow I_M-like current despite their slow dynamics are capable of producing high-frequency oscillation of the membrane potential. As demonstrated in neocortical pyramidal neurones, the presence of the subthreshold sustained I_Na,Pper se results in an amplification of synaptic currents (Schwindt & Crill, 1995). A non-linear summation of oscillation waves and EPSPs was observed in neurones of the inferior olivary nucleus (Lampl & Yarom, 1993). In these cells, a super-linear summation of oscillation waves and EPSPs occurred during the rising phase of the waves, while a less than linear summation occurred during the falling phase of the waves, i.e. the efficacy of EPSPs was enhanced during the rising phase while it was attenuated during the falling phase. In addition, a significant change in the delay of the synaptic response was observed, resulting in the maximum amplitude of the response at the peak of oscillation waves, regardless of the exact time of stimulation. Thus, the function of subthreshold oscillation in the inferior olive was interpreted in terms of a synchronizing and timing device. In magnocellular neurones of the supraoptic nucleus the latter function may be less important compared to the olivary input of the cerebellum. However, in supraoptic neurones, subthreshold oscillation of the membrane potential may be important for inter-neuronal synchronization as was observed in a simultaneous recording of supraoptic neurones during the milk ejection reflex (Lincoln & Wakerley, 1974) and in paired recordings from supraoptic and paraventricular oxytocin cells (Belin & Moos, 1986; for review see Wakerley & Ingram, 1993). In the context of neuronal synchronization, the phase-dependent amplification of EPSPs may provide a mechanism to increase the susceptibility of magnocellular neurones to any type of specific afferent activity, e.g. from osmoreceptors during hyper-osmotic stimulation or from mechanoreceptors of the nipples during suckling of the offspring, resulting in an orchestrated discharge of a neuronal population.

Furthermore, as indicated by the correlation of the oscillation frequency and the discharge frequency in magnocellular neurones examined in the present study, the interplay between the subthreshold oscillatory activity and the ionic mechanisms involved in the generation and adaptation of action potentials seems to be essential for the determination of continuous discharge in these neurones. It may be speculated that, like cortical neurones (Gutfreund et al. 1995), magnocellular neurones of the supraoptic nucleus may have the tendency to generate voltage signals at a certain frequency and to preferentially respond to the same frequency of input activity, thus promoting the population discharge at that preferred frequency.