Abstract
Magnetoencephalographic (MEG) and electromyographic (EMG) signals were recorded from six subjects during isometric contraction of four different muscles.
Cortical sources were located from the MEG signal which was averaged timelocked to the onset of motor unit potentials. A spatial filtering algorithm was used to estimate the source activity. Sources were found in the primary motor cortex (M1) contralateral to the contracted muscle. Significant coherence between rectified EMG and M1 activity was seen in the 20 Hz frequency range in all subjects.
Interactions between the motor cortex and spinal motoneuron pool were investigated by separately studying the non-stationary phase and amplitude dynamics of M1 and EMG signals.
Delays between M1 and EMG signals, computed from their phase difference, were found to be in agreement with conduction times from the primary motor cortex to the respective muscle. The time-dependent cortico-muscular phase synchronization was found to be correlated with the time course of both M1 and EMG signals.
The findings demonstrate that the coupling between the primary motor cortex and motoneuron pool is at least partly due to phase synchronization of 20 Hz oscillations which varies over time. Furthermore, the consistent phase lag between M1 and EMG signals, compatible with conduction time between M1 and the respective muscle with the M1 activity preceding EMG activity, supports the conjecture that the motor cortex drives the motoneuron pool.
A number of recent studies have provided evidence for modulation of motor unit firing by central oscillatory activity. These modulations have been investigated directly in simultaneous electro- or magnetoencephalographic (EEG/MEG) and electromyographic (EMG) recordings. During isometric contractions, significant coherence, typically in the 15–33 Hz frequency range, has been observed between EEG/MEG signals from the primary motor cortex and the rectified EMG of various muscles (Conway et al. 1995; Salenius et al. 1996, 1997b; Halliday et al. 1998b; Kilner et al. 1999).
Experimentally, Baker et al. (1997) reported coherence at 20–30 Hz between local field potentials (LFPs) in the primary motor cortex and EMG recordings from the contralateral hand and forearm muscles in monkeys that was present only during the periods of steady hold. Indirect evidence for central modulation of motor unit firing was obtained from measurements of peripheral oscillations during voluntary finger muscle contraction (McAuley et al. 1997). The results reported in these studies are consistent with the hypothesis that oscillatory activity in the primary motor cortex drives the spinal motoneuron pool during isometric muscle contraction or during the hold phase of a tracking task by modulating the firing probability of a population of motor units (McAuley et al. 1997).
Linked to the still-debated functional significance of these cortico-muscular interactions is the controversy about the phase relationship between the interacting cortical and peripheral oscillations (Farmer, 1998; Hari & Salenius, 1999). Conway et al. (1995) reported zero delays whereas Salenius et al. (1997b) found non-zero delays between cortex and muscle.
The aim of this study was, first, to determine the phase difference between MEG and EMG and, second, to further characterize interactions between motor cortex and spinal motoneuron pool by separating phase and amplitude dynamics.
The techniques used to estimate the delay between MEG and EMG signals usually assume stationarity of the signals and typically comprise the cumulant density or a linear fit to the phase spectrum. ‘Stationarity’ here is taken to be weak stationarity as defined by Koopmans (1983), i.e. the expectation of the process is time independent and the autocovariance function of the process C(t1, t2) depends only on the time difference, t2–t1. Since MEG and EMG signals are non-stationary, we address the question of delay by employing a tool for the detection of phase synchronization in non-stationary, noisy data; this tool was recently introduced to MEG signal analysis (Tass et al. 1998). Using this approach, the delay between MEG and EMG signals is estimated from mutual phase relationships. The analysis is based on a separation of amplitude and phase information by means of the Hilbert transform (Panter, 1965) which works successfully even in the case of chaotic oscillators (Rosenblum et al. 1996; Rosenblum & Kurths, 1998). In contrast to the classical coherence, which depends both on the phase and the amplitude dynamics of the two signals, this approach allows us to study phase and amplitude dynamics separately.
METHODS
Six healthy right-handed subjects (3 females, 3 males; 22–34 years old) participated in the study and gave their informed consent before the experiments. The study was performed according to the Declaration of Helsinki and approved by the local ethics committee (Heinrich-Heine University, Düsseldorf). The data derive in part from the study of Salenius et al. (1997b). The subjects were asked to perform isometric contraction of four different muscles in separate runs: abduction of the index finger (∼20 deg), extension of fingers II–IV (∼30 deg), elevation of the foot (∼30 deg) and flexion of the big toe (∼30 deg). Each run lasted 4–5 min. Before each run the contraction force was optimized for all muscles to reveal distinct motor unit potentials in the surface electromyogram. The estimated strength was very weak (∼10% of maximum voluntary contraction, MVC) for the interosseus muscle and slightly higher (∼20% MVC) for the foot, tibialis anterior and index finger extensor muscles. No quantitative force measurements were made.
Recording procedure
Cortical signals were recorded with a whole scalp neuromagnetometer in a magnetically shielded room simultaneously with surface EMG from the contracting muscle. The subject's head was supported against the helmet-shaped lower surface of the Neuromag-122 magnetometer (Ahonen et al. 1993). MEG and EMG signals were recorded with passbands of 0.03–330 Hz and 3–300 Hz, respectively, and stored on magneto-optical disks for off-line analysis. The exact position of the head with respect to the sensor array was determined by measuring magnetic signals from three indicator coils placed on the scalp. The position of the indicator coils relative to anatomical landmarks was determined beforehand.
Analysis
The coherence between the rectified EMG and all MEG channels was calculated with a frequency resolution of about 1 Hz by averaging the Fourier transforms across the whole contraction period (Halliday et al. 1995). A Hanning window was used and windows were overlapped by half the window length. The frequency range of coherence above the 99% confidence level was identified. The 99% confidence level was determined by calculating both the coherence with the EMG signal shifted by the width of the fast Fourier-transform (FFT) window (mean, 0.018; standard deviation (s.d.), 0.0037) and according to Halliday et al. (1995) (mean, 0.012; s.d., 0.0015). The first method resulted in higher confidence limits in all cases and was used for further analysis.
In addition to classical coherence, the synchronization index (ρ) was computed according to the procedure described in Tass et al. (1998). ρ quantifies the phase synchronization between two oscillatory signals, where phase synchronization means that two oscillators are able to maintain a preferred phase difference irrespective of perturbing influences like noise. The extent of phase synchronization is quantified by characterizing the distribution of the phase difference. With this aim in view the separation of phase and amplitude of the signal s(t) was achieved by employing the analytical signal concept , where a(t) denotes the analytical signal and the Hilbert transform of s(t) which results in an unambiguous definition of the instantaneous phase Φ(t) and amplitude A(t) (Gabor, 1946; see also Rosenblum & Kurths, 1998). The Hilbert transform was computed with a 256-point linear-phase finite-duration impulse response (FIR) filter which was designed using the Parks-McClellan algorithm (Mathworks, 1998). Computation of the Hilbert transform using the FFT instead of the FIR filter did not change the results significantly. The Hilbert transform was applied to the MEG signals and to the rectified EMG signal. Since Φ(t) and A(t) are only meaningful for a narrowband signal s(t), MEG and EMG signals were bandpass filtered in the frequency range of significant coherence before applying the Hilbert transform. For the phase detection of a signal generated by a number of oscillatory subsystems like an EMG or MEG signal a narrowband signal corresponding to the dominant frequency peak is typically not a sufficient approximation of the signal provided the frequency components vary rapidly in time. In this case one has to take into account higher harmonics too (Tass, 1999). However, as will be shown in the Results section (Fig. 1), a narrowband signal is a sufficient approximation for the signals analysed here.
Figure 1. An arbitrary 1 s segment of rectified EMG recorded from the left tibialis anterior muscle before (A) and after (B) filtering with a bandpass of 17–23 Hz.
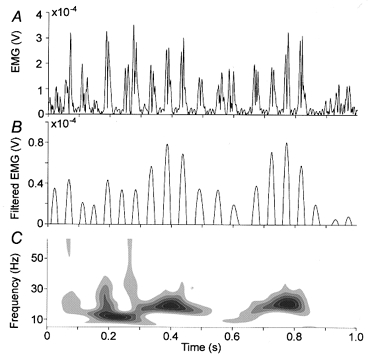
For the sake of clarity just the positive part of the filtered signal is shown in B. C, scalogram of the signal shown in A. This time–frequency representation is based on Morlet wavelets and displays the distribution of power in the time–frequency plane (Auger et al. 1999).
The Hilbert transform provides an instantaneous phase that allows a preferred phase in the histogram of the phase differences (modulo 2π) between EMG and MEG signals to be identified. The histograms were computed for 5 s long, non-overlapping windows with number of bins N = exp(0.626 + 0.4ln(M–1)) (Otnes & Enochson,1972), where M is the number of samples. This results in a bin-width of ∼0.1 rad. Depending on the total recording time, 60–80 histograms were obtained. Results were robust against changes of window length and bandwidth of the filter. If the phases evolve independently from each other, the histogram converges to a uniform distribution with increasing number of phase differences. In the case of phase locking, a peak is apparent in the histogram, indicating a preferred phase difference. This peak is identified after smoothing the histogram with a median filter of the order 9. The corresponding phase can be translated to a delay between the EMG and MEG signals (with an ambiguity of 2π due to the modulus operation). The deviation of the distribution of the phase difference of the actual data from a uniform distribution is quantified by an entropy measure and yields ρ. Surrogate data were used to establish the significance level (Tass et al. 1998). Delays were computed for the 50% of windows with the highest synchronization index. In addition, the 20% highest local maxima of the M1 amplitude in the 20 Hz frequency band were identified and M1–EMG phase differences were computed for the 30 samples closest to each maximum. Since the synchronization index was found to correlate with the M1 amplitude, this delay estimate is based on phase differences at times of strongest cortico-muscular synchronization.
The MEG–EMG delay was computed from the MEG signals displaying the highest synchronization index as well as from the underlying source activity in the motor cortex. The locations and orientations of the source currents were estimated by fitting a single dipole to phase-triggered averages of the MEG signal, i.e. the MEG signal averaged timelocked to the onset of motor unit potentials in the EMG. The onsets and thus the trigger points were identified in the instantaneous EMG phase Φ as local maxima of the function −sinΦ which was checked by visual inspection. The average number of trigger points was 6115 (s.d., 1325). A dipole was also fitted to the real part of the EMG-MEG cross-spectral density in the frequency band of maximum coherence. The dipole positions obtained from both methods differed by only a few millimetres (consistent with the uncertainty expected from the signal-to-noise ratio of the data) and no systematic differences were observed.
The MEG signal is invariant against a simultaneous change of the sign of the dipole orientation and the dipole time course which would nevertheless lead to a π-phase shift between dipole time course and EMG signal. The sign of the dipole orientation was chosen due to the following argument. Simultaneous recordings of local field potentials (LFPs) and single or multiple unit discharges in monkeys have revealed a tendency of the unit firing to occur at the negative LFP peak in the depth of the cortex (Murthy & Fetz, 1996; Baker et al. 1997, 1999; Donoghue et al. 1998). The pattern of surface-positivity and depth-negativity corresponds to an intracellular current flow from the depth to the surface of M1. The MEG signal is mainly sensitive to postsynaptic currents and to a negligible extent to cortical action potential-related currents (Hämäläinen et al. 1993). Thus the MEG signal is a representation of synchronized (also subthreshold) membrane potential fluctuations of a large number of neurons and resembles the spatially integrated LFPs. Consequently the M1 activation was estimated for backward pointing dipoles (see also Brown et al. 1998; Hari & Salenius, 1999).
A spatial filtering method was used to estimate the time course of the source (Robinson & Vrba, 1997; Gross & Ioannides, 1999). This method is based on a linear transformation of the data. The transformation vector A is designed by constrained optimization in order to pass signals from the desired source with unit gain while suppressing contributions from all other sources. Specifically A is computed as:
where R is the moment matrix of the zero-mean data matrix M (R=E(MMT) where E(x) denotes the statistical expectation of x and xT denotes the transpose of x), α is a regularization parameter, I is the unit matrix and L(r0, q0) is the solution of the forward problem of the dipole with position r0 and orientation q0. The estimate of the source activation is finally computed as the linear combination of the sensor signals weighted by the coefficients A. The coherence between rectified EMG and the estimated M1 activation increased on average by 34% compared with coherence between rectified EMG and the signal of the sensor above the contralateral primary motor cortex.
RESULTS
Figure 1 illustrates that the unfiltered rectified EMG signal (A) is sufficiently represented by the EMG signal filtered around 20 Hz (B). Peaks in the filtered EMG signal generally coincide with the centre of mass of the EMG bursts. Figure 1 also demonstrates the necessity to employ techniques which are not based on the assumption of stationarity. The scalogram (C, the distribution of power in the time- frequency plane, Auger et al. 1999) of an arbitrary 1 s EMG trace shows clear variations of power. Nevertheless both MEG and EMG signals showed distinct frequency bands typically centred on 10 Hz and 20 Hz containing most of the power. Since cortex-muscle coherence is almost exclusively restricted to the 20 Hz band, we focus our analysis on this part of the signal.
The coherence and ρ between the estimated source and the rectified EMG exceeded the 99% confidence level in all data sets. The distribution across channels was similar for coherence and ρ (Fig. 2A and B). In contrast to classical coherence, ρ is a function of time and thus allows observation of variations in the phase synchronization between both non-stationary signals.
Figure 2. Coherence and synchronization index ρ between EMG and MEG signals.
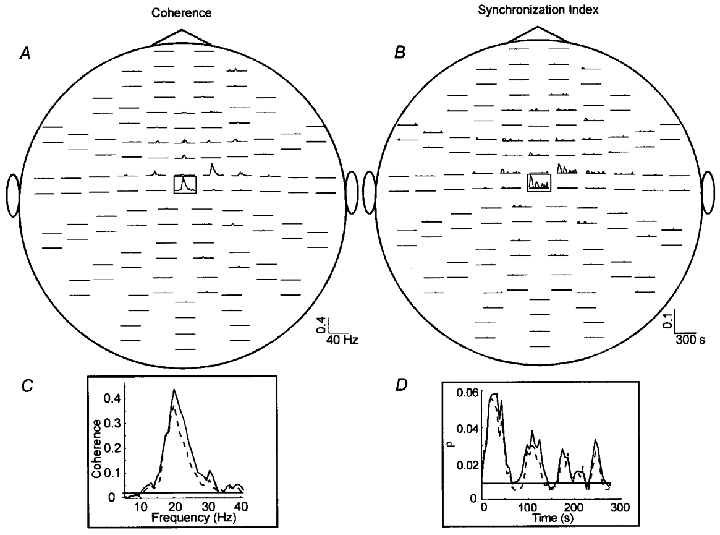
Coherence as function of frequency (A) and ρ as function of time (B) between rectified EMG recorded from the left tibialis anterior muscle and all MEG signals. Only values exceeding the 99% confidence level are shown. The sensor array is viewed from above. Traces are plotted in pairs corresponding to the two orthogonal planar gradiometers at each sensor location. C, coherence as function of frequency between EMG and M1 (continuous line) and between EMG and the MEG signal with the highest coherence (dashed line). D, ρ as function of time between EMG and M1 (continuous line) and between EMG and the MEG signal with the highest coherence (dashed line). The horizontal lines in Cand Dmark the 99% confidence level.
Figure 2C and D shows the increase of coherence and ρ between EMG and the source in the primary motor cortex (continuous lines) compared with the sensor signal (dashed lines). Variations over time are clearly evident for ρ indicating a variable degree of phase locking between M1 and the muscle.
Table 1 summarizes the delays between M1 maxima and the onset of motor unit potentials for M. extensor indicis, M. interosseus dorsalis I, M. tibialis anterior and M. flexor hallucis brevis. Delays were computed with different methods. Values in the first row of Table 1 correspond to estimates obtained from the phase spectrum calculated according to Halliday et al. (1995). The values in the second row were obtained from the phase-triggered average of the M1 activation. The point of zero phase in the 20 Hz band (as calculated by the Hilbert transform) preceding the EMG peak was taken as the onset of the motor unit potential. The third row contains values computed from phase differences in 5 s windows and the fourth row shows estimates from phase differences at times of strongest synchronization. The rows are ordered according to their expected sensitivity to periods of weak synchronization (with the fourth row being least sensitive to these periods). The phase spectrum is computed over the whole data set as is the phase-triggered average. The third estimate is obtained on a selection of 5 s windows with the highest synchronization index. The fourth estimate specifically relies on phase differences at times of M1 amplitude maxima (with associated high synchronization) and agrees best with conduction times.
Table 1.
Comparison of delays
| M. extensor indicis | M. interosseus dorsalis I | M. tibialis anterior | M. flexor hallucis brevis | |
|---|---|---|---|---|
| Phase spectra | 21.0 ± 1.9 | 42.1 ± 3.7 | 41.0 ± 6.9 | 63.6 ± 6.7 |
| Phasetriggered averages | 16.0 ± 2.6 | 23.0 ± 0.8 | 29.0 ± 1.9 | 47.0 ± 4.0 |
| Phase differences | 16.0 ± 2.7 | 26.8 ± 5.1 | 32.0 ± 2.9 | 49.5 ± 5.0 |
| Phase differences at strongest synchronization | 15.7 ± 1.6 | 23.6 ± 1.6 | 26.7 ± 2.3 | 41.7 ± 6.6 |
| Corticomuscular conduction times | 15.2 ± 0.9† | 23.0 ± 0.6* | 27.4 ± 1.2* | 41.2 ± 3.4* |
Comparison between delays (given as means ±s.d. in ms) obtained from phase spectra, phasetriggered averages, phase differences and phase differences at times of strongest synchronization and corticomuscular conduction times. Conduction times are taken from magnetic stimulation studies with tonic preinnervation of target muscle
Figure 3A shows the unfiltered averaged MEG signal timelocked to the motor units of the right extensor indicis muscle (phase-triggered average). Clearly damped oscillations are evident in the channels above the hand area of the left hemisphere. The spatial distribution of the magnetic field at the time of the first negative peak preceding the EMG onset (−15 ms) shows a dipolar field pattern (Fig. 3B) that can be modelled by a single dipole in the hand area of the left primary motor cortex (Fig. 3C).
Figure 3. Averaged MEG signals timelocked to the onsets of the motor unit potentials of the right extensor indicis muscle.
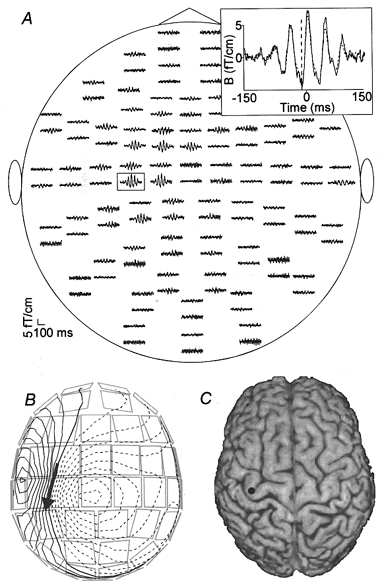
A, unfiltered averaged MEG signals timelocked to onsets of the motor unit potentials (phase-triggered average). The channels are arranged in the same way as in Fig. 2 (viewed from the top). The dashed vertical line at −15 ms in the inset marks the minimum in the signal and the dashed trace shows the part of the signal that is accounted for by the dipole. B, the isocontour map of the estimated magnetic field component normal to the sensor surface at −15 ms. The contour lines are separated by 0.2 fT. The arrow represents the dipole that explains the magnetic field best in the least-squares sense. C, the dipole superimposed on the subject's brain.
Amplitude dynamics
ρ was computed in a 20 s window that was moved in 5 s steps. To study the amplitude dynamics and its possible interactions with the phase dynamics we used the same windows to compute the mean amplitudes for the EMG signal and the M1 activation. Figure 4A shows recordings from the tibialis anterior muscle. The patterns were similar in the amplitude and the ρ modulations. The correlation is 0.79 between EMG and M1 amplitude, 0.77 between MEG amplitude and ρ and 0.86 between EMG amplitude and ρ.
Figure 4.
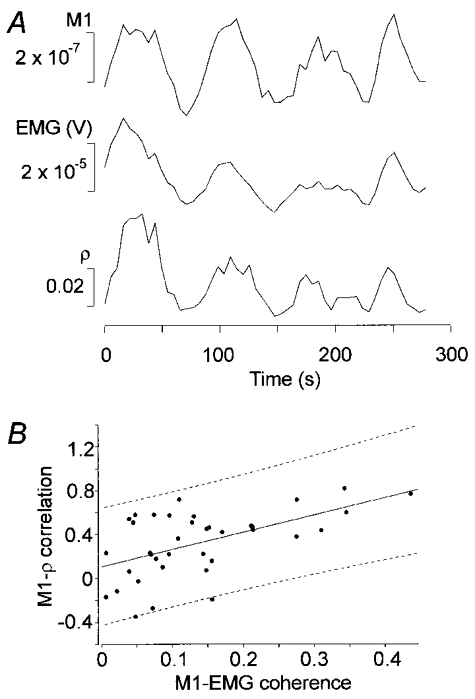
A, amplitudes of M1 activation and rectified EMG, and the synchronization index ρ as a function of time. All traces show mean values in a 20 s window moving across the signal in 5 s steps. B shows the dependence of the M1–ρ correlation on the M1–EMG coherence, together with the linear fit with the 95% confidence region (r2 = 0.30 and P < 0.0005).
These correlations were computed for all data sets. The different correlations were not independent from each other.
Figure 4B shows the dependence between M1–EMG coherence and M1–ρ correlation together with a linear fit and the corresponding 95% confidence region.
DISCUSSION
By separating phase and amplitude information we have shown that in addition to coherence, significant phase locking is present between oscillatory ∼20 Hz activity of the rectified EMG signal and the activity of the contralateral primary motor cortex (M1) during voluntary isometric contraction. The delay between the EMG and motor cortex signals, computed from the phase difference and phase-triggered averages of the MEG signal, is consistent with the conduction time from M1 to the corresponding hand or leg muscle. In addition, slow amplitude variations of the 20 Hz motor cortex activity were correlated with amplitude variations in the EMG.
The results of previous studies reporting on delays between motor cortex and coherent EMG oscillations are controversial. Conway et al. (1995), who were the first to report on the coupling between human motor cortex and spinal motoneuronal pool, found a zero-phase lag using the cumulant density.
However, Salenius et al. (1997b) found non-zero delays by averaging MEG signals timelocked to the onset of motor unit potentials. The differences between the delays to foot and hand muscles were consistent with differences of conduction times. However, the absolute delays between motor cortex and EMG signal could not readily be reconciled with the respective conduction times. Non-zero delays were also found by using cross-correlograms (Brown et al. 1998).
Using similar methods Halliday et al. (1998a) were unable to derive a consistent delay at all. They observed a constant phase spectrum in the frequency region of significant coherence which leads to a physiologically meaningless frequency-dependent delay between motor cortex and EMG signal. A potentially meaningful delay requires a linear frequency dependence (of non-zero slope) of the phase. Although such a relation has been demonstrated in some subjects with strong coherence (Salenius et al. 1997b; Brown et al. 1998, 1999; Marsden et al. 1999; Mima & Hallet, 1999), the assumption of a broad region with a linear dependence of phase difference on frequency is not always valid. Furthermore, the results are sensitive to the width of the frequency region chosen for the linear fit and the degree of linearity in that region.
In addition, coherence and delay estimates depend on how well the oscillatory outflow from M1 is represented by the time series used in the computation. For example, in EEG recordings it has been shown that coherence and phase spectra crucially depend on commonly applied signal transformations such as spatial derivatives (Mima & Hallet, 1999). Thus it is critical to obtain the best possible representation of the M1 activity to study its interdependence with the EMG signal. EEG derivations have a rather broad sensitivity profile leading to a possibly poor representation of the underlying activity. Together with the problematic choice of the reference electrode position this could lead to less reliable delay estimates.
Our finding of temporal variations in the synchronization of EMG and M1 activity may also help to explain the conflicting reports on delays between motor cortex and EMG. Since the final phase spectrum consists of the averaged cross-spectrum of the full data set it is also affected by the periods of weak synchronization. In our approach, phase differences are computed from epochs of strongest synchronization which probably improves the delay estimation. This effect can be clearly seen in Table 1 where rows are ordered according to their expected sensitivity to segments of weak synchronization. The temporal variability of coherence and phase spectra is also noted and discussed in McAuley et al. (1999).
In addition to possible differences in the execution of the experimental task, these points are likely to account for the inconsistent results on delays between motor cortex and EMG in different studies.
We addressed the above-mentioned problems in the analysis of both EEG and MEG signals in relation to EMG activity by optimizing the M1 activity estimate, by calculating the delays with methods that are not based on the FFT and by analysing segments of strong synchronization for the delay estimation. First, we recorded MEG with planar gradiometers (as did Salenius et al. 1997b and Brown et al. 1998) which have a more focused sensitivity than EEG electrodes or a magnetometer. Second, the representation of the M1 activity was improved by applying a spatial filter resulting in a further attenuation of unrelated interferences. The subsequent analysis was carried out on the source activation, thus avoiding problems originating from the complex sensitivity profile of the sensors. Third, and most important, we used instantaneous phases from the Hilbert transform to calculate delays between EMG and MEG signals in two different ways, which are more appropriate than FFT-based techniques since they do not require stationarity of the signals: delays were determined from the phase differences between EMG and MEG signals and from the latency of M1 activity peak to EMG onset calculated from signals averaged with respect to zero phase of the EMG (phase-triggered average).
The resulting delays are in good agreement with absolute cortico-muscular conduction times (Rothwell et al. 1991; Kloten et al. 1992). Delays computed in patients with cortical myoclonus support these results (Brown et al. 1999).
By using the instantaneous phase we also demonstrated variations in the synchronization index ρ that correlate with the M1 amplitude and the EMG amplitude in the 20 Hz frequency range. Since the M1–EMG coupling is known to be due to a modulation of the motor unit firing rate our observations are consistent with the view that the modulation strength correlates with the amplitude of the rhythmic motor commands. Variations in the modulation strength are reflected in the time course of ρ. A contribution of the signal-to-noise ratio (SNR) of the two time series on ρ can also not be excluded. If we assume that the M1 activation estimate consists of the MEG correlate of the descending oscillatory motor commands plus interfering noise, then an increase of the M1 power results in a higher coherence and synchronization index due to the increased SNR. A dependence of MEG–EMG coherence on MEG power in the 20 Hz range was also reported by Salenius et al. (1997a) (see also Hari & Salenius, 1999).
Although the functional role of the coherent cortico-motoneuronal interaction is still unclear, our results support the view of a rhythmic drive from motor cortex to motoneuron pool (Salenius et al. 1997b; Hari & Salenius, 1999). Conway et al. (1995) suggested that cortico-muscular coherence is a manifestation of motor binding due to a zero-phase loop incorporating descending motor activity and peripheral feedback. In contrast, our results, specifically the time delay and the M1–EMG amplitude correlation, suggest a cortical drive mechanism which may be relatively independent of peripheral feedback. This is in line with findings of McAuley et al. (1997) who suggested a central origin of peripheral 20 Hz oscillations which were shown to be at least partly independent of peripheral feedback. Further support comes from Marsden et al. (1999) who found coherence between electrocorticographic signals and contralateral EMG during tonic contraction in a subject with hemianaesthesia and from Farmer et al. (1993) who reported a 16–32 Hz motor unit synchronization in a deafferented patient.
These arguments seem to be compatible with a different type of motor binding where cortical oscillations reflect the selection and coordination of specific neuronal populations within the motor system. It is known that the multitude of possible movements is realized through a flexible and dynamic grouping of spinal motoneurons which requires a likewise dynamic representation in the cortical motor system. Since the observed coherence reflects the cortical drive to the muscle we can identify this representation with the generator of the coherent 20 Hz oscillations which is localized in the primary motor cortex representation of the muscle. Different co-activated muscles show a coherent EMG at the same frequency of about 20 Hz suggesting a common oscillatory drive from their motor cortex representations. This has been shown in normal subjects (Farmer et al. 1993; Gibbs et al. 1995; Conway et al. 1998) and in patients with cortical myoclonus (Brown et al. 1999). The representations of the different co-activated muscles which have shown to be organized in a mosaic like, distributed fashion within the primary motor cortex (Sanes et al. 1995) may be connected or bound together by common 20 Hz oscillations.
One might speculate that the 20 Hz motor cortex oscillations arise under stationary conditions. For example, during isometric contraction no dynamics of motor control need to be encoded. Thus, such a task can be achieved by the motor cortex continously sending the same motor commands at regular time intervals to the muscle leading to an oscillatory signal. Similarly, approaching the problem from an information-theory point of view, Baker et al. (1999) suggested that whenever the required information to be transferred is low enough, oscillatory motor commands are sent yielding an efficient recruitment of motoneurons (see also Hari & Salenius, 1999).
Another interesting issue which needs further investigation is the functional significance of other frequency components. Although strong 10 Hz components are evident in the power spectra of EMG and M1, the coherence is restricted to the 20 Hz range. This supports the findings of different functional roles of the 10 and 20 Hz components (Salmelin & Hari, 1994). Nevertheless the absence of coherent 10 Hz oscillations does not imply the absence of any influence of cortical 10 or 20 Hz oscillations on peripheral 10 Hz oscillations. Although the preferred firing rate of most motor units during weak isometric contraction is at about 10 Hz (Freund et al. 1975), an at least partly central origin of 10 Hz EMG oscillations during finger muscle contraction has been reported (McAuley et al. 1997) as well as possibly centrally induced movement discontinuities at about 10 Hz during slow finger movements (Vallbo & Wessberg, 1993). More sophisticated algorithms may be needed to describe the interdependencies of these oscillations.
In summary, we have further characterized the interaction between oscillatory 20 Hz activity of M1 and contralateral limb muscles using instantaneous phase and amplitude. Our analysis revealed a consistent phase difference between M1 and EMG signal, agreeing well with known conduction times. In addition, we found temporal variations in the synchronization index that correlated both with the 20 Hz power in M1 and the 20 Hz power of the EMG signal. These results suggest a hierarchical organization of the 20 Hz interaction, with the motor cortex leading or driving the spinal motoneuron pool.
Acknowledgments
This work was supported by the Volkswagen-Stiftung, the Deutsche Forschungsgemeinschaft and the Academy of Finland.
References
- Ahonen AI, Hämäläinen MS, Kajola MJ, Knuutila JET, Laine PP, Lounasmaa OV, Parkkonen LT, Simola JT, Tesche CD. 122-channel SQUID instrument for investigating the magnetic signals from the human brain. Physica Scripta. 1993;49:198–205. [Google Scholar]
- Auger F, Flandrin P, Goncalves P, Lemoine O. Time Frequency Toolbox. France: CNRS, Rice University, USA; 1999. [Google Scholar]
- Baker SN, Kilner JM, Pinches EM, Lemon RN. The role of synchrony and oscillations in the motor output. Experimental Brain Research. 1999;128:109–117. doi: 10.1007/s002210050825. [DOI] [PubMed] [Google Scholar]
- Baker SN, Olivier E, Lemon RN. Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. The Journal of Physiology. 1997;501:225–241. doi: 10.1111/j.1469-7793.1997.225bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown P, Farmer SF, Halliday DM, Marsden J, Rosenberg JR. Coherent cortical and muscle discharge in cortical myoclonus. Brain. 1999;122:461–472. doi: 10.1093/brain/122.3.461. [DOI] [PubMed] [Google Scholar]
- Brown P, Salenius S, Rothwell JC, Hari R. Cortical correlate of the piper rhythm in humans. Journal of Neurophysiology. 1998;80:2911–2917. doi: 10.1152/jn.1998.80.6.2911. [DOI] [PubMed] [Google Scholar]
- Conway BA, Halliday DM, Bray K, Cameron M, McLelland D, Mulcahy E, Farmer SF, Rosenberg JR. Inter-muscle coherence during co-contraction of finger and wrist muscles in man. The Journal of Physiology. 1998;509.P:175–176P. [Google Scholar]
- Conway BA, Halliday DM, Farmer SF, Shahani U, Maas P, Weir AI, Rosenberg JR. Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. The Journal of Physiology. 1995;489:917–924. doi: 10.1113/jphysiol.1995.sp021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donoghue JP, Sanes JN, Hatsopoulos NG, Gaal G. Neural discharge and local field potential oscillations in primate motor cortex during voluntary movements. Journal of Neurophysiology. 1998;79:159–173. doi: 10.1152/jn.1998.79.1.159. [DOI] [PubMed] [Google Scholar]
- Farmer SF. Rhythmicity, synchronization and binding in human and primate motor systems. The Journal of Physiology. 1998;509:3–14. doi: 10.1111/j.1469-7793.1998.003bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farmer SF, Bremner FD, Halliday DM, Rosenberg JR, Stephens JA. The frequency content of common synaptic inputs to motoneurones studied during voluntary isometric contraction in man. The Journal of Physiology. 1993;470:127–155. doi: 10.1113/jphysiol.1993.sp019851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freund H-J, Budingen HJ, Dietz V. Activity of single motor units from human forearm muscles during voluntary isometric contractions. Journal of Neurophysiology. 1975;38:933–946. doi: 10.1152/jn.1975.38.4.933. [DOI] [PubMed] [Google Scholar]
- Gabor D. Theory of communication. Proceedings of the IEE. 1946;93:429–457. [Google Scholar]
- Gibbs J, Harrison LM, Stephens JA. Organization of inputs to motoneurone pools in man. The Journal of Physiology. 1995;485:245–256. doi: 10.1113/jphysiol.1995.sp020727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross J, Ioannides AA. Linear transformations of data space in MEG. Physics in Medicine and Biology. 1999;44:2081–2097. doi: 10.1088/0031-9155/44/8/317. [DOI] [PubMed] [Google Scholar]
- Halliday DM, Conway BA, Farmer SF, Rosenberg JR. Using electroencephalography to study functional coupling between cortical activity and electromyograms during voluntary contractions in humans. Neuroscience Letters. 1998a;241:5–8. doi: 10.1016/s0304-3940(97)00964-6. [DOI] [PubMed] [Google Scholar]
- Halliday DM, Conway BA, Farmer SF, Rosenberg JR, McLelland D, Vourekas G. Correlation between EEG and motor output during voluntary contractions in man. The Journal of Physiology. 1998b;506.P:82P. [Google Scholar]
- Halliday DM, Rosenberg JR, Amjad AM, Breeze P, Conway BA, Farmer SF. A framework for the analysis of mixed time series/point process data – theory and application to the study of physiological tremor, single motor unit discharges and electromyograms. Progress in Biophysics and Molecular Biology. 1995;64:237–278. doi: 10.1016/s0079-6107(96)00009-0. [DOI] [PubMed] [Google Scholar]
- Hämäläinen M, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography – theory, instrumentation, and application to noninvasive studies of the working human brain. Reviews of Modern Physics. 1993;65:413–497. [Google Scholar]
- Hari R, Salenius S. Rhythmical corticomotor communication. NeuroReport. 1999;10:R1–10. [PubMed] [Google Scholar]
- Kilner JM, Baker SN, Salenius S, Jousmaki V, Hari R, Lemon RN. Task-dependent modulation of 15–30 Hz coherence between rectified EMGs from human hand and forearm muscles. The Journal of Physiology. 1999;516:559–570. doi: 10.1111/j.1469-7793.1999.0559v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kloten H, Meyer BU, Britton TC, Benecke R. Normal values and age-related changes in magneto-electric evoked compound muscle potentials. EEG-EMG Zeitschrift für Elektroenzephalographie, Elektromyographie und verwandte gebiete. 1992;23:29–36. [PubMed] [Google Scholar]
- Koopmans LH. Handbook of Statistics. Vol. 3. Amsterdam: Elsevier Science Publishers; 1983. A spectral analysis primer; pp. 169–183. chap. 9. [Google Scholar]
- McAuley JH, Farmer SF, Rothwell JC, Marsden CD. Common 3 and 10 Hz oscillations modulate human eye and finger movements while they simultaneously track a visual target. The Journal of Physiology. 1999;515:905–917. doi: 10.1111/j.1469-7793.1999.905ab.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAuley JH, Rothwell JC, Marsden CD. Frequency peaks of tremor, muscle vibration and electromyographic activity at 10 Hz, 20 Hz and 40 Hz during human finger muscle contraction may reflect rhythmicities of central neural firing. Experimental Brain Research. 1997;114:525–541. doi: 10.1007/pl00005662. [DOI] [PubMed] [Google Scholar]
- Marsden JF, Ashby P, Rothwell JC, Brown P. Coherence between muscle and electrocorticographic signals during isometric contraction in man. The Journal of Physiology. 1999;518.P:73P. [Google Scholar]
- Mathworks . Signal Processing Toolbox. User's Guide. Natick, MA, USA: The Mathworks, Inc.; 1998. [Google Scholar]
- Mima T, Hallet M. Electroencephalographic analysis of cortico-muscular coherence: reference effect, volume conduction and generator mechanism. Clinical Neurophysiology. 1999;110:1892–1899. doi: 10.1016/s1388-2457(99)00238-2. [DOI] [PubMed] [Google Scholar]
- Murthy VN, Fetz EE. Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. Journal of Neurophysiology. 1996;76:3968–3982. doi: 10.1152/jn.1996.76.6.3968. [DOI] [PubMed] [Google Scholar]
- Otnes RK, Enochson L. Digital Time Series Analysis. New York: John Wiley & Sons; 1972. [Google Scholar]
- Panter P. Modulation, Noise, and Spectral Analysis. New York: McGraw-Hill; 1965. [Google Scholar]
- Robinson SE, Vrba J. Functional neuroimaging by synthetic aperture magnetometry (SAM) In: Yoshimoto T, Kotani M, Kuriki S, Karibe H, Nakasato B, editors. Recent Advances in Biomagnetism. Sendai: Tohoku University Press; 1997. pp. 302–305. [Google Scholar]
- Rosenblum MG, Kurths J. Analysing synchronization phenomena from bivariate data by means of the hilbert transform. In: Kantz H, Kurths J, Mayer-Kress G, editors. Nonlinear Analysis of Physiological Data. Berlin: Springer; 1998. pp. 91–99. [Google Scholar]
- Rosenblum MG, Pikovsky AS, Kurths J. Phase synchronization of chaotic oscillators. Physical Review Letters. 1996;76:1804–1807. doi: 10.1103/PhysRevLett.76.1804. [DOI] [PubMed] [Google Scholar]
- Rothwell JC, Thompson PD, Day BL, Boyd S, Marsden CD. Stimulation of the human motor cortex through the scalp. Experimental Physiology. 1991;76:159–200. doi: 10.1113/expphysiol.1991.sp003485. [DOI] [PubMed] [Google Scholar]
- Salenius S, Forss N, Hari R. Rhythmicity of descending motor commands covaries with the amount of motor cortex 20–30 Hz rhythms. Society for Neuroscience Abstracts. 1997a;23:1948. [Google Scholar]
- Salenius S, Portin K, Kajola M, Salmelin R, Hari R. Cortical control of human motoneuron firing during isometric contraction. Journal of Neurophysiology. 1997b;77:3401–3405. doi: 10.1152/jn.1997.77.6.3401. [DOI] [PubMed] [Google Scholar]
- Salenius S, Salmelin R, Neuper C, Pfurtscheller G, Hari R. Human cortical 40 Hz rhythm is closely related to EMG rhythmicity. Neuroscience Letters. 1996;213:75–78. doi: 10.1016/0304-3940(96)12796-8. [DOI] [PubMed] [Google Scholar]
- Salmelin R, Hari R. Spatiotemporal characteristics of sensorimotor neuromagnetic rhythms related to thumb movement. Neuroscience. 1994;60:537–550. doi: 10.1016/0306-4522(94)90263-1. [DOI] [PubMed] [Google Scholar]
- Sanes JN, Donoghue JP, Thangaraj V, Edelman RR, Warach S. Shared neural substrates controlling hand movements in human motor cortex. Science. 1995;268:1775–1777. doi: 10.1126/science.7792606. [DOI] [PubMed] [Google Scholar]
- Tass P, Rosenblum MG, Weule J, Kurths J, Pikovsky A, Volkmann J, Schnitzler A, Freund H-J. Detection of n:m phase locking from noisy data: Application to magnetoencephalography. Physical Review Letters. 1998;81:3291–3294. [Google Scholar]
- Tass PA. Phase Resetting in Medicine and Biology – Stochastic Modelling and Data Analysis. Berlin: Springer; 1999. [Google Scholar]
- Vallbo Å B, Wessberg J. Organization of motor output in slow finger movements in man. The Journal of Physiology. 1993;469:673–691. doi: 10.1113/jphysiol.1993.sp019837. [DOI] [PMC free article] [PubMed] [Google Scholar]


