Intersample fluctuations in phosphocreatine concentration determined by ³¹P-magnetic resonance spectroscopy and parameter estimation of metabolic responses to exercise in humans

Abstract

1. The ATP turnover rate during constant-load exercise is often estimated from the initial rate of change of phosphocreatine concentration ([PCr]) using ³¹P-magnetic resonance spectroscopy (MRS). However, the phase and amplitude characteristics of the sample-to-sample fluctuations can markedly influence this estimation (as well as that for the time constant (τ) of the [PCr] change) and confound its physiological interpretation especially for small amplitude responses.

2. This influence was investigated in six healthy males who performed repeated constant-load quadriceps exercise of a moderate intensity in a whole-body MRS system. A transmit- receive surface coil was placed under the right quadriceps, allowing determination of intramuscular [PCr]; pulmonary oxygen uptake (V̇_O2) was simultaneously determined, breath-by-breath, using a mass spectrometer and a turbine volume measuring module.

3. The probability density functions (PDF) of [PCr] and V̇_O2 fluctuations were determined for each test during the steady states of rest and exercise and the PDF was then fitted to a Gaussian function. The standard deviation of the [PCr] and V̇_O2 fluctuations at rest and during exercise (s_r and s_w, respectively) and the peak centres of the distributions (xc_r and xc_w) were determined, as were the skewness (γ₁) and kurtosis (γ₂) coefficients.

4. There was no difference between s_r and s_w for [PCr] relative to the resting control baseline (s_r= 1.554%Δ (s.d.= 0.44), s_w= 1.514%Δ (s.d.= 0.35)) or the PDF peak centres (xc_r=−0.013 %Δ (s.d.= 0.09), xc_w−0.197 %Δ (s.d.= 0.18)). The standard deviation and peak centre of the ‘noise’ in V̇_O2 also did not vary between rest and exercise (s_r= 0.0427 l min⁻¹ (s.d.= 0.0104), s_w= 0.0640 l min⁻¹ (s.d.= 0.0292); xc_r=−0.0051 l min⁻¹ (s.d.= 0.0069), xc_w 0.0022 l min⁻¹ (s.d.= 0.0034)).

5. Our results demonstrate that the intersample ‘noise’ associated with [PCr] determination by ³¹P-MRS may be characterised as a stochastic Gaussian process that is uncorrelated with work rate, as previously described for V̇_O2. This ‘noise’ can significantly affect the estimation of τ[PCr] and especially the initial rate of change of [PCr], i.e. the fluctuations can lead to variations in estimation of the initial rate of change of [PCr] of more than twofold, if the inherent ‘noise’ is not accounted for. This ‘error’ may be significantly reduced in such cases if the initial rate of change is estimated from the time constant and amplitude of the response.

The profile of the non-steady-state response of a physiological system to a particular dynamic forcing regime provides important information concerning the process (or processes) of the underlying system control. For example, it is possible to make inferences concerning the putative high-energy phosphate control of muscle oxygen consumption in humans by establishing the kinetic parameters of the intramuscular high-energy phosphate and pulmonary oxygen uptake (V̇_O2) responses to muscular exercise, either on different occasions (Barstow et al. 1994; McCreary et al. 1996) or simultaneously (Whipp et al. 1999; Rossiter et al. 1999). However, the appropriateness of inferences which can be drawn from such studies is dependent on the ability to discriminate sufficiently small differences between the kinetic parameters of these systems (Milsum, 1966; Lamarra et al. 1987).

Using ³¹P-MRS there is an appreciable sample-to-sample fluctuation evident in human muscle phosphocreatine concentration ([PCr]) at rest and during exercise (e.g. Meyer, 1988; Blei et al. 1993; McCreary et al. 1996; Conley et al. 1998; Rossiter et al. 1999) which by its nature can impair both the confidence of the parameter estimation and the limits of its physiological interpretation.

The steady-state oxygen cost of exercise is not appreciably different among humans differing in age, sex or physical fitness (Hagberg et al. 1980; Babcock et al. 1994). As the time course of V̇_O2 to a step increase in work rate has been shown to conform to an exponential response, after a short delay (reviewed in Whipp & Ozyener, 1998), the time constant (τ) (or the mean response time; MRT, τ′) may be considered its defining parameter characterising the system function. When establishing the parameters of the V̇_O2 and intramuscular [PCr] responses, the confidence limits of the estimation must be narrow enough to allow appropriate levels of physiological interpretation. The factors which influence the confidence of τV̇_O2 estimation have previously been determined in normal healthy adults (Lamarra et al. 1987; Myers et al. 1990) and children (Potter et al. 1999), i.e. the response amplitude, the standard deviation of the intersample fluctuations in the measurement, the sample density, and the underlying time constant itself.

In order to minimize some of these concerns, repeats of like experiments are commonly averaged for V̇_O2 parameter estimation (e.g. Whipp et al. 1982; Rossiter et al. 1999). This is based upon the demonstration that the intersample ‘noise’ for this variable is normally distributed about the mean value with uncorrelated Gaussian characteristics which are unchanged at different levels of V̇_O2. Thus, when comparing parameters from two separate responses (such as τ[PCr] and τV̇_O2; Barstow et al. 1994; McCreary et al. 1996; Rossiter et al. 1999), the confidence (K₁) with which these parameters can be estimated must be taken into account. However, the characterisation of the intersample variations in the ³¹P-MRS determination of intramuscular [PCr] has not, to our knowledge, previously been determined.

The characterisation of these fluctuations has important implications also for the estimation of the initial rate of change of [PCr] (d[PCr]/dt) which is commonly used to estimate the ATP turnover rate during constant-load exercise (Kemp et al. 1993, 1994; Conley et al. 1998). However, even small fluctuations in the sample-to-sample measurement of [PCr], especially for small amplitude responses, can lead to marked variations in the estimation of ATP turnover rate with consequences for computing transients in hydrogen ion production rate and glycolytic flux. It was, therefore, the purpose of this investigation to characterise the sample-to-sample fluctuation of [PCr] measurement by ³¹P-MRS and assess the influence of these fluctuations on parameter estimation.

METHODS

Six healthy male volunteers with a mean age of 28 years (range 20–59) provided informed consent (as approved by the Local Research Ethics Committee for Human Experimentation, St George’s Hospital Medical School) to participate in the study, and were cleared to exercise inside the bore of the MR scanner. Each subject initially performed a series of habituation tests in the Laboratory of Human Physiology. This included the determination of work rates that were moderate in intensity for each subject (i.e. not associated with a slow phase of V̇_O2 kinetics (Linnarsson, 1974; Whipp, 1987)). For the subsequent MR studies work rates were chosen that produced the largest possible moderate intensity increment in V̇_O2 with the work rate increments varying among the subjects between approximately 30 and 80 W.

The subjects lay prone inside the bore of the MR scanner with their feet suspended in rubber stirrups that formed an integral part of a custom-designed, plastic insert into the magnet bore (Whipp et al. 1999). Rhythmic knee extension exercise of constant amplitude (i.e. the extent of the magnet bore diameter, approx. 30 cm) and constant frequency (32 pulses leg⁻¹ min⁻¹) was performed against the rubber stirrups (Whipp et al. 1999). The subjects received an audible cue at 32 pulses min⁻¹, such that the contraction of the quadriceps of the non-dominant leg occurred in unison with the interrogation of the quadriceps of the dominant leg by magnetic resonance. ³¹P-MRS free induction decay (FID) values were obtained every 1875 ms throughout the entire square wave exercise test protocol. Data were averaged over eight acquisitions (a ³¹P spectrum every 15 s).

The subject was ‘strapped down’ to the MR scanner table by means of a non-distensible strap placed over the hips in order to minimise any extraneous movement. Each subject performed a repeated constant load ‘square wave’ exercise protocol of 4 min at rest, 6–15 min of constant-load moderate intensity exercise, and 6 min recovery at rest. Each subject had at least 6 min recovery before each subsequent test. Work rate approximations (∼W) were determined as the product of the amplitude of deflection of the exercising limbs, the frequency of deflection and the elastic coefficient of the rubber stirrups, which had been previously calculated over this length of deflection.

Determination of intramuscular high-energy phosphates by ³¹P-MRS

The experiments were performed using a one-pulse ³¹P-MRS acquisition from a 1.5 Tesla superconducting magnet (GE, Signa Advantage). A surface coil (20 cm transmit and 13 cm receive), tuned to a frequency of 25.85 MHz for phosphorus was placed under the quadriceps of the dominant leg (in all cases the right leg) midway between the knee and hip joint (as previously described in Rossiter et al. 1999). The coil was securely fastened to the table, and displacement of the leg over the coil was prevented by the broad non-elastic strap over the hips. This allowed knee extensor exercise to be performed with the region of interest (ROI) always stationary with the leg in the relaxed position.

Prior to the data acquisition, a series of axial gradient recall echo (GRE) images of the thigh were acquired in order to optimise the RF coil position. Shimming was performed on the ROI using an automated shimming package provided by the manufacturers. Shimming to the proton signal of muscle water allowed the homogeneity of the magnetic field to be optimised for the muscle ROI in its stationary position. The ³¹P radio frequency excitation pulse was set at a level to give maximum [PCr] signals at a 5 s repetition rate from an 80 mm thick axial slice of muscle. FIDs for ³¹P spectra were collected every 1875 ms with a spectral width of 2500 Hz and 512 data points. Data were averaged every eight acquisitions and the dynamic signals for the three ATP peaks (α, β and γ), PCr and P_i could be determined every 15 s throughout the rest-exercise-rest protocol. This maximised the signal-to-noise ratio of the spectra and the time resolution of the data set. Signal intensities of each resonance were calculated (as a batch job) by means of the time-domain VARPRO fitting program (Van der Veen et al. 1988), using the appropriate prior knowledge of the ATP multiplets (Stubbs et al. 1996).

The T₁ saturation factor was assumed to remain constant for each resonance throughout the experiment, and all phosphate metabolite levels are presented relative to their pre-exercise control values.

Simultaneous breath-by-breath gas exchange measurement

Pulmonary gas exchange was measured using a computer, and the algorithms of Beaver et al. (1973) (Clinical and Scientific Equipment (CaSE), Gillingham, Kent, UK; as previously described by Whipp et al. 1999). Expired volume was measured by a volume measuring module (VMM) with a custom designed non-magnetic turbine with stainless steel mountings and extended interface cable (Interface Associates, Laguna Niguel, CA, USA), and calibrated with a 3 l syringe over a range of flows which extended beyond the values achieved during exercise (Hans Rudolph, Kansas City, MO, USA). The concentrations of respired gas (O₂, CO₂ and N₂) were measured every 20 ms using a QP9000 quadrupole mass spectrometer (CaSE) calibrated against precision-analysed gas mixtures. Gas was drawn continuously from the mouthpiece along the extended 14 m sampling capillary line, which had a 5–95 % rise time of <80 ms and a delay of 2680 ms (Whipp et al. 1999).

Analysis of the [PCr] and fluctuations

Having established the area of the PCr peaks using the VARPRO fitting program, the data were converted to relative changes (%Δ) as determined by their percentage relationships, using the average during the 4 min of controlled rest to establish the 100 % level.

The probability density function (PDF) of [PCr] measurements was determined by calculating the mean [PCr] value for rest and the steady-state portion of the exercise bout (i.e. after at least 3 min of exercise, depending on the underlying kinetics of the response). This value was assumed to represent a constant intramuscular [PCr] value, about which the fluctuation of measurement was defined as the ‘noise’ function. Using commercially available software (Microcal Origin), a frequency analysis of the residual from this mean was made using bins of 0.5 %Δ fluctuation for [PCr]. A similar analysis was performed for V̇_O2 using bins of 20 ml min⁻¹. As suggested by Lamarra et al. (1987), occasional breath values were omitted from the analysis, using an exclusion criterion of greater than four standard deviations about the local mean. Exclusion of these aberrant values of V̇_O2 is justified by the fact that they typically arise due to swallowing or coughing or some other reason unrelated to the physiological response of interest. We did not, however, exclude the occasional ‘unusually’ large individual variations in [PCr] as there is no similar physiological reason for these values not to be associated with the actual fluctuation in measurement.

The PDFs for both V̇_O2 and [PCr] were compared to a Gaussian distribution and their skewness and kurtosis values were calculated. The ‘goodness of fit’ to a Gaussian distribution was also evaluated using the chi squared (χ²) test. The autocorrelation factor was also assessed using regression analysis to estimate the correlation of a single sample (n) with samples occurring at some time in the past and future, up to four (i.e. n+ 4) sample delays. This allows assessment ‘randomness’ of the time distribution of the samples within the PDF function.

Values are given as means ± standard deviation, or 95 % confidence intervals where indicated, and a P value of less than 0.05 was used to determine the rejection of the null hypothesis.

RESULTS

A typical response of intramuscular [PCr] and V̇_O2 to two single 6 min moderate ‘square wave’ forcings, each separated by 6 min rest, for a single subject is shown in Fig. 1. The intersample fluctuations for both V̇_O2 and [PCr] can clearly be seen both at rest and during exercise, with the residuals of the steady-state fits shown below as a fluctuation around zero (i.e. the steady-state mean). The time constants of these responses were approximately 30 s, and it was necessary to leave a minimum of approximately 4 times the τ before a steady state could be assumed; only data that were expected to be steady state were, therefore, included in the analysis process.

Figure 1. Intramuscular [PCr] and V̇_O2 dynamic responses to two square wave forcings of moderate intensity exercise in a representative subject (subject 1).

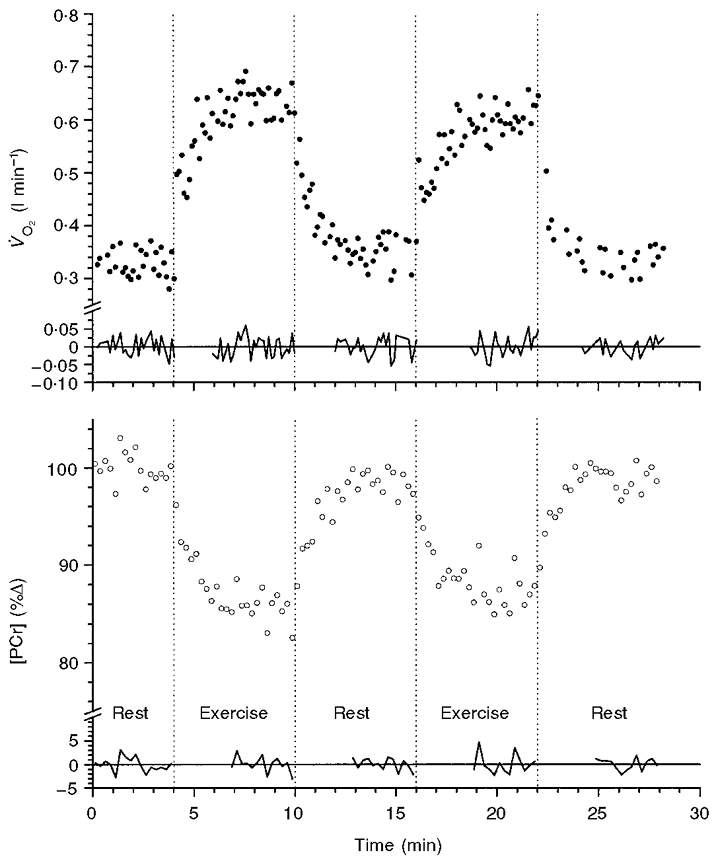
The response shows an ‘exponential-like’ fall of [PCr] and the associated ‘exponential-like’ rise in V̇_O2 to a new steady state from a resting value in two successive bouts of 6 min duration, separated by a 6 min rest period. The residuals to a linear fit of gradient zero are shown in the relevant regions. The vertical dotted lines indicate onset or cessation of exercise.

In the case of the [PCr] responses, occasional ‘errant’ values were apparently artifacts of the measurement design, reflecting factors such as mis-timing of the contraction with the audio cue of the measurement and the inherently poor signal-to-noise characteristics of MRS measurements. Such values were included in the description process, at this point, in order to fully describe the standard deviation of this ‘noise’ process. For V̇_O2 these measurement artifacts were removed (as described by Lamarra et al. 1987). These calculation errors were obvious, giving rise to, for example, negative V̇_O2 values or positive values an order of magnitude greater than the typical response.

The standard deviation of the [PCr] fluctuations at rest and moderate work (s_r and s_w, respectively) and the peak centres of the distributions (xc_r and xc_w) were determined for each subject (a typical example is shown in Fig. 2) and are given in Table 1. As there was no difference between s_r and s_w for [PCr] (s_r= 1.554%Δ (s.d.= 0.44), s_w= 1.514%Δ (s.d.= 0.35)), or between xc_r and xc_w (xc_r=−0.013 %Δ (s.d.= 0.09), xc_w−0.197 %Δ (s.d.= 0.18)) within the six subjects, the PDF data were summed within the rest or exercise condition, thereby increasing the number of samples (n) during rest and work to 800 and 445, respectively (Fig. 3). This yielded s_r and s_w values of 1.37 and 1.60 %Δ, and xc_r and xc_w of 0.002 and −0.124 %Δ, respectively. During exercise, there was a tendency for the peak to be smaller in relative frequency than at rest, suggestive of a small broadening of the standard deviation from rest to exercise (as demonstrated by the peak heights in Figs 2 and 3). However, this was not the case when each subject was considered individually (s_r= 1.554%Δ (s.d.= 0.44), vs.s_w= 1.514%Δ (s.d.= 0.346)) (Table 1). The skewness (γ₁) values changed from 0.97 to 0.68 between rest and exercise; both these values, however, are well within acceptable limits for absence of skewness (Wetherill, 1981). The small increase in s_w compared to s_r was reflected in the kurtosis (γ₂) coefficients of −0.36 at rest and −1.06 during exercise. Nevertheless, kurtosis is a symmetrical characteristic and thus would not affect appropriate averaging of repeat responses.

Figure 2. Examples of amplitude probability density functions for intersample fluctuations of [PCr] and V̇_O2 measurements during the steady state at rest (A) and moderate exercise (B) for subject 1.

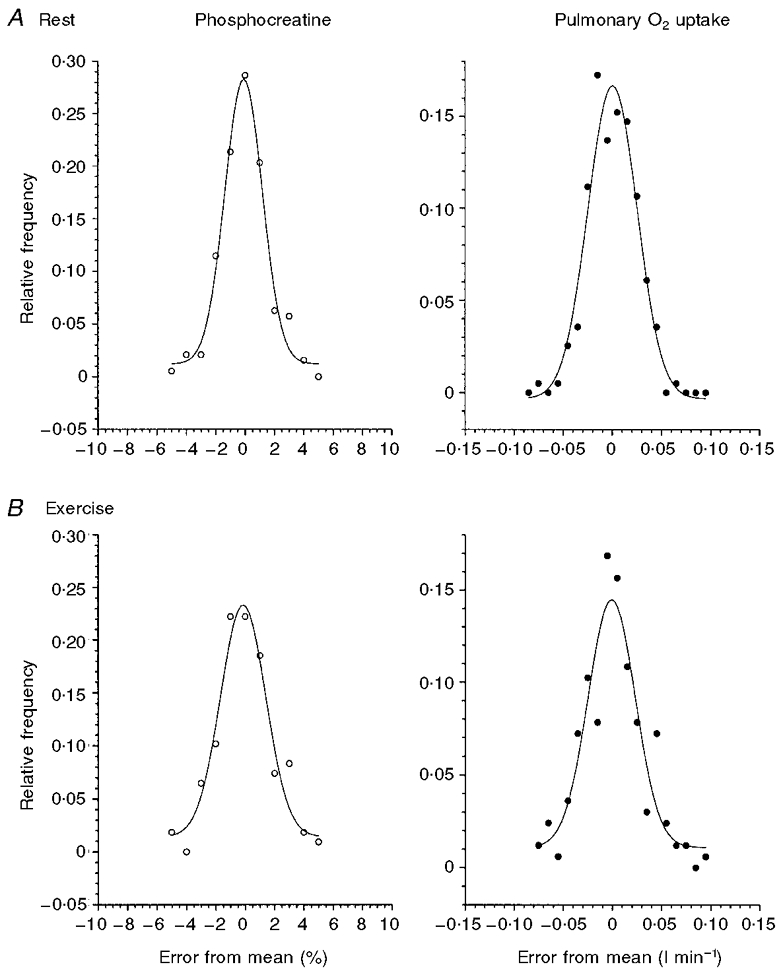
Relative frequency is calculated as the actual frequency relative to the total sample number (n) for that subject.

Table 1.

Parameters of a Gaussian model applied to the PDF of the fluctuations in [PCr] measurement

	Rest						Moderate exercise
Subject no.	n	xcr (%)	xcrC95 (%)	w (%)	wC95 (%)	sr	n	xcw (%)	xcwC95 (%)	w (%)	wC95 (%)	sw
1	192	−0.103	0.148	2.549	0.366	1.275*	108	−0.146	0.278	3.073	0.773	1.537*
2	82	−0.132	0.429	3.990	2.514	1.995*	47	−0.220	0.309	2.066	0.762	1.033*
3	192	0.094	0.103	2.485	0.253	1.243*	114	−0.093	0.159	4.113	0.645	2.057*
4	75	0.058	0.081	2.432	0.197	1.216*	35	−0.101	0.233	2.775	0.603	1.388*
5	210	−0.021	0.211	2.752	0.544	1.376	100	−0.066	0.167	2.737	0.430	1.369*
6	49	0.026	0.668	4.435	3.145	2.218*	41	−0.556	0.755	3.397	2.278	1.699*
Mean	133	−0.013	0.273	3.107	1.170	1.554*	74	−0.197	0.317	3.027	0.915	1.514*
s.d.	72	0.090	0.230	0.874	1.306	0.437	37	0.184	0.223	0.691	0.679	0.346
Group response: all data	800	0.002	0.130	2.745	0.335	1.37*	445	−0.124	0.181	3.209	0.522	1.60*

Model parameters of the probability density function for the ‘noise’ fluctuation in [PCr] measurement for each subject at rest and during the steady state of moderate exercise, and fitted with a Gaussian function. n, number of points; xc_r and xc_w, centre of peak at rest and work, respectively; w, 2 × variance (ω); C₉₅, 95% confidence interval of estimation; s_r and s_w, standard deviation from the Gaussian model during rest and work, respectively.

^*Not significantly different from a Gaussian distribution using χ² goodness-of-fit (P > 0.05).

Figure 3. The PDF for the distribution of intersample fluctuations of [PCr] in the steady state at rest (A), or during exercise (B).

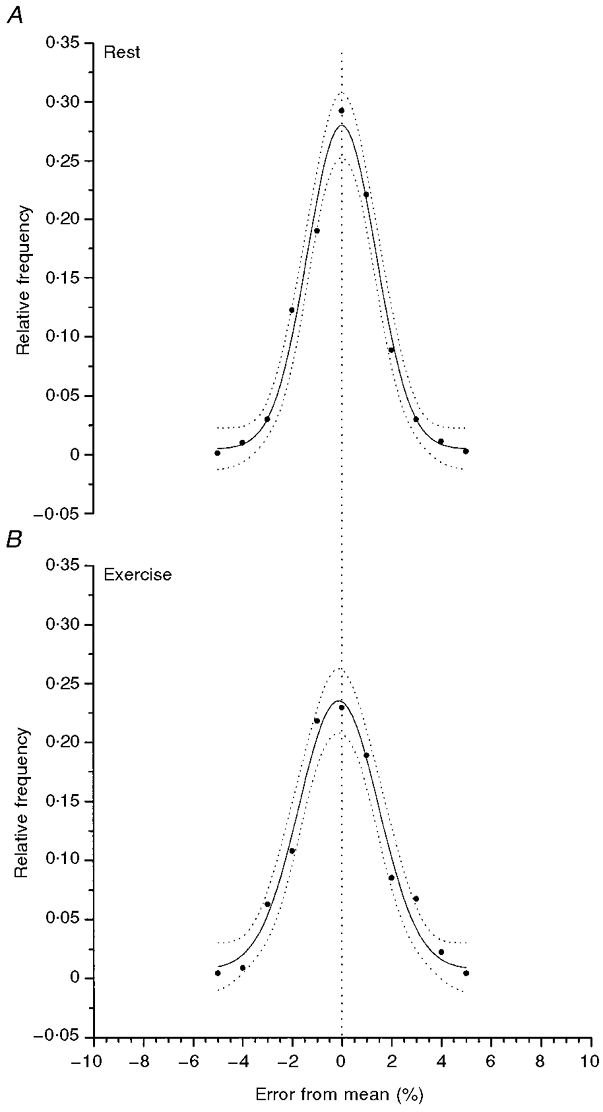
The data are the average for all six subjects. The Gaussian distribution provides a good description of the PDF and the dotted lines give the 95 % confidence intervals of the estimation.

The resulting standard deviations of the fluctuation of the ‘noise’ in V̇_O2 during rest (s_r) and moderate work (s_w) are illustrated by the probability density function (PDF) for a single subject in Fig. 2. The standard deviation values were not different between subjects (Table 2) at rest or during exercise being 0.0427 l min⁻¹ (s.d.= 0.0104) for s_r and 0.0640 l min⁻¹ (s.d.= 0.0292) for s_w. Similarly the centre of the peak (xc) was not different from zero in either condition (xc_r=−0.0051 l min⁻¹ (s.d.= 0.0069), xc_w= 0.0022 l min⁻¹ (s.d.= 0.0034)). The PDFs for the six subjects were summed, in the same fashion as for [PCr], and the mean is shown in Fig. 4. These data appeared to have general characteristics similar to those described by Lamarra et al. (1987). Lamarra et al. (1987), however, studied the fluctuation process of V̇_O2 in humans sitting upright or cycling on a cycle ergometer whereas the subjects in the present study were lying prone. Despite these general similarities, the standard deviation of the interbreath fluctuations in this study was, in fact, smaller than that of Lamarra et al. (1987); this could reflect the comprehensive familiarisation our subjects underwent prior to this study.

Table 2.

Parameters of a Gaussian model applied to the PDF of the fluctuations in V̇ measurement

	Rest						Moderate exercise
Subject no.	n	xcr (l min−1)	xcrC95(l min−1)	w(l min−1)	wC95 (l min−1)	sr	n	xcw (l min−1)	xcwC95 (l min−1)	w (l min−1)	wC95(1 min−1)	sw
1	175	0.0006	0.0027	0.0562	0.0100	0.0281*	149	−0.0025	0.0058	0.0656	0.0170	0.0328
2	258	−0.0018	0.0037	0.0755	0.0095	0.0378*	152	0.0024	0.0084	0.1035	0.0452	0.0518*
3	356	−0.0065	0.0058	0.1065	0.0154	0.0533*	177	0.0008	0.0109	0.2090	0.0371	0.1045*
4	138	−0.0015	0.0040	0.0727	0.0107	0.0364*	79	0.0068	0.0169	0.0911	0.0579	0.0456*
5	323	−0.0032	0.0044	0.0925	0.0116	0.0463*	130	0.0005	0.0139	0.1060	0.0405	0.0530*
6	168	−0.0183	0.0078	0.1089	0.0190	0.0545*	267	0.0053	0.0120	0.1921	0.0345	0.0961*
Mean	236	−0.0051	0.0047	0.0854	0.0127	0.0427*	159	0.0022	0.0113	0.1279	0.0387	0.0640*
s.d.	90	0.0069	0.0018	0.0208	0.0037	0.0104	62	0.0034	0.0039	0.0583	0.0135	0.0292
Group response: all data	1418	−0.0044	0.0019	0.0883	0.0043	0.0442*	954	0.0013	0.0039	0.0995	0.0086	0.0498*

Model parameters of the probability density function for the [noise] fluctuation in V̇_O2 measurement for each subject at rest and during the steady state of moderate exercise, and fitted with a Gaussian function. n, number of points; xc_r and xc_w, centre of peak at rest and work, respectively; w, 2 × variance (ω); C₉₅, 95% confidence interval of estimation; s_r and s_w, standard deviation from the Gaussian model during rest and work, respectively.

^*Not significantly different from a Gaussian distribution using χ² goodness-of-fit (P > 0.05).

Figure 4. The PDF for the distribution of intersample fluctuations of V̇_O2 measurement in the steady state at rest (A), or during exercise (B).

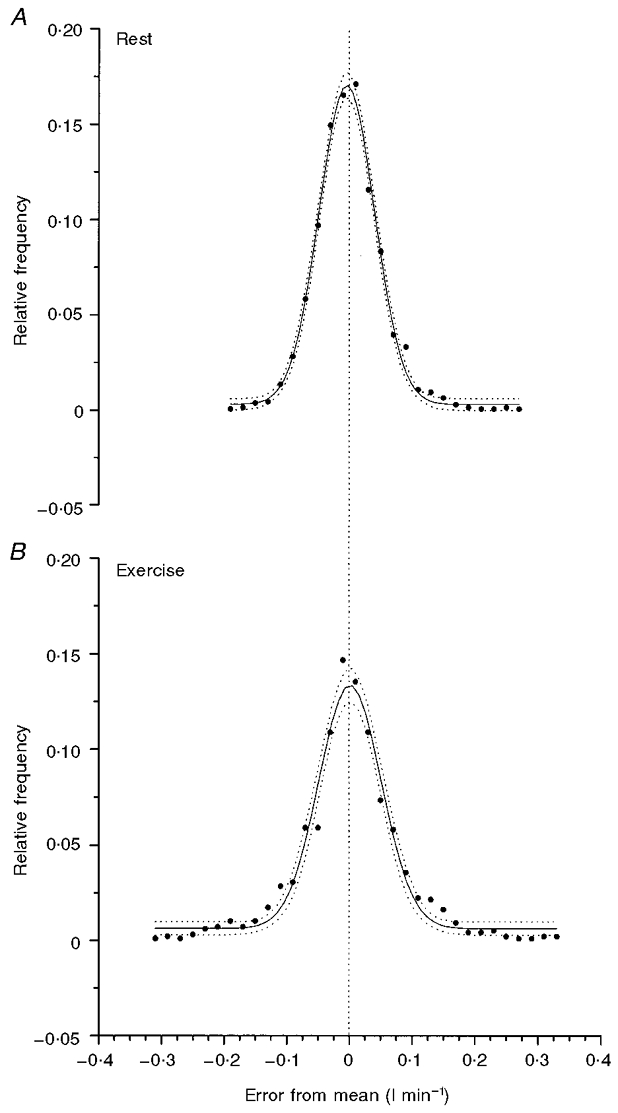
The data are the average for all six subjects. The Gaussian distribution provides a good description of the PDF and the dotted lines give the 95 % confidence intervals of the estimation.

The PDFs, shown in Figs 3 and 4 are fitted with Gaussian curves (with appropriate 95 % confidence limits), the parameters for which are given in Tables 1 and 2. Figures 3 and 4 illustrate how the Gaussian ‘normal’ distribution was a sufficient approximation of the ‘noise’ associated with the determination of intramuscular [PCr] by MRS and simultaneously determined V̇_O2. The average goodness-of-fit was determined by the χ² values at rest and during exercise and when each individual was considered separately all but one PDF for [PCr] and one for V̇_O2 (see Tables 1 and 2) were well described by a Gaussian normal distribution. When the [PCr] and V̇_O2 PDFs for each subject were summed within a condition (Tables 1 and 2, and Figs 3 and 4) the resulting distribution was well fitted by a Gaussian function, using the χ² value to determine the goodness-of-fit.

Furthermore, it was important to describe the randomness of the PDF distribution in the time domain, i.e. the temporal features with which the noise fluctuated around the mean and whether this could be described by a systematic process. The randomness and flatness of the residuals from the fit to the original data provide a means of testing this; however, the autocorrelation factors were also calculated for both [PCr] and V̇_O2 and are shown for each subject in Fig. 5 and Table 3 for up to four sample or breath delays. Figure 5 demonstrates the rapid fall of the autocorrelation factor to a value close to zero for any sample delays of 1 to 4 (i.e. up to 1 min): this did not differ when sample delays of up to 12 were considered. The fluctuation may, therefore, be considered to occur in a random fashion around the mean of approximately zero, suggesting that the ‘noise’ associated with one sample bore little relation with the ‘noise’ of an adjacent or subsequent sample.

Figure 5. The autocorrelation coefficients for [PCr] and in all six subjects at both rest and exercise for sample delays of n from n to n+ 4.

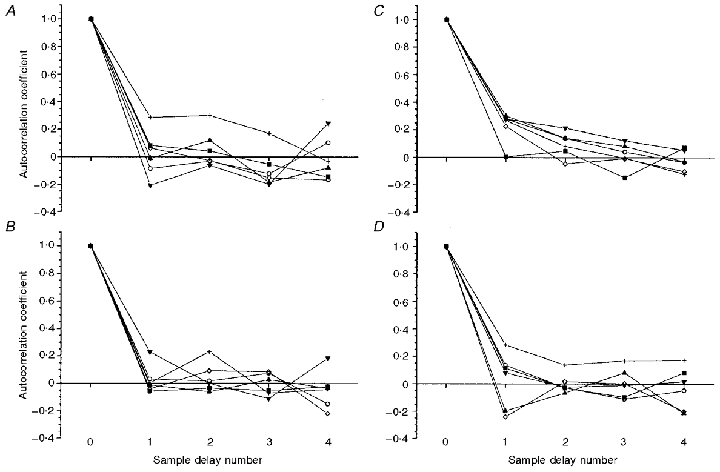
A, [PCr], rest; B, [PCr], exercise; C, V̇_O2, rest; D, V̇_O2, exercise.

Table 3.

Autocorrelation factors (R-values) for PCr and V̇_O2 measurements at rest and during exercise for n samples up to n+ 4

	PCr, sample delay number				V̇O2, sample delay number
Subject no.	1	2	3	4	1	2	3	4
Rest
1	0.083	0.043	−0.053	−0.145	0.005	0.046	−0.146	0.072
2	−0.085	−0.031	−0.122	0.104	0.280	0.140	0.041	−0.033
3	−0.011	0.120	−0.184	−0.079	0.303	0.141	0.082	−0.030
4	−0.207	−0.062	−0.199	0.246	0.279	0.214	0.123	0.053
5	0.064	−0.026	−0.152	−0.167	0.226	−0.045	−0.007	−0.101
6	0.287	0.301	0.171	−0.034	0.269	0.080	−0.003	−0.120
Mean	0.022	0.058	−0.090	−0.013	0.227	0.096	0.015	−0.027
s.d.	0.168	0.136	0.138	0.159	0.112	0.090	0.093	0.078
Exercise
1	−0.057	−0.034	−0.051	−0.024	0.115	−0.029	−0.096	0.082
2	0.031	0.017	0.073	−0.149	0.136	−0.027	−0.111	−0.048
3	−0.012	−0.061	0.027	−0.035	−0.197	−0.066	0.081	−0.213
4	0.229	0.000	−0.111	0.184	0.080	−0.024	−0.010	0.017
5	−0.041	0.092	0.085	−0.220	−0.242	0.017	0.002	−0.199
6	0.002	0.231	−0.071	−0.043	0.284	0.138	0.169	0.174
Mean	0.025	0.041	−0.008	−0.048	0.029	0.002	0.006	−0.031
s.d.	0.105	0.107	0.081	0.137	0.205	0.072	0.106	0.154

DISCUSSION

The fluctuations of [PCr] measurement at different energy states from rest to the limits of moderate exercise, in this study, were well described by a Gaussian distribution. This has significant implications, not only for the use of non-linear least squares fitting procedures to estimate the time-course of intramuscular [PCr] change but also for the efficacy of using the initial rate of change of [PCr] to calculate the rate of ATP turnover at the onset of exercise. As determined by Lamarra et al. (1987) the confidence interval for the estimation of kinetic parameters, such as τ, is greatly dependent upon the standard deviation of the noise function and the magnitude of the increment by the relationship:

(1)

where K₁ is the 95 % confidence interval for the estimation of τ for a single transition of variable x of steady-state magnitude change Δx_ss, with standard deviation of S₀. The value L^ is a constant determined by the data density and the underlying time constant of the ‘actual’ response. This confidence interval can be decreased by averaging repeats of like experiments. However, this is only justified if the ‘noise’ is determined to fluctuate ‘normally’ about the mean value. This demonstration that the fluctuation of [PCr] using ³¹P-MRS is normally distributed at a range of energy states in the quadriceps muscles allows these averaging procedures to be justifiably applied. Without these averaging techniques, adequate estimates (i.e. to within approximately 10 %) of the time course of [PCr] change on transition from rest to exercise are not possible.

The sample-to-sample fluctuations in [PCr] are likely to be determined by a number of factors. The finding here that the standard deviation of the PCr fluctuations does not change at different energy states implies that the fluctuations are a constant factor of the measurement technique, rather than actual fluctuations in the [PCr] in the region of interest of the muscle under investigation. Furthermore, it also shows that there is no loss of fidelity with the exercise protocol used in these studies, i.e. that the movement of the contraction quadriceps is finished by the time that each sample is taken and the region of interest is in the same position relative to the B₀ magnetic field at the time of sampling. The coil also remains stationary relative to the B₀ field as it is fixed to the patient bed. Therefore, these ‘noise’ characteristics are likely to be improved by factors such as increasing the muscle mass under investigation, increasing the strength of the magnetic field employed, and lengthening the repetition time of sampling. However, these factors tend to conflict with the requirements for kinetic analysis as represented in eqn (1). For instance, increasing the muscle mass investigated often requires a weaker B₀ field, as a whole-body, rather than a small bore, MRS is usually required. Also, lengthening the sample frequency decreases the temporal resolution of the sampling and, therefore, the data density (i.e. L^ in eqn (1) is increased). In this study eight acquisitions were used per sample. By reducing this to four, the signal-to-noise ratio reduces dramatically (i.e. S₀ in eqn (1) is greatly increased); by increasing this value to 12 the time-domain data density required for kinetic analysis is reduced to unacceptable levels, with only one data sample per 22.5 s (again by increasing L^ in eqn (1)). Therefore, the measurements presented here have been made with the premise that L^ and S₀ were to be titrated to give the smallest possible K₁. These data are, therefore, likely to express a standard deviation of ‘noise’ that is small compared to studies that employ plantar flexor or forearm handgrip exercise for the exercised muscle group, but also time-domain data density adequate for kinetic analysis in order to investigate aspects of control (Blei et al. 1993; Kemp et al. 1994; McCreary et al. 1996; Conley et al. 1998).

The fact that the standard deviation of breath-by-breath V̇_O2 noise fluctuation was small in these studies enables greater confidence to be expressed when comparing the kinetics of another variable ([PCr] for instance) with V̇_O2 (e.g. Rossiter et al. 1999): the confidence expressed in the parameters of both variables must be adequately small to allow appropriate discrimination of the potential differences.

The fluctuations in [PCr] determination in this and previous studies have important implications for the estimation of the ATP turnover rate from the initial rate of change of [PCr]. The confidence of the determination of d[PCr]/dt by estimating the initial slope between the baseline and the first data point for an exponential with a modelled Gaussian ‘noise’ function superimposed is shown in Fig. 6. For a given standard deviation (1.5 %Δ) and size of [PCr] signal (i.e. the equivalent volume of the contracting unit interrogated), the resulting confidence of the determination of d[PCr]/dt is predominantly dependent on the magnitude of the steady-state decrement in [PCr]. For small changes in [PCr], expected in calf or forearm muscle for instance, the errors are likely to be greater than those shown in Fig. 6, which are based on measurements from a large volume of the quadriceps. With small [PCr] decrements, such as those observed during moderate intensity work rates, the errors in the estimation of d[PCr]/dt can be as great as approximately 100 %, giving 95 % confidence intervals of approximately 80 % for d[PCr]/dt determination. The confidence intervals for estimating d[PCr]/dt may be significantly reduced by exercising a large muscle mass and reducing the [PCr] value to at least 50 %. Even with these large decrements in steady-state [PCr] the 95 % confidence limits are as much as 16 %. As shown in Fig. 6, these confidence limits may be reduced by averaging data from like experiments, but the improvement is of diminishing return by a factor of 1/✓n, where n is the number of like runs averaged.

Figure 6. The 95 % confidence limits (K_n) for the estimation of the initial rate of change of [PCr] (d[PCr]/dt) using the initial slope estimated from data with a superimposed noise function at different levels of work.

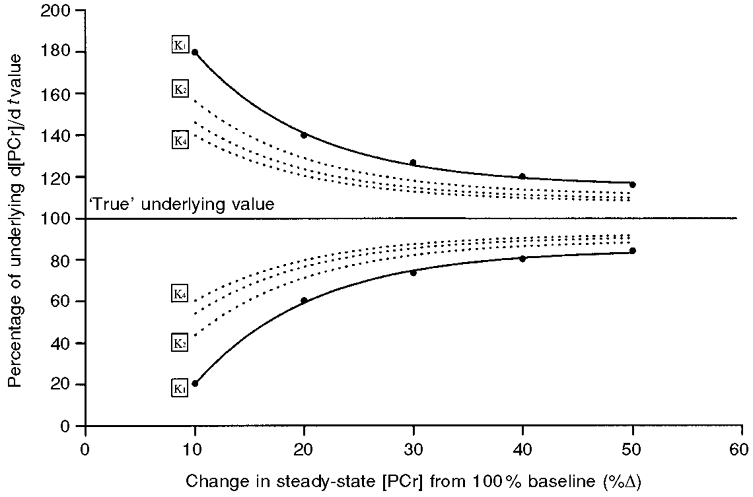
The lines for K₁ give the confidence of d[PCr]/dt estimation from a single data sample with a s.d. of 1.5 %Δ. K₂ to K₄ show the improvement of estimation as successive like bouts are included in the average. The estimation also improves as the steady-state amplitude of response is increased.

We attempted to characterize the effect of the actual variability in the response on d[PCr]/dt using the two methods previously discussed, in each of the six subjects. In Fig. 7 the estimations of d[PCr]/dt made both from the slope of the regression between the resting baseline at time zero and the first item of data acquired in each of the identical exercise transitions (open circles) and the best fit exponential (i.e. Δ[PCr]_ss/τ) of each individual run (filled circles). The bars in this figure represent the high-confidence estimation of the initial rate of change using Δ[PCr]_ss/τ determined from the average of n repeats (i.e. this reduces S₀ by a factor of 1/✓n). However, even for a single exercise transition the estimation is greatly improved using the Δ[PCr]_ss/τ method. Figure 7 also highlights the bias resulting from slope estimation; d[PCr]/dt varies as a tan function, which ranges between zero and infinity. This influence is clearly seen in Fig. 7 where subjects 4 and 6 in particular show very large overestimations of d[PCr]/dt.

Figure 7. Estimation of the initial rate of change of [PCr] (d[PCr]/dt) using two methods in six subjects.

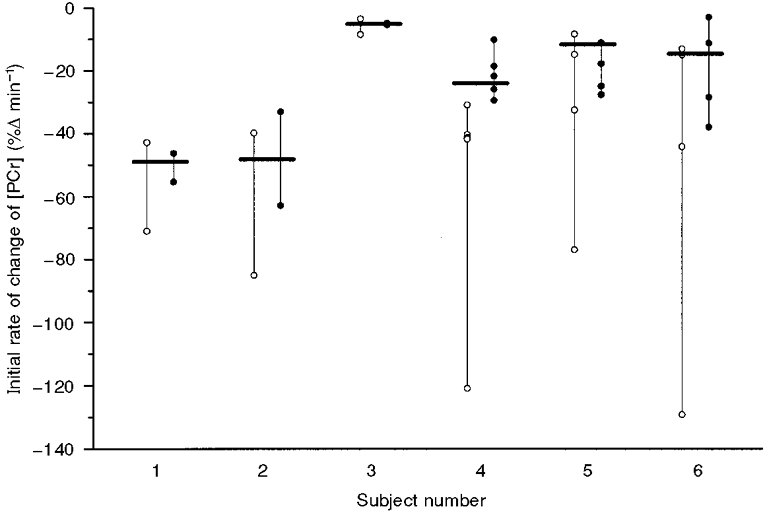
d[PCr]/dt is estimated from the regression from the baseline at time zero to the first item of data acquired (i.e. 15 s into the exercise) (○). Alternatively, d[PCr]/dt is estimated from the kinetic parameters of the best fit exponential (•). The black bars represent the estimation of d[PCr]/dt with the highest confidence, i.e. estimated from the best fit exponential to the averaged data where the standard deviation (S₀) of the fluctuations is reduced.

The determination of d[PCr]/dt from Δ[PCr]_ss and τ may be significantly influenced by the data density (i.e. the number of spectra per minute). If the sampling interval is decreased, the error would reduce only if the standard deviation of the noise remained constant. However, this is not the case when using the ³¹P-MRS technique to determine [PCr] as this technique is itself highly dependent on increasing signal-to-noise ratios by averaging multiple acquisitions. The signal that can be expected from the interrogation of muscle by ³¹P-MRS will be itself dependent on the [PCr] relaxation time (T₁) in relation to the sampling interval, as alluded to by Newcomer & Boska (1999). It is possible that the T₁ relaxation time of [PCr] may change abruptly on exercise (i.e. with a t_1/2 of approximately 5–10 s; Newcomer et al. 1999). This could potentially have a significant effect on the determination of Δ[PCr], because partial saturation of the [PCr] signal will alter the apparent amplitude of the [PCr] fall as a function of the magnitude of the T₁ change. This is unlikely to affect the determination of the time course of the [PCr] kinetics, however, due to the small t_1/2 of the T₁ change. The potential of reducing the apparent Δ[PCr]_ss and therefore further increasing the K_n of d[PCr]/dt (Fig. 5) should, however, be considered. The aspect of T₁ changes with exercise have, thus far, only been investigated in the gastrocnemius/soleus muscle group during repeated isometric contractions, i.e. where the acidic stress is likely to be high unlike the moderate intensity rhythmic exercise employed here. The relevant, important studies of the [PCr] relaxation time during moderate dynamic exercise have yet to be made.

In this study we found that the optimal compromise between spectral signal-to-noise ratio and temporal resolution was achieved by a repetition time of 1875 ms with eight FIDs summed to produce one spectrum. Therefore, in order to avoid severe errors in estimating d[PCr]/dt it is necessary to maximize the magnitude of the [PCr] fall and minimise those factors that increase the standard deviation of the ‘noise’ component of the response.

Our results demonstrate that the intersample noise associated with [PCr] determination by ³¹P-MRS may be characterised as a stochastic Gaussian process uncorrelated to work rate, i.e. allowing valid subsequent kinetic analysis using relevant methods, similar to those previously described for pulmonary oxygen uptake (Lamarra et al. 1987). Accounting for this Gaussian ‘noise’ process may also help in distinguishing the underlying kinetic process or processes. Appropriate averaging will reduce the ‘low confidence’ signal of a single acquisition sequence to that of a ‘high confidence’ one, allowing confident parameter assignment from the kinetic analysis and appropriately distinguish small deviations from dynamic linearity (e.g. Rossiter et al. 2000). The variation, however, will significantly affect the subsequent calculation of the initial rate of change of [PCr], i.e. a possible modulation of more than twofold in the estimation of the initial rate of change of [PCr], if the inherent noise is not accounted for. It may, therefore, be more appropriate to estimate the ATP turnover rate (and the rate of hydrogen ion production and glycolytic flux) by parameters estimated from the entire dynamic response rather than those relying upon the accuracy of a small number of samples.