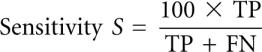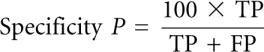Skip to main content
PMC home page
RNA logoLink to RNA
. 2008 Apr;14(4):630–640. doi: 10.1261/rna.968808

KnotSeeker: Heuristic pseudoknot detection in long RNA sequences

Jana Sperschneider 1,2, Amitava Datta 1
PMCID: PMC2271355  PMID: 18314500

Abstract

Pseudoknots are folded structures in RNA molecules that perform essential functions as part of cellular transcription machinery and regulatory processes. The prediction of these structures in RNA molecules has important implications in antiviral drug design. It has been shown that the prediction of pseudoknots is an NP-complete problem. Practical structure prediction algorithms based on free energy minimization employ a restricted problem class and dynamic programming. However, these algorithms are computationally very expensive, and their accuracy deteriorates if the input sequence containing the pseudoknot is too long. Heuristic methods can be more efficient, but do not guarantee an optimal solution in regards to the minimum free energy model. We present KnotSeeker, a new heuristic algorithm for the detection of pseudoknots in RNA sequences as a preliminary step for structure prediction. Our method uses a hybrid sequence matching and free energy minimization approach to perform a screening of the primary sequence. We select short sequence fragments as possible candidates that may contain pseudoknots and verify them by using an existing dynamic programming algorithm and a minimum weight independent set calculation. KnotSeeker is significantly more accurate in detecting pseudoknots compared to other common methods as reported in the literature. It is very efficient and therefore a practical tool, especially for long sequences. The algorithm has been implemented in Python and it also uses C/C++ code from several other known techniques. The code is available from http://www.csse.uwa.edu.au/∼datta/pseudoknot.

Keywords: RNA pseudoknots, minimum free energy, dynamic programming, heuristic algorithms, minimum weight independent set, RNA structure prediction

INTRODUCTION

A central dogma in biology states that sequence determines structure determines function. This has been successfully applied to protein tertiary structure prediction. Over the past decades, the protein folding problem has attracted worldwide attention from many research groups and is seen as the holy grail of biochemistry. However, proteins are not the only important catalytically active macromolecules. It is clear that RNA can no longer be seen solely as a carrier of genetic information from DNA to proteins. RNA easily keeps up with the countless functions and structures proteins exhibit, adopts diverse three-dimensional folds, and can act like a catalyst. It is an extremely versatile molecule and facilitates various functions, including translational regulation, intron splicing, gene expression, and cell regulation. Novel noncoding RNAs are discovered continuously and the exciting RNA world is far from being fully explored.

Recent studies on RNA emphasize the fact that pseudoknots are a prevalent structural part, occurring in most classes of RNA (e.g., mRNA, tmRNA, rRNA, ribozymes, aptamers) (Staple and Butcher 2005). Pseudoknots are functionally diverse and can induce viral ribosomal frameshift or readthrough, be part of the catalytic core of ribozymes, or promote telomerase activity (Brierley et al. 2007). Especially retroviruses (e.g., HIV), coronaviruses (e.g., SARS), and most plant viruses use pseudoknots for proliferation and replication (Baril et al. 2003; Thiel et al. 2003). This draws attention to the high relevance of pseudoknots in antiviral drug design.

RNA secondary structure prediction methods by free energy minimization require O(n 3) time and O(n 2) space using dynamic programming (Zuker and Stiegler 1981). However, including a tertiary structure element like the pseudoknot dampens the optimism of solving the RNA structure prediction problem. The general pseudoknot structure prediction problem is NP-complete (Lyngso and Pedersen 2000). Practical dynamic programming algorithms run in O(n 6), O(n 5), or O(n 4) time for a restricted class of pseudoknots (Rivas and Eddy 1999; Akutsu 2000; Dirks and Pierce 2003; Reeder and Giegerich 2004). Dynamic programming methods for pseudoknot prediction guarantee an optimal solution in regards to the minimum free energy (MFE) model, yet suffer from two major drawbacks: a high running time even for a restricted class of pseudoknots and decreasing accuracy for long sequences due to sparse knowledge about pseudoknot thermodynamics. Nevertheless, if presented with a sequence fragment exactly harboring a pseudoknot, dynamic programming methods are able to fold it into the correct structure with high base-pair accuracy (Huang et al. 2005). Detection of true positive pseudoknots as a first step in RNA structure prediction can greatly improve the overall performance. The route followed in this article is to perform efficient pseudoknot detection preliminary to structure prediction. The advantage is clear: if we can find pseudoknots with high accuracy, the remaining sequence can be folded in O(n 3) time according to the MFE model.

Apart from dynamic programming, several other techniques exist for RNA structure prediction including pseudoknots. Early methods comprise Monte Carlo simulations (Abrahams et al. 1990), genetic algorithms (Gultyaev et al. 1995; van Batenburg et al. 1995), stochastic context-free grammars (Brown and Wilson 1996; Cai et al. 2003), and maximum weighted matching (MWM) based on graph theory (Tabaska et al. 1999). Elaborated ab initio folding simulations are performed in KineFold (Xayaphoummine et al. 2003). Recent heuristic procedures include iterated loop matching (ILM) (Ruan et al. 2004) and HotKnots (Ren et al. 2005). ILM is a hybrid method employing dynamic programming and comparative information, which iteratively chooses the highest scoring helical region and adds it to the predicted structure. HotKnots expands this idea by considering several alternative secondary structures and returning a fixed number of suboptimal folding scenarios. HPknotter is a detection tool for pseudoknots based on structural matching and dynamic programming kernels (Huang et al. 2005). PLMM_DPSS was recently designed for predicting a limited class of pseudoknots with very high sensitivity (Huang and Ali 2007). All of these heuristic approaches do not guarantee returning an optimal solution with regard to the MFE model, however run in reasonable CPU time.

Overall, there is very high demand for RNA prediction algorithms including pseudoknots. In this article, we present a new approach, called KnotSeeker, for detecting pseudoknots in primary RNA sequences. Our algorithm works as follows: Given an RNA sequence, we find sequence fragments possibly and exactly harboring a pseudoknot using certain criteria. The small number of candidate pseudoknot sequences is folded by a well-established dynamic programming algorithm to see whether they indeed form a stable pseudoknot as the minimum free energy structure. In a second step, these verified pseudoknot candidates are tested if they are likely to exist in the structure with minimal free energy. Only stable, nonoverlapping pseudoknots are returned as the final result. The main advantage of this heuristic pseudoknot detection is that it handles long sequences fast and finds the correct pseudoknots with higher accuracy compared to other methods.

A deeper understanding of pseudoknot thermodynamics will yield better energy parameters and folding results. However, it is unlikely that this will improve the efficiency of dynamic programming methods. Hence, the KnotSeeker detection tool is a substantial improvement and support for rapid ab initio RNA structure prediction including pseudoknots. Additionally, KnotSeeker will benefit from pseudoknot thermodynamic parameter improvements in the future.

RESULTS

RNA structure and pseudoknots

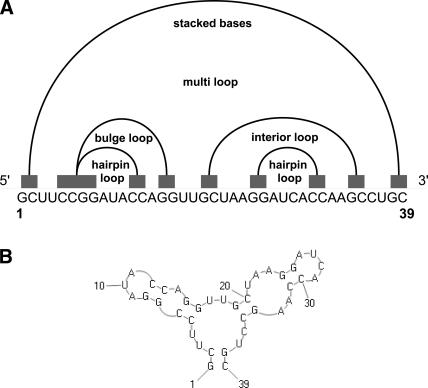
The foundation of RNA structure formation is continuous base pairing, resulting in so-called helical regions or stems. RNA comprises various secondary structure elements, e.g., single-stranded regions, stacked base pairs, hairpin loops, multiple loops, interior loops, and bulge loops (Fig. 1). Naturally, we can represent a stem si with start point ai and end point bi as an interval on the line. Formally, we define a stem interval si as follows:

FIGURE 1.

FIGURE 1.

Open in a new tab

(A) Representation of RNA secondary structure elements as intervals on the line. Note that all secondary structure elements can be nested, but have to be noncrossing. (B) Corresponding secondary structure.

  • si = [ai : bi] with an associated stem length len(si).

  • [ai, ai + 1, …, ai + len(si) − 1] is base-paired with [bi, bi − 1, …, bi − len(si) + 1].

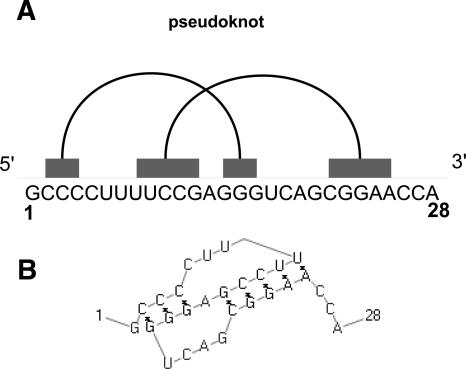
A pseudoknot basically consists of two crossing stems si and sj (Fig. 2).

FIGURE 2.

FIGURE 2.

Open in a new tab

(A) Representation of a pseudoknot on the line. It consists of two crossing stem intervals. (B) Corresponding pseudoknot structure generated by PseudoViewer (Byun and Han 2006).

In contrast to proteins, RNA can form independently stable secondary structures, which is crucial for RNA folding (Brion and Westhof 1997). The common assumption is that starting with the single-stranded sequence, the majority of secondary structure elements (e.g., hairpin loops in close vicinity) form that determine tertiary structure (Tinoco and Bustamente 1999). There are exceptions to this rule, like secondary structure rearrangements during RNA folding (Tinoco and Wu 1998). However, it is widely accepted in the research community that standard RNA folding is a hierarchical two-step process (Schroeder et al. 2004).

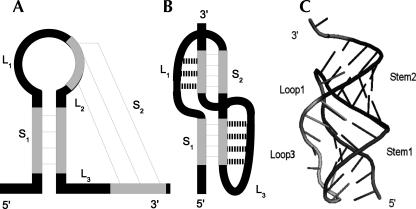
Pseudoknots are tertiary interactions between a loop region and unpaired residues outside the loop. After secondary structure formation, nucleotides in a hairpin loop can base-pair with complementary ones in a single-stranded sequence. These tertiary contacts result in a so-called H-type pseudoknot consisting of two stems (S 1, S 2) and three loops (L 1, L 2, L 3) (Fig. 3). H-type pseudoknots are the simplest and most abundant pseudoknot structures. Over 78% of all 246 in PseudoBase reported pseudoknots are of H-type (van Batenburg et al. 2000).

FIGURE 3.

FIGURE 3.

Open in a new tab

Representations of an H-type pseudoknot. (A) General formation: base-pairing between a loop and single-stranded region. (B) A coaxially stacked pseudoknot: loop–stem interactions are indicated with dotted lines. (C) Three-dimensional view of a pseudoknot.

Pseudoknot folding and formation is a combination of thermodynamics, molecular physics, and sequence composition. It is essential to survey pseudoknots in three-dimensional space for a deeper understanding. The A-form helix forces loops L 1 and L 3 to span the major groove of S 2 and minor groove of S 1, respectively (Pleij et al. 1985). Dependent on the loops, stems, and helical junction, the A-form geometry can deviate from the standard RNA helix. The two stems can coaxially stack with an absent loop L 2. Bent and overtwisted pseudoknot conformations also occur (Giedroc et al. 2000).

Additionally, residues in the loop regions can form tertiary interactions with nucleotides from the minor and major grooves. The shallow and wide minor groove allows tertiary contacts and triple helical regions between S 1 and L 3 (Batey et al. 1999). A-minor interactions resulting from hydrogen bonds between loop adenines and the minor groove are common (Nissen et al. 2001).

Pseudoknot thermodynamic parameters are not very well understood. It is assumed that the free energy of a pseudoknot consists of destabilizing (positive) energy values for loop regions and stabilizing (negative) energy values for stem regions (Gultyaev et al. 1999). The stacked stem energy for S 1 and S 2 can be calculated using the additive sum of the nearest-neighbor model. However, the entropic loop energies for L 1 and L 3 still have to be estimated. The loops are not equivalent stereochemically, as they cross different grooves. The simple nearest-neighbor model also neglects the important stem–loop correlations (Cao and Chen 2006). Additionally, stabilizing coaxial stacking and base triples at the helical junction need to be taken into account.

Detection of pseudoknots

The detection of pseudoknots must be clearly distinguished from RNA structure prediction including pseudoknots. Pseudoknot detection is a self-contained step without simultaneous secondary structure prediction aimed to return only pseudoknots. If pseudoknots can be detected with high accuracy, the remaining sequence can efficiently be folded using state-of-the-art secondary structure prediction programs in O(n 3) time and O(n 2) space. There are several programs for RNA structure prediction including pseudoknots; however HPknotter is the only tool performing sheer pseudoknot detection so far (Huang et al. 2005). HPknotter can improve RNA secondary structure prediction including pseudoknots. However, it suffers from a high number of returned false positive pseudoknots. HPknotter finds pseudoknots using the following steps: First, RNAMotif's structural matcher returns a great number of possible pseudoknot fragments for a given input sequence. The NUPACK energy calculation tool is used for removing hits with lower nonpseudoknotted MFE structure. Second, pseudoknot verification is performed by pknots, NUPACK, or pknotsRG to see if a filtered hit indeed folds into the desired pseudoknot structure. A minimum weight independent set calculation returns a mutually disjoint pseudoknot set as the result.

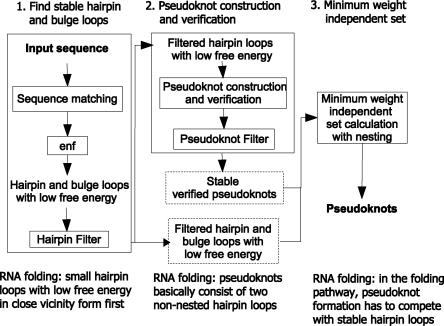
The new approach for pseudoknot detection followed in this article is presented in Figure 4. Unlike HPknotter, KnotSeeker is based on RNA folding assumptions and free energy minimization considering stable secondary structure elements. Detailed descriptions of the three main steps can be found in the Materials and Methods section.

FIGURE 4.

FIGURE 4.

Open in a new tab

New approach for pseudoknot detection and details of its three stages. In the first stage, enf stands for free energy evaluation.

Experimental results

We tested KnotSeeker on 34 sequences covering various RNA classes. The sequence lengths range from 73 nucleotides (nt) to 1340 nt. As KnotSeeker is designed for detecting pseudoknots in primary RNA sequences, we report sensitivity and specificity only for pseudoknotted base pairs using the following notation as in Baldi et al. (2000):

  • Inline graphic

  • Inline graphic

TP (true positive) corresponds to the number of correctly predicted base pairs in the predicted pseudoknot, FN (false negative) to the number of base pairs in the published pseudoknot that were not predicted, and FP (false positive) to the number of incorrectly predicted base pairs in the predicted pseudoknot. We also report the ratio r = (number of correctly predicted pseudoknots)/(number of predicted pseudoknots).

We compared the results to three other methods, namely the dynamic programming algorithm pknotsRG (mfe mode) (Reeder and Giegerich 2004) and the heuristic approaches HPknotter (general descriptor) (Huang et al. 2005) and ILM (Ruan et al. 2004). We also obtained the results achieved by HotKnots (Ren et al. 2005), which heuristically finds 20 structures with lowest free energy. However, we discovered that HotKnots did not return any correct pseudoknots in the best structure with lowest free energy for our test sequences. A comparison of the remaining suboptimal folding scenarios with the other algorithms would be biased and thus we excluded HotKnots in our evaluation. We were unable to obtain results from pknots (Rivas and Eddy 1999) and NUPACK (Dirks and Pierce 2003) due to running out of memory for sequences longer than 150 nt and 200 nt, respectively. We discovered that ILM tends to predict very complex pseudoknots for long sequences. In many cases, we found that long-range pseudoknotted helices with several internal H-type pseudoknots cover the whole sequence. Therefore, it is hard to correctly assign the ratio r, because the number of predicted pseudoknots is ambiguous. Whenever this is the case, we omit the r value for the results obtained by ILM.

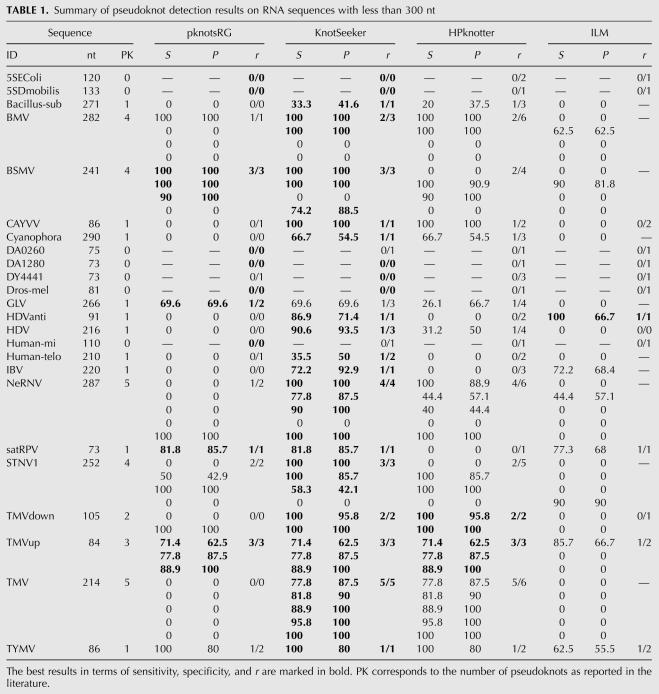
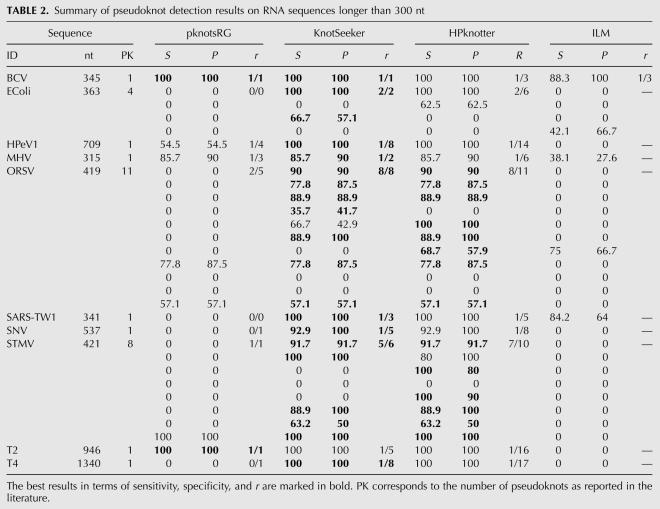
The pseudoknot detection results are displayed in detail in Tables 1 and 2 and the best results for a sequence are highlighted. One should note that more than one method can give best results for one sequence. For sequences shorter than 300 nt, pknotsRG gives best results for 10 of the 24 sequences. HPknotter and ILM show poor performance, dominating on only 2 and 1 sequences, respectively. KnotSeeker clearly outperforms the other methods with best results on 21 of the 24 sequences. For the set of long sequences (>300 nt), there is a similar scenario. KnotSeeker achieves the best results on 9 of the 10 sequences, whereas pknotsRG and HPknotter dominate on only two of the 10 sequences. Both sensitivity and specificity of the ILM predictions are significantly lower than those for the other methods.

TABLE 1.

Summary of pseudoknot detection results on RNA sequences with less than 300 nt

graphic file with name 630tbl1.jpg

Open in a new tab

TABLE 2.

Summary of pseudoknot detection results on RNA sequences longer than 300 nt

graphic file with name 630tbl2.jpg

Open in a new tab

The results emphasize that the strategy followed by KnotSeeker and HPknotter greatly improves the pseudoknot prediction results. The dynamic programming algorithm pknotsRG misses most pseudoknots in the test sequences. This illustrates the limitations of the dynamic programming approach and underlying energy model for long sequences. However, pknotsRG has very high sensitivity and specificity for short sequence fragments exactly harboring a pseudoknot. This becomes clear because KnotSeeker and HPknotter mainly achieve higher sensitivity and specificity because of the correct pseudoknot verification results returned by pknotsRG. Our approach clearly outperforms HPknotter for all test sequences. HPknotter returns many false positive pseudoknots, especially for longer sequences. Even though both procedures follow a similar idea (find sequence fragments possibly harboring a pseudoknot and verify them), KnotSeeker is significantly more accurate. This is due to the fact that our approach is based on RNA folding assumptions and takes into account competing secondary structure elements in the minimum weight independent set (MWIS) calculation.

We also report the running time for all approaches (Table 3; see Materials and Methods for experimental details). HPknotter runs in the order of minutes for sequences longer than 200 nt. pknotsRG is very efficient on short sequences; however, it becomes computationally expensive for long sequences due to its time requirements of O(n 4). In contrast to that, KnotSeeker is a rapid tool and runs in the order of seconds. It is significantly faster than pknotsRG and HPknotter on longer sequences. KnotSeeker takes less than 2 min to detect the pseudoknot in the very long T4 gene 32 mRNA sequence (1340 nt), whereas pknotsRG requires more than 40 min to fold the sequence. ILM is also a very efficient approach; however with the drawback of low sensitivity and specificity for ab initio structure prediction.

TABLE 3.

A comparison of running times for all RNA sequences

graphic file with name 630tbl3.jpg

Open in a new tab

DISCUSSION

Our approach gives the best results for pseudoknot detection when compared to pknotsRG, HPknotter, and ILM. KnotSeeker detects almost all predicted pseudoknots and returns significantly less incorrect pseudoknots than HPknotter. Especially for long sequences, our method is a substantial improvement for RNA structure prediction including pseudoknots. Pseudoknot detection prior to structure prediction is a successful and computationally efficient route. This was first demonstrated by HPknotter (Huang et al. 2005) and is now emphasized by the work presented in this article. KnotSeeker returns significantly more accurate results than the heuristic approaches ILM and HotKnots for long RNA sequences. This is mainly due to the fact that we perform a pseudoknot verification step that is consistent with the MFE model, whereas ILM and HotKnots simply combine highest scoring crossing helices. However, one should acknowledge that the heuristic approaches ILM and HotKnots perform well for different frameworks. ILM produces good results for a set of aligned sequences, whereas HotKnots is a reliable heuristic approach for short sequences.

The pseudoknot detection approach KnotSeeker is limited by a few factors. At this stage only certain pseudoknots that can be folded by pknotsRG are detected. These are so-called canonical, recursive pseudoknots (Reeder and Giegerich 2004). Using pknots with a high running time of O(n 6) can improve the results, especially for detecting more complex pseudoknots as in tmRNA or IRES elements (Rivas and Eddy 1999). An experiment using different pseudoknot thermodynamic parameters as in Cao and Chen (2006) or including partition function information (McCaskill 1990) is also an option. Furthermore, one can think of performing an alignment with known pseudoknot classes like retroviral frameshift sites to achieve more accurate results. During the MWIS calculation for nested structures, a free energy evaluation considering the secondary structure can be implemented. This should improve the results considerably and even lead to a fast novel RNA secondary structure prediction method including pseudoknots.

MATERIALS AND METHODS

In this section, we give a detailed description of the algorithmic details and the sequence data used for testing.

The KnotSeeker algorithm

Find stable hairpin and bulge loops

GUUGle is a search tool that finds all exact matches (under RNA base-pairing rules) of a minimum specified length between target and query sequences (Gerlach and Giegerich 2006). It makes use of suffix arrays and runs fast. A target sequence vs. target sequence search can be used to detect helical regions within a sequence.

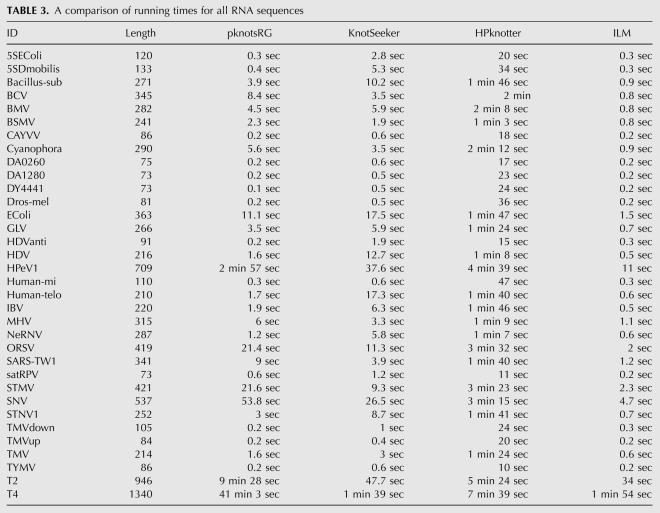
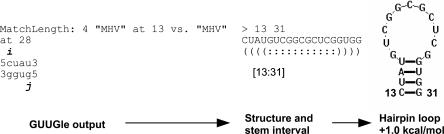
In the first step, we let GUUGle detect exact matches with length larger or equal to 3 base pairs (bp). These matches correspond to helical regions. GUUGle returns sequence fragments of a certain length k and two indices i,j (Fig. 5). The output usually consists of a large number of matches. The goal is to identify relevant matches. Following the initial assumption, we keep only those intervals with j − i ≥ 6, according to minimal hairpin loop lengths. Given the sorted stem interval list derived from the GUUGle output, bulge loops of size one are found as well through a simple combination of intervals (Fig. 6).

FIGURE 5.

FIGURE 5.

Open in a new tab

GUUGle output, corresponding structural interval representation and hairpin loop with free energy. Note that the stem interval for the GUUGle output correlates to si = [i : j + k − 1].

FIGURE 6.

FIGURE 6.

Open in a new tab

Construction of stem intervals with bulge loops of size one from the given sorted list of stem intervals. A partial overlap of size one is allowed in the second case.

As the corresponding secondary structure is known for each hairpin or bulge loop, we let RNAeval (Vienna RNA package 1.7) evaluate the free energy using the Turner parameters (Hofacker et al. 1994; Mathews et al. 1999). We only keep secondary structures with free energy < +2.0 kcal/mol with the motivation that stems with low free energy are likely to form in the native structure. Formally, each stem interval si = [ai : bi] has an associated weight w(si) corresponding to its free energy value. To further limit the size of the hairpin and bulge loop set, the following assumption is used: RNA folding is a two-step process and small structures with low free energy in close vicinity form first. The set of hairpin loop intervals is parsed as follows:

  • Given two intervals [i : k] and [i : l] with k < l. If w([i : k]) < w([i : l]), then delete longer interval [i : l].

  • Given two intervals [k : i] and [l : i] with k < l. If w([k : i]) > w([l : i]), then delete longer interval [k : i].

As an output for the first step, we get a list of filtered hairpin and bulge loops with their corresponding free energy values.

Pseudoknot construction and verification

A simple H-type pseudoknot basically consists of two crossing stems with low free energy. Given the list of filtered hairpin loops from the first step, two entries can be combined to potentially form a pseudoknot. An examination of entries in PseudoBase led us to use certain pseudoknot loop length restrictions similar to HPknotter (van Batenburg et al. 2000; Huang et al. 2005). The goal of this heuristic is to keep the set of candidate pseudoknots as small as possible while considering naturally occurring stem and loop lengths.

  • 1 nt ≤ size (Loop L 1) ≤ 20 nt.

  • 0 nt ≤ size (Loop L 2) ≤ 35 nt.

  • 1 nt ≤ size (Loop L 3) ≤ 75 nt.

Overall, we assume that a pseudoknot has to have a length ≤90 nt, as this returns the most significant results. These simple pseudoknots are among the best studied, whereas thermodynamics of very long pseudoknots are not well understood. Additionally, the following observation was made by us during preliminary testing: the two hairpin loop intervals potentially forming a pseudoknot need to have a combined free energy sum of less than −2.5 kcal/mol. This improves the runtime drastically, as only a small portion of intervals need to be combined as a pseudoknot candidate. Two important points should be noted. First, certain secondary structure rearrangements during pseudoknot formation are allowed, e.g., stems can partially overlap. Second, three-stemmed pseudoknots with an additional stem in their loops are also naturally included in pseudoknot construction.

Given the list of possible pseudoknots, we test with pknotsRG in O(n 4) time and O(n 2) space if they actually fold into stable pseudoknots (Reeder and Giegerich 2004). This verification is fast, as the list of candidates is small and the test runs on short sequence fragments exactly harboring a potential pseudoknot. Our pseudoknot filter procedure returns the desired and verified pseudoknots. However, pknotsRG returns several false positive verified pseudoknots, which do not occur in the native structure. This issue is tackled in the next step.

Minimum weight independent set

The verified pseudoknots plus filtered hairpin and bulge loops form our candidate structure elements set. To eliminate false positive pseudoknots from the second step, an MWIS calculation is performed. This corresponds to the following RNA folding assumption: in the folding pathway, pseudoknot formation has to compete with stable secondary structure elements.

The MWIS problem on a weighted interval set can be solved in linear time and space with an additional O(n log n) sorting step (Hsiao et al. 1992). It is based on a sweep line strategy and returns the set of nonoverlapping intervals with minimum weight as an output. For the MWIS calculation required here, one additional assumption regarding RNA folding has to be added. There can be nested structures; a hairpin or bulge loop can have several internally nested hairpin and bulge loops or pseudoknots. Like before, no two structure elements are allowed to overlap. For the calculation we assume that nesting results in an additional −1.5 kcal/mol free energy gain for the outer stem interval, as this is an energetically favorable process. The final output consists of the pseudoknots that are likely to occur in the native structure with minimum free energy. The following notations and assumptions are required for the MWIS algorithm:

  • Let si = [ai : bi] be a structure element interval with an associated weight w(si) corresponding to its free energy value.

  • Let S = {s 1, s 2, …, sn} be the set of candidate structure elements.

  • The sorted endpoints list L = {e 1, e 2, …, e 2n} is given.

  • temp min is a temporary variable that stores the MWIS weight of the set of intervals whose right endpoints have been scanned.

  • μ(i) = w(si) + min{μ(j) | bj < ai} for any 1 ≤ i ≤ n.

The MWIS algorithm scans the endpoints list. If the endpoint scanned is a left endpoint ai, the weight w(si) plus temp min is stored in μ(i). If the endpoint scanned is a right endpoint bi, μ(i) is checked to see whether it is smaller than temp min or not. For μ(i) < temp min, the value of temp min is replaced by μ(i). At the end of the calculation, the MWIS weight of S is stored in temp min and the resulting interval set can be recovered through a traceback step.

First step: Including nested structures

The first step delivers nested intervals and their corresponding updated energy values. The sorted endpoints list is scanned from left to right. If the right endpoint bi of a hairpin or bulge loop interval si is discovered, a search is performed to find all stems and pseudoknots contained in the interval [ai + len(si) − 1 : bi − len(si) + 1]. However, the resulting set Snested(i) can have overlapping structure elements. Therefore, a standard MWIS calculation is performed on the set Snested(i) to find only nonoverlapping nested structures of minimum weight. The updated weight w(si) of the outer stem si is the weight of the MWIS plus an additional −1.5 kcal/mol. This value turned out to give the best results during preliminary testing. The output of this first step is the list of structure elements with new updated weights accounting for nested structures.

Second step: MWIS calculation

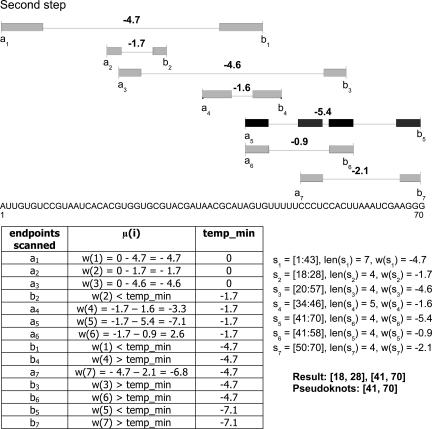
In the second step, an overall MWIS calculation is performed on the new structure element candidate set including nesting in linear time and space. The result consists of pseudoknots, hairpin loops, and bulge loops with combined minimum free energy. As this approach is designed for pseudoknot detection, the final output only returns pseudoknots. The different steps of the MWIS calculation are illustrated in Figures 7 and 8.

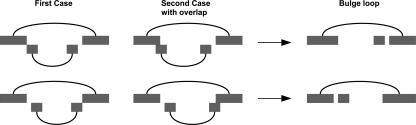
FIGURE 7.

FIGURE 7.

Open in a new tab

(A) Initial interval set with six stem intervals and one pseudoknot interval s 5. (B) Interval set after first step to include nested structures with new updated weights.

FIGURE 8.

FIGURE 8.

Open in a new tab

MWIS calculation using a sweep line strategy. The final result consists of the pseudoknot interval s 5.

Sequence test data

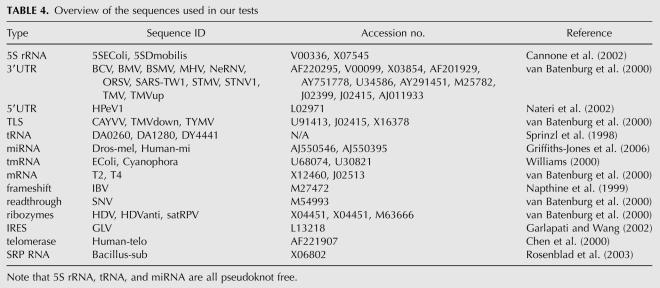
An overview of the sequences selected for testing is provided in Table 4. We chose both pseudoknotted and pseudoknot-free sequences from the literature.

TABLE 4.

Overview of the sequences used in our tests

graphic file with name 630tbl4.jpg

Open in a new tab

Experimental and implementation details

The KnotSeeker pipeline was implemented in Python 2.5 incorporating several existing programs, namely GUUGle (Gerlach and Giegerich 2006), RNAeval (Vienna RNA package 1.7; Hofacker et al. 1994), and pknotsRG (Reeder and Giegerich 2004). The experiments and time measurements for pknotsRG (mfe mode), KnotSeeker, and ILM were carried out with a dual Intel 1.66 GHz processor and 1 GB main memory. The results for HPknotter were obtained from its Web server, which returns also the computation time.

Footnotes

Article published online ahead of print. Article and publication date are at http://www.rnajournal.org/cgi/doi/10.1261/rna.968808.

REFERENCES

  1. Abrahams, J.P., van den Berg, M., van Batenburg, E., Pleij, C.W.A. Prediction of RNA secondary structure, including pseudoknotting, by computer simulation. Nucleic Acids Res. 1990;18:3035–3044. doi: 10.1093/nar/18.10.3035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Akutsu, T. Dynamic programming algorithms for RNA secondary structure prediction with pseudoknots. Discrete Appl. Math. 2000;104:45–62. [Google Scholar]
  3. Baldi, P., Brunak, S., Chauvin, Y., Andersen, C.A.F., Nielsen, H. Assessing the accuracy of prediction algorithms for classification: An overview. Bioinformatics. 2000;16:412–424. doi: 10.1093/bioinformatics/16.5.412. [DOI] [PubMed] [Google Scholar]
  4. Baril, M., Dulude, D., Steinberg, S.V., Brakier-Gingras, L. The frameshift stimulatory signal of human immunodeficiency virus type 1 group O is a pseudoknot. J. Mol. Biol. 2003;331:571–583. doi: 10.1016/S0022-2836(03)00784-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Batey, R.T., Rambo, R.P., Doudna, J.A. Tertiary motifs in RNA structure and folding. Angew. Chem. Int. Ed. Engl. 1999;38:2326–2343. doi: 10.1002/(sici)1521-3773(19990816)38:16<2326::aid-anie2326>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
  6. Brierley, I., Pennell, S., Gilbert, R.J.C. Viral RNA pseudoknots: Versatile motifs in gene expression and replication. Nat. Rev. Microbiol. 2007;5:598–610. doi: 10.1038/nrmicro1704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brion, P., Westhof, E. Hierarchy and dynamics of RNA folding. Annu. Rev. Biophys. Biomol. Struct. 1997;26:113–137. doi: 10.1146/annurev.biophys.26.1.113. [DOI] [PubMed] [Google Scholar]
  8. Brown, M., Wilson, C. RNA pseudoknot modeling using intersections of stochastic context free grammars with applications to database search. In: Hunter L., Klein T.E., editors. Proceedings of the 1996 Pacific Symposium on Biocomputing. World Scientific Publishing; Singapore: 1996. pp. 109–125. [PubMed] [Google Scholar]
  9. Byun, Y., Han, K. PseudoViewer: Web application and web service for visualizing RNA pseudoknots and secondary structures. Nucleic Acids Res. 2006;34:W416–W422. doi: 10.1093/nar/gkl210. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cai, L., Malmberg, R.L., Wu, Y. Stochastic modeling of RNA pseudoknotted structures: A grammatical approach. Bioinformatics. 2003;19:66–73. doi: 10.1093/bioinformatics/btg1007. [DOI] [PubMed] [Google Scholar]
  11. Cannone, J.J., Subramanian, S., Schnare, M.N., Collett, J.R., D'Souza, L.M., Du, Y., Feng, B., Lin, N., Madabusi, L.V., Müller, K.M., et al. The comparative RNA web (CRW) site: An online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinformatics. 2002;3:2. doi: 10.1186/1471-2105-3-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cao, S., Chen, S.-J. Predicting RNA pseudoknot folding thermodynamics. Nucleic Acids Res. 2006;34:2634–2652. doi: 10.1093/nar/gkl346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Chen, J., Blasco, M., Greider, C. Secondary structure of vertebrate telomerase RNA. Cell. 2000;100:503–514. doi: 10.1016/s0092-8674(00)80687-x. [DOI] [PubMed] [Google Scholar]
  14. Dirks, R.M., Pierce, N.A. A partition function algorithm for nucleic acid secondary structure including pseudoknots. J. Comput. Chem. 2003;24:1664–1677. doi: 10.1002/jcc.10296. [DOI] [PubMed] [Google Scholar]
  15. Garlapati, S., Wang, C. Identification of an essential pseudoknot in the putative downstream internal ribosome entry site in giardiavirus transcript. RNA. 2002;8:601–611. doi: 10.1017/s135583820202071x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gerlach, W., Giegerich, R. GUUGle: A utility for fast exact matching under RNA complementary rules including G-U base pairing. Bioinformatics. 2006;22:762–764. doi: 10.1093/bioinformatics/btk041. [DOI] [PubMed] [Google Scholar]
  17. Giedroc, D.P., Theimer, C.A., Nixon, P.L. Structure, stability, and function of RNA pseudoknots involved in stimulating ribosomal frameshifting. J. Mol. Biol. 2000;298:167–185. doi: 10.1006/jmbi.2000.3668. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Griffiths-Jones, S., Grocock, R.J., van Dongen, S., Bateman, A., Enright, A.J. miRBase: MicroRNA sequences, targets, and gene nomenclature. Nucleic Acids Res. 2006;34:D140–D144. doi: 10.1093/nar/gkj112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gultyaev, A.P., van Batenburg, F.H.D., Pleij, C.W.A. The computer simulation of RNA folding pathways using a genetic algorithm. J. Mol. Biol. 1995;250:37–51. doi: 10.1006/jmbi.1995.0356. [DOI] [PubMed] [Google Scholar]
  20. Gultyaev, A.P., van Batenburg, F.H.D., Pleij, C.W.A. An approximation of loop free energy values of RNA H-pseudoknots. RNA. 1999;5:609–617. doi: 10.1017/s135583829998189x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hofacker, I.L., Fontana, W., Stadler, P.F., Bonhoeffer, S., Tacker, M., Schuster, P. Fast folding and comparison of RNA secondary structures. Monatsh. Chem. 1994;125:167–188. [Google Scholar]
  22. Hsiao, J.Y., Tang, C.Y., Chang, R.S. An efficient algorithm for finding a maximum weight 2-independent set on interval graphs. Inf. Process. Lett. 1992;43:229–235. [Google Scholar]
  23. Huang, X., Ali, H. High sensitivity RNA pseudoknot prediction. Nucleic Acids Res. 2007;35:656–663. doi: 10.1093/nar/gkl943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Huang, C.-H., Lu, C.L., Chiu, H.-T. A heuristic approach for detecting RNA H-type pseudoknots. Bioinformatics. 2005;21:3501–3508. doi: 10.1093/bioinformatics/bti568. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lyngso, R.B., Pedersen, C.N. RNA pseudoknot prediction in energy-based models. J. Comput. Biol. 2000;7:409–427. doi: 10.1089/106652700750050862. [DOI] [PubMed] [Google Scholar]
  26. Mathews, D., Sabina, J., Zuker, M., Turner, D.H. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
  27. McCaskill, J.S. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
  28. Napthine, S., Liphardt, J., Bloys, A., Routledge, S., Brierley, I. The role of RNA pseudoknot stem 1 length in the promotion of efficient −1 ribosomal frameshifting. J. Mol. Biol. 1999;288:305–320. doi: 10.1006/jmbi.1999.2688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Nateri, A.S., Hughes, P.J., Stanway, G. Terminal RNA replication elements in human parechovirus 1. J. Virol. 2002;76:13116–13122. doi: 10.1128/JVI.76.24.13116-13122.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Nissen, P., Ippolito, J.A., Ban, N., Moore, P.B., Steitz, T.A. RNA tertiary interactions in the large ribosomal subunit: The A-minor motif. Proc. Natl. Acad. Sci. 2001;98:4899–4903. doi: 10.1073/pnas.081082398. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Pleij, C.W.A., Rietveld, K., Bosch, L. A new principle of RNA folding based on pseudoknotting. Nucleic Acids Res. 1985;13:1717–1731. doi: 10.1093/nar/13.5.1717. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Reeder, J., Giegerich, R. Design, implementation, and evaluation of a practical pseudoknot folding algorithm based on thermodynamics. BMC Bioinformatics. 2004;5:104. doi: 10.1186/1471-2105-5-104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ren, J., Rastegari, B., Condon, A., Hoos, H.H. HotKnots: Heuristic prediction of RNA secondary structures including pseudoknots. RNA. 2005;11:1494–1504. doi: 10.1261/rna.7284905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Rivas, E., Eddy, S.R. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J. Mol. Biol. 1999;285:2053–2068. doi: 10.1006/jmbi.1998.2436. [DOI] [PubMed] [Google Scholar]
  35. Rosenblad, M.A., Gorodkin, J., Knudsen, B., Zwieb, C., Samuelsson, T. SRPDB: Signal Recognition Particle Database. Nucleic Acids Res. 2003;31:363–364. doi: 10.1093/nar/gkg107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Ruan, J., Stormo, G.D., Zhang, W. An iterated loop matching approach to the prediction of RNA secondary structures with pseudoknots. Bioinformatics. 2004;20:58–66. doi: 10.1093/bioinformatics/btg373. [DOI] [PubMed] [Google Scholar]
  37. Schroeder, R., Barta, A., Semrad, K. Strategies for RNA folding and assembly. Nat. Rev. Mol. Cell Biol. 2004;5:908–919. doi: 10.1038/nrm1497. [DOI] [PubMed] [Google Scholar]
  38. Sprinzl, M., Horn, C., Brown, M., Ioudovitch, A., Steinberg, S. Compilation of tRNA sequences and sequences of tRNA genes. Nucleic Acids Res. 1998;26:148–153. doi: 10.1093/nar/26.1.148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Staple, D.W., Butcher, S.E. Pseudoknots: RNA structures with diverse functions. PLoS Biol. 2005;3:956–959. doi: 10.1371/journal.pbio.0030213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tabaska, J.E., Cary, R.B., Gabow, H.N., Stormo, G.D. An RNA folding method capable of identifying pseudoknots and base triples. Bioinformatics. 1999;14:691–699. doi: 10.1093/bioinformatics/14.8.691. [DOI] [PubMed] [Google Scholar]
  41. Thiel, V., Ivanov, K.A., Putics, A., Hertzig, T., Schelle, B., Bayer, S., Weissbrich, B., Snijder, E.J., Rabenau, H., Doerr, H.W., et al. Mechanisms and enzymes involved in SARS coronavirus genome expression. J. Gen. Virol. 2003;84:2305–2315. doi: 10.1099/vir.0.19424-0. [DOI] [PubMed] [Google Scholar]
  42. Tinoco, I., Bustamente, C. How RNA folds. J. Mol. Biol. 1999;293:271–281. doi: 10.1006/jmbi.1999.3001. [DOI] [PubMed] [Google Scholar]
  43. Tinoco, I., Wu, M. RNA folding causes secondary structure rearrangement. Proc. Natl. Acad. Sci. 1998;95:11555–11560. doi: 10.1073/pnas.95.20.11555. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. van Batenburg, F.H.D., Gultyaev, A.P., Pleij, C.W.A. An APL-programmed genetic algorithm for the prediction of RNA secondary structure. J. Theor. Biol. 1995;174:269–280. doi: 10.1006/jtbi.1995.0098. [DOI] [PubMed] [Google Scholar]
  45. van Batenburg, F.H.D., Gultyaev, A.P., Pleij, C.W.A., Ng, J., Oliehoek, J. PseudoBase: A database with RNA pseudoknots. Nucleic Acids Res. 2000;28:201–204. doi: 10.1093/nar/28.1.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Williams, K.P. The tmRNA website. Nucleic Acids Res. 2000;28:168. doi: 10.1093/nar/28.1.168. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Xayaphoummine, A., Bucher, T., Thalmann, F., Isambert, H. Prediction and statistics of pseudoknots in RNA structures using exactly clustered stochastic simulations. Proc. Natl. Acad. Sci. 2003;100:15310–15315. doi: 10.1073/pnas.2536430100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zuker, M., Stiegler, P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 1981;9:133–148. doi: 10.1093/nar/9.1.133. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from RNA are provided here courtesy of The RNA Society

RESOURCES