Low dimensionality of supraspinally induced force fields

Abstract

Recent experiments using electrical and N-methyl-d-aspartate microstimulation of the spinal cord gray matter and cutaneous stimulation of the hindlimb of spinalized frogs have provided evidence for a modular organization of the frog’s spinal cord circuitry. A “module” is a functional unit in the spinal cord circuitry that generates a specific motor output by imposing a specific pattern of muscle activation. The output of a module can be characterized as a force field: the collection of the isometric forces generated at the ankle over different locations in the leg’s workspace. Different modules can be combined independently so that their force fields linearly sum. The goal of this study was to ascertain whether the force fields generated by the activation of supraspinal structures could result from combinations of a small number of modules. We recorded a set of force fields generated by the electrical stimulation of the vestibular nerve in seven frogs, and we performed a principal component analysis to study the dimensionality of this set. We found that 94% of the total variation of the data is explained by the first five principal components, a result that indicates that the dimensionality of the set of fields evoked by vestibular stimulation is low. This result is compatible with the hypothesis that vestibular fields are generated by combinations of a small number of spinal modules.

Is the motor behavior of vertebrates based on simple units (“movement primitives”) that can be flexibly combined to accomplish a variety of motor tasks? This fundamental and long-standing question has been addressed from many different perspectives. A recent set of experiments based on electrical and chemical (N-methyl-d-aspartate) microstimulation of the frog’s spinal cord and on cutaneous stimulation of the frog’s hindlimb have provided evidence for a modular organization of spinal cord circuitry (1–4). A “module” is a functional unit of the spinal cord’s circuitry that generates a specific motor output by producing a muscle synergy, a specific pattern of muscle activation. The output of a module can be characterized as a force field. A force field is a mapping that associates each position of the frog’s hindlimb with a corresponding force generated by the neuromuscular system. Force fields have been measured by placing the ankle at different locations in the leg’s workspace and recording at each location the response to electrical stimulation of the same site in the spinal cord. The majority of force fields generated by the stimulation of different areas of the lumbar gray matter of spinalized frogs were found to converge toward an equilibrium point. In addition, the force fields were grouped into a few classes (2). Costimulation experiments have shown further that different force fields can be combined independently. The simultaneous stimulation of two sites in the lumbar gray matter gives rise to a field that is the vector sum of the fields generated at each site separately (5). These observations have led to the hypothesis that the supraspinal systems as well as the spinal reflex pathways may control motor behavior by selecting combinations of spinal modules and linearly combining their force-field output. Such a control scheme may simplify the problem of how a wide repertoire of movements is generated by the central nervous system(6).

To investigate whether the descending pathways generate limb movements and postures as combinations of a small number of modules, we studied the force fields generated by the activation of the vestibular system of the frog. We chose to study the movements produced by the vestibular system for three main reasons. First, the vestibular nerve and the peripheral vestibular apparatus are easily accessible, and a chronic implantation of stimulating electrodes is possible. Second, it is known from anatomical and physiological studies (7–11) that the vestibular afferents, through secondary neurons in the vestibular nucleus, directly project to the lumbar spinal cord. Vestibulospinal fibers therefore could activate directly the different modules in the spinal cord circuitry responsible for the generation of the spinal force fields. Finally, the vestibulo-spinal system is capable of producing a range of different motor outputs (12, 13), making this system suitable for this study.

In this paper, we have tested the hypothesis that the supraspinal systems generate motor output as a linear combination of a small number of force fields by studying the dimensionality of a set of force fields generated by vestibular stimulation. If a supraspinal control structure produces a motor output exclusively through the activation of spinal modules and if the force fields generated are linear combinations of the fields associated with the modules, then the supraspinally induced force fields will lie on the linear subspace generated by the spinal fields. Moreover, if the number of spinal modules is small, the dimensionality of the subspace should be low.

METHODS

Surgical Procedures.

We performed electrical stimulation of the vestibular afferents in seven adult bullfrogs (Rana catesbeiana). All surgeries were performed under standard tricaine anesthesia. The skull was opened dorsally by removing part of the frontoparietal and exoccipital bones. The brain was transected rostral to the brain stem, keeping the roots of the VIIIth cranial nerve and the vestibular nuclear complex intact. The completeness of the transection and the integrity of brainstem were determined visually. In four animals, the ampullae of the horizontal and anterior-vertical semicircular canal were exposed by drilling a small opening in the otic capsule. Two or three fine stainless steel microelectrodes were implanted in both the horizontal and vertical ampullae under visual guidance through a high power microscope. The electrodes were cemented in place by using two small bone screws for support. In the remaining three animals, the VIIIth nerve was approached through the roof of the mouth. A small opening was drilled into the parasphenoid to expose the distal end of the anterior branch of the nerve, which contains only vestibular afferents (14). Two or three insulated silver wires with ≈1 mm of the tip exposed were positioned close to the nerve, and the assembly was cemented to the parasphenoid by using a bone screw as support. In all but one animal, the electrodes were implanted bilaterally.

Stimulation Technique.

Trains of bipolar current pulses applied through pairs of implanted electrodes were used to elicit motor responses. The current was controlled and delivered by a constant-current stimulus isolator (BSI-2, Bak Electronics, Germantown, MD). Train duration ranged between 300 and 600 ms at a frequency ranging between 40 and 100 Hz. The pulse duration ranged between 0.1 and 0.5 ms. The current was increased gradually until a stable response was elicited. Different combinations of electrodes were tried before the experiment, and the motor responses of the unconstrained animal were observed. Only electrode combinations eliciting a clear vestibular reflex, identifiable by the rotation of the head and postural adjustments of the forelimbs and hindlimbs, were used during the experiments.

Data Collection.

For each stimulation condition, we collected a set of isometric force measurements at the ankle over a grid of ankle positions. Animals were placed on a horizontal stand and were immobilized by pelvis and head clamps. The right ankle, at the distal end of the tibia, was attached to a six-axis force transducer mounted on a three-axis Cartesian manipulator. The transducer held the femur and the tibia on a horizontal plane with the ankle at the level of the acetabulum. In each animal, we measured the length of the femur and the tibia from an x-ray of the leg. We also computed the coordinates of a set of ankle positions corresponding to a fixed grid in hip and knee-joint coordinates. The resulting Cartesian grid extended over the same portion of the frog’s leg workspace irrespective of the animal’s size.

A computer was used to trigger the stimulation and to collect the force data. The ankle was placed at each grid position and, after a delay of at least 30 s, a train of stimuli was applied to the vestibular afferents. The force was sampled at 50 Hz for 2 s. The force recording started at least 100 ms before the onset of the stimulation to allow a baseline force measurement.

Force Field Analysis.

A force field is a mapping of a vector, x, and a scalar, t, into a vector F(x, t) that represents the force generated at the ankle, at the location x on the horizontal plane, after a latency t from the onset of the stimulation. We used the measured force vectors at discrete time intervals over a set of ankle locations as a sample of the continuous field. We limited our analysis to the two horizontal components of the force at the time of its peak magnitude. The time of peak magnitude was defined as the time at which the average force magnitude over all locations was maximal. Because we were interested in the active force produced by the stimulation, for each configuration we subtracted the mean force recorded before the onset of the stimulus from the force at the peak time. In cases where repeated measurements at the same location were available, the forces were averaged. To better visualize the structure of the fields, we estimated the forces across the convex hull of the sampled ankle locations by using a piecewise linear interpolation procedure based on a Delaunay triangulation of the data (15).

To compare directly the results from different animals, we transformed the Cartesian coordinates of the ankle positions and the forces into joint coordinates and torques. Because the femur–tibia system constrained into the horizontal plane is nonredundant, it is possible to transform the Cartesian coordinates of the ankle location, x, into hip and knee coordinates, q, and, by using the Jacobian matrix J = δx/δq, the horizontal forces into hip and knee torques (16). For each stimulation condition, the resulting data used for subsequent analysis was, therefore, a vector F of 2N hip and knee torque components, where N is the number of locations sampled.

Dimensionality Analysis.

We investigated the implications of the hypothesis that the supraspinal fields were generated as linear combination of a set of “primitive fields”, that is

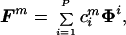where F^m is a supraspinal field, Φⁱ is a primitive field, and c_i^m is the combination coefficient expressing the projection of the mth supraspinal field into the direction of the ith primitive field. If P is the number of independent primitive fields, the subspace of the 2N dimensional vectors (force fields sampled over N configurations) that are combinations of the primitive fields has linear dimension P. This fact implies that, given M samples drawn from this subspace, {F^m}_m=1,M, the sample covariance matrix, s, whose elements re given by

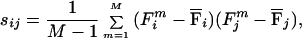has rank P, smaller than the full rank 2N for N large enough.

To study the structure of the covariance matrix, it is convenient to diagonalize it: that is, to perform a principal component analysis (PCA) (17). The principal components constitute an orthonormal basis of eigenvectors of the covariance matrix. Therefore, the eigenvalues of the covariance matrix represent the variance of the data when projected along each of the principal components. The sum of the first n largest eigenvalues divided by the sum of all of them represent the proportion of the total variation, tr(s), explained by the respective n principal components. Therefore, the first P principal components will explain all of the variation present in the data if the covariance matrix has rank P.

If we take into account the presence of random noise in the data, the model can be rewritten as:

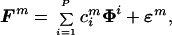where ɛ^m is a random vector with covariance Σ. In this case, the covariance matrix will in general have full rank. Nonetheless, if the total variation of the noise, tr(Σ), is small compared with the total variation caused by the combination of primitives, most of the variation of the data will be explained by the first P principal components. Using those fields for which repeated measurements of the force at each position were available, we estimated tr(Σ) as the mean of the traces of the sample covariance matrices of each of the fields.

We also performed a PCA on a set of random fields whose components were generated independently to have a set with the highest possible dimensionality to compare with the observed vestibular set. A number of fields equal to the number of observed fields were generated from a multinormal distribution with diagonal covariance equal to the diagonal elements of the covariance matrix of the data. The fraction of total variation explained by the first n components was computed for these random fields, and the procedure was repeated for 1,000 sets of fields to estimate mean value and SD.

RESULTS

Ankle Forces Generated by Vestibular Stimulation.

A brief electrical stimulation of the anterior branch of the vestibular nerve generated a pulse of force at the ankle. The force directions were constant during the duration of the pulse. The time course of the force’s magnitude recorded at different ankle locations under the same stimulation condition was, in most cases, a scaled version of the same waveform (Fig. 1). Consequently, the structure of a force field did not change over time, and it was well described by the forces at their peak magnitude.

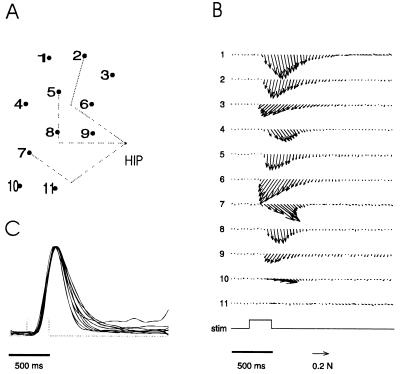
Figure 1.

The construction of a force field. (A) Grid of ankle positions in the horizontal plane used to measure the isometric forces (dorsal view of the right leg; top is caudal and bottom is rostral). The dotted segments represent the position of the femur and the tibio-fibula in three different configurations. (B) Time course of the horizontal forces generated at different ankle locations by the same train of impulses applied to the vestibular nerve (the number on the left of each trace corresponds to the number of the location on the grid). The envelope of the stimulation train is shown in the trace labeled “stim.” (C) Time course of the normalized magnitude of the horizontal forces generated at different ankle locations by the same stimulation. The forces at the time of the maximal magnitude are used to construct the force field.

Vestibular Fields.

We observed different types of responses to different stimulation conditions. We stimulated either the left or the right vestibular nerve and, on each side, different combinations of electrodes. In the animals with dorsal implants, force fields were obtained by stimulating different pairs of electrodes in the horizontal and in the vertical ampullae. In the animals with ventral implants, force fields were obtained by stimulating different pairs of the three electrodes implanted close to the distal end of the anterior branch of the nerve. In general, the force orientations varied smoothly throughout the leg’s workspace. Different fields were characterized by different average orientations, which appeared to be distributed continuously from rostral to lateral to caudal. In Fig. 2, sample fields recorded in four different animals are shown.

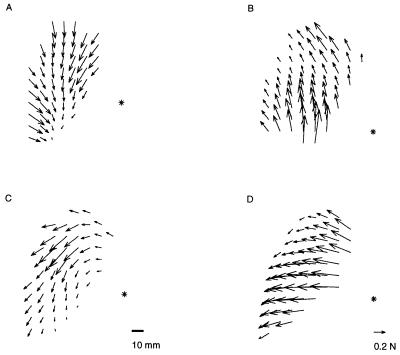
Figure 2.

Sample vestibular force fields from four different animals. The asterisk indicates the position of the frog’s right hip. The forces shown are obtained by a linear interpolation of the measured forces over a dense grid. The field in A is the same detailed in Fig. 1.

Dimensionality of Vestibular Fields: Principal Component Analysis.

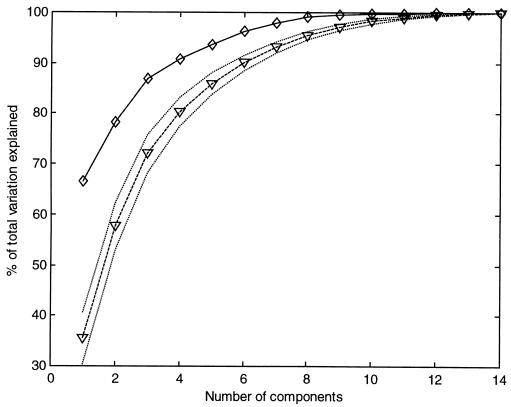
To investigate the hypothesis that the observed vestibular fields were produced from the combination of a small number of primitives, we studied the covariance structure of a set of 20 vestibular fields. We performed a PCA on this set of 20 14-dimensional vectors, composed by the hip and joint torque collected over the same seven configurations for each of fields. As described in the Methods section, we computed the proportion of the total variation explained by the first n principal component as a function of n (Fig. 3). We found that 91% of the total variation was explained by the first four principal components, and 94% was explained by the first five. The total variation of a vestibular field due to experimental noise was estimated to be 9 ± 4% of the total variation of the data. This result indicated that the dimensionality of the set of vestibular fields is low.

Figure 3.

Result of the principal component analysis and comparison with random fields. The solid line represents the fraction of the total variation explained by the first n principal components as a function of n computed for the vestibular data. The broken line represents the same quantity computed for an equal number of randomly generated fields with maximal dimensionality. The dotted lines are one SD above and below the mean.

To test the sensitivity of the PCA method, we randomly generated a set of 20 fields with maximal dimensionality (see Methods). We then compared the result obtained with PCA of the vestibular fields with that of the random fields. As seen in Fig. 3, the curve of the fraction of total variation explained as a function of the number of principal components for the random fields is significantly below the curve for the vestibular fields.

DISCUSSION

The analysis of vestibular force fields presented here shows that the dimensionality of a set of supraspinally induced force fields is low. This result indicates that the supraspinal set can be expressed as combinations of a small number of primitive fields.

Such a result is compatible with the hypothesis that supraspinal fields are linear combinations of a small number of fields generated by the modules of the spinal cord circuitry. The existence of spinal modules in the frog’s spinal cord has been shown by electrical and chemical microstimulation (2, 3). Costimulation of different modules has shown that the spinal force fields combine linearly; a field elicited by the simultaneous stimulation of two sites is the vector sum of the fields generated at each site separately (5). The supraspinal structures, therefore, could activate the spinal modules and generate a variety of force fields simply by controlling the time-varying set of coefficients in the linear combination of the spinal force fields. This control scheme provides a simple account of how the central nervous system may generate the motor output required for a particular task. The central nervous system would represent the desired output as a force field and would select the combination of spinal force fields that best approximate the output (6). According to this hypothesis, the motor-control system would be solving a vector-field approximation problem, an operation that does not require the knowledge of the internal structure of the controlled system (i.e., the musculoskeletal apparatus) but only to have a representation of the force fields generated by each module. A recent simulation study (18) has shown how a three-layered neural network can implement a mechanism by which supraspinal structures activate spinal modules whose force field output are linearly combined.

Although further investigations will be necessary to identify what kind of primitives give rise to the vestibular fields, the observation of the low dimensionality of the supraspinal fields provides an unexpected and remarkable insight into the operation of the motor-control system.

ABBREVIATION

PCA

principal component analysis