Recombinant Temporal Aberration Detection Algorithms for Enhanced Biosurveillance

Abstract

Objective

Broadly, this research aims to improve the outbreak detection performance and, therefore, the cost effectiveness of automated syndromic surveillance systems by building novel, recombinant temporal aberration detection algorithms from components of previously developed detectors.

Methods

This study decomposes existing temporal aberration detection algorithms into two sequential stages and investigates the individual impact of each stage on outbreak detection performance. The data forecasting stage (Stage 1) generates predictions of time series values a certain number of time steps in the future based on historical data. The anomaly measure stage (Stage 2) compares features of this prediction to corresponding features of the actual time series to compute a statistical anomaly measure. A Monte Carlo simulation procedure is then used to examine the recombinant algorithms’ ability to detect synthetic aberrations injected into authentic syndromic time series.

Results

New methods obtained with procedural components of published, sometimes widely used, algorithms were compared to the known methods using authentic datasets with plausible stochastic injected signals. Performance improvements were found for some of the recombinant methods, and these improvements were consistent over a range of data types, outbreak types, and outbreak sizes. For gradual outbreaks, the WEWD MovAvg7+WEWD Z-Score recombinant algorithm performed best; for sudden outbreaks, the HW+WEWD Z-Score performed best.

Conclusion

This decomposition was found not only to yield valuable insight into the effects of the aberration detection algorithms but also to produce novel combinations of data forecasters and anomaly measures with enhanced detection performance.

Introduction

Modern automated syndromic surveillance systems can be divided into three steps. In the first step (denoted preprocessing or preconditioning), medical records such as emergency room visits or over-the-counter medication sales are filtered and aggregated to form daily counts, proportions, weekly aggregates, or other quantities based on predefined syndromic classifications. These classifications are generally fixed but may also be created or altered dynamically in response to public health information. In the second step (aberration detection), algorithms are used to detect temporal and/or spatial changes in the preprocessed data that may be indicative of a disease outbreak. In the third step (response), surveillance system users manage alerts by seeking corroboration across time, space, and other sources of evidence and initiating a public health response when appropriate. A demonstrably consistent algorithm improvement can often be rapidly integrated into an operational system, offering immediate return on investment. Increased specificity translates directly into reduced resource requirements because users have fewer alarms to investigate. In this article, we investigate one novel approach to discovering such new algorithms to obtain increased detection performance.

Background

Over the past ten years, various researchers have developed numerous algorithms for the detection of aberrations (Step 2) in univariate time series, drawing from such diverse fields as statistical process control, radar signal processing, and finance. The C1 and C2 algorithms of the Centers for Disease Control and Prevention’s (CDC’s) Early Aberration Reporting Systems (EARS) are based on the Xbar control chart, ¹ and C3 is related to the Cumulative Summation (CUSUM) chart. Reis et al. have used a trimmed-mean seasonal model fit with an Auto-Regressive Moving Average coupled to multiday filters. ^2,3 Brillman et al. have used regression-based models. ⁴ Naus and Wallenstein examined the Generalized Likelihood Ratio Test (GLRT) applied to time series. ⁵ The Electronic Surveillance System for Early Notification of Community-based Epidemics (ESSENCE) biosurveillance systems automatically select between a regression-based algorithm and an adaptive Exponentially Weighted Moving Average (EWMA) chart, with the selection determined by a goodness-of-fit measure for the regression model. ⁶ Burkom et al. ⁷ obtained promising results in adapting the generalized exponential smoothing technique of Holt and Winters ^8,9 to biosurveillance data.

As the field of biosurveillance continues to expand, the situation for researchers and practitioners has become unclear at best. Temporal aberration detection algorithms continue to increase in complexity even while more enter the literature. No general consensus exists as to which algorithm is most effective at detecting potential outbreaks, even though some of these algorithms are deployed in operational biosurveillance systems. Even if all algorithms were freely available (many are proprietary), it is resource intensive for individual researchers to evaluate the performance of each algorithm on their own data.

Exacerbating this situation is the diversity of syndromic time series that challenges the algorithms. Some series have a median count of zero, whereas others have a median in the hundreds. Some exhibit complex cyclic behaviors including day-of-week (DOW) effects and seasonal fluctuations. For the time series derived from data sources with multiple locations such as hospital groups or pharmacy chains, the series’ statistical properties can change significantly over the course of months and even weeks as the participation of large-scale data providers increases or decreases and as data processing systems and networks improve. Finally, the manifestation of a potential outbreak in a time series may be significantly impacted by a number of different factors, including the pathogen, its infectivity, the method of introduction to the susceptible population, and the population’s underlying social network. Thus, the unknown shape of the resulting time series signal adds another layer of complexity to the problem. With numerous algorithms, data types, and outbreak shapes, two very important questions remain: Which temporal aberration detection algorithm works best on a specific combination of data type and outbreak, and why?

To help answer these questions, we decompose temporal aberration detection algorithms into two sequential stages. The first, the forecast stage, attempts to capture the expected behavior of the time series in the absence of an outbreak signal. The second, the anomaly measure stage, produces a test statistic based on the difference between the observed and expected data. Both stages are not always explicit and may be abbreviated or omitted in some temporal aberration detection algorithms.

Stage 1: Data Forecast

The data forecasting stage uses some historic portion of the time series to make n-sample-ahead predictions of the expected number of counts. Stage 1 can be simple or complex. The simplest forecaster would simply use the previous day’s value or the value from a week ago without further modification. The EARS family of algorithms—C1, C2 and C3—all use a 7-day moving average to generate the expected values. The only difference among forecasts in these techniques is that C1 uses the last 7 days of data whereas C2 and C3 use data from 3 to 9 days in the past, ignoring the current and two most recent days of data. This 2-day buffer, referred to as a guardband, helps to prevent outbreak effects from contaminating the predictions. The g-scan implementation in Wallenstein and Naus ⁵ used a spline fit of historic data for estimation purposes.

Data forecasters can also be adaptive, updating their procedures based on recent data. The Holt-Winters exponential smoother makes predictions using three components: a simple exponential smoother, an adjustment for trends, and a cyclic multiplier to handle repetitive patterns. Brillman et al. ⁴ fit an ordinary least-squares loglinear model to a set of training series values to obtain regression coefficients. These coefficients are used to extrapolate for expected values beyond the training data. Regardless of the complexity of the forecaster, one of the fundamental assumptions in this stage is that the disease outbreaks cannot be predicted a priori. In other words, it is assumed that the predicted series will not contain an outbreak signal and that the appropriate comparison to the actual data will allow timely outbreak identification. For detection of gradual signals, this assumption necessitates the use of a temporal guardband between the baseline period and the interval to be tested to avoid loss of sensitivity because of the presence of the early part of the outbreak signal in the baseline.

Stage 2: Anomaly Measurement

For each time interval in which data are to be tested, the anomaly measurement stage calculates a numeric value to quantify the severity of positive differences between observation and prediction. Even though unusual decreases in a time series can result from a public health event (imagine a dropoff in reported values caused by an emergency that interrupts the reporting procedure), the need to control alert rates for sensitivity to high values mandates that such overpredictions not be tested for anomaly. The calculated numeric value or test statistic can then be used to decide whether or not to investigate the cases causing the anomaly for evidence of a public health event.

Typically, the comparison between observed and forecast values is a simple differencing, resulting in a time series of residuals that are then used to form a test statistic as the basis for an alerting decision. Many anomaly measures normalize the residuals either explicitly or implicitly to account for natural variance in the baseline data. The Z-Score, related to the Xbar chart of statistical quality control, performs this normalization explicitly by dividing the residual by a standard deviation estimate. The quotient then serves as the test statistic. The 7-day filtering method employed by Reis does not normalize explicitly but attempts to account for global variability with the determination of an empirical alerting threshold. Often, statistical process control charts such as the CUSUM or EWMA chart are used for the anomaly measure stage.

Motivation

Decoupling temporal aberration detection algorithms affords several potential advantages. ▶ lists a variety of published algorithms and shows one way of decomposing them into two stages. Many combinations of these implementations are possible, but few have been explored. Once an algorithm becomes associated with a specific organization, publication, or acronym, developers, implementers, and users treat the underlying combination of forecast and anomaly measure stages as a monolithic unit, preventing alternative combinations from being explored. However, this study’s findings demonstrate that novel couplings of data forecasters and anomaly measures can yield enhanced algorithms. Individual consideration of each stage may suggest new approaches or variations to explore. Either Stage 1 or Stage 2 can be fixed while varying the other stage for testing on a certain type of data and/or outbreak effects. Finally, examining the multitude of possible permutations may also help categorize existing techniques and, importantly, understand performance differences among them. The only caveat is the necessity to ensure that the assumptions demanded of the input into the second stage are met by the output produced by the first; otherwise, nonsensical results could be produced.

Table 1.

Table 1 Decomposition of Several Existing Aberration Detection Algorithms from the Literature into Data Forecast and Anomaly Measure Stages

Algorithm	Data Forecasting	Anomaly Measure	Threshold
Fixed Data Threshold	Not applicable	Not applicable	Predetermined number of counts
C1 (EARS)	Moving average with 7-Day window	Z-Score	Three standard deviations above the mean (7-day)
C2 (EARS)	Moving average with 7-day window and 2-day guardband	Z-Score	Three standard deviations above the mean (7-day)
C3 (EARS)	Moving average with 7-day window and 2-day guardband	Sum of last three Z-Scores	Three standard deviations above the mean (7-day)
Reis [3]	Auto regressive moving average applied to trimmed seasonal model	7-day filter applied to residuals	Empirically derived based on desired sensitivity
GScan [5]	Spline fit to historic data	GLRT applied to sum of values in fixed-size moving window	Empirically derived based on simulation studies
Brillman [4]	Loglinear regression model with a fixed baseline	Page’s test applied to the residuals in log space	Empirically derived

This study decomposes several popular temporal aberration detection algorithms—an adaptive regression, a Holt-Winters exponential smoother, sliding z-score variations generalizing the EARS family of algorithms, and a temporal scan statistic—into two stages. We then evaluate the effectiveness of all possible recombinant temporal aberration detection algorithms assembled from the possible combinations of the various stages for the detection of two different types of stochastically generated outbreaks inserted into authentic syndromic time series. Our hypothesis is that there exist novel combinations that yield improved detection performance over a broad class of background data and target signal types.

Methods

The goal of our study was to decompose existing algorithms into two separate stages and evaluate the outbreak detection performance of different combinations of these stages. The outbreak detection capabilities of the various Stage 1 and Stage 2 combinations were evaluated on real syndromic data with stochastically generated outbreak signals inserted in repeated Monte Carlo simulation runs.

Background Data

The background data for this study were time series of aggregated de-identified counts of health indicators derived from the BioALIRT program conducted by the U.S. Defense Advanced Research Projects Agency (DARPA). ¹⁰ (The appropriate formal agreements to use these data were signed by the authors. Others wishing access may contact the corresponding author for the required procedures.) This data set contains three types of daily syndromic counts: military clinic visit diagnoses, filled military prescriptions, and civilian physician office visits. These records, gathered from ten U.S. metropolitan areas, were categorized as Respiratory (RESP), Gastrointestinal (GI), or Other. Although 30 time series were available, 14 series were excluded because they contained artifacts such as temporary dropouts and permanent step increases not representative of routine consumer behavior or disease trends. The remaining 16 included 10 time series of RESP counts and 6 time series of GI counts, each 700 days in length. All series demonstrated strong DOW effects with a difference of over 200 between median weekday and weekend counts. The RESP series also demonstrated cyclic annual fluctuations, peaking during the winter season; whereas, the GI series did not.

Stochastic Injects

For the signal to be detected, injected cases attributable to a presumed outbreak were added to the background data. Our injection process assumes that the number of outbreak-attributable data counts on a given day is proportional to the number of newly symptomatic cases on that day. We consider the signal to be the number of additional data counts attributable to a point-source outbreak on each day after exposure; together, these attributable counts form the “data epicurve.” These data epicurves were stochastically drawn from two different lognormal distributions chosen to represent outbreaks that were sudden or gradual relative to the data time scale. The first, representing a sudden 1- to 3-day jump in cases (Spike), used lognormal parameters ζ = 1 and σ = 0.1. (See Sartwell et al. for details). ¹¹ The second outbreak type, representing a more gradual rise in the number of cases over time (SlowRise), used ζ = 2.4 and σ = 0.3. The stochastic epicurves were drawn from the resulting lognormal distribution. To challenge the algorithms, we set the total number of cases, N, of the outbreak one, two, three, or four times the standard deviation of the 4 weeks of detrended background data immediately preceding the start of the injected outbreak. Individual incubation periods were then chosen with a set of N random lognormal draws and rounded to the nearest day. The number of cases added to the observed case count each day after the outbreak onset was equal to the number of draws rounded to that day.

For each Monte Carlo trial, a single stochastic epicurve was injected (added) to a background time series as previously described, beginning at a randomly chosen start day beyond an 8-week startup period. This startup period was to accommodate the longest warmup interval required by any of the methods chosen for testing. Each data forecaster was then applied successively to make predictions of the time series after inject counts had been added to the selected subinterval of the authentic data. Residuals were computed from each set of predictions (generated by each data forecaster) and were then run through each anomaly measure, producing a time series of test statistics for possible alerting for each forecaster/anomaly measure combination. This process was repeated 600 times for each possible combination of syndromic time series, outbreak size, and outbreak type. The number of trials was chosen heuristically to obtain stable estimates of detection probability in reasonable simulation execution time.

As the precise start and stop day of each outbreak signal were calculated and saved, an exact determination of an algorithm’s performance could be determined. We accounted for the nonuniform, sometimes multimodal and long-tailed shape of the stochastic outbreak signals by counting toward empirical detection probabilities only those anomaly measure values from days containing the first 80% of total inject counts. Thus, algorithms were not credited for late detections of no use to public health response. Receiver Operator Characteristic (ROC) curves were generated, summarizing the relationship between the probability of detection (sensitivity, y-axis) and the probability of a false alarm (specificity, x-axis) for a range of practical detection threshold values. The same set of epicurves and outbreak start dates was used for testing each forecaster/anomaly measure pair to minimize the variance of the findings, a technique known as common random numbers. ¹²

Decoupling Aberration Detection Algorithms

Six different data models were used to generate n-day-ahead predictions of time series with and without injects.

Exponentially Weighted Moving Average (EWMA)

The first predictor used was a simple exponential moving average using a smoothing coefficient α of 0.4. If y(t) represents the original time series and p(t) represents the smoothed or predicted time series, the EWMA prediction is given by

(1)

(2)

Moving Average (MovAvg)

The second and third predictors used moving averages with window lengths of 7 (MovAvg7) and 56 days (MovAvg56), respectively. The shorter-window average represents the expected value used in the EARS algorithms, ¹ and the longer one was added to give less volatile baseline parameters for more stable predictions.

Weekend/Weekday Moving Average (WEWDMovAvg)

The fourth predictor used the average of the last 7 weekdays or weekend/holiday days to predict n days ahead according to whether the day of the predicted count was a non-holiday weekday. ¹³ This stratification of the simple moving average reflects the W2 modification being tested by the BioSense program. ¹⁴

Holt-Winters General Exponential Smoother (HW)

The fifth predictor used was a generalized exponential smoother based on the Holt-Winters method detailed by Burkom et al. ⁷ In that reference, this approach compared well against regression models on a day-to-day prediction basis. Along with the level L_t, the method includes two additional recursive terms, one for the trend T_t and one for a seasonal component S_t. The k-step ahead forecast is given by

(3)

where M is the number of seasons in a cycle (e.g., for a monthly periodicity M=12); L_t, T_t, and S_t are updated as follows:

(4)

(5)

(6)

The three smoothing coefficients, α, β and γ, were fixed at 0.4, 0, and 0.15, respectively.

Adaptive Regression

The last predictor was an adaptive regression model with a sliding 8-week baseline interval. ⁴ This model is given by

(7)

where c₁-c₆ are coefficients for DOW indicators, c₈ is a constant intercept, c₉ is the slope of a linear trend using a centered ramp function, and c₁₀ is a coefficient for a holiday indicator. This method recomputes the regression coefficients for each forecast using only the series values from the 8 weeks before the forecast day. The short baseline is intended to capture recent seasonal and trend patterns. The holiday indicator helps to avoid exaggerated forecasts on known holidays and also avoid the computation of spurious values for c₁-c₇ when holidays occurred in the short baseline interval. A similar model is applied for anomaly detection in ESSENCE biosurveillance systems when an automated goodness-of-fit criterion is satisfied. ⁶

The number, n, of advance prediction days was set to 2 for the detection of spike outbreaks and to 7 for the slow-rise outbreaks. The purpose of this look ahead or prediction buffer is to prevent the early portion of an outbreak from contaminating the segment of recent data used for time series prediction. In practice, depending on monitoring objectives, one would choose a single value for n or could use multiple values for general surveillance capability.

We used six different anomaly measures to compute test statistics from the observed values and the model predictions.

CUSUM

The first anomaly measurement method used in this study was the fast initial response variation of a cumulative summation applied to the Z-Score of the forecast residuals. If z_t represents the Z-Score of the residuals, the CUSUM, S_t, is given by

(8)

with k set to 1. ¹⁵ When the detection statistic exceeded a reset threshold of 4, the sum was set back to 2 to retain rapid response capability as in ¹⁵ .

Adaptive EWMA

The second anomaly measure, an EWMA-based algorithm, smoothes a time series of forecast residuals using dual smoothing coefficients of 0.4 and 0.9 for sensitivity to gradual and spike outbreaks. ⁶ The measure then computes a modified Z-Score (z_0.4, z_0.9) for each of the two smoothed series of residuals, scaling for the length of the baseline used (28 days for this study), and returns the probability that the test statistic will fall in the interval [-infinity, max(z_0.4, z_0.9)] given a t-distribution with 27 degrees of freedom.

G-Scan Statistic (gScan)

The third and fourth methods implemented the g-scan statistic, G_t(w), described by Naus and Wallenstein with a 7-day and 3-day window, respectively, shown in the following equation ⁵

(9)

09 where Y_t(w) represents the number of counts in the time series within window, w, and E_t(w) captures the expected number of counts within the window using the predictions provided by the data forecaster.

Z-Score

The fifth method computed a Z-Score based on the prediction residuals (actual count minus predicted count), with the mean of the previous 28 days of residuals subtracted from the current estimate and divided by the standard deviation of the last 28 residuals as given by

(10)

Weekend/Weekday Z-Score (WEWD Z-Score)

The sixth method, the weekend/weekday (WEWD) Z-Score, is a slight modification to the Z-Score. For the WEWD baseline, we restricted residuals to the last 28 weekdays. Similarly, when computing the output for a prediction of a weekend day or a holiday, only weekend/holiday residuals were used.

All data forecast and anomaly measure stages used and that adjust for holidays use the following set of dates: New Year’s Day, the Birthday of Martin Luther King, Jr., Washington’s Birthday (Presidents’ Day), Memorial Day, Independence Day, Labor Day, Columbus Day, Veterans Day, Thanksgiving Day, and Christmas Day.

Performance Measurement

The six data models coupled to each of the six anomaly detectors yielded 36 temporal aberration detection algorithms. Each of these 36 composites was applied to the 16 different background time series discussed in the section called Stage 1: Data Forecast. Each algorithm/background pair was tested with two different inject types (spike and slow-rise), each with four different sizes (one, two, three, and four times the standard deviation of the detrended data). Computations in this procedure produced 4608 ROC curves. We extracted two summary scalar measures from each such curve to simplify the analysis. The first measure was a detection probability denoted PD84 and taken from the point of the ROC curve corresponding to an expected background alert rate of one every 84 days or 12 weeks. The second measure was the average detection probability for expected alarm rates between one per 16 weeks and one per 12 weeks, denoted Area because it was computed as the percentage area under the portion of the ROC curve deemed relevant for public health monitoring. Because of the large volume of data generated, Spotfire Design Explorer (DXP) (http://www.spotfire.com/products/dxp_pro.cfm) was used to rapidly visualize the relationships among all variables and to produce several of the graphs in this publication.

Results

Sample Results

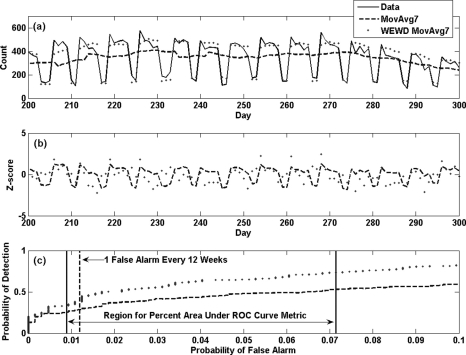
▶ displays sample output from each stage (forecast and anomaly measure) of two different, decomposed aberration detection algorithms applied to one RESP time series along with an ROC curve, demonstrating the two recombinant algorithms’ performance. Panel (a) shows the original time series (solid black line) along with the output of the data forecasting stage for two different forecasters, a 7-day moving average (MovAvg7, dashed line) and the WEWD 7-day moving average (WEWD MovAvg7, dotted line). The time scale, in days, shows a magnified portion of the 700-day series. Panel (b) shows the output of the Z-Score anomaly measure applied to the MovAvg7 residuals (dashed line) and the WEWD MovAvg7 residuals (dotted line) calculated from the values plotted in panel (a).

Figure 1.

Prediction output of two different data forecasters applied to an RESP time series; (a) output of Z-Score anomaly measure applied to the corresponding residuals and (b) resulting ROC curves produced with Monte Carlo simulation.

From panel (a), it is apparent that the series predicted by MovAvg7 lacks the original data’s weekly trend, resulting in residuals with undesirable DOW fluctuations. The Z-Score values in panel (b) also show a strong DOW trend when based on the MovAvg7 predictor output and a slight 7-day fluctuation when based on the WEWD MovAvg7. Neither forecaster completely eliminates the weekly pattern from the original data, resulting in biased output from the anomaly measure stage and decreased detection performance. Decomposing the algorithms into constituent stages helps to identify and isolate this problem. Notably, the MovAvg7+Z-Score predictor-detector combination is used indiscriminately by many public health institutions for routine health monitoring.

Panel (c) demonstrates the ROC curves produced with the Monte Carlo stochastic inject simulation using a spike outbreak (1-σ signal: total injected cases set to one standard deviation above the mean) for the two aberration detection algorithms from panel (b) (using the same line-marking scheme) and graphically illustrates the two performance metrics. PD84 is the y-value or detection probability at the intersection of the dashed vertical line and the ROC curve, and Area is the percentage of area beneath the ROC curve between the two solid vertical lines. The aggregate information of the ROC curve cannot show that the DOW problem is the principal cause of the performance difference. One benefit of algorithm decoupling is to clarify such sources of bias.

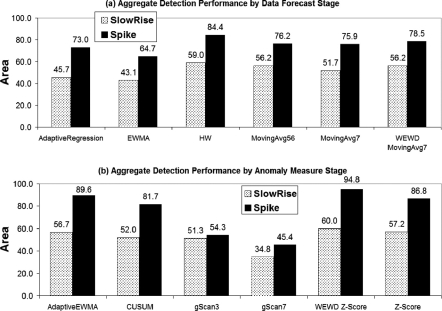
Aggregate Results

Because this study yielded several thousand results, we begin this analysis by first examining highly aggregated results before performing more stratified analyses. Each of the 36 possible aberration detection algorithms resulting from the different combinations of data forecasters and anomaly measures was applied to the 16 time series as in ▶. ▶ presents two bar charts with each bar in both panels representing the average Area detection metric with one of the two algorithm stages held constant. On the left, panel (a) shows the Area detection metric for each data forecaster averaged over all other variables (outbreak size, time series, and anomaly measure). On the right, panel (b) shows the Area detection metric for each anomaly measure averaged over all other variables (outbreak size, time series, and data forecaster). Because of the similarity of the data series in scale and in behavior, we averaged the Area measures over all 16 time series in these charts. The top chart gives these averaged measures for SlowRise outbreaks and the bottom chart for Spike outbreaks. The solid dark line shows the average performance across all recombinant algorithms for the associated outbreak type.

Figure 2.

Comparison of performance influence of all algorithm stages using relevant detection probabilities averaged across all time series and 3- and 4-sigma outbreak sizes for (a) data forecast stages averaged across all anomaly measure stages and (b) anomaly measure stages averaged across all data forecast stages.

Performance of the recombinant algorithms was greater for Spike than SlowRise outbreaks with an average Area of approximately 60% versus 43%. This observation is a result of the evaluation methodology for the two signal types and the relative difficulty of detection. The SlowRise outbreaks are variably intermittent events spread over a 2- to 3-week interval, and they are important because they represent the likely data effects of non-communicable disease outbreaks for which the disease has a long incubation period, as well as communicable disease outbreaks with certain transmission characteristics.

When the anomaly measure was held constant, recombinant algorithms using either the HW or WEWD MovingAvg7 data forecasters yield the highest aggregate performance for SlowRise outbreaks, and the HW data forecaster yielded the best performance for Spike outbreaks. When the data forecaster was held constant, recombinant algorithms using the WEWD Z-Score were followed by the Z-Score because their anomaly measure offered the top performance for SlowRise outbreaks. In the case of Spike outbreaks, recombinant algorithms using the WEWD Z-Score followed closely by the AdaptiveEWMA yielded the best performance.

▶ shows Area performance results averaged over 3- and 4-sigma outbreaks and all 16 time series for SlowRise outbreaks in the top chart and Spike outbreaks in the bottom chart. Data forecasters are listed vertically as rows (top performer in a column is bold), and anomaly measures are listed horizontally as columns (top performer in a row is shaded) to explore the individual contributions of each stage of the recombinant algorithms. The top four performing recombinant algorithms in each section of the table are denoted parenthetically.

Table 2.

Table 2 Percent Area Under the ROC Curve Averaged Across All 16 Data Series and 3- and 4-sigma Outbreak Sizes for All Possible Combinations of Data Forecasters and Anomaly Measures for Both SlowRise and Spike outbreaks

	CUSUM	Adaptive EWMA	GScan3	GScan7	Z-Score	WEWD Z-Score	Mean	Range
SlowRise
EWMA	37.97	46.19	46.61	37.74	46.91	43.13	43.097	9.17
MovAvg7	50.02	53.59	51.32	33.43	59.81	61.97	51.69	28.54
MovAvg56	54.16	57.44	55.97	42.61	63.50	63.66 (4)	56.22	21.05
WEWD MovAvg7	57.67	65.84 (2)	52.32	34.21	58.31	68.69 (1)	56.17	34.48
Holt Winters	58.16	61.22	65.13 (3)	46.51	59.81	63.28	59.02	18.62
AdaptiveRegression	53.82	55.66	36.33	14.02	54.64	59.47	45.66	45.45
Mean	51.97	56.66	51.28	34.75	57.16	60.03
Range	20.19	19.65	28.8	32.49	16.59	25.56
Spike
EWMA	71.17	71.00	59.25	48.18	58.78	79.70	64.68	31.52
MovAvg7	74.83	86.20	68.62	43.56	83.92	98.12	75.88	54.56
MovAvg56	74.01	86.80	60.77	53.52	84.51	97.35	76.16	43.83
WEWD MovAvg7	93.08	98.78 (2)	45.73	38.73	97.39	97.57	78.55	60.05
Holt Winters	95.27	98.76 (3)	50.57	63.98	98.73 (4)	98.90 (1)	84.37	48.33
AdaptiveRegression	82.14	96.33	40.67	24.23	97.60	97.29	73.04	73.37
Mean	81.75	89.65	54.27	45.37	86.82	94.82
Range	24.10	27.78	27.95	39.75	39.95	19.20

▶ demonstrates several general results. Large performance differences among the various recombinant algorithms are apparent, with high scores observed for some unexpected/untested combinations of data forecasters and anomaly measures. For SlowRise outbreaks, the top four algorithms were WEWD MovingAverage7+WEWD Z-Score (68.69%), WEWD MovingAverage7+AdaptiveEWMA (65.84%), HW+gScan3 (65.13%), and MovingAvg56+WEWD Z-Score (63.66%). For Spike outbreaks, the top four algorithms, all tightly clustered, were HW+WEWD Z-Score (98.90%), WEWD MovAvg7+AdaptiveEWMA (98.78%), HW+AdvancedEWMA (98.76%), and HW+Z-Score (98.73%). All of these combinations included at least one stage that modeled the prominent DOW effect, and the best values came from the combination that included day-of-week effects in both stages.

The detection scores of the WEWD Z-score were consistently high for Spike outbreaks and relatively high for SlowRise signals. The combination of this detector with MovAvg7 is much like the W2 algorithm under testing by the BioSense program at CDC. ¹⁴ A likely explanation of the relative performance of this stratified Z-Score is that none of the other detectors accounts for either modeled or unmodeled DOW effects in residuals and the weekly pattern is the most prominent feature of the city-level data series of this study.

The six anomaly measures produced their weakest results when coupled with the EWMA forecaster, although the EWMA-based anomaly detector performed well. The gScan anomaly measures gave poor performance for Spike outbreak detection for 3- and 7-day window sizes, regardless of the underlying forecaster. Area measures for 7-day gScan were also low for the SlowRise outbreaks. These findings agree with past experience that, for syndromic data, the utility of the gScan methods is for sparse data streams unlike those of the current study. Furthermore, coupling the AdaptiveRegression forecaster to either gScan anomaly measure resulted in a larger performance drop when compared to other forecasters, suggesting that the predictions made by the AdaptiveRegression forecaster were particularly ill-suited for this anomaly measure.

Among the six forecasters (rows) of ▶, the bottom three account in some way for the DOW patterns, whereas the top three ignore these patterns. As noted, the gScan algorithms are not well matched to the study data, and if we set the gScan columns aside, the anomaly detector Area measures are almost uniformly higher for the bottom three forecasters for both types of signal. For the Spike outbreaks, this difference is over 10% for the CUSUM, EWMA, and Z-Score detectors; this difference is small but consistent for the WEWD Z-Score. The only exception to the advantage of the DOW modeling is that the Z-Score detector for SlowRise outbreaks has a higher score for the MovAvg56 (63.50) forecaster than for the WEWD MovAvg7 (58.31), and this difference is likely a combination of the volatility of the 7-day baseline of the latter forecaster and the difficulty of detection of the SlowRise signals.

It is interesting to compare the Area scores of the WEWD Z-score (which accounts for DOW effects) and the Z-score (that does not) applied to the three data forecasters that include DOW adjustment. The small but consistent improvements of the WEWD Z-score suggest that the residuals produced by these three data forecasters still contain DOW effects that may bias aberration detection. Furthermore, the performance jump for WEWD Z-Score versus Z-score Spike outbreak detection applied to residuals of the EWMA and moving average forecasters is sizable and seemingly indicates that the anomaly measure alone can effectively correct for DOW and DOW correction is more important for Spike detection than gradual signal detection because of the relative temporal concentration and difficulty of detecting these signal types.

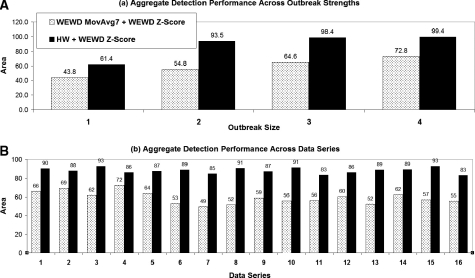
▶ shows results for the top performing SlowRise (left) and Spike (right) recombinant algorithms (WEWD MovAvg7+WEWD Z-Score and HW+WEWD Z-Score, respectively) stratified by outbreak size and time series. In panel (a), the gray bars show the Area detection metric of the WEWD MovAvg7+WEWD Z-Score recombinant algorithm applied to different size SlowRise outbreaks; whereas, the black bars show the Area detection metric of the HW+WEWD Z-Score recombinant algorithm applied to different size Spike outbreaks. The Area detection performance metric scaled linearly with SlowRise outbreak size. Also, there appears to be a large jump in detection capability for HW+WEWD Z-Score algorithm applied 1- and 2-sigma Spike outbreaks. In panel (b), gray bars again show the performance (standard deviation of 6.5) of the WEWD MovAvg7+WEWD Z-Score recombinant algorithm averaged over all four SlowRise outbreak sizes stratified by time series. Likewise, the black bars show the Area performance (standard deviation of 3.0) of the HW+WEWD Z-Score algorithm averaged over all four Spike outbreak sizes stratified by time series. Both series of bars show relatively consistent performance by the top performing recombinant algorithms across all 16 time series.

Figure 3.

Comparison of average detection probabilities for practical false alarm rates for top performing algorithms for SlowRise (gray bars) and Spike (black bars) signals across signal strengths averaged over all data series and individual time series averaged over all signal strengths.

Discussion

The aggregate performance results indicate that novel recombinant algorithms offer excellent temporal aberration detection capabilities. For SlowRise outbreaks, WEWD MovAvg7+WEWD Z-Score recombinant algorithm performed best; for Spike outbreaks, the HW+WEWD Z-Score recombinant algorithm performed best. The localization of the surge of counts over 1 or 2 days from the spike outbreak makes it critically important that either the data forecaster or anomaly measure or both compensate for this DOW effect when detecting such outbreaks in time series with strong weekly fluctuations. For SlowRise outbreaks that last longer than a week, DOW compensation does not appear to be as important. Even though not all data will have such weekly patterns, their presence in the test data set afforded an excellent opportunity to evaluate how effectively different stages of each recombinant algorithm removed or handled this type of systemic bias.

A primary systematic feature of the data streams in this study is the DOW day-of-week effect, and algorithms may be classified according to how this effect is modeled. The sliding 7-day average of the widely used C1-C3 ignores this effect, treating all days as equivalent, i.e., a count on a Sunday is equivalent to a count on a Monday. For a second management strategy, the CDC W2 algorithm divides the data into weekday and weekend-plus-holiday counts. The most detailed strategy handles each day uniquely. Muscatello’s 7-day differencing technique ¹⁶ and the regression of Brillman et al., ⁴ with DOW indicator covariates, fall into this category. This categorization suggests numerous variations of pre-existing techniques. Treating weekends and weekdays separately improved the Z-Score anomaly measure producing the WEWD Z-Score. It is also possible to modify other anomaly measures, such as the CUSUM and gScan, in a similar fashion to handle weekends and weekdays. These three could then be stratified by DOW, yielding three additional anomaly measures.

It also appears that some forecasters have a far more detrimental effect on certain control-chart approaches than others. For example, the detection probabilities found with the gScan measure applied to adaptive regression residuals were significantly below those found when they were applied to Holt-Winters residuals. This difference may result from the reduced autocorrelation in the residuals of the latter forecaster, as discussed by Chatfield. ⁹ Moreover, although most statistical process control charts typically require independent and identically distributed input data, the detection performance penalty for violation of these conditions needs to be better understood for use with residuals computed for the evolving data streams characteristic of biosurveillance.

Furthermore, recombinant algorithms offer numerous research directions. There are many more data forecaster and anomaly measure combinations to test, including simple parameter changes in existing techniques. Also, the anomaly measure variations suggested should be evaluated, affording a more precise investigation into the balance between temporal stratification and data adjacency. One can imagine an automated biosurveillance system that would automatically switch from a standard Z-Score to a WEWD Z-Score when the data’s temporal 7-day autocorrelation increased above a particular threshold. Forecast techniques from many other fields could also be matched with various control chart ideas. Many novel combinations could be efficiently evaluated with the methodology given herein.

A surveillance designer or manager wishing to seek additional detection performance from the recombinant approach might follow the following procedure:

• a) Obtain a quantity of historic data thought to be similar to the series that will need to be monitored. For monitoring daily data that are nonsparse (in the sense of a positive median daily counts) with the methods described above, a year of data could give reasonable results. For very sparse data or for more complex prediction modeling, several years of data would be preferable.

• b) Restrict attention to prediction methods that seem reasonable for the time series to be monitored. For example, to monitor counts of a syndrome grouping known to be nonseasonal, one would not use a predictor that includes covariates for annual trending.

• c) In selecting the anomaly detection methods to be applied to the residuals, consider the outbreak signal types that are consistent with the public health goals of the system. For example, a temporal scan statistic with a long time window might not be appropriate for monitoring gastrointestinal syndrome data for evidence of a food poisoning outbreak.

• d) Given the available data and size of the monitored population, how small an outbreak effect is the system required to detect? Having chosen a small, plausible set of prediction and anomaly detection methods, apply them to the test data with inject data scaled to the required detection size, and compare the resultant detection probabilities at the required alert rates, i.e., choose among the algorithms based on a few selected points on the ROC curves.

Aside from detection performance, additional factors for choosing among algorithm combinations are the difficulty of implementation and expected need for technical expertise as the data streams change. A complex predictor based on autoregressive error modeling is likely to be more sensitive to nonstationary behavior than a Holt-Winters predictor, though it may give smaller errors on a training set.

We discuss two limitations beyond those already noted. First, this research was limited to time series that contain strong DOW patterns. Not all syndromic time series contain such patterns. Second, synthetic outbreaks were inserted randomly into the data on all days of the week. Because of the strong DOW effect in the data, the outbreaks peaking on weekends will represent far greater deviations from the expected count than those peaking on weekdays. One can argue that the DOW effect should impact outbreak shape proportional to the severity and novelty of the symptoms. A patient with apparently life-threatening symptoms will take drastic measures to seek health care regardless of local clinic hours or daily schedule. However, the diseases of most interest to syndromic surveillance are those that present like other common illnesses, such as the common cold or influenza. ¹⁷ In this situation, the syndromic records from an outbreak would show the same DOW dependence as the underlying data. Thus, future studies may want to modulate the outbreak signal based on DOW effects to make the research more relevant to plausible outbreak situations.

Conclusion

This study found that the decomposition of aberration detection algorithms into two separate, sequential stages yielded new aberration detection algorithms with improved performance. The analysis of each stage separately offers insight into performance differences among candidate algorithms. This understanding can be used to develop a classification system to select the best aberration detection algorithm to surveil syndromic time series based on data characteristics. For example, the current default method used in ESSENCE applies a regression model goodness-of-fit measure and automatically selects the algorithm based on the result. ¹⁸ When aberration detection algorithms are treated as monolithic techniques, opportunities for substantial improvement are lost.