Fossil ghost ranges are most common in some of the oldest and some of the youngest strata

Abstract

Biologists routinely compare inferences about the order of evolutionary branching (phylogeny) with the order in which groups appear in the fossil record (stratigraphy). Where they conflict, ghost ranges are inferred: intervals of geological time where a fossil lineage should exist, but for which there is no direct evidence. The presence of very numerous and/or extensive ghost ranges is often believed to imply spurious phylogenies or a misleadingly patchy fossil record, or both. It has usually been assumed that the frequency of ghost ranges should increase with the age of rocks. Previous studies measuring ghost ranges for whole trees in just a small number of temporal bins have found no significant increase with antiquity. This study uses a much higher resolution approach to investigate the gappiness implied by 1000 animal and plant cladograms over 77 series and stages of the Phanerozoic. It demonstrates that ghost ranges are indeed relatively common in some of the oldest strata. Surprisingly, however, ghost ranges are also relatively common in some of the youngest, fossil-rich rocks. This pattern results from the interplay between several complex factors and is not a simple function of the completeness of the fossil record. The Early Palaeozoic record is likely to be less organismically and stratigraphically complete, and its fossils—many of which are invertebrates—may be more difficult to analyse cladistically. The Late Cenozoic is subject to the pull of the Recent, but this accounts only partially for the increased gappiness in the younger strata.

1. Introduction

There are essentially two independent narratives on the history of life. Neither can be read uncritically. The first derives from the distributions of characters in living and fossil organisms and takes the form of inferences about evolutionary relationships (phylogeny). The second derives from the stratigraphic or temporal sequence in which groups appear as fossils. Biologists often compare these two narratives by mapping cladograms onto stratigraphic range charts (Norell & Novacek 1992; Benton & Hitchin 1997; Clyde & Fisher 1997). Where they convey similar stories, their confidence in the accuracy and completeness of both is reinforced. Where the order of phylogenetic branching is at odds with the order in the rocks, the interpretation is often problematic.

Gaps or ghost ranges are implied where sister taxa originate at different times (figure 1), and can be summed over the whole tree (Wills 1999). A modest number and extent of ghost ranges can serve to concentrate research efforts towards finding older or transitional fossil forms and refining dates. For example, details of the evolution of tetrapods from fishes were sketchy for many years, but research was fruitfully focused within a ghost range called ‘Romer's Gap’ (Clack 2002). The revelation of extensive ghost ranges, by contrast, usually suggests a very gappy record and/or a spurious phylogeny. This is a wider problem for macroevolutionary studies, which seek to document trends through the history of life and often rely upon both accurate phylogenies and a fossil record of determinate quality (Paul & Donovan 1998; Foote & Sepkoski 1999).

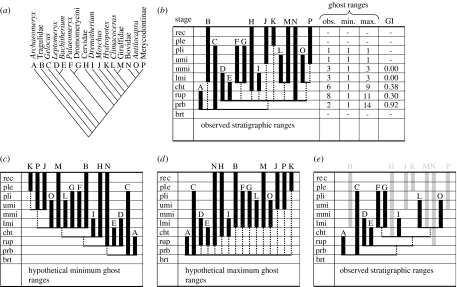
Figure 1.

Comparing a phylogeny and fossil dates to infer ghost ranges. (a) Example phylogeny of Ruminantia (Gentry & Hooker 1988). Taxa are assigned letters A to P for simplicity. (b) Cladogram in (a) plotted onto observed stratigraphic ranges (black vertical bars) to reveal the locations of ghost ranges (broken vertical lines). Values for the Gap Index (GI) are calculated by scaling the number of ghost ranges in each stratigraphic interval between the minimum and maximum possible (see (c,d); Wills 1999). The distribution of stratigraphic data that yields the (c) smallest and (d) largest number of ghost ranges for each interval. (e) The observed distribution of ghost ranges when omitting the contribution of lineages that persist to the Recent (grey bars). brt, Bartonian; prb, Priabonian; rup, Rupelian; cht, Chattian; lmi, Lower Miocene; mmi, Middle Miocene; umi, Upper Miocene; pli, Pliocene; ple, Pleistocene; rec, Recent.

Historically, it was assumed that the frequency of ghost ranges would increase with antiquity. This was principally because a decline in fossil record quality with age was thought to be an inevitable consequence of the increased likelihood that older fossils will have been crushed, deformed, melted or eroded. There are also difficulties associated with inferring phylogenies for some older (less familiar, less complete and otherwise problematic) fossil taxa (Wagner 2000; Briggs & Fortey 2005). The only study to directly investigate this assumption (Benton et al. 2000) reached the counter-intuitive conclusion that gappiness was uniform throughout the Phanerozoic—an extremely seductive prospect—but offered the rider that differences at finer levels of taxonomic and stratigraphic resolution had probably been masked. This finding remains largely unchallenged. More refined methods are used here to reveal a more complex pattern in these data.

A number of indices quantify the extent of ghost ranges implied by whole cladograms. Common to many of these (e.g. the relative completeness index (Benton & Storrs 1994), the gap excess ratio (GER; Wills 1999), the Manhattan Stratigraphic Measure (Siddall 1998; Pol & Norell 2001)) is a direct or indirect tally of the number of stratigraphic intervals containing implied gaps. Since these indices assess whole trees, previous workers investigating temporal trends (Benton et al. 2000) divided the Phanerozoic into just three bins, with most cladograms plotting solely within the Palaeozoic, Mesozoic or Cenozoic. Intermediate bins were added for cladograms spanning two eras, but these contained a biased sample of longer trees, frequently containing greater numbers of taxa. Both factors are known to influence the above indices (Finarelli & Clyde 2002; Pol et al. 2004). Monte Carlo simulations (permuting range data over each tree topology; see electronic supplementary material, figures 1 and 2) offer some control (Wills 1999). They indicate that gappiness deviates less from the random expectation for the Palaeozoic and Cenozoic time bins than for the Mesozoic (i.e. the Palaeozoic and Cenozoic are more gappy). This ‘convex’ pattern is unexpected, and the present study investigates it more fully by counting gaps in individual stratigraphic intervals.

2. Material and methods

(a) The database

The dataset comprised 1000 cladograms (Benton et al. 2000), including 1 cladogram of all life, 33 of plants, 9 of cnidarians, 1 of molluscs, 179 of arthropods, 14 of brachiopods, 1 each of bryozoans and graptolites, 60 of echinoderms, 34 of basal deuterostomes (including calcichordates), 157 of fishes, 26 of amphibians, 203 of reptiles, 8 of birds, 269 of mammals and 4 of other tetrapods. Cladograms were derived from numerous sources, including a search of Web of Science. The principal source of stratigraphic data for families and higher taxa was The fossil record 2 (Benton 1993), rationalized with data from the published sources where appropriate. Data on uncertain origination dates are not included, although this represents a refinement for particular, detailed case studies where ages are disputed (Pol & Norell 2006). Range data for lower taxonomic groups were taken from the papers that presented the cladograms. Origins were dated to stratigraphic series and stages, with the Phanerozoic divided into 77 intervals (Gradstein 2004). The most inclusive taxa were used, coding origins for the highest taxon represented by each terminal. A summary of the dataset is available in the electronic supplementary material, table 1 and references.

(b) The frequency of ghost ranges

Existing indices of cladistic and stratigraphic congruence derive just a single value for each cladogram. However, matches and mismatches between stratigraphy and cladistic branching are often in different portions of the tree, and therefore potentially at different times. Moreover, previous surveys have crudely divided the Phanerozoic into three arbitrary bins, corresponding to the Palaeozoic, Mesozoic and Cenozoic. This study markedly increases the temporal resolution to 77 Phanerozoic series and stages (the maximum resolution of the stratigraphic data), calculating the number of ghost ranges passing through the interval for each cladogram spanning it (figure 1).

In order to investigate the patterns through time, a simple count of the number of ghost ranges in each interval would be too simplistic. Firstly, the maximum number of ghost ranges implied by a cladogram increases as a function of the number of terminal taxa that it includes. Hence, observed numbers of ghost ranges have been scaled between the maximum and minimum possible for a given number and distribution of observed ranges. For shorthand, this is referred to here as the gap index (GI), ranged between 0.0 (maximum gappiness) and 1.0 (minimum gappiness) by analogy with the GER (Wills 1999). Secondly, some intervals are traversed by many trees, others by far fewer, so that the mean GI values are reported for each interval.

The number of ghost ranges that a given cladogram can imply traversing a given interval is a function of the stratigraphic distribution of observed ranges, the size and topology of the cladogram, and the position of the interval relative to the full stratigraphic range of the cladogram. As well as the distribution of range data and tree topology, the number of ghost ranges that a given cladogram can imply traversing a given interval is a function of both the size of the cladogram and the position of the interval relative to the full stratigraphic range of the cladogram. Intervals near the bottom or top of a tree (or those traversed only by small cladograms) can yield only a limited range of possible GI values (just 0.0 or 1.0 in the most extreme cases). This may artificially inflate or depress the mean GI values for some intervals. Hence, regions of individual trees for which the difference between the minimum and the maximum number of gaps was less than six were filtered out (figure 2a). This is an arbitrary number, but similar results were obtained for differences between five and nine, with the sample size becoming too small for many intervals above this level (see also electronic supplementary material, figures 3 and 4). In practical terms, this omitted the top and bottom of the largest trees, and removed smaller trees altogether. Fortunately, there was no large, systematic temporal bias in cladogram size in the dataset, with no significant relationship between the mean age of first occurrence (as a proxy for cladogram age) and the number of taxa in the sample of 1000 cladograms (Spearman's ρ=−0.029, p=0.362).

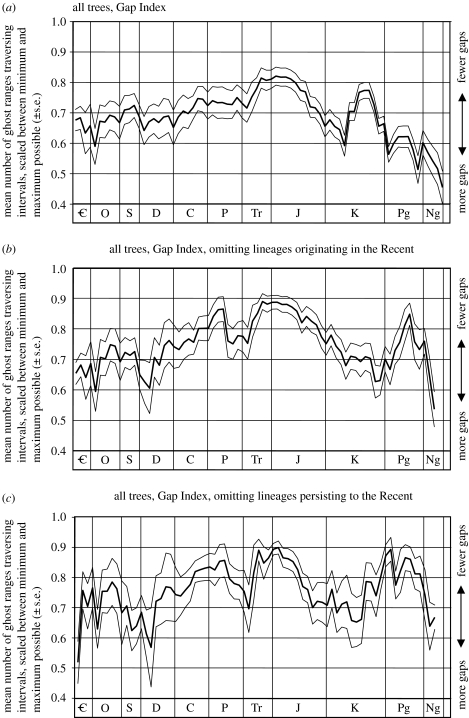
Figure 2.

How common are ghost ranges in individual stratigraphic stages? Data based on 1000 cladograms, encompassing all taxa. Data are filtered to exclude those cladograms where the range of possible gap values is less than 6 for a given interval. (a) Mean number of observed gaps±s.e., scaled between the maximum (1.0) and minimum (0.0) number of gaps for each tree's distribution of range data (i.e. Gap Index). Low values indicate gappier intervals. (b) As in (a), but weeding out ghost ranges subtended between one or more taxa not known as fossils. This controls for one interpretation of the ‘pull of the Recent’. (c) As in (a), but weeding out ghost ranges subtended between one or more taxa persisting to the Recent (i.e. known from the extant biota). This controls for a more restrictive interpretation of the pull of the Recent.

(c) The pull of the Recent

Living diversity has been sampled and described in much greater detail than the fossil biota. Unsurprisingly, the majority of living species and genera have no fossil record. However, many higher taxa are also known only from extant material. Most phyla, for example, first appear either in the Cambrian (predominantly those of medium to large size with reasonable preservation potential) or in the Recent (mostly the small and meiofaunal groups). In general, cladograms spanning strata nearer the Recent are more likely to contain taxa with no fossil record. These can be minute organisms, those with no resistant parts or known from isolated and small populations. Hence, the inclusion of groups with no fossil record may generate long gaps between the extant taxa and their nearest fossil relatives. It has been argued, therefore, that diversity estimates in the Late Cenozoic (and the Neogene in particular) are made higher than they would otherwise be by the extension of fossil ranges to the Recent. This ‘pull of the Recent’ (Jablonski et al. 2003) could also, in principle, artificially inflate the apparent number of ghost lineages approaching the present day, since all of the groups with no fossil record must be related to groups containing fossils at some level. This possibility was tested in two ways. Firstly, ghost ranges subtended by one or more taxa with no fossil record were individually weeded out from the calculations (figure 2b). Secondly, a much more inclusive definition of ‘Recent’ was used, removing the contributions of all those taxa persisting to the Recent, irrespective of whether or not they were also known as fossils (figure 2c). This last approach is excessively strict, since ghost ranges are subtended only between the first occurrences of taxa, and not their last occurrences. Moreover, several groups that are very abundant as fossils are known from just a handful of living representatives (e.g. the primitive frilled shark Chlamydoselachus anguineus (Winchell et al. 2004) and the Laotian rock rat Laonastes aenigmamus (Dawson et al. 2006)) or occasionally from single living specimens (e.g. the beetle Sikhotealinia zhiltzovae; Leschen & Beutel 2004). Under such logic, these fortuitous finds invalidate the incorporation of ghost ranges between the (potentially much more abundant) fossil representatives and their sister groups. Had the finds not been made, then the ghost ranges would be acceptable, and moreover should the groups go extinct in the future, then they become acceptable again.

(d) Other edge effects

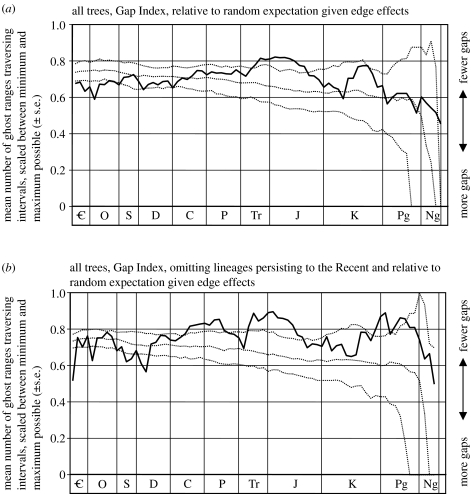
In addition to the putative pull of the Recent, there are other edge effects influencing apparent gappiness. The Recent provides an upper boundary, as no lineages can be known to persist beyond the Recent. There is also an effective lower stratigraphic bound for all of the cladograms in the dataset: the origins of multicellular organisms in the fossil record. As such, the Cambrian will tend to sample the ‘bases’ of trees, while the Neogene will tend to sample closer to the ‘tops’. Because the likelihood of gaps may be variable with tree ‘height’, this could, at least in principle, produce a spurious trend in gappiness. Some non-uniform pattern of gappiness would be expected from cladograms with the same distribution of size, stratigraphic range, topological balance and other parameters as found in this sample when constrained by the same edge effects. This null expectation was determined empirically by redating randomly all 1000 trees independently, and repeating this for 200 iterations. For each iteration, individual trees were ‘displaced’ up or down by a random number of stratigraphic intervals, redating all of their constituent taxa in concert such that their relative ages (within a tree) remained unchanged. The latest Precambrian and the Recent were treated as reflective boundaries, such that the oldest origin and the youngest extinction, respectively, for a given tree were never allowed to predate or supersede these dates. Randomly redated trees were therefore constrained to ‘fit’ within the Phanerozoic. The 200 iterations of the simulation also yielded upper and lower 95% CIs for each stratigraphic interval (figure 3).

Figure 3.

Is the pattern of GI through time significantly different from that expected for randomly redated cladograms with the same properties as our sample (see text for further explanation)? All 1000 trees were randomly redated in absolute age, while retaining the relative ages of their constituent lineages. Two-hundred Monte Carlo simulations were run to yield 95% CIs above and below the median (dotted lines). Observed patterns of GI as solid line. (a) All lineages, including those persisting to the Recent. (b) Weeding out the contribution of lineages persisting to the Recent.

3. Results and discussion

(a) Overall trends in gappiness

There is significant variation in the amount of gappiness implied through time by all treatments and partitions of the dataset. In the plot for all taxa with no corrections for edge effects or the pull of the Recent (figure 2a), the GI shows a systemic trend, with the highest values in the Late Triassic/Early Jurassic, and gaps being more frequent towards both the Cambrian and the Recent (see also electronic supplementary material, figures 3–5). The systemic increase in GI from the Triassic back to the Cambrian would be predicted from deterioration in the quality of the fossil record, and also increasing difficulty of finding appropriate characters and producing well-supported cladograms for older groups (Mishler 2000). Moreover, the sample reflects temporal trends in the taxonomic composition of the global biota, with a greater proportion of invertebrates in older, Palaeozoic strata (Benton et al. 2000). There is evidence that homoplasy is more abundant among some invertebrate groups than vertebrates, making cladograms more difficult to resolve (Wagner 2000). This, in turn, may imply reduced accuracy. The lower gappiness in strata of intermediate age (figure 2a) may be partly a function of taxonomic rarefaction, yielding longer gaps but fewer of them. Cladograms with fewer, morphologically more distinct taxa may be easier to infer accurately than those with many similar taxa.

(b) Why are there more ghost ranges approaching the Recent?

The finding of increasing gappiness towards the present is counter-intuitive, and might result from the pull of the Recent. Weeding out the contributions of taxa with no fossil record should remove this effect, since ghost ranges are only subtended between dates of first occurrences (and are not influenced by times of last occurrence). This caused an increase in GI over most of the time profile, and preferentially towards the Recent (figure 2b). However, despite the appearance of an additional GI peak in the Palaeogene, the overall trend of increasing gappiness from the beginning of the Jurassic to the Recent remained. A more restrictive interpretation is to remove the contributions of all taxa persisting up to the Recent (so that values are based on lineages known only as fossils). This yielded a much more complex pattern (figure 2c), with an irregular decrease in GI from the earliest Jurassic back to the Cambrian, and a decrease from the Jurassic to the Mid-Cretaceous. However, there was also a second peak in GI from the Late Cretaceous into the Early Palaeogene, with a steep decline thereafter (such that ghost ranges become more common through the Cenozoic). Therefore, depending upon the interpretation of the pull of the Recent, the effect may account for some of the systemic and sustained increase in gappiness from the Jurassic to the Recent observed in figure 2a (but see also electronic supplementary material, figures 3–5). However, such pruning of taxa from phylogeny/stratigraphy comparisons is not routine in the literature: ghost ranges and indices are usually reported with living taxa retained (Benton 2001; Kerr & Kim 2001; Marivaux et al. 2004).

(c) Do some periods have more or less ghost ranges than we would expect?

Simulations randomizing the absolute age of each tree (while retaining the relative ages of taxa within them) demonstrated the impact of edge effects. The expected GI values were not invariant with time, but rather showed a shallow decline of approximately 8% from the Cambrian to the Late Palaeogene, and then much more precipitously thereafter (figure 3a). Hence, an increase in gappiness in the Neogene is expected, probably because this period tends to preferentially sample the tops of trees. This edge effect is distinct from that anticipated from the pull of the Recent. The observed GI values mostly lie within the 95% CIs for the randomized data. However, in the Late Triassic and Early to Mid-Jurassic, the GI is significantly higher than expected, whereas in the Cambrian and Ordovician it is significantly lower (i.e. more ghost ranges) than expected. While the GI decreases towards the Recent, this is within the expectation for random data. Repeating the simulation while simultaneously pruning out the contribution of lineages persisting to the Recent revealed a slightly more variable pattern (figure 3b). GI was intermittently and significantly lower than expected from the Cambrian to the Devonian, while intermittently and significantly higher than expected from the Carboniferous to the Jurassic, and again briefly in the Late Cretaceous and Early Palaeogene.

(d) Trends for partitions of the data

All other things being equal, trees of phyla and classes will tend to be rooted deep in time, while those of genera and species are more likely, in principle, to be rooted anywhere. In order to remove the effects of taxonomic level, the profile was recalculated for just those 344 trees predominantly comprising families (see electronic supplementary material, figure 6). The GI was high (approx. 0.9) from the Devonian to the Mid-Jurassic, declining steeply and markedly into the Cretaceous (approx. 0.5) and more gradually thereafter. Removing the contribution of non-fossil lineages damped the post-Jurassic decline in GI, but increased the apparent gappiness of the Late Neogene. Considering lineages known only from the fossils prohibitively reduced the sample size (less than 6) from the Cretaceous onwards, but revealed a systemic decrease in the GI from the Devonian to the end of the Jurassic. Plots for trees predominantly above (n=388) and below (n=268) the family level were also generated (see electronic supplementary material, figure 7). While family-level trees had a good temporal spread, there were few trees at lower taxonomic levels for much of the Cambrian to Jurassic. Nonetheless, the Jurassic to Recent showed a systemic albeit irregular decline in GI. This largely disappeared when the contributions of lineages persisting to the Recent were removed, although sample sizes were severely reduced. For trees above the family level, there was no clear trend in GI through time. An otherwise systemic but irregular decrease in GI throughout the Phanerozoic was broken by a large peak in the Mid- to Late Cretaceous. Removing the contribution of lineages persisting to the Recent reduced the mean interval sample size down to just three, affecting the oldest record as much as the Cenozoic. The pattern for all taxonomic levels is therefore a composite of the trends for these data partitions. However, in no case is the number of ghost ranges uniform with time, neither is there a simple increase with antiquity.

Although the taxonomic composition of the biota at a given time is a legitimate part of what makes the record gappy or otherwise, the data for tetrapods were also analysed separately (n=512), with the added advantage that these animals are predominantly non-marine. This curve extends back only as far as the Early Carboniferous (see electronic supplementary material, figure 8). There are cladograms predating this, but no intervals with sufficient variation in numbers of ghost ranges. Considering all lineages, or removing the contribution of non-fossil lineages, the GI showed a systemic decrease from the Permian to the Recent. The pattern from fossil taxa alone was more complex, with an irregular decline from the Permian to the Mid-Cretaceous, but higher values in the Late Cretaceous and Palaeogene, declining again into the Neogene.

4. Conclusions

1. The distribution of ghost ranges through the Phanerozoic in this sample of 1000 cladograms is not uniform (cf. Benton et al. 2000). Ghost ranges are least abundant in the latter half of the Palaeozoic and Early Mesozoic, while gappiness increases approaching the Cambrian, and also the Recent. This is important because (irrespective of the reasons for this pattern) plots of phylogenies against fossil dates are more likely to reveal large numbers of ghost ranges at different times in the geological past. Assuming that this sample is representative, palaeontologists should not be surprised, for example, to find relatively large numbers of ghost ranges in the Cenozoic. It need not be suggested that their data are uniquely inferior.

2. The increased number of ghost ranges in the Early Palaeozoic probably reflects deterioration in the fossil record. The oldest record is almost certainly less complete (both organismically and stratigraphically), largely as a function of the reduced exposure of rocks and its corollaries. Coupled with this, it is more difficult to infer stable cladograms for problematic and/or fragmentary fossils, and these are disproportionately found in the Early Palaeozoic (Briggs & Fortey 2005). Moreover, the majority of Palaeozoic taxa are invertebrates, many of which have a low fossilization potential and typically offer fewer morphological character states with higher levels of homoplasy (Wagner 2000).

3. The increased gappiness of the Late Cenozoic is probably largely artefactual. The number of ghost ranges is inflated by the pull of the Recent (at least where this is defined most strictly as the influence of all taxa with living representatives, not just those with no fossil record) and other edge effects, but this is within the range expected for randomly redated samples of similar cladograms.

4. The latter half of the Palaeozoic and Early Mesozoic has the fewest ghost ranges across all trees, and these are less frequent than expected for randomly redated trees. Herein, for example, lie the much-studied origins of mammals and dinosaurs; vertebrate groups generating huge interest and whose cladograms tend to match the fossil record better than most (Benton 2001; Wills 2001). These trees could be closer to the historical truth than some other groups. However, there is also a potentially powerful pruning effect when investigating the origins of well-known higher taxa: series of putatively transitional fossils are preferentially selected for study at the expense of those with unfamiliar distributions of characters. Investigators actively seek out ‘missing links’. This leads to a greater number of pectinate, unbalanced trees than models of random branching and fossilization predict (Pearson 1999), and this may also favour artefactually decreased gappiness.

5. This study demonstrates that inferences about the completeness of the fossil record cannot be made directly or straightforwardly from the distribution of ghost ranges. Individual stratigraphically gappy cladograms are only suggestive of a gappy fossil record (Angielczyk & Fox 2006). Gaps may result from an inaccurate cladogram and/or a poor record, while even a spurious cladogram may be congruent with a poor record in some circumstances. Without an independent test for cladogram accuracy or record quality, the two remain conflated in particular cases. However, where hundreds of cladograms are sampled across disparate groups of animals and plants, an incomplete record is a more plausible explanation for wholesale mismatching (Benton & Hitchin 1997; Benton et al. 2000). Nevertheless, while stratigraphic incompleteness is an important factor, taxonomic and organismic incompleteness may also compromise the taxon and character sampling necessary for accurate cladistics (Wagner 2000). Some periods may have been dominated by very small or soft-bodied individuals, and these are much less likely to have left fossils than large organisms with heavily mineralized skeletons. The relationship between the preservation probability for individuals and species is poorly understood, still more so that between individuals and the series of character changes necessary to construct accurate cladograms. Ghost ranges are not just a function of a stratigraphically patchy record and/or inaccurate cladograms. Rather, they result from the interaction of these factors with each other and with the intensity of taxon sampling through time, which may itself be a function of the intensity and agenda of study (Weishampel 1996).

Supplementary Material

Additional figures 1–8

Trends in GI and other indices for alternative temporal and taxonomic partitions of the data

Table 1. Summary data for 1,000 cladograms

GER values are for whole cladograms, and are indicative only. Taxonomic level refers to the most common taxonomic level of terminals. The following abbreviations are used: S, species; G, genus; F, family; O, order; C, class; P, phylum; K, kingdom. Prefixes: S, sub-; Sup, super-

References for 1,000 cladograms

Table 2. Summary statistics for all stratigraphic intervals. Numbers pertaining to the Gap Index (GI) are for trees and intervals where the difference between the maximum and minimum number of ghost ranges was 6 or more