Skip to main content
NCBI home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2007 Dec 20;36(4):1120–1128. doi: 10.1093/nar/gkm1125

Kinking the double helix by bending deformation

Quan Du 1, Alexander Kotlyar 1, Alexander Vologodskii 1,*
PMCID: PMC2275110  PMID: 18096619

Abstract

DNA bending and torsional deformations that often occur during its functioning inside the cell can cause local disruptions of the regular helical structure. The disruptions created by negative torsional stress have been studied in detail, but those caused by bending stress have only been analyzed theoretically. By probing the structure of very small DNA circles, we determined that bending stress disrupts the regular helical structure when the radius of DNA curvature is smaller than 3.5 nm. First, we developed an efficient method to obtain covalently closed DNA minicircles. To detect structural disruptions in the minicircles we treated them by single-strand-specific endonucleases. The data showed that the regular DNA structure is disrupted by bending deformation in the 64–65-bp minicircles, but not in the 85–86-bp minicircles. Our results suggest that strong DNA bending initiates kink formation while preserving base pairing.

INTRODUCTION

The regular structure of the double helix can experience local disruptions under sufficient bending and/or unwinding torsional stress. Large bending and torsional deformations often appear during DNA functioning, and thus we need to know the conformational features and conditions of appearance of such disruptions in of the regular DNA structure. Local structural disruptions appearing under negative torsional stress have been studied in detail (1,2), but disruptions created by bending stress have not been studied experimentally. For a long time, however, such structural disruptions were a subject of theoretical discussion and modeling. Crick and Klug (3) were the first to suggest that large bending deformations should cause formation of kinks with preserved base pairing. Although such kinks have been observed in structures of DNA–ligand and DNA–protein complexes (4–7), the energetic cost of their appearance remains unknown. Simple theoretical estimations and molecular dynamics simulations show that kinks should appear in DNA circles of about 100 bp in length (8,9). Kinks easily appear at DNA nicks (10), but their energetic cost should be substantially lower in this case due to the much larger conformational flexibility of single DNA strand. A hinge for double helix bending can also be provided by opening of a single base pair (11). The energetic cost of the latter disruption is rather high, however, and the probability to find a base pair in an opened conformation in unstressed DNA equals 10–7 – 10–5, at room temperature (12,13). This is understandable since the opening involves disruption of stacking in 2 bp steps. Kinks eliminate only one stacking interaction and therefore may have higher probability of appearance. Subsequently, under the term ‘disruption’ we will mean either base pair opening or kinks of the double helix.

Recent interest in the problem was initiated by Cloutier and Widom (CW) (14) who reported that the cyclization probability for DNA fragments of about 100 bp in length exceeds the theoretical expectation by 3–5 orders of value. The theory of DNA cyclization is based on the wormlike chain model, which considers only small fluctuations of angles between adjacent base pairs (15). The DNA model based on the wormlike chain accurately describes practically all known quantitative experimental data on DNA conformational properties (16). However, theoretical studies confirmed the suggestion made by CW that cyclization of very short DNA fragments has to deviate from the theoretical predictions based on the wormlike chain, if it involves sharp kinks of the double helix (11,17,18). The conclusion simply means that beyond a certain limit of the bending deformation, the regular DNA structure experiences local disruptions. This limit remained unknown, however, since a later study found that the cyclization probability for DNA fragments with length above 100 bp follows the predictions of the wormlike-chain model (17). We determined the limit in the current study by probing the structure of DNA minicircles.

First, we developed an efficient method to obtain covalently closed DNA minicircles. To detect disruptions of the regular DNA structure in these minicircles we treated them by single-strand-specific endonucleases. This method has been widely used to study local conformational changes in supercoiled plasmids (19–24). Any conformational changes in the minicircles are also influenced by their supercoiling, therefore we carefully accounted for this coupling. Choosing the experimental conditions where the influence of torsional stress is minimized, we found that the double helix is disrupted by bending deformation in the minicircles of 64–65 bp, but not in the 85–86 bp minicircles. Our data show that two different single-strand-specific endonucleases used in the study have different sensitivities to the disruptions created by bending and torsional deformations. We suggest, using this observation, that torsional stress creates open regions in the double helix while strong DNA bending initiates formation of kinks that preserve the base pairing. If the suggestion is correct, this is the first experimental observation of kinks in DNA free of bound proteins. Our results are very important for better understanding of small loop formation in DNA–protein complexes, since kinks greatly facilitate strong DNA bending.

MATERIALS AND METHODS

DNA minicircles

The sequences of all minicircles have GC-content near 50% and do not contain intrinsically bent motifs (Table S1 in Supplementary Data). Each minicircle ≤106 bp in length is assembled from two linear double-stranded DNA substrates that are obtained from one another by circular permutation of the fragment halves (Figure 1). For each minicircle one linear substrate carries EcoRV blunt ends, while the other carries StuI blunt ends.

Figure 1.

Figure 1.

Open in a new tab

Preparation of DNA minicircles from linear duplexes with very long cohesive ends. (a) DNA duplexes with N/2 base pairs and cohesive ends of N/2 nucleotides easily form minicircles, due to larger flexibility and contour length of the single-stranded regions. (b) Ligase-Assisted Minicircle Accumulation (LAMA). The same fragments paired with complementary strands were mixed together with Taq DNA ligase. In step 1, the fragments are denatured, then in step 2 they are quickly cooled. As a result, a fraction of them form the minicircles with two single-stranded nicks; the rest go back into linear duplexes. In step 3, the nicks are ligated. The cycle may be repeated a few times.

The linear substrates were cloned between EcoRV or StuI sites of separate plasmids, and verified individually by DNA sequencing. The substrates were PCR amplified by high-fidelity Phusion Polymerase (Finnzymes) using the cloned plasmids as templates. The universal PCR primers were designed to hybridize only with the vector sequences flanking each substrate. The PCR products were purified by PCR Purification Kit (Qiagen). Each PCR product was subsequently cleaved by either EcoRV or StuI restriction enzyme, producing the final blunt-end fragments for the minicircle assembly. The restriction enzymes were heat inactivated at the end of the reactions.

About 0.4 μg each of the two substrates were mixed in 100 μl Taq DNA ligase reaction buffer (30 mM Tris–HCl, pH 7.7, 25 mM NaCl, 3 mM MgCl2, 25 mM potassium acetate, 10 mM magnesium acetate, 10 mM DTT, 1 mM NAD, 0.1% Triton X-100), with 80 U of Taq DNA ligase for the Ligase-Assisted Minicircle Accumulation (LAMA) procedure (explained in Results section). The mixture was placed in a thermal cycler that performs the following temperature program: step 1, DNA denaturation at 95°C for 20 s; step 2, cooling at maximum rate to 4°C and holding for 1 min; step 3, ligation at 65°C for 20 min. Seven consecutive thermal cycles were able to convert up to 90% of the substrate fragments into minicircles. The minicircles ranging from 84 to 106 bp were produced by this procedure.

The LAMA protocol described above, however, failed to produce DNA minicircles of sizes between 63 and 66 bp, possibly due to the denaturation of circularly assembled DNA intermediates at the elevated ligation temperature of 65°C. These 63–66 bp minicircles were produced by a modified protocol, which switches to T4 DNA ligase and a 25°C ligation step. In this protocol, the substrates were mixed in the reaction buffer (60 mM Tris–HCl, pH 7.6, 25 mM NaCl, 13 mM MgCl2, 10 mM DTT, 1 mM ATP, 25 μg/ml BSA), heated to 95°C for 2 min and then chilled immediately on ice for 5 min. The mixture was brought to 25°C and incubated with 10 U of T4 DNA ligase for 1 h. Additional cycles do not improve the yield because T4 DNA ligase converted all remaining substrate molecules into various multimeric products during the first cycle. Minor fractions of the 63–66 bp DNA substrates were able to form minicircles.

Minicircles of 200, 205, 400 and 410 bp were obtained by ligase-catalyzed ring closure of linear DNA with HindIII cohesive ends (25).

After the minicircle assembly and ligation steps, the DNA products were treated by Exonuclease I and Exonuclease III at 37°C to digest the remaining single and double-stranded linear DNA. The minicircles were purified subsequently by the PCR Purification Kit or the Nucleotide Removal Kit (Qiagen). The minicircles did not contain chemically synthesized oligonucleotides to assure the consistency of DNA quality in the nuclease reactions.

Detection of local disruptions

BAL 31 nuclease digestion reactions were performed in 10 mM Tris–HCl, pH 8.0, 120 mM NaCl, 2 mM MgCl2, 2 mM CaCl2. DNA minicircles were incubated with 0.005 U/μl BAL 31 at 25°C for 10 and 60 min. The reaction was stopped by the addition of 15 mM EDTA.

S1 nuclease (USB) reactions were performed in 30 mM sodium acetate, pH 5.2, 50 mM NaCl, 1 mM ZnCl2. DNA minicircles were incubated with 0.2 U/μl S1 nuclease at 25°C for 30 min. The reaction was stopped by the addition of 10 mM EDTA.

DNA samples were electrophoresed in 10% (unless indicated otherwise) preheated denaturing polyacrylamide gels with 7 M urea, in Tris–borate EDTA buffer. The gels were stained with SYBR Gold (Invitrogen) and scanned by Storm 840 imager (Molecular Dynamics) in fluorescence mode. The Image Quant software was used to quantify the bands.

Enzymes and oligonucleotides

All DNA oligonucleotides were purchased from Integrated DNA Technologies. All enzymes were purchased from New England Biolabs unless otherwise noted.

RESULTS

Preparing DNA minicircles

Our major attention in this study is on DNA minicircles around 100 bp and smaller. It is very difficult to obtain such small circles by the ligation of DNA fragments with short cohesive ends since the probability of cyclization is extremely low in this case (17). Therefore, to make these minicircles we developed a different strategy, DNA Circularization by Long Cohesive Ends (DCLCE). A circle of N base pair in length can be assembled by mixing two single-stranded DNA of N nucleotides, which are capable of forming a linear duplex with N/2 base pairs and two long cohesive ends of N/2 nucleotides each (Figure 1a). These long cohesive ends are very flexible and their contour length is larger than the length of the double-stranded part of the duplexes, so nucleation and propagation of the cyclization is possible without substantial deformation of the double-stranded part. This provides higher efficiency of cyclization compared to the multimerization, under the condition that the concentration of substrate oligonucleotides is not too high. The final product is the double-stranded circular DNA with two nicks located diametrically, which can be subsequently ligated by DNA ligase. By using the DCLCE strategy one can obtain DNA minicircles of nearly any sequence.

In our tests, DCLCE was able to convert chemically synthesized oligonucleotide substrates to nicked double-stranded minicircles with nearly 100% yield. However, we found the homogeneity of the synthetic DNA unsatisfactory for our goals (see Note in Supplementary Data). Thus, we extended the strategy to allow the use of double-stranded DNA substrates (Figure 1b). When a generic DNA strand A precisely matches strand B by DCLCE, their complementary strands will do this as well. By successive processes of heat denaturation and annealing, a fraction of the linear DNA is converted to the minicircles. These minicircles are a mixture of two isomers, differing only in the sites of two nicks. After ligation of the nicks by DNA ligase, all covalently closed minicircles are identical. In our experiment, each DNA template was cloned into a plasmid vector, amplified by high-fidelity PCR, and restricted to blunt end DNA of a designated length. In order to improve the yield of circles, we developed a one-pot method named LAMA. In LAMA, the pair of matched substrates was mixed in a 1:1 ratio with thermophilic Taq DNA ligase. By repeating the temperature program of 95°C (denaturation) → 4°C (annealing) → 65°C (nick ligation) in a thermal cycler, the remaining linear substrates can be reused in the following rounds; thus more circles can be accumulated (Figure 2a). Two key factors help ensure the high efficiency of the procedure: (i) Taq DNA ligase does not ligate the blunt ends of linear DNA; and (ii) formation of covalently closed minicircles is irreversible.

Figure 2.

Figure 2.

Open in a new tab

Analysis of the minicircle preparation. (a) Preparation of 86 bp minicircles by LAMA. The lanes of denaturing polyacrylamide gel show single-stranded linear (86 nt L) and circular (86 and 172 nt C), as well as denatured covalently closed double-stranded minicircles (86 and 172 bp C) accumulation after various numbers of cycles. After seven cycles the mixture was treated by exonucleases I and III (lane 6). (b) Confirmation of the circular structure of the 86 bp ligation product by restriction and nicking endonucleases. Samples were separated in denaturing polyacrylamide gel with 10 bp linear DNA marker M (Invitrogen). Lane 1, 86 bp linear DNA; lane 2, 86 bp DNA minicircle; lanes 3–5, 86 bp minicircle treated with single or double digestion by EcoRV and StuI, whose restriction cleavage sites are 43 bp apart by design; lane 6, 86 bp minicircle singly nicked by Nt.BstNBI that runs as a single-stranded circle and a single-stranded linear DNA in denaturing conditions; lane 7, singly-nicked 86 p minicircle treated by Exonuclease I and Exonuclease III which leave only the single-stranded circular DNA.

In our experiments, LAMA successfully produced minicircles of 84–106 bp. However, the protocol failed to produce closed minicircles of 63–66 bp. To obtain these minicircles, we first assembled them in the absence of DNA ligase, and then incubated the mixture with T4 DNA ligase at room temperature to close the nicks.

The double-stranded circular nature of the samples was established from the restriction by EcoRV and StuI, and the nicking by Nt.BstNBI (Figure 2b). The verification of the minicircle sizes is presented in Supplementary Data (Figure S1).

Theoretical analysis of conformational changes in supercoiled minicircles

Proper interpretation of the experimental data presented below requires theoretical analysis of the thermodynamic equilibrium between the minicircle conformations with and without local disruptions. For this goal we need to estimate the corresponding conformational free energies. We will assume that a certain number of disruptions appear in the minicircle. This changes both the DNA bending free energy, Gb, and the free energy of the torsional deformation, Gt. The change of Gt occurs since local disruptions of the double helix can be associated with DNA unwinding. Such unwinding occurs during base pair opening (26,27). It also occurs in DNA kinks that preserve base pairing, according to the theoretical analysis (3,9) and structural data on DNA–protein complexes (5,28). This unwinding, δTw, affects the value of Gt and, therefore, the probability of the disruption appearance. In addition, formation of the disruptions has their internal free energy cost, Gk. The value of Gk is specified by local conformational changes only and does not depend on the torsional and bending stress in the minicircles.

DNA supercoiling (the excessive torsional deformation in the case of minicircles) is specified by the linking number difference, ΔLk. The value of ΔLk equals Lk − N/γ, where Lk is the linking number of the DNA complementary strands and γ is the average number of base pairs per helix turn in the torsionally unstressed DNA under particular conditions (29). We are interested here in DNA minicircles <200 bp in length, which maintain a planar conformation if −1.5 ≤ ΔLk ≤ 1.5 (30). Therefore, in the absence of local disruptions the elastic energy of minicircles consists of Gt and Gb only and can be written as

graphic file with name gkm1125m1.jpg 1

where L is the minicircle contour length, C is the torsional rigidity constant, and 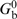Inline graphic is the bending energy in the absence of any disruptions. After appearance of disruptions the number of helix turns in torsionally unstressed molecules is (N/γ + δTw) rather than N/γ, so the supercoiling is specified by the value Lk − (N/γ + δTw), or (ΔLk − δTw). Correspondingly, Gt depends on (ΔLk − δTw) rather than on ΔLk Thus, in the presence of the disruptions the minicircle energy can be written as

graphic file with name gkm1125m2.jpg 2

where Inline graphic is the bending energy in the presence of the disruptions.

The change of the minicircle energy, δG = G1 − G0, resulting from the disruption appearance, equals

graphic file with name gkm1125m3.jpg 3

where Inline graphic. Since Inline graphic, Equation (3) shows that the energy of torsional deformation always promotes local disruptions if ΔLk < δTw/2. The above analysis is illustrated in Figure 3.

Figure 3.

Figure 3.

Open in a new tab

The effect of local DNA unwinding on the disruption formation. Changes of DNA torsional free energy, Gt are specified by the value of (ΔLk−δTw) where δTw is the DNA unwinding by the disruptions (δTw < 0). These changes are shown by arrows on the plots. (a) Sufficiently large negative supercoiling reduces Gt and therefore promotes the disruption appearance. (b) Gt increases by the disruption formation if the minicircles were initially relaxed (ΔLk = 0). In this case, the torsional deformation inhibits the disruption formation. (c) If the minicircle ΔLk equals δTw/2, the torsional free energy does not change on the disruption formation and, therefore, does not affect the disruption appearance.

We will assume in the subsequent analysis that DNA helical repeat is not changing in strongly bent DNA fragments. The assumption is supported by the crystallographic data on nucleosome structure, where the double helix is bent with a curvature similar to the curvature of our minicircles (31). Also, the cyclization data show that γ does not change in free minicircles of 95–105 bp (17,32).

Structural disruptions caused by negative torsional stress

Different methods were used to detect structural disruptions in negatively supercoiled DNA, and among them an important role belongs to probing DNA structure by endonucleases specific to single-stranded DNA segments (19–24). These enzymes introduce single-stranded cuts at DNA sites with structural disruptions. We used two of these enzymes, BAL 31 and S1, to probe the structure of the minicircles. The nucleases are commonly used probes for noncanonical structures in double-stranded DNA (33). Both enzymes are capable of cleaving the single-stranded loops in DNA hairpins. It has been reported that BAL-31 and S1 nucleases can cleave DNA lesions which are generated by mutagenic agents such as ultraviolet radiation and by treatment of N-acetoxy-N-2-acetylaminofluorene (AAAF) (34–36). Solution structure of a duplex DNA containing a cyclobutane thymidine dimer, the major DNA photoproduct by UV radiation, shows base pair destabilization and distortion at the lesion (37). The DNA product of AAAF treatment also introduced evident unwinding in the DNA helix (36). In addition, BAL-31 and S1 nucleases are also known to specifically cleave B-Z DNA junctions (38,39). The first atomic structure of a B–Z junction was revealed by X-ray crystallography recently, showing only one broken base pair with extruded bases at the junction (40). The base stacking between the B and Z DNA segments is continuous in the structure. Both the mutagenic lesions and the B–Z junction can be considered as abrupt DNA backbone distortions, but they do not include segments of single-stranded DNA in a conventional sense. Still, they are well recognized by both endonucleases. Albeit no apparent single-stranded structure is present in a kink, the inherent small unwinding and the large base pair roll within a kink are possibly the features which can be recognized by the enzymes. It is worth noting that S1 endonuclease works under low pH, although above the pKa values of the DNA bases.

First, we investigated 200 bp and 205 bp minicircles. For the 200 bp minicircles ΔLk is close to zero (25), so they are represented by a single topoisomer. The minicircles are very stable to the digestion by both nucleases (under chosen standard conditions), as was expected (Figure 4). The fragments of 205 bp in length have ∼19.5 helix turns and therefore form two topoisomers after cyclization, with Inline graphic and Inline graphic (Figure 4). The topoisomers are not digested by either BAL 31 or S1 nuclease. This result shows that even the (–) topoisomer keeps essentially intact regular structure in the minicircles of this size.

Figure 4.

Figure 4.

Open in a new tab

Probing the structure of 200 bp and 205 bp DNA circles by single-strand-specific endonucleases. The 6% denaturing polyacrylamide gels show results of 60 min treatment by BAL 31 (a) and 30 min treatment by S1 (b). The only topoisomer of the 200 bp minicircles (CM, Lk = 19) is relaxed; the two topoisomers of the 205 bp minicircles (Lk of 19 and 20) have ΔLk of –0.5 and 0.5. The minicircles of 400 and 410 bp (CD) are relaxed. The size of linear fragments which served as a substrate in the minicircles preparation is shown at the bottom of the figure.

Second, we studied the nuclease digestion of 106 and 100 bp minicircles. The data in Figure 5 show that the DNA structure is not disrupted in the 106 bp minicircles that are represented by the single torsionally unstressed topoisomer (ΔLk = 0) (17). The fragment of 100 bp has a semi-integer number of helix turns, so one could expect that its cyclization gives two topoisomers. The minicircles, however, are presented by only one topoisomer that is quickly digested by BAL 31 (Figure 5a). Thus, the topoisomer has well-pronounced local disruptions. It means that its ΔLk equals –0.5 rather than +0.5, since only negative torsional stress can promote the disruptions [see Equation (3)]. Correspondingly, the free energy of the (+) topoisomer is higher than that of (–) topoisomer, and (+) topoisomer does not appear during the ligation. S1 endonuclease also digests the topoisomer, although the reaction proceeds very slowly (Figure 5b).

Figure 5.

Figure 5.

Open in a new tab

Probing the structure of 100 bp and 106 bp DNA minicircles by single-strand-specific endonucleases. The denaturing polyacrylamide gels show the results of 60 min treatment by BAL 31 (a) and 30-min treatment by S1 (b). The minicircles (ds circular) of 100 bp are negatively supercoiled (Inline graphic), while minicircles of 106 bp are relaxed. The other labels refer to single-stranded linear fragments (ss linear) and circles (ss circular). The minicircle size is shown at the bottom of the figure.

The fact that disruptions appear in this topoisomer is not surprising. The topoisomer superhelix density, σ, is close to –0.055, which corresponds to extremely high torsional stress, equivalent to σ of –0.22 in a large circular DNA (41–43). Torsional stress of this magnitude should cause local unwinding of the double helix in the minicircle. The reduction of the bending stress further shifts the equilibrium to the conformation with local disruptions. However, the bending stress per se is insufficient to create disruptions in the minicircles of about 100 bp in length since torsionally unstressed minicircles of this size are not digested by the nucleases.

DNA distortion by bending deformation

Since the minicircles of 106 bp in length (Inline graphic) are highly resistant to nuclease digestion, we applied the approach to minicircles of smaller sizes. The data on the nuclease digestion of 63 bp circles are shown in Figure 6 [lanes 2 and 3 in panels (a) and (b)]. Although the linear fragment of this length has nearly an integer number of the helix turns, the corresponding circles appear as two topoisomers, the upper one with ΔLk of –1 and the lower one with ΔLk of 0 (Figure S2 in Supplementary Data). Figure 6a and b shows that (–) topoisomer is quickly digested by both endonucleases, so the topoisomer definitely has local disruptions. Such local disruptions would create positive torsional stress in the intact regions of the second topoisomer with Inline graphic, so their formation has to be suppressed. This second topoisomer is only slowly digested by BAL 31 endonuclease and resistant to S1 treatment (Figure 6a and b). Thus, the disruptions appear in the topoisomer with rather small probability.

Figure 6.

Figure 6.

Open in a new tab

Probing the structure of DNA minicircles by single-strand-specific endonucleases. The denaturing polyacrylamide gels (10% for a and b; 8% for c and d) show results of 60-min treatment by BAL 31 (a, c) and 30-min treatment by S1 (b, d). The minicircle size in base pair is shown for panels (a) and (b) at bottom of panel (b) and for panels (c) and (d) at bottom of panels (d). Minicircles of 63–66 bp were obtained by nick ligation at 25°C, while minicircles of 84–87 bp were ligated at 65°C except for the 84 bp minicircles shown at lane 1 of panel (c) which were ligated at 25°C. Some minicircles are represented by two topoisomers; the topoisomers with lower value of Lk correspond to the upper band. (e) Quantitative comparison of BAL 31 digestion rates for two sets of minicircles (for 63, 84 and 85 bp minicircles the plot represents topoisomers with higher values of Lk). The digestion kinetics is specified by the first-order rate constant, k. The data from panels (a) and (c) and from SI Figure 3 were used for the plot.

The energy of the upper topoisomer (Inline graphic) is specified by Equation (2), while the energy of the lower topoisomer (Inline graphic) can be approximated by Equation (1). Since the fractions of both topoisomers are nearly equal, so they have nearly equal energies. This gives us the following equation

graphic file with name gkm1125m4.jpg 4

Since the first and third terms in the equation are positive, we conclude that for DNA minicircles of this size the decrease in the bending energy (the second term) has a larger absolute value than the energetic cost of the disruptions, Gk. Thus, in these minicircles the bending deformation alone is sufficient to cause the local disruptions. This conclusion is confirmed by the digestion analysis of the minicircles 64–66 bp in length.

The effect of the supercoiling energy on the appearance of the disruptions would be close to zero if [see Equation (3)].

graphic file with name gkm1125m5.jpg 5

We can estimate that each of the disruptions, kinks or open base pairs, introduces DNA unwinding of 0.05–0.2 of the helix turn and a couple of such disruptions should appear in a minicircle to reduce the bending energy substantially, so δTw = (−0.1)÷(−0.4) (3). We conclude that ΔLk satisfying Equation (3) should be in the range of (−0.05)÷(−0.2). If ΔLk > δTw/2, the disruptions are suppressed by the supercoiling; if ΔLk < δTw/2, they are promoted by supercoiling. Supercoiling definitely suppresses the disruptions in the second topoisomer of 63 bp circles (Inline graphic). Therefore, we investigated the minicircles of 64–66 bp, where the values of ΔLk are close to –0.1, –0.2 and –0.3, correspondingly. The data presented in Figure 6 [panels (a) and (e)] show that the rate of digestion by BAL 31 increases greatly when the circle size is growing and ΔLk is decreasing. This confirms that δTw < 0 for the appearing disruptions [see Equation (3)]. The value of ΔLk for some circles of this set should approximately satisfy Equation (5), and they are well digested by BAL 31 nuclease. Thus, we conclude from the digestion data that DNA bending alone disrupts the regular DNA structure in 64–66 bp minicircles.

Figure 6b shows that 64–66 bp minicircles are hardly digested by S1 nuclease, while the enzyme quickly digests the (–) topoisomer of 63 bp circles. It is possible that DNA disruptions in the latter case have a different nature and this makes them more accessible to the digestion by S1 nuclease.

The results presented so far show that the bending stress alone causes disruptions of the double helix in 64–66 bp minicircles, but not in 106 bp minicircles. To address the critical size of the minicircles where the bending-induced disruptions appear with higher precision, we investigated minicircles of 84–87 bp in length.

The 84 bp linear fragment has nearly an integer number of helix turns (N/γ = 8), and in this respect is similar to the 63 bp fragment. However, it forms only one topoisomer with Inline graphic during the nick ligation at 25°C (the first lane in Figure 6c). Two topoisomers of the minicircles are obtained by ligation at 65°C [Figure 6, lane 2 in panels (c) and (d)]. In this case, DNA unwinding by Inline graphic of the helix turn promotes appearing of the upper, negatively supercoiled topoisomer. Also, the local disruptions are more probable at 65°C, and this facilitates the formation of (–) topoisomer.

The (–) topoisomer is digested very fast by both endonucleases (Figure 5c, lanes 2 and 3). Of course, this was expected since the topoisomer has very high (–) supercoiling (Inline graphic). The lower topoisomer, with Inline graphic, is resistant to both endonucleases. As it was for the lower topoisomer of 63 bp, the supercoiling has to suppress the appearance of disruptions in this case. To eliminate this factor we investigated digestion of 85–87-bp minicircles. Figure 6c–e shows that all these minicircles are resistant to the digestion by both endonucleases (except the upper topoisomer of 85 bp minicircles). Only a very slight digestion by BAL 31 was observed for 87 bp minicircles. In the latter case, however, negative supercoiling may promote the disruption appearance. Therefore, we concluded that DNA bending alone does not create disruptions in this set of minicircles.

DISCUSSION

To determine the limit of elastic bending deformation of the double helix, we probed the DNA structure in minicircles of various sizes by single-strand-specific endonucleases. This method was used to study alternative structures in negatively supercoiled plasmids for many years. We tested, using minicircles with different supercoiling, that the method strongly discriminates the minicircles with and without disruptions of the regular DNA structure. The negatively supercoiled minicircles are well digested in the cases when they are expected to have unwound regions.

It was important to minimize the effect of torsional stress in the experiments, in order to address double-helix disruption by bending stress alone. Our analysis showed that it should be the case for DNA fragments with the number of the helix turns slightly exceeding an integer number. Under such condition, the net change of the torsional free energy due to the disruption formation will be close to zero. Using the corresponding circles we showed that bending causes disruptions of the double helix in the minicircles of 64–65 bp, although the helix structure is intact in the minicircles of 85–86 bp and 106 bp.

Our results are in a very good agreement with the measurements of j-factors for short DNA fragments. First, we found that minicircles of Inline graphic bp in length with ΔLk of –0.5, 0 and +0.5 are resistant to digestion by both endonucleases used in the study, BAL 31 and S1, confirming that the minicircles contain no disruptions of the double helix structure (Figure 4). This is in agreement with the fact that the values of j-factor for these minicircles are very well described by the model which accounts only for DNA elastic deformations (25). The same agreement between theory and experiment was observed for the 106-bp minicircles (17). Our current data confirmed that the minicircles of this size, with Inline graphic, do not contain disruptions of the double helix (Figure 4). The 100-bp minicircles, on the other hand, appear in the form of a highly negatively supercoiled topoisomer (σ = –0.055). These minicircles are easy digested by BAL 31 nuclease, in full agreement with theoretical estimations showing that minicircles with such negative supercoiling have to have unwound regions. Thus, it is not surprising that the j-factor oscillations for the set of minicircles 94–105 bp in length are much smaller than they should be for minicircles of these sizes with the intact helical structure (32). Cyclization of DNA fragments 100–106 bp in length gives minicircles without disruptions for topoisomers with small torsional stress and minicircles with disrupted regions for topoisomers with Inline graphic. Bending stress alone does not disrupt the double helix in the minicircles of these sizes.

Our results show disruptions of the regular DNA structure by bending deformation if the average angles between adjacent base pairs approach 6°. This is a relatively small angle, and such bending does not destroy the stacking interaction between two chosen adjacent base pairs. Indeed, the average amplitude of the angle thermal fluctuations corresponds to 6–7° (25), and these fluctuations do not disrupt regular DNA structure. The disruptions appear in the minicircles because they create localized sharp bends which reduce the bending deformation in all other base pair steps of the minicircles. It is a different question what angle between two chosen adjacent base pairs would break the stacking interaction between them. It should be noted in this context that the value of DNA curvature causing the disruption formation is not relevant to kink formation in tight DNA–protein complexes. In such complexes nearly each base pair interacts with protein and kink formation at a particular base pair step hardly affects conformations at the adjacent base pair steps. Our study addresses conformations of DNA loops which do not interact with proteins along their entire contour, like one formed by lac repressor in lac operon (44).

Our approach cannot determine what kind of local unwound structures appear in the minicircles. We can only suggest some speculations on the issue, based on the different sensitivity of the minicircles to two single-strand-specific nucleases used in the study. Quick digestion by S1 nuclease was only observed for minicircles with ΔLk of –1 [(–) topoisomers for 63 and 84 bp minicircles, Figure 6b and d]. We suggest that the disruptions in these cases have larger unwinding and correspond to small regions with opened base pairs. The disruptions created by the bending stress alone in 64–66 bp minicircles are resistant to S1 nuclease, although they are well digested by BAL 31. Certainly, DNA unwinding should be smaller in these cases, and we think that the disruptions represent sharp kinks of the double helix which preserve base pairing. Although there are no doubts that such kinks can appear in DNA free of bound proteins, our study presents probably the first case in which they were observed experimentally.

A different type of disruption, which involves two consecutive base pair steps, was observed in the recent molecular dynamic simulation of DNA minicircles (9). In this disruption, the hydrogen bonds are intact in two flanking base pairs while the central base pair is broken and the bases are stacked with the 5′ bases of the corresponding strands. We cannot exclude that this kind of disruption also appears in the studied minicircles.

The 100-bp minicircles represent a special case, since they have ΔLk of –0.5. This ΔLk is sufficiently large to promote base pair opening. The minicircles have some sensitivity to S1 nuclease, indicating that base pair opening can occur there with a certain probability. On the other hand, the minicircles are digested very fast by BAL 31 enzyme, which indicates that they have stable disruptions. It is probable that both base pair opening and kinks appear in these minicircles with comparable probabilities.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

[Supplementary Data]
nar_gkm1125_index.html (601B, html)

ACKNOWLEDGEMENTS

The work was supported by the National Institutes of Health grants GM54215 to A.V. This investigation used a facility constructed with support from Research Facilities Improvement Grant Number C06 RR-16572-01 from the National Center for Research Resources, National Institutes of Health. Funding to pay the Open Access publication charges for this article was provided by A.V.

Conflict of interest statement. None declared.

REFERENCES

  • 1.Vologodskii AV. Topology and Physics of Circular DNA. Boca Roton: CRC Press; 1992. [Google Scholar]
  • 2.Sinden RR. DNA Structure and Function. San Diego: Academic Press; 1994. [Google Scholar]
  • 3.Crick FH, Klug A. Kinky helix. Nature. 1975;255:530–533. doi: 10.1038/255530a0. [DOI] [PubMed] [Google Scholar]
  • 4.Sobell HM, Tsai CC, Jain SC, Gilbert SG. Visualization of drug-nucleic acid interactions at atomic resolution. III. Unifying structural concepts in understanding drug-DNA interactions and their broader implications in understanding protein-DNA interactions. J. Mol. Biol. 1977;114:333–365. doi: 10.1016/0022-2836(77)90254-6. [DOI] [PubMed] [Google Scholar]
  • 5.Suzuki M, Yagi N. Stereochemical basis of DNA bending by transcription factors. Nucleic Acids Res. 1995;23:2083–2091. doi: 10.1093/nar/23.12.2083. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Werner MH, Gronenborn AM, Clore GM. Intercalation, DNA kinking, and the control of transcription. Science. 1996;271:778–784. doi: 10.1126/science.271.5250.778. [DOI] [PubMed] [Google Scholar]
  • 7.Dickerson RE. DNA bending: the prevalence of kinkiness and the virtues of normality. Nucleic Acids Res. 1998;26:1906–1926. doi: 10.1093/nar/26.8.1906. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Sussman JL, Trifonov EN. Possibility of nonkinked packing of DNA in chromatin. Proc. Natl Acad. Sci. USA. 1978;75:103–107. doi: 10.1073/pnas.75.1.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Lankas F, Lavery R, Maddocks JH. Kinking occurs during molecular dynamics simulations of small DNA minicircles. Structure. 2006;14:1527–1534. doi: 10.1016/j.str.2006.08.004. [DOI] [PubMed] [Google Scholar]
  • 10.Protozanova E, Yakovchuk P, Frank-Kamenetskii MD. Stacked-unstacked equilibrium at the nick site of DNA. J. Mol. Biol. 2004;342:775–785. doi: 10.1016/j.jmb.2004.07.075. [DOI] [PubMed] [Google Scholar]
  • 11.Yan J, Marko JF. Localized single-stranded bubble mechanism for cyclization of short double helix DNA. Phys. Rev. Lett. 2004;93:108108. doi: 10.1103/PhysRevLett.93.108108. [DOI] [PubMed] [Google Scholar]
  • 12.Gueron M, Kochoyan M, Leroy JL. A single mode of DNA base-pair opening drives imino proton exchange. Nature. 1987;328:89–92. doi: 10.1038/328089a0. [DOI] [PubMed] [Google Scholar]
  • 13.Russu IM. Probing site-specific energetics in proteins and nucleic acids by hydrogen exchange and nuclear magnetic resonance spectroscopy. Methods Enzymol. 2004;379:152–175. doi: 10.1016/S0076-6879(04)79009-6. [DOI] [PubMed] [Google Scholar]
  • 14.Cloutier TE, Widom J. Spontaneous sharp bending of double-stranded DNA. Mol. Cell. 2004;14:355–362. doi: 10.1016/s1097-2765(04)00210-2. [DOI] [PubMed] [Google Scholar]
  • 15.Shimada J, Yamakawa H. Ring-closure probabilities for twisted wormlike chains. Application to DNA. Macromolecules. 1984;17:689–698. [Google Scholar]
  • 16.Vologodskii A. In: Computational Studies of DNA and RNA. Lankas F, Sponer J, editors. Dordrecht, The Netherlands: Springer; 2006. pp. 579–604. [Google Scholar]
  • 17.Du Q, Smith C, Shiffeldrim N, Vologodskaia M, Vologodskii A. Cyclization of short DNA fragments and bending fluctuations of the double helix. Proc. Natl Acad. Sci. USA. 2005;102:5397–5402. doi: 10.1073/pnas.0500983102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Wiggins PA, Phillips R, Nelson PC. Exact theory of kinkable elastic polymers. Phys. Rev. E. 2005;71 doi: 10.1103/PhysRevE.71.021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Beard P, Morrow JF, Berg P. Cleavage of circular, superhelical simian virus 40 DNA to a linear duplex by S1 nuclease. J. Virol. 1973;12:1303–1313. doi: 10.1128/jvi.12.6.1303-1313.1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Wang JC. Interactions between twisted DNAs and enzymes: the effects of superhelical turns. J. Mol. Biol. 1974;87:797–816. doi: 10.1016/0022-2836(74)90085-0. [DOI] [PubMed] [Google Scholar]
  • 21.Gray HB, Jr, Ostrander DA, Hodnett JL, Legerski RJ, Robberson DL. Extracellular nucleases of pseudomonas BAL 31. I. Characterization of single strand-specific deoxyriboendonuclease and double-strand deoxyriboexonuclease activities. Nucleic Acids Res. 1975;2:1459–1492. doi: 10.1093/nar/2.9.1459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Lilley DM. The inverted repeat as a recognizable structural feature in supercoiled DNA molecules. Proc. Natl Acad. Sci. USA. 1980;77:6468–6472. doi: 10.1073/pnas.77.11.6468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Singleton CK, Klysik J, Stirdivant SM, Wells RD. Left-handed Z-DNA is induced by supercoiling in physiological ionic conditions. Nature. 1982;299:312–316. doi: 10.1038/299312a0. [DOI] [PubMed] [Google Scholar]
  • 24.Lyamichev VI, Mirkin SM, Frank-Kamenetskii MD. Structures of homopurine-homopyrimidine tract in superhelical DNA. J. Biomol. Struct. Dyn. 1986;3:667–669. doi: 10.1080/07391102.1986.10508454. [DOI] [PubMed] [Google Scholar]
  • 25.Vologodskaia M, Vologodskii A. Contribution of the intrinsic curvature to measured DNA persistence length. J. Mol. Biol. 2002;317:205–213. doi: 10.1006/jmbi.2001.5366. [DOI] [PubMed] [Google Scholar]
  • 26.Murchie AI, Bowater R, Aboul-ela F, Lilley DM. Helix opening transitions in supercoiled DNA. Biochim. Biophys. Acta. 1992;1131:1–15. doi: 10.1016/0167-4781(92)90091-d. [DOI] [PubMed] [Google Scholar]
  • 27.Benham CJ. Energetic of the strand separation transition in superhelical DNA. J. Mol. Biol. 1992;225:835–847. doi: 10.1016/0022-2836(92)90404-8. [DOI] [PubMed] [Google Scholar]
  • 28.Olson WK, Gorin AA, Lu XJ, Hock LM, Zhurkin VB. DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proc. Natl Acad. Sci. USA. 1998;95:11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Fuller FB. The writhing number of a space curve. Proc. Natl Acad. Sci. USA. 1971;68:815–819. doi: 10.1073/pnas.68.4.815. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Le Bret M. Twist and writing of short circular DNAs according to the first-order elasticity. Biopolymers. 1984;23:1835–1867. doi: 10.1002/bip.360231004. [DOI] [PubMed] [Google Scholar]
  • 31.Richmond TJ, Davey CA. The structure of DNA in the nucleosome core. Nature. 2003;423:145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
  • 32.Cloutier TE, Widom J. DNA twisting flexibility and the formation of sharply looped protein-DNA complexes. Proc. Natl Acad. Sci. USA. 2005;102:3645–3650. doi: 10.1073/pnas.0409059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Desai NA, Shankar V. Single-strand-specific nucleases. FEMS Microbiol. Rev. 2003;26:457–491. doi: 10.1111/j.1574-6976.2003.tb00626.x. [DOI] [PubMed] [Google Scholar]
  • 34.Shishido K, Ando T. Cleavage of ultraviolet light-irradiated DNA by single strand-specific S1 endonuclease. Biochem. Biophys. Res. Com. 1974;59:1380–1388. doi: 10.1016/0006-291x(74)90466-5. [DOI] [PubMed] [Google Scholar]
  • 35.Fuchs RP. In vitro recognition of carcinogen-induced local denaturation sites native DNA by S1 endonuclease from Aspergillus oryzae. Nature. 1975;257:151–152. doi: 10.1038/257151a0. [DOI] [PubMed] [Google Scholar]
  • 36.Legerski RJ, Gray H.B., Jr, Robberson DL. A sensitive endonuclease probe for lesions in deoxyribonucleic acid helix structure produced by carcinogenic or mutagenic agents. J. Biol. Chem. 1977;252:8740–8746. [PubMed] [Google Scholar]
  • 37.Lee J-H, Choi Y-J, Cho B-S. Solution structure of the DNA decamer duplex containing a 3′-T·T base pair of the cis–syn cyclobutane pyrimidine dimer: implication for the mutagenic property of the cis–syn dimer. Nucleic Acids Res. 2000;28:1794–1801. doi: 10.1093/nar/28.8.1794. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Kilpatrick MW, Wei CF, Gray H.B., Jr, Wells RD. BAL 31 nuclease as a probe in concentrated salt for the B-Z DNA junction. Nucleic Acids Res. 1983;11:3811–3822. doi: 10.1093/nar/11.11.3811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Singleton CK, Kilpatrick MW, Wells RD. S1 nuclease recognizes DNA conformational junctions between left-handed helical (dT-dG)n·dC-dA)n and contiguous right-handed sequences. J. Biol. Chem. 1984;259:1963–1967. [PubMed] [Google Scholar]
  • 40.Ha SC, Lowenhaupt K, Rich A, Kim YG, Kim KK. Crystal structure of a junction between B-DNA and Z-DNA reveals two extruded bases. Nature. 2005;437:1183–1186. doi: 10.1038/nature04088. [DOI] [PubMed] [Google Scholar]
  • 41.Shore D, Baldwin RL. Energetics of DNA twisting. II. Topoisomer analysis. J. Mol. Biol. 1983;170:983–1007. doi: 10.1016/s0022-2836(83)80199-5. [DOI] [PubMed] [Google Scholar]
  • 42.Horowitz DS, Wang JC. Torsional rigidity of DNA and length dependence of the free energy of DNA supercoiling. J. Mol. Biol. 1984;173:75–91. doi: 10.1016/0022-2836(84)90404-2. [DOI] [PubMed] [Google Scholar]
  • 43.Frank-Kamenetskii MD, Lukashin AV, Anshelevich VV, Vologodskii AV. Torsional and bending rigidity of the double helix from data on small DNA rings. J. Biomol. Struct. Dyn. 1985;2:1005–1012. doi: 10.1080/07391102.1985.10507616. [DOI] [PubMed] [Google Scholar]
  • 44.Becker NA, Kahn JD, Maher L.J., 3rd Bacterial repression loops require enhanced DNA flexibility. J. Mol. Biol. 2005;349:716–730. doi: 10.1016/j.jmb.2005.04.035. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
nar_gkm1125_index.html (601B, html)
nar_gkm1125_1.pdf (415.2KB, pdf)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES