Abstract
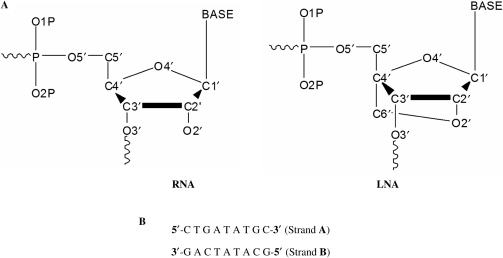
Locked nucleic acid (LNA) is a chemically modified nucleic acid with its sugar ring locked in an RNA-like (C3′-endo) conformation. LNAs show extraordinary thermal stabilities when hybridized with DNA, RNA or LNA itself. We performed molecular dynamics simulations on five isosequential duplexes (LNA–DNA, LNA–LNA, LNA–RNA, RNA–DNA and RNA–RNA) in order to characterize their structure, dynamics and hydration. Structurally, the LNA–DNA and LNA–RNA duplexes are found to be similar to regular RNA–DNA and RNA–RNA duplexes, whereas the LNA–LNA duplex is found to have its helix partly unwound and does not resemble RNA–RNA duplex in a number of properties. Duplexes with an LNA strand have on average longer interstrand phosphate distances compared to RNA–DNA and RNA–RNA duplexes. Furthermore, intrastrand phosphate distances in LNA strands are found to be shorter than in DNA and slightly shorter than in RNA. In case of induced sugar puckering, LNA is found to tune the sugar puckers in partner DNA strand toward C3′-endo conformations more efficiently than RNA. The LNA–LNA duplex has lesser backbone flexibility compared to the RNA–RNA duplex. Finally, LNA is less hydrated compared to DNA or RNA but is found to have a well-organized water structure.
INTRODUCTION
Nucleic acids are central to transmission, expression and conservation of genetic information. Consequently, high-affinity binding of complementary nucleic acids has a plethora of applications in biotechnology and medicine. Pragmatic in this context is the development of nucleic acids with chemical modifications rendering them high affinity and stability, since unmodified DNA or RNA oligonucleotides have moderate affinities for complementary targets and low stability in biological fluids (1). One such modification results in a Locked Nucleic Acid (LNA) molecule, where the furanose conformation is chemically locked in an RNA like (C3′-endo) conformation by introduction of a 2′-O, 4′-C methylene linkage (Figure 1A). LNAs show extraordinary thermal affinities when hybridized with either DNA (ΔTm = 1–8°C per modification), RNA (ΔTm = 2–10°C per modification) or LNA itself (ΔTm > 5°C per modification) (2–4). Eventually, LNA–LNA duplex formation constitutes the most stable Watson–Crick base pairing system yet developed. LNA has therefore found applications in several areas of therapeutics and diagnostics, recently. For instance, LNAs have been employed as aptamers for transcription factor NF-κB (5), incorporated into DNAzymes (6), used as molecular beacons (7), used as probes to improve RNA in situ hybridization (8,9) and applied to improve siRNA stability and functionality (10).
Figure 1.
(A) Structural differences in the ribonucleotide units forming RNA and LNA. (B) Sequence of the bases present in nucleic acid strands A and B. In case of RNA, Thymine (T) bases are changed to Uracil (U) bases. The numbering starts from 1 to 9 beginning with the first base in the 5′ to 3′ direction in both the strands.
With such immense potential, it is of fundamental importance to understand the structural nature of complexes formed by LNA with RNA or DNA. There have been some studies in this direction, mainly with NMR spectroscopy and X-ray crystallography, where in most cases only selected nucleotides have been replaced by LNA nucleotides in a regular RNA or DNA-based duplex (11–13), and in one recent study, NMR structure of a fully modified LNA strand hybridized with an RNA strand was reported (14). These studies have given useful information on the nature of duplex structure, with the introduction of LNA. For instance, these studies show that with incorporation of an increasing number of LNA nucleotides, duplexes achieve an increasing A-like character (14) and the duplexes containing LNA nucleotides show an increase in the values of NMR order parameters compared to unmodified duplexes (15).
We undertook the present computational study of duplexes containing a fully modified LNA strand to be able to find answers to some questions of broad interest: (a) what are the characteristics of LNA–DNA and LNA–LNA duplexes, which are rather new to the structural arsenal of LNA based duplexes, (b) what are the differences and similarities amongst the LNA–RNA, LNA–DNA and LNA–LNA duplexes, (c) how do the structure and dynamics of LNA-based duplexes differ from the regular, unmodified RNA–DNA and RNA–RNA duplexes, (d) how does the aqueous solvent behave in each of the five different (LNA–DNA, LNA–LNA, LNA–RNA, RNA–DNA and RNA–RNA) duplexes and (e) to what extent the LNA strand induces its characteristics (in terms of flexibility, dynamics, sugar conformation, etc.) onto partner strands, compared to unmodified duplexes. An understanding of these fundamental properties will not only be instrumental in more efficient applications of LNA in biotechnology and medicine, but also provide a paradigm platform to plan future nucleic acid modifications effectively.
Molecular dynamics (MD) simulations in explicit solvent have been regularly used in order to address the kind of questions posed above in both regular (16–18) and modified (19–21) nucleic acids. These simulations have given excellent agreement with experimental results, besides providing a very detailed picture of the conformational space and thermodynamics of these molecules along with a clear representation of the behavior of solvent. Here we report the results of a total of 50 ns of MD simulations in aqueous solvent with periodic boundary conditions of three nucleic acid duplexes including a fully modified LNA strand (LNA–DNA, LNA–LNA and LNA–RNA) and two regular duplexes (RNA–DNA and RNA–RNA), for comparison.
COMPUTATIONAL METHODS
Duplex modeling and simulation setup
The 20 NMR structures of the 9-mer LNA–RNA duplex (Figure 1B, PDB ID 1h0q) were reported to have an average pairwise RMSD of 1.06 Å (14). The first structure out of these 20 was used as a starting structure and four new duplexes (LNA–LNA, LNA–RNA, RNA–DNA and RNA–RNA) were modeled using this structure as a template with the introduction of appropriate modifications in bases and ribose units (Figure 1B). All LNA-containing duplexes have their LNA strand fully modified and all five duplexes are isosequential. Initial modeling of new duplexes was performed using the Insight II (Accelrys Inc., San Diego, CA) molecular modeling package and CHARMM (version c33a1) (22) was used for force-field-based calculations. Parameters for bonds, angles, dihedrals and impropers for LNA were derived based on existing parameters for DNA or RNA within the CHARMM27 force-field (23) for nucleic acids. Point charges for LNA were based on the RESP charges derived by Nielsen et al. (14). The new topology and parameters relevant to LNA are provided in the Supplementary Data of this article. Each duplex was immersed in a rhombic dodecahedron shaped box containing ∼3500 pre-equilibrated TIP3P (24) water molecules. Each side of the box extended at least 10 Å away from any solute atom and water molecules within a distance of 2.2 Å of any solute atom were deleted. Sixteen sodium ions were randomly added to the water box in each case to neutralize the net charge.
Molecular dynamics simulation protocol
To avoid the duplex ends from fraying apart during the simulation, weak harmonic distance restraints were imposed on the Watson–Crick hydrogen bonds present in the terminal base steps with a force constant of 4 kcal/mol/Å2. The system was subjected to an equilibration protocol first involving solvent minimization using 2500 steps of steepest descent and 5000 steps of Adopted Basis Newton Raphson (ABNR) algorithms, while holding the solute atoms restrained to their initial positions by means of a harmonic force constant of 50 kcal/mol/Å2. Following this, while still keeping the positional restraints on the solute, the solvent was heated from 100 to 300 K in a 4 ps phase while maintaining a constant pressure of 1 atm. Solvent dynamics was performed for 25 ps in this stage followed by a gradual release of positional restraints from the solute in decrements of 5 kcal/mol/Å2 mediated by series of minimization steps and dynamics. This equilibrated system was then subject to an unrestrained (except the hydrogen bonding restraints on the terminal base pairs) simulation at a constant temperature of 300 K and a constant pressure of 1 atm for 10 ns in each case.
The SHAKE algorithm (25) was used to constrain all covalent bonds involving a hydrogen atom, allowing a time step of 2 fs and the leapfrog algorithm was used to integrate the equations of motion. Constant pressure was maintained using the Langevin piston method (26) with a piston of mass 400 amu and a collision frequency of 20 ps−1, coupled to a temperature bath of 300 K. The system was maintained at 300 ± 10 K, once heated, by scaling the velocities accordingly. Furthermore, a dielectric constant of 1 was used, and atom-based non-bonded interactions were truncated beyond 12 Å using a force shift approach (27), which has been proven to accurately represent the long-range electrostatic effects in nucleic acids (28). The non-bonded lists were maintained for pairs within a distance of 14 Å and updated heuristically whenever an atom had moved more than 1 Å since last update. Periodic boundary conditions were applied and coordinates were saved every picosecond for further analysis.
Analysis of trajectories
Rotational and translational motion was removed from the trajectories by superimposing the solute (nucleic acid duplex) onto the starting structure, and the solvent was recentered around the solute atoms. All properties were calculated for the last 8 ns of the 10 ns trajectories. RMSD was calculated for all heavy atoms in each case, with respect to starting structure. The interstrand phosphate distance was calculated as the distance between the phosphorus atom of a nucleotide in one strand and the phosphorus atom of the nucleotide in partner strand. Since phosphate groups are not present in one of the strands of both terminal steps, these distances were calculated for all base pair steps, except the terminals, in each case. The intrastrand phosphate distance was calculated as the distance between the phosphorous atoms of two successive nucleotides within a strand. The helicoidal and step parameters were calculated with the program CURVES version 5.1 (29).
Hydration numbers were calculated for sets of major groove (O6, N7, O4, H61 and H62), minor groove (N3, O2, H21 and H22) and phosphate oxygen (O1P, O2P, O3′ and O5′) atoms in each case, representing the number of water molecules present at a distance of <3.0 Å of the solute atoms. Additionally, the radial distribution, g(r) of water protons was calculated for the set of phosphate oxygen atoms in each case. Next, solvent occupancy analysis of intrastrand hydrogen bond bridging water molecules was performed. A hydrogen bond was considered to be present when the distance between hydrogen atom and the hydrogen bond acceptor atom was <2.4 Å, which has been shown as a sufficient criterion (30). The solvent occupancy was interpreted by counting the number of solute atoms that formed a bridged hydrogen bond via any water molecule (water molecule donating and hence bridging two hydrogen bonds, simultaneously) resulting in a net occupancy of more than 100%.
Root mean square fluctuations (RMSFs) were calculated around average structures for the heavy atoms composing backbone atoms (P, O1P, O2P, O3′, C5′ and O5′) of each nucleotide. Additionally, entropy calculations for all nucleic acid duplexes and their structural components (base, ribose and backbone atoms of each strand) were performed with the quasiharmonic analyses facility implemented in CHARMM. The configurational entropy estimator used is based on the use of the quasiharmonic analysis with the covariance (covariance matrix of atomic positional fluctuations accumulated during MD) related to the quantum-mechanical harmonic oscillator expression for the entropy (31). The entropies and their contribution to the free energy (TS) were calculated at 300 K.
RESULTS AND DISCUSSION
Overall structure and dynamics
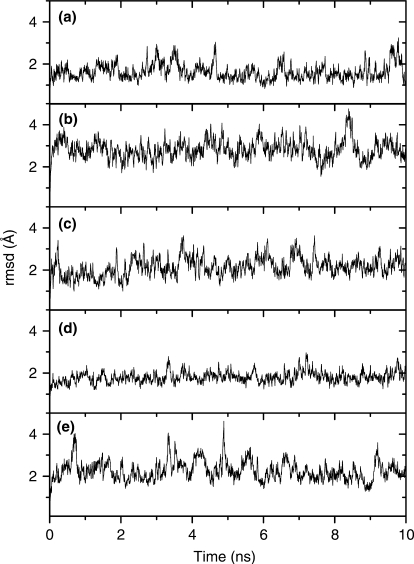
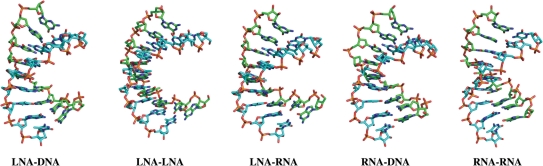
All the simulated structures depict an ensemble of conformations with stable 2–3Å RMSDs from the starting structure (Figure 2). The simulation of the LNA–RNA duplex was able to very closely reproduce the NMR-derived structure (final, energy minimized snapshot shows an RMSD of 1.2 Å when superimposed with starting experimental structure; whereas average pairwise RMSD for the set of NMR structures is 1.06 Å, see Supplementary Data). Figure 3 shows energy minimized, final snapshots from the MD simulations of the five duplexes. All the structures adopt typical A-type duplex geometries. The general structure of LNA–DNA and LNA–RNA duplexes resemble the RNA–DNA and RNA–RNA duplexes. However, the LNA–LNA duplex exhibits a slight unwinding of the helix (see twist angles in section on base stacking), resulting in relatively shallower grooves, compared to other duplexes.
Figure 2.
Time evolution during the entire simulation of the root mean square deviation (rmsd) from the starting structures for all the heavy atoms of (a) LNA–DNA, (b) LNA–LNA, (c) LNA–RNA, (d) RNA–DNA and (e) RNA–RNA duplexes.
Figure 3.
Energy minimized structures of the last snapshots of duplexes studied with MD simulations in explicit solvent for 10 ns. Hydrogen atoms are omitted for clarity. Carbon atoms of Strand A are in cyan and that of Strand B in green for each duplex.
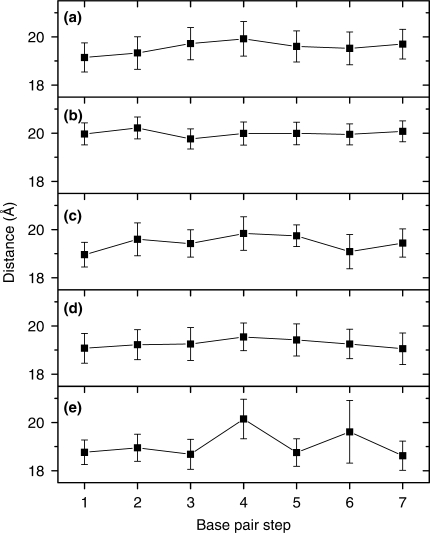
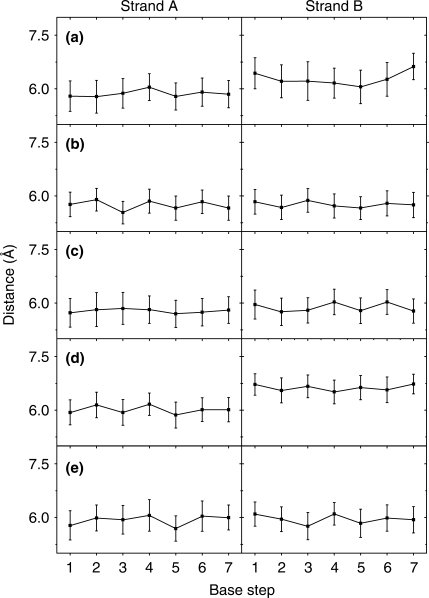
To further characterize the general structural and dynamic features, we calculated interstrand phosphate and intrastrand phosphate distances during the simulation in each case. Figure 4 shows the interstrand phosphate distances, which describe a duplex structure in its girth. LNA strand containing duplexes have on average longer distances (upto 20 Å for LNA–LNA duplex) compared to RNA–DNA and RNA–RNA duplexes. Furthermore, intrastrand phosphate distances (Figure 5) show that LNA strands have around 5.7 Å intrastrand phosphate distance, whereas DNA strands have a longer distance of around 6.4 Å. RNA strands are closer to LNA strands in their intrastrand phosphate lengths (around 5.9 Å), however at several base steps RNA strands have their average intrastrand phosphate distances exceeding 6 Å.
Figure 4.
Average ± SD interstrand phosphate distances in (a) LNA–DNA, (b) LNA–LNA, (c) LNA–RNA, (d) RNA–DNA and (e) RNA–RNA duplexes, calculated during the last 8 ns of the 10 ns MD trajectory.
Figure 5.
Average ± SD intrastrand phosphate distances in (a) LNA–DNA, (b) LNA–LNA, (c) LNA–RNA, (d) RNA–DNA and (e) RNA–RNA duplexes, calculated during the last 8 ns of the 10 ns MD trajectory.
Sugar puckering
Previous NMR studies (14,32) have determined that, in general, the locked C3′-endo conformation of LNA drives the conformation of the base paired strand into larger populations of north sugar puckers, in an attempt to achieve an overall A-type geometry. This behavior is indeed expected, as RNA is also known to influence DNA sugar puckering in DNA–RNA duplexes (18). However, the relative extent of such a conformational coupling between sugar puckers in case of LNA is not known. Here we focused on this sugar pucker conformation, and calculated the extent to which LNA induces its C3′-endo pucker [pucker phase (33) values between 0° and 36°] on to a partner strand. Table 1 depicts the frequency of occurrence of C3′-endo pucker in all the strands during the simulation. We also report the frequency of north (0° ± 90°) conformation in all strands. Sugars in all LNA strands stay locked in a C3′-endo pucker (and north conformation). Sugars in all the RNA strands show greater than 90% instances of C3′-endo pucker (and almost 100% north conformations). The DNA strand in the LNA–DNA duplex shows around 36% instances of C3′-endo pucker and 44% instances of north conformation of its sugars. On the other hand, sugars of the DNA strand in the RNA–DNA duplex show only around 9% of C3′-endo pucker and around 15% of north conformation. These results show that LNA tunes the sugar puckering in partner DNA strand towards C3′-endo pucker or north conformations more efficiently than does RNA.
Table 1.
Frequency of sugar C3′-endo pucker and North conformation in the nucleic acid duplexes
| Duplex | C3′-endo pucker (%a) in strand A | C3′-endo pucker (%a) in strand B | North conformation (%a) in strand A | North conformation (%a) in strand B |
|---|---|---|---|---|
| LNA(A)–DNA(B) | 100 | 37 | 100 | 44 |
| LNA(A)–LNA(B) | 100 | 100 | 100 | 100 |
| LNA(A)–RNA(B) | 100 | 90 | 100 | 100 |
| RNA(A)–DNA(B) | 92 | 9 | 100 | 16 |
| RNA(A)–RNA(B) | 91 | 90 | 100 | 99 |
aPercent count of occurrence of the C3′-endo pucker and North conformation of sugar moieties during the last 8 ns of the 10 ns MD trajectory.
Backbone flexibility
In order to probe the influence of rigid sugar conformation of LNA on nucleic acid backbone flexibility, we calculated the RMSF values for backbone atoms of each nucleotide (Figure 6). It is clear that DNA backbone is slightly more flexible than LNA/RNA backbone and that LNA does not impose its low backbone flexibility onto partner strands. Also, the LNA–LNA duplex has lesser backbone flexibility compared to the RNA–RNA duplex. To further understand the nature of conformational flexibility, we calculated absolute conformational entropies for all the structural elements (backbone, sugar and bases) in the five duplexes (see Supplementary Data). For backbone atoms, we do not find any apparent influence of LNA in lowering the entropy of partner strands and the LNA–LNA duplex is calculated to have the lowest backbone entropy. Hence LNA tunes the sugar pucker of DNA to a significant extent; it does not influence the backbone flexibility of DNA or RNA.
Figure 6.
Root mean square fluctuations of the backbone atoms (P, O1P, O2P, O3′, C5′ and O5′) of (a) LNA(A)–DNA(B), (b) LNA(A)–LNA(B), (c) LNA(A)–RNA(B), (d) RNA(A)–DNA(B) and (e) RNA(A)–RNA(B) duplexes. All A strands are plotted in black and all B strands in red.
Water structure and dynamics
The aqueous solvent has a crucial role in nucleic acid structure, stability and dynamics and has been a subject of study for a long time (34–37). We calculated the hydration numbers in the first solvation shell of duplex groove and phosphodiester backbone atoms (Table 2). Minor groove hydration in RNA–RNA duplex is the highest (average 17.4 water molecules) and in the LNA–LNA duplex it is the lowest (average 15.6 water molecules). The partially unwound helix of the LNA–LNA duplex, resulting in a shallower minor groove, may lead to its low minor groove hydration. Major groove hydration in the RNA–RNA is also the highest compared to other duplexes. LNA–DNA and RNA–DNA duplexes have similar major groove hydration (hydration numbers ∼14.5), which is lower than the RNA–RNA duplex (hydration number ∼18.5). Next, the hydration numbers for backbone oxygen atoms (Table 2) reveal that RNA and LNA are lesser hydrated (hydration numbers ∼41) than DNA (hydration numbers ∼46). Yet, the LNA strand in LNA–RNA duplex is slightly lesser hydrated than the RNA strand. To further characterize the backbone hydration, we calculated the radial distribution function (RDF), which describes how on average, the water molecules are radially packed around the various nucleic acid atoms. RDF plots show that the backbone of DNA is more hydrated than RNA or LNA and LNA is the least hydrated, even after the first shell of solvation (Figure S2, Supplementary Data). This result is in agreement with a recent experimental finding where it is proposed that introduction of LNA nucleotides into DNA duplexes results in a net lower uptake of water molecules (38).
Table 2.
Hydration numbers at specific sites in the nucleic acid duplexes
| Hydration numbera | ||||
|---|---|---|---|---|
| Duplex | Major Groove | Minor Groove | Backbone Oxygens (Strand A) | Backbone Oxygens (Strand B) |
| LNA–DNA | 14.9 ± 0.5 | 16.6 ± 0.5 | 41.3 ± 1.2 | 45.3 ± 1.3 |
| LNA–LNA | 15.3 ± 0.6 | 15.6 ± 0.4 | 41.1 ± 1.2 | 42.0 ± 1.2 |
| LNA–RNA | 16.8 ± 0.6 | 16.2 ± 0.5 | 40.8 ± 1.2 | 41.7 ± 1.2 |
| RNA–DNA | 14.5 ± 0.5 | 16.7 ± 0.5 | 41.7 ± 1.2 | 46.5 ± 1.4 |
| RNA–RNA | 18.7 ± 0.7 | 17.4 ± 0.5 | 41.2 ± 1.2 | 41.6 ± 1.2 |
aAverage ± SD number of water molecules present at a distance less than 3.0 Å of the specified set of atoms during the last 8 ns of the 10 ns MD trajectory.
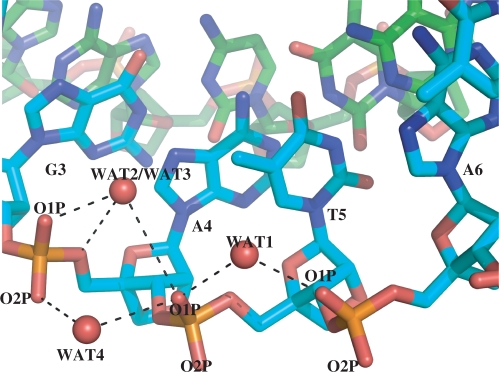
In order to probe the structure of water at an atomic level, we studied the hydrogen bonding pattern in nucleic acid backbone. We calculated the occupancy of water-mediated hydrogen bonding bridges in the backbone of each strand during the simulation (Table 4). Phosphate oxygen atoms (O1P and O2P) are capable of accepting multiple hydrogen bonds from water molecules and they can also participate as one of the members in water-mediated hydrogen bonding bridge involving other backbone oxygen atoms. Interestingly, we find that whereas DNA and RNA only form very infrequent multiple hydrogen bonding bridges during the course of the simulation, LNA strands have the most frequent (resulting in high occupancy) hydrogen-bonding bridges. Table 3 shows the number of atoms (eventually O1P and O2P atoms) in a strand involved in multiple, water-mediated hydrogen bonding interactions that result in a net occupancy of 100% or more (see Supplementary Data for a complete list of all specific fractions of occupancy). Figure 7 depicts a snapshot from the simulation of the LNA–LNA duplex where the O1P atom of T5 is shown forming four water-bridged hydrogen bonds with other backbone oxygen atoms, although not all possible simultaneously, but distributed over the course of simulation resulting in a net occupancy of more than 100%. The water molecules bridging hydrogen bonds were exchanged by other water molecules from the bulk solvent and the average residence time for such a bridge ranged from 5 to 15 ps, quite similar to what has been reported for double-stranded DNA(39).
Table 4.
X-Displacement values for the base pairs in the nucleic acid duplexes
| Base pair | X-Displacement (Å) | ||||
|---|---|---|---|---|---|
| LNA–DNA | LNA–LNA | LNA–RNA | RNA–DNA | RNA–RNA | |
| 1–9 | −4.2 ± 0.9 | −6.7 ± 1.8 | −4.9 ± 1.1 | −3.2 ± 0.6 | −1.0 ± 1.1 |
| 2–8 | −4.3 ± 0.9 | −6.7 ± 1.7 | −4.9 ± 1.1 | −3.2 ± 0.6 | −1.1 ± 1.1 |
| 3–7 | −4.4 ± 0.9 | −6.8 ± 1.7 | −4.8 ± 1.2 | −3.3 ± 0.6 | −1.0 ± 1.1 |
| 4–6 | −4.3 ± 0.9 | −7.0 ± 1.7 | −5.0 ± 1.1 | −3.2 ± 0.6 | −0.9 ± 1.0 |
| 5–5 | −4.2 ± 0.9 | −7.0 ± 1.7 | −4.8 ± 1.1 | −3.2 ± 0.6 | 0.7 ± 1.5 |
| 6–4 | −4.3 ± 0.9 | −6.9 ± 1.7 | −4.8 ± 1.3 | −3.2 ± 0.6 | −0.6 ± 1.0 |
| 7–3 | −4.2 ± 0.9 | −6.9 ± 1.7 | −4.8 ± 1.2 | −3.2 ± 0.6 | 0.6 ± 1.7 |
| 8–2 | −4.1 ± 0.9 | −6.9 ± 1.7 | −4.7 ± 1.3 | −3.2 ± 0.6 | −0.2 ± 1.3 |
| 9–1 | −4.0 ± 0.9 | −6.9 ± 1.8 | −4.7 ± 1.3 | −3.2 ± 0.6 | −0.0 ± 1.4 |
Table 3.
Occupancy analyses for water-mediated hydrogen bonding bridges (number of solute atoms involved) in the nucleic acid duplexes
| Atom Set | LNA (A)–DNA (B) | LNA (A)–LNA (B) | LNA (A)–RNA (B) | RNA (A)–DNA (B) | RNA (A)–RNA (B) |
|---|---|---|---|---|---|
| Intra A strand water bridges | 7a | 7 | 8 | 0 | 2 |
| Intra B strand water bridges | 0 | 6 | 2 | 0 | 2 |
aUnique number of solute atoms that formed a hydrogen bond via any water molecule resulting in a net occupancy of more than 100% (representing multiple hydrogen bonds, see supporting information for a complete list) during the last 8 ns of the 10 ns MD trajectory.
Figure 7.
A snapshot from the MD trajectory of LNA–LNA duplex depicting water-mediated hydrogen-bonding bridges formed by O1P of T5 in Strand A (carbon atoms in cyan) with other backbone oxygen atoms during the course of simulation resulting in a net occupancy of more than 100%. Similar hydrogen-bonding bridges have lower occupancies in both DNA and RNA strands. Hydrogen atoms are omitted and water oxygen atoms are shown as spheres. The water molecules were exchanged by other water molecules during the simulation.
It is an interesting finding that LNA is less hydrated compared to DNA or RNA but has a well-organized water structure, in context of the backbone. DNA may be more hydrated than RNA or LNA around the backbone oxygen atoms because the intrastrand phosphate distances in DNA are longer than in RNA or LNA (Figure 5), which may allow for more space and hence increase in the number of water molecules in the first shell of hydration (owing to individual shell of hydration for each phosphate oxygen atom). LNA may also be less hydrated because of the apolar nature of the methylene linkage in the sugar. Furthermore, the overall backbone conformation and chemical environment of LNA, in addition to its shorter intrastrand phosphate distances and lower backbone flexibility allow for the formation of simultaneous water-mediated hydrogen bonding bridges with greater occupancy than DNA or RNA. The multiple water bridges in LNA may provide it with an extra stability compared to DNA or RNA.
Base stacking
Stacking of bases plays a prominent role in the structural stability of nucleic acid duplexes. The stacking mode can be specified by helicoidal and step parameters. Helicoidal parameters demonstrate the orientation of a base pair relative to the global helical axis, and step parameters are required to describe the position and orientation of one base pair relative to another (29). Here, in order to characterize the structure of nucleic acid duplexes further, we present values of four parameters—x-displacement of base pairs from helix axis (defined as the perpendicular distance from the long axis of the base pair to the helix axis), propeller twist angles of base pairs (formed between two base planes that form a base pair), roll angles and twist angles of stacking base pairs, calculated directly from the simulation snapshots (Tables 4–7). For comparison, we also calculated the values of these parameters for the 20 NMR structures of the LNA–RNA duplex, and found them to be in good agreement with those of the experimental structures (see Supplementary Data).
Table 5.
Propeller twist angles of the base pairs in the nucleic acid duplexes.
| Base pair | Propeller Twist (in degrees) | ||||
|---|---|---|---|---|---|
| LNA–DNA | LNA–LNA | LNA–RNA | RNA–DNA | RNA–RNA | |
| 1–9 | −11.2 ± 9.9 | −7.0 ± 9.0 | −5.8 ± 9.5 | −18.0 ± 10.1 | −13.7 ± 11.0 |
| 2–8 | −14.0 ± 7.8 | −12.1 ± 7.9 | −15.4 ± 8.1 | −15.4 ± 8.3 | −13.3 ± 9.2 |
| 3–7 | −10.6 ± 10.6 | −10.1 ± 7.5 | −9.7 ± 8.4 | −13.0 ± 11.0 | −6.8 ± 10.4 |
| 4–6 | −15.7 ± 9.1 | −12.4 ± 7.0 | −12.9 ± 8.9 | −15.5 ± 9.3 | −10.5 ± 11.8 |
| 5–5 | −10.0 ± 8.1 | −10.2 ± 6.8 | −9.9 ± 8.0 | −13.0 ± 8.5 | 15.5 ± 13.8 |
| 6–4 | −16.2 ± 9.8 | −9.8 ± 6.9 | −14.7 ± 10.6 | −16.1 ± 9.9 | −6.1 ± 10.2 |
| 7–3 | −12.4 ± 8.6 | −9.3 ± 7.1 | −13.2 ± 9.3 | −14.8 ± 8.7 | 4.4 ± 18.2 |
| 8–2 | −9.3 ± 11.0 | −6.8 ± 7.7 | −12.9 ± 10.5 | −6.8 ± 8.9 | −8.1 ± 9.6 |
| 9–1 | 5.2 ± 9.9 | −7.6 ± 7.9 | −4.2 ± 9.7 | 1.7 ± 9.7 | −6.8 ± 9.3 |
Table 6.
Roll angles of the stacking base pairs in the nucleic acid duplexes
| Stacking pair | Roll (in degrees) | ||||
|---|---|---|---|---|---|
| LNA–DNA | LNA–LNA | LNA–RNA | RNA–DNA | RNA–RNA | |
| 1–2:9–8 | 8.5 ± 5.0 | 7.1 ± 5.0 | 10.6 ± 5.9 | 10.4 ± 5.7 | 13.5 ± 7.1 |
| 2–3:8–7 | 13.0 ± 7.1 | 10.5 ± 5.2 | 11.7 ± 6.6 | 15.5 ± 7.2 | 14.1 ± 7.0 |
| 3–4:7–6 | 11.8 ± 7.2 | 11.6 ± 4.6 | 11.6 ± 5.5 | 8.5 ± 7.1 | 9.7 ± 6.2 |
| 4–5:6–5 | 4.4 ± 5.1 | 4.2 ± 3.9 | 5.8 ± 5.0 | 7.5 ± 5.9 | 7.6 ± 6.7 |
| 5–6:5–4 | 14.4 ± 6.7 | 12.9 ± 4.8 | 15.8 ± 6.2 | 17.6 ± 6.9 | 15.5 ± 7.3 |
| 6–7:4–3 | 5.11 ± 5.2 | 3.1 ± 3.9 | 5.7 ± 5.1 | 7.9 ± 6.5 | 11.1 ± 6.7 |
| 7–8:3–2 | 11.9 ± 7.2 | 11.7 ± 5.1 | 13.8 ± 6.5 | 13 ± 6.9 | 11.4 ± 6.8 |
| 8–9:2–1 | 4.8 ± 5.0 | 5.4 ± 4.0 | 4.5 ± 4.6 | 6.2 ± 4.8 | 5.5 ± 4.7 |
Table 7.
Twist angles of the stacking base pairs in the nucleic acid duplexes
| Stacking pair | Twist (in degrees) | ||||
|---|---|---|---|---|---|
| LNA–DNA | LNA–LNA | LNA–RNA | RNA–DNA | RNA–RNA | |
| 1–2:9–8 | 30.7 ± 4.9 | 24.5 ± 4.0 | 29.1 ± 4.1 | 33.6 ± 5.0 | 30.7 ± 4.6 |
| 2–3:8–7 | 28.6 ± 4.1 | 22.7 ± 4.0 | 26.6 ± 5.1 | 31.3 ± 4.1 | 29.1 ± 4.9 |
| 3–4:7–6 | 26.4 ± 4.7 | 24.6 ± 3.6 | 26.6 ± 3.9 | 31.2 ± 5.3 | 28.9 ± 4.7 |
| 4–5:6–5 | 25.3 ± 4.3 | 22.6 ± 3.3 | 24.0 ± 3.8 | 28.9 ± 3.7 | 18 ± 11.9 |
| 5–6:5–4 | 28.2 ± 4.3 | 24.1 ± 3.8 | 28.0 ± 4.2 | 30.6 ± 4.1 | 33.5 ± 14.2 |
| 6–7:4–3 | 26.1 ± 4.2 | 21.8 ± 3.4 | 24.9 ± 3.4 | 28.6 ± 3.9 | 29.9 ± 8.4 |
| 7–8:3–2 | 29.4 ± 4.8 | 24.0 ± 3.8 | 27.3 ± 5.2 | 31.2 ± 3.9 | 22.5 ± 9.1 |
| 8–9:2–1 | 26.6 ± 5.0 | 22.5 ± 3.6 | 27.0 ± 4.2 | 30.8 ± 4.5 | 31.3 ± 4.4 |
The x-displacement is positive if the helix axis passes by the major groove of the base pair and negative if it passes by the minor groove. On average, the LNA–LNA duplex is calculated to have the lowest x-displacement and the RNA–RNA duplex the highest (Table 4). The propeller twist angle is found to have a similar pattern along the length of the duplex for LNA–DNA and RNA–DNA duplexes, but in the RNA–RNA duple the otherwise negative propeller twist has positive values for base pairs 5–5 and 7–3 (Table 5). The roll angles (angles between two successive base pair planes) show similar trends in all the duplexes (Table 6). Finally, the twist angles (defined as the angle by which one base pair has to rotate to match with the next base pair around the helical axis), vary from one base pair to the next and these variations are probably influenced at least in part, by the attempt to maximize the base stacking overlap as one base pair encounters the next base pair. For the LNA–LNA duplex, the values for twist angles are generally lower compared to other duplexes (Table 7). This reflects the slight unwinding of the helix that the LNA–LNA duplex undergoes. This may also explain why a fully modified LNA strand is unable to form a triplex with a DNA duplex as found in a recent study (40). It is possible that a fully modified LNA strand does not have the ability to twine enough as a helix so as to form a stable triplex with the helical DNA duplex in a network of non Watson–Crick hydrogen bonds.
CONCLUSIONS
In the present computational study we have used state-of-the-art MD simulations to understand in detail the structure, dynamics and hydration of nucleic acid duplexes formed by a fully modified LNA strand. We also performed two simulations on regular, unmodified duplexes for comparison. Although LNA is an RNA mimic we have found that the RNA–RNA duplex differs from the LNA–LNA duplex in a number of properties. A fully modified LNA strand, according to our calculations, has only subtle differences from an equivalent RNA strand but these subtle differences altogether impart to LNA certain unique physical properties. In conclusion, this study has deepened our understanding of LNA-based nucleic acid duplexes in the following specific aspects:
The overall structure of LNA–DNA and LNA–RNA duplexes resemble the RNA–DNA and RNA–RNA duplexes. However, the LNA–LNA duplex exhibits a slight unwinding of the helix.
Duplexes with an LNA strand have on average longer interstrand phosphate distances compared to RNA–DNA and RNA–RNA duplexes. Intrastrand phosphate distances in LNA strands are however shorter than DNA and slightly shorter than RNA.
LNA tunes the sugar puckering in partner DNA strand towards C3′-endo pucker or North conformations more efficiently than RNA.
The DNA backbone is slightly more flexible than LNA or RNA backbones and LNA does not show any conformational coupling of its reduced backbone flexibility onto partner strands. Also, the LNA–LNA duplex has lesser backbone flexibility compared to the RNA–RNA duplex.
LNA is less hydrated compared to DNA or RNA but has a well-organized water structure, in context of the backbone. DNA and RNA only form very infrequent multiple hydrogen-bonding bridges via water molecules during the course of the simulation, however LNA strands have the most frequent hydrogen-bonding bridges, resulting in a net higher occupancy of water bridged backbone.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
ACKNOWLEDGEMENT
This work was supported by the Swedish Research Council and the Swedish Foundation for Strategic Research through the BioX program.
Conflict of interest statement. None declared.
REFERENCES
- 1.Crooke ST. Progress in antisense technology. Annu. Rev. Med. 2004;55:61–95. doi: 10.1146/annurev.med.55.091902.104408. [DOI] [PubMed] [Google Scholar]
- 2.Braasch DA, Corey DR. Locked nucleic acid (LNA): fine-tuning the recognition of DNA and RNA. Chem. Biol. 2001;8:1–7. doi: 10.1016/s1074-5521(00)00058-2. [DOI] [PubMed] [Google Scholar]
- 3.Koshkin AA, Nielsen P, Meldgaard M, Rajwanshi VK, Singh SK, Wengel J. LNA (locked nucleic acid): an RNA mimic forming exceedingly stable LNA: LNA duplexes. J. Am. Chem. Soc. 1998;120:13252–13253. [Google Scholar]
- 4.Obika S, Nanbu D, Hari Y, Andoh J, Morio K, Doi T, Imanishi T. Stability and structural features of the duplexes containing nucleoside analogues with a fixed N-type conformation, 2′-O,4′-C-methyleneribonucleosides. Tetrahedron Lett. 1998;39:5401–5404. [Google Scholar]
- 5.Crinelli R, Bianchi M, Gentilini L, Magnani M. Design and characterization of decoy oligonucleotides containing locked nucleic acids. Nucleic Acids Res. 2002;30:2435–2443. doi: 10.1093/nar/30.11.2435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vester B, Lundberg LB, Sorensen MD, Babu BR, Douthwaite S, Wengel J. LNAzymes: incorporation of LNA-type monomers into DNAzymes markedly increases RNA cleavage. J. Am. Chem. Soc. 2002;124:13682–13683. doi: 10.1021/ja0276220. [DOI] [PubMed] [Google Scholar]
- 7.Wang L, Yang CYJ, Medley CD, Benner SA, Tan WH. Locked nucleic acid molecular beacons. J. Am. Chem. Soc. 2005;127:15664–15665. doi: 10.1021/ja052498g. [DOI] [PubMed] [Google Scholar]
- 8.Kloosterman WP, Wienholds E, de Bruijn E, Kauppinen S, Plasterk RHA. In situ detection of miRNAs in animal embryos using LNA-modified oligonucteotide probes. Nat. Methods. 2006;3:27–29. doi: 10.1038/nmeth843. [DOI] [PubMed] [Google Scholar]
- 9.Thomsen R, Nielsen PS, Jensen TH. Dramatically improved RNA in situ hybridization signals using LNA-modified probes. RNA. 2005;11:1745–1748. doi: 10.1261/rna.2139705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Elmen J, Thonberg H, Ljungberg K, Frieden M, Westergaard M, Xu YH, Wahren B, Liang ZC, Urum H, et al. Locked nucleic acid (LNA) mediated improvements in siRNA stability and functionality. Nucleic Acids Res. 2005;33:439–447. doi: 10.1093/nar/gki193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bondensgaard K, Petersen M, Singh SK, Rajwanshi VK, Kumar R, Wengel J, Jacobsen JP. Structural studies of LNA : RNA duplexes by NMR: conformations and implications for RNase H activity. Chemistry. 2000;6:2687–2695. doi: 10.1002/1521-3765(20000804)6:15<2687::aid-chem2687>3.0.co;2-u. [DOI] [PubMed] [Google Scholar]
- 12.Nielsen KE, Singh SK, Wengel J, Jacobsen JP. Solution structure of an LNA hybridized to DNA: NMR study of the d(CT(L)GCT(L)T(L)CT(L)GC): d(GCAGAAGCAG) duplex containing four locked nucleotides. Bioconjug. Chem. 2000;11:228–238. doi: 10.1021/bc990121s. [DOI] [PubMed] [Google Scholar]
- 13.Petersen M, Bondensgaard K, Wengel J, Jacobsen JP. Locked nucleic acid (LNA) recognition of RNA: NMR solution structures of LNA : RNA hybrids. J. Am. Chem. Soc. 2002;124:5974–5982. doi: 10.1021/ja012288d. [DOI] [PubMed] [Google Scholar]
- 14.Nielsen KE, Rasmussen J, Kumar R, Wengel J, Jacobsen JP, Petersen M. NMR studies of fully modified locked nucleic acid (LNA) hybrids: solution structure of an LNA: RNA hybrid and characterization of an LNA : DNA hybrid. Bioconjug. Chem. 2004;15:449–457. doi: 10.1021/bc034145h. [DOI] [PubMed] [Google Scholar]
- 15.Nielsen KE, Spielmann HP. The structure of a mixed LNA/DNA : RNA duplex is driven by conformational coupling between LNA and deoxyribose residues as determined from C-13 relaxation measurements. J. Am. Chem. Soc. 2005;127:15273–15282. doi: 10.1021/ja051026z. [DOI] [PubMed] [Google Scholar]
- 16.Foloppe N, Nilsson L. Toward a full characterization of nucleic acid components in aqueous solution: simulations of nucleosides. J. Phys. Chem. B. 2005;109:9119–9131. doi: 10.1021/jp044513u. [DOI] [PubMed] [Google Scholar]
- 17.Norberg J, Nilsson L. Molecular dynamics applied to nucleic acids. Acc. Chem. Res. 2002;35:465–472. doi: 10.1021/ar010026a. [DOI] [PubMed] [Google Scholar]
- 18.Noy A, Perez A, Marquez M, Luque FJ, Orozco M. Structure, recognition properties, and flexibility of the DNA-RNA hybrid. J. Am. Chem. Soc. 2005;127:4910–4920. doi: 10.1021/ja043293v. [DOI] [PubMed] [Google Scholar]
- 19.Sen S, Nilsson L. Molecular dynamics of duplex systems involving PNA: structural and dynamical consequences of the nucleic acid backbone. J. Am. Chem. Soc. 1998;120:619–631. [Google Scholar]
- 20.Sen S, Nilsson L. MD simulations of homomorphous PNA, DNA, and RNA single strands: characterization and comparison of conformations and dynamics. J. Am. Chem. Soc. 2001;123:7414–7422. doi: 10.1021/ja0032632. [DOI] [PubMed] [Google Scholar]
- 21.Soliva R, Sherer E, Luque FJ, Laughton CA, Orozco M. Molecular dynamics simulations of PNA center dot DNA and PNA center dot RNA duplexes in aqueous solution. J. Am. Chem. Soc. 2000;122:5997–6008. [Google Scholar]
- 22.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. Charmm - a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 23.Foloppe N, MacKerell AD. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000;21:86–104. [Google Scholar]
- 24.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 25.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical-integration of Cartesian equations of motion of a system with constraints - molecular-dynamics of N-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 26.Feller SE, Zhang YH, Pastor RW, Brooks BR. Constant-pressure molecular-dynamics simulation - the Langevin Piston method. J. Chem. Phys. 1995;103:4613–4621. [Google Scholar]
- 27.Steinbach PJ, Brooks BR. New spherical-cutoff methods for long-range forces in macromolecular simulation. J. Comput. Chem. 1994;15:667–683. [Google Scholar]
- 28.Norberg J, Nilsson L. On the truncation of long-range electrostatic interactions in DNA. Biophys. J. 2000;79:1537–1553. doi: 10.1016/S0006-3495(00)76405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lavery R, Sklenar H. The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic-acids. J. Biomol. Struct. Dyn. 1988;6:63–91. doi: 10.1080/07391102.1988.10506483. [DOI] [PubMed] [Google Scholar]
- 30.Deloof H, Nilsson L, Rigler R. Molecular-dynamics simulation of Galanin in aqueous and nonaqueous solution. J. Am. Chem. Soc. 1992;114:4028–4035. [Google Scholar]
- 31.Andricioaei I, Karplus M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys. 2001;115:6289–6292. [Google Scholar]
- 32.Petersen M, Nielsen CB, Nielsen KE, Jensen GA, Bondensgaard K, Singh SK, Rajwanshi VK, Koshkin AA, Dahl BM, et al. The conformations of locked nucleic acids (LNA) J. Mol. Recognit. 2000;13:44–53. doi: 10.1002/(SICI)1099-1352(200001/02)13:1<44::AID-JMR486>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 33.Altona C, Sundaralingam M. Conformational-analysis of sugar ring in nucleosides and nucleotides - new description using concept of pseudorotation. J. Am. Chem. Soc. 1972;94:8205–&. doi: 10.1021/ja00778a043. [DOI] [PubMed] [Google Scholar]
- 34.Auffinger P, Westhof E. Water and ion binding around RNA and DNA (C,G) oligomers. J. Mol. Biol. 2000;300:1113–1131. doi: 10.1006/jmbi.2000.3894. [DOI] [PubMed] [Google Scholar]
- 35.Saenger W, Hunter WN, Kennard O. DNA conformation is determined by economics in the hydration of phosphate groups. Nature. 1986;324:385–388. doi: 10.1038/324385a0. [DOI] [PubMed] [Google Scholar]
- 36.Auffinger P, Westhof E. Water and ion binding around r(UpA)(12) and d(TpA)(12) oligomers - comparison with RNA and DNA (CpG)(12) duplexes. J. Mol. Biol. 2001;305:1057–1072. doi: 10.1006/jmbi.2000.4360. [DOI] [PubMed] [Google Scholar]
- 37.Westhof E. Water: an integral part of nucleic acid structure. Annu. Rev. Biophys. Biophys. Chem. 1988;17:125–144. doi: 10.1146/annurev.bb.17.060188.001013. [DOI] [PubMed] [Google Scholar]
- 38.Kaur H, Arora A, Wengel J, Maiti S. Thermodynamic, counterion, and hydration effects for the incorporation of locked nucleic acid nucleotides into DNA duplexes. Biochemistry. 2006;45:7347–7355. doi: 10.1021/bi060307w. [DOI] [PubMed] [Google Scholar]
- 39.Pastor N. The B- to A-DNA transition and the reorganization of solvent at the DNA surface. Biophys. J. 2005;88:3262–3275. doi: 10.1529/biophysj.104.058339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Sorensen JJ, Nielsen JT, Petersen M. Solution structure of a dsDNA: LNA triplex. Nucleic Acids Res. 2004;32:6078–6085. doi: 10.1093/nar/gkh942. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.