Evidence for the existence of a robust pattern of prey selection in food webs

Abstract

Food webs aim to provide a thorough representation of the trophic interactions found in an ecosystem. The complexity of empirical food webs, however, is leading many ecologists to focus dynamic ecosystem studies on smaller microcosm or mesocosm studies based upon community modules, which comprise three to five species and the interactions likely to have ecological relevance. We provide here a structural counterpart to community modules. We investigate food-web ‘motifs’ which are n-species connected subgraphs found within the food web. Remarkably, we find that the over- and under-representation of three-species motifs in empirical food webs can be understood through comparison to a static food-web model, the niche model. Our result conclusively demonstrates that predation upon species with some ‘characteristic’ niche value is the prey selection mechanism consistent with the structural properties of empirical food webs.

1. Introduction

Food webs are a description of who eats whom in an ecosystem (Sugihara 1984; Cohen et al. 1990). The food webs reported in the literature, however, appear increasingly complex (Williams & Martinez 2000; Dunne et al. 2002; Garlaschelli et al. 2003; Cattin et al. 2004; van Veen & Murrell 2005; Pascual & Dunne 2006; Stouffer et al. 2006; Camacho et al. 2007). Therefore, many ecologists have attempted to gain insight into the dynamics and stability of natural ecosystems in terms of small subwebs—‘community modules’ (Holt 1997; Holt & Hochberg 2001)—which bridge the gap between ‘the baroque complexity of entire communities and the bare bones of single and pairwise population dynamics’ (Holt 1997). Community modules provide a set of ecologically relevant subgraphs upon which to perform dynamic studies.

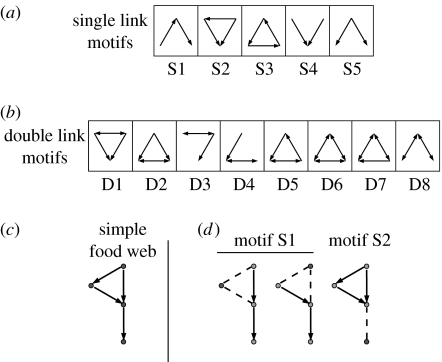
Intriguingly, the structural complexity of natural food webs masks a number of striking statistical regularities (Cohen et al. 1990; Dunne et al. 2002; Garlaschelli et al. 2003; Bascompte & Melián 2005; Camacho & Arenas 2005; Stouffer et al. 2005, 2006; van Veen & Murrell 2005; Camacho et al. 2007), such as the existence of universal forms for the distributions of numbers of prey and predators (Camacho et al. 2002a,b; Stouffer et al. 2005) Motivated by this fact, we investigate here whether there are any robust patterns in the structural counterparts to community modules. Specifically, we consider n-species ‘food-web’ motifs, which consist of the complete set of unique connected subgraphs containing n species (Milo et al. 2002). In this study, we focus on the case n=3, for which there are 13 distinct motifs (figure 1). For comparison, there are 199 and 9364 distinct motifs for n=4 and n=5, respectively.

Figure 1.

Food-web motifs. When neglecting cannibalism, there are 13 unique food-web motifs composed of three species (Milo et al. 2002). To simplify our analysis and presentation, we separate the 13 motifs into two groups: (a) motifs S1–S5 that include only single links and (b) motifs D1–D8 that include double links (mutual predation). (c) A simple food web. (d) If we search the food web in (c) for food-web motifs, we find two instances of motif S1 and one instance of motif S2. Note that enumeration of food-web motifs counts separately all connected species triplets.

Our quantification of food-web motifs will allow us to study all interactions at a given scale. Notably, this will include subgraphs less explored previously in dynamic studies. As a consequence, our results could provide new templates upon which to conduct future dynamic microcosm, mesocosm and field studies.

(a) Food-web motifs

The trophic interactions in food webs are directed and we use the convention here that links point from predator to prey. Neglecting cannibalism, i.e. self links, there are two possible motifs comprising a pair of species: (i) single links, A→B, and (ii) double links, A↔B. For triplets of species, there are 13 possible distinct motifs when neglecting cannibalism (figure 1). We have labelled these three-species motifs as S1–S5 and D1–D8, where ‘S’ denotes that the motif includes only single links and ‘D’ denotes that the motif includes at least one double link. We quantify the over- or under-representation of these motifs within food webs (Milo et al. 2002). We hypothesize that comparing the profiles of over- and under-representation from model-generated and empirical food webs will allow us to identify the mechanisms responsible for the observed food-web structure.

Three recently proposed models (Williams & Martinez 2000; Cattin et al. 2004; Stouffer et al. 2005) correctly reproduce key statistical properties of food webs from a variety of environments, including deserts, rainforests, lakes and estuaries. We have recently demonstrated that two key features common to these three models are responsible for the models' ability to reproduce the structure of empirical food webs. These are: (i) the species niche values form a totally ordered set and (ii) each species has an exponentially decaying probability of preying on a given fraction of the species with lower niche values (Stouffer et al. 2005). The former mechanism was first proposed in the cascade model of Cohen & Newman (1985). They hypothesized that intermediate species and top predators in an ecosystem can be ranked, i.e. assigned an ordered set of ‘niche values’. Remarkably, a single factor—species mass—is thought to provide an excellent proxy for niche value (Warren & Lawton 1987; Cohen 1989; Lawton 1989; Cohen et al. 1993, 2003).1

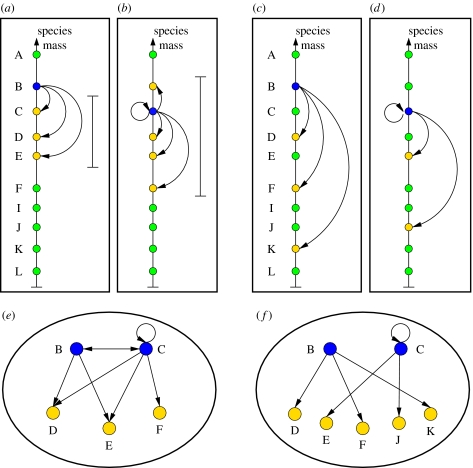
The latter condition is shared by the three models; however, the manner in which prey are selected is different in each. In the generalized cascade model (Stouffer et al. 2005)—approximately, in the nested-hierarchy model (Cattin et al. 2004)—predators select their prey at random from species with niche values less than or equal to their own, i.e. species of smaller or equivalent mass (figure 2). In the niche model (Williams & Martinez 2000), in contrast, predators consume prey falling within a contiguous range of niche values (figure 2). Using mass as a proxy, the generalized cascade and nested-hierarchy models implicitly assume that predators are indifferent to the size of their prey, provided only that they are of smaller or equivalent mass; the niche model implicitly assumes that selection pressures force predators to most efficiently prey upon species whose mass is close to a ‘characteristic value’.

Figure 2.

Two possible mechanisms for prey selection. Top and intermediate species can be assigned to trophic niches according to some ‘niche value’. This value is typically thought to be species mass, as predators predominantly prey on other species with mass less than or equal to their own. We represent predators as blue circles and prey as yellow circles. Other species are represented by green circles. (a) and (b) The predator preys upon species within a contiguous range, represented by the solid bar, as in the niche model. (c) and (d) The predator consumes prey with lower or equal niche value at random, as in the generalized cascade model. (e) Network representation of the corresponding food web. Under this prey selection mechanism, if two species appear in a double link and consume each other, they must be close together on the niche axis. In addition, their contiguous range of prey will overlap, making it likely that they have common prey. Similarly, two species which are close together on the niche axis are very likely to share predators owing to the contiguous range. (f) Network representation of the corresponding food web. Owing to the random prey selection mechanism, there is a substantially weaker relationship between the location of the two predators on the niche and the likelihood that they share predators and prey.

We recently proposed a new ‘generalized niche model’ in which all predators select a specified fraction of their prey contiguously and the remainder at random from species with niche values less than or equal to their own (Stouffer et al. 2006). Using this model, we were able to demonstrate that empirical food webs exhibit a strong bias towards intervality, i.e. there exists a strong empirical bias towards diet contiguity (Stouffer et al. 2006). With this in mind, the local motif structure of empirical food webs should provide an important additional means to validate any static food-web model as well as the conclusions regarding intervality.

Past studies of network motifs have uncovered relevant subgraphs within a variety of empirical networks (Milo et al. 2002, 2004), be they biological, technological, and social, or model networks (Artzy-Randrup et al. 2004; Vázquez et al. 2004; Middendorf et al. 2005). Studies have also investigated a subset of motifs or modules in food webs (Milo et al. 2002; Arim & Marquet 2004; Bascompte & Melián 2005). However, none of these investigations has been able to mechanistically predict a complete pattern of motif over- and under-representation, analytically or otherwise. Thus, the approach we follow here is a clear departure from what has been done before. Our approach enables us to concretely validate mechanism-based hypotheses upon analysis of the empirical data.

2. Material and methods

(a) Quantifying motif representation

To test the significance of the appearance of a particular motif in a network, the number of appearances N_real of a motif in the real network is compared to the appearances in an ensemble of randomized networks as a null hypothesis (Milo et al. 2002). This comparison yields the z-score

$$z_i=\frac{N_{\text{real}}-\langle N_{\text{rand}}\rangle }{{\sigma }_{N_{\text{rand}}}},$$ (2.1)

where 〈N_rand〉 and ${\sigma }_{N_{\text{rand}}}$ are the average and standard deviation of the random ensemble, respectively. The z-score of motif i thus measures the significance of deviations of the real network from the null hypothesis. We represent the set of z-scores for three-species motifs as a vector Z={z_i}, which has one component each for the motifs S1–S5 and D1–D8. Williams & Martinez (2000) used the z-score as an important means to validate the niche model, as did Cattin et al. (2004) in their validation of the nested-hierarchy model. It is important to note that use of the z-score implicitly assumes that the underlying values are normally distributed, and that, in this case, this assumption would apply to the distribution of N_rand.

The profile of z-scores indicates whether particular motifs are over- or under-represented relative to the null hypothesis provided by randomized networks. A key point to emphasize is that these are relative descriptors for the appearances of a given motif. Therefore, over-representation implies that a motif appears more frequently than in the randomized network, while under-representation implies less frequent occurrence. Under-representation rarely implies absence, particularly in larger networks.

(b) Randomizing networks

For the purpose of generating the ensemble of random networks, one must specify the constraints to be fulfilled while randomizing the network (Artzy-Randrup et al. 2004; Itzkovitz et al. 2004). These constraints correspond in practice to specifying the correct null hypothesis. In our analysis of the motifs, we conserve the following attributes for every species during the randomizations: (i) number of prey, (ii) number of predators, (iii) number of single links, A→B, (iv) number of double links, A↔B, and (v) whether or not a species is a cannibal. This preserves the overall distributions of each of these properties, numbers of prey and predators, single links, double links and cannibal links. This process guarantees that all subsequent results are due to other network properties (Milo et al. 2002; Artzy-Randrup et al. 2004; Itzkovitz et al. 2004). It is clear that this randomization scheme maintains the same species as cannibals before and after. Owing to this fact, and the fact that the appearance of cannibalism in food webs is consistent with the random hypothesis (Williams & Martinez 2000; Stouffer et al. 2005), we neglect cannibalism in our investigation of prey selection mechanisms.

It is important for the randomization process to preserve the distributions of lower-order motifs when considering motifs of a specified size to maintain consistency and validity between results at different levels (Milo et al. 2002). Therefore, when examining motifs of size n, one must preserve motifs of size n−1. This is why we preserve the distributions of single and double links in the examination of three-species motifs.

To randomize a network while conserving all of these properties, we use the Markov chain Monte Carlo switching algorithm (Itzkovitz et al. 2004) and treat single, double and cannibal links separately. For example, two single links A→B and C→D can become A→D and C→B, provided both A→D and C→B do not already exist in the network and they do not form new double links. Similarly, two double links A↔B and C↔D can become A↔D and C↔B, provided both A, D and C, B are unconnected by a link in any direction.

(c) Comparing empirical and model-generated food webs

To compare the data against the models, we first generate a model food web with the same number of species S and directed connectance C=L/S² as the empirical food web, where L is the number of trophic links within the food web. The implementation of the niche model (Williams & Martinez 2000), nested-hierarchy model (Cattin et al. 2004) and generalized cascade model (Stouffer et al. 2005) is followed as originally detailed. It is interesting to note that all three models require no free parameters as the only required inputs are the number of species S and number of links L, both of which are obtained directly from the empirical data.

We then compute the z-scores of the model-generated food web. To measure how well the model compares to the empirical data, we calculate two quantities: the uncentred correlation coefficient r and ratio d between the empirical and model-generated data. For each empirical food web, this process is repeated at least 250 times per model.

(d) Uncentred correlation coefficient

The uncentred correlation coefficient r between the z-score vectors Z_a and Z_b of two food webs a and b, respectively, is defined as

$$r=\sum _{j=1}^m\left(\frac{z_{a,j}}{{\sigma }_{{\mathit{Z}}_a}^{\left(0\right)}}\right)\left(\frac{z_{b,j}}{{\sigma }_{{\mathit{Z}}_b}^{\left(0\right)}}\right),$$ (2.2)

where

$${\sigma }_{{\mathit{Z}}_a}^{\left(0\right)}=\sqrt{\sum _{j=1}^m{\left(z_{a,j}\right)}^2},$$ (2.3)

a specifies the food web and j is an index over motifs. From the mathematical viewpoint, the uncentred correlation coefficient is the scalar product of the unit vectors in the directions of Z_a and Z_b and thus is equal to the cosine of the angle between the two data vectors in an m-dimensional space.

Since the vector Z describes the shape of over- and under-representation of motifs in a food web (figure 3), a value of r close to 1 indicates that the two food webs have similar directions, i.e. very similar profiles; a value of r close to 0 indicates little similarity, and close to -1 indicates that the two behave oppositely (i.e. the motifs under-represented in one food web are typically over-represented in the other and vice versa). Therefore, two similarly characterized food webs will have r values close to 1 upon comparing their respective z-scores. We would observe the same upon comparing an empirical food web and a model food web which exhibit similar behaviours.

Figure 3.

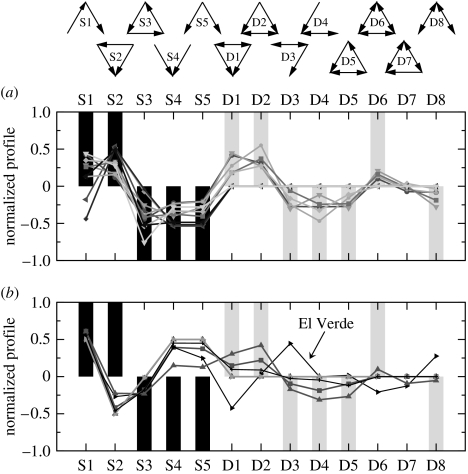
Three-species motif over- and under-representation. To facilitate visual comparison between food webs of different sizes and linkage densities, we plot the normalized profile ${\mathcal{P}}_i=z_i/\sqrt{{\sum }_j{z}_j^2}$, which is the vector of z-scores normalized to length 1 (Milo et al. 2004). The normalization aids in graphical comparison because larger and more densely connected networks tend to exhibit stronger patterns of over- and under-representation; the converse is also true for smaller and less densely connected networks (Milo et al. 2004). (a) Normalized profiles of the 10 empirical food webs characterized by over-representation of motif S2 and under-representation of motifs S4 and S5. (b) Normalized profiles of the six food webs characterized by under-representation of motif S2 and over-representation of motifs S4 and S5. The bars represent predictions of the generalized cascade and niche models for over- ($\mathcal{P}$>0) or under-representation ($\mathcal{P}$<0) of the individual motifs. The black bars represent the predictions of both the generalized cascade and the niche models, while the grey bars represent the predictions of only the niche model. The empirical webs in (a) are correctly predicted by the niche model, while those in (c) do not match the predictions for motifs S2, S4 and S5. Nevertheless, all food webs with double links, except the El Verde Rainforest, follow the pattern predicted by the niche model for motifs D1–D8.

(e) Ratio of the z-score norms

The uncentred correlation coefficient compares the directions of the z-score vectors, but ignores their magnitudes. In order to fully evaluate the similarity of two profiles, we must consider the similarity of the magnitudes as well. To this end, we introduce the ratio d of norms of the z-score vectors Z_a and Z_b of two food webs a and b, respectively, defined as

$$d=\frac{\left|{\mathit{Z}}_a\right|}{\left|{\mathit{Z}}_b\right|},$$ (2.4)

where

$$\left|{\mathit{Z}}_a\right|=\sqrt{\sum _{j=1}^m{\left(z_{a,j}\right)}^2},$$ (2.5)

a specifies the food web and j is an index over motifs. The ratio d provides a measure of the relative length of the two z-score vectors in an m-dimensional space. This ratio is a measure of how similar two food webs are in the magnitudes of their motif over- and under-representation.

Unlike previous studies which focused upon p-values (e.g. Milo et al. (2002) and Bascompte & Melián (2005)) we choose to compare the empirical and model motif patterns using our two metrics, r and d, for the following reasons. Earlier studies were concerned with individual motifs with respect to some null hypothesis model. By using our two metrics r and d, in contrast, our investigation is able to quantify the representation of the complete pattern of motifs simultaneously. This is because a comparison between, for example, a model and empirical food web, can only be considered in good agreement if both r and d give favourable results. The p-values, in contrast, could be significant if the measure has a broad distribution, and thus provides little indication of a lack of strong agreement.

3. Results

(a) Motifs in the models

We first investigate model food webs constructed according to each of the two prey selection mechanisms discussed above. For simplicity, we focus on the generalized cascade and niche models for our theoretical arguments. Let us initially, however, hypothesize using only the ranking induced by species mass discussed earlier. We would find it unsurprising to observe over-representation of motif S1, as this motif is the simple food chain (Cohen et al. 1990; figure 3). Likewise, we would expect to find over-representation of motif S2, since it represents omnivory (Polis 1991)—a predator consuming species from two different, but lower, trophic levels—and thus continues to uphold the mass ranking within the food web (figure 3). In contrast, we would expect under-representation of motif S3, again on the basis of species having ranked niche values (figure 3). Motif S3 is a clear example of species ‘violating’ the presumed ranking by consuming a species of greater mass.

The generalized cascade model can, in fact, be treated analytically and the over- and under-representation we derived explicitly for motifs S1–S5 confirm these arguments (Camacho et al. 2007). Food webs generated by the generalized cascade model display an over-representation of motifs S1–S2 and an under-representation of motifs S3–S5. Since the niche and nested-hierarchy models are, in essence, specialized implementations of the generalized cascade model (Stouffer et al. 2005), we expect them to generate similar profiles for motifs S1–S5. Numerical simulations demonstrate that this is indeed the general case (see electronic supplementary material). The nested-hierarchy model, however, exhibits a small tendency to deviate from this pattern for given combinations of S and L.

We were unable to obtain analytical results for motifs D1–D8 beyond the trivial case of the generalized cascade model, which does not generate double links. Nevertheless, we can still gain insight through heuristic arguments based upon the mechanisms being implemented in the models. Let us first assume that predators consume a contiguous range of species, as in the niche model. Then species with similar niche values are likely to share predators. In addition, for two species to be connected by a double link, they must have similar niche values. This implies that their respective ranges of prey are likely to have substantial overlap (figure 2). These observations can be trivially translated into predictions of motif representation. Since two species connected by a double link are likely to share prey, we predict over-representation of motif D1 and under-representation of motif D3, and since two species connected by a double link are likely to share predators, we predict over-representation of motif D2 and under-representation of motif D4. These two cases together further enable us to predict under-representation of motif D5.

Additionally, if A↔B and C↔B, it is necessary for all of A, B and C to have similar niche values. It is then likely that A and C are also connected by a double link, and unlikely that they have no connection between them. We therefore predict over-representation of motif D6 and under-representation of motif D8. These predictions provided by the contiguous range of prey are indicated by the grey bars in figure 3.

Let us now consider the case in which prey selection among species of smaller or equivalent mass is random, as in the generalized cascade model, but where some double links are possible. Since prey are chosen at random, species do not need to have similar niche values to be connected by a double link, and further, species connected by a double link are no more (or less) likely to share prey or predators. This is similar to what one expects for the nested-hierarchy model as the ranking imposed by species mass is indeed relaxed in the implementation (Stouffer et al. 2005). For motifs D1–D8, we then expect little difference between food webs generated by the nested-hierarchy model and their randomizations, in contrast to the strongly correlated and systematic pattern exhibited by the niche model. This is confirmed by numerical simulations (see electronic supplementary material).

(b) Motifs in the empirical food webs

In order to test our model-based predictions, we study 16 empirical food webs from a variety of environments: three estuarine—Chesapeake Bay (Baird & Ulanowicz 1989), St Marks (Christian & Luczkovich 1999) and Ythan (Hall & Raffaelli 1991); five freshwater—Bridge Brook Lake (Havens 1992), Canton Creek (Townsend et al. 1998), Little Rock Lake (Martinez 1991), Skipwith Pond (Warren 1989) and Stony Stream (Townsend et al. 1998); three marine—Benguela (Yodzis 1998), Caribbean Reef (Opitz 1996) and Northeast US Shelf (Link 2002); and five terrestrial—Coachella Valley (Polis 1991), El Verde Rainforest (Waide & Reagan 1996), Grassland (Martinez et al. 1999), Scotch Broom2 (Hawkins et al. 1997) and St Martin (Goldwasser & Roughgarden 1993). We present the profiles of over- and under-representation for the 16 empirical food webs studied in figure 3.

We first consider motifs S1–S5. We find that under-representation of motif S3 is common among all 16 webs and over-representation of motif S1 for all but three webs. These three food webs, Chesapeake Bay, Scotch Broom and Grassland, have the lowest linkage density L/S of the 16 webs, where S is the number of trophic species in the food web and L is the number of trophic interactions between these species. It has been shown previously that many properties of the niche model exhibit greater variance at low size, linkage density and/or directed connectance (Stouffer et al. 2005). Many of these properties represent averages across the food web; therefore, the smaller these three attributes, the more sensitive the calculations are to fluctuations within the data.

For the remaining motifs, S2, S4 and S5, we gain additional insight upon comparison to the analytical predictions for the generalized cascade model. Using this basis, we can separate the food webs into two groups: 10 food webs which exhibit over-representation of motif S2 and under-representation of motifs S4–S5, just as in the generalized cascade and niche models; and 6 remaining food webs which exhibit under-representation of motif S2 and over-representation of motifs S4–S5, opposite the generalized cascade model's predictions. The larger group includes Benguela, Chesapeake Bay, Coachella Valley, Grassland, Little Rock Lake, Caribbean Reef, Northeast US Shelf, Scotch Broom, St Marks Seagrass and St Martin Island.

The differences we find for motifs S2, S4 and S5 in Bridge Brook Lake, Canton Creek, El Verde Rainforest, Skipwith Pond, Stony Stream and Ythan Estuary are very intriguing. Canton Creek and Stony Stream are, for example, time specific rather than community food webs (Townsend et al. 1998); therefore, we would expect that they may not be directly comparable to the other food webs considered here. It would be interesting to explore further the ecological or environmental reasons why these two food webs exhibit over-representation of isolated exploitative competition and isolated generalist predation. It is additionally intriguing to note that these six are the only food webs for which the nested-hierarchy model has better predictive power than the niche model, due precisely to the deviations for motifs S2, S4 and S5.

Next, we consider motifs D1–D8. Remarkably, we find the same pattern of over- and under- representation for all food webs with double links except El Verde Rainforest (figure 3). This pattern includes over-representation of motifs D1, D2 and D6 and under-representation of motifs D3–D5 and D8. Significantly, this is the exact pattern we predict when assuming that predators consume a contiguous range of prey, as in the niche model. We emphasize here that a double link is truly mutual predation, and that in food webs, particularly aquatic systems, different trophic species are traditionally defined for juveniles and adults of a single taxonomic species when dietary differences are present (e.g. Warren (1989)).

We can quantify the robustness of these patterns by calculating the uncentred correlation coefficient between the z-score profiles from the 16 empirical food webs (figure 4). When we consider just motifs S1–S5, as in figure 4a, it is visually apparent that the six food webs exhibit different properties from the rest. Likewise, upon examining figure 4b which considers motifs D1–D8, it is apparent how similar all of the food webs with double links, except El Verde Rainforest, are to each other.

Figure 4.

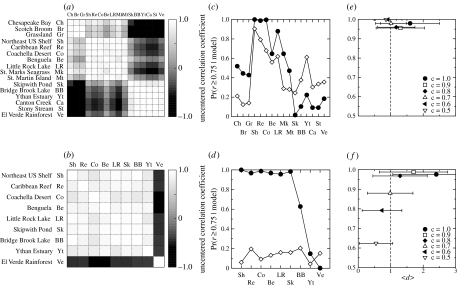
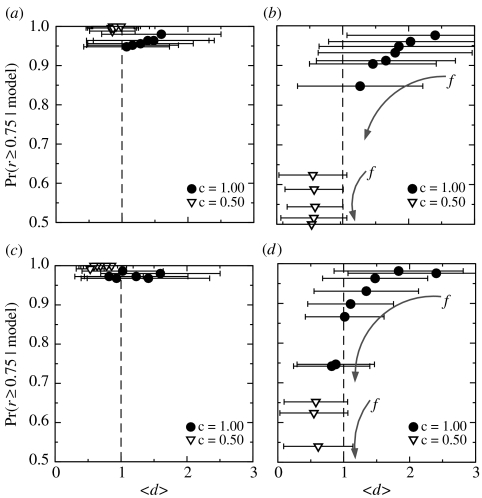
Uncentred correlation coefficient between pairs of empirical food webs for (a) motifs S1–S5 and (b) motifs D1–D8. The uncentred correlation coefficient r measures the degree of similarity between two food webs: a value of r close to 1 indicates high similarity; that close to 0 indicates little similarity; and that close to 1 indicates that the two behave oppositely. (c) Motifs S1–S5 and (d) motifs D1–D8: we show here the fraction of model-generated food webs with uncentred correlation coefficient r≥0.75 when compared to the empirical food webs for the niche (solid circles) and nested-hierarchy (open diamonds) models. When examining the uncentred correlation coefficient, the two models reproduce the empirical profile of over- and under-representation for motifs S1–S5 with similar success (c), with the niche model typically performing only slightly better than the nested-hierarchy model. For motifs D1–D8 (d), however, only the niche model successfully reproduces the empirical patterns, significantly outperforming the nested-hierarchy model. (e) Motifs S1–S5 and (f) motifs D1–D8: we repeat the analysis but also consider the ratio d for the Caribbean Reef food web and the generalized niche model for $c\in [0.5,1.0]$. The original niche model (generalized niche model with c=1.0) is unable to fully capture the magnitude of the empirical z-scores for motifs D1–D8; however, the introduction of slight discontiguity in species diets (e.g. c=0.95) allows the generalized niche model to completely capture the motif behaviour exhibited by the Caribbean Reef food web. Note that, in (b) (d) and (f), we only consider the empirical food webs which contain double links.

(c) Robustness of the empirical patterns

We now examine quantitatively the hypothesis that the contiguous range of prey is responsible for the pattern of over- and under-representation observed in empirical food webs. We also examine the models' ability to reproduce these patterns, beyond the analytical and heuristic arguments. To do this, we compare each empirical food web to simulations of the niche, generalized cascade and nested-hierarchy models. Each of these models have been shown to accurately reproduce other key properties of empirical food webs (Williams & Martinez 2000; Cattin et al. 2004; Stouffer et al. 2005); however, never to this level of structural detail.

To quantify the relationship between the model and empirical food webs, we determine the fraction of the model-generated food webs with uncentred correlation coefficient 0.75≤r≤1.0, i.e. the fraction of model food webs well aligned with the empirical results and by computing the average norm-ratio 〈d〉, i.e. whether the model food webs typically have norm comparable with the empirical food webs.

In our comparisons, we find again that the niche model and its underlying mechanism reproduce the empirically observed z-score profiles remarkably well (figure 4c). With regard to motifs S1–S5, both the niche and generalized cascade models perform almost equally as well in their comparison with the empirical food webs, whereas the nested-hierarchy model performs slightly worse.

With respect to motifs D1–D8, however, it is clear that the niche model and its underlying mechanism reproduce the empirical observed the z-score profile with remarkable accuracy (figure 4d). The niche model is highly successful for the food webs which have double links, while the nested-hierarchy model, in contrast, is at best only marginally successful. In fact, by quantifying this comparison using Bayesian model selection analysis, we find that considering the uncentred correlation coefficient for motifs D1–D8, we would effectively always select the niche model over the nested-hierarchy model ($p_{\text{Niche}}/p_{\text{Nested}}\approx 1\times {10}^6$; see electronic supplementary material).

Our results thus demonstrate that network motifs are a robust feature of empirical food webs and that their presence can be explained by predators consuming a contiguous range of prey. There is, of course, the possibility that other models could likewise offer similar predictions with regard to motifs. In fact, while the niche model is able to explain the overall pattern of motif over- and under-representation, it fails to accurately capture the magnitude, as measured by d. This implies that some additional ingredient or understanding is missing.

A recent study indicates that these deviations may be solely attributed to small deviations from the explicit dietary contiguity observed empirically (Stouffer et al. 2006). We investigate the proposed generalized niche model which is a synthesis of the niche and generalized cascade models in which the fractional contiguity of species diets is explicitly specified by an additional parameter c∈[0, 1]. A value of c=0 indicates that prey are selected at random from species with niche values less than or equal to their own, just as in the generalized cascade model. A value of c=1, in contrast, indicates that prey are selected from a contiguous range of niche values, just as in the niche model. When considering food-web intervality, it was concluded that empirical food webs exhibit diet contiguity consistent with $c\simeq 1$ (Stouffer et al. 2006).

Just as was the case for intervality, we find that only a few random predation events are sufficient for the generalized niche model to reproduce not only the correlation observed between motif representation but also the precise magnitude of these representation patterns (figure 4e,f). This fact supports both the conclusion of dietary contiguity observed in empirical food webs and the larger conclusion that food-web structure is almost entirely explained by species diets and how these prey are selected.

An important question arises with regard to whether or not the observed patterns could be a result of the aggregation of taxonomic species into trophic species commonly observed in empirical food webs. In fact, all of the food webs we consider in our analysis are trophic; furthermore, each of the models we consider was specifically designed to explain observed properties of trophic, not taxonomic, food webs.

To examine the effect of aggregation, we consider two aggregation strategies. First, we construct a generalized niche model food web with specified diet contiguity c. Each of these model webs has S′=S(1+f) species and linkage density z=L/S. Here, f is defined as the fraction of species in an observed food web, which are the result of aggregating two species; therefore, $f\in [0,1]$. The limit f=0 corresponds to no aggregated species while f=1 means every species is the result of aggregation. We then lump together fS pairs of species, resulting in a food web with S species and linkage density $z\approx L/S$.

In the first aggregation strategy, we lump together the fS pairs of species which are closest together in niche value; this creates a single species with all prey and predators of the original two species. This is synonymous with lumping together species that are likely to share predators. In the second aggregation strategy, we lump together the fS pairs of species that have the greatest overlap in both prey and predators. We quantify the overlap as the number of prey and predators two species share divided by the total number of unique prey and predators of the two species. This is very close to the procedure which occurs in the collection of empirical food-web data in lumping similarly behaving species into a single trophic species.

To quantify the effect of aggregation, we examine how changes in the value of $f\in [0,0.50]$ influence the results of our analysis (figure 5). For both aggregation strategies, as f increases, the agreement between the model webs and the empirical data decreases for any fixed value of c, mirroring the effect of decreasing diet contiguity c. By the two mechanisms examined here, it is therefore unlikely that the strong agreement we observe between the motifs in the empirical data and niche model could be explained by aggregation of taxonomic species into trophic species. In fact, large amounts of aggregation would have the effect of strongly reducing the strength of the patterns observed empirically.

Figure 5.

Effect of aggregation of taxonomic species into trophic species on the conclusion of diet contiguity in empirical food webs. We show here the fraction of model-generated food webs with uncentred correlation coefficient r≥0.75 against the average ratio d which compares the magnitudes of model and empirical z-score vectors. Each model food web is a realization of the generalized niche model with differing specified levels of diet contiguity c and differing fractions of aggregated species f. (a) Motifs S1–S5 and (b) motifs D1–D5: we lump species which are closest together in niche value. This is equivalent to lumping together species which are likely to share predators. (c) Motifs S1–S5 and (d) motifs D1–D8: we lump species which have the greatest overlap in both prey and predators. This is equivalent to the procedure which occurs in the collection of empirical food-web data when lumping similarly behaving species into a single trophic species. We see little effect upon motifs S1–S5 but pronounced effects for motifs D1–D8. As f increases (as indicated by the arrows), the agreement between the model webs and the empirical data decreases for any fixed value of c, mirroring the effect of decreasing diet contiguity c. It is therefore unlikely that the strong agreement we observe between the empirical data and niche model would be due to aggregation of taxonomic species into trophic species, at least by the two mechanisms examined here. All error bars are two standard deviations of the observed values.

4. Discussion

Our comparisons of both the model and empirical food webs indicate that a significant mechanism for prey selection in natural ecosystems is consumption of species whose niche value is close to some characteristic value. The idea that this value is related to species mass is, in fact, well documented. Morphologically, it has been demonstrated that features such as mouth size of birds or fishes can greatly limit the size of prey that can be consumed (Werner & Hall 1977; Wheelwright 1985). Energetically, it has been shown that increasing predator size is associated with increasing mean prey size (Gittleman 1985; Vézina 1985; Carbone et al. 1999), and the energy increase from prey consumption must justify that spent during prey capture (Wainwright 1996; Carbone et al. 1999; Radloff & Toit 2004). Furthermore, it has been shown that prey size specialization can play a tremendous role in the coexistence of predators and thus maintaining biodiversity (Karanth & Sunquist 1995, 2000).

Our ecosystem-wide investigation of the mechanism for prey selection provides us with several significant implications. First, our results provide additional evidence for the conclusion that empirical food webs are well approximated by diet contiguity as in the niche model. Just as in Stouffer et al. (2006), we find that the contiguity assumption is well justified and only small deviations from perfectly contiguous diets are necessary to accurately explain empirical food-web structure.

Second, our results demonstrate that omnivory occurs much more than one would expect to find by chance alone. Moreover, omnivory represents a significant component of a complete food-web structure. This result is congruent with the theoretical studies that emphasize the stabilizing impact of omnivory (McCann et al. 1998). As our motifs consist of only three species, however, it is not decisive whether they represent true omnivory across trophic levels or simply intraguild predation. This discrepancy helps to explain why Bascompte & Melián (2005) concluded that there is an ambiguous role of omnivory in food webs. Therefore, the debate regarding omnivory's true significance remains open (Yodzis 1984; Pimm 2002; Williams & Martinez 2004; Tanabe & Namba 2005).

Third, we uncover motifs which are frequently observed within food-web structure but to date have not been studied to the depth of others such as apparent competition and exploitative competition (Holt 1997; Holt & Hochberg 2001). These two motifs have been investigated in the laboratory owing to their relative simplicity and assumed ecology relevance. It would be intriguing to see whether there are dynamic explanations, for example, for the abundance or lack of motifs D1–D8 in addition to the dietary explanation we have uncovered. An intriguing possibility is that future theoretical investigations into motifs with additional species would likewise uncover larger ecologically relevant subgraphs.

Lastly, it is unlikely that there exists systematic bias in food-web data collection or in the strategies for aggregating taxonomic species into trophic species. The existence of any such bias would make it substantially more difficult to obtain the quantitatively robust motif patterns we report.

In conclusion, we would like to note that it is quite remarkable for something as complex as the pattern of representation of motifs in a food web can be understood using only very simple but plausible rules. It is also remarkable that the same patterns emerge independently from the specific details of the food web studied, notably its environment or the particular species present. These facts open up the possibility that similar solutions may exist for even more daunting ecological problems. We believe that these static food-web patterns will enable us to gain insight into, for example, how an invasive species might select its prey upon entering a new environment.

Supplementary Material

Supporting text

Numerical simulations of motif representation in model food webs